matlab数值计算符号计算练习

1 将(x -6)(x -3)(x -8)展开为系数多项式的形式。

2 求解多项式x 3-7x 2+2x +40的根。

3 求解在x =8时多项式(x -1)(x -2) (x -3)(x -4)的值。

4 计算多项式乘法(x 2+2x +2)(x 2+5x +4)。

5 计算多项式除法(3x 3+13x 2+6x +8)/(x +4)。

6 对下式进行部分分式展开：27243645232345234+++++++++x x x x x x x x x7 计算多项式9514124234++--x x x x 的微分和积分。

8 用符号函数法求解方程a t 2+b*t +c=0。

9用符号计算验证三角等式：sin(ϕ1)cos(ϕ2)-cos(ϕ1)sin(ϕ2) =sin(ϕ1-ϕ2) 10 因式分解：6555234-++-x x x x 11 ⎥⎥⎦⎤⎢⎢⎣⎡=)sin()log(12x x e x x a f ax ，用符号微分求df/dx 。

12 求代数方程组⎪⎩⎪⎨⎧=+=++002y x c by ax 关于x,y 的解。

13， 用符号函数法求解方程a t 2+b*t +c=0。

(应用solve)14， 因式分解：6555234-++-x x x x (应用syms, factor) 15， ⎥⎥⎦⎤⎢⎢⎣⎡=)sin()log(12x x e x x a f ax ，用符号微分求df/dx 。

(应用syms,diff)16计算极限求极限：n n h n x M hx h x L )1(lim )2(,)ln()ln(lim )1(0-=-+=∞→→ 17 计算导数22d d ,d d ,d d ,sin x y C a y B x y A ax y ====求．18计算不定积分、定积分、反常积分 x x x x I d )22(1222⎰+-+=，x x x x J d cos sin cos 2/0⎰π+=，⎰+∞-=0d e 2x K x ．19 符号求和求级数 ∑∞=121n n 的和S, 以及前十项的部分和S1． 20解代数方程和常微分方程例如：求一元二次方程a*x^2+b*x+c=0的根． 21求微分方程x y ='的通解．22求微分方程⎩⎨⎧==+=0)0(' ,1)0('"y y y x y 的特解． 23求微分方程组⎩⎨⎧=+=x y xy x 2''的通解．。

以下是一个MATLAB符号计算作业的例子，该作业要求计算一个表达式的值，并将其结果与另一个表达式的结果进行比较。

作业题目：
计算以下两个表达式的结果，并比较它们的大小：
1. 计算e^((-4+sqrt(16))) 的值。

2. 计算(1/3)*e^((-1/3)) 的值。

作业要求：
1. 使用MATLAB的符号计算功能来计算这两个表达式的值。

2. 比较这两个表达式的值，并输出它们的大小关系。

作业步骤：
1. 打开MATLAB软件，并输入以下命令来创建一个符号变量：
syms x
2. 使用exp函数和sqrt函数来计算第一个表达式的值，如下所示：
expr1 = exp(-4 + sqrt(16));
3. 使用符号计算功能来计算第二个表达式的值，如下所示：
expr2 = (1/3)*exp(-1/3);
4. 比较这两个表达式的值，并输出它们的大小关系，如下所示：
disp(['The value of expr1 is ', num2str(expr1)]);
disp(['The value of expr2 is ', num2str(expr2)]);
disp(['The relationship between expr1 and expr2 is: ', num2str(expr1-expr2)]);。

Matlab上机操作2——符号计算1、%创建数值常量和符号常量a1=2*sqrt(5)+pi %创建数值常量a2=sym('2*sqrt(5)+pi') %按符号表达式创建符号常量a3=sym(2*sqrt(5)+pi) %按最接近的两个正整数表示符号常量a4=sym(2*sqrt(5)+pi,'d') %按最接近的十进制浮点数表示符号常量a31=a3-a1 %数值常量和符号常量的计算a5='2*sqrt(5)+pi' %字符串常量2、%创建符号变量和符号表达式f1=sym('a*x^2+b*x+c') %创建符号表达式syms a b c x %创建符号变量f2=a*x^2+b*x+c %创建符号表达式syms('a','b','c','x') %注意这里是syms，不是sym>> sym('a','b','c','x')错误使用sym输入参数太多。

f3=a*x^2+b*x+c; %创建符号表达式syms x y real %创建实数符号变量z=x+i*y; %创建z为复数符号变量real(z) %复数z的实部是实数xsym('x','unreal'); %清除符号变量的实数特性real(z) %复数z的实部3、%比较符号矩阵与字符串矩阵A=sym('[a,b;c,d]') %创建符号矩阵B='[a,b;c,d]' %创建字符串矩阵C=[a,b;c,d] %创建数值矩阵C=sym(B) %转换为符号矩阵whos4、%计算符号矩阵的行列式值、非共轭转置和特征值syms a11 a12 a21 a22A=[a11 a12;a21 a22] %创建符号矩阵det(A) %计算行列式A.' %计算非共轭转置eig(A)%计算特征值5、%符号表达式的代数运算f=sym('2*x^2+3*x+4')g=sym('5*x+6')f+g %符号表达式相加f*g %符号表达式相乘6、%对符号表达式进行任意精度控制并用三种运算方式表示同一符号常量a=sym('2*sqrt(5)+pi')digits %显示默认的有效位数vpa(a) %用默认的位数计算并显示vpa(a,20) %按指定的精度计算并显示digits(15) %改变默认的有效位数vpa(a) %按digits指定的精度计算并显示a1 =2/3 %数值型a2 = sym(2/3) %有理数型digitsa3 =vpa('2/3',32) %VPA型format longa17、%符号变量与数值变量进行转换a1=sym('2*sqrt(5)+pi')b1=double(a1) %转换为数值变量a2=vpa(sym('2*sqrt(5)+pi'),32)b2=numeric(a2) %转换为数值变量b2=numeric(a2)未定义函数或变量'numeric'。

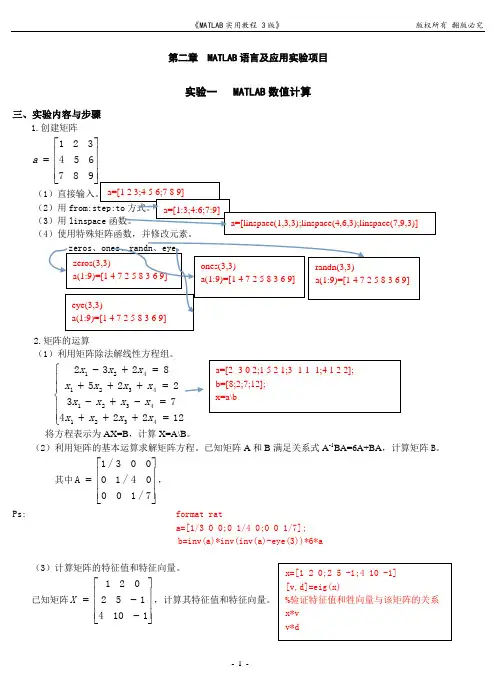
第二章 MATLAB 语言及应用实验项目实验一 MATLAB 数值计算三、实验内容与步骤1.创建矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321a（1（2）用（3）用（42.矩阵的运算（1）利用矩阵除法解线性方程组。

⎪⎪⎩⎪⎪⎨⎧=+++=-+-=+++=+-12224732258232432143214321421x x x x x x x x x x x x x x x 将方程表示为AX=B ，计算X=A\B 。

（2）利用矩阵的基本运算求解矩阵方程。

已知矩阵A 和B 满足关系式A -1BA=6A+BA ，计算矩阵B 。

其中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=7/10004/10003/1A ，Ps: format rata=[1/3 0 0;0 1/4 0;0 0 1/7];b=inv(a)*inv(inv(a)-eye(3))*6*a（3）计算矩阵的特征值和特征向量。

已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=1104152021X ，计算其特征值和特征向量。

（4）Page:322利用数学函数进行矩阵运算。

已知传递函数G(s)=1/(2s+1),计算幅频特性Lw=-20lg(1)2(2w )和相频特性Fw=-arctan(2w),w 的范围为[0.01，10]，按对数均匀分布。

3.多项式的运算（1）多项式的运算。

已知表达式G(x)=(x-4)(x+5)(x 2-6x+9),展开多项式形式，并计算当x 在[0，20]内变化时G(x)的值，计算出G(x)=0的根。

Page 324（2）多项式的拟合与插值。

将多项式G(x)=x 4-5x 3-17x 2+129x-180，当x 在[0，20]多项式的值上下加上随机数的偏差构成y1，对y1进行拟合。

对G(x)和y1分别进行插值，计算在5.5处的值。

Page 325 四、思考练习题1.使用logspace 函数创建0～4π的行向量，有20个元素，查看其元素分布情况。

Ps: logspace(log10(0),log10(4*pi),20) (2) sort(c,2) %顺序排列 3.1多项式1）f(x)=2x 2+3x+5x+8用向量表示该多项式，并计算f(10)值. 2）根据多项式的根[-0.5 -3+4i -3-4i]创建多项式。

第9章 MATLAB符号计算习题9一、选择题1．设有a=sym(4)。

则1/a+1/a的值是（）。

BA．0.5 B．1/2 C．1/4+1/4 D．2/a2．函数factor(sym(15))的值是（）。

DA．'15' B．15 C．[ 1, 3, 5] D．[ 3, 5]3．在命令行窗口输入下列命令：>> f=sym(1);>> eval(int(f,1,4))则命令执行后的输出结果是（）。

AA．3 B．4 C．5 D．14．MA TLAB将函数展开为幂级数，所使用的函数是（）。

DA．tailor B．tayler C．diff D．taylor5．MATLAB用于符号常微分方程求解的函数是（）。

CA．solve B．solver C．dsolve D．dsolver二、填空题1．在进行符号运算之前首先要建立，所使用的函数或命令有和。

符号对象，sym，syms2．对于“没有定义”的极限，MATLAB给出的结果为；对于极限值为无穷大的极限，MA TLAB给出的结果为。

NaN，Inf3．在命令行窗口输入下列命令：>> syms n;>> s=symsum(n,1,10)命令执行后s的值是。

554．在MATLAB中，函数solve(s,v)用于代数方程符号求解，其中s代表，v 代表。

符号代数方程，求解变量5．在MA TLAB符号计算中y的二阶导数表示为。

D2y三、应用题1．分解因式。

（1）x9-1 （2）x4+x3+2x2+x+1（3）125x6+75x4+15x2+1 （4）x2+y2+z2+2(xy+yz+zx)(1):2x=sym('x'); A=x^9-1; factor(A) (2):x=sym('x');B=x^4+x^3+2*x^2+x+1; factor(B) 2．求函数的极限。

（1）4586lim 22++x x x x --4→x （2）xx -0→x lim(1):x=sym('x');A=(x^2-6*x+8)/(x^2-5*x+4); limit(A,x,4) (2):x=sym('x'); B=abs(x)/x; limit(B)3．求函数的符号导数。

MATLAB符号计算（收藏版）1 符号计算基础1.1符号运算•与数值运算的区别▪数值运算中必须先对变量赋值，然后才能参与运算。

▪符号运算无须事先对独立变量赋值，运算结果以标准的符号形式表达。

•特点▪运算对象可以是没赋值的符号变量▪可以获得任意精度的解1.2 符号对象•建立符号变量和符号常数▪sym函数sym函数用来建立单个符号量，例如，a=sym(‘a’)建立符号变量a，此后用户可在表达式中使用变量a进行各种运算。

▪syms函数syms函数调用格式为：syms var1 var2 … varn变量间用空格而不要用逗号分隔例1考察符号变量和数值变量的差别a=sym('a');b=sym('b');c=sym('c');d=sym('d');%定义4个符号变量w=10; x=5; y=-8; z=11; %定义4个数值变量A=[a, b; c, d] %建立符号矩阵AB=[w, x; y, z] %建立数值矩阵Bdet(A)%计算符号矩阵A的行列式det(B)%计算数值矩阵B的行列式a=sym('a');b=sym('b');c=sym('c');d=sym('d');%定义4个符号变量w=10; x=5; y=-8; z=11;%定义4个数值变量A=[a, b; c, d]%建立符号矩阵AB=[w, x; y, z]%建立数值矩阵Bdet(A)%计算符号矩阵A的行列式det(B)%计算数值矩阵B的行列式例2比较符号常数与数值在代数运算时的差别pi1=sym('pi');k1=sym('8');k2=sym('2');k3=sym('3');% 定义符号变量pi2=pi;r1=8;r2=2;r3=3;% 定义数值变量sin(pi1/3)% 计算符号表达式值sin(pi2/3) % 计算数值表达式值sqrt(k1) % 计算符号表达式值sqrt(r1) % 计算数值表达式值sqrt(k3+sqrt(k2))% 计算符号表达式值sqrt(r3+sqrt(r2))% 计算数值表达式值•建立符号表达式▪sym函数▪syms函数▪利用单引号建立符号表达式例3利用3种方法建立符号表达式U=sym('3*x^2+5*y+2*x*y+6')%定义符号表达式Usyms x y; %建立符号变量x、yV=3*x^2+5*y+2*x*y+6%定义符号表达式V2*U-V+6%求符号表达式的值W='3*x^2+5*y+2*x*y+6'%定义符号表达式W例4建立x, y的一般二元函数f = sym('f(x,y)');f = ‘f(x,y)’;•基本的符号运算▪基本四则运算例5符号表达式的四则运算示例syms x y z;f=2*x+x^2*x-5*x+x^3%符号表达式的结果为最简形式f=2*x/(5*x)%符号表达式的结果为最简形式f=(x+y)*(x-y)%符号表达式的结果不是x^2-y^2，而是(x+y)*(x-y)•基本的符号运算▪因式分解与展开1.factor(S) 对S分解因式，S是符号表达式或符号矩阵;2.expand(S) 对S进行展开，S是符号表达式或符号矩阵;3.collect(S) 对S合并同类项，S是符号表达式或符号矩阵;4.collect(S, v) 对S按变量v合并同类项，S是符号表达式或符号矩阵。

Matlab 练习习题1． 设a=1.2,b=-4.6,c=8.0,e=-4.0,计算⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+=d bc e a t ππ22arctan2． 设a=5.67,b=7.811,计算)lg(b a e ba ++3． 已知园半径为15，求其直径、周长和面积。

4． 已知三角形三边a=8.5,b=14.6,c=18.5,求三角形面积2/)(,))()(((c b a s c s b s a s s area ++=---=5． 下列命令执行后，L1、L2、L3、L4的值分别是多少？A=1:9；B=10-A ； L1=A==B ； L2=A<=5； L3=A>3&A<7;L4=find(A>3&A<7)； 习题1． 设矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=321212113A⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=111012111B求：（1）2A+B ；（2）4A 2-3B 2；（3）AB ；（4）BA ；（5）AB-BA2.设三阶矩阵A 、B ，满足A -1BA=6A+BA⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=71000410031A 求矩阵B2． 设（2E-C -1B ）A T =C -1,其中E 是4阶单位矩阵，A T 是4阶矩阵A 的转置，⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---=1021000032231021B ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1021000002101021C求矩阵A3． 有一4阶魔方矩阵a ，找出矩阵中大于7的元素，并将它们重新排列成列向量b 。

4． 给定矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=054000031A ,删去整行和整列的0。

5． 设2阶矩阵A 、B 、X ，满足X-2A=B-X,⎥⎦⎤⎢⎣⎡--=2112A⎥⎦⎤⎢⎣⎡--=0220B 求矩阵X6． 求矩阵的主对角元素、逆矩阵、行列式的值、秩、特征值和特征向量⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=163053064A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=1124111221B7． 分别用矩阵求逆、矩阵除法求方程组的解⎪⎩⎪⎨⎧=+--=+-=+-1074453932z y x z y x z y x 8． 已知多项式P 1(x)=3x+2,P 2(x)=5x 2-x ＋2，P 3(x)=x 2-0.5,求：（1） P(x)=P 1(x)+P 2(x)+P 3(x) （2） P(x)=P 1(x)*P 2(x)*P 3(x) （3） P(x)=0的全部根计算x i =0.2*i,i=0,1,2各点上的P(x i )。

第 2 章符号计算符号计算：解算数学表达式、方程不是在离散化的数值点上进行，而是凭借一系列恒等式，数学定理，通过推理和演绎，获得解析结果。

符号计算建立在数值完全准确表达和推演严格解析的基础之上，所得结果完全准确。

特点：一．相对于MATLAB的数值计算“引擎”和“函数库”而言，符号计算的“引擎”和“函数库”是独立的。

二．在相当一些场合，符号计算解算问题的命令和过程，显得比数值计算更自然、更简明。

三．大多数理工科的本科学生在学过高等数学和其他专业基础课以后，比较习惯符号计算的解题理念和模式。

2.1符号对象和符号表达式MATLAB依靠基本符号对象（包括数字、参数、变量）、运算符及一些预定义函数来构造和衍生符号表达式和符号方程。

2.1.1基本符号对象和运算算符1.生成符号对象的基本规则●任何基本符号对象（数字、参数、变量、表达式、函数）都必须借助专门的符号命令sym、syms、symfun定义。

●任何包含符号对象的表达式或方程，将继承符号对象的属性。

2.精准符号数字和符号常数符号（类）数字的定义：sym(Num) 采用精准数值类数创建精准的符号数字（推荐格式!）sc=sym(Num) 采用精准数值类数创建精准的符号常数sc（推荐格式!）说明：若输入量Num是精准的浮点数（如0.321、10/3等），能生成精准的符号数字；若输入量Num是诸如sin(0.3)的数值表达式，那么就只能生成由数字表达式获得的16位精度的近似符号数字。

sym('Num') 采用有理分数字符串创建精准的符号数字sc=sym('Num') 采用有理分数字符串创建精准的符号常数sc说明： Num必须处于（英文状态下的）单引号内，构成字符串（关于字符串参见附录A）；只有当字符串数字'Num'采用诸如321/1000、10/3等整数构成的有理分数形式表达时，sym('Num') 才能生成精准的符号数字；若字符串数字用诸如0.321、3.21e-1等“普通小数或科学记述数”表达，那么只能产生“近似符号数字”。

Matlab 教程 第二章 符号计算课堂练习1 创建符号变量有几种方法？MA TLAB 提供了两种创建符号变量和表达式的函数：sym 和syms 。

sym 用于创建一个符号变量或表达式，用法如x=sym(‘x’) 及 f=sym(‘x+y+z’)，syms 用于创建多个符号变量，用法如syms x y z 。

f=sym(‘x+y+z’) 相当于syms x y z f= x+y+z2 下面三种表示方法有什么不同的含义？ （1）f=3*x^2+5*x+2 （2）f='3*x^2+5*x+2' （3）x=sym('x') f=3*x^2+5*x+2 （1）f=3*x^2+5*x+2表示在给定x 时，将3*x^2+5*x+2的数值运算结果赋值给变量f ，如果没有给定x 则指示错误信息。

（2）f='3*x^2+5*x+2'表示将字符串'3*x^2+5*x+2'赋值给字符变量f ，没有任何计算含义，因此也不对字符串中的内容做任何分析。

（3）x=sym('x')f=3*x^2+5*x+2表示x 是一个符号变量，因此算式f=3*x^2+5*x+2就具有了符号函数的意义，f 也自然成为符号变量了。

3 用符号函数法求解方程a t 2+b*t +c=0。

>> r=solve('a*t^2+b*t+c=0','t') r =[ 1/2/a*(-b+(b^2-4*a*c)^(1/2))] [ 1/2/a*(-b-(b^2-4*a*c)^(1/2))]4 用符号计算验证三角等式：sin(ϕ1)cos(ϕ2)-cos(ϕ1)sin(ϕ2) =sin(ϕ1-ϕ2) >> syms phi1 phi2;>> y=simple(sin(phi1)*cos(phi2)-cos(phi1)*sin(phi2)) y =sin(phi1-phi2)5 求矩阵⎥⎦⎤⎢⎣⎡=22211211a a a a A 的行列式值、逆和特征根。