Gold序列产生及特性分析实验

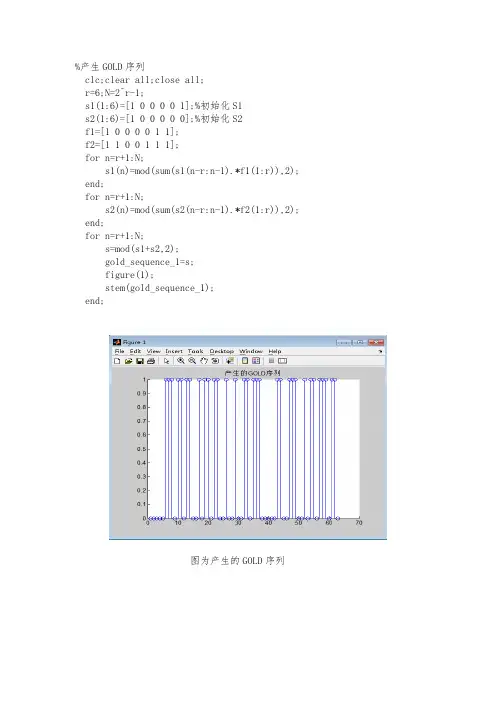
%产生GOLD序列clc;clear all;close all;r=6;N=2^r-1;s1(1:6)=[1 0 0 0 0 1];%初始化S1s2(1:6)=[1 0 0 0 0 0];%初始化S2f1=[1 0 0 0 0 1 1];f2=[1 1 0 0 1 1 1];for n=r+1:N;s1(n)=mod(sum(s1(n-r:n-1).*f1(1:r)),2); end;for n=r+1:N;s2(n)=mod(sum(s2(n-r:n-1).*f2(1:r)),2); end;for n=r+1:N;s=mod(s1+s2,2);gold_sequence_1=s;figure(1);stem(gold_sequence_1);end;图为产生的GOLD序列%自相关分析clc;clear all;close all;r=6;N=2^r-1;s1(1:6)=[1 0 0 0 0 0];%初始化S1s2(1:6)=[1 0 0 0 0 0];%初始化S2f1=[1 0 0 0 0 1 1];f2=[1 1 0 0 1 1 1];for n=r+1:N;s1(n)=mod(sum(s1(n-r:n-1).*s1(1:r)),2);end;for n=r+1:N;s2(n)=mod(sum(s2(n-r:n-1).*s2(1:r)),2);end;s=mod(s1+s2,2);gold_sequence_1=s;figure(1);stem(gold_sequence_1);grid on;gold_sequence_1=2*gold_sequence_1-1;for j=0:N-1s3(j+1)=sum(gold_sequence_1.*[gold_sequence_1(1+j:N),gold_sequence_1( 1:j)])/N;end;j=-N+1:N-1;rho=[fliplr(s3(2:N)),s3];figure(2)plot(j,rho);axis([-30 30 -1 1.2])title('第一个gold序列的自相关函数')图为产生的GOLD序列图为GOLD序列对应的自相关函数图%互相关分析clc;clear all;close all;r=6;N=2^r-1;s1(1:6)=[1 0 0 0 0 0];%初始化S1s2(1:6)=[1 0 0 0 0 0];%初始化S2f1=[1 0 0 0 0 1 1];f2=[1 1 0 0 1 1 1];for n=r+1:N;s1(n)=mod(sum(s1(n-r:n-1).*f1(1:r)),2);end;for n=r+1:N;s2(n)=mod(sum(s2(n-r:n-1).*f2(1:r)),2);end;s=mod(s1+s2,2);gold_sequence_1=s;figure(1);stem(gold_sequence_1);grid on;r=6;M=2^r-1;s1(1:6)=[1 0 0 0 1 0];%初始化S1s2(1:6)=[1 0 0 0 1 0];%初始化S2f1=[1 0 0 0 0 1 1];f2=[1 1 0 0 1 1 1];for n=r+1:M;s1(n)=mod(sum(s1(n-r:n-1).*f1(1:r)),2);end;for n=r+1:N;s2(n)=mod(sum(s2(n-r:n-1).*f2(1:r)),2);end;s=mod(s1+s2,2);gold_sequence_2=s;figure(2);stem(gold_sequence_2);grid on;gold_sequence_1=2*gold_sequence_1-1;gold_sequence_2=2*gold_sequence_2-1;for j=0:M-1s3(j+1)=sum(gold_sequence_1.*[gold_sequence_2(1+j:N),gold_sequence_2( 1:j)])/N;end;j=-M+1:M-1;rho=[fliplr(s3(2:N)),s3];figure(3)plot(j,rho);axis([-30 30 -1 1.2])title('第一个gold序列的互相关函数')图为GOLD序列1图为GOLD序列2图为GOLD序列的互相关函数。

实验二 GOLD 序列码产生及特性分析实验一、实验目的1. 了解Gold 码的性质和特点；2. 熟悉Gold 码的产生方法；二、实验内容1. 熟悉Gold 码的的产生方法；2. 测试Gold 码的的波形；三、实验原理m 序列虽然性能优良，但同样长度的m 序列个数不多，且m 序列之间的互相关函数值并不理想（为多值函数）。

1967年，R ．Gold 提出和讨论了一种新的序列，即Gold 码序列。

这种序列有较为优良的自相关和互相关特性，构造简单，产生的序列数多，因而得到广泛的应用。

a) m 序列优选对m 序列优选对是指在m 序列集中，其互相关函数最大值的绝对值满足下式的两条n 阶m 序列：表2－1给出了部分m 序列优选对。

表2－1 部分优选对码表 级数 基准本原多项式 配对本原多项式 7 211 217,235,277,325,203,357,301,323 9 1021 1131,133310 2415 2011,3515,317711 4445 4005,5205,5337,52632．Gold 码的产生方法Gold 码是m 序列的组合码，由同步时钟控制的两个码字不同的m 序列优选对逐位模2加得到，其原理如图2-1所示。

这两个码发生器的周期相同，速率也相同，因而两者保持一整除为偶数，但不能被位奇数41212)(2/)2(2/)1(n n R n n xy ⎩⎨⎧++≤++τ定的相位关系，这样产生的组合码与这两个子码序列的周期也相同。

当改变两个m 序列的相对位移时，会得到一个新的Gold 码。

Gold 码虽然是m 序列模2加得到的，但它已不再是m 序列，不过仍具有与m 序列近似的优良特性，各个码组之间的互相关特性与原来两个m 序列之间的互相关特性一样，最大的互相关值不会超过原来两个m 序列间最大互相关值。

Gold 码最大的优点是具有比m 序列多得多的独立码组。

图2-1 Gold 码序列发生器Gold 码序列具有以下性质：（1）两个m 序列优选对经不同移位相加产生的新序列都是Gold 序列，两个n 级移位寄存器可以产生2n +1个Gold 序列，周期均为2n -1。

gold序列的⽣成与相关特性仿真Gold序列⽣成与相关性仿真1.1 references[1] 基于Matlab的Gold码序列的仿真与实现.[2] Code Selection for CDMA Systems.1.2 m序列的⽣成原理1.2.1⽣成本原多项式利⽤Matlab编程环境求解本原多项式，其运⾏结果如表1所⽰．选择n=7，采⽤7级移位寄存器，产⽣的序列周期是127，其程序如下所⽰．N=7; %以7级寄存器为例，并组其中的⼀组优选对：211，,217connections=gfprimfd(N,'all');表（1）n=7 本原多项式上⾯的多项式中，仅有9个是独⽴的．因为第⼀⾏和第⼗⾏，第⼆⾏和四⾏，第三⾏和第⼗六⾏，第五⾏和第⼋⾏，第六⾏和第⼗四⾏，第七⾏和第⼗三⾏，第九⾏和第⼗⼋⾏，第⼗⼀⾏和第⼗⼆⾏，第⼗五⾏和第⼗七⾏是两两对称的．⽤⼋进制数表⽰时，所选择的本原多项式为211、217、235、367、277、325、203、313和345共9条．在这9条本原多项式中，选择⼀个基准本原多项式，再按要求选择另⼀本原多项式与之配对，构成m序列优选对，对7级m序列优选对如下表：表（2）n=7 m序列所以优选对1.2.2构成移位寄存器根据产⽣Gold码序列的⽅法，从上述本原多项式中选择⼀对m序列优选对，以211作为基准本原多项式，217作为配对本原多项式，通过并联结构形式来产⽣Gold序列，⽣成gold 序列的结构如图（6）所⽰：图（6）Gold序列⽣成结构1.3 ⾃相关函数仿真参数及初始值设定如下：N=7; %以7级寄存器为例，并组其中的⼀组优选对：211，,217connections=gfprimfd(N,'all');f1=connections(4,:); %取⼀组本原多项式序列，211f2=connections(16,:); %取另⼀组本原多项式序列,217registers1=[1 0 0 0 0 0 0];%给定寄存器的初始状态registers2=[1 0 0 0 0 0 0];%取相同的初始状态⽣成的gold 序列⾃相关函数如图（7）、（8）所⽰图（7） Gold 序列周期⾃相关函数结论：⾃相关函数取值集合{127，15，-1，-17}图（8）Gold 序列⾮周期⾃相关函数020406080100120140gold 序列周期⾃相关函数020406080100120140-40-2020406080100120140gold 序列⾮周期⾃相关函数1.4 互相关函数仿真时改变m序列寄存器初始状态，从⽽⽣成两个gold序列，求得互相关函数如图（9）（10）所⽰。

通信08-1 艾盼盼0850283101设计Gold序列发生器姓名：艾盼盼学号：0850283101 班级：通信08-1摘要：m序列，尤其是m序列优选对，是特性很好的伪随机序列。

但是，它们能彼此构成优选对的数目很少，不便于在码分多址系统中应用。

R.Gold于1967年提出了一种基于m 序列优选对的码序列，称为Gold序列。

它是m序列的组合码，由优选对的两个m序列逐位模2加得到，当改变其中一个m序列的相位（向后移位）时，可得到一新的Gold序列。

Gold 序列虽然是由m序列模2加得到的，但它已不是m序列，不过它具有与m序列优选对类似的自相关和互相关特性，而且构造简单，产生的序列数多，因而获得广泛的应用。

【关键词】：m序列优选对，Gold序列，模2加，自相关1. Gold码的概述1.1 gold码定义R.Gold于1967年提出了一种基于m序列优选对的码序列，称为Gold序列。

它是m序列的组合码，由优选对的两个m序列逐位模2加得到，当改变其中一个m序列的相位（向后移位）时，可得到一新的Gold序列。

Gold序列虽然是由m序列模2加得到的，但它已不是m 序列，不过它具有与m序列优选对类似的自相关和互相关特性，而且构造简单，产生的序列数多，因而获得广泛的应用。

1.2 gold码基本功能单元Gold码发生器的基本功能单元为线性反馈移位寄存器LFSR（Linear Fdddback Bhift Register）。

2.Gold序列的设计2.1 m序列优选对寻找方法产生gold序列的必要条件是m序列优选对，设A是对应于n级本原多项式f（x）所产生的m序列，B是对应于n级本原多项式g（x）所产生的m序列，当它们的互相关函数|Ra.b（k）|满足：则f（x）和g（x）所产生的m序列A和B构成一对优选对。

寻找m序列优选对的方法还有硬件计算法，分圆陪集法，逐步移位模2加法，三值判别法。

2.2gold序列设计的理论证明证明，若F1（x），F2（x）为两个不同的本原多项式，令F1（x）产生的序列为G（F1），F2（x）产生的序列为G（F2），F1（x）. F2（x）所产生的序列为G（F1，F2），则有上式表明两本原多项式乘积所产生的序列等于两个本原多项式分别产生的模2和序列。

m序列与gold序列性能分析比较赵新宁北京邮电大学信息工程学院，北京（100876）E-mail：zhaoxinning106@摘要：在扩频系统中，伪随机序列具有十分重要的作用。

m序列和gold序列作为最常用和实用的伪随机序列，各有其特点。

本文分析其基本原理和产生方式，并特别对其性能方面做了仿真比较。

关键词：扩频；m序列；gold序列中图分类号：TN91在扩频通信系统中，伪随机序列是关键技术之一。

伪随机序列码的码型影响码序列的相关特性，序列长度决定了扩展频谱的宽度。

因此，在扩频系统中，对于伪随机序列有如下的要求：首先，伪随机序列的长度（即伪码比特率）应该足够长，能够满足扩展带宽的需要；第二，伪随机序列要具有尖锐的自相关特性（用作地址码），和良好的互相关特性；第三，伪随机序列要有足够多的数量，以满足码分多址的需求；第四，应具有近似噪声的频谱特性，即近似连续谱，且均匀分布；工程上易于实现。

通常，作为扩频通信系统工程实现上的伪随机序列一般是m序列和gold序列。

目前，在cdma2000系统中采用伪随机序列中的m序列（长码）来区分用户，wcdma系统中则用gold码来区分用户。

1.m序列的原理和产生在所有的伪随机序列中，m序列是最重要、最基本的一种伪随机序列。

而另外的多种伪随机序列都是由它引出并且产生的。

m序列是一种周期性的伪随机序列，又被称作最长线性移位寄存器序列；是由带线性反馈的移位寄存器产生的周期最长的序列[1]。

其周期为2n-1（n 为移位寄存器级数）。

m序列具有与随机噪声类似的尖锐的自相关特性，但它不是真正随机的，而是按照一定的规律周期性的变化。

这种特性使得m序列适合于工程应用。

m序列最大长度决定于移位寄存器的级数，而序列构成则决定于反馈系数的不同设置。

并非所有的反馈系数的设置都可以产生对应长度的m序列。

m序列具有平衡性和其游程特性，即一个序列周期中，“1”的数目与“0”的数目最多相差一个；同时，长度为n的元素游程出现的次数比长度为n+1的游程出现的次数多一倍。

m序列和G o l d序列特性研究要点Harbin Institute of Technology扩频通信实验报告课程名称：扩频通信实验题目：Gold码特性研究院系：电信学院班级：通信一班姓名：学号：指导教师：迟永钢时间： 2012年5月8日哈尔滨工业大学第1章实验要求1.以r=5 1 45E为基础，抽取出其他的m序列，请详细说明抽取过程；2.画出r=5的全部m序列移位寄存器结构，并明确哪些序列彼此是互反多项式；3.在生成的m序列集中，寻找出m序列优选对，请确定优选对的数量，并画出它们的自相关和互相关函数图形；4.依据所选取的m序列优选对生成所有Gold序列族，确定产生Gold序列族的数量，标出每个Gold序列族中的所有序列，并实例验证族内序列彼此的自相关和互相关特性；5.在生成的每个Gold序列族内，明确标出平衡序列和非平衡序列，并验证其分布关系。

6.完整的作业提交包括：纸质打印版和电子版两部分，要求两部分内容统一，且在作业后面附上源程序，并加必要注释。

7.要求统一采用Matlab软件中的M文件实现。

第2章 实验原理2.1 m 序列二元m 序列是一种伪随机序列，有优良的自相关函数，是狭义伪随机序列。

m 序列易于产生于复制，在扩频技术中得到了广泛应用。

2.1.1 m 序列的定义r 级非退化的移位寄存器的组成如图1所示，移位时钟源的频率为c R 。

r 级线性移位寄存器的反馈逻辑可用二元域GF(2)上的r 次多项式表示2012() {0,1}r r i f x c c x c x c x c =++++∈L (1)图 2-1 r 级线性移位寄存器式(1)称为线性移位寄存器的特征多项式，其给出的表示反馈网络的而逻辑关系式是现行的。

因此成为线性移位寄存器。

否则称为，非线性移位寄存器。

对于动态线性移位寄存器，其反馈逻辑也可以用线性移位寄存器的递归关系式来表示112233 {0,1}i i i i r i r i a c a c a c a c a c ----=++++∈L (2) 特征多项式(1)与递归多项式(2)是r 级线性移位寄存器反馈逻辑的两种不同种表示法，因其应用的场合不同而采用不同的表示方法。

用MATLAB进行Gold序列的产生Gold序列因为其良好的伪噪声特性,经常作为CDMA扩频系统仿真中的用户扩频序列,用MATLAB可以产生各种长度的Gold序列优选对,用MATLAB进行Gold序列的产生Gold序列因为其良好的伪噪声特性，经常作为CDMA扩频系统仿真中的用户扩频序列，用MATLAB可以产生各种长度的Gold序列优选对，在此基础上，产生混沌序列等其他性质的扩频序列也很容易。

下面给出完整的源程序% MATLAB script for Illustrative Gold sequence generation. echo on % first determine the maximal length shift register sequences %We'll take the initial shift register content as "00001".connections1=[1 0 1 0 0];connections2=[1 1 1 0 1];sequence1=ss_mlsrs(connections1);sequence2=ss_mlsrs(connections2);% cyclically shift the second sequence and add it to the first one L=2^length(connections1)-1;;for shift_amount=0:L-1,temp=[sequence2(shift_amount+1:L) sequence2(1:shift_amount)];gold_seq(shift_amount+1,:)=(sequence1+temp) -floor((sequence1+temp)./2).*2;end;% find the max value of the cross correlation for these sequences max_cross_corr=0;for i=1:L-1,for j=i+1:L,% equivalent sequencesc1=2*gold_seq(i,:)-1;c2=2*gold_seq(j,:)-1;for m=0:L-1,shifted_c2=[c2(m+1:L) c2(1:m)];corr=abs(sum(c1.*shifted_c2));if (corr>max_cross_corr),max_cross_corr=corr;end;end;end;end;% note that max_cross_corr turns out to be 9 in this example...调用的子函数ss_mlsrs.mfunction [seq]=ss_mlsrs(connections);% [seq]=ss_mlsrs(connections)% SS_MLSRS generates the maximal length shift register sequence when the% shift register connections are given as input to the function. A "zero" % means not connected, whereas a "one" represents a connection. m=length(connections);L=2^m-1; % length of the shift register sequence requestedregisters=[zeros(1,m-1) 1]; % initial register contentsseq(1)=registers(m); % first element of the sequence for i=2:L, new_reg_cont(1)=connections(1)*seq(i-1);for j=2:m,new_reg_cont(j)=registers(j-1)+connections(j)*seq(i-1);end;registers=new_reg_cont; % current register contentsseq(i)=registers(m); % the next element of the sequence end;。

目录一．基本原理 (1)1.1伪随机序列 (1)1.11伪随机序列的相关概念 (1)1.12伪随机序列的数学 (1)1.13伪随机序列的相关特性 (2)1.2m序列 (3)1.3Gold序列 (5)1.31Gold序列的产生原理 (5)1.32Gold序列的基本性质 (6)二．设计过程 (6)2.1 MATLAB编程简介 (6)2.2 设计思路与流程图 (7)2.3 仿真程序 (8)三．仿真结果 (9)四．结果分析 (9)4.1相关性的理论分析 (9)4.2自相关 (11)4.3互相关 (13)五．总结 (17)一：基本原理Gold序列是R·Gold提出的一种基于m序列的码序列，这种序列有较优良的自相关和互相关特性，构造简单，产生的序列数多，因而获得了广泛的应用。

1.1伪随机序列1.1.1伪随机序列相关概念伪随机序列作为扩频通信系统中的一部分是十分关键的，它关系到扩频系统的性能。

四十年代末，信息论的奠基人香农(C.E.Shannon)提出的编码定理指出：只要信息速率Rb小于信道容量C，则总可以找到某种编码方法，在码周期相当长的条件下，能够几乎无差错的从收到高斯噪声干扰的信号中复制出原发信息。

这里有两个条件，一是Rb<=C，二是编码的码周期足够长。

同时香农在证明编码定理的时候，提出用具有白噪声统计特性的信号来编码。

白噪声是一种随机过程，它的瞬时值服从正态分布，功率谱在很宽频带内都是均匀的。

但是至今无法实现对白噪声放大、调制、检测、同步及控制等，而只能用具有类似于限带白噪声统计特性的伪随机序列信号来逼近它，并作为扩频系统的扩频码。

六十年代末，一些易于产生、加工和复制且具有白噪声性质的“伪噪声编码技术”日趋成熟，因此高效抗干扰编码通信变得蓬勃发展起来。

同时用各种不同波形的正交码来实现波形分割的码分多址通信也相继出现，实现了无线用户的随意呼叫通信。

这种技术在地面多址通信和卫星通信中都可采用。

gold序列产生原理Gold序列是一种特殊的数列，其产生原理可以通过递归函数来描述。

Gold序列的特点是，每个数都是前面两个数的和，即第n个数等于第n-1个数加上第n-2个数。

具体来说，第一个数和第二个数是预先给定的，接下来的每个数都是前面两个数的和。

为了更好地理解Gold序列的产生原理，我们可以通过一个简单的例子来说明。

假设我们规定第一个数为0，第二个数为1。

那么根据递归函数，第三个数就是0+1=1，第四个数是1+1=2，第五个数是1+2=3，以此类推。

通过上述例子，我们可以看出，Gold序列的产生过程是通过不断将前面两个数相加而得到的。

这个过程可以用递归函数来表示，即f(n) = f(n-1) + f(n-2)，其中f(n)表示第n个数。

通过递归函数的定义，我们可以根据已知的前两个数，依次计算出后面的数。

值得注意的是，Gold序列的产生原理并不依赖于具体的初始值。

无论我们规定第一个数和第二个数是什么，只要按照递归函数的规则计算，最终得到的数列都是Gold序列。

这是因为递归函数的定义保证了每个数都是前面两个数的和。

Gold序列在数学和计算机科学中都有广泛的应用。

在数学中，Gold序列被用来研究一些数论和代数的问题，例如斐波那契数列和黄金分割数等。

在计算机科学中，Gold序列常常被用来生成随机数序列或用作密码学中的密钥序列。

在生成随机数序列的应用中，Gold序列通过将两个序列进行异或运算来产生新的序列。

这样做的好处是，由于递归函数的特性，Gold 序列的数值分布相对均匀，具有较好的随机性质。

这使得Gold序列在随机数生成算法中得到了广泛应用。

在密码学中，Gold序列常被用作加密算法中的密钥序列。

由于Gold序列具有较好的随机性质和良好的扩散性质，使得生成的密钥序列能够提供较高的安全性。

因此，Gold序列在密码学中被广泛应用于对称加密算法和流密码算法中。

总结起来，Gold序列是一种通过递归函数产生的数列，其产生原理是每个数都是前面两个数的和。

Gold 序列实验报告一、实验过程及分析1 m 序列&G old 序列的产生（1）选取本原多项式367()1f x x x x x =++++，产生m 序列。

fbconnection_m=[1 0 1 0 0 1 1]; mseq=m_sequence(fbconnection_m);（2）由本原多项式37237()1&()1f x x x f x x x x x =++=++++生成的m 序列为m 序列优选对，以此优选对来产生Gold 序列。

fbconnection_op_1=[0 0 1 0 0 0 1]; fbconnection_op_2=[1 1 1 0 0 0 1];goldseq=gold_seq(fbconnection_op_1,fbconnection_op_2);2 m 序列的相关特性-150-100-50050100150kR (k )autocorrelation function of m sequence图1 m 序列自相关函数kR (k )图 2 m 序列互相关函数3 G old 序列的相关特性kR (k )autocorrelation function of gold sequence图3 G old 序列自相关函数-20-15-10-5051015kR (k )cross-correlation function of gold sequence图4 G old 序列互相关函数图2-5 m 序列&G old 序列最小，最大相关值4 m 序列&G old 序列相关特性比较-200-1000100200-20020406080100120140kR (k )autocorrelation function of m sequence -200-1000100200-20020406080100120140kR (k )autocorrelation function of gold sequence图6 m 序列&G old 序列自相关函数比较-200-1000100200-50-40-30-20-100102030kR (k )cross-correlation function of m sequence -200-1000100200-20-15-10-551015kR (k )cross-correlation function of gold sequence图7 m 序列&G old 序列互相关函数比较gold 序列在时延不为0是三值的，这一点不如m 序列，在时延为0处具有与m 序列相同的峰值特性。

实验 GOLD 序列特性实验一、实验目的1、掌握GOLD 序列的特点。

2、了解GOLD 序列在直接扩频通信中所起的作用二、实验器材1、移动通信原理实验箱 一台2、20M 双踪示波器 一台3、频谱分析仪或带FFT 功能的数字示波器（选配）一台三、实验内容1、观察GOLD 序列的波形（频谱）。

2、观察GOLD 序列的自相关和互相关特性。

四、实验原理1、伪随机序列工程上常用二元{0，1}序列来产生伪噪声码。

它具有如下特点： （1） 每一周期内“0”和“1”出现的次数近似相等。

（2） 每一周期内，长度为n 比特的游程出现的次数比长度为n+1比特的游程出现的次数多一倍。

（游程是指相同码元的码元串）（3） 序列具有双值自相关函数，即：⎪⎩⎪⎨⎧-≤≤=11k 01)(p pR τττ当－＝当（4.1-1）在（4.1-1）式中，p 为二元序列周期，又称码长，k 为小于p 的整数，τ为码元延时。

2、m 序列二元m 序列是一种基本的伪随机序列，有优良的自相关函数，易于产生和复制，在扩频技术中得到了广泛的应用。

长度为2n -1位的m 序列可以用n 级线性移位寄存器来产生。

如图4.1-1所示：图4.1-1 线性移位寄存器m 序列的特性如下（1） 在每一周期p= 2n -1内，“0”出现2n －1-1次，“1”出现2n －1次，“1”比“0”多出现一次。

（2） 在每一周期内共有2n －1个元属游程，其中“0”的游程和“1”的游程数目各占模二加法器一半。

并且，对n>2，当1≤k ≤n-1时，长为k 的游程占游程总数的1/ 2 k ，其中“0”的游程和“1”的游程各占一半。

长为n –1的游程只有一个，为“0”的游程；长为n 的游程也只有一个，为“1”的游程。

（3） m 序列（a k ）与其位移序列（τ-k a ）的模二和仍然是m 序列的另一位移序列（τ'-k a ），即：{}{}{}ττ'--=+k k k a a a（4） m 序列的自相关函数为：⎪⎩⎪⎨⎧≠-=ppp R mod 01mod 01)(τττ当＝当（4.1-2）3、Gold 序列虽然m 序列有优良的自相关特性，但是使用m 序列作CDMA （码分多址）通信的地址码时，其主要问题是由m 序列组成的互相关特性好的互为优选的序列集很少，对于多址应用来说，可用的地址数太少了。

中南大学扩频通信实验报告实验一：扩频与解扩观测实验时间：4月9号一、实验目的1、了解直接序列扩频的原理。

2、了解扩频前后信号在时域及频域上的变化。

二、实验器材⒈主控&信号源模块、2号、14号、11号模块各一块⒉双踪示波器一台⒊连接线若干三、实验原理1、实验原理框图数字信号源扩频解扩DoutMUXBSOUT2# 模块14# 模块11# 模块NRZ1NRZ-CLK1扩频序列1序列1（TP8）扩频序列2序列2（TP8）CDMA1AD 输入1AD 输入2CDMA2Dout实验框图2、实验框图说明本实验选择【扩频与解扩观测实验】菜单。

如框图所示，我们用2号模块作为信号源，DoutMUX 输出32K 数字信号，送入至14号模块的NRZ1。

14号模块此时完成扩频功能，扩频序列由14号模块内部产生，将开关S1设置为0000，开关S2设置为0111，即可设置该路扩频序列1的码型（测试点为TP8序列1）。

扩频信号由端口CDMA1输出。

同时，当14号模块的开关S3设置为0111、开关S4设置为0000且端口NRZ2和NRZ-CLK2无信号输入时，端口CDMA2输出的伪随机序列与14号模块的扩频序列1相同，本实验中将该序列“CDMA2”可作为后续的解扩序列。

此时的11号模块完成解扩功能，其中扩频信号从端口“AD 输入1”输入，解扩序列从“AD 输入2”输入，解扩信号从11号模块的“Dout ”输出。

该实验【扩频与解扩观测实验】中扩频序列的长度可通过PN 序列长度设置开关S6进行选择15位或16位。

当开关S6拨至“127位”时，表示该实验的扩频为15位；当开关S6拨至“128位”时，表示该实验的扩频为16位。

注：为配合示波器调节，为了较好的对比观测扩频前和扩频后的码元，建议选择16位。

四、实验步骤1、按框图所示连线。

源端口目标端口连线说明 模块2：DoutMUX模块14：TH3(NRZ1)数据送入扩频单元模块2：BSOUT 模块14：TH1(NRZ-CLK1) 时钟送入扩频单元模块14：TH4(CDMA1) 模块11：TH2(AD输入1) 送入解扩单元模块14：TH5(CDMA2) 模块11：TH3(AD输入2) 提供解扩序列2、选择主菜单【移动通信】→【扩频与解扩观测实验】，此时2号模块DoutMUX输出速率为32K。

Gold序列的仿真研究摘要: Gold序列是R?Gold提出的一种基于m序列的码序列,这种序列有较优良的自相关和互相关特性,构造简单,产生的序列数多,因而获得了广泛的应用。

本文对Gold序列进行仿真研究,首先介绍了扩频通信中常用的m序列和Gold 序列码产生的方法原理和性质,运用Matlab对Gold码的生成和性能进行了仿真分析。

关键词:伪随机序列;Gold序列;m序列;Matlab仿真SIMULATION OF GOLD SEQUENCESAbstract: Gold sequences is proposed by RGold which is based on m sequences. Gold sequences has good properties, such as good autocorrelation and cross-correlation, easy to construct and more sequences, etc, therefore it has wide applications.This paper investigates the Gold sequences. The principle and performance of m sequences and Gold sequences in spread spectrum communication are first introduced in the paper. Simulation by Matlab is also provided in the paper to analyze the nature of Gold sequences.Key words: Pseudo-random sequence;Gold sequence;m sequence;Matlab simulation目录1 引言11.1研究的背景及意义 11.2 CDMA通信技术简介 11.2.1 扩频的理论基础11.2.2 扩频通信的分类21.2.3 CDMA扩频通信系统的构成 21.2.4 伪随机序列在CDMA通信系统中的应用 22 m序列 32.1 伪随机序列相关概念 32.1.1 伪随机序列的数学定义 32.1.2 随机序列的相关特性 42.2 m序列的产生原理 53 Gold序列 63.1 Gold序列的产生原理 63.2 Gold序列的基本性质74 Matlab仿真实现84.1 产生m序列84.2 产生Gold序列94.3 相关性仿真104.3.1 相关性的理论分析104.3.2 Matlab仿真115 结束语14致谢16参考文献171 引言1.1研究的背景及意义移动通信由于具有时实性、机动性、具有不受时空限制等特点,己经成为一种深受人们欢迎的通信方式,并融入了现代生活当中。

实验一GOLD序列特性实验②用示波器观察测试点“GOLD1”处的波形。

改变拨位开关“扩频码速率”的设置，按“发射机复位”键，再观察“GOLD1”处的波形。

“GOLD1置位”设置为10000000时100kbit/s的GOLD1波形“GOLD1置位”设置为10000000时200kbit/s的GOLD1波形观察Gold序列的自相关和互相关特性用示波器测“TX3”处波形，该波形即为Gold序列的GOLD序列的自相关特性用示波器测“TX3”处波形，该波形即为Gold序列的互相关特性。

GOLD序列的互相关特性1、顺时针将“跟踪”电位器旋到底，用示波器测“VCO-C”处波形，该波形即为延迟锁相环的鉴相特性曲线。

2、用示波器双踪分别观察“G1-BS”和“G3-BS”处的波形，调节“跟踪”旋钮，直到二个波形完全一致，没有相差为止。

此时表明接收机的Gold序列和发射机的Gold序列在相位与码速率上都一致。

3、用示波器双踪分别观察“GOLD1”和“GD-TX”处的波形，二者的波形应完全一致。

说明：由于本系统的Gold序列频率较高，且周期很长，模拟双踪示波器应在“断续（CHOP）”模式下比较“GOLD1”和“GD-TX”处的波形，如果在“交替（ALT）”模式下即使两者输出波形一致，观察结果也可能不一致。

数字示波器则不存在该问题。

实验三扩频与解扩实验①将“SIGN1置位”设置成不为全0或全1的码字，设置“GOLD1置位”。

用示波器分别观察“SIGN1”和“S1-KP”的波形，并做对比。

信码速率为1kbit/s、扩频码速率为100kbit/s时“SIGN1”和“S1-KP”处波形②（选做）用带FFT功能的数字示波器分别观察“SIGN1”和“S1-KP”的频谱，并做对比。

③分别改变发射机的信码速率和扩频码速率，重复上一步骤。

5、（选做）观察扩频前后PSK调制频谱的实验①码字设置不变，将“扩频”开关拨下，用频谱仪观察“PSK1”的频谱。

实验八GOLD 码特性实验一、实验目的1、掌握GOLD 码的编解码原理。

2、掌握GOLD 码的软件仿真方法。

3、掌握GOLD 码的硬件仿真方法。

4、掌握GOLD 码的硬件设计方法。

二、预习要求1、掌握GOLD 码的编解码原理和方法。

2、熟悉matlab 的应用和仿真方法。

3、熟悉Quatus 的应用和FPGA 的开发方法。

三、实验原理1、GOLD 序列简介GOLD 序列是由m 序列的“优选对”构成的。

所谓优选对是指m 序列中互相关值为[－1，－t(n),t(n)-2]的一对序列。

其中(1)/21(2)/212,2,(){n n n n t n ++++=为奇数，为偶数下表为部分m 序列的部分优选对 表1 部分m 序列的部分优选对上表中的m 序列采用8进制（可参见PN 码实验）。

2、GOLD 序列由m 序列中的优选对{xi}和{yi}本身加上它们的相对移位模二相加构成的2n －1个序列组成，序列总数为2n ＋1。

任一队序列之间的互相关函数都是三值的，即(1)/2(1)/21(1)/2(1)/211{(21)(),(21)()2R {1{(21)(),(21)()2n n cn n t n n t n t n n t n ++++++--+=--=-=--+=--=-为奇数为偶数，但不被4整除即，GOLD 序列的最大互相关值为|R |()c m t n下表为GOLD 序列的t(n)值及其与自相关峰值Rs （0）的比值，同时给出GOLD 序列族中的序列数。

表为 部分GOLD 序列的t(n)值、Rs （0）、序列数表1、建立GOLD 的仿真文件(GOLD.MDL)GOLD1…GOLD7的Sample Time 均设置为SampleTime ；Preferred polynomial （1）设置为[1 0 1 1]；Initial states （1）设置为[0 0 1]; Preferred polynomial （2）设置为[1 1 0 1]；Initial states （2）设置为[0 0 1]。