安培环路定理和磁通量

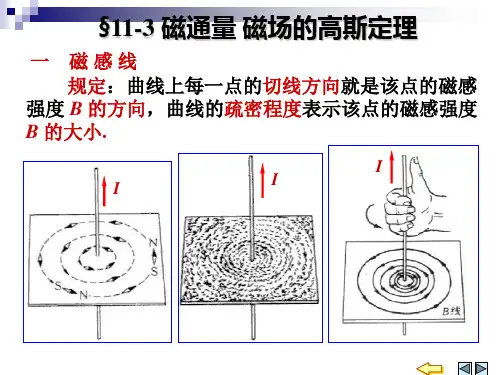
磁场中的磁通量与安培环路定理磁通量与安培环路定理是电磁学中两个重要的概念，它们之间存在着密切的联系。

磁通量是衡量磁场强度的物理量，而安培环路定理则描述了电流在闭合路径上产生的磁场。

它们的关系既有理论基础，又有实际应用。

首先，我们来了解一下磁通量的概念。

磁通量是在磁场中通过一个给定面积的总磁场线数，用符号Φ表示。

它是在单位时间内通过单位面积的磁场线数，即磁场线的密度。

磁通量是用于描述磁场的强弱的一个重要参量，单位是韦伯(Wb)。

磁通量与磁场的关系可以用下式表示：Φ = B·A·cosθ其中，Φ表示磁通量，B表示磁场强度，A表示面积，θ表示磁场线与法线之间的夹角。

从这个式子可以看出，当磁场线垂直于面积时，磁通量最大；当磁场线平行于面积时，磁通量为零。

接下来，我们来了解一下安培环路定理。

安培环路定理是在1836年由法国物理学家安培提出的，它描述了电流在闭合路径上产生的磁场。

根据安培环路定理，沿着一条闭合路径，磁场的总磁通量等于该路径内的电流的代数和的N倍，即Φ=A·μ_0·I_N。

在这个公式中，Φ表示磁通量，A表示路径的面积，μ_0表示真空磁导率，I_N 表示通过该路径内的电流的代数和。

公式中的N表示电流回路的圈数，它表示电流环路绕行的次数。

根据安培环路定理，电流越大、回路圈数越多，产生的磁场强度就越大。

安培环路定理与磁通量的关系可以通过一个简单的实验来说明。

我们可以将一个螺线管放在一个磁场中，然后通过螺线管中的电流产生一个磁场。

根据安培环路定理，螺线管所包围的磁通量等于螺线管中的电流的代数和的N倍。

通过这个实验可以得出一个结论：当电流通过螺线管增大时，螺线管所包围的磁通量也会增大。

这就说明了电流对磁场强度的影响。

这一结论对于理解和应用电磁学理论有着重要意义。

磁通量与安培环路定理不仅有理论上的意义，还有着广泛的应用。

例如，在发电机和变压器中，磁通量的变化可以产生感应电动势，从而实现电能的相互转换。

磁场中的磁通量与安培环路定律磁通量是描述磁场强度的物理量，而安培环路定律则是磁场与电流之间的重要定律。

本文将详细介绍磁通量和安培环路定律以及它们之间的关系。

一、磁通量的概念和计算磁通量是描述磁场穿过某个曲面的总磁力线数目的物理量。

它的符号为Φ，单位为韦伯（Wb）。

磁通量的计算可以使用以下公式：Φ = B·A·cosθ其中，B表示磁场的磁感应强度，A表示曲面的面积，θ表示磁场线与法线之间的夹角。

在实际应用中，我们常常需要计算通过一个闭合曲面的磁通量。

根据高斯定律，当闭合曲面内没有磁单极子存在时，通过闭合曲面的总磁通量为零。

这一定律被称为高斯磁定理。

二、安培环路定律的基本原理安培环路定律描述了磁场强度和绕过电流的闭合曲线之间的关系。

它的基本原理可以概括为：“磁场强度的环流等于通过这一环路所包围的总电流”。

安培环路定律可以用以下公式表示：∮B·dl = μ0·I其中，∮B·dl表示沿闭合曲线的磁场强度的环流积分，μ0表示磁导率，I表示通过闭合曲线所包围的总电流。

通过安培环路定律，我们可以计算封闭曲线上的磁场强度。

这在磁场计算和电磁感应等领域具有重要的应用价值。

三、磁通量与安培环路定律的关系磁通量和安培环路定律之间存在着密切的关系。

根据安培环路定律，对于任意封闭曲线，通过该曲线所包围的总电流等于封闭曲线上的磁场强度的环流积分。

根据高斯定律，当通过一个封闭曲面的磁通量为非零时，该封闭曲面内存在磁单极子。

然而，根据实验观察和理论研究，至今尚未发现磁单极子的存在。

因此，磁通量为零的情况更符合实际情况。

根据这一观察和推理，我们可以得出结论：通过任意封闭曲面的磁通量等于零。

换句话说，磁通量的总和为零。

这与通过安培环路定律得到的结果相吻合。

四、磁通量和安培环路定律的应用磁通量和安培环路定律在许多领域都有广泛的应用，特别是在电磁感应和电路分析中。

在电磁感应中，根据法拉第电磁感应定律，当磁通量通过一个线圈变化时，线圈中会感应出电动势。

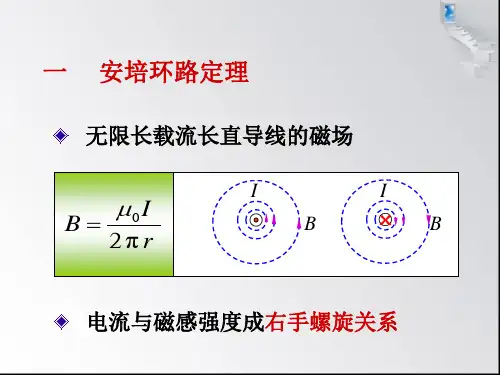
无限长载流圆柱导体内外磁场的分布载流圆柱导体内外磁场的分布是电磁学中的一个重要问题。

在这篇文章中，我们将以此为主题，详细讨论这个问题，并一步一步解答。

一、导体内外磁场的形成原理载流圆柱导体内外磁场的形成原理可以通过安培环路定理来解释。

根据安培环路定理，磁场的总磁通量等于该环路上所有电流元的磁通量之和。

对于一段长度为L的导线，其磁通量可以表示为：Φ= B ×A ，其中，B表示磁感应强度，A表示过该面积的磁场线的数量。

由于导线内部存在电流，通过安培环路定理可知，导体内外磁场的形成原理是由导体内部的电流元和其它电流元产生的。

导体内外的磁场由导体内部电流元的磁场叠加而成，并随着距离导体表面的距离不断减小。

二、导体内磁场的分布在讨论导体内磁场的分布之前，我们首先需要确定正交坐标系。

在本文中，我们选择柱坐标系。

在柱坐标系中，磁场的分布可以表示为B = (B_r, B_θ, B_z)。

其中，B_r表示径向磁场分量，B_θ表示角向磁场分量，B_z表示轴向磁场分量。

为了计算导体内磁场的分布，我们可以应用安培定理。

根据安培定理，电流周围的磁场线是以电流元为轴线的圆周。

根据对称性，我们可以得出导体内电流元的磁场与其它电流元在磁场线中的贡献是一样的。

这意味着在任意一个彼此距离相等的电流元上，它们对磁场的贡献相等。

所以，在导体内部的圆柱体积元上，径向磁场分量B_r = 0。

同理，角向磁场分量B_θ= 0。

因此，在导体内部，只存在轴向磁场分量B_z。

它的大小可以通过安培环路定理计算。

假设导体内流过的电流为I，半径为R，那么在径向表面上环路定理可以表示为：B_z ×2πrL = μ_0I,其中，r是径向表面到轴线的距离，L是导体的长度，μ_0是真空中的磁导率。

由此可以得到导体内的轴向磁场分量为：B_z = (μ_0I)/(2πrL)。

在导体外，磁场的计算较为复杂。

但有一种常用的简化方法是采用比例法和对称性法。

磁介质中的安培环路定理
安培环路定理是描述电流在一个闭合环路内的磁场强度的定量关系的定理。

在磁介质中，安培环路定理可以表述为：闭合环路内的磁通量等于环路内电流所产生的磁场强度与环路中磁化强度的代数和。

换句话说，如果我们将一个磁介质的闭合环路划分成若干小段，对每一小段进行磁场分析，然后将它们按照一定的方向按顺序排列，就形成了一个完整的安培环路。

在磁介质中，该安培环路的总磁通量等于环路内任意一个小段上的磁场强度与该小段上的磁化强度的代数和。

这个定理主要用于计算磁介质中的磁场分布及其对电路的影响。

对于任意一个闭合环路，我们都可以通过安培环路定理求得环路内的磁通量，再根据法拉第电磁感应定律计算出环路内的感应电动势，从而分析电路中的电磁现象。

总之，安培环路定理是一种描述磁介质中电流与磁场强度之间关系的基本定理，是电磁学研究中不可或缺的重要工具。

安培环路定理的适用范围安培环路定理，也称为安培第二定律，是电磁学中重要的定理之一。

它表明了在一个封闭的电路中，电流通过每个点的总和等于所围面积中磁通量的变化率。

这个定理的适用范围比较广泛，下面我们将进一步探讨。

首先，安培环路定理适用于理想的电路模型。

在理想电路中，电路元件的内阻为零，电路中的电流可以自由地流过。

这样，我们就能够在一个封闭的电路中应用安培环路定理来分析电路的行为。

其次，安培环路定理适用于直流电路和交流电路。

对于直流电路，磁通量随时间不变，因此，磁通量变化率等于零。

而对于交流电路，磁通量随时间变化，因此磁通量变化率不为零。

因此，安培环路定理在直流电路和交流电路的分析中都可以得到应用。

第三，安培环路定理适用于恒定电场的电路。

电场与磁场是两种不同的物质，它们在物理性质上也有着很大的差异。

在一个恒定电场中，磁场的存在比较微弱，因此电场的贡献至关重要。

第四，安培环路定理适用于涉及电感的电路。

电感是电路中的一种被动元件，它具有存储电能的能力。

当电流通过一个电感时，会产生一个磁场。

这个磁场会随着电流的变化而变化，因此，磁通量也会随着电流的变化而变化。

安培环路定理在涉及到电感的电路分析中也可以得到应用。

最后，安培环路定理适用于涉及电流的系统。

当电流通过导线时，它可以产生磁场。

由于导线通常是弯曲的，因此在某些情况下，我们需要考虑导线的形状来分析电路的行为。

在这种情况下，安培环路定理可以帮助我们计算由于导线形状变化而引起的磁场变化。

在总体上，安培环路定理在电磁学的研究中具有重要的作用。

它不仅可以用于电路的分析，也可以用于磁场和电流的相互作用的研究。

随着科学技术的不断发展，我们相信安培环路定理的适用范围还将得到进一步的扩展和深入研究。