当前位置：文档之家 › 静电场的环路定理表达式及其物理意义

静电场的环路定理表达式及其物理意义

  • 格式：docx
  • 大小：36.55 KB
  • 文档页数：2

下载文档原格式

  / 2

合集下载

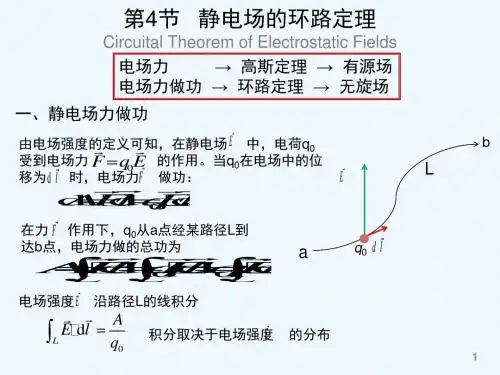
7.4+5 静电场的环路定理、电势及其与场强关系 - 副本

7.4+5 静电场的环路定理、电势及其与场强关系 - 副本

电荷 q 在静电场中 r 点处的电势能:
r
W(r) q
E(r ) dr
势能零点
(积分路径任选)
数值上等于把电荷从该点移到势能零点过程中静电力 对该电荷所做的功。
例：电荷q0 在点电荷Q产生的静电场中的电势能 (无穷远处为0)：
W
(r
)
q0
Q
40 r
rQ
电势（Electric Potential） [§7.4]
前知，静电力所做的功可写成
b
Aab a q0E dl [W (rb ) W (ra )]
其中函数W (r ) 称为电荷 q0 在电场 E 中的电势能。
关于静电场力的功能原理： A W
注意： ➢ 电势能反映电荷在静电场中特定位置处的势能， 它与电荷所处在静电场中的位置有关； ➢ 电势能是系统的能量，属于电荷与静电场共有； ➢ 电势能也存在零点选择问题。 ［视方便而选；常选无穷远处为0］
λ
UP
E dl
P
r
E(r)dr
无意义
λ dr λ (ln ln r) o
r 2πε0r
2πε0
选取某一距带电直导线为rB 的B点为电势零点，
E λ 2πε0r
rB
rP B r
UP
B
E dl
P
rB
dr
r 20r
ln rB 2 0 r
当电荷分布扩展到无穷远时，电势零点不能再选在
静电场的环路定理 电势能 (§7.4)
Circulation Theorem of Electrostatic Field and Electric Potential Energy
静电场的性质： 1）电荷在电场中受到电场力

6-3 静电场的环路定理和电势

6-3 静电场的环路定理和电势

V(r>R)

1
4 0
q r
练习 在点电荷 +2q 的电场中，如果取图中P点处 为电势零点，则 M点的电势为
2q P M
a
a
（A） q
2π 0a
（C）
q
8π
0
a
q
（B）
4π 0a
（D） q
4π 0a
练习 在点电荷q的电场中，选取以q为中心，R为半 径的球面上一点P处作电势零点，则与点电荷q距离 为r的P’点电势为
A

（D）电场力作的功 W 0
电势的求解方法
（1）利用电势叠加原理
VP
dq
4π0r
使用条件：有限大带电体且选无限远处为电势零点.
（2）利用电势的定义
V 0点
VA E dl
A
使用条件：场强分布已知或很容易确定.
均匀带电球面：
V( r R )

1
4 0
q R
四 电势
1、电势
VA

EpA q0

E dl
AB
(VB 0)
q0
A
B E
物理意义：描述电场能的性质，某点的电势在数值上等于将单 位正电荷从该点沿着任意路径移到零势能点时电场力所做的功.
B
电势差（电压）：U AB VA VB
E dl
A
WAB q0 (VA VB ) (EPB EPA)
位置有关，与路径无关.
B
dr
dl
q0
E

二 静电场的环路定理


q0 E dl q0 E dl

静电场的环路定理

静电场的环路定理





q
j
V V V 1 2 k q q q 1 2 n 4 r r 4 r 0 1 4 0 2 0 n
q i
电势叠加原理
V V P i r 0 i i i 4
任意带电体场中的电势
VP q
4 0r
dq
a b
即：a、b两点的电势差 = A/q0
将单位正电荷 从ab电场力作的功 与路径无关
6
例: 已知真空中两金属圆筒电极间电压为U ，半径分别为 R1、 R2 。 求：负极上静止电子到正极时的速度？ 解：由电势差的定义可得
A q ( V V )
( e)( U )
R
R
2
1
F
c
dl
q0
dr
b
r +dr
r
a
rb
+
积分
1 1 q q q q 0 0 A d r 2 a4 r 4 r 0 0 a r b
b
ra
q
——点电荷的电场力作功 只与被移动电荷距离场源电荷的距离相关 与路径无关
2
2.在点电荷系的电场中(或连续带电体的电场)

结论
b b b A q E d l q E d l q E d l 0 1 0 2 0 n a a a



电场强度的线积分与路径无关
电场力是保守力，静电场是保守力场。
3
二、环路定理
在任意电场中, 将q0从a
b L2 经L1
经L2
b电场力作功：
A q E d l 0 L

简述静电场的环路定理

简述静电场的环路定理

简述静电场的环路定理静电场的环路定理是电磁学中的基本定理之一，它描述了静电场中电场强度的分布以及其与电荷分布之间的关系。

本文将对静电场的环路定理进行简述，重点介绍定理的含义和应用。

静电场的环路定理，又称为库仑定律或环路定理，是由法国物理学家库仑在18世纪末提出的。

定理的核心思想是在闭合路径上，电场强度沿着路径的积分等于路径内电荷的代数和与真空介电常数的乘积。

简单来说，静电场的环路定理可以用以下公式表示：∮E·dl = q/ε₀其中，∮E·dl表示电场强度沿闭合路径的环路积分，q表示路径内的总电荷，ε₀表示真空介电常数。

根据静电场的环路定理，可以推导出一些重要的结论和应用。

首先，对于闭合路径上没有电荷的情况，环路积分必然等于零。

这意味着在没有电荷存在的区域，电场强度沿着任意闭合路径的环路积分都等于零。

这个结论可以用来验证电场的无旋性，即电场强度的旋度为零。

对于闭合路径上存在电荷的情况，环路积分不等于零。

根据路径内电荷的正负情况以及电场强度的方向，可以确定环路积分的正负。

如果路径内的总电荷为正，则环路积分为正，表示电场强度沿路径的方向与路径的方向一致；如果路径内的总电荷为负，则环路积分为负，表示电场强度沿路径的方向与路径的方向相反。

静电场的环路定理可以应用于计算电场强度、电势差等物理量。

例如，在计算电场强度时，可以通过选择合适的闭合路径，利用环路定理求解电场强度的大小和方向。

在计算电势差时，可以利用环路定理将电场强度的环路积分转化为电势差的差值，从而简化计算过程。

静电场的环路定理还可以应用于电场的分布和电势的计算。

通过选择合适的闭合路径，可以根据路径内的电荷分布和已知的电场强度，求解路径上任意点的电场强度和电势。

同时，环路定理也为电场强度的计算提供了一种简便的方法，避免了直接积分计算的繁琐过程。

静电场的环路定理是电磁学中的重要定理之一，它描述了静电场中电场强度与电荷分布之间的关系。

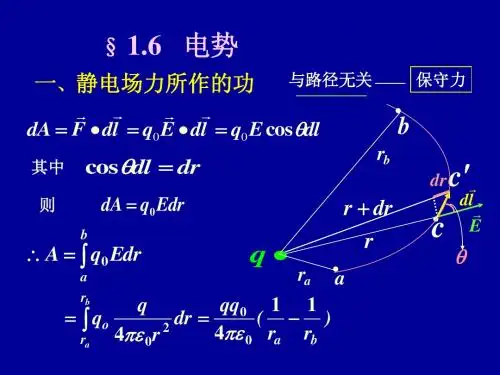
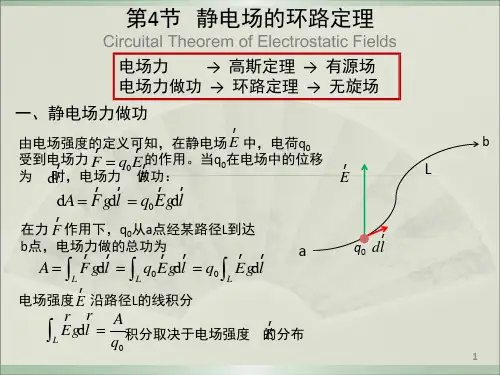
静电场的环路定理

静电场的环路定理

它是反映电场本身“能的属性”的物理量，与 场中是否存在电荷无关。 要注意，电势和电势能是两个不同的概念，不 能混为一谈。
Wa E dl 定义电势 ua q0 a
单位正电荷在该点 所具有的电势能

Wa q0 E dl
a

单位正电荷从该点到无穷远 点(电势零)电场力所作的功
三 电势
电势差
1、电势能 分析：当检验电荷 q 0 从a点移到b点，电 场力要做功，而功是能量转化的量度， 这说明 q 0 从a点移到b点有能量变化。不 管 q 0 从a点沿哪一条路径移到b点，电 场力对电荷 q 0 做的功都是相同的，这说 明电荷 q 0 在a﹑b两点的能量差是一定 的，其值由这两点的位置决定。这种由 电荷在电场中的位置决定的能量，叫做 电势能。显然，电势能是电荷 q 0 和电场 共同具有的。检验电荷在a﹑b两点的电 位能，分别用 W a ﹑W b 表示。
电势能
例2、求均匀带电圆环轴线 上的电势分布。 已知：R、q
解:方法一 微元法
Y
dl




r
x
P

Z
R
X
O


方法二 定义法 由电场强度的分布 qx E 2R 3 dl 2R 2 2 2 4 0 ( x R ) uP du 4 0 r 4 0 r 0 qxdx u Edx 3 q 2 2 2 xp x p 4 ( x R ) 0 2 2 4 0 R x
则ab电场力的功 Aab q0 E dl Wa Wb
b
取 W 0
注意
Wa Aa
q0 E dl

静电场的环路定理 电场的电势(势函数)：静电场的保守性意味着,对静电场来说,存在着一个由电场中各点位

静电场的环路定理 电场的电势(势函数)：静电场的保守性意味着,对静电场来说,存在着一个由电场中各点位

9-6 电势
物理学教程 （第二版）
三 电势的叠加原理
点电荷系 E Ei
i
VA E dl Ei dl
A
iA
q1
q2 q3
r1 r2 r3
E3
E2
A
E1
VA
VAi
i
i
qi
4π 0ri
电荷连续分布
VP
dq
4π 0r
dqqdrqP
dV
dE
第九章 静电场
9-6 电势
第九章 静电场
9-6 电势
物理学教程 （第二版）
此标量函数（电势）在 A、B 两点的数值之差等 于从A到B移动单位正电荷时静电场力所做的功.
E dl
( EpB
EpA )
AB
q0 q0
q0
E dl AB
(VB
VA )
A
B E
B 点电势
VB
EpB
q0
A 点电势
VA
EpA q0
VA AB E dl VB （ VB为参考电势，值任选）
由
V外 (r)
Q
4π 0r
可得
V (R)
Q
4π 0R
V内
或
V内(r)
R r
E1
dr
R
E2
dr
Q
4π 0R
Q
V外 (r) 4π 0r
Q
V内(r) 4π 0R
V
Q
4 π 0R
oR
Q
4π 0r物理中能量单位 1eV 1.602 1019 J
第九章 静电场
9-6 电势
物理学教程 （第二版）
二 点电荷的电势

第10章静电学-3-静电场环路定理

第10章静电学-3-静电场环路定理

+q
11
(2)电荷分布如图所示, 将点电荷qo从a 经半圆b移到c的 过程中, 电场力对qo的功？
解 Aac qo (Ua Uc )
b
Ua
q
4o R
q
4o R
0
-q
a
+q R
o
c
Uc
q
4 o (3 R)
q
4o R
R
R
q
6o R
Aac
qqo
6o R
12
例10-14 一均匀带电直线段，长为L，电量为q ;取无穷远为电 势零点，求直线延长线上离一端距离为d 的P点的电势。
9
③对于电荷连续分布的带电体，可将其分割为无数多电荷元
dq，每个电荷元dq当作点电荷，其电势为
dU dq 4πε0r
根据电势叠加原理
U
V
dq
4 0r
dl dq dS
dV
积分遍及整个带电体，V是带电体的体积。
电势叠加原理也可以计算多个带电体所产生电场的总电 势，总电势应等于各带电体所产生电场的电势的代数和。
(3)电势差：
b
Uab Ua Ub E dl
a
静电场中a、b两点的电势差等于将单位正电荷由a沿任意路 径移至b过程中电场力做的功。
电势差是绝对量，与电势零点的选择无关。
6
由Wa
q
零势点 E
a
dl ,
得 Wa qUa
由Aab
q
b
E dl
a
Wa Wb ,
得 Aab q(Ua Ub )
(3)等于场强从该点沿任意路径到零势点的线积分。
说明：
(1)电势是相对量，要确定场中各点的电势必须选定电势零点。

静电场的环路定理

静电场的环路定理

已知q的电场分布 E
根据定义, P点的电势为
4
q
0r
2
er
VP


P

E dl

r
q
40r
2Pdr4q04r2qe0rrP dl
q > 0时, VP为正, r V, r处V= 0 min q < 0时, VP为负, r V, r处V = 0 max
2.电场强度与电势梯度的关系
根据电势差的定义, 把单位正电荷从P1移到P2 电场力所作的功为：
dA E dn V (V dV )
r E
dn
n
P1
P2
V V dV
E dn dV
E


dV dn
grad V
E
ቤተ መጻሕፍቲ ባይዱ

dV dn
n
r E grad V
r 即:电场中某点的场强 E 等于该点电势梯度的负值
无意义
VP

P
E
dr
rP
2 0r
dr

2 0
ln
rP
r
P
P'
令某处 r = r0（有限值） V=0，则
VP

P0
P
E
dl

P
P
E dl

P0
P
E dl
r0 P0

P
P
2
0r
dr

2 0
ln
r0 r
可见：当电荷分布到无穷远时，
22
归纳 电场强度与电势的关系
积分关系：

练习三(电)解答

练习三(电)解答

练习三（电）解答1、半径为R 的均匀带电球体的静电场中各点的电场强度的大小E 与距球心的距离r 的关系曲线为： ［ ］答：应用高斯定理很容易求得均匀带电球体的场强分布为⎪⎪⎩⎪⎪⎨⎧=,4,43020R qr r qE πεπε R r R r <≤>0 所以，应该选择答案(B)。

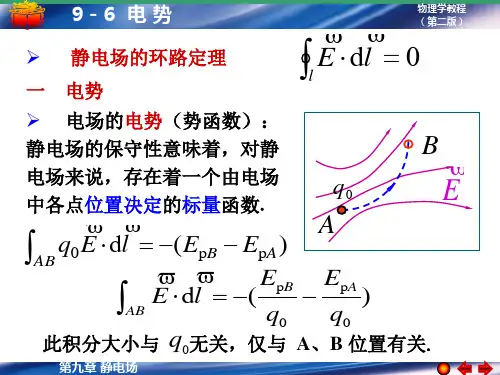
2、如图所示，两个无限长的半径分别为R 1和R 2的共轴圆柱面，均匀带电，沿轴线方向单位长度上的电量分别为λ1和λ2，则在外圆柱面外、距离轴线为r 处的P 点的电场强度大小为 (A)()()r 0212πελλ+(B)()]()[]20210122R r R r -+-πελπελ (C)()()[]20212R r -+πελλ(D)))20210122R R πελπελ+ [ ]答：根据场强叠加原理，P 点的场强应该是两个无限长带电圆柱面各自产生的场强的叠加：rr r E E E P 021020122221πελλπελπελλλ+=+=+= 所以应当选择答案(A)。

3、A 、B 为真空中两个平行的无限大的均匀带电平面，已知两平面间的电场强度大小为E 0，两平面外侧电场强度大小都为E 0/3，方向如图，则A 、B 两平面上的电荷面密度分别为=A σ ，=B σ 。

解：如图，设向右为正方向，且A 、B 两平面上的电荷面密度均大于零，则根据Er R E ∝1/r 2 (A) O Er R O E ∝1/r 2 (B) EOR E ∝1/r 2 (C)ErO RE ∝1/r 2E ∝1/r (D)λ2P场强叠加原理Ⅰ区： 0003122E B A -=--εσεσ Ⅱ区： 00022E BA -=-εσεσ联立以上二式可得⎪⎩⎪⎨⎧=-=00003432E E B Aεσεσ ［注：用Ⅱ、Ⅲ区列式联立求解亦可］4、静电场的环路定理的数学表达式为： ，该式的物理意义是： ；该定理表明，静电场是 场。

答：0=⋅⎰Ll d E，静电场的环流为零，保守。

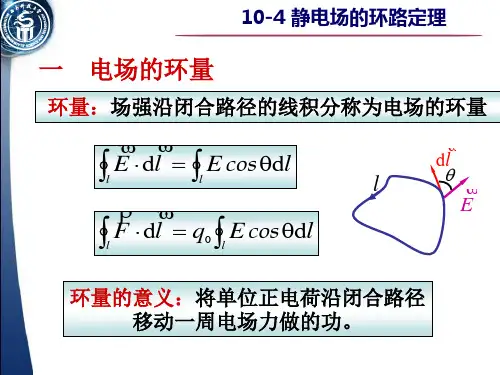
静电场环路定理

静电场环路定理
l
i
l
结论：静电场力做功，与路径无关.
10-4 静电场的环路定理
静电场的环路定理
q0 E dl q 0
q 0 ( E dl
ABC
ABC
E dl 0
l
CDA
E dl ) 0
A
ADC
E dl
B
D
C
E
结论：沿闭合路径一 周，电场力作功为零.
q1
r1

n
n
U i
i 1
i 1
Ei dl
E3

q2
r2
E2
q3
r3
A
E1
10-4 静电场的环路定理
电荷连续分布时 dq dV
dq dU 4πε0 r
1 dq UA 4πε0 r
dq
r
A
10-4 静电场的环路定理
计算电势的方法
q
令 U 0 qdr U E dl r 2
r
4πε0 r
er
r
q U 4 πε0 r
10-4 静电场的环路定理
四
电势的计算
点电荷系 E Ei
i
qi UA i 1 4 π ε0 ri
n
UA

A
E dl
A
10-4 静电场的环路定理
一
电场的环量
E dl E cos dl
l l
环量：场强沿闭合路径的线积分称为电场的环量
dl
l
F dl q0 E cos dl

环流定理

环流定理

11.6.3 电势
一、电势 电势差
1、电势
W Va = a = ∫ E • dl q0 a
b
Vb = 0
任意场点的电势等于单位正电荷在该点所具有的电势能 单位正电荷从该点到电势零点电场力所作的功 当场源电荷分布在有限区域内时通常电势零点取在无限远处！ 当场源电荷分布在有限区域内时通常电势零点取在无限远处！
∞ n 1
up = ∫ E ⋅ dl
p
有
p
∑E ⋅ dl
i
= ∑(∫ Ei ⋅ dl )
1 p
n
∞
= ∑Vip
1
n
在点电荷系的电场中， 在点电荷系的电场中，某一点的电势等于各点电荷单独 存在时，在该点产生的电势的代数和。 存在时，在该点产生的电势的代数和。这一结论称为电 n 势叠加原理。 势叠加原理。
Vp = ∫ E ⋅ dl
p
Z
+
+
• P
X
E=
x
qx 4πε0 (R + x )
2 2 3 2
3 2
Vp = ∫ E ⋅ dl = ∫
p
∞
qx
4πε0 (R2 + x2 )
⋅ dx
11-11求均匀带电球面电场中电势的分布， 11-11求均匀带电球面电场中电势的分布，已知R ，q 求均匀带电球面电场中电势的分布
电势及电势差的单位都是“伏特” 符号: 电势及电势差的单位都是“伏特”, 符号: V
a
b
.
电势差、 功、电势差、电势能之间的关系
A = q∫ E • dl = q(Va −Vb ) =W −W ab a b
a b
二、电势的计算

静电场中环路定理和环流定理

静电场中环路定理和环流定理

静电场中环路定理和环流定理
在静电场中，环路定理是基本电磁定律之一，它描述的是沿着闭合回路的路径积分
（环路积分）与围绕路径的电场强度之积的相等关系。

具体而言，环路定理可以表示为：
∮ E·dℓ = 0
其中，E表示电场强度，dℓ表示环路上的微小位移元素，∮表示对整个环路沿着闭合
路径的积分。

这个定理的物理意义是：在一个静电场中，当你绕着一个闭合回路走一圈时，得到的
电场积分总是等于零。

这个定理对于描述物体的电荷分布和电场的特性非常重要。

同时，
环路定理也可以用于确定电场的解析表达式，来计算电势差和电荷分布的影响。

与环路定理相比，环流定理是一个更为广泛和深入的物理定律，它描述了磁场产生的
物理原理。

在静电场中，环流定理指的是一个围绕电流线路的环曲面上的积分，等于线路
内的电流的总和。

数学上，环流定理可以表述为：
其中，B表示磁场强度，dS表示环曲面上的微小面积元素，μ0表示真空中的磁导率，而I则表示通过线路内的电流强度。

物理上，环流定理描述了磁场沿着封闭路径的总和，或者说，从一个特定区域流出和
流入的总量。

直观上，环流定理也可以用来计算磁场的速率和强度，以及它在不同场合下
的表现形式。

总的来说，环路定理和环流定理都是物理学家和工程师们经常使用的基本定律。

通过
这两个定理，我们可以更加深入地理解力学、电学等自然现象，从而为相关的技术和应用
开发提供更为坚实的基础。

08.3静电场的环路定理、电势

08.3静电场的环路定理、电势
E a E b
b
a
u 3
u 2 u 1
2.电势梯度 电势梯度 单位正电荷从 a到 b电场力的功 到 电场力的功
u+d +u
E•d = Ec sθ l =u−(u+d ) l o d u Ec sθ l =− u o d d
在 l E d 方向上的分量 电场强度沿某 一方向的分量 一般
u
E l
n
a
b
l 由电势定义得 u =∫ E•d =∫ P
r
∞
4 ε0r π
d = r
q 4 ε0r π
讨论 大小
q>0 u>0 r ↑ u↓ r → u 小 ∞ 最 q<0 u<0 r ↑ u↑ r → u 大 ∞ 最
为球心的同一球面上的点电势相等 对称性 以q为球心的同一球面上的点电势相等
点电荷系的电势 由电势叠加原理， 的电势为 由电势叠加原理，P的电势为
单位正电荷在该点 所具有的电势能
∞
W = ∫q E•d l a 0
a
∞
单位正电荷从该点到无穷远 电势零)电场力所作的功 点(电势零 电场力所作的功 电势零
定义电势差 a b 定义电势差 u −u 电场中任意两点 的 电势之差（电压） 电势之差（电压）
u =u −u =∫ E•d −∫ E•d =∫ E•d l l l ab a b
d q −q A =u −u =0−( ) + oc o c 4 03R 4 0R a πε πε b c q +q 0 −q = 6 0R πε R R R
② 将单位负电荷由 ∞ O电场力所作的功
A O =u −u =0 o ∞ ∞
功、电势差、电势能之间的关系 电势差、

物理-环路定理

物理-环路定理

三、电势
1、定义
说明：
U E p
“0” E dr
q
A
（1）对有限带电体，通常 选 无限 远为电势零点
U A
E dl
A
但在工程技术中，取大地、仪器外壳等为电势零点；
（2）电场的电势分布确定后，电场力做功
W势
2、电势的计算 (1) 点电荷的电势
Q
dq
e
带电体
r
A
UdUA
? dq
4 0r
dq
U A Q 4πε0r
三、电势
例2 求一均匀带电细圆环，半径为R，带正电
荷量Q。求圆环轴线上任意点P 的电势。
dU p
z
r
O
R dl
三、电势
例3 求均匀带电薄圆盘轴线上任意点P 的电
势。设圆盘半径为R，盘上电荷面密度为 σ 。
dUp
dq 4πε0(r 2
即：静电场是无 旋场。 E 0
二、静电势能
(1) 电势能是电荷与静电场
B
所构成的系统共有的。
L1
(2) 某点电势能的大小与势
能零点的选取有关。
q
A
L2
E
但任意两点间的电势能差 与势能零点选取无关。
“0”
E pA A Fe dr
1E8pA11E年pB泊 松W把eA势B 能
(3) 库用 电仑于 学力静 的F电 解与e 学 析电， 理势发论能E展。p的了关静系：
q+
A
积分至无穷远
E
r
U(r) q
4πε0r
三、电势
(2) 点电荷系的电势
U A
推广：
i
qi 4 π ε0ri

大学物理：第7章-静电场3-环路定理和电势

大学物理：第7章-静电场3-环路定理和电势

如何形象表示电势？
找到相等的电势： ( x, y, z) C(常量）
三维空间 + 限定条件 = 二维曲面 1. 定义等势面：电场中电势相等的各个点所构成的曲面。
作图规则：相邻等势面之间电势差相等
2. 等势面的性质 1) 沿等势面，电场力不做功（定义） 2) 闭合，不相交（数学上，单值，连续） 3) 等势面与电场线处处正交（直观表达）
解：(1) 选无限远处为电势零点，根据 q1
q2
电势叠加原理，O点电势为
O 1 2 3 4
O
41
4q1
4π 0
r
4.1103 V
q4
q3
(2) A q0( O ) 4.1 106 J
(3) o点电势能高，增加了4.1106 J
例4：均匀带电直线，长L，线电荷密度为 ，求直线延
长线上到其一端距离为d的一点P的电势。
解：在直线上取电荷元dl，它到P点 距离为l，在P点产生的电势为
电势叠加法
L
d
d
dq
dx
O
4π0 (d L x) 4π0 (d L x) dx
d+L-x
P
d L dx dL dy ln d L
4π0 0 (d L x) 4π0 d y 4π0 d
例5：均匀带电球层，内半径为R1，外半径为R2，体电
带电量为q。 解：场强已由高 E
斯定理求得
0
q
4π 0r
2
er
(r R) (r R)
以无限远为电势零点。
球面外：从场点积分到电势零点，各场点电场=点电荷
电场，积分结果等同点电荷。即： q
(r R)
球面外，电势和场点半径成反比

二、静电场的保守性——环路定理

二、静电场的保守性——环路定理
9
3.电势迭加原理 由场强叠加原理和电势的定义，可得电势叠加原理。 一个电荷系的电场中,任一点的电势等于每一个 表述： 带电体单独存在时在该点所产生电势的代数和。 表达式：U ( p)
p


p
E dl p ( E1 E2 ) dl
U ( p)
U2
14

r
1 E2 dl r E2dr r
rR
q q dr 2 4 0r 4 0 r
I区：球面内
r R, E1 0
1
U1
q 4 0 R
q q II区：球面外 r R, E2 U2 2 4 0 r 4 0 r
dl
dAMN
E dl Edl cos 0 E dl
E
M
19
3.由于规定了两个相邻等势面的电势差相等，所以等 势面较密集的地方，场强较大。等势面较稀疏的地方 ，场强较小。
4.电力线的方向指向电势降低的方向。等势面 证明：假设电荷q0由2移到1，
因沿电力线方向移动正电荷场力做正 功，电势能减少。
dA q0
1
从 r到r
dr ,电场做的功：
b rb
q0 ra
r dr
dl r
a
cdr F
E

4 0 r
2
dr
dA q0
q 4 0 r
2
dr
rb
b
r dr
在 q 的电场中将检验电荷 q0 从 a 点移动到 b 点，电场 力作功为：
4 q q UO i 1 4 0 ri 4 0 r 0 r

第10章 静电学 - 3 - 静电场环路定理

第10章 静电学 - 3 - 静电场环路定理

由此可见, 在点电荷q的电场中, 电场力的功只与路径的起 点和终点位置有关, 而与路径形状无关。 此结论可通过场强叠加原理推广到任意点电荷系(包括带电 体)的电场。
2
即：电场力做功只与路径的起点和终点位置有关, 而与所经
过的路径无关——电场力是保守力。
A F dl q0 E dl 0 E dl 0
R2 ln 1 R1
dV R2 E0 ln E0 0 令 dR1 R1
A
R2 e R1
B
R1
Vmax
R2 E0 =33kV e
R2
22
例10-19一半径为R的均匀带电球面，带电量为q；球面外有一 均匀带电细线，电荷线密度为 , 长为l, 细线近端离球心距离 为ro, 求细线受的力和细线在球面电场中的电势能。
A
A e(U A U B ) eV
B
1 eV m 2 , =1.03107(m/s) 2
21
(4)若击穿场强Eo=200kV/cm, R1可调整, 能承受的最大电压是 多少?
E
V R2 r ln R1
显然r=R1处的场强最强，最先击穿，令E=E0
R2 得： V E0 R1 ln R1
§10. 4 1.电场的环量
静电场环路定理 l
dl
----场强沿闭合路径的线积分。即
E dl E cos dl
l l
E
设想将试验电荷q0沿闭合路径移动一周，则电场力作功
A l F dl l q0 E dl q0 l E cos dl
n
n
4 o ri
qi
式中: Ui代表第i个点电荷qi单独存在时在a点产生的电势。

3.3 静电场的环路定理 大学物理

3.3 静电场的环路定理 大学物理

R
+
o + + +
4 0 r （3）确定电势分布；
2
E

er
(r R)
主讲：张国才
U P E dl E dr + r+ r r + + 1 q q r p + + 2 dr R R 4 + + 4 o R 0 r o + + (2)当r>R时 + + + + U P E dl E dr + + "P" r
主讲：张国才
3.3 静电场的环路定理
基础物理学
4
试验电荷q0在静电场中沿任意闭合路径 L运动一周时，电场力对q0做的功W=？
L
W q0 E dl 0
E dl 0
L
主讲：张国才
3.3 静电场的环路定理 静电场的 Nhomakorabea路定理基础物理学
5
在静电场中，场强沿任意闭合路径的线积 分（称为场强的环流）恒为零。
2 2
0

主讲：张国才
q 4 0 R x
2 2
基础物理学 3.3 静电场的环路定理 二、从电荷分布求场强，从场强分布求电势。 例2 计算均匀带电球面的电场中的电势分布。球面半 径为R，总带电量为q。
13
解：
q
+
+ + + +
+ +
+
（1）取无穷远处为电势零点； + （2）由高斯定律可知电场分布为； + E 0 (r R) + + 1 q

4. 3 静电场的环路定理 电势

4. 3 静电场的环路定理 电势

r
U
(2) r>R

r
R E dl 0 dl E dl
r R
q q = ———2 dr = ——— 40R R 40r

q q U = ——— d r = ——— 40 r r 40r2 求电势方法小结
(4-46) 简便！
P P
n
取 U=0
q1 q2 q3
qn
•P
q U= ——— 40r
1 qi U =U1+ U2+Un U i i 1 4 0 ri i 1
P
n
(4-40)
电势叠加原理 ： 点电荷系所激发的电场中某点的电势，等于各
点电荷单独存在时在该点产生的电势的代数和。P129 dU 3．带电体的电场中的电势 P dq r dq 元电势 dU = ——— 40r + ++ ++ 1 dq + (4-43) = dU 总电势 U ++ + V 4 r
= 2000 V a点电势低 O
E
ra
• a(3,2) • b(1,0)
rb
x
ab rb ra
i (3i 2 j )
四、电势的计算 方法一：按电势定义 U a
dl与 E 同向或反向


a
E d l E cos d l
P128 场中任意两点a、b的 Uab在数值上等于将单位正电荷从a点 相关问题 ——静电场力作功的简单表达式 q ab
a
a
b
经任意路径移到b点时,电场力所作的功。与电势零点的选择无关
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

静电场的环路定理表达式及其物理意义
静电场的环路定理是利用有限定义的电流环路来描述静电场中电场强度的一个重要定理。

这个定理有两个版本，即古典环路定理和现代环路定理。

环路定理的实质是说明了在有限的环路中，电流的大小和方向可以由电位差来确定，这个电位差是环路中电、电阻器及其他元件所产生的。

对于古典环路定理，它定义了环路中电位差与电流之间的关系，它可以用来求解电流环路中的电流大小和方向。

现代环路定理是由普朗克提出的，主要是为了求解电流环路中的电动势，它可以表达为：在有限的电流环路中，环路中定义的每个电和电阻器之间的电势差的积分，加上环路中的电动势，等于零。

环路定理的物理意义是，在有限的电流环路中，电流的大小和方向可以由电位差来确定。

电位差是指电和电阻器之间的电势差，这个电势差是由于环路中定义的电和电阻器所产生的。

环路定理的物理意义是，在有限的电流环路中，电流的大小和方向可以由电位差来确定，而电位差是指电和电阻器之间的电势差，这个电势差是由于环路中定义的电和电阻器所产生的。

古典环路定理和现代环路定理可以用来求解电流环路中的电流大小和方向，古典环路定理定义了环路中电位差与电流之间的关系，而现代环路定理描述了在有限的电流环路中，环路中定义的每个电和电阻器之间的电势差的积分，加上环路中的电动势，等于零。

环路定理是电路理论的基础，它可以用来解决复杂的电路问题，也可以用来研究复杂的电路系统。

环路定理可以用来描述复杂的静电场，电路中的电势差和电流的关系，从而有助于理解电路的工作原理，并且可以用来求解复杂的电路问题。

环路定理可以用来描述复杂的静电场，使用它可以更好地理解电路工作原理，并且可以用来求解复杂的电路问题。