三角函数与向量的基本概念及综合应用prt

三角函数1. 终边相同的角是指与某个角α具有同终边的所有角，它们彼此相差2k π(k ∈Z)，即Z}k ,2k |{∈+=∈απβββ，根据三角函数的定义，终边相同的角的各种三角函数值都相等。

2.区间角区间角是介于两个角之间的所有角，如]65,6[}656|{πππαπαα=≤≤∈3.象限角：角的顶点与原点重合，角的始边与x 轴的非负半轴重合。

那么，角的终边（除端点外）在第几象限，我们就说这个角是第几象限角。

第一象限角：{α|k ⋅360︒<α<k ⋅360︒+90︒，（k ∈Z ）}； z}k ,22k 2k |{∈+<<ππαπα第二象限角：{α|k ⋅360︒+90︒<α<k ⋅360︒+180︒，（k ∈Z ）}； z}k ,2k 22k |{∈+<<+ππαππα第三象限角：{α|k ⋅360︒+180︒<α<k ⋅360︒+270︒，（k ∈Z ）}； z}k ,232k 2k |{∈+<<+ππαππα第四象限角：{α|k ⋅360︒+270︒<α<k ⋅360︒+360︒，（k ∈Z ）}；或{α|k ⋅360︒-90︒<α<k ⋅360︒，（k ∈Z ）}z}k ,22k 232k |{∈+<<+ππαππα或z}k ,2k 22k |{∈<<-παππα要特别注意:如果角的终边在坐标轴上,就认为这个角不属于任何一个象限,称为非象限角。

O xyO xyO xy角的概念任意角的三角函数的定义 同角三角函数的关系三角函数 弧度制弧长公式、扇形面积公式三角函数线诱导公式 和角、差角公式 二倍角公式公式的变形、逆用、“1”的替换化简、求值、证明（恒等变形）三角函数 的 图 象 定义域奇偶性 单调性 周期性最值 对称轴（正切函数除外）经过函数图象的最高（或低）点且垂直x 轴的直线，对称中心是正余弦函数图象的零点，正切函数的对称中心为(k π2，0)（k ∈Z ）.正弦函数y ＝sin x= 余弦函数y ＝cos x 正切函数y ＝tan xy ＝A sin(ωx ＋ϕ)＋b①图象可由正弦曲线经过平移、伸缩得到，但要注意先平移后伸缩与先伸缩后平移不同；②图象也可以用五点作图法；③用整体代换求单调区间（注意ω的符号）； ④最小正周期T ＝2π| ω |；⑤对称轴x ＝(2k ＋1)π－2ϕ2ω，对称中心为(k π－ϕω，b )（k ∈Z ）.值域图象对称性{α|α=k ⋅360︒, k ∈Z} {α|α=k ⋅360︒+180︒,k ∈Z} {α|α=k ⋅180︒,k ∈Z}O x yO x yO xy{α|α=k ⋅360︒+90︒,k ∈Z} {α|α=k ⋅360︒+270︒,k ∈Z} {α|α=k ⋅180︒+90︒,k ∈Z}O x yO x yO xy{α|α=k ⋅90︒, k ∈Z} {α|α=k ⋅90︒+45︒, k ∈Z} {α|α=k ⋅45︒, k ∈Z} 4．弧度制长度等于半径长的圆弧所对的圆心角叫做1弧度角，记作1rad ，或1弧度，或1(单位可以省略不写)。

向量三角函数知识点归纳向量和三角函数是高中数学中的重要内容，下面是关于这两个知识点的归纳总结。

一、向量1.向量的定义向量是有大小和方向的量，用箭头在平面或空间中表示。

向量的大小叫做模，用，a，或，a，表示；向量的方向用一个角度或另一向量表示。

2.向量的基本运算-向量的加减：向量的加减使用平行四边形法则，即将两个向量的起点相接，然后将两个向量的终点用直线连接。

- 向量的数量积：向量 a 和 b 的数量积（内积或点积）定义为abcosθ，其中θ 表示 a 和 b 之间的夹角。

-向量的数量积的性质：交换律、结合律、分配律等。

-向量的夹角：可以使用向量的点积公式计算向量之间的夹角。

-向量的投影：一个向量在另一个向量上的投影是一个标量，表示一个向量在另一个向量上的投影长度。

3.向量的应用-分解力的合力：当一个力可以分解为多个力的合力时，可以使用向量的方法表示这个过程。

-平行四边形法表示速度：当一个物体以两个向量之和的速度在平面内运动时，可以使用平行四边形法则来表示其速度。

二、三角函数1.三角函数的定义三角函数是一组用于描述角和边之间关系的函数。

常见的三角函数有正弦函数、余弦函数和正切函数。

- 正弦函数：sinθ = 对边 / 斜边- 余弦函数：cosθ = 邻边 / 斜边- 正切函数：tanθ = 对边 / 邻边2.三角函数的性质和关系-三角函数的周期性：正弦函数和余弦函数的周期都为2π，正切函数的周期为π。

-三角函数的奇偶性：正弦函数和正切函数是奇函数，余弦函数是偶函数。

-三角函数的和差化积公式：- 正弦函数的和差化积：sin(A ± B) = sinAcosB ± cosAsinB- 余弦函数的和差化积：cos(A ± B) = cosAcosB ∓ sinAsinB- 正切函数的和差化积：tan(A ± B) = (tanA ± tanB) / (1 ∓tanAtanB)-三角函数的平方和差公式：- 正弦函数的平方和差：sin²A ± sin²B = 2sinAcosA，cos²A ± cos²B = 2cosAcosB- 余弦函数的平方和差：cos²A + cos²B = 2cosAcosB，cos²A - cos²B = -2sinAsinB- 正切函数的平方和差：tan²A ± tan²B = 1 ∓ 2tanAtanB3.三角函数的应用-三角函数的性质可以用于求解各种三角形的边长和角度。

向量在三角函数中的应用一、引言向量是数学中一个重要的概念，它广泛应用于几何、物理等领域。

在三角函数中，向量同样具有重要的应用。

本文将对向量在三角函数中的应用进行详细介绍。

二、向量的基本概念1. 向量的定义向量是具有大小和方向的物理量，通常用带箭头的字母表示。

例如，$\vec{a}$表示一个向量。

2. 向量的表示方法向量可以用坐标表示，也可以用模长和方向角表示。

设$\vec{a}$是一个非零向量，则其坐标为$(x,y)$，模长为$|\vec{a}|=\sqrt{x^2+y^2}$，方向角为$\theta=\arctan\frac{y}{x}$。

3. 向量的运算向量可以进行加减乘除等运算。

其中加法和减法都是按照分量分别相加或相减；乘法有数量积和叉乘两种形式；除法则是将一个向量乘以另一个向量的倒数。

三、三角函数中的应用1. 正弦定理和余弦定理正弦定理：$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$。

余弦定理：$a^2=b^2+c^2-2bc\cos A$，$b^2=a^2+c^2-2ac\cos B$，$c^2=a^2+b^2-2ab\cos C$。

其中，$a,b,c$为三角形的边长；$A,B,C$为对应的角度；$R$为三角形外接圆半径。

这两个定理中都涉及到向量的叉乘运算。

例如，在正弦定理中，可以将$\vec{a}$、$\vec{b}$和$\vec{c}$看作三个向量，则有$\vec{a}\times\vec{b}=|\vec{a}||\vec{b}|\sin A\cdot\hat{n}$，其中$\hat{n}$为垂直于$\vec{a}$和$\vec{b}$所在平面的单位向量。

因此，正弦定理可以写成$\frac{\vec{a}}{\sin A}=\frac{\vec{b}}{\sinB}=\frac{\vec{c}}{\sin C}=2R\cdot\hat{n}$。

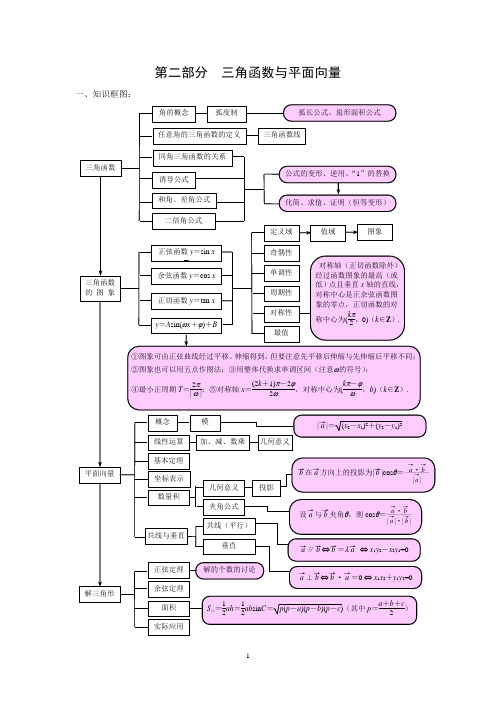
第二部分三角函数与平面向量一、知识框图：二、基础知识要点剖析：1、与角α终边相同的角的集合{}Z k k ∈+=,2|απββ; 十六条终边所对应的角能记住吗？集合⎭⎬⎫⎩⎨⎧∈±=Z k k ,3|ππγγ表示怎样的终边的角？区分锐角、小于090的角、090~0的角、钝角、对顶角、区域角、区间角、象限角等。

2、弧长公式：||l R α=，扇形面积公式：211||22S lR R α==，1弧度(1rad)57.3≈3、三角函数的定义（r y x ,,三个量的比值）：r y =αsin ，r x =αcos ，)0(tan ≠=x xyα。

㈠任意角的三角函数值在各个象限的符号知道吗？特别是特殊角的三角函数值记准了吗？㈡正弦线、余弦线、正切线会画吗？利用它们求三角不等式很简便哦！有印象吗？ ㈢常见三角不等式：（1）若(0,)2x π∈，则sin tan x x x <<，(2) 若(0,)2x π∈，则1sin cos x x <+≤(3) 2cos sin 1,≤+≤∈x x R x 则若.4、同角三角函数的基本关系式 ：①22sin cos 1θθ+=，②tan θ=θθcos sin ，注意公式变形： 2)cos (sin cos sin 21)1(θθθθ±=±.)42sin(22cos 2sin sin 1πθθθθ±=±=± 2sin 2cos 1θθ=-， 2cos 2cos 1θθ=+（2）如t =±ααcos sin ,d =ααcos sin ,αtan 之间互相转换懂吗？知一求二：(3)若t =+ααcos sin ，则21c o s s i n 2-=t αα；12sin 2-=t α；22cos sin t -±=-αα（4）若t =ααcos sin ，则t 21cos sin +±=+αα；t 21cos sin -±=-αα.5、诱导公式分两大类：为偶数与奇数）k k(2απ±。

三角函数与向量的综合应用在数学领域中，三角函数与向量是两个重要的概念。

它们在各自的领域中拥有广泛的应用，并且可以相互结合，产生更强大的数学工具。

本文将讨论三角函数与向量的综合应用，并探究它们在实际问题中的应用。

一、三角函数与向量的基础知识1. 三角函数三角函数是描述角度关系的函数，其中最常用的三角函数包括正弦函数、余弦函数和正切函数。

它们可以通过三角比值或单位圆上的点坐标来定义。

三角函数在几何、物理和工程等领域中广泛应用，用于求解角度、距离、速度等问题。

2. 向量向量是具有大小和方向的量，可用于表示物体的位移、力和速度等。

向量通常用有序数组表示，其中包括了向量的分量或坐标。

向量在几何、物理、计算机图形学等领域中有重要的应用，用于描述与计算空间中的各种问题。

二、三角函数与向量的结合运用1. 正弦函数与向量的应用正弦函数可以用于求解两个向量之间的夹角。

对于给定的两个向量A和B，它们的夹角θ可以通过以下公式求得：θ = arcsin(|A × B| / (|A| |B|))其中，|A|和|B|分别表示向量A和向量B的模长，A × B表示两个向量的叉乘，|A × B|表示叉乘结果的模长。

这个夹角的计算提供了求解向量运动方向、力的方向以及判断向量共线性等问题的重要依据。

2. 余弦函数与向量的应用余弦函数可以用于求解两个向量之间的夹角以及向量在特定方向上的投影。

对于给定的两个向量A和B，它们的夹角θ可以通过以下公式求得：θ = arccos(A · B / (|A| |B|))其中，|A|和|B|分别表示向量A和向量B的模长，A · B表示两个向量的点乘。

此外，余弦函数还可以用于求解向量在特定方向上的投影长度，从而实现对向量分解和向量运动路径的分析。

3. 正切函数与向量的应用正切函数可以用于求解向量的斜率。

对于给定的向量A，它的斜率可以通过以下公式求得：m = tan(θ) = (A.y / A.x)其中，A.x和A.y分别表示向量A在x轴和y轴上的分量。

高中数学的三角函数与向量总结在高中数学学习中，三角函数与向量是两个重要的主题。

三角函数研究角的度量与各种三角关系，而向量则研究物体的位移与力的方向。

本文将总结高中数学中三角函数与向量的相关知识点，帮助读者更好地理解与应用这些概念。

一、三角函数1. 正弦函数正弦函数是三角函数中最基本的函数之一，用于研究角的正弦关系。

表示为sin(x)，其中x为角的度数。

正弦函数的定义域为全体实数，值域为[-1, 1]。

在直角三角形中，正弦函数可表示为对边与斜边之比。

2. 余弦函数余弦函数是三角函数中另一个基本的函数，用于研究角的余弦关系。

表示为cos(x)，其中x为角的度数。

余弦函数的定义域为全体实数，值域为[-1, 1]。

在直角三角形中，余弦函数可表示为邻边与斜边之比。

3. 正切函数正切函数是三角函数中较为特殊的函数，用于研究角的切线关系。

表示为tan(x)，其中x为角的度数。

正切函数的定义域为全体实数，但在某些角度上不存在值，需要注意避免这些角度。

在直角三角形中，正切函数可表示为对边与邻边之比。

4. 三角函数的基本关系三角函数之间存在一些基本的关系。

例如，sin(x)与cos(x)互为倒数，即sin(x) = 1/cos(x)。

另外，tan(x) = sin(x)/cos(x)。

通过利用这些基本关系，可以简化求解三角函数的过程。

二、向量1. 向量的定义向量是有大小和方向的量，通常用箭头表示。

在平面几何中，向量可以表示为有序数对 (a, b)，其中 a 为横坐标的变化量，b 为纵坐标的变化量。

向量也可以用矩阵表示。

2. 向量的运算向量有多种运算，包括向量的加法、减法、数量乘法和点乘法。

其中，向量的加法和减法符合平行四边形法则，数量乘法可以改变向量的大小，而点乘法可以得到两个向量的数量积，用于求夹角等相关性质。

3. 向量的模和方向角向量的模表示向量的大小，可通过勾股定理计算得出。

向量的方向角表示向量与平行于坐标轴的正方向之间的夹角。