燕山大学理论力学内部资料——刚体的平面运动
- 格式:pdf
- 大小:332.09 KB
- 文档页数:9



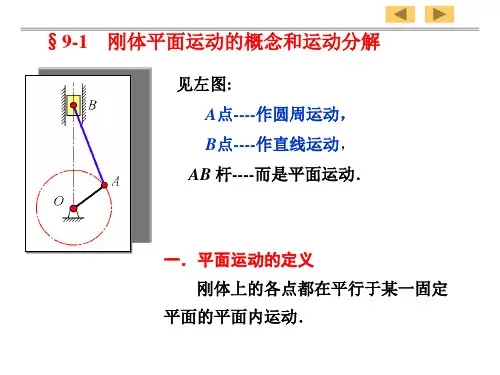

基础部分——运动学第7 章刚体平面运动连杆作什么运动呢?行星齿轮机构行星轮作什么运动?第7章刚体平面运动运动过程中,刚体上任一点到某一固定平面的距离保持不变刚体上任一点都在与某一固定平面平行的平面内运动沿直线轨道滚动的车轮机械臂小臂的运动平面运动的刚体在自身平面内运动的平面图形SxyOxyOASIIxyOA SII平面图形上任一线段的位置位置x Ay AϕB )(1t f x A =)(2t f y A =)(3t f =ϕ平面运动平移+ 转动xyOASIIxAyAϕB基点⇒O ′O O ′O O ′O′三种运动?平面运动基点平移基点转动注意:平移动系不一定固结与某一实际刚不一定固结与某一实际刚体。
O ′xyO平移动系O'x'y'x ′y ′O ′基点推广结论:刚体的平面运动可以分解为随基点的平移和绕基点的转动问题一:x yOA SIIx Ay AϕB问题二:随基点的平移与基点的选择有无关系绕基点的转动与基点的选择有无关系结论:同一瞬时平面图形绕任一基点转动的ω、α都相同。
动点re a 点的速度合成定理SAv ωABB v A v ?=B v x ′y ′基点BA v 三种运动?大小? 方向?BAA B v v v +=AωA Av BAv Bv平面图形上任一点的速度等于基点的速度与该点随图形绕基点转动速度的矢量和。
SAv ωABAv BAv Bv BAA B v v v +=试一试:基点法作平面运动。
[例7-1] 曲柄—滑块机构解:转动。
r 3ABOωϕAv Bv BAv 基点大小方向?AvBA3ABOωϕAv B v BAv Av ABω转向?= v 滑块Bϕ大小方向A 32SAv ωAB Av BAv Bv 平面图形上任意两点的速度在该两点连线上的投影(大小和正负号)相等。
速度投影定理[][]ABA AB B v v =[]ABBA vr 3再分析例7-1ABOωϕAv Bv Bv解:请比较两种方法A 32如何解释这种现象?观察到了什么现象?[先看一照片]若选取速度为零的点作为基点,则求解速度问题•基点法•速度投影法优点:缺点:优点:缺点:SAv ωAv BAv Bv AA 为基点B有没有更好的方法呢?Aω0≠ω唯一存在AL ′证明:MAA M v v v +=SA v v MAv LMPωAv PA =∴0=⋅−=ωPA v v A P ∵该瞬时瞬时速度中心速度瞬心唯一性:瞬时性:不共线,故速度均不为零。


中科院研究生院硕士研究生入学考试《理论力学》考试大纲本理论力学考试大纲适用于中国科学院研究生院力学专业的硕士研究生入学考试。
理论力学是力学各专业的一门重要基础理论课,本科目的考试内容主要包括静力学、运动学和动力学三大部分。
要求考生对其中的基本概念有很深入的理解,系统掌握理论力学中基本定理和分析方法,具有综合运用所学知识分析问题和解决问题的能力。
一、考试内容:(一)静力学基本概念与物体受力分析物体受力分析,常见约束与约束反力,平衡力系作用下的物体受力。
几个静力学公理。
(二)力系简化和力系平衡汇交力系的几何法和解析法;力偶系的概念。
平面和空间力系和力偶系的平衡方程,考虑摩擦的平衡问题。
(三)点的运动学和点的合成运动质点的运动及其数学描述,点的绝对运动,牵连运动和相对运动的概念,点的速度和加速度的合成。
(四)刚体的简单运动和刚体平面运动刚体的平动和定轴转动,平面运动刚体上任意点的速度和加速度表示。
(五)质点动力学的基本方程牛顿三个定律,质点运动微分方程和质点动力学问题的求解,质心和转动惯量的计算。
(六)动量定理动量和冲量的概念,动量定理和动量守恒。
质心运动定理和质心运动守恒定律。
(七)动量矩方程动量矩和动量矩定理,刚体绕定轴转动的微分方程。
质点系相对于质心的动量矩定理。
(八)动能定理各种作用力的功;质点和刚体的动能;质点和质点系的动能定理。
功率和功率方程,势力场,势能和机械能守恒定律。
(九)达朗贝尔原理质点和质点系的达朗贝尔原理。
(十)虚位移原理约束,广义坐标,自由度和理想约束的概念,虚位移原理。
(十一)碰撞碰撞的分类与特点,碰撞过程的基本定理,恢复系数,撞击中心。
(十二)分析力学基础动力学普遍方程,拉格朗日方程,拉格朗日方程的初积分。
(十三)机械振动基础单自由度系统的自由振动和受迫振动,计算固有频率的能量法,隔震原理。
二、考试要求:(一)静力学基本概念与物体受力分析(1) 熟练掌握刚体和力的基本概念、力的三要素。




燕山大学理论力学燕山大学理论力学((力学类力学类))考研专业课复习大纲考研专业课复习大纲 考研加油站收集整理 一、静力学:1、静力学公理与物体的受力分析:静力学公理、约束与约束反力、受理分析与受力图。
2、平面汇交力系:平面汇交力系合成与平衡的几何法、解析法、力的分解与力在轴上的投影。
3、力矩、平面力偶理论:力对点之矩、合力矩定理、平面力偶理论、平面力偶系的合成和平衡方程。
4平面任意力系:力的平移定理、平面任意力系向一点的简化、平面任意力系的平衡方程、静定与静不定的概念、物体系统的平衡、平面简单桁架的内力计算。
5摩擦及其平衡问题:滑动摩擦和滚动摩阻、摩擦角和自锁现象、考虑摩擦时平衡问题的解法。
6空间力系:空间汇交力系、空间力偶理论、力对轴之矩与力对点之矩、空间任意力系的简化、空间任意力系的平衡方程。
二、运动学:1、点的运动学:确定点运动位置的基本方法、点的速度与加速度的矢量表示、点的速度与加速度的直角坐标表示、点的速度与加速度的弧坐标表示。
2、刚体的简单运动:刚体的平动、刚体绕定轴的转动、转动刚体上各点的速度与加速度、定轴轮系的传动问题。
3、点的合成运动:点的合成运动的几个基本概念、点的速度合成定理、牵连运动为平动时的加速度合成定理、牵连运动为转动时的加速度合成定理。
4、刚体的平面运动:刚体的平面运动的分解、求平面图形上各点速度的基点法和投影法、求平面图形上各点速度的瞬心法、求平面图形上各点加速度的基点法。
三、动力学:1、质点动力学的基本方程:动力学的基本定律、质点的运动微分方程、质点动力学的两类基本问题。
2、动量定理:质点的动量定理、质点系的动量定理、质心运动定理。
3、动量矩定理:质点的动量矩定理、质点系的动量矩定理、刚体绕定轴的转动微分方程、刚体对轴的转动惯量、刚体的平面运动微分方程。
4、动能定理:力的功、质点的动能定理、质点系的动能定理、功率、功率方程、机械效率、势力场、势能、机械能守恒定律、基本定理的综合应用。
9-1、如图所示,在筛动机构中,筛子的摆动是由曲柄连杆机构所带动的。
已知曲柄的转速OA r/min 40=oA n ,m 3.0=OA 。
当筛子运动到与点O 在同一水平线上时,。
求此瞬时筛子的速度。
BC 090=∠BAO
BC
9-2、图示两齿条以速度1v 和2v 同方向运动()21v v >。
在两齿条间夹一齿轮,其半径为r ,求齿轮的角速度及其中心的速度。
O
9-3、四连杆机构中,连杆上固连一块三角板,如图所示。
机构由曲柄带动。
已知:曲柄的角速度AB ABD A O 1rad/s 21=A O ω;曲柄m 1.01=A O ,水平距离,m 05.021=O O m 05.0=AD ;当铅直时,平行于,且与在同一直线上;角。
求三角板的角速度和点的速度。
A O 1A
B 21O O AD 1AO 030=ϕABD
D
9-4、图示配汽机构中,曲柄OA 的角速度rad/s 20=ω为常量。
已知,m 4.0=OA m 372.0==BC AC 。
求当曲柄OA 在两铅直线位置和水平位置时,配汽机构中气阀推杆DE 的速度。
9-5、半径为R的轮子沿水平面滚动而不滑动,如图所示。
在轮上有圆柱部分,其半径为r。
将线绕于圆柱上,线的B端以速度v和加速度a沿水平方向运动。
求轮的轴心的速度和加速度。
O
9-6、曲柄OA 以恒定的角速度rad/s 2=ω绕O 转动,并借助连杆驱动半径为AB r 的轮子在半径为R 的圆弧槽中作无滑动的滚动。
设OA ==AB R =m 12=r ,求图示瞬时点B 和点的速度和加速度。
C
9-7、在图示曲柄连杆机构中,曲柄OA 绕轴转动,其角速度为O 0ω,角加速度为0α。
在某瞬时曲柄与水平线间成角,而连杆与曲柄垂直。
滑块060AB OA B 在圆形槽内滑动,此时半径与连杆间成角。
如,B O 1AB 030r OA =r AB 32=,r B O 21=,求在该瞬时,滑块B 的切向和法向加速度。
9-8、图示平面机构中,杆以不变的速度AB v 沿水平方向运动,套筒B 与杆的端点铰接,并套在绕O 轴转动的杆OC 上,可沿该杆滑动。
已知和两平行线间的垂直距离为,求在图示位置(,,)时杆的角速度和角加速度,滑块AB AB OE b 060=γ030=βBD OD =OC E
的速度和加速度。
*9-9、已知图示机构中滑块的速度为常值,A m/s 2.0=A v ,。
求当,时杆的速度和加速度。
m 4.0=AB CB AC =030=θ
CD。