叠合梁正应力计算表格

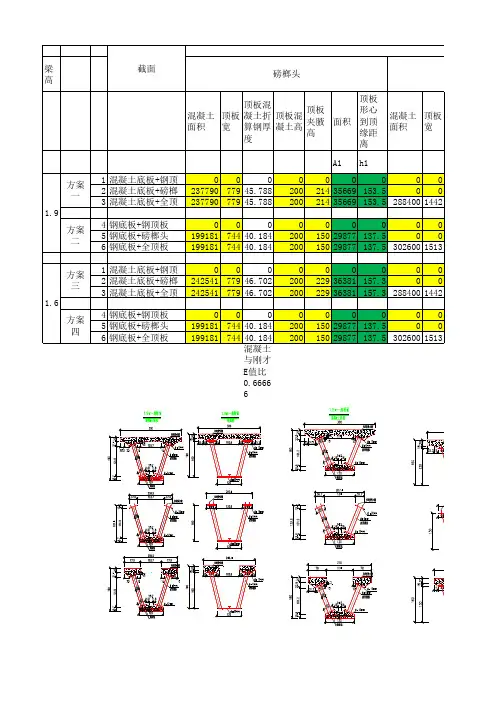
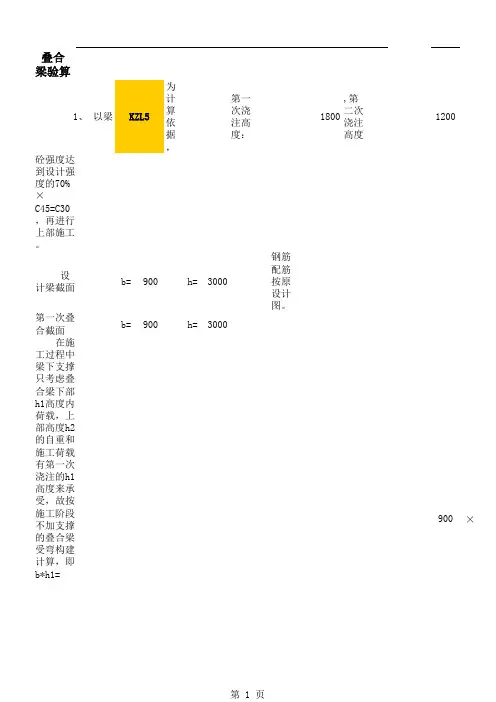
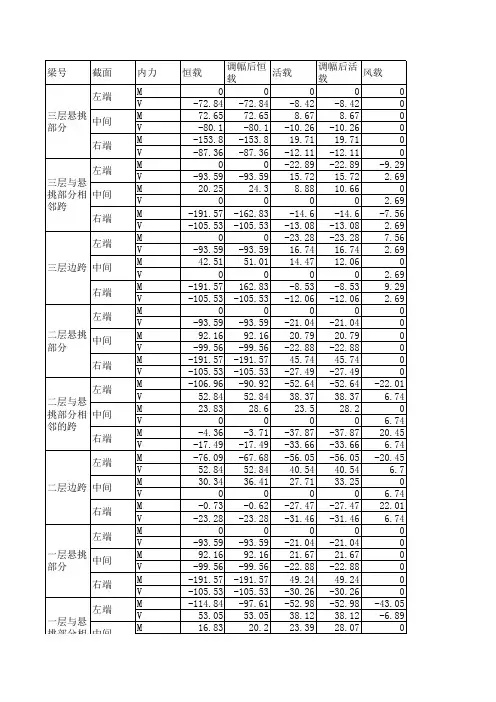
计算书工程名称：计算内容：目录1.工程概况 (1)2.结构描述 (1)3.计算分析依据及技术标准 (1)3.1计算分析依据 (1)3.2技术标准 (1)4.计算方法和内容 (1)4.1计算方法 (1)4.2计算分析内容 (1)5.计算模型及参数 (2)5.1计算模型 (2)5.2计算参数 (2)6.计算工况及荷载 (3)6.1恒载 (3)6.2活载及其它荷载 (3)7.作用组合 (3)8.施工阶段描述 (4)9.主要计算结果 (4)10.剪力钉验算 (7)11.高强螺栓数量计算 (8)12.钢梁腹板抗剪验算 (9)13.挠度验算 (9)1. 工程概况2. 结构描述3. 计算分析依据及技术标准3.1 计算分析依据1）《公路桥涵设计通用规范》（JTG D60-2004）；2）《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG D62－2004）；3）《公路桥涵地基与基础设计规范》（JTG D63－2007）；4）《钢结构设计规范》（GB 50017-2003）；5）《钢-混凝土组合桥梁设计规范》（GB 50917-2013）；6）《公路钢结构桥梁设计规范》（JTG D64-2015）。

3.2 技术标准1）设计荷载：公路-Ⅰ级；2）桥梁设计安全等级：一级；结构重要性系数：1.1。

4. 计算方法和内容4.1 计算方法4.2 计算分析内容计算支反力；验算结构正应力（拉应力、压应力）；验算结构变形；验算剪力钉的抗剪强度；验算钢梁拼接缝；验算钢梁腹板抗剪强度。

5. 计算模型及参数5.1 计算模型5.2 计算参数(1)混凝土混凝土材料性能表(2)钢材(3)预应力钢束采用φs15.2。

6. 计算工况及荷载6.1 恒载1）一期恒载:(1)混凝土容重：26kN/m³；钢材容重：78.5kN/m³(2)横隔板及加劲肋：钢梁横隔板、腹板竖向加劲肋及剪力钉等的重量以1.3倍主梁重量计。

2）二期恒载:(1)混凝土桥面铺装(2)防撞护栏：每侧取10kN/m；6.2 活载及其它荷载1）汽车及人群的横向分布系数：2）温度梯度15规范：箱梁日照温差依据《公路桥涵设计通用规范》（JTG D60—2015）取值。

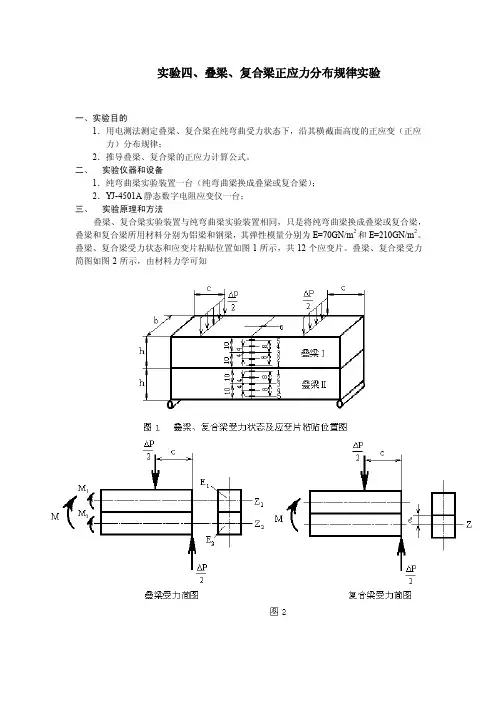
实验四、叠梁、复合梁正应力分布规律实验一、实验目的1．用电测法测定叠梁、复合梁在纯弯曲受力状态下，沿其横截面高度的正应变（正应力）分布规律；2．推导叠梁、复合梁的正应力计算公式。

二、实验仪器和设备1．纯弯曲梁实验装置一台（纯弯曲梁换成叠梁或复合梁）；2．YJ-4501A静态数字电阻应变仪一台；三、实验原理和方法叠梁、复合梁实验装置与纯弯曲梁实验装置相同，只是将纯弯曲梁换成叠梁或复合梁，叠梁和复合梁所用材料分别为铝梁和钢梁，其弹性模量分别为E=70GN/m2和E=210GN/m2。

叠梁、复合梁受力状态和应变片粘贴位置如图1所示，共12个应变片。

叠梁、复合梁受力简图如图2所示，由材料力学可知叠梁横截面弯矩：M=M 1+M 222112221111Z Z Z Z I E I E MI E MI E M+===ρI Z1为叠梁1截面对Z 1轴的惯性距；I Z2为叠梁2截面对Z 2轴的惯性距。

因此，可得到叠梁Ⅰ和叠梁Ⅱ正应力计算公式分别为2211111111Z Z I E I E Y M E Y E +==ρσ2211222222Z Z I E I E Y M E Y E +==ρσ式中Y 1——叠梁Ⅰ上测点距Z 1轴的距离；Y 2——叠梁Ⅱ上测点距Z 2轴的距离。

复合梁 设： E 2 / E 1 = n22111Z Z I E I E M+=ρI Z1为梁1截面对中性Z 轴的惯性距； I Z2为梁2截面对中性Z 轴的惯性距。

中性轴位置的偏移量为： )1(2)1(+-=n n h e因此，可得到复合梁Ⅰ和复合梁Ⅱ正应力计算公式分别为2211111Z Z I E I E MY E Y E +==ρσ2211222Z Z I E I E MY E YE +==ρσ在叠梁或复合梁的纯弯曲段内，沿叠梁或复合梁的横截面高度已粘贴一组应变片，见图1。

当梁受载后，可由应变仪测得每片应变片的应变，即得到实测的沿叠梁或复合梁横截面高度的应变分布规律，由单向应力状态的虎克定律公式εσE =，可求出应力实验值。

一.1b=100t=10h=230s=6B=200T=104380mm2152mm98mm4.6E+07mm 4302773mm 3469607mm 32混凝土等级C208.08板厚h d 100梁跨度6000梁左相邻净距1800梁右相邻净距1800板托顶宽b 0300板托高度h t150b 1 =600b 2 =6001500mm150000mm 222944.4mm 2402mm混凝土板顶面至组合截面中和轴的距离 x= [b e *h d 2/(2*αE )+A*y]/A 0 =117mm 混凝土截面惯性矩 I c = b e *h d 3/12=1.3E+08mm4换算成钢截面的组合截面惯性矩 I 0 = I c /αE + A c *(x-0.5h d )2/αE + I + A(y-x)2 =5E+08mm 43.5E+07mm42.4E+08mm 43763855mm 41307031mm4313662.2mm 2混凝土板顶面至组合截面中和轴的距离x c = [b e *h d 2/(4*αE )+A*y]/A 0c=162mm 4.2E+08mm 44.2E+07mm 41.1E+08mm 44800913mm 41249942mm 4二施工阶段的验算1弯矩和剪力钢梁自重：0.41kN/m 板自重： 6.00kN/m 2000mm)板托重：0.90kN/m 6.09kN/m 自重标准值 g 1：7.31kN/m施工荷载： 2.80kN/m 施工阶段弯矩设计值M 45.51kN.m (梁跨度：6000mm)施工阶段剪力设计值V 30.34kN2钢梁抗弯强度设计143.14N/mm 2<215N/mm 2PASS!92.29N/mm2<215N/mm2PASS!3钢梁剪应力计算面积矩 S=207492mm 322.80N/mm 2<125N/mm 2PASS!4挠度计算考虑混凝土徐变的组合截面特征计算换算成钢截面的组合截面面积 A 0c = A c / 2αE + A =换算成钢截面的组合截面惯性矩 I 0c = I c /(2*αE ) + A c *(x c -0.5h d )2/(2*αE) + I + A(y-x c )2 =(平台梁间距：钢梁剪应力τ1max = v 1*s 1/I*t w =混凝土板截面面积A c = b e * h d =换算成钢截面的组合截面面积A 0=A c /αE +A =对混凝土板底面的组合截面弹性抵抗矩 w 0c b=αE *I 0 / (x - h d ) =对钢梁上翼缘的组合截面弹性抵抗矩 w 0t = I 0 / (d-x) =对混凝土板顶面的组合截面弹性抵抗矩 w 0c tc = 2αE *I 0c / x c =对钢梁下翼缘的组合截面弹性抵抗矩 w 0b = I 0 / (H-x) =组合梁计算截面特征计算钢梁面积 A ＝b*t + h*s +B*T =钢梁中和轴至钢梁顶面的距离为 y t = [0.5b*t 2 + h*s*(0.5h + t) + B*T*(t+h+0.5T)] / A =钢梁截面特征计算：钢梁中和轴至钢梁顶面的距离为 y b = h + t + T - y t =钢梁截面惯性矩 I= (b*t 3 + s*h 3 + B*T 3) / 12 + b*t*(yt-0.5t)2 + s*h*(y t -0.5h-t)2 + B*T*(0.5T+h+t-y t )2 =钢梁上翼缘的弹性抵抗矩 W 1 = I / y t =混凝土板顶面至钢梁截面中和轴的距离 y = h d + h t +y t =对混凝土板顶面的组合截面弹性抵抗矩 w 0c t = αE *I 0 / x=混凝土板计算宽度b e =钢梁上翼缘的弹性抵抗矩 W 2 = I / y b =组合截面特征计算：钢与混凝土弹性模量比αE =自重标准值 g 1k ：对混凝土板底面的组合截面弹性抵抗矩 w 0c bc =2αE *I 0c / (x c - h d ) =对钢梁上翼缘的组合截面弹性抵抗矩 w 0tc= I 0c/ (d-x c) =对钢梁下翼缘的组合截面弹性抵抗矩 w 0bc = I 0c / (H-x c ) =钢梁上翼缘应力 M / r x *W 1 =钢梁下翼缘应力 M / r x *W 2 =△=5*g*l 4/(384*E*I)=10.8mm < L/400 =15mm PASS!三使用阶段的验算1弯矩及剪力找平层重： 1.9kN/m 活荷载：15.6kN/m （活荷载：6kn/m 2)78.84kN.m 52.56kN22.1-2.28N/mm 2<10N/mm 2PASS!-0.33N/mm 2<10N/mm 2PASS!-87.74N/mm 2<215N/mm2PASS!130.39N/mm2<215N/mm 2PASS!2.2-2.24N/mm 2<10N/mm 2PASS!-0.37N/mm2<10N/mm2PASS!-88.23N/mm 2<215N/mm 2PASS!130.69N/mm 2<215N/mm 2PASS!2.3(略）2.4(略)3钢梁的剪应力147000mm 31105812mm 319.35N/mm 2<125N/mm 2PASS!4组合梁的挠度3.46mm < L/400 =15mm PASS!τ＝V 1S 1/It w +V 2S o /I o T w =两个受力阶段的荷载对组合梁的钢梁产生的剪应力△＝5q k l 4/384EI o +5g k l 4/384EI o c =组合梁中由于混凝土收缩引起的内力钢梁腹板顶面处对钢梁中和轴的面积矩S 1=钢梁腹板顶面以外的砼及钢梁上翼缘对组合截面中和轴的面积矩S o =使用阶段弯矩设计值M 使用阶段剪力设计值V 组合梁的抗弯强度在垂直荷载作用下的正应力考虑混凝土徐变在垂直荷载作用下的正应力混凝土板顶面应力:σ0c tc =-(M 2g /W 0c tc +M 2q /W 0c t )=混凝土板顶面应力σ0c t =-M/W 0c t =混凝土板底面应力σ0c b =-M/W 0c b =钢梁上翼缘应力σ0t = -M 1/W 1+M 2/W 0t =钢梁下翼缘应力σ0b = -M 1/W 2+M 2/W 0b =σ0bc = -M 1/W 2+(M 2g /W 0bc +M 2q /W 0b )=钢梁下翼缘应力温度差产生的应力σ0c bc =-(M 2g /W 0c bc +M 2q /W 0c b )=混凝土板底面应力:钢梁上翼缘应力σ0tc = -M 1/W 1+(M 2g /W 0tc +M 2q /W 0t )=。

excel计算大全-钢结构计算表格-组合梁一.1b=180t=6h=336s=6B=180T=84536mm 2187mm163mm9.2E+07mm 4493514.82mm 3566179.58mm 32混凝土等级C257.36板厚h d 100梁跨度6000梁左相邻净距1820梁右相邻净距1820板托顶宽b 0180板托高度h t 0b 1 =600b 2 =6001380mm138000mm 223286mm 2287mm混凝土板顶面至组合截面中和轴的距离x= [b e *h d 2/(2*αE )+A*y]/A 0 =96mm混凝土截面惯性矩 I c = b e *h d 3/12= 1.2E+08mm4换算成钢截面的组合截面惯性矩I 0 = I c /αE + A c *(x-0.5hd )2/αE + I + A(y-x)2 = 3.1E+08mm 42.4E+07mm 4-5.76E+08mm 47.8E+07mm 4884365mm 4313911mm 2混凝土板顶面至组合截面中和轴的距离x c = [b e *h d 2/(4*αE )+A*y]/A 0c =127mm271805747mm 431503784mm 4148184467mm 4-1E+07mm 4841504mm 4二施工阶段的验算1弯矩和剪力钢梁自重：0.43kN/m板自重： 6.00kN/m 2000mm)板托重：0.00kN/m5.36kN/m 自重标准值 g 1：6.43kN/m施工荷载： 2.80kN/m 考虑混凝土徐变的组合截面特征计算换算成钢截面的组合截面面积A 0c = A c / 2αE + A =换算成钢截面的组合截面惯性矩I 0c = I c /(2*αE ) + A c *(x c -0.5h d )2/(2*αE) + I + A(y-x c )2 =(平台梁间距：混凝土板截面面积A c = b e * h d =换算成钢截面的组合截面面积A 0=A c /αE +A =对混凝土板底面的组合截面弹性抵抗矩w 0c b =αE *I 0 / (x - h d ) =对钢梁上翼缘的组合截面弹性抵抗矩 w 0t = I 0 / (d-x) =对混凝土板顶面的组合截面弹性抵抗矩w 0c tc = 2αE *I 0c / x c =对钢梁下翼缘的组合截面弹性抵抗矩 w 0b = I 0 / (H-x) =楼面次梁组合梁计算截面特征计算钢梁面积 A ＝b*t + h*s +B*T =钢梁中和轴至钢梁顶面的距离为y t = [0.5b*t 2 + h*s*(0.5h + t) + B*T*(t+h+0.5T)] / A =钢梁截面特征计算：钢梁中和轴至钢梁底面的距离为 y b = h + t + T - y t =钢梁截面惯性矩 I= (b*t 3 + s*h 3 + B*T 3) / 12 + b*t*(yt-0.5t)2 + s*h*(y t -0.5h-t)2 + B*T*(0.5T+h+t-y t )2 =钢梁上翼缘的弹性抵抗矩 W 1 = I / y t =混凝土板顶面至钢梁截面中和轴的距离 y = h d + h t +y t =对混凝土板顶面的组合截面弹性抵抗矩w 0c t = αE *I 0 / x=混凝土板计算宽度b e =钢梁上翼缘的弹性抵抗矩 W 2 = I / y b =组合截面特征计算：钢与混凝土弹性模量比αE =自重标准值g 1k ：对混凝土板底面的组合截面弹性抵抗矩w 0c bc =2αE *I 0c / (x c - h d ) =对钢梁上翼缘的组合截面弹性抵抗矩 w 0tc = I 0c / (d-x c ) =对钢梁下翼缘的组合截面弹性抵抗矩 w 0bc = I 0c / (H-x c) =施工阶段弯矩设计值M 41.52kN.m (梁跨度：6000mm)施工阶段剪力设计值V 27.68kN2钢梁抗弯强度设计80.13N/mm 2<215N/mm 2PASS!69.85N/mm 2<215N/mm 2PASS!3钢梁剪应力计算面积矩 S=297003mm 314.85N/mm 2<125N/mm 2PASS!4挠度计算△=5*g*l 4/(384*E*I)= 4.8mm < L/250 =24mm PASS!三使用阶段的验算1弯矩及剪力找平层重： 2.4kN/m活荷载：20.8kN/m （活荷载：8kn/m 2)104.40kN.m69.60kN22.1-4.35N/mm 2<12.5N/mm 2PASS!0.18N/mm 2<12.5N/mm 2PASS!-57.27N/mm 2<215N/mm 2PASS!169.14N/mm 2<215N/mm 2PASS!2.2-4.24N/mm 2<12.5N/mm 2PASS!0.09N/mm 2<12.5N/mm 2PASS!-58.48N/mm 2<215N/mm 2PASS!169.76N/mm 2<215N/mm 2PASS!2.3(略）2.4(略)3钢梁的剪应力198720mm 3854940mm 331.68N/mm 2<125N/mm 2PASS!4组合梁的挠度6.28mm < L/250 =24mmPASS!四。

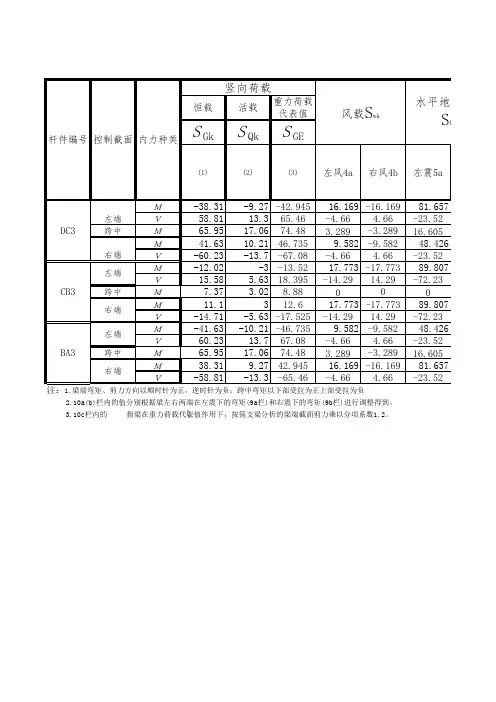
一.1b=100t=10h=230s=6B=200T=104380mm 2152mm 98mm4.6E+07mm 4302773mm 3469607mm 32混凝土等级C208.08板厚h d 100梁跨度6000梁左相邻净距1800梁右相邻净距1800板托顶宽b 0300板托高度h t150b 1 =600b 2 =6001500mm150000mm 222944.4mm 2402mm混凝土板顶面至组合截面中和轴的距离 x= [b e *h d 2/(2*αE )+A*y]/A 0 =117mm混凝土截面惯性矩 I c = b e *h d 3/12=1.3E+08mm 4换算成钢截面的组合截面惯性矩 I 0 = I c /αE + A c *(x-0.5h d )2/αE + I + A(y-x)2 =5E+08mm 43.5E+07mm 42.4E+08mm 43763855mm 41307031mm 4313662.2mm 2混凝土板顶面至组合截面中和轴的距离x c = [b e *h d 2/(4*αE )+A*y]/A 0c =162mm4.2E+08mm 44.2E+07mm 41.1E+08mm 44800913mm 41249942mm 4二施工阶段的验算1弯矩和剪力钢梁自重：0.41kN/m板自重： 6.00kN/m 2000mm)板托重：0.90kN/m6.09kN/m 自重标准值 g 1：7.31kN/m施工荷载： 2.80kN/m施工阶段弯矩设计值M 45.51kN.m (梁跨度：6000mm)施工阶段剪力设计值V 30.34kN2钢梁抗弯强度设计143.14N/mm 2<215N/mm 2PASS!92.29N/mm 2<215N/mm 2PASS!3钢梁剪应力计算面积矩 S=207492mm 322.80N/mm 2<125N/mm 2PASS!4挠度计算考虑混凝土徐变的组合截面特征计算换算成钢截面的组合截面面积 A 0c = A c / 2αE + A =换算成钢截面的组合截面惯性矩 I 0c = I c /(2*αE ) + A c *(x c -0.5h d )2/(2*αE) + I + A(y-x c )2 =(平台梁间距：钢梁剪应力τ1max = v 1*s 1/I*t w =混凝土板截面面积A c = b e * h d =换算成钢截面的组合截面面积A 0=A c /αE +A =对混凝土板底面的组合截面弹性抵抗矩 w 0c b =αE *I 0 / (x - h d ) =对钢梁上翼缘的组合截面弹性抵抗矩 w 0t = I 0 / (d-x) =对混凝土板顶面的组合截面弹性抵抗矩 w 0c tc = 2αE *I 0c / x c =对钢梁下翼缘的组合截面弹性抵抗矩 w 0b = I 0 / (H-x) =组合梁计算截面特征计算钢梁面积 A ＝b*t + h*s +B*T =钢梁中和轴至钢梁顶面的距离为 y t = [0.5b*t 2 + h*s*(0.5h + t) + B*T*(t+h+0.5T)] / A =钢梁截面特征计算：钢梁中和轴至钢梁顶面的距离为 y b = h + t + T - y t =钢梁截面惯性矩 I= (b*t 3 + s*h 3 + B*T 3) / 12 + b*t*(yt-0.5t)2 + s*h*(y t -0.5h-t)2 + B*T*(0.5T+h+t-y t )2 =钢梁上翼缘的弹性抵抗矩 W 1 = I / y t =混凝土板顶面至钢梁截面中和轴的距离 y = h d + h t +y t =对混凝土板顶面的组合截面弹性抵抗矩 w 0c t = αE *I 0 / x=混凝土板计算宽度b e =钢梁上翼缘的弹性抵抗矩 W 2 = I / y b =组合截面特征计算：钢与混凝土弹性模量比αE =自重标准值 g 1k ：对混凝土板底面的组合截面弹性抵抗矩 w 0c bc =2αE *I 0c / (x c - h d ) =对钢梁上翼缘的组合截面弹性抵抗矩 w 0tc = I 0c / (d-x c ) =对钢梁下翼缘的组合截面弹性抵抗矩 w 0bc = I 0c / (H-x c ) =钢梁上翼缘应力 M / r x *W 1 =钢梁下翼缘应力 M / r x *W 2=△=5*g*l 4/(384*E*I)=10.8mm < L/400 =15mm PASS!三使用阶段的验算1弯矩及剪力找平层重： 1.9kN/m活荷载：15.6kN/m （活荷载：6kn/m 2)78.84kN.m52.56kN22.1-2.28N/mm 2<10N/mm 2PASS!-0.33N/mm 2<10N/mm 2PASS!-87.74N/mm 2<215N/mm 2PASS!130.39N/mm 2<215N/mm 2PASS!2.2-2.24N/mm 2<10N/mm 2PASS!-0.37N/mm 2<10N/mm 2PASS!-88.23N/mm 2<215N/mm 2PASS!130.69N/mm 2<215N/mm 2PASS!2.3(略）2.4(略)3钢梁的剪应力147000mm 31105812mm 319.35N/mm 2<125N/mm 2PASS!4组合梁的挠度3.46mm < L/400 =15mm PASS!τ＝V 1S 1/It w +V 2S o /I o T w =两个受力阶段的荷载对组合梁的钢梁产生的剪应力△＝5q k l 4/384EI o +5g k l 4/384EI o c =组合梁中由于混凝土收缩引起的内力钢梁腹板顶面处对钢梁中和轴的面积矩S 1=钢梁腹板顶面以外的砼及钢梁上翼缘对组合截面中和轴的面积矩S o =使用阶段弯矩设计值M 使用阶段剪力设计值V 组合梁的抗弯强度在垂直荷载作用下的正应力考虑混凝土徐变在垂直荷载作用下的正应力混凝土板顶面应力:σ0c tc =-(M 2g /W 0c tc +M 2q /W 0c t )=混凝土板顶面应力σ0c t =-M/W 0c t =混凝土板底面应力σ0c b =-M/W 0c b =钢梁上翼缘应力σ0t = -M 1/W 1+M 2/W 0t =钢梁下翼缘应力σ0b = -M 1/W 2+M 2/W 0b =σ0bc = -M 1/W 2+(M 2g /W 0bc +M 2q /W 0b )=钢梁下翼缘应力温度差产生的应力σ0c bc =-(M 2g /W 0c bc +M 2q /W 0c b )=混凝土板底面应力:钢梁上翼缘应力σ0tc = -M 1/W 1+(M 2g /W 0tc +M 2q /W 0t )=。

注意：表中数据填写自己实验时所记录的进行计算！！！！！！！有的图也可能每组不同，自己看了改改实验九叠合梁正应力测试工程意义1、在建筑工程中经常将２种或３种以上的材料组合在一起共同承载这种梁称为层合梁鉴于层合梁在工程中的广泛应用有必要对层合梁的弯曲正应力进行测试分析为工程计算提供实验依据。

2、工程中常用的现浇式框架和装配式框架都有各自的优点与缺点。

前者整体性好，抗震性好，刚度大，但模板用量大且在现浇过程中需设置临时支撑，因而施工周期长；后者模板用量小，构件预制且可省去临时支撑，施工周期短，但整体性差，抗震性能也较差。

叠合框架具有上述两种结构的优点，其整体性好，抗震性好，节省临时支撑，有较好的应用前景。

3、叠梁是指一根梁自然叠放在另一根梁上而形成的组合结构,上部的梁受到外荷载的作用而产生变形，从而将一部分力传递到下部的梁上,形成梁间的接触力。

叠梁在实际工程中并不少见,较为常见的供电、供水等工程的管道桥梁就属于此类结构。

电缆套在钢管内,钢管又搁放在桥梁上,于是钢管与桥梁便组成了叠梁形式的结构。

这类结构上部的梁有多少力传递到下部梁上以及其分布情况常需要获得其具体数据。

一、实验目的1、通过对由两种材料固结而成的梁的应力测试，加深对纯弯曲梁平面假设的理解；2、观察复合梁和叠合梁正应力分布情况，了解如何组合梁合理；3、测定梁纯弯曲时横截面上正应力的分布规律，并与理论计算结果进行比较，以验证弯曲正应力公式。

4、进一步熟悉电测的操作方法。

二、实验装置、设备1.叠合梁应变计布片位置见下图1，有关截面尺寸均已标注于梁上。

2.WYS-1弯曲实验台架。

见图23.程控静态数字应变仪，型号：YE2538。

4.用联结螺栓连接的叠合梁，钢梁与铝梁叠合（钢梁置于下方）。

5.加载用铁块，4块，10kg/块。

三、实验步骤1、测量尺寸用游标卡尺测量实验梁横截面尺寸b，计算各应变片轴线至梁的中性层的距离yi，用钢尺测量力的作用点到支座的距离a，计入表中。

由两种不同材料组成的胶接叠梁弯曲实验实验指导一、 目的1、 测定由两种不同材料组成的胶接叠梁正应力分布规律。

2、 由实验结果探索胶接叠梁的弯曲正应力计算公式并和实验结果作比较。

二、 实验装置、设备和叠梁应变计布置图1、 叠梁应变计布片位置见下图，有关截面尺寸均已标注于梁上。

2、 WYS-1弯曲实验台架。

3、 数字电阻应变仪。

三、 加载方案按ΔP=800N ，P max =4000N 分五级加载分别测各点应变。

四、 数据分析1、 实验要求学生按上述加载方案分别测出各测点应变，然后计算ΔP=800N 时，各测点的增量应变Δεi ，对于2、3、4、5、6、7测点应取前后应变的平均值，例2''2'22εεε∆+∆=∆，用坐标纸按比例绘制实测应变ε（或Δε），应力σ（或Δσ）沿梁高分布图，实验数据及理论计算结果应用表格表示。

2、 根据分布图可直接求出实验梁中性轴的位置。

3、 进行理论探讨，求出应力沿两种材料分布的解析表达式（包括中性轴位置的计算公式）。

4、 把解析解的结果与实测值比较，计算1，2（2′），7（7′），8四点的误差和中性轴理论值和实测值的误差（误差较大时应讨论其原因或对解析解进行修正）。

5、 实验总结或体会。

h 1=h 2实验报告实验名称： 胶结叠合梁的弯曲正应力实验 指导老师：一、实验目的和要求3、测定由两种不同材料组成的胶接叠梁正应力分布规律。

4、由实验结果探索胶接叠梁的弯曲正应力计算公式并和实验结果作比较。

二、实验内容和原理本次实验为胶结叠合梁的内应力测试探索其受外力矩作用时的规律。

两梁的内力分析及中性轴的位置分析：两梁为胶结拼贴而成，在相接面，有两梁的曲率相同，故曲率半径相同，设上梁为1，下梁为2，则有1/ρ1=1/ρ2，而ρ=EI/M ，故M1/(E1 x I1)=M2/(E1 x I2),且有M1+M2=M ，解得 M1=M/(1+E2 x I2/E1 x I1),M2= M/(1+E1 x I1/E2 x I2) (其中M=Fa/2) 而σ=My/I ，故σ1max=M1 x h/2I1，σ2max=M2 x h/2I2中性轴位置：由E1 x S1+E2 x S2=0，设中性轴在交合面的上方yc 处，其中S1=∫ydA 在A1的积分，S2=∫ydA 在A2的积分，解得yc=（E1-E2）h / 2(E1+E2) 三、主要仪器设备4、实验材料如图所示，叠合梁的中间部分前后贴14枚应变片，尺寸和材料的一些力学参数如图5、 WYS-1弯曲实验台架。