机械原理课后习题答案
- 格式:doc
- 大小:971.50 KB
- 文档页数:20
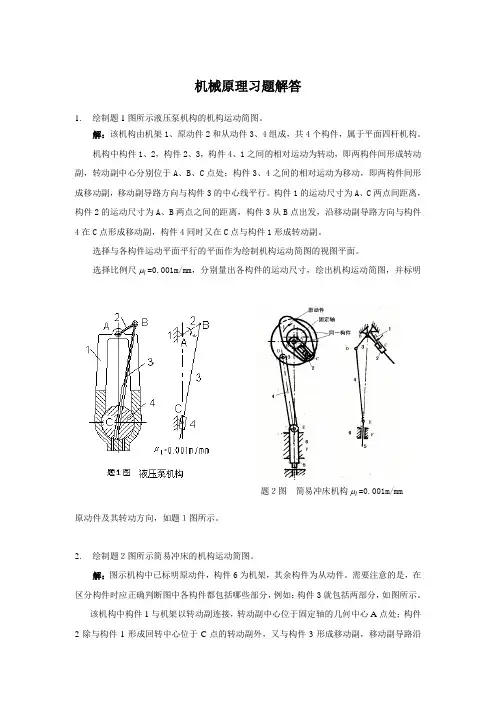
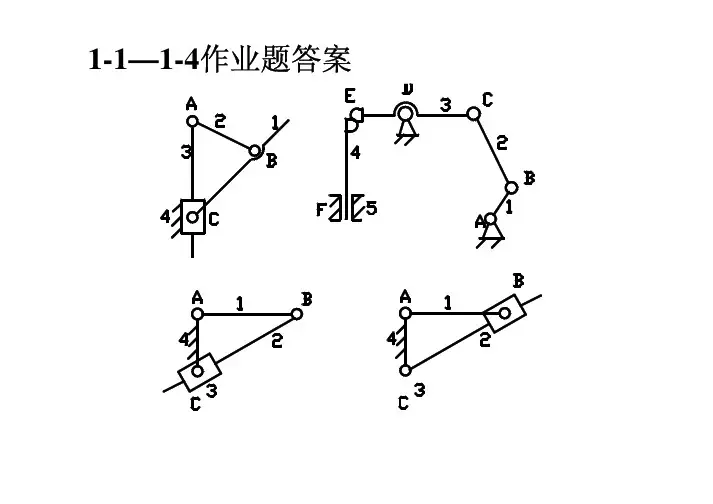
机械原理习题解答1.绘制题1图所示液压泵机构的机构运动简图。
解:该机构由机架1、原动件2和从动件3、4组成,共4个构件,属于平面四杆机构。
机构中构件1、2,构件2、3,构件4、1之间的相对运动为转动,即两构件间形成转动副,转动副中心分别位于A、B、C点处;构件3、4之间的相对运动为移动,即两构件间形成移动副,移动副导路方向与构件3的中心线平行。
构件1的运动尺寸为A、C两点间距离,构件2的运动尺寸为A、B两点之间的距离,构件3从B点出发,沿移动副导路方向与构件4在C点形成移动副,构件4同时又在C点与构件1形成转动副。
选择与各构件运动平面平行的平面作为绘制机构运动简图的视图平面。
选择比例尺μ=0.001m/mm,分别量出各构件的运动尺寸,绘出机构运动简图,并标明l题2图简易冲床机构lμ=0.001m/mm原动件及其转动方向,如题1图所示。
2.绘制题2图所示简易冲床的机构运动简图。
解:图示机构中已标明原动件,构件6为机架,其余构件为从动件。
需要注意的是,在区分构件时应正确判断图中各构件都包括哪些部分,例如:构件3就包括两部分,如图所示。
该机构中构件1与机架以转动副连接,转动副中心位于固定轴的几何中心A点处;构件2除与构件1形成回转中心位于C点的转动副外,又与构件3形成移动副,移动副导路沿BC 方向;构件3也绕固定轴上一点B 转动,即构件3与机架形成的转动副位于B 点,同时构件3与构件2形成移动副,又与构件4形成中心位于D 点的转动副;构件4与构件5形成中心位于E 点的转动副;构件5与机架6形成沿垂直方向的移动副。
该机构属于平面机构,因此选择与各构件运动平面平行的平面作为绘制机构运动简图的视图平面。
选择比例尺l μ=0.001m/mm ,量出各构件的运动尺寸,绘出机构运动简图,并标明原动件及其转动方向,如题2图所示。
3. 题3图为外科手术用剪刀。
其中弹簧的作用是保持剪刀口张开,并且便于医生单手操作。
忽略弹簧,并以构件1为机架,分析机构的工作原理,画出机构的示意图,写出机构的关联矩阵和邻接矩阵,并说明机构的类型。
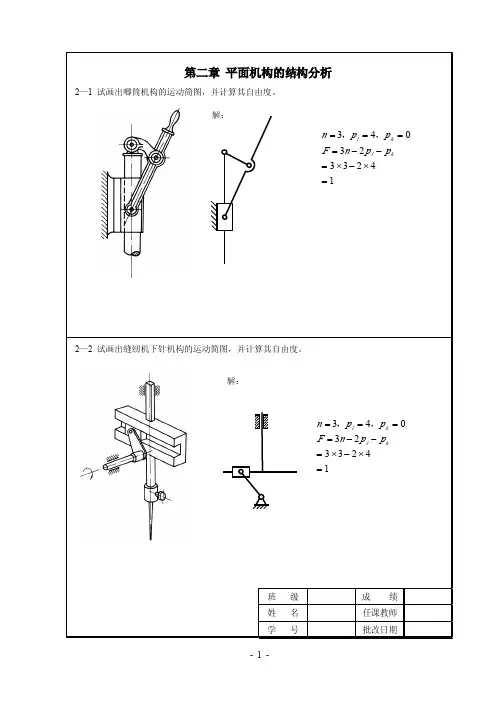

第二章 机构的结构分析题2-11 图a 所示为一简易冲床的初拟设计方案。
设计者的思路是:动力由齿轮1输入,使轴A 连续回转;而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构使冲头4上下运动,以达到冲压的目的。
试绘出其机构运动简图(各尺寸由图上量取),分析是否能实现设计意图,并提出修改方案。
解:1)取比例尺,绘制机构运动简图。
(图2-11a)2)要分析是否能实现设计意图,首先要计算机构的自由度。
尽管此机构有4个活动件,但齿轮1和凸轮2是固装在轴A 上,只能作为一个活动件,故 3=n 3=l p 1=h p01423323=-⨯-⨯=--=h l p p n F原动件数不等于自由度数,此简易冲床不能运动,即不能实现设计意图。
分析:因构件3、4与机架5和运动副B 、C 、D 组成不能运动的刚性桁架。
故需增加构件的自由度。
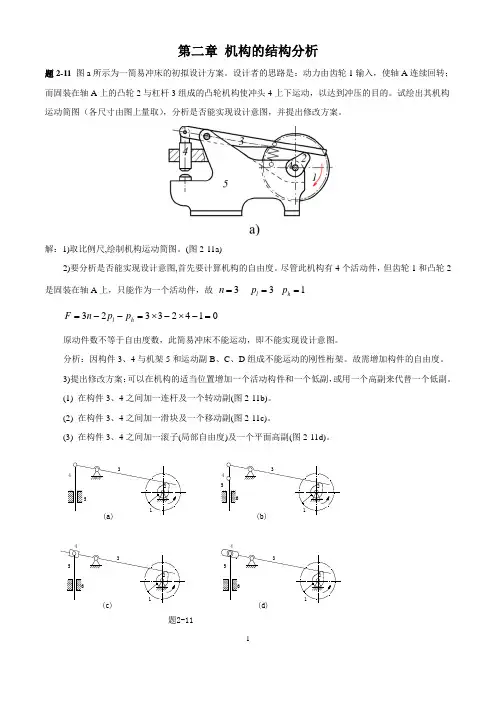
3)提出修改方案:可以在机构的适当位置增加一个活动构件和一个低副,或用一个高副来代替一个低副。
(1) 在构件3、4之间加一连杆及一个转动副(图2-11b)。
(2) 在构件3、4之间加一滑块及一个移动副(图2-11c)。
(3) 在构件3、4之间加一滚子(局部自由度)及一个平面高副(图2-11d)。
题2-11讨论:增加机构自由度的方法一般是在适当位置上添加一个构件(相当于增加3个自由度)和1个低副(相当于引入2个约束),如图2-1(b )(c )所示,这样就相当于给机构增加了一个自由度。
用一个高副代替一个低副也可以增加机构自由度,如图2-1(d )所示。
题2-12 图a 所示为一小型压力机。
图上,齿轮1与偏心轮1’为同一构件,绕固定轴心O 连续转动。
在齿轮5上开有凸轮轮凹槽,摆杆4上的滚子6嵌在凹槽中,从而使摆杆4绕C 轴上下摆动。
同时,又通过偏心轮1’、连杆2、滑杆3使C 轴上下移动。
最后通过在摆杆4的叉槽中的滑块7和铰链G 使冲头8实现冲压运动。
试绘制其机构运动简图,并计算自由度。

机械原理习题答案篇一:机械原理_课后习题答案第七版《机械原理》作业题解第二章机构的构造分析F=3n-2pl-ph =3×-2×-1=0 34 F = 3n ? (2pl + ph )= 3 ×4 ? (2 ×5 + 1) = 17 438 5 2 9 1-1' F = 3n ?(2pl + ph ? p') ? F'= 3 ×8 ? (2 ×10 + 2 ? 0) ?1= 1篇二:机械原理第七版西北工业大学习题答案(特别全答案详解).doc第二章平面机构的构造分析题2-1 图a所示为一简易冲床的初拟设计方案。
设计者的思路是:动力由齿轮1输入,使轴A连续回转;而固装在轴A上的凸轮2与杠杆3组成的凸轮机构使冲头4上下运动,以到达冲压的目的。
试绘出其机构运动简图(各尺寸由图上量取),分析是否能实现设计意图,并提出修改方案。
解:1)取比例尺,绘制机构运动简图。
(图2-1a) 2)要分析是否能实现设计意图,首先要计算机构管此机构有4个活动件,但齿轮1和凸轮2是固装能作为一个活动件,故n?3 pl?3 ph?1F?3n?2pl?ph?3?3?2?4?1?0的自由度。
尽在轴A上,只原动件数不等于自由度数,此简易冲床不能运动,即不能实现设计意图。
分析:因构件3、4与机架5和运动副B、C、D组成不能运动的刚性桁架。
故需增加构件的自由度。
3)提出修改方案:可以在机构的适当位置增加一个活动构件和一个低副,或用一个高副来代替一个低副。
(1) 在构件3、4之间加一连杆及一个转动副(图2-1b)。
(2) 在构件3、4之间加一滑块及一个移动副(图2-1c)。
(3) 在构件3、4之间加一滚子(局部自由度)及一个平面高副(图2-1d)。
置上添加一个构件(相当于增加3个自由度)和1个低副(相当于引入2个约束),如图2-1(b)(c)所示,这样就相当于给机构增加了一个自由度。

机械原理朱理版习题答案机械原理是一门研究机械运动规律、机械结构设计原理和机械系统性能分析的学科。
朱理版的《机械原理》是众多教材中的一种,它以其系统性、实用性和理论性而受到广泛欢迎。
以下是一些习题的答案示例,供学习者参考。
# 第一章:机械运动的基本概念习题1:解释什么是自由度,并给出一个机械系统的自由度计算示例。
答案:自由度是指一个机械系统在空间中能够独立运动的方向数。
例如,一个平面机械系统,如果它有3个独立的运动方向,则它的自由度为3。
计算自由度的公式是:\( F = 3n - 2j - h \),其中\( n \)是系统内的运动副数,\( j \)是低副数,\( h \)是高副数。
习题2:阐述平面四杆机构的类型及其特点。
答案:平面四杆机构主要有双曲柄机构、双摇杆机构和曲柄摇杆机构三种类型。
双曲柄机构具有两个曲柄,运动平稳;双摇杆机构没有曲柄,运动速度变化较大;曲柄摇杆机构则有一个曲柄和一个摇杆,兼具两者的特点。
# 第二章:平面连杆机构习题3:根据给定的连杆长度,设计一个满足特定运动要求的平面四杆机构。
答案:设计平面四杆机构时,需要根据给定的连杆长度和所需的运动轨迹来选择合适的连杆类型和长度比例。
例如,如果需要实现近似直线运动,可以选择双曲柄机构,并调整连杆长度以满足运动学要求。
# 第三章:凸轮机构习题4:描述凸轮机构的工作原理,并给出设计一个简单凸轮机构的步骤。
答案:凸轮机构通过凸轮的旋转来驱动从动件做往复或摆动运动。
设计凸轮机构的步骤通常包括确定运动规律、计算凸轮轮廓曲线、选择合适的材料和加工方法。
# 结束语机械原理的学习不仅要求理解理论知识,还需要通过习题来加深对概念的理解和应用。
希望上述习题答案能够帮助学习者更好地掌握机械原理的相关知识,并在实际设计中灵活运用。
请注意,上述内容仅为示例,具体的习题答案会根据实际的习题内容而有所不同。
如果需要针对特定习题的答案,请提供具体的习题信息。

第二章 平面机构的结构分析题2-1 图a 所示为一简易冲床的初拟设计方案。
设计者的思路是:动力由齿轮1输入,使轴A 连续回转;而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构使冲头4上下运动,以达到冲压的目的。
试绘出其机构运动简图(各尺寸由图上量取),分析是否能实现设计意图,并提出修改方案。
解:1)取比例尺,绘制机构运动简图。
(图2-1a) 2)要分析是否能实现设计意图,首先要计算机构的自由度。
尽管此机构有4个活动件,但齿轮1和凸轮2是固装在轴A上,只能作为一个活动件,故3=n3=l p 1=h p01423323=-⨯-⨯=--=h l p p n F原动件数不等于自由度数,此简易冲床不能运动,即不能实现设计意图。
分析:因构件3、4与机架5和运动副B 、C 、D 组成不能运动的刚性桁架。
故需增加构件的自由度。
3)提出修改方案:可以在机构的适当位置增加一个活动构件和一个低副,或用一个高副来代替一个低副。
(1) 在构件3、4之间加一连杆及一个转动副(图2-1b)。
(2) 在构件3、4之间加一滑块及一个移动副(图2-1c)。
(3) 在构件3、4之间加一滚子(局部自由度)及一个平面高副(图2-1d)。
1(c)题2-154364(a)53221讨论:增加机构自由度的方法一般是在适当位置上添加一个构件(相当于增加3个自由度)和1个低副(相当于引入2个约束),如图2-1(b )(c )所示,这样就相当于给机构增加了一个自由度。
用一个高副代替一个低副也可以增加机构自由度,如图2-1(d)所示。
题2-2 图a所示为一小型压力机。
图上,齿轮1与偏心轮1’为同一构件,绕固定轴心O连续转动。
在齿轮5上开有凸轮轮凹槽,摆杆4上的滚子6嵌在凹槽中,从而使摆杆4绕C轴上下摆动。
同时,又通过偏心轮1’、连杆2、滑杆3使C轴上下移动。
最后通过在摆杆4的叉槽中的滑块7和铰链G使冲头8实现冲压运动。
试绘制其机构运动简图,并计算自由度。

机械原理习题答案机械原理习题答案机械原理是工程学中的重要基础课程,它研究物体在外力作用下的运动和力学性质。
通过学习机械原理,我们可以了解力的作用规律、运动的原理以及机械结构的设计等方面的知识。
为了帮助大家更好地掌握机械原理的相关知识,下面将给出一些典型习题的答案,希望对大家的学习有所帮助。
1. 一个物体以匀速运动通过一个水平圆弧形的轨道,求物体所受的合外力。
答:由于物体以匀速运动通过轨道,所以物体受到的合外力为零。
根据牛顿第一定律,物体在不受合外力作用时,将保持匀速直线运动或静止状态。
2. 一个质量为2kg的物体在水平面上受到一个5N的水平拉力,求物体的加速度。
答:根据牛顿第二定律F=ma,其中F为物体所受合外力,m为物体的质量,a 为物体的加速度。
将已知数据代入公式中,可得5N=2kg*a,解得a=2.5m/s²。
所以物体的加速度为2.5m/s²。
3. 一个质量为10kg的物体静止在斜面上,斜面的倾角为30°,求物体所受的重力分解到斜面上的分力大小。
答:将物体的重力分解为垂直于斜面的分力和平行于斜面的分力。
根据三角函数的定义,可知物体所受的重力分解到斜面上的分力大小为10kg * 9.8m/s² * sin30° ≈ 49N。
4. 一个质量为5kg的物体通过一个光滑的斜面下滑,斜面的倾角为45°,求物体下滑的加速度。
答:物体下滑的加速度等于斜面的倾角的正弦值乘以重力加速度。
根据已知数据,可得物体下滑的加速度为5kg * 9.8m/s² * sin45° ≈ 34.6m/s²。
5. 一个质量为3kg的物体通过一个粗糙的斜面下滑,斜面的倾角为30°,摩擦系数为0.2,求物体下滑的加速度。
答:物体下滑的加速度等于斜面的倾角的正弦值减去摩擦系数乘以斜面的倾角的余弦值,再乘以重力加速度。
根据已知数据,可得物体下滑的加速度为3kg * 9.8m/s² * (sin30° - 0.2*cos30°) ≈ 25.9m/s²。

机械原理习题集答案第一章:机械运动学1. 问题:简述平面运动的基本概念。
答案:平面运动是指物体在平面内的运动,其轨迹可以是直线或曲线。
在平面运动中,物体的每一个点都在同一平面内移动。
2. 问题:什么是四杆机构的运动规律?答案:四杆机构是最基本的机械机构之一,其运动规律取决于杆的长度和连接方式。
常见的四杆机构有双曲柄机构、曲柄滑块机构等。
第二章:机械动力学1. 问题:牛顿运动定律在机械设计中的应用是什么?答案:牛顿运动定律是描述物体运动的基本定律,包括惯性定律、力的作用与反作用定律和作用力与加速度的关系。
在机械设计中,这些定律用于预测和计算机械系统的运动状态和受力情况。
2. 问题:简述达朗贝尔原理。
答案:达朗贝尔原理是动力学中的一个基本原理,它指出在没有外力作用的系统中,系统内各部分的动量守恒。
在机械设计中,这一原理常用于分析和计算机械系统的动态平衡。
第三章:机构设计与分析1. 问题:什么是机构的自由度?答案:机构的自由度是指在没有约束的情况下,机构能够独立进行的运动的数量。
自由度的计算公式为:\( F = 3n - 2j - h \),其中\( n \)是机构中杆件的数量,\( j \)是铰链的数量,\( h \)是高副的数量。
2. 问题:如何确定一个机构的运动类型?答案:确定机构的运动类型需要分析机构的几何形状和连接方式。
例如,如果机构中存在曲柄和滑块,它可能是一个曲柄滑块机构,其运动类型为往复直线运动。
第四章:机械结构设计1. 问题:机械结构设计中需要考虑哪些因素?答案:在机械结构设计中,需要考虑的因素包括材料的选择、强度和刚度的计算、尺寸的确定、成本控制、维护的便利性等。
2. 问题:什么是疲劳强度?答案:疲劳强度是指材料在反复加载和卸载过程中抵抗断裂的能力。
在机械结构设计中,需要考虑疲劳强度以确保结构的可靠性和耐久性。
第五章:机械传动1. 问题:什么是齿轮传动?答案:齿轮传动是一种利用齿轮啮合来传递运动和动力的机械传动方式。
2-8解:(1)取μ= m/mml作机构位置图如(a)图(2)求v、ω、列矢量方程式取μ,作速度(b)图v(3)求a、α列矢量方程式作加速度(c)图题5-8解αa1=arccos(rb/ra1)=arccos[(z1cosα)/(z1+2ha*)] =31°46′O1 α PN2B2N1αa2=26°14′10″B1P=B1N1-N1PB1 PbⅠ=mz1/2·cosα(tgαa1- tgα′)=11.39mm B2P=12.72mm B1B2=24.11mm 作用弧CD=B1B2cosα′=25.66mm 作用角 ϕ 1 =CD/r1′=25.66/47.5=30°58 ′αⅡO2εα=B1B2/Pb=1.63题5-12解N 1 N 2 = 2 N 1 P = 2r sin α N 1 N 2 2r sin α ∴ tgα a = = = 2tgα = 0.7279 O1 N 1 r cos α 3′ α a = 36° 9″ rb r cos α z cos α 又 cos α a = = = * ra r + ha z + 2ha* 2ha cos α ∴z = = 12.323 cos α − cos α aO1 α ra rb (B2) αa P rb ra αa α O2 N1(B1) N2∴不根切,z最少为13题5-13解h m − xm = MN* aMN = PN sinα = OPsin2 α mz 2 = sin α 2* az 2 x = h − sin α 2x=1-35/2 sin 20° =-1.0471 or x=(17-35)/17=-1.05882题5-15解解题思路: 1.设计题,主要确定尺寸 r 、ra、r f 、rb 2.变位齿轮传动设计步骤:由 a 、 a ′、 α → α ′ → x Σ → x 1、 x 2 ← x min ← 据 z = 12 z Σ、 α 、 α ′ → y 、 x Σ → ∆ y 计算: r 、 ra、 r f 、 rb 3 .验证 s a < 0 .2 m 、 ε α ≥ 1题5-15解1.选择传动类型 2. 求 α ′和 x Σα ′ = arccos(m a = ( z1 + z 2 ) = 120mm < a ′ 2a cos α ) = 29 ° 5 0 ′ 2 8 ′′ a′x∑( z 1 + z 2 )( inv α ′ − inv α ) = = 1 . 2505 2 tg α17 − 12 z1 = z2 = 12 < 17,∴ x1.2 > = 0.2941 17 ∴ x1 = x2 = x∑ / 2 = 1.2505/ 2 = 0.62533.分配 x 1 和 x 24.求y和∆y y = (a ′ − a ) / m = (130 − 120) / 10 = 1; ∆y = x ∑ − y = 0.2505 mz 1.2 = 60mm 5.r1.2 = 2 * ra 1.2 = r1.2 + ( ha + x1.2 − ∆y )m = 73.75mm* r f 1.2 = r1.2 − ( ha + c * − x1.2 )m = 53.75mmmz 1.2 rb1.2 = cos α = 56.38mm 2 6.验算sa 和ε α ′23 s = (π / 2 + 2 x1.2 tgα )m = 20.26mm ;α a 1.2 = arccos(rb1.2 / ra 1.2 ) = 40°8 ″ sa 1.2 = s ra 1.2 − 2ra 1.2 ( invα a 1.2 − invα ) r1.2 73.75 − 2 × 73.75(0.142715 − 0.014904) = 6.05mm > 0.2m 60= 20.26 ×题5-15解1 [ z1 ( tgα a 1 − tgα ′ ) + z 2 ( tgα a 2 − tgα ′ )] εα = 2π 1 = z1 ( tgα a 1 − tgα ′ ) = 1.03π题5-16解 用等变位修复,小正变位;大负变位* * ∆d a 2 = d 2 + 2( ha + x 2 )m − ( d 2 + 2ha m ) = 2 x 2 m则 x 2 = ∆d a 2 / 2m = −1 而 x1 = − x 2 = 1d 1 = 96mm ; d 2 = 384mm ; d a 1 = 112mm ; d a 2 = 384mm ; d f 1 = 94mm ; d f 2 = 366mm ; d b1 = 90.21mm ; d b 2 = 360.84mm ; a ′ = a = 240mm .验算sa 和ε α d b1 α a 1 = arccos( ) = 36°21′; d a1α a 2 = 20° sa 1 = πm / 2 • d a 1 / d 1 − d a 1 ( invα a 1 − invα )= 1.02mm > 0.2m sa 2 ↑ 不验算 1 εα = [ z1 ( tgα a 1 − tgα ) + z 2 ( tgα a 2 − tgα )] 2π = 1.42mn (1 ) a ′ = a 12 = ( z3 + z4 ) 34 2 cos β ∴ cos β = 0 . 79412 , β = 37 ° 25 ′ 41 ″ m n z3 ( 2 )d 3 = m t z 3 = = 45 .33 mm ; d 4 = m t z 4 = 90 .67 mm ; cos β* d f 3 = d 3 − 2 ( han + c * ) m = 40 .33 mm ; d f 4 = 85 .67 mm ; * d a 3 = d 3 + 2 han m = 49 .33 mm ; d a 4 = 94 .67 mm tg α t = tg α n / cos β = 0 .4583 ; α t′ = α t = 24 ° 37 ′ 25 ″题5-20解d b 3 = d 3 cos α t = 41 .21 mm ; d b 4 = 82 . 42 mmα at 3 = arccos( d b 3 / d a 3 ) = 33 ° 20 ′ 35 ″; α at 4 = 29 ° 28 ′ 16 ″ εγ = εα + ε β= 3 . 118 1 = [ z 3 ( tg α at 3 − tg α t ) + z 4 ( tg α at 4 − tg α t )] 2π。
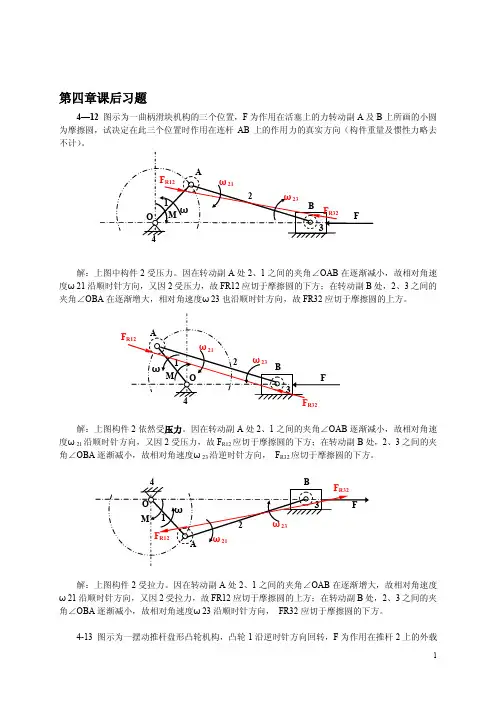
第四章课后习题4—12图示为一曲柄滑块机构的三个位置,F为作用在活塞上的力转动副A及B上所画的小圆为摩擦圆,试决定在此三个位置时作用在连杆AB上的作用力的真实方向(构件重量及惯性力略去不计)。
解:上图中构件2受压力。
因在转动副A处2、1之间的夹角∠OAB在逐渐减小,故相对角速度ω21沿顺时针方向,又因2受压力,故FR12应切于摩擦圆的下方;在转动副B处,2、3之间的夹角∠OBA在逐渐增大,相对角速度ω23也沿顺时针方向,故FR32应切于摩擦圆的上方。
R32解:上图构件2依然受压力。
因在转动副A处2、1之间的夹角∠OAB逐渐减小,故相对角速度ω21沿顺时针方向,又因2受压力,故F R12应切于摩擦圆的下方;在转动副B处,2、3之间的夹角∠OBA逐渐减小,故相对角速度ω23沿逆时针方向,F R32应切于摩擦圆的下方。
解:上图构件2受拉力。
因在转动副A处2、1之间的夹角∠OAB在逐渐增大,故相对角速度ω21沿顺时针方向,又因2受拉力,故FR12应切于摩擦圆的上方;在转动副B处,2、3之间的夹角∠OBA逐渐减小,故相对角速度ω23沿顺时针方向,FR32应切于摩擦圆的下方。
4-13 图示为一摆动推杆盘形凸轮机构,凸轮1沿逆时针方向回转,F为作用在推杆2上的外载荷,试确定凸轮1及机架3作用给推杆2的总反力FR12及FR32方位(不考虑构件的重量及惯性力,解:经受力分析,FR12的方向如上图所示。
在FR12的作用下,2相对于3顺时针转动,故FR32应切于摩擦圆的左侧。
补充题1 如图所示,楔块机构中,已知γ=β=60°,Q =1000N 格接触面摩擦系数f =0.15,如Q 为有效阻力,试求所需的驱动力F 。
解:对机构进行受力分析,并作出力三角形如图。
对楔块1,R 21R310F F F ++=由正弦定理有21sin(602sin(90R F F ϕϕ+-=))o o ① 对楔块2,同理有R12R 320Q F F ++=sin(90sin(602ϕϕ+-=))o o ②sin(602sin(602F Q ϕϕ+=⋅-))o o且有2112R R F F = ,8.53arctgf ϕ==o③联立以上三式,求解得F =1430.65N2 如图示斜面机构,已知:f (滑块1、2与导槽3相互之间摩擦系数)、λ(滑块1的倾斜角)、Q (工作阻力,沿水平方向),设不计两滑块质量,试确定该机构等速运动时所需的铅重方向的驱动力F 。
错误!解:滑块1、2受力情况及力三角形如图所示。
由正弦定理有对滑块1:21sin 90()sin(2R F F ϕλλϕ⎡⎤-++⎣⎦=)o ① 对滑块2:12sin(902sin(90)R Q F ϕϕ-+=)o o ② 并且有2112,R R F F arctgf ϕ== ③ 解之得cos sin(2)cos 2cos()F Q ϕλϕϕλϕ⋅+=⋅⋅+第五章课后习题5—8图示为一带式运输机,由电机1经平带传动及一个两级齿轮减速器带动运输带8。
设已知运输带8所需的引力F=5500N ,运送速度v=1.2m/s 。
平带传动(包括轴承)的效率1η=0.95,每对齿轮(包括轴承)的效率2η=0.97,运输带8的机械效率3η=0.92(包括支承和联轴器)。
试求该系统的总效率及电动机所需的效率。
解:该系统的总效率为822.092.097.095.023221=⨯⨯=⋅⋅=ηηηη电机所需的功率为3d 5500 1.2108.029(Kw)0.822F N υη-⨯⨯===5—9 如图所示,电动机通过V 带传动及圆锥、圆柱齿轮传动带动工作机A 及B 。
设每对齿轮的效率1η=0.97(包括轴承的效率),带传动的效率3η=0.92,工作机A 、B 的功率分别5Kw A P = 、KW P B 1= ,效率分别为8.0=A η,5.0=B η ,试求电动机所需的功率。
解:输入功率22.7)/(221'==ηηηA A A P P 31.2)/(221'==ηηηB B B P P5—12 a)图示为一焊接用楔形夹具,利用这个夹具把要焊接的工件1和1'预先夹妥,以便焊接。
图中2为夹具,图中2为夹具体,3为楔块,若已知各接触面间的摩擦系数均为f , 试确定此夹具的自锁条件。
解法1 根据反行程时η'≤0的条件来确定。
反行程时(楔块3退出)取楔块3为分离体,其受工件1(及1')和夹具2作用的反作用力R 13和R 23 以及支持力P ,各力方向如图a 所示,根据楔块3的平衡条件,作封闭三角形如图c 所示。
反行程时R 23为驱动力,由正弦定理可得当φ=0(不考虑摩擦)时,得理想驱动力为:于是得此机构反行程的机械效率为 :令,可得自锁条件为。
解法2 根据反行程时生产阻力小于或等于零的条件来确定。
根据楔块3的力三角形(图c ),由正弦定理有23sin(2)cos P R αϕϕ-=⋅若楔块3不自动松脱,则应使P≤0,即得自锁条件为: 2αϕ≤解法3 根据运动副的自锁条件确定。
由于工件被夹紧后P 力就被撤消,故楔块3的受力如图b 所示,楔块3就如同一个受到R 23(此时为驱动力)作用而沿水平面移动的滑块。
故只要R 23作用在摩擦角φ之内,楔块3即发生自锁。
R 23与垂直方向之间的夹角是α-φ,要使R 23作用在摩擦角φ之内,即αϕϕ-≤ 所以,楔块3发生自锁的条件是: 2αϕ≤(b )设矿石的重量为Q ,矿石与颚板间的摩擦因数为f ,则摩擦角为f arctan =ϕ矿石有向上被挤出的趋势时,其受力如图,由力平衡条件知:R12R 320Q F F ++=由正弦定理得R12sin(2)sin(90)F Qαϕϕ=-+R12sin(2)cos Q F αϕϕ-=⋅令Q ≤0,得sin(2)0αϕ-≤故自锁条件为:ϕα2≤[参考方法二:0)2sin(2F R =--Q ϕα即 )2(s i n 2F R ϕα-=Q∴ 2s i n )2(s i n 0'αϕαη-==RR F F 当'η<0时,即02≤-ϕα,矿石将不被挤出,即自锁条件为ϕα2≤]补充题:如图示斜面机构,已知:f (滑块1、2与导槽3相互之间摩擦系数)、λ(滑块1的倾斜角)、F (驱动力,铅重方向),Q (工作阻力,沿水平方向),设不计两滑块质量,试确定该机构的效率及自锁条件(包括正、反行程)。
解:ϕ(1)反行程:受力分析如图 由正弦定理得,21sin(2)sin(90)R F Fλϕλϕ=--+12sin 90sin(90)R F Q ϕ=-2112R R F F =所以cos()cos sin(2)Q F λϕϕλϕ-=⋅-可得'0sin(2)tan cos()Q Q λϕηλλϕ-==⋅- '0η≤令,则ϕλ2≤为自锁条件。
(2)正行程效率:由第4章受力分析知cos sin(2)cos 2cos()F Q ϕλϕϕλϕ⋅+=⋅⋅+所以0tan cos 2cos()cos sin(2)F F λϕλϕηϕλϕ⋅⋅+==⋅+R32第七章课后习题7-6 如图所示为一机床工作台的传动系统。
设已知各齿轮的齿数,齿轮3的分度圆半径r 3,各齿轮的转动惯量J 1、J 2、J 2’、J 3,齿轮1直接装在电动机轴上,故J 1中包含了电动机转子的转动惯量。
工作台和被加工零件的重量之和为G 。
当取齿轮1为等效构件时,求该机械系统的等效转动惯量J e (ω1/ω2=Z 2/Z 1)。
解:根据式(7-17)221nsi i e i si i J m J υωωω=⎡⎤⎛⎫⎛⎫=+⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦∑得2222224122311113e GJ J J J J g ωωυωωωωω⎛⎫'⎛⎫⎛⎫⎛⎫'=++++ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭① 又因21221121123322143311322,,,z z z z z z r z z ωωωωωωωωωυωωωω'==='⋅=⨯==⋅⋅' ②由①、②得22231211223232()()e Gr z z z J J J J J z g z z ⎛⎫'⎛⎫⋅'=++++ ⎪ ⎪ ⎪⋅⎝⎭⎝⎭7-11某内燃机的曲柄输出力矩Md 随曲柄转角ψ的变化曲线如图所示,其运动周期ψT =π,曲柄的平均转速nm =620r/min 。
当用该内燃机驱动一阻抗力为常数的机械时,如果要求其运转不均匀系数δ=0.01。
试求1) 曲柄的最大转速n max 和相应的曲柄转角位置φmax ;2) 装在曲轴上的飞轮转动惯量J F (不计其余构件的转动惯量)。
M r Ⅰ Ⅱ Ⅲ ⅠⅢ能量指示解:(1)设阻力矩为M r ,由驱动功等于阻抗功有r 0d M d M d ππϕϕ=⎰⎰ 即r 120130130200()2002180180M πππ+⋅=⨯+⨯ 解得:r 700116.67.6M N m =≈直线OA 的方程为:200180020180y x x ππ== 直线BC 的方程为:2003600()()13013180y x x ππππ=--=-- 直线Me 与分别与OA 、BC 交于D 、E 点,则可求得D 、E 坐标为:7700125700(,),(,)10862166D E ππ 由能量指示图知, E 点时速度达到最大值n max ,max (1)620(10.005)623.1/min 2m n n r δ=+=⨯+=max125180104.17216πϕπ=⨯≈o o (2)由能量指示图知,D 到E 区间内的盈亏功为最大盈亏功 max w ∆,其在数值上应等于梯形ABED 所围成的面积max 13012577006125()(200)21802161086216w ππππ⎡⎤∆=+-⨯-=⎢⎥⎣⎦22max 900/([])F m J w n πδ≥∆将max ,,m w n δ∆代入上式得,22.11.F J kg m ≥补充题:图示铰链四杆机构,已知l 1=100mm ,l 2=390mm ,l 3=200mm ,l 4=250mm ,若阻力矩M 3=100N·m 。
试求:(1)当φ=π/2时,加于构件1上的等效阻力矩M er (2)当φ=π时,加于构件1上的等效阻力矩M er 。
解(1)先确定速度瞬心P 13的位置,如图所示。
p131131431334p p p p νωω=⋅=⋅313141131334p p 12p p l l ωω∴=== 3er 31110050(N m)2M M ωω=⋅=⨯=⋅ (2)先确定速度瞬心P 13的位置,如图所示。