数学建模论文-肥猪最佳销售时机问题

数学建模论文课题：猪的最佳销售时期的数学模型问题重述：一般从事猪的商业性饲养和销售总是希望获得利润，因此，饲养某种猪是否获利，怎样获得最大利润，是饲养者必须首先考虑的问题。

如果把饲养技术水平、猪的类型等因素视为不变的，且不考虑市场的需求变化，那么影响获利大小的一个主要因素是如何选择猪的售出时机。

也许有人认为，猪养得越大，售出后获利越大。

其实不然，因为随着猪的生长，单位时间消耗的饲养费用也就越多，但同时其体重增长的速度却不断下降，所以饲养时间太长是不合算的。

试作适当的假设，引入相应的参数，建立猪的最佳销售时机的数学模型。

一、模型假设1、猪的市场价格的变化是连续的，即市场猪肉价格随时间变化的函数可以视为连续函数。

2、饲料市场价格的变化是连续的，即饲料价格随时间变化的函数可以视为连续函数。

3、成本主要由猪苗价格与饲料消耗组成，不考虑其他因素。

4、饲养技术水平、猪的类型等因素视为不变的，且不考虑市场的需求变化。

二、符号说明1、市场猪肉价格为q(t) 元/公斤2、饲料价格为p(t) 元/公斤3、猪苗价格为r 元/公斤4、猪苗重量为m 公斤5、饲养了t 时间后，猪的重量为M(t)公斤6、t 时刻，单位时间增加重量为a(t)公斤7、t 时刻，每消耗1公斤饲料增加的重量为d(t)公斤8、t 时刻，单位时间消耗的饲料为c(t)公斤9、0~t 内消耗饲料的总花费为Z(t)元10、在t 时刻出售可获的利润为Q(t)元三、模型建立1、饲养了t 时间后，猪的重量M(t)的估计由上述符号说明可知：a(t)=c(t)d(t)当时间很短时，即：t~t +⊿t 内增加的重量可由下式表示：M(t~t +⊿t)-M(t )≈a(t) *⊿t= c(t)d(t) *⊿t 即为：()()()dM t c t d t dt =——————————①初值条件：M(0)=m故：0()()()tM t m c s d s ds =+⎰——————————②2、0~t 内消耗饲料的总花费Z(t)的估计当时间很短时，即：t~t +⊿t 内的总花费可由下式表示：Z(t~t +⊿t)-Z(t )≈c(t)p(t) *⊿t 即为：()()()dZ t c t p t dt=——————————③ 初值条件：Z(0)=0故：0()()()t Z t c s p s ds =⎰———————————④3、在t 时刻出售可获利润Q(t)的估计由于：利润=t 时刻售价*猪重量-饲料总花费-猪苗单价*猪苗重量即为：()()*()()*Q t q t M t Z t r m =--——————————⑤ 将②④式代入可得：00()*(())()*()()()()t tQ t m q t r q t c s d s ds c s p s ds =-+-⎰⎰————————————⑥4、在t 时刻出售可获利润Q(t)最大值的估计由⑥式：要求时刻t ，使得Q(t)最大，必须令()0d Q t d t =即： 0()()*[()()]()*[()*()()]0t dQ t dq t m c s d s ds c t q t d t p t dt dt =++-=⎰———————————⑦由⑦式的方程即可解出使Q(t)达到最大的时间,记为T则最大利润为：00()*(())()*()()()()T TQ T m q T r q T c s d s ds c s p s ds =-+-⎰⎰———————————⑧（模型中的函数p(t)、q(t)、c(t)、d(t)均可由统计数据回归得出）四、模型简化与模型求解如果市场猪肉价格与饲料价格取为长期价格水平的平均值(即为常数)，分别为p 元/公斤与q 元/公斤。

猪的最佳销售时机问题分析：设g(t)为一头猪在t 时刻的重量，则有g(0)=0x ,g(t)≤X 其中X 为该品种住的最大体重，猪生长速度随着体重的增加就会减慢下来，到达最大体重X 时，生长速度为零，依此可设： dg/dt =α(1-g(t)/X)g(0)=0x ,t≥0 ① 其中，α是反映住的生长速度快慢的常数又设f(t)为一头猪饲养到t 时刻共消耗的饲养费用（饲养费+人员工薪）s x 为猪可上市销售的最小体重；ts 为猪从体重0x 增至s x 所需饲养时间C(t,x)为t 时刻体重为x 的猪的单位售价，t 时刻将猪售出则:纯利润 :W(t)=C(t,x)×g(t)-f(t)-C00x ② 0<ts≤t②为问题的主模型，g(t)由①确定，只需求出 f(x)与C(t,x)即可。

假设模型（1）该模型只对某一品种猪进行讨论，涉及猪的性质的其他有关参数均视为常数；（2）猪随着体重的增长,生长速度不断减慢；（3）猪随着体重的增加饲养费用越来越多，达到最大体重后，单位时间消耗的饲养费为一常数 ；（4）C(t,x)为常数C依假设（3），单位时间消耗的饲养费可分为两部分： 一部分与体重有关（如饲料费用）记为β另一部分为固定费用（如饲养员薪金）为r-β由平衡原理，单位时间间隔[t,t+Δt]为饲养费用的增加量为f(t+Δt)-f(t)=(r-β)Δt+⎰∆+tt t m x z g )(βdz其中右端第一项为固定费总值，第二项为与体重有关费用 由积分中值定理可得这一部分结果为：t t t x x m ∆∆+)(θβ,(0<θ<1)于是f(t+Δt)-f(t)=(r-β)Δt+mx βx(t+θΔt)Δt 两边同除以 Δt 且Δt 0→得：])(1[)()(mm x t g r t g x r dt df--=+-=βββ 由f(0)=0，另得)1(m x x r dt df--=β 及))(1(m x t g dt dg -=αY(0)=0 ③ x(0)=0x t≥0的方程是一阶线性非齐次微分方程： g(t)’+)(t g x m α=α带入一阶线性非其次微分方程的求解公式可解得： g(t)=)()(m m m m x t m t x dt x dt x e x e c dt ke e αααα----=+⎰⎰⎰又 g(0)=0x 即得①的解为：g(t)=m x +(0x －m x )t x m eα- 由④可解出：1-g(t)/m x =(1-t x m m e x x α-)0代入方程③，便有其变形m x t m e x x r dt dfαβ---=)1(0直接积分而获得 f(t)=rt-)1)((0m x t m e x x ααβ---易见，α越大，f(t)越小，即增长速度越大，饲养费越小，符合实际。

论文：数学建模养猪策略(一)摘要本文根据养猪场某头猪的重量增长数据建立数学模型对该地区未来猪的体重作出相应的预测，首先我们建立了Logistic模型，通过matlab数据拟合并求解出第25天的体重预测,通过数据检验和误差分析，发现相对误差较大。

通过拟合求解,根据利润公式, 获得最大利润时的天数，所以取得最大利润.(二)关键字猪重量预测，阻滞增长模型（Logistic模型），误差分段加权(三)问题重述：三．问题分析问题1：初步判断，猪的体重与饲养时间成正比例关系，我们可以对比指数模型、二次模型和阻滞增长模型寻找他们最适合的关系。

把第25天带入关系式中求解出25天时猪的体重。

问题2：投入资金可使生猪体重随时间增加，但预测生猪出售的市场价格随时间下降，应该存在一个最佳的出售时机，使获得的利润最大。

实际上，在较短的时段内，成本大致不会改变，而生猪的体重较容易得到准确的估计值，但是生猪的出售的市场价格会经常发生波动。

根据题意，可以先假设农场每天投入的成本、生猪每天增加的体重和生猪出售的市场价格的每天的降幅都是常数，建立和求解数学模型，得到生猪出售的最佳时机，然后讨论参数变化对模型解答的影响，最后讨论模型解答对模型假设的依赖性。

四.建模过程问题一：模型建立模型一：指数增长模型模型假设、模型变量和函数定义1.猪的体重增长率r 其中)0(>r2.t 时间时，猪的体重为x （t ）符号说明1．r 猪的体重增长率2．x 当前猪体重模型分析与模型建立已假定猪的体重增长率为一常数r ，则由指数增长模型，可以得到猪体重的指数增长公式，由此预测未来猪的体重。

依照上面的定义和假设，有： 指数增长模型：rx dtdx =，0)0(x x = 可解得：rt e x t x 0)(=把1.10)1(=x 代入上述方程二式解之得：)(r 00)(t t e x t x -= 其中（10=t ）模型求解及检验通过对模型的求解，我们得到0.074916=r /1天。

售猪问题的讨论分析摘要本文针对猪的日增重量和出售价格及养猪成本随时间的变化，建立了出售猪的时间和收益的函数模型。

并分析了猪的饲养成本对最佳售猪时间的灵敏度。

由于题目中未明确说明猪的日增重量及价格的日减少率是否相同，我们在建模时假定猪的日增重量和价格的日减少率保持不变，并且假设猪在待售期间不再有其他花费。

做出模型后再对相关变量做灵敏度分析。

我们令继续饲养的时间的天数为t，猪的日增重量为g(KG)，生猪的初始售价为p0，生猪价格的日减少量为r，饲养生猪不到前期投入为k0，每天饲养的花费为k,在继续饲养期间生猪的重量变化为w(t)=w0+gt，令在继续饲养期间生猪的出售价格变化P(t)=p0-rt，令在继续饲养期间生猪的饲养的总花费为C(t)=k0+kt，令在继续饲养期间生猪的总收益为R(t)=p(t)w(t)。

则可得到饲养天t后售猪得到的净收益的模型为为：P(t)=R(t)-C(t)=(p0-rt)(w0+gt)-(k0+kt)关键词：售猪收益收益最大化日增重量养猪成本价格减少率一，问题的重述在售猪问题中，1. 对每天的饲养花费做灵敏性分析，分别考虑饲养花费对最佳售猪时间和相应收益的影响。

2. 进一步考虑，如果有新的饲养方式，每天的饲养花费为8元，会使猪按2.2 公斤/天增重，那么是否值得改变饲养方式？求出使饲养方式值得改变的最小的增重率。

二，问题的分析1.1：问题一的分析：第一题是求解饲养花费对最佳售猪时间和相应收益的影响，求出最佳销售时间和净收益对每天的饲养花费的灵敏度在每天的饲养花费估计值附近的值，进行最佳销售时间和净收益对每天的饲养花费的灵敏度分析。

关键是要建立最佳销售时间和净收益对每天的饲养花费的灵敏度的表达式。

.2：问题二的分析第二题中需要考虑当生猪的每天的饲养花费为8元，会使猪按2.2 公斤/天增重时是否值得改变饲养方式并且求出使饲养方式值得改变的最小的增重率。

要知道是否值得改变饲养方式就需要先算出饲养花费为8元，增重为2.2公斤每天饲养方式的最大收益及出售的最佳时机。

生猪的出售时机二、问题分析投入资金使生猪体重随时间增加，出售单价随时间减少，故存在最佳出售时机，使利润最大。

一、问题描述饲养场每天投入4元资金，用于饲料、人力、设备，估计可使80千克重的生猪体重增加2公斤。

市场价格目前为每千克8元，但是预测每天会降低0.1元，问生猪应何时出售。

如果估计和预测有误差，对结果有何影响。

三、问题求解设生猪每天增重为r=2，市场价格每天下降为g=0.1。

若当前出售，利润为80×8=640（元）t 天出售,生猪体重：w=80+rt出售价格：p=8-gt 销售收入：R=pw资金投入：C=4t 利润：Q=R-C=pw -C则Q(t)=(8-gt)(80+rt)-4t；求t，使Q(t)最大。

用mathematica求解：D[(8-g*t)*(80+r*t)-4t,t]-4+r (8-g t)-g (80+r t)Solve[-4+r (8-g t)-g (80+r t) 0,t]即敏感性分析研究 r, g 变化时对模型结果的影响 估计r=2，g=0.1 1、 设g=0.1不变 , 4060, 1.5r t r r-=≥ 用mathematica 画图： Plot[(40*r-60)/r, {r,1.5,3},Frame->True,PlotLabel->"t 对r", PlotStyle->{RGBColor[0,0,1]}]t 对r 的（相对）敏感度Δ/(,)Δ/t t S t r r r = dt r dr t ≈ 60(,)34060S t r r ≈=- 即：生猪每天体重增加量r 增加1%，出售时间推迟3%。

4402r g t rg--=2、设r=2不变，320,00.15g t g g -=≤≤用mathematica 画图：Plot[(3-20*g)/g, {g,0.06,0.15},Frame ->True, PlotLabel->"t 对r", PlotStyle ->{RGBColor[0,0,1]}]t 对g 的（相对）敏感度Δ/(,)Δ/t t dt g S t g g g dg t =≈ 3(,)3320S t g g =-=-- 即：生猪价格每天的降低量g 增加1%，出售时间提前3%。

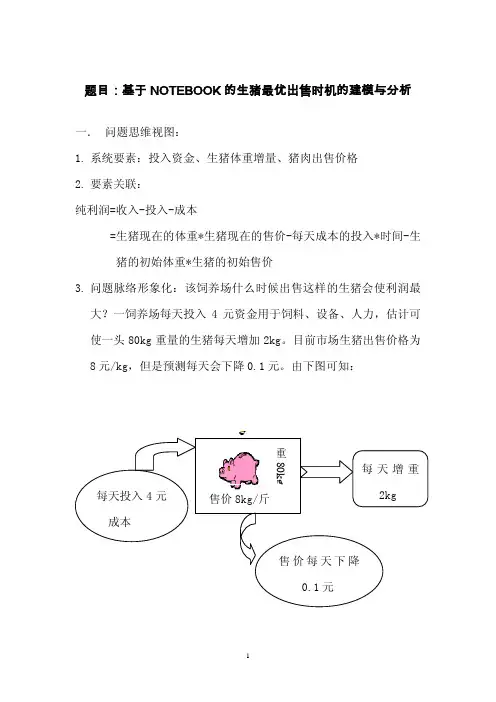
题目：基于NOTEBOOK的生猪最优出售时机的建模与分析 一． 问题思维视图：1.系统要素：投入资金、生猪体重增量、猪肉出售价格2.要素关联：纯利润=收入-投入-成本=生猪现在的体重*生猪现在的售价-每天成本的投入*时间-生猪的初始体重*生猪的初始售价3.问题脉络形象化：该饲养场什么时候出售这样的生猪会使利润最大？一饲养场每天投入4元资金用于饲料、设备、人力，估计可使一头80kg重量的生猪每天增加2kg。

目前市场生猪出售价格为8元/kg，但是预测每天会下降0.1元。

由下图可知：二． 数学刻画：1.给定每天投入4元资金使生猪体重每天增加常数r（=2kg）；生猪出售的市场价格每天降低常数g(=0.1)。

2.给出如下符号列表：符号 t w p C Q R含义 时间 生猪体重单价 t天资金投入纯利润出售收入单位 天 kg 元/kg 元 元 元三． 模型推演：假设r=2，g=0.1，t天后出售，则：生猪体重：w=80+r*t（r=2）; 出售单价：p=8-g*t;出售收入：R=p*w； 资金投入: C=4*t;于是利润为：Q=R-C-8*80.从而得到目标函数(纯利润)：Q(t)=（8-g*t）(80+r*t)-4*t-640 （1）其中，求t（>=0）使Q(t)最大。

这是二次函数最值问题，而且是个现实中的优化问题，故Q(t)的一阶导数为零的t（t>=0）值可使Q（t）取最大值。

先求Q(t)一阶导数：syms t;Q(t)=(8-g*t)*(80+r*t)-4*t-640;y=diff(Q(t),t)y =- r*(g*t-8) - g*(r*t + 80) - 4[g,t,r]=solve('-r*(g*t-80)-g*(r*t+80)=4','g=g','r=r')g =z1t =( 40*z1 + 2)/(z*z1)r =z即： t=(4*r-40*g-2)./(r*g ) (2)在这个模型中：取r=2，g=0.1，则：Q（t）=（8-0.1*t)*(80+2*t)-4*t-640）目标函数MATLAB作图如下：ezplot('(8-0.1*t)*(80+2*t)-4*t-640',[0,20])hold onxlabel('t坐标'); ylabel('Q(t)坐标');从图象可知t=10时，Q（t）max=10。

猪的出栏时机与销售渠道选择猪的养殖是当前农业养殖业中非常重要的一部分，而猪的出栏时机和销售渠道的选择更是养殖业者需要考虑的重要问题。

作为一名兽医专家，我深知这些问题对于养殖业者来说至关重要。

在本文中，我将从猪的出栏时机和销售渠道两个方面进行深入探讨。

首先，猪的出栏时机对于养殖业者来说至关重要。

猪出栏的时机需要根据猪的品种、饲养环境、饲料配方、饲养技术等因素进行合理决策。

一般来说，猪的出栏时间应该在猪达到市场重量的同时，也要考虑到猪肉市场的需求情况。

在市场需求旺盛的时候，出栏的时间可以稍微提前，以获取较高的销售价格。

而在市场需求相对较低的时候，可以适当延迟出栏时间，以避免价格下跌对养殖业者的影响。

其次，选择合适的销售渠道是猪养殖业者不可忽视的问题。

不同的销售渠道在市场定价和客户群体方面都有所不同。

养殖业者可以选择直接销售给个体户或者肉类加工厂，也可以通过合作社、批发市场甚至是电商平台进行销售。

在选择销售渠道时，养殖业者需要考虑自身实力和资源，并根据市场需求和竞争情况进行合理决策。

同时，养殖业者还需要了解销售渠道的政策规定和相关法律法规，确保自己的销售行为符合规范。

在选择销售渠道时，养殖业者还需要考虑交通条件和销售环境。

交通条件好的地方可以选择远离养殖场的地方进行销售，以获得更好的销售价格和更广阔的销售市场。

而交通条件相对较差的地方，可以选择找寻附近的加工厂和批发市场进行销售，以减少运输成本和销售经验。

另外，大型超市和电商平台也是一些养殖业者选择的销售渠道，这些渠道拥有更广泛的销售网络和稳定的销售市场，但需要注意与平台合作的合同和规则。

此外，养殖业者在选择销售渠道时还需要考虑金融服务、物流配送和售后服务等方面的支持。

一些市场较大的销售渠道可以为养殖业者提供贷款、保险和售后服务等支持，这有助于提高养殖业者的销售能力和竞争力。

同时，养殖业者也需要与物流公司合作，确保猪肉能够按时安全送达目的地。

综上所述，猪的出栏时机和销售渠道选择是养殖业者需要认真考虑的问题。

2010高教社杯全国大学生数学建模竞赛承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人（包括指导教师）研究、讨论与赛题有关的问题。

我们知道，抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。

我们郑重承诺，严格遵守竞赛规则，以保证竞赛的公正、公平性。

如有违反竞赛规则的行为，我们将受到严肃处理。

我们参赛选择的题号是（从A/B/C/D中选择一项填写）：我们的参赛报名号为（如果赛区设置报名号的话）：所属学校（请填写完整的全名）：鄂东职业技术学院参赛队员(打印并签名) ：1. 吴永兵2.3.指导教师或指导教师组负责人(打印并签名)：徐金华日期： 2010 年 7 月 5 日2010高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号（由赛区组委会评阅前进行编号）：全国统一编号（由赛区组委会送交全国前编号）：全国评阅编号（由全国组委会评阅前进行编号）：生猪的出售时机摘要这篇论文介绍生猪长大后的出售时机问题。

考察生猪出售的最佳时机，使获得的利益最大。

其中涉及的因素有价格、生长速度，采用预测的方式构建数学模型分析，并对这些因素进行敏感性分析和强健性分析。

关键词：价格变化生长速度敏感性分析强健性分析一、背景介绍某一饲养场每天投入4元资金用于饲料、设备、人力，工作人员估计可使一头80公斤重的生猪每天增加2公斤．目前生猪出售的市场价格为每公斤8元，但是预测每天会降低0．1元，那么该场应该什么时候出售这样的生猪，才能使收益最大．如果上面的估计和预测有出入，对结果有多大影响呢．二、问题分析投入资金可使生猪体重随时间增长，那么是不是投入越多的资金获得的利益越大呢，很显然不是的，大家由背景可知售价(单价)随时间减少，应该存在一个最佳的出售时机，使获得利润最大．这是一个优化问题，根据给出的条件，可作如下的简化假设．三、模型假设每天投入4元资金使生猪体重每天增加常数r (=2公斤)；生猪出售的市场价格每天降低常数g(=0．1元)．四、模型建立给出以下记号：t～时间(天)．w～生猪体重(公斤)；~p单价 (元／公斤)；R-出售的收入(元)；C-t天投入的资金(元)；Q-纯利润(元)．按照假设，)1.0rrtgtw．又知道tp=g=，再考虑,=R4Cpw2),8((80===-+到纯利润应扣掉以当前价格(8元／公斤)出售80公斤生猪的收入，有80R8⨯=CQ，--得到目标函数(纯利润)为其中1.0t使)(≥,2=r．求)0=gQ最大．(t五、模型求解这是求一个二次函数最大值问题，用代数或微分法容易得到当1.0,10=t，即10天后出售，可得最大纯利润20元．(=Q,2==gr时，20)10六、敏感性分析由于模型假设中的参数(生猪每天体重的增加r和价格的降低g)是估计和预测的，所以应该研究它们有所变化时对模型结果的影响．1．设每天生猪价格的降低1.0g元不变，研究r变化的影口向，由(2)式可得t是r的增函数，表1和图3给出它们的关系．2．设每天生猪体重的增加r=2公斤不变，研究g变化的影响，由(2)式可得t是r的减函数，表2和图4给出它们的关系．可以用相对改变量衡量结果对参数的敏感程度．t 对r 的敏感度记作).(r t S ，定义为由(3)式，当r =2时可算出即生猪每天体重r 增加1％，出售时间推迟3％． 类似地定义t 对g 的敏感度).(g t S ，由(4)式，当g=0．1时可算出即生猪价格每天的降低g 增加1％，出售时间提前3％。

数学建模论文肥猪的最佳销售时机作者:摘要：人们通过对猪的饲养和销售，总希望获阿得最大收益。

因此建立与此相关的数学模型来求解最大收益与最佳销售时间就有着重要的实际意义。

对于收入部分，由于市场价格受多种不确定因素的影响且变化较大，我们假设价格保持不变，所以收入正比于猪的体重；猪的体重与时间的关系可以用Gompertz模型来模拟。

对于成本部分，认为由饲料成本和猪仔价格组成。

通过对饲料消耗量和体重的实际数据的分析，发现线性拟合的效果较理想，由此利用该关系确定饲料的消耗。

至此问题转化为建立猪的生长模型和饲料消耗模型。

对于最优化模型，我们从两个方面进行了考虑，一是总利润的最大值，二是日均利润最大值。

通过以上分析，较好地解决了肥猪最佳销售时机问题，对养殖户有一定参考意义。

肥猪的最佳销售时机关键词：数学建模；肥猪最佳销售时机；饲料消耗模型；Gompertz模型问题的叙述与分析：一般从事猪的饲养和销售总希望获得利润，因此饲养某种猪是否获利，怎样获得最大利润，是饲养者必须考虑的问题。

如果把饲养技术水平，猪的性质等因素看成不变的，且不考虑市场的需求变化，那么影响获利大小的一个主要因素是如何选择猪的售出时机，即何时把猪卖出获利最大。

也许有人认为，猪养的越大，售出后获利愈大，其实不然，因为随着猪的生长，单位时间消耗的饲养费用也就愈多，但同时其体重的增长速度却不断下降，所以饲养时间过长是不合算的。

考虑某个品种猪的最佳销售时机的数学模型。

要求猪的最佳销售时机，目标是寻求最大利润的取得，由此实际上需要找出收入和支出分别是什么，受什么影响。

为了简化问题，我们只考虑一头猪的利润，并且做了一系列的理想化的假设，比如生猪价格固定等，所以收入与猪的体重成正比，而成本则由固定成本（如猪仔价格，防疫费用）和变化成本（主要是饲料的消耗）组成，最终问题转化成建立猪的生长模型和饲料消耗模型。

通过查阅大量相关资料，我们选择了用Gompertz模型来模拟猪的生长情况，而对于后者，我们对实际原始数据进行了分析，建立了较理想的模型。

生猪的出售时机模型随着经济的发展，养殖业一直是重要的农业产业之一，而猪肉作为人均消费量最大的肉类，也成为了养殖业中的主要产品之一。

然而，在养殖业中，猪的出售时机成为了一个重要的问题，因为在错误的时机出售猪可能会导致养殖业的损失。

因此，针对猪的出售时机问题，建立一个猪的出售时机模型，本文主要分为以下几个方面进行探讨：（一）养殖周期首先从猪的养殖周期来分析，从生猪出生到出栏，需要3-6个月的时间，因此，养殖业主可以根据养殖周期预测猪的出售时机。

根据猪肉市场行情变化，可以预计未来的猪肉价格，从而在适当的时机出手猪肉。

如果养殖业主在市场行情高峰期出售猪肉，可以获得更好的销售价格。

（二）饲料价格养殖猪的另一个重要因素是饲料，因此，饲料价格对养殖业主出售猪的时机也有很大的影响。

当饲料价格高时，养殖成本会增加，因此养殖业主可以选择在饲料价格下降时出售猪肉，以减少成本和获得更好的利润。

（三）猪重猪的重量是另一个值得考虑的因素。

成熟的生猪一般在120-150公斤左右，但不同地区、不同品种、不同年龄段的猪重不尽相同。

因此，养殖业主应该根据猪的生长情况和销售市场需求来决定出售猪肉的时机。

例如，在某些地区，一些消费者更喜欢优质的五花肉，因此，养殖业主可以在猪的脂肪含量达到最佳水平时出售猪肉，从而获得更好的销售价格。

（四）销售渠道出售生猪的时机还与销售渠道有关。

如果养殖业主将猪肉出售给猪肉加工厂或超市，可以根据猪肉的需求来决定出售时机。

然而，如果养殖业主选择直接面向消费者销售猪肉，则需要更加谨慎，选择在消费者需求高峰期出售猪肉，以获得更好的销售利润。

总之，猪的出售时机是养殖业主需要考虑的重要问题，其出售时机需要充分考虑猪的养殖周期、饲料价格、猪重、销售渠道等多种因素。

此外，养殖业主还需要根据市场行情预测未来的猪肉价格，从而选择适当的出售时机，以获得更好的销售价格和营利。

生猪出售时机的数学模型[推荐]猪肉是国人最喜爱的一种肉类产品，也是世界上最消费的肉类之一。

对于养殖户来说，合理的出售时间很重要，可以使得收益最大化，同时也可以保证市场的供需平衡。

在本文中，我们将建立一个数学模型来预测生猪出售的最佳时间，以帮助养殖户做出更加准确的决策。

1. 市场需求变化趋势首先，我们需要了解市场需求的变化趋势。

因为市场需求的变化会直接影响到生猪价格的波动。

一般来说，猪肉的需求与季节、人口、经济因素等紧密相关。

下面就以一些常见因素为例，简单分析需求趋势的变化规律。

（1）季节性需求猪肉是我国重要的春节离不开的食品，季节性需求是猪肉价格波动的重要因素。

春节前各地的销售市场都会陆续大幅增加猪肉品种的销售，销售量的提高占据了市场的主要推动力量。

过年过节，猪肉是各个家庭的必备品，所以春节前后不仅销量大增，而且价格也会慢慢上升。

（2）人口增长和改变的消费习惯随着我国人口增长和生活习惯、消费观念的改变，猪肉消费的需求也发生了很大的变化。

由于人口数量不断增长，猪肉的总需求量也在不断提升，所以在这种市场背景下，生猪的价格会保持较为长期的上升趋势。

（3）经济因素人们消费能力与市场经济环境密切相关，市场经济催生了人们消费需求的增长，生猪价格一般也会随着市场经济的发展而稳步提高。

2. 生猪价格波动规律了解到市场需求的变化趋势后，我们需要在此基础上分析生猪价格波动的规律。

生猪价格的波动可以分为短期和长期两种趋势，短期波动受季节和政策等因素的影响比较大，而长期波动则受到供需关系等因素的影响比较大。

（1）短期波动规律短期波动受到季节和政策等因素的影响，波动幅度相对较小。

一般在春节、端午节、中秋节等节假日前期，生猪价格仍会有所上升。

而在政府宏观调控政策出现较大变动时，也会对生猪价格产生影响。

长期波动受到供需关系等因素的影响。

由于生猪属于周期性消费品，所以在市场需求增长的时期，生猪价格总体上呈现上升趋势。

但是随着养殖场数量的增加和技术的不断发展，生猪生产能力不断提高，当供大于求时，猪肉价格也会出现下跌现象。

饲养场牲畜的出售时机数学建模毕业论文摘要：饲养场饲养的牲畜出售时机的决策对于饲养场的盈亏影响很大。

本文通过建立数学模型，在分析饲料成本、市场情况、生长周期等因素的基础上，探究了饲养场牲畜的最佳出售时机，并通过实例验证了模型的可行性和准确性。

关键词：饲养场，牲畜，出售时机，数学模型第一章前言随着社会经济的发展，畜牧业在国民经济中的地位日益重要，饲养场成为了畜牧业发展的重要力量。

饲养场在饲养过程中需要考虑很多因素，其中牲畜出售时机的决策对于饲养场的盈亏影响很大。

因此，如何选择合适的出售时机，成为了饲养场必须面对的问题。

本文在饲养场牲畜出售时机的问题上展开研究，并通过建立数学模型，分析饲料成本、市场情况、生长周期等因素，探究了饲养场牲畜的最佳出售时机，并通过实例验证了模型的可行性和准确性。

第二章相关研究牲畜的出售时机问题在畜牧业的发展中一直是一个关注的问题。

在国内外对牲畜出售时机问题的研究中，许多学者通过建立模型，分析市场环境、生长周期和饲料成本等因素，提出了不同的决策方案。

例如，曹志强等人（2013）通过建立数学模型，综合考虑生产成本、市场价格、还贷周期等因素，提出了一套系统的牛出售时机决策模型。

此外，王吉平等人（2017）也建立了一个数学模型，通过分析市场需求和饲料成本等因素，提出了合适的出售时机。

以上研究表明，建立数学模型对牲畜出售时机的决策具有很大的帮助。

本文将在前人研究的基础上，分析饲养场牲畜出售时机的最佳决策，并建立数学模型进行验证。

第三章模型建立3.1 模型假设1. 假设牲畜饲养周期为T个单位时间。

2. 假设饲养场每单位时间需要支付k元饲料基础成本。

3. 假设每单位时间出售一头牲畜可以获利p元。

4. 假设饲料价格不受外部因素影响。

3.2 模型建立根据以上假设，我们可以建立如下的决策模型：首先，我们可以用C(t)表示第t个单位时间时，一头牲畜饲养的成本。

由于每单位时间需要支付k元基础成本，因此可以得到：C(t) = k * t其次，每单位时间出售一头牲畜可以获利p元，因此我们可以用P(t)表示第t个单位时间时，出售一头牲畜的收益。

猪的最佳销售一、猪的最佳销售时机问题： 1、问题的提出：对于猪的商业性饲养和销售，人们总是希望获得最大的利润，在市场需求不变的情况下，如果我们不考虑猪的饲养技术、水平，猪的类型等因素的影响，那么影响销售利润的主要因素，就是销售时机问题，由于随着猪的生长，单位时间消耗的饲养费用逐渐增多，而猪的体重增长却逐渐变慢，因此对猪的饲养时间过长是不合算的。

假定一头猪在开始饲养时的重量为x 0，在饲养后任意时刻t 的重量为x (t )，对于某一品种的猪，它的最大重量假定为X 0，猪的最小出售体重为x s ，相应的饲养时间为t s 。

一头猪从开始饲养到时刻t 所需的费用为y (t )，同时我们假定反映猪体重变化速度的参数为α，猪在达到最大体重后，单位时间的饲养费为y ，反映饲养费用变化大小的参数为λ，请根据上面的假设，建立起猪的最佳销售时机的数学模型，并用下面所给的数据验证你的模型。

假设X 0=200（kg ），x s =75（kg ），α=0.5（kg/天），猪的市场销售价设为c =6元/kg ，γ=1.5（元/天），λ=1（元/天），x 0=5kg 。

2、问题分析：由于猪在进行饲养时已具有一定的体重，而其体重的增加随饲养时间的延长逐渐减慢，因此由Logistic 模型可得)1(0X x dt dx -=α；又由于猪的体重增加，单位时间消耗的饲养费用就越多，达到最大体重后，饲养费用为常数γ，所以有)1(0X x dt dy --=λγ，因此，得到微分方程：⎪⎪⎪⎩⎪⎪⎪⎨⎧==--=-=0)0()0()1()1(000y x x X x dt dy X x dt dx λγα 求解可得：⎪⎪⎩⎪⎪⎨⎧---=--=--)1)(()()()(0000000t X t X e x X t t y e x X X t x αααλγ （1） 养猪能否获利，主要看猪从出生到t s 时，如果出售是否可以获利，因此，获利的充要条件为：)(00s s t y c x c x +≥ （2）其中c 0为仔猪的价格。