《刚体的角动量守恒》PPT课件

i
12
M外 Mi外 ri Fi
i
i
----各质点所受外力矩的矢量 和称为质点系所受合外力矩
M内 Mi内 (ri fij ) 0
i
i
ji
----各质点所受内力矩 的矢量和
（证明如下：）
Fi
m2
m1
mi
fij ri
f ji m j
0
rj
13
内力总是成对出现的，所以内力矩也是成对出
：质量线密度
线积分
对质量面分布的刚体： dm dS
：质量面密度
对质量体分布的刚体：dm dV
：质量体密度
面积分
体积分 26
计算转动惯量 I 的三条有用的定理：
（1）叠加定理:对同一转轴 I 有可叠加性
I Ii
I mr mr mr
m2
I
r1
m1
r2 r3
m3
转轴
（2）平行轴定理: I Ic md 2
常矢量
7
若 M 0 ，则 L 常矢量
M 0
的条件是
— 质点角动量守恒定律
F 0
或 F 过固定点：有心力
（如行星受的万有引力）
角动量守恒定律是物理学的基本定
律之一，它不仅适用于宏观体系，也 适用于微观体系，而且在高速低速范 围均适用。
8
角动量守恒定律可导出行星运动的开
普勒第二定律：
L
（书P79页例3.1）
i
与内力矩无关 v
守恒条件 M i 0 i
20
§3.3 定轴转动刚体的角动量 转动惯量 一、定轴转动刚体的角动量
把刚体看作非常多质元构成 的质点系，第i个质元对原点o
z v vvi

M M1 M2 M3
（2）刚体内作用力和反作用力的力矩互相抵消．
M ij
rj
j

O
d ri
i Fji
Fij
Mij M ji
M ji
（3）力矩必须明确是对哪个点（或轴） 8
三、角动量定理 角动量守恒
1.质点的角动量定理
将角动量 L r p 两边对时间求导
14
角动量守恒定律是一条普遍的规律，存在
于很多自然现象中，例如，行星受恒星引力作
用作椭圆轨道运动，引力的作用线始终通过恒
星中心，这样的力称为有心力。由于有心力对
力心的力矩恒为零，因此，受有心力作用的质
点对力心的角动量守恒。 掠面速度
·m
f
r
dS 1 r v dt 2
o r
vdt
12
将角动量定理的微分形式 M dL 两边乘以
dt 并积分得
t
dt
0 M dt L L0
t
0 M
dt :
质点或质点系的合外力矩的冲量矩；
L0 与L 分别是质点或质点系始末状态的角动量。
在一段时间内，质点（系）角动量的增量
等于作用于质点（系）的合外力矩的冲量
矩——质点（系）角动量定理的积分形式
Lrp
(xi yj zk ) (pxi py j pzk )
各坐标轴的分量
Lx ypz zpy Ly zpx xpz Lz xpy ypx
分别称为对 x、y 、z 轴的角动量
2
例 质点L沿某r一 p方向r作 m直v线运动，对O点的角动量 角动量大小为
L rm vsin m v d

角动量守恒定律
一、角动量定理
由转动定律
4-3 角动量守恒定律
M dL dt
Mdt dL
L L t2 Mdt L2 dL
t1
L1
21
系统所受合外力矩的冲量矩等于系统 角动量的增量。
4-3 角动量守恒定律
二、角动量守恒定律
由角动量定理：
t2 t1
M
d
t
L2
L1
若 M 0，则 L J =恒矢量
4-3 角动量守恒定律
一、角动量定理：
t2 tL1
二、角动量守恒定律：
若 M 0，则 L J =恒量
1、刚体： J不变， 也不变（大小、方向） 2、非刚体： J变， 变 → J ，；J ，
课后思考：
4-3 角动量守恒定律
试分析为什么直升机要安装尾翼螺旋桨呢？
4-3 角动量守恒定律
内容：当系统所受合外力矩为零时，则 系统的总角动量保持不变。
应用：
4-3 角动量守恒定律
1、刚体： J不变， 也不变 （大小、方向）
应用：
4-3 角动量守恒定律
2、非刚体： J变， 变 → J ，；J ，
4-3 角动量守恒定律
2、非刚体： J变， 变 → J ，；J ，
J ，
J ，
小结：

匀直细杆对端垂轴旳
平行移轴定理
对质心轴旳转动惯量 对新轴旳转动惯量
质心
例如：
时
新轴对心轴旳平移量
新轴 质心轴
代入可得 端
匀质薄圆盘对圆心垂盘轴算旳 例
取半径为 微宽为 旳窄环带旳质量为质元
球体算例 匀质实心球对心轴旳 可看成是许多半径不同旳共轴 薄圆盘旳转动惯量 旳迭加 距 为 、半径为 、微厚为 旳薄圆盘旳转动惯量为
a = Rb
T2 – m2 g = m2a ( T1 – T2 ) R = Ib
及
I
=
1 2
mR2
得
b=
(m1-m2)g
R(m1+ m2+ m
2)
常量
故
由
m2
a
G2
m1
a
G1
(m1-m2)g
R(m1+ m2+ m 2)
t (m1-m2)g
g 2 (rad)
R(m1+ m2+ m 2)
两匀直细杆
q
转动定两律者瞬例时题角加五速度之比
与 时刻相应，何时
则何时
，
何时 恒定 则何时 恒定。
匀直 细杆一 端为轴 水平静 止释放
转动定律例转题动 二( T2 – T1 ) R = Ib
I=mR2 2
R
m
T2
T1
a
m2
m1
b
平动 m2 g – T2 = m2a
T2
T1
T1 – m1 g = m1a
线-角 a = Rb
T2
T1
联立解得
a
G2
力矩旳功算例 拨动圆盘转一周，摩擦阻力矩旳功旳大小

若转轴不动，称定轴转动。 O
1. 定轴转动特征
(1) 刚体上各点都在垂直于固定轴的平面内(转动平面) 做圆周运动.其圆心都在一条固定不动的直线(转轴)上.
(2) 刚体上各点到转轴的垂直线在同样的时间内所转过 的角度都相同。因而用角量描述刚体的运动.
www. ******.com
3.3 刚体的运动
2. 定轴转动的描述
解：
N

R
T
Mg
T' M.
a R
mg
m
www. ******.com
3.4 刚体的角动量 转动定律 转动惯量
根据转动定律 根据牛顿第二定律
TR=Jβ
1 MR2
2
mg-T=ma
因绳与滑轮间无滑动，所以 a=Rβ
解以上三式得
a mg mM /2
a
mg
R R( m M / 2 )
rF
www. ******.com
3.1 质点的角动量 力矩
3.1.2 质点的角动量定理
力矩定义：
M rF
力矩大小：
M r F sinθ 式中 rsinθ d 为力臂，则
M Fd
因 Fsin θ F ，即合力切向分量，所以：
M r F
www. ******.com
3.2 质点的角动量守恒定律
(1) 角坐标 称角位置或角坐标。
规定逆时针转向 为正。

p x
O
刚体定轴转动的运动学方程
= (t) (2) 角位移
为 t时间内刚体所转过的角度。
p x O
www. ******.com
3.3 刚体的运动
(3) 角速度 角速度 lim Δ d Δt0 Δt dt 在定轴转动中，转向只可能有

转动惯量的特性
只与刚体的质量和各质点到转动轴 的距离有关，与转动角速度的大小 无关。
02
角动量定理
角动量的定义与性质
角动量的定义
角动量是描述刚体转动状态的物理量 ，等于刚体的转动惯量乘以角速度。
角动量的性质
角动量是矢量，具有方向和大小；对 于定轴转动，角动量位于转轴上；角 动量是相对量，与参考系的选择有关 。
理解角动量守恒定律的证明方法是深入理解该定律的重要途径。
详细描述
证明角动量守恒定律的方法主要有两种，一种是基于牛顿第二定律和转动定理推导，另一种是通过分析系统的能 量变化来证明。通过这些证明方法，可以更深入地理解角动量守恒定律的物理意义和适用条件。
04
刚体定轴转动的实例 分析
刚体定轴转动的实例介绍
角动量守恒定律的内容及应用
总结词
掌握角动量守恒定律的内容及应用是解决实际问题的关键。
详细描述
角动量守恒定律表明，对于不受外力矩或所受外力矩的矢量和为零的系统，其总角动量保持不变。这 一原理在日常生活、工程技术和科学研究中有广泛的应用，如行星运动、陀螺仪、火箭飞行等。
角动量守恒定律的证明方法
总结词
陀螺仪
风扇
陀螺仪是一个典型的刚体定轴转动实 例，其工作原理就是角动量守恒定律 。
当风扇的扇叶旋转时，可以将其视为 刚体定轴转动，这个过程涉及到角动 量定理的应用。
自行车轮
自行车轮在转动时，也是一个刚体定 轴转动的例子，其转动惯量对于理解 角动量定理和角动量守恒定律非常有 帮助。
刚体定轴转动的角动量定理应用实例
舞蹈演员在进行旋转动作时，可以通过改变身体的姿势来改变转动惯量，从而控制旋转的 速度。
刚体定轴转动的角动量守恒定律应用实例

i 1
可见即使对定轴转动，角动量L也不一定与方向相同
（本例中方向还一直在改变）。
第 49 页
z
本章中我们感兴趣的是定
L
ri
D Li
轴转动，即要研究角动量
v i 在z轴的分量Lz
q
Dmi
Ri
DLiz DLi cosq
O
Dmi Rivi cosq
Dmiri2
Lz DLiz (Dmiri2)
JZ
r 2dm
m
r2 r r (r h) (r h)
r2 h2 2h r
rdm 0 质心的定义 m
Jz
r2dm
m
h2dm 2h
m
m r2dm JC mh2
第 21 页
例3 一质量为 m ，半径为 R 的均匀薄圆盘，求通 过盘中心并与盘面垂直的轴的转动惯量。
解 dm 2 rdr
特别要注意： 转动惯量与转轴的位置有关。
转动惯量具有可相加性。
第 17 页
第 18 页
例2 计算质量为 m ，长为 l 的细棒绕通过其端点的 垂直轴的转动惯量。
解 J r2dm
dm dx m dx
l
J l x2 m dx 1 m x3 l
0l
3l 0
J 1 ml2 3
第 19 页
J r2dm
J 2 R r3dr 0 R4 1 mR2 22
r dr Ro
第 22 页
例4 质量m1、半径为 R的实心滑轮，可绕通过其质心 的轴无摩擦的转动。一根轻绳绕在其上，绳端挂一质
量为 m2的物体，绳子与滑轮间无相对滑动。求物体下 落的加速度和绳子的张力。
解
T
R

应该理解和掌握。 如果忽略滑轮的质量，则有
T1
T2
m1m2 g m1 m2
15
第15页/共59页
例题6 长度为l、质量为m 的均匀棒悬挂在通过
其顶端的水平轴上，并可绕此轴在竖直平面内作
无摩擦的摆动。如果棒自由摆动通过平衡位置时，
低端的速率为v，试求：
（1）棒通过平衡位置时的转动动能;
（2）棒摆动的最大偏角m ； （3）在从平衡位置到达最大偏角m 的过程中， 在任一位置时棒的角加速度。
M z
dM z
l g m ldl 1 Lmg
0
L
2
（2）求角加速度
根据转动定律 Mz J
其中，棒相对一端的转动惯量
3 g
2L
J 1 mL2 3
角加速度为负值，表示为减速转动
22
第22页/共59页
（3）求外力矩撤去后棒转过的转数 选求转过的总角度。根据匀变速定轴转动规律
0 02 2
m2R2 )1
1 2
m1R22
2
1 2
m1R2 m2R2
1 2
m1R2
1
1 2
m1 1 2
m2 m1
1
2.31rad
s1
38
第38页/共59页
例3如图所示，细杆（l，m）可绕端点O的水平轴转动，从水 平位置自由释放，在竖直位置与物体M相碰，物体与地面摩擦 系数为μ，相撞后，物体沿水平地面滑行一段s 后停止。 求：碰后杆质心C离地最大高度，并说明杆向左右摆的条件。 解（1） 自由下落过程 （E守恒）
将 代入上式： o2 1 o2L
2 3 g
转动的转数为： n 1 o2L 2 6 g
（4）求摩擦力矩所作的功

均为m. 问: 欲使细杆以恒定的角速度转动, 小虫应以多
大速率向细杆端点爬行? 解: 碰撞前后系统角动量 守恒
mv04l 112m2lm(4l)2
12v0 7l
7
12 v0
7l
角动量定理
MdLd(J)dJ
dt dt
dt
mcg o rsd(1m 2 m l2 ) r2 md r r
d t12
Mdt t0
L0 dL L L0 J J 0
定轴转动的刚体所受合外力矩的冲量矩等于刚体在
这段时间内对该轴的角动量的增量．
10
三 刚体对轴的角动量守恒定律
t
Mdt (J) t0
若 Miz 0 则JJ0
外力对某轴的力矩之和为零，则该物体对 同一轴的角动量守恒.
11
➢花样滑冰
➢跳水运动员跳水
i
刚体对某定轴的角动量等于刚体对该轴的 转动惯量与角速度的乘积．方向沿该转动 轴，并与这时转动的角速度方向相同．
9
2.刚体定轴转动的角动量定理
M J Jd d (J ) d L即 M = d L
d t d t d t
d t
定轴转动的刚体所受的合外力矩等于此时刚体角动
量对时间的变化率．
t
L
➢ 质点角动量（相对圆心） 例 质量很小长度为l 的均匀细杆, 可绕过其中心 O 并与纸面垂直的轴在竖直平面内转动 .
9 0 若 ，则
质点在垂直于 z 轴平面上以角速度 作半径为 的圆运动.
A
刚体对转轴的角动量就是刚体上各质元的角动量之和．
Lrpr m 这就是质点的角动量守恒定律。 v z 质点所受外力对某固定点的力矩为零，则质点对该固定点的角动量守恒。
刚体对转轴的角动量就是刚体上各质元的角动量之和．

第22页/共29页
2 .有心力场,对力心角动量守恒.
例: 质量为m的小球系在绳的一端，另一端通过圆孔向
下，水平面光滑，开始小球作圆周运动（r1,v1)然
后向下拉绳，使小球的运动轨迹为r2的圆周
求：v2=？
解： 作用在小球的力始
v2
终通过O点（有 心力）由质点角
v1
动量守恒：
r r O
1
2
mv1r1 mv2r2
第28页/共29页
谢谢您的观看！
第29页/共29页
r
0!
第11页/共29页
二、角动量守恒定律
质点角动量守恒
当M 0
,
L r (mv)
=恒矢量
当质点所受对参考点O的合力矩为零时，质点
对该参考点O的角动量为一恒矢量。
例：
L
v
m r
行星对太阳的径矢在相等的时间内扫过相等的面积. —–开普勒第二定律 Kepler laws
第12页/共29页
讨论：行星受力方向与矢径在一条直线（中心力），
第19页/共29页
1.孤立系.
第20页/共29页
1.孤立系.
为什么星系是扁状，盘型结构？
第21页/共29页
18世纪哲学家提出星云说，认为太阳系是由气云组 成的。气云原来很大，由自身引力而收缩，最后聚 集成一个个行星、卫星及太阳本身。但是万有引力 为什么不能把所有的天体吸引在一起而是形成一个 扁平的盘状？康德认为除了引力还有斥力，把向心 加速的天体散射到个方向。19世纪数学家拉普拉斯 完善了康德的星云说，指出旋转盘状结构的成因是 角动量守恒。我们可以把天体系统看成是不受外力 的孤立系统。原始气云弥漫在很大的范围内具有一 定的初始角动量J，当r变小的时，在垂直J的横方 向速度要增大，而平行J方向没有这个问题，所以 天体就形成了朝同一个方向旋转的盘状结构。 数学推导

如图质点m以速率v 做圆锥运动,求对O 点和对O点
的角动量. 设摆长为b.
[解] 如图对O点
Lmsvib n
O
b
L
L'
方向: 向上,是常矢量.
Om
对O´点
L m v b（b与v夹 角 为π）
2
方向 : 垂直摆线向外,方向始终在变,其端亦在水
平面内画一圆.不是常矢.
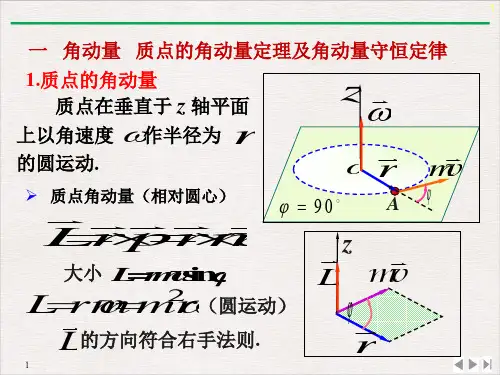
2. 质点的角动量定理
(牛顿第二定律)：质点所受合力等于质点动
z
L
p
r
单位
z
or
mv
90
说明
• a角).动并量非a .质点b d作周r 期p 性c曲线质沿点是运点直与d动以 线 直动 运 线才量 动 的有， 距p 原 离在
Lrprm v
o
Lrpsindp
• Lb参)是.考质矢点量点,定是的状义角态的量动..它量与是参相考系对和于参选考点定都的有关.
大学物理角动量守恒与刚体的定 轴转动
怎样思想，就有怎样的生活
第五章
角动量守恒与刚体的定轴转动
5－1 角动量与角动量守恒定律
角动量（也称动量矩）定义
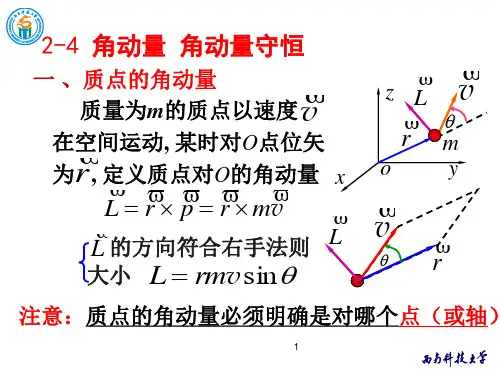
质量为 m的质点以速度 v在
空矢间为运r,动质, 点某相时对刻于相原对点原的点角O动的量位
定义为:
Lrprm v
L
mv
o
r
m
角动量在动量的基础上考虑了角度的因素。
这是质点角动量定理的积分形式
牛顿定律
导出
适用
质点角动量定理
惯性系
3. 质点的角动量守恒定律
M 0 , L r m v 恒矢量
质点所受合外力对某一固定点的力矩为零, 则质点 对该点的角动量保持不变.