下载文档原格式
第五讲万有引力定律一行星的运动1．地心说2. 日心说二开普勒天文学三定律：1. 开普勒第一定律（轨道定律）2. 开普勒第二定律（面积定律）3. 开普勒第三定律（周期定律）三万有引力定律1. 内容任意两个物体之间都存在着相互作用的引力，引力的大小与这两个物体质量的乘积成正比，与它们之间的距离的平方成反比。
表达式：221 r mmGF2. 万有引力常量引力常量G是英国物理学家卡文迪许，巧妙利用扭秤装置，在牛顿发现万有引力定律一百多年以后，于1798年第一次在实验室里比较准确地测量出来。
G=6.67×10-11N·m2 /kg23. 万有引力定律的适用条件仅仅适用于质点或可以看作质点的物体。
相距较远（相对于物体自身的尺寸）的物体和质量均匀分布的球体可以看作质点，此时，式中的r指两质点间的距离或球心间的距离。
4. 万有引力定律的应用（1）计算中心天体的质量和密度（2）发现未知天体四天体的运动1. 运动模型天体运动可看成是匀速圆周运动──其引力全部提供天体做圆周运动的向心力。
２．人造地球卫星（1）第一宇宙速度：也叫环绕速度，是人造地球卫星在地球表面附近做匀速圆周运动的速度。
既是卫星绕地球圆周运动的最大速度，也是发射卫星的最小速度，大小为7.9km/s。
（2）第二宇宙速度：也叫脱离速度，是使物体挣脱地球引力束缚的最小发射速度，大小为11.2km/s。
（3）第三宇宙速度：也叫逃逸速度，使物体挣脱太阳引力束缚的最小发射速度，大小为16.7km/s。
3. 地球同步卫星（1）同步卫星：所谓地球同步卫星，是相对于地面静止，和地球自转具有相同周期的卫星。
同步卫星必须位于赤道正上方距地面一定高度处。
（2）地球同步卫星的“六个一定”：①位置和绕行方向一定。
所有同步卫星都在赤道的正上方，运行方向与地球自转方向一致。
②周期一定。
同步卫星的运转周期与地球自转周期相同，即T =24h ③角速度一定。
同步卫星的角速度等于地球的自转角速度。
高中物理天体运动多星问题高中物理天体运动多星问题高中物理天体运动多星问题一直是物理教学中的难点，它涉及到天体的运动规律、万有引力、圆周运动等多个知识点。
下面我们将从定义、原理、解题方法三个方面来探讨这个问题。
一、什么是多星问题？多星问题是指在一个宇宙空间内，有两个或多个星球相互吸引，它们绕着共同的质心做圆周运动。
类似于我们太阳系中的双星系统，其中太阳和地球在相互引力作用下绕着共同质心运动。
二、多星问题的原理是什么？多星问题的原理仍然是万有引力定律。
根据万有引力定律，任何两个物体之间都存在相互吸引的力，其大小与它们的质量乘积成正比，与它们之间距离的平方成反比。
在多星系统中，每个星球都受到其他星球的引力作用，因此它们会相互绕转。
三、如何解决多星问题？解决多星问题需要用到圆周运动和万有引力的知识。
首先，我们需要找到各个星球之间的相互作用力，然后根据牛顿第二定律列出方程。
在处理多星问题时，需要注意各个星球的运动轨迹是绕着共同质心做圆周运动，因此我们需要先求出共同质心的位置。
在实际解题过程中，我们可以先根据题意画出图形，标出各个星球的位置和质量，然后根据万有引力定律和圆周运动的规律列出方程。
通常需要求解的是各个星球的运动轨迹和速度等物理量。
四、举例说明例如，在太阳系中，地球和太阳之间的距离是变化的，它们的共同质心位于太阳内部。
如果我们忽略其他行星的影响，那么地球围绕这个共同质心做圆周运动。
根据万有引力定律和牛顿第二定律，我们可以列出方程，求解出地球绕太阳运动的轨迹和速度等物理量。
总之，多星问题是高中物理天体运动中的一个难点，但只要我们掌握了万有引力定律、圆周运动等基本知识，通过认真分析题意，画出图形，列出方程，就可以正确求解问题。
通过研究多星问题，我们可以更深入地了解天体的运动规律，为未来的科学研究打下坚实的基础。
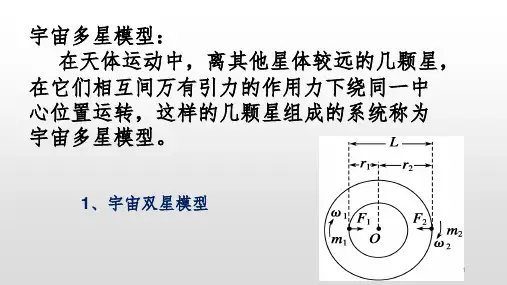
双星模型、三星模型、四星模型天体物理中的双星，三星，四星，多星系统是自然的天文现象，天体之间的相互作用遵循万有引力的规律，他们的运动规律也同样遵循开普勒行星运动的三条基本规律。
双星、三星系统的等效质量的计算，运行周期的计算等都是以万有引力提供向心力为出发点的【例题1】天文学家将相距较近、仅在彼此的引力作用下运行的两颗恒星称为双星。
双星系统在银河系中很普遍。
利用双星系统中两颗恒星的运动特征可推算出它们的总质量。
已知某双星系统中两颗恒星围绕它们连线上的某一固定点分别做匀速圆周运动，周期均为T，两颗恒星之间的距离为r，试推算这个双星系统的总质量。
（引力常量为G）【例题2】神奇的黑洞是近代引力理论所预言的一种特殊天体，探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系大麦哲伦云时，发现了LMCX3双星系统，它由可见星A和不可见的暗星B构成，两星视为质点，不考虑其他天体的影响.A、B围绕两者连线上的O点做匀速圆周运动，它们之间的距离保持不变，如图4-2所示.引力常量为G，由观测能够得到可见星A的速率v 和运行周期T.(1)可见星A所受暗星B的引力F a可等效为位于O点处质量为m′的星体(视为质点)对它的引力，设A 和B的质量分别为m1、m2，试求m′(用m1、m2表示).(2)求暗星B的质量m2与可见星A的速率v、运行周期T和质量m1之间的关系式；(3)恒星演化到末期，如果其质量大于太阳质量m s的2倍，它将有可能成为黑洞.若可见星A的速率v=2.7×105 m/s，运行周期T=4.7π×104 s，质量m1=6m s，试通过估算来判断暗星B有可能是黑洞吗？（G=6.67×10-11 N·m2/kg2，m s=2.0×1030 kg）【例题3】天体运动中，将两颗彼此相距较近的行星称为双星，它们在万有引力作用下间距始终保持不变，并沿半径不同的同心轨道作匀速园周运动，设双星间距为L，质量分别为M1、M2，试计算（1）双星的轨道半径（2）双星运动的周期。
【例题4】我们的银河系的恒星中大约四分之一是双星.某双星由质量不等的星体S1和S2构成,两星在相互之间的万有引力作用下绕两者连线上某一定点C做匀速圆周运动.由天文观察测得其运动周期为T,S1到C点的距离为r1,S1和S2的距离为r,已知引力常量为G.由此可求出S2的质量为（ D ）A.212)(4GTrrr2πB.2312π4GTrC.232π4GTrD.2122π4GTrr【例题5】如右图，质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速周运动，星球A和B两者中心之间距离为L。
已知A、B的中心和O三点始终共线，A和B分别在O的两侧。
引力常数为G。
⑴求两星球做圆周运动的周期。
⑵在地月系统中，若忽略其它星球的影响，可以将月球和地球看成上述星球A和B，月球绕其轨道中心运行为的周期记为T1。
但在近似处理问题时，常常认为月球是绕地心做圆周运动的，这样算得的运行周期T2。
已知地球和月球的质量分别为5.98×1024kg 和7.35 ×1022kg 。
求T2与T1两者平方之比。
（结果保留3位小数）【例题6】【2012•江西联考】如右图，三个质点a、b、c质量分别为m1、m2、M（M>>m1，M>>m2）。
在c的万有引力作用下，a、b在同一平面内绕c沿逆时针方向做匀速圆周运动，它们的周期之比T a∶T b=1∶k；从图示位置开始，在b运动一周的过程中，则（）A．a、b距离最近的次数为k次B．a、b距离最近的次数为k+1次C．a、b、c共线的次数为2kD．a、b、c共线的次数为2k-2【例题7】宇宙中存在一些离其他恒星较远的、由质量相等的三颗星组成的三星系统,通常可忽略其他星体对它们的引力作用.已观测到稳定的三星系统存在两种基本的构成形式:一种是三颗星位于同一直线上,两颗星围绕中央星在同一半径为R的圆轨道上运行;另一种形式是三颗星位于等边三角形的三个顶点上,并沿外接于等边三角形的圆形轨道运行.设每个星体的质量均为m.(1)试求第一种形式下,星体运动的线速度和周期.(2)假设两种形式下星体的运动周期相同,第二种形式下星体之间的距离应为多少?【例题8】（2012•湖北百校联考）宇宙中存在由质量相等的四颗星组成的四星系统，四星系统离其他恒星较远，通常可忽略其他星体对四星系统的引力作用.已观测到稳定的四星系统存在两种基本的构成形式:一种是四颗星稳定地分布在边长为a的正方形的四个顶点上，均围绕正方形对角线的交点做匀速圆周运动，其运动周期为；另一种形式是有三颗星位于边长为a的等边三角形的三个项点上，并沿外接于等边三角形的圆形轨道运行，其运动周期为，而第四颗星刚好位于三角形的中心不动.试求两种形式下，星体运动的周期之比12TT.例题1【解析】：设两颗恒星的质量分别为m 1、m 2r 1、r 2，角速度分别为ω1、ω2。
根据题意有21ωω=①r r r =+21② 根据万有引力定律和牛顿定律，有G1211221r w m rm m =③G 1221221r w m rm m =④联立以上各式解得2121m m rm r +=⑤根据解速度与周期的关系知Tπωω221==⑥联立③⑤⑥式解得322214r GT m m π=+例题2 解析：设A 、B 的圆轨道半径分别为，由题意知，A 、B 做匀速圆周运动的角速度相同，设其为。
由牛顿运动定律，有121r m F A ω=，222r m F B ω=，B A F F =设A 、B 间距离为，则21r r r += 由以上各式解得1221r m m m r +=由万有引力定律，有221r mm G F A =，代入得21221321)(r m m m m G F A += 令211r m m GF A '=，通过比较得22132)(m m m m +=' （2）由牛顿第二定律，有121221r v m rm m G = 而可见星A 的轨道半径π21vT r = 将代入上式解得G Tv m m m π2)(322132=+ （3）将s m m 61=代入上式得G Tv m m m s π2)6(32232=+ 代入数据得s s m m m m 5.3)26(232=+ 设)0(2>=n nm m s ，将其代入上式得s s s m m nnm m m 5.3)16(}6(2232=+=+s s s m m nnm m m 5.3)16(}6(2232=+=+可见，2232)6(m m m s +的值随的增大而增大，试令2=n ，得s s s m m m nn 4.3125.0)16(2<=+可见，若使以上等式成立，则必大于2，即暗星B 的质量s m 必大于s m 2，由此可得出结论：暗星B 有可能是黑洞。
例题3 .解析：双星绕两者连线上某点做匀速圆周运动，即：222121221L M L M LMM G ωω==---------①..L L L =+21-------② 由以上两式可得：L M M M L 2121+=，L M M M L 2122+=又由12212214L T M L M M G π=.----------③ 得：)(221M M G LL T +=例题4解析 双星的运动周期是一样的,选S 1为研究对象,根据牛顿第二定律和万有引力定律得221121π4Tr m =r m Gm 2,则m 2=2122π4GT r r .故正确选项D 正确. 例题5【解析】 ⑴A 和B 绕O 做匀速圆周运动，它们之间的万有引力提供向心力，则A 和B 的向心力相等。
且A 和B 和O 始终共线，说明A 和B 有相同的角速度和周期。
因此有R M r m 22ωω=，L R r =+，连立解得L Mm m R +=，L M m Mr +=对A 根据牛顿第二定律和万有引力定律得L m M MT m L GMm +=22)2(π 化简得 )(23m M G L T +=π⑵将地月看成双星，由⑴得)(231m M G L T +=π将月球看作绕地心做圆周运动，根据牛顿第二定律和万有引力定律得L T m L GMm 22)2(π=化简得 GML T 322π=所以两种周期的平方比值为01.11098.51035.71098.5)(242224212=⨯⨯+⨯=+=M M m T T 例题6【解析】在b 转动一周过程中，a 、b 距离最远的次数为k-1次，a 、b 距离最近的次数为k-1次，故a 、b 、c 共线的次数为2k-2，选项D 正确。
例题7解析 (1)对于第一种运动情况,以某个运动星体为研究对象,根据牛顿第二定律和万有引力定律有:F 1=22222)2(R Gm F RGm = F 1+F 2=mv 2/R运动星体的线速度:v =RGmR25周期为T ,则有T =vRπ2T =4πGmR 53(2)设第二种形式星体之间的距离为r ,R ′=︒30cos 2/r由于星体做圆周运动所需要的向心力靠其它两个星体的万有引力的合力提供,由力的合成和牛顿运动定律有：F 合=222rGm cos30°F 合=m22π4TR′ 所以r =31)512(R例题8【解析】对三绕一模式，三颗绕行星轨道半径均为a ，所受合力等于向心力，因此有22222142m +G =m a a T π⋅︒ ①解得21T ②对正方形模式，四星的轨道半径均为2a ，同理有22222cos 45m G a ⋅︒ ③ 图4 解得23224(47a T =Gmπ ④故12T T。
