四点共圆基本判断方法超全.pdf

证明四点共圆的基本方法证明四点共圆有下述一些基本方法：方法1从被证共圆的四点中先选出三点作一圆，然后证另一点也在这个圆上，若能证明这一点，即可肯定这四点共圆．方法2把被证共圆的四个点连成共底边的两个三角形，且两三角形都在这底边的同侧，若能证明其顶角相等，从而即可肯定这四点共圆．（若能证明其两顶角为直角，即可肯定这四个点共圆，且斜边上两点连线为该圆直径。

）方法3把被证共圆的四点连成四边形，若能证明其对角互补或能证明其一个外角等于其邻补角的内对角时，即可肯定这四点共圆．方法4把被证共圆的四点两两连成相交的两条线段，若能证明它们各自被交点分成的两线段之积相等，即可肯定这四点共圆；或把被证共圆的四点两两连结并延长相交的两线段，若能证明自交点至一线段两个端点所成的两线段之积等于自交点至另一线段两端点所成的两线段之积，即可肯定这四点也共圆．(根据的逆定理)方法5证被证共圆的点到某一定点的距离都相等，从而确定它们共圆．上述五种基本方法中的每一种的根据，就是产生四点共圆的一种原因，因此当要求证四点共圆的问题时，首先就要根据命题的条件，并结合图形的特点，在这五种基本方法中选择一种证法，给予证明．判定与性质：圆内接四边形的对角和为π,并且任何一个外角都等于它的内对角。

如四边形ABCD内接于圆O，延长AB和DC交至E，过点E作圆O的切线EF，AC、BD交于P，则A+C=π，B+D=π，角DBC=角DAC（同弧所对的圆周角相等）。

角CBE=角ADE（外角等于内对角）△ABP∽△DCP（三个内角对应相等）AP*CP=BP*DP（）四点共圆的图片EB*EA=EC*ED（）EF*EF= EB*EA=EC*ED（）（切割线定理，割线定理，相交弦定理统称）AB*CD+AD*CB=AC*BD（托勒密定理Ptolemy）证明四点共圆的原理四点共圆证明四点共圆基本方法：方法1把被证共圆的四个点连成共底边的两个三角形，且两三角形都在这底边的同侧，若能证明其顶角相等，从而即可肯定这四点共圆．方法2把被证共圆的四点连成四边形，若能证明其对角互补或能证明其一个外角等于其邻补角的内对角时，即可肯定这四点共圆．四点共圆的判定是以四点共圆的性质的基础上进行证明的。

四点共圆的判定与性质一、四点共圆的判定〔一〕判定方法1、假设四个点到一个定点的距离相等，那么这四个点共圆。

2、假设一个四边形的一组对角互补〔和为180°〕，那么这个四边形的四个点共圆。

3、假设一个四边形的外角等于它的内对角，那么这个四边形的四个点共圆。

4、假设两个点在一条线段的同旁，并且和这条线段的两端连线所夹的角相等，那么这两个点和这条线的两个端点共圆。

5、同斜边的直角三角形的顶点共圆。

6、假设AB、CD两线段相交于P点，且PA×PB=PC×PD，那么A、B、C、D四点共圆(相交弦定理的逆定理)。

7、假设AB、CD两线段延长后相交于P。

且PA×PB=PC×PD，那么A、B、C、D四点共圆(割线定理)。

8、假设四边形两组对边乘积的和等于对角线的乘积，那么四边形的四个顶点共圆(托勒密定理的逆定理。

〔二〕证明1、假设四个点到一个定点的距离相等，那么这四个点共圆。

假设可以判断出OA=OB=OC=OD，那么A、B、C、D四点在以O为圆心OA为半径的圆上。

2、假设一个四边形的一组对角互补〔和为180°〕，那么这个四边形的四个点共圆。

假设∠A+∠C=180°或∠B+∠D=180°，那么点A、B、C、D四点共圆。

3、假设一个四边形的外角等于它的内对角，那么这个四边形的四个点共圆。

假设∠B=∠CDE，那么A、B、C、D四点共圆证法同上。

4、假设两个点在一条线段的同旁，并且和这条线段的两端连线所夹的角相等，那么这两个点和这条线的两个端点共圆。

假设∠A=∠D或∠ABD=∠ACD，那么A、B、C、D四点共圆。

5、同斜边的直角三角形的顶点共圆。

如图2，假设∠A=∠C=90°，那么A 、B 、C 、D 四点共圆。

6、假设AB 、CD 两线段相交于P 点，且PA ×PB=PC ×PD ，那么A 、B 、C 、D 四点共圆(相交弦定理的逆定理)。

四点共圆的判定与性质一、四点共圆的判定（一）判定方法1、若四个点到一个定点的距离相等，则这四个点共圆。

2、若一个四边形的一组对角互补（和为180°），则这个四边形的四个点共圆。

3、若一个四边形的外角等于它的内对角，则这个四边形的四个点共圆。

4、若两个点在一条线段的同旁，并且和这条线段的两端连线所夹的角相等，那么这两个点和这条线的两个端点共圆。

5、同斜边的直角三角形的顶点共圆。

6、若AB、CD两线段相交于P点，且PA×PB=PC×PD，则A、B、C、D四点共圆(相交弦定理的逆定理)。

7、若AB、CD两线段延长后相交于P。

且PA×PB=PC×PD，则A、B、C、D四点共圆(割线定理)。

8、若四边形两组对边乘积的和等于对角线的乘积，则四边形的四个顶点共圆(托勒密定理的逆定理。

（二）证明1、若四个点到一个定点的距离相等，则这四个点共圆。

若可以判断出OA=OB=OC=OD，则A、B、C、D四点在以O为圆心OA为半径的圆上。

2、若一个四边形的一组对角互补（和为180°），则这个四边形的四个点共圆。

若∠A+∠C=180°或∠B+∠D=180°，则点A、B、C、D四点共圆。

3、若一个四边形的外角等于它的内对角，则这个四边形的四个点共圆。

若∠B=∠CDE，则A、B、C、D四点共圆证法同上。

4、若两个点在一条线段的同旁，并且和这条线段的两端连线所夹的角相等，那么这两个点和这条线的两个端点共圆。

若∠A=∠D或∠ABD=∠ACD，则A、B、C、D四点共圆。

5、同斜边的直角三角形的顶点共圆。

如图2，若∠A=∠C=90°，则A 、B 、C 、D 四点共圆。

6、若AB 、CD 两线段相交于P 点，且PA ×PB=PC ×PD ，则A 、B 、C 、D 四点共圆(相交弦定理的逆定理)。

7、若AB 、CD 两线段延长后相交于P 。

四点共圆的7种判定方法证明要证明四个点共圆，可以使用以下七种判定方法。

方法1：使用相交弧的性质假设四个点A、B、C、D共圆。

我们可以通过观察四个点连线所形成的相交弧的性质来进行判定。

即如果从A到B的弧和从C到D的弧的起点和终点重合，或者从B到C的弧和从D到A的弧的起点和终点重合，或者从C到D的弧和从A到B的弧的起点和终点重合，则可以证明四个点共圆。

方法2：使用余弦定理假设四个点A、B、C、D共圆，并且以A为圆心，AB为半径做圆，那么可以使用余弦定理证明。

首先，假设O为C到D的中点，我们可以根据余弦定理得出：AC² = AO² + OC² - 2 * AO * OC * cos∠AOC，同样地，我们可以得出：BD² = BO² + OD² - 2 * BO * OD * cos∠BOD。

由于共圆的性质，我们可以得到∠AOC = ∠BOD，因此AC² = BD²，从而可以证明四个点共圆。

方法3：使用向量运算假设四个点A、B、C、D共圆，我们可以使用向量运算进行证明。

首先，我们可以构建向量AB和向量AC，然后计算它们的叉乘，得到一个向量N。

同样地，我们可以构建向量AD和向量AC，并计算它们的叉乘，得到另一个向量M。

如果向量N和向量M垂直（即内积等于0），那么可以证明四个点共圆。

方法4：使用角平分线的性质假设四个点A、B、C、D共圆，并且AC和BD相交于点P。

那么根据角平分线的性质，我们可以得知∠APC=∠BPD。

同样地，由于共圆的性质，我们可以得到∠APC=∠BPC，因此∠BPD=∠BPC。

这意味着点P在角BPD的角平分线上，所以我们可以得出AD与BC也相交于点P，从而可以证明四个点共圆。

方法5：使用Miquel点的性质假设四个点A、B、C、D共圆，并且以AC为直径作圆，那么D一定在这个圆上。

同样地，以BD为直径作圆，C也一定在这个圆上。

四点共圆的判定方法四点共圆是指四个点在同一圆周上，这种情况在几何学中经常会遇到。

那么如何判断四个点是否共圆呢？本文将介绍四种方法，包括解析几何法、向量法、余弦定理法和三角形面积法。

以下是详细的方法：一、解析几何法1. 假设已知四个点的坐标分别为A（x1, y1）、B（x2, y2）、C（x3,y3）和D（x4, y4）。

2. 计算出AB、AC和AD三条线段的长度，分别记作a、b和c。

3. 根据勾股定理可以求出三角形ABC、ABD和ACD的面积S1、S2和S3。

4. 如果S1+S2+S3等于ABC三角形的面积，则说明四个点共圆。

二、向量法1. 假设已知四个点A、B、C和D。

2. 分别计算出向量AB、AC和AD的叉积，得到三个向量的模长，分别记作a、b和c。

3. 计算出向量AB与AC之间的夹角α，向量AB与AD之间的夹角β，以及向量AC与AD之间的夹角γ。

4. 如果α+β+γ等于180度，则说明四个点共圆。

三、余弦定理法1. 假设已知四个点A、B、C和D。

2. 计算出AB、AC、AD、BC、BD和CD三对线段之间的夹角，分别记作α、β和γ。

3. 根据余弦定理可以求出三个角的余弦值cosα、cosβ和cosγ。

4. 如果cosα+cosβ+cosγ等于0，则说明四个点共圆。

四、三角形面积法1. 假设已知四个点A、B、C和D。

2. 构造三角形ABC和ABD，分别计算出它们的面积S1和S2。

3. 构造三角形ACD和BCD，分别计算出它们的面积S3和S4。

4. 如果S1+S2等于S3+S4，则说明四个点共圆。

总结：以上就是判断四点共圆的四种方法，其中解析几何法比较简单易懂，适用于初学者；向量法需要一些向量知识，但计算较为简便；余弦定理法需要一些三角函数知识，但也比较容易掌握；三角形面积法则需要计算多个三角形的面积，稍微有些繁琐。

根据实际情况选择合适的方法进行判断即可。

四点共圆的判定方法证明嘿，咱今儿个就来好好唠唠这四点共圆的判定方法证明！你说这四点共圆，就像是四个小伙伴，要想知道它们是不是真的能凑成一个圆，那可得有几招厉害的法子呢！先来说说这第一种判定方法。

如果四个点到一个定点的距离相等，那它们不就乖乖地在一个圆上啦！这就好比是一群孩子围着一个糖果罐子，离罐子距离一样的不就在一个圈里嘛！你想想是不是这个理儿？还有一种呢，就是如果一个四边形的一组对角互补，那这四个点也能共圆哟！这就好像是两个人，一个喜欢吃甜，一个喜欢吃辣，互补得很，那他们就能愉快地一起玩耍啦，这四个点也是一样的道理呀！要是这对角不互补，那它们可就凑不到一块儿去咯！再有呢，就是如果两个三角形有一条公共边，且在公共边同侧的两个顶点所对的边相等，那这四个点也能共圆。

这就跟玩拼图似的，这几块正好能拼成一个完整的图案，那它们就是一伙儿的呀！你可别小瞧了这些判定方法，它们就像是一把把钥匙，能帮我们打开四点共圆这个神秘大门呢！在解决很多几何问题的时候，那可真是大显身手呀！比如说，当我们遇到一些图形里有几个点，想要判断它们是不是能共圆，这时候这些方法不就派上用场啦？就好像有一次，我在做一道题的时候，怎么看那几个点都觉得它们应该在一个圆上，但是又不确定。

然后我就试着用这些判定方法一个一个去试，嘿，还真让我给试出来了！那种感觉，就像是找到了宝藏一样兴奋！而且啊，这些判定方法不仅仅是在数学里有用，在生活中有时候也能找到类似的道理呢！比如说，一群人要合作完成一件事情，那是不是也得有一些条件让他们能团结在一起呀？这和四点共圆不是有点像嘛！总之呢，这四点共圆的判定方法证明可真是有趣又实用！我们可得好好掌握它们，让它们为我们解决问题助一臂之力呀！这就是我对四点共圆判定方法证明的理解啦，你觉得怎么样呢？是不是也觉得很有意思呀？。

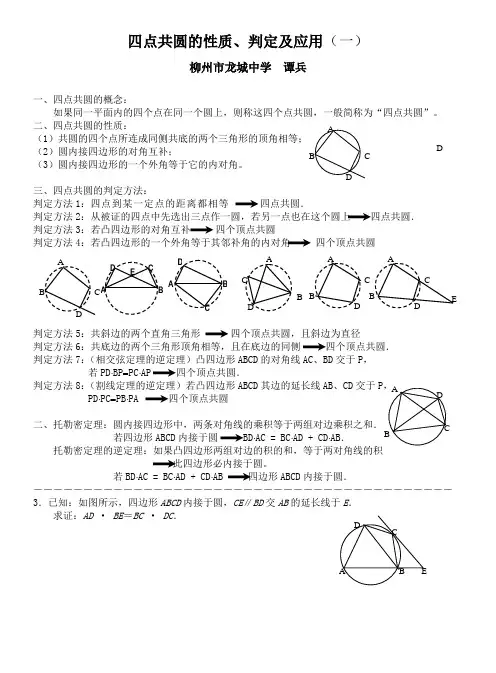
四点共圆的性质、判定及应用（一）柳州市龙城中学 谭兵一、四点共圆的概念：二、四点共圆的性质： （1（2）圆内接四边形的对角互补； （3）圆内接四边形的一个外角等于它的内对角。

三、四点共圆的判定方法：判定方法1：四点到某一定点的距离都相等 四点共圆．判定方法2：从被证的四点中先选出三点作一圆，若另一点也在这个圆上 四点共圆． 判定方法3：若凸四边形的对角互补 四个顶点共圆判定方法4：若凸四边形的一个外角等于其邻补角的内对角 判定方法5：共斜边的两个直角三角形 四个顶点共圆，且斜边为直径判定方法6：共底边的两个三角形顶角相等，且在底边的同侧 四个顶点共圆． 判定方法7：（相交弦定理的逆定理）凸四边形ABCD 的对角线AC 、BD 交于P ，若PD⋅BP =PC ⋅AP 四个顶点共圆．判定方法8：（割线定理的逆定理）若凸四边形ABCD 其边的延长线AB 、CD 交于PD ⋅PC =PB ⋅PA 四个顶点共圆若四边形ABCD 内接于圆 BD ⋅AC = BC ⋅AD + CD ⋅AB ．此四边形必内接于圆。

若BD ⋅AC = BC ⋅AD + CD ⋅AB 四边形ABCD 内接于圆．―――――――――――――――――――――――――――――――――――――――――― 3．已知：如图所示，四边形ABCD 内接于圆，CE ∥BD 交AB 的延长线于E ．求证：AD · BE ＝BC · DC ．D ED C A D CA6．如图，已知在△ABC中，AB＝AC，BD平分∠B，△ABD的外接圆和BC交于E．求证：AD＝EC．性质1．如图，在△ABC中，AD⊥BC，DE⊥AB，DF⊥AC．求证：B、E、F、C四点共圆．判定*5．正方形ABCD的中心为O，面积为1989 cm2．P为正方形内一点，且∠OPB＝45°，PA∶PB＝5∶14．求PB判定．A B7．已知：梯形ABCD中，AD＝BC，AB∥CD．求证：BD2＝BC2＋AB ·CD．托勒密定理DC9．在△ABC 中，∠A 的内角平分线AD 交外接圆于D ．连结BD,CD ．求证：)． 托勒密*8．如图，以Rt △ABC 的斜边BC 为一边在△ABC 的同侧作正方形BCEF ，设正方形的中心为O ，连结AO ，如果AB ＝4，AO ＝26，求AC 的长.**10．如图，AD 、BC 为过圆的直径AB 两端点的弦，且BD 与AC 相交于E 。