专题25平面几何的最值问题

５ 一
数 学教 学
２１ 年第 ５ ００ 期
平 面几何 的最值 问题 及 求法
５５ ２１ ３ ０广东 省东莞市常 学（ 部 平中 高中 ）陈 洪波
一
、
利用三角形的性质
利用三 角形 “ 两边之和大 于第三边， 两边之
设正 △ＡＢ 的边长为 ２ Ｍ 是 Ｊ 边上的中点， ， Ｅ ； ｊ是边Ｂ ［ ） 上的任意一点， ＋Ｐ 的最大值 Ｐ Ｍ 和最小值分别记为ｓ ， 和ｔ 则求 ｓ 一ｔ的值． 解： 如图 ２ ． Ｐ ≤ ，’ ，Ｆ ≤ Ｍ， ’ Ｊ ） ＰＡ＋ ＰＭ ≤ ＣＡ＋ ＣＭ ＝ ２＋ 、３ ／． ／
所 以Ｐ Ｐ ＝ ｘＯｐ ２ ／ ＇ ＋Ｏ ＂ Ｐ
例２ （ ０ 年全国初中数学联合竞赛试题） ２ ０ ０
２１ 年第 ５ ００ 期
＝ ￣ ＯＰ２＋ ＯＰ２＝ １ ｖ － ／ ０ ／ ２
．
数 学教 学
５２ —５
解： 以点 为旋转 中心， ＡＢＣ 将 Ｅ按顺时针 方向旋转 ６ 。 ＡＢＧ 连结 ＥＦ， ＡＢ ０到 Ｆ， 则 ＥＦ为
Ａ１
、
‘ ＼ ，
‘
、 ＼＼ Ｍ 、１ ＾
＝
３ 。 ０ ．
ｊ、 、 ‘ ， Ｎ
图４
设 正方 形 边 长 为 ， ＢＧ ＝ ， 则 ＧＨ ＝ － ， ４ ｘ
Ｂ 日 ： 日 ：
（ ） ＋ ．
由Ｇ Ｈ 十 日 ＝ＡＧ ， 得
１ ２ ＋
分析： 因河宽一定的， 以桥 Ｍ Ⅳ 的长度一 所 定， 只须使 Ｍ ＋ＢⅣ 最短即可． 可平移 Ｍ （ 或
于 Ｂ． ’Ｒｃ ． △ＤＤ Ｇ中， ＤＧ． 。ＤＤ ． ＤＤ ＞ ． ．
＞
Ｍ 连结 ＣＭ 则 ． ， Ｍ ＝ ９ 。 所以 ０， Ｍ ｘＡ ＋Ｃ ＝ ／ Ｃ２ ＝ 、７ ． ＝ 、 ． ／，’ ／ ．￡ ／ ／ ７ 从而 ８ 一ｔ ＝（ 十 ） 一７ ４ ． 。 。 ２ 。 ＝４ ５ 二、 利用对称变换 例３ （００ ２０ 年黄 冈初 中数学竞赛试题） 如图 ３ ， （Ｂ ＝ ４ 。 二 ） ５ 角内有一 点Ｐ， ＰＯ ＝ １， ０ 在 角的两条 边上有两点 Ｑ 均不 同于点 Ｄ， 、 求 ＡＰ Ｒ的周长的最小值． Ｑ

几何中的最值问题作为一门重要的数学学科，几何中有许多重要的概念和方法，其中最值问题是一个广泛研究的内容。

在几何中，最值问题是指在某些条件下，某个几何量（如长度、面积、体积等）的最大值或最小值问题。

本文将从不同角度介绍几何中的最值问题及其应用。

一、最值问题的基础概念在几何问题中，最值问题最常见的便是一些面积、长度和体积的最值问题。

最常见的方法是使用微积分的极值定理，通过计算导数为0的点来找到函数的最大值和最小值。

此外，还有最大和最小的边界问题。

这些问题需要考虑的是给定条件下的最大可行解或最小可行解。

例如，给定一个面积固定的矩形，我们需要求出其长度和宽度的最大或最小值。

这些问题与微积分密切相关，但在解决这些问题时需要更多的几何知识和直觉。

二、平面几何中的最值问题在平面几何中，最值问题通常涉及三角形、四边形和圆形等形状。

这些形状的特性可以用来求解最值问题，通常需要使用各种几何知识和技巧。

例如，对于一个给定面积的三角形，在其周长恒定的情况下，需要求出该三角形的最大或最小长度。

为解决这类问题，我们可以利用三角形的海涅定理或余弦定理，通过微积分的极值定理得到最优解。

对于圆形，最值问题可能涉及到面积和周长问题，这些需要用到圆相关的特点和公式，如半径、直径、周长和面积等，通常需要通过微积分的方法求解。

另一方面，对于四边形最值问题，我们需要利用它们的对角线和相邻边的关系来解决，这通常需要将四边形划分为三角形或矩形来计算。

三、空间几何中的最值问题在空间几何中，最值问题通常涉及立体体积，包括长方体、正方体、棱锥和棱柱等。

这些问题需要利用空间几何的特点和公式来求解，常用的方法包括微积分的极值定理和立体几何的体积计算公式。

例如，对于一个矩形长方体，在其表面积固定的情况下，需要求出其有最大或最小的体积。

如果我们设该矩形长方体的长、宽和高分别为x、y和z，那么该矩形长方体的体积可以表示为V(x,y,z)=xyz。

通过微积分的方法，可以证明只有当x=y=z时，该方体的体积最大。

专题25 费马点、布洛卡点、拿破仑三角形问题一．选择题（共4小题）1．（2021春•顺德区期末）点P 为ABC ∆所在平面内一点，当PA PB PC ++取到最小值时，则称该点为ABC ∆的“费马点”．当ABC ∆的三个内角均小于120︒时，费马点满足如下特征：120APB BPC CPA ∠=∠=∠=︒．如图，在ABC ∆中，AB AC ==BC 点到A ，B ，C 三点的距离之和为( )A ．4B ．2C ．2-D ．2+2．（2020秋•新华区校级期末）“费马点”是指位于三角形内且到三角形三个顶点距离之和最小的点，当三角形三个内角均小于120︒时，“费马点”与三个顶点的连线正好三等分“费马点”所在的周角，即该点所对的三角形三边的张角相等均为120︒，根据以上性质，函数()f x =的最小值为( )A ．2BC ．2-D ．2+3．（2020秋•安徽月考）17世纪法国数学家费马曾提出这样一个问题：怎样在一个三角形中求一点，使它到每个顶点的距离之和最小？现已证明：在ABC ∆中，若三个内角均小于120︒，当点P 满足120APB APC BPC ∠=∠=∠=︒时，则点P 到三角形三个顶点的距离之和最小，点P 被人们称为费马点．根据以上性质，已知a 为平面内任意一个向量，b 和c 是平面内两个互相垂直的单位向量，则||||||a b a b a c -+++-的最小值是( )A ．2B ．2C 1-D 1+4．（2014春•鹿城区校级期末）设点F 为锐角ABC ∆的“费马点”，即F 是在ABC ∆内满足120AFB BFC CFA ∠=∠=∠=︒的点．若||3FA =，|4FB =，||5FC =，且实数x ，y 满足AF xAB y AC =+，则(x y= ) A ．54 B ．2516 C ．32 D ．94二．填空题（共15小题）5．（2021•泰安模拟）在一个三角形ABC 中到三个顶点距离之和最小的点叫做这个三角形的费马点，经证明它也满足120APB BPC CPA ∠=∠=∠=︒，因此费马点也称为三角形的等角中心如图，在ABC ∆外作等边ACD ∆，再作ACD ∆的外接圆，则外接圆与线段BD 的交点P 即为费马点．若1AB =，2BC =，90CAB ∠=︒，则PA PB PC ++= ．6．（2021•深圳模拟）著名的费马问题是法国数学家皮埃尔⋅德费马(16011665)-于1643年提出的平面几何极值问题：“已知一个三角形，求作一点，使其与此三角形的三个顶点的距离之和最小．”费马问题中的所求点称为费马点，已知对于每个给定的三角形，都存在唯一的费马点，当ABC ∆的三个内角均小于120︒时，则使得120APB BPC CPA ∠=∠=∠=︒的点P 即为费马点．已知点P 为ABC ∆的费马点，且AC BC ⊥，若||||||PA PB PC λ+=，则实数λ的最小值为 ．7．（2021•江西模拟）费马点是指位于三角形内且到三角形三个顶点距离之和最小的点．当三角形三个内角都小于23π时，费马点与三角形三个顶点的连线构成的三个角都为23π．已知点P 为ABC ∆的费马点，角A ，B ，C 的对边分别为a ，b ，c ，若cos 2sin()cos 6A C B π=-，且22()6b a c =-+，则PA PB PB PC PA PC ⋅+⋅+⋅的值为 ．8．（2020秋•全国月考）费马点是指到三角形三个顶点距离之和最小的点，当三角形三个内角均小于120︒时，费马点在三角形内，且费马点与三个顶点连线正好三等分费马点所在的周角，即该点对三角形三边的张角相等，均为120︒．已知ABC ∆的三个内角均小于120︒，P 为ABC ∆的费马点，且3PA PB PC ++=，则ABC ∆面积的最大值为 ．9．（2020•江西模拟）我们把三角形三个顶点距离之和最小的点称为费马点，若三角形内角均小于120︒，则该三角形的费马点与三角形三边的张角均为120︒．已知三角形ABC 中内角A ，B ，C 所对的边分别是a ，b ，c ．若||a b -=，60C =︒，若三角形ABC 的费马点为O ，则OA OB OB OC OC OA ++= ．10．（2018秋•上虞区期末）费马点是指三角形内到三角形三个顶点距离之和最小的点，当三角形三个内角均小于120︒时，费马点与三个顶点连线正好三等分费马点所在的周角，即该点所对的三角形三边的张角相等均为120︒．根据以上性质，已知(1,0)A -，(1,0)B ，(0,2)C ，P 为ABC ∆内一点，记()||||||f P PA PB PC =++，则()f P 的最小值为 ，此时sin PBC ∠= ．11．（2019•凉山州模拟）点M 是ABC ∆内部或边界上的点，若M 到ABC ∆三个顶点距离之和最小，则称点M 是ABC ∆的费马点（该问题是十七世纪法国数学家费马提出）．若(0,2)A ，(1,0)B -，(1,0)C 时，点0M 是ABC ∆的费马点，且已知0M 在y 轴上，则000||||||AM BM CM ++的大小等于 ．12．（2018秋•荆州区校级期中）以三角形边BC ，CA ，AB 为边向形外作正三角形BCA '，CAB '，ABC '，则AA '，BB '，CC '三线共点，该点称为ABC ∆的正等角中心．当ABC ∆的每个内角都小于120︒时，正等角中心点P 满足以下性质：（1）120APB APC BPC ∠=∠=∠=︒；（2）正等角中心是到该三角形三个顶点距离之和最小的点（也即费马点）．由以上性质得的最小值为 ．13．（2019春•石家庄期末）费马点是指三角形内到三角形三个顶点距离之和最小的点．当三角形三个内角均小于120︒时，费马点与三个顶点连线正好三等分费马点所在的周角，即该点所对的三角形三边的张角相等均为120︒．根据以上性质，函数()f x =的最小值为 ．14．（2021春•湖北期末）拿破仑定理是法国著名军事家拿破仑⋅波拿巴最早提出的一个几何定理：“以任意三角形的三条边为边，向外构造三个等边三角形，则这三个等边三角形的外接圆圆心恰为另一个等边三角形（此等边三角形称为拿破仑三角形）的顶点．”已知ABC ∆内BC ，AC ，AB 为边向外作三个等边三角形，其外接圆圆心依次记为A '，B '，C '．若30ACB ∠=︒，则△A B C '''的面积最大值为 ．15．（2021春•润州区校级期中）拿破仑定理是法国著名军事家拿破仑⋅波拿巴最早提出的一个几何定理：“以任意三角形的三条边为边，向外构造三个等边三角形，则这三个等边三角形的外接圆圆心恰为另一个等边三角形（此等边三角形称为拿破仑三角形）的顶点．”已知ABC ∆内接于单位圆，以BC ，AC ，AB 为边向外作三个等边三角形，其外接圆圆心依次记为A '，B '，C '．若90ACB ∠=︒，则△A B C '''的面积最大值为 ．16．（2021•泉州二模）拿破仑定理：“以任意三角形的三条边为边，向外构造三个正三角形，则这三个正三角形的中心恰为另一个正三角形的顶点．”利用该定理可为任意形状的市区科学地确定新的发展中心区位置，合理组织人流、物流，使城市土地的利用率，建筑的使用效率达到最佳，因而在城市建设规划中具有很好的应用价值．如图，设ABC ∆代表旧城区，新的城市发展中心1O ，2O ，3O 分别为正ACD ∆，正ABE ∆，正BCF ∆的中心．现已知2AB =，30ACB ∠=︒，△123O O O ABC 的面积为 ．17．（2021•浔阳区校级模拟）法国著名的军事家拿破仑．波拿巴最早提出的一个几何定理：“以任意三角形的三条边为边向外构造三个等边三角形，则这三个三角形的外接圆圆心恰为另一个等边三角形的顶点”．在三角形ABC 中，角60A =︒，以AB 、BC 、AC 为边向外作三个等边三角形，其外接圆圆心依次为1O 、2O 、3O ，若三角形123O O O 角形ABC 的周长最小值为 ．18．（2021•淮安模拟）拿破仑定理是法国著名的军事家拿破仑⋅波拿马最早提出的一个几何定理：“以任意三角形的三条边为边，向外构造三个等边三角形，则这三个三角形的外接圆圆心恰为另一个等边三个角形的顶点”．在ABC ∆中，120A ∠=︒，以AB ，BC ，AC 为边向外作三个等边三角形，其外接圆圆心依次为1O ，2O ，3O ，若△123O O O ABC ∆的周长的取值范围为 ．19．（2021•江苏模拟）法国著名的军事家拿破仑．波拿巴最早提出的一个几何定理：“以任意三角形的三条边为边向外构造三个等边三角形，则这三个三角形的外接圆圆心恰为另一个等边三角形的顶点”．在三角形ABC 中，角60A =︒，以AB 、BC 、AC 为边向外作三个等边三角形，其外接圆圆心依次为1O 、2O 、3O ，若三角形123O O O ，则三角形ABC 的周长最小值为 ．三．解答题（共3小题）20．（2021春•台江区校级期中）法国数学家费马被称为业余数学之王，很多数学定理以他的名字命名．对ABC ∆而言，若其内部的点P 满足120APB BPC CPA ∠=∠=∠=︒，则称P 为ABC ∆的费马点．如图所示，在ABC ∆中，已知45BAC ∠=︒，设P 为ABC ∆的费马点，且满足45PBA ∠=︒，2PA =．（1）求PAC ∆的面积；（2）求PB 的长度．21．如图，在ABC∆中，90ABC∠=︒，AB，1BC=，P为ABC∆内一点，90BPC∠=︒．（1）若12PB=，求PA；（2）若150APB∠=︒，求tan PBA∠．22．在ABC∆内存在一点O，满足BAO CAO CBO ACO∠=∠=∠=∠，求证：ABC∆的三边构成等比数列．。

几何中的最值问题在平面几何问题中，当某几何元素在给定条件变动时，求某几何量（如线段的长度、图形的面积、角的度数）的最大值或最小值问题，称为最值问题。

最值问题的解决方法通常有两种：（1）应用几何性质：①三角形的三边关系：两边之和大于第三边，两边之差小于第三边；②两点间线段最短；③连结直线外一点和直线上各点的所有线段中，垂线段最短；④定圆中的所有弦中，直径最长。

⑵运用代数证法：①运用配方法求二次三项式的最值；②运用一元二次方程根的判别式。

例1、A、B两点在直线l的同侧，在直线L上取一点P，使PA+PB最小。

变式1：A、B两点分别在直线L的两侧，在直线L上取一点P使P A－PB最大。

ALB例2、如图所示，△ABC中，AB＝3，AC＝2，以BC为边的△BCP是等边三角形，求AP的最大值、最小值。

A'例3、已知：如图⊙O1与⊙O2相交于C、D,A是⊙O1上一点，直线AD交⊙O2于点B。

⑴当点A在弧CAD上运动到A’点时，作直线A’D交⊙O2于点B’，连结A’C、B’C。

证明：△A’B’C ∽△ABC。

(2)问点A’在弧CAD上什么位置时，S△A’B’C最大，说明理由。

（3）当O1 O2＝11，CD＝9时，求S△A’B’C的最大值。

BB图1 图2例4、已知：如图△ABC是一块锐角三角形余料，边长BC＝120mm，高AD＝80mm,要把它加工成一个矩形零件，使矩形的一边在BC上，其余两个顶点分别在AB、AC上，设矩形的长QM＝y mm ，宽MN＝x mm（1）求证：y=120- x(2)当x与y分别取什么值时，矩形PQMN的面积最大？最大面积是多少？。

专题25 平面几何的最值问题例】等提示：当CM ®吋，CM 值最小，g 営:晋MN 的最小值为点厅到AB 的距离B'F, BE= —— = 4^5 cm, AC阳=8亦cm, AE=-BE 1=(20, -(4⑹'=8辰m.在△ABB'中，由丄 的“/^二丄血叩乍，得B'F=16cm ・故BM+2 2MN 的最小值为16cm. 例3 由厶APDs 厶BPQ,得(例2题咔“ 、A/竺=如,即盹=竺竺二好2 -P+BQ=x+冬"・・・・x+《4 BP BQAP x x x2 lx — = 14ab ,・••当且仅当x=—即x=V^时，上式等号成立.故当4PV XXp= 伤时，AP+BQ 最小，其最小值为2 后 _b.例4 (1”；=25 +亍，仔= 49”，故要选择路线/较短•⑵Z+EM +b ，(例5题图)X —呂=才(沪一4)厂一4八・当r=-^—时，片=1?,当r>-^—时，/,2>^,当r<-^— 1 2 LV ) 」 兀$ _4 1 - 兀—4 1 2亍-4时，/.2< /； • 例 5 设 DN=x, PN=y,则 S=xy,由厶APQs'ABF,得4f 3，.=-即-2 — (4 — x) 2不在自变量y 的取值范围内，所以y=—不是极值点，当y=3时，S {3)=12,当y=4时，S (4)=8,故S m ”=12.此时，钢板的最大利用率 ---------- : ---- =80%. 例6设PD=x(x>l),42 -Zx2xl2 则 PC=厶—,由 RtMCDsZAB,得&B=S"'= "I ,令 y=&3・Sz^B ，则 Y= ~ PC J7~[2(P)x=10 — 2y,代入 S=xy 得 S=xy=y(10—2小 即 S=~225 +因 3WyW4,而 y=2AB X PA X AB = (x + 厅2(x-l)求y 的最小值，有下列不同思路：①配方：y =2,即当x=3时，y 有最小值4.②例2如图，B f M+x-\ 2 ------ 1 ----- 2 x-1+ 4 , A 当2运用基本不等式：y=X_1 232x-l 2 二当——=——，即当尸3吋，尹有最小值4.③借用判别式，去2 x — 1分母，得 “+2 (l-y)x+l+2y=0,由厶=4(1一尹)2—4(1+2尹)=4尹(p-4)N0,得比 4,・\y 的最小值为4.1.17提示：当两张纸条的对角重合时，菱形周长最人.2.83. ^744.D5.D6.B7. C 提示：当点P 与点D 重合时，四边形ACBP 的周长最大.8. (1)连结 ME,过 N 作 NFA.AB 于 F,可证明 RUEB 4竺Rt^MNF,得 MF=AE=x. VME 2=AE 2+AM 2f故 MB 1=X 1+AM 1,即(2—力M) 2=x 2+.4M 2, AM=\~-x.:・S=4AM十 DN xq= "M + " x2=/M+/M+MF=2/M+Ag=2 (l--x 2) +x=~-x 22 24 2+x+2.(2) S=~- (X 2-2 X +1)(x —l)讣丄.故当亦=x= 1 时，四边形ADNM2 2 2 2的面积最大，此吋最大值为仝.29. (1) 3C 长为竺二(2)提示：连结3D (3)过点3作丄力D 于由(2)知四3AB?边形/BCD 为等腰梯形，从而BC=AD-2 AM=2r-2 /M.由厶BAM^/\DAB,得 -------------------ADX YY EF=2 r- —./=4x+2 (2 厂一一)=-- rr r(0<x< V2 r)..当兀=厂时，/取得最大值6— 2+2=4,2 x-lY・・・BC=2厂一一.(x —r) 2+6 r (第8題图)10. (1) V ZAPE= ZADQ.Z4EP= ZAQD,:. ^APE^/\ADQ. (2)由厶4PEs △力DQ,1J 1333'PDFs£\ADQ,S、PEF = — S DPEQF ，得 S、PEF = — — 7+x= — — (x ——)2+ — •故当 x=—2 3 3 2 42时，即P 是/D 的中点时，取得最大值，(3)作A 关于直线BC 的对称点连结DA 交BC 于0,则这个0点就是使LADO 周长最小的点，此时0是BC 的中点. 11. (1)点P 恰好在3C 上时，由对称性知MN 是LABC 的中位线，.••当BC=3时，2点P 在BC 上.(2)由己知得ZUBC 底边上的高〃=“扌=4.①当0＜疋3时，如图1,连结并延长交BC 于点、D, 4D 与MN 交于点O.(第11题图)图22J 2 1 o 1 市△/A/Ns △/3C,得 AO= — X J y=S、PMN =S、AMN =—x — x=—x?即尹=—x?•当=3 时，v3 ■‘233 3'的值最大，最大值是3.②当3<x<6时，如图2,设△PMN 与BC 相交于点E, F, 4P 与 244相交于D.由①屮知AO=-x, :.AP=-x, :.PD=AP~AD=-x-A, T \PEFs 厶ABC.,3 33尹的最大值为4.综上，当兀=4时，夕的值最大，最大值为4.1.8 8^232提示：当ZCAB=ZACD=90°时，四边形ABCD 的面积达到最大值.S MB C(x-3)・••吵=S“wv _c — 1 2b“EF—~ 入3(x —3) 2=-X 2 + 8X -12 = - (X —4) 2 + 4.故当 x=4 时,Q'PE F・• SbPEF=~即2. 0</<1 提示：设BC=a, CA=b, AB=c, b+c=2观(r+1),又—/)csin60°=5A/i5c:=—2 2Ca+b+c) F,即、bc^~ = L [2\/3 +2A/3 G+l)]『，.bc=4r (r+2) . b, c 为方程2 2 2X2-2A/3 (r+1) x+4r (r+2) =0 的两个根，由—0,得(r+1) <22.H r>0, r+l>0,故 r+l<2,即 0</<l.3如7提示:过P 作垂直于"的弦倔此时弓形面积最小•4.丄提示：设 —=x,则 —= 1-^= —,也型=/,3 AB BA CA S’％° ° 2 1S 梯形DEFG = 1 —工厶—2 ( 1 —X ) 2 = — 3 (.X — — ) ' + —・33n:]5. 7 + °提示：当= 时，OC 的长最大.6. C27. (1)由 RtzUBPsRtAPC 。

平面几何中的最值江苏省泗阳县李口中学沈正中在平面几何中，我们常常遇到各种求最大值和最小值的问题，有时它和不等式联系在一起，统称最值问题。

如果把最值问题和生活中的经济问题联系起来，可以达到最经济、最节约和最高效率。

在平面几何问题中，当某几何元素在给定条件变动时，求某几何量（如线段的长度、图形的面积、角的度数）的最大值或最小值问题, 称为最值问题。

最值问题的解决方法通常有两种：一、应用几何性质：1.三角形的三边关系：两边之和大于第三边，两边之差小于第三边；2.两点间线段最短；3.连结直线外一点和直线上各点的所有线段中，垂线段最短；4.定圆中的所有弦中，直径最长。

二、运用代数证法：1.运用配方法求二次三项式的最值；2.运用一元二次方程根的判别式。

下面介绍几例。

【题例1】①图1所示，A、B两点在直线/的同侧，在直线，上取一点P,使PA +PB最小。

②图2所示，A、B两点在直线/的两侧，在直线，上图 1 图 2P ，A —P ，B ，VAB\ 所以 即PA-PB 最大。

(A0 - BO)2 『AO 2 + BO 2 AB22=—取一点P ，使PA-PB 最大。

【解答】①图1中，在直线I 上任取一点P',再取点A 关于直 线/的对称点 A 、连 AP\ AT\ A ，B 、BP\ 则 AP ，= A ，P\在△A ，BP ，中,A'P'+BP'>A'B,当P'在A ，B 与直线，的交点处P 点时,A"+BP ，=AB 即 A ，P+BP=A'B,此时 PA+PB 最小。

②图2中，在直线Z 上任取一点P,再取点B 关于直线/的对 称点B ，，连AB 、并延长交,于P,连AP ，、BP\ BT\ BP,则PB = P ，B, PB ，= PB,所以 AB 9= PA-PBoP ,A-P ,B = P ,A-P ,B\ 在左AB ，P ，中, 唯有P ，在p 点时，才有P ，A —P ，B ，=AB\【题例2】如图3所示，已知直角AAOB 中，直角顶点o 在单位圆心上，斜边与单 位圆相切，延长AO, B0分别与单位圆交 于C, D.试求四边形ABCD 面积的最小值。

初中数学：平面几何的最值问题-例题与求解（培优25）平面几何的最值问题【阅读与思考】几何中的最值问题是指在一定的条件下，求平面几何图形中某个确定的量(如线段长度、角度大小、图形面积)等的最大值或最小值.求几何最值问题的基本方法有:1.特殊位置与极端位置法:先考虑特殊位置或极端位置，确定最值的具体数据，再进行一般情形下的推证.2.几何定理(公理)法:应用几何中的不等量性质、定理.3.数形结合法等:揭示问题中变动元素的代数关系，构造一元二次方程、二次函数等.【例题与求解】【解析】作点B关于直线AC的对称点B'，交AC与E，连接B'M，过B'作B'G⊥AB于G，交AC于F，再由对称性可知B'M+MN=BM+MN≥B'G，再由等号成立条件得出AC=10√5，再根据△ABC的面积分别求出BE、BB'的值，由相似三角形的判定定理得出△B'GB~△ABC，再根据相似三角形的性质即可求解.【点评】本题考查的是最短路线问题及相似三角形的判定与性质，根据题意作出辅助线是解答此题的关键.【点评】本题考查了三角形相似的判定与性质.也考查了平行四边形的性质以及一元二次方程根的判别式运用.【解析】(1)根据勾股定理易得路线1:l₁²=AC²=高²+(底面周长一半)²；路线2:l₂²=(高+底面直径)²；让两个平方比较，平方大的，底数就大.(2)根据(1)得到的结论让两个代数式分三种情况进行比较即可.【点评】此题考查了平面展开一最短路径问题，比较两个数的大小，有时比较两个数的平方比较简便，比较两个数的平方，通常让这两个数的平方相减，注意运用类比的方法做类型题.【解析】根据题意画图分析.用含表示某一边的字母的代数式表示面积，关键是表示另一边的长.借助三角形相似建立关系.【点评】根据函数求出的最值与实际问题中的最值不一定相同，需注意自变量的取值范围.【点评】本题主要考查对三角形的面积，相似三角形的性质和判定，勾股定理，面积和等积变形等知识点的理解和掌握，能求出方程x²+2(1-y)x+1+2y=0中y的最小值是解此题的关键.。

，
∴当 x 1 2 ，即当 x＝3 时，y 有最小值 4．
2
x 1
②运用基本不等式：y＝ x 1 2 2 2 2 x 1
x 1 2 ＋2＝4， 2 x 1
∴当 x 1 ＝ 2 ，即当 x＝3 时，y 有最小值 4. 2 x 1
③借用判别式，去分母，得 x2＋2（1－y）x＋1＋2y＝0，
由△＝4（1－y）2－4（1＋2y）＝4y（y－4）≥0，得 y≥4，
①求 y 关于 x 的函数关系式；
②当 x 为何值时，△PBC 的周长最小？求出此时 y 的值．
（南通市中考试题）
第 9 题图
第 10 题图
第 11 题图
第 12 题图
11．如图，已知直线 l ： y kx 2 4k ( k 为实数)．
(1) 求证：不论 k 为任何实数，直线 l 都过定点 M，并求点 M 的坐标； (2) 若直线 l 与 x 轴、y 轴的正半轴交于 A，B 两点，求△AOB 面积的最小值．（太原市竞赛试题）
例 1 在 Rt△ABC 中，CB=3，CA=4，M 为斜边 AB 上一动点．
过点 M 作 MD⊥AC 于点 D，过 M 作 ME⊥CB 于点 E，
则线段 DE 的最小值为
．（四川省竞赛试题）
解题思路：四边形 CDME 为矩形，
连结 CM，则 DE= CM，将问题转化为求 CM 的最小值．
解： 12 5
解： 如图，B′M＋MN 的最小值为点 B′到 AB 的距离 B′F，
BE＝ AB BC 4 5 cm，BB′＝ 8 5 cm， AC
AE＝
AB2 BE 2
202
4
5
2
8
5 cm．
在△ABB′中，由 1 BB′•AE＝ 1 AB•B′F，得 B′F＝16cm．

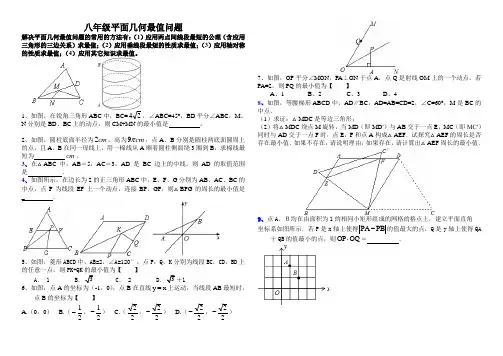
八年级平面几何最值问题解决平面几何最值问题的常用的方法有：（1）应用两点间线段最短的公理（含应用三角形的三边关系）求最值；（2）应用垂线段最短的性质求最值；（3）应用轴对称的性质求最值；（4）应用其它知识求最值。

1、如图，在锐角三角形ABC 中，BC=24，∠ABC=45°，BD 平分∠ABC ，M 、N 分别是BD 、BC 上的动点，则CM+MN 的最小值是 。

2、如图，圆柱底面半径为2cm ，高为9cm π，点A 、B 分别是圆柱两底面圆周上的点，且A 、B 在同一母线上，用一棉线从A 顺着圆柱侧面绕3圈到B ，求棉线最短为 cm 。

3、在△ABC 中，AB ＝5，AC ＝3，AD 是BC 边上的中线，则AD 的取值范围是 ．4、如图所示，在边长为2的正三角形ABC 中，E 、F 、G 分别为AB 、AC 、BC 的中点，点P 为线段EF 上一个动点，连接BP 、GP ，则△BPG 的周长的最小值是 _ ．5、如图，菱形ABCD 中，AB=2，∠A=120°，点P ，Q ，K 分别为线段BC ，CD ，BD 上的任意一点，则PK+QK 的最小值为【 】A ． 1B ．3C ． 2D ．3＋1 6、如图，点A 的坐标为（-1，0），点B 在直线y x =上运动，当线段AB 最短时，点B 的坐标为【 】A.（0，0）B.（21-，21-） C.（22，22-） D.（22-，22-）7、如图，OP 平分∠MON ，PA ⊥ON 于点A ，点Q 是射线OM 上的一个动点，若PA=2，则PQ 的最小值为【 】 A 、1 B 、2 C 、3 D 、48、如图，等腰梯形ABCD 中，AD ∥BC ，AD=AB=CD=2，∠C=60°，M 是BC 的中点．（1）求证：△MDC 是等边三角形；（2）将△MDC 绕点M 旋转，当MD （即MD ′）与AB 交于一点E ，MC （即MC′）同时与AD 交于一点F 时，点E ，F 和点A 构成△AEF ．试探究△AEF 的周长是否存在最小值．如果不存在，请说明理由；如果存在，请计算出△AEF 周长的最小值．9、点A 、Ｂ均在由面积为1的相同小矩形组成的网格的格点上，建立平面直角 坐标系如图所示．若P 是x 轴上使得PA PB -的值最大的点，Q 是y 轴上使得QA十QB 的值最小的点，则OP OQ ⋅＝ ．答案：1.4 2.15 3.1<AD<4 4.3 5.B 6.B 7.B 8.2+9.5。

平面几何中的最值问题最值问题的解决方法通常有两种：1、应用几何性质：①三角形的两边之和大于第三边，两边之差小于第三边；②两点之间，线段最短；③垂线段最短；④定圆中，直径最长。

2、运用代数证法：①运用配方法②运用判别式。

例1、A、B两点在直线l的同侧，在直线L上取一点P，使PA+PB最小。

例2、A、B两点在直线l的同侧，在直线L上取一点P，使|PA-PB|最大。

已知AB是半圆的直径，AB=10,如果这个半圆是一块铁皮，ABDC是内接半圆的梯形，试问怎样剪这个梯形，才能使梯形ABDC的周长最大？2 .如图是半圆与矩形结合而成的窗户，如果窗户的周长为8米(m)，怎样才能得出最大面积，使得窗户透光最好？几何的定值与最值基本方法是：分清定量和变量，运用特殊位置、极端位置，直接计算等方法，先探求出定值，再给出证明．求几何最值问题的基本方法有：1．特殊位置与极端位置法；2．几何定理(公理)法；3．数形结合法等．【例1】 如图，已知AB=10，P 是线段AB 上任意一点，在AB 的同侧分别以AP 和PB 为边作等边△APC 和等边△BPD ，则CD 长度的最小值为 ．思路点拨 如图，作CC ′⊥AB 于C ，DD ′⊥AB 于D ′，DQ ⊥CC ′，CD 2=DQ 2+CQ 2，DQ=21AB 一常数，当CQ 越小，CD 越小， 本例也可设AP=x ，则PB=x -10，从代数角度探求CD 的最小值．注：从特殊位置与极端位置的研究中易得到启示，常能找到解题突破口，特殊位置与极端位置是指：(1)中点处、垂直位置关系等；(2)端点处、临界位置等．【例3】 如图，已知平行四边形ABCD ，AB=a ，BC=b (a >b )，P 为AB 边上的一动点，直线DP 交CB 的延长线于Q ，求AP+BQ 的最小值．思路点拨 设AP=x ，把AP 、BQ 分别用x 的代数式表示，运用不等式ab b a 222≥+ (当且仅当b a =时取等号)来求最小值．【例4】 如图，已知等边△ABC 内接于圆，在劣弧AB 上取异于A 、B 的点 ⌒M，设直线AC与BM相交于K，直线CB与AM相交于点N，证明：线段AK 和BN的乘积与M点的选择无关．思路点拨即要证AK·BN是一个定值，在图形中△ABC的边长是一个定值，说明AK·BN与AB有关，从图知AB为△ABM与△ANB的公共边，作一个大胆的猜想，AK·BN=AB2，从而我们的证明目标更加明确．注：只要探求出定值，那么解题目标明确，定值问题就转化为一般的几何证明问题．1．如图，正方形ABCD的边长为1，点P为边BC上任意一点（可与B点或C点重合），分别过B、C、D作射线AP的垂线，垂足分别是B′、C′、D′，则BB′+CC′+DD′的最大值为，最小值为．2．如图，∠AOB=45°，角内有一点P，PO=10，在角的两边上有两点Q，R(均不同于点O)，则△PQR的周长的最小值为．3．如图，两点A、B在直线MN外的同侧，A到MN的距离AC=8，B到MN的距离BD=5，CD=4，P在直线MN上运动，则PBPA 的最大值等于．。

平面直角坐标系中的最值问题解决方法
平面直角坐标系中的最值问题是一个非常重要的问题，通常涉及到求函数在给定区域内的最大值和最小值。

下面是一些解决最值问题的方法：
1. 观察函数图像：通过观察函数的图像，可以直观地看到函数在哪些区域内的值较大或较小。

这种方法适用于一些简单函数的图像。

2. 利用导数：对于一些可导函数，可以利用导数来判断函数的单调性，从而确定函数的最大值和最小值。

3. 利用极坐标：将平面直角坐标系转化为极坐标系，可以将问题转化为求极径的最大值和最小值。

这种方法适用于一些具有圆形边界的问题。

4. 利用几何意义：对于一些具有几何意义的函数，可以利用几何意义来求解最值。

例如，对于圆上的点到原点的距离，可以利用圆的半径和圆心位置来求解最值。

解决平面直角坐标系中的最值问题需要综合考虑多种方法，根据具体问题选择合适的方法进行求解。

专题25 平面几何的最值问题例题与求解【例1】在Rt △ABC 中，CB =3，CA =4，M 为斜边AB 上一动点．过点M 作MD ⊥AC 于点D ，过M 作ME ⊥CB 于点E ，则线段DE 的最小值为 ．解题思路：四边形CDME 为矩形，连结CM ，则DE = CM ，将问题转化为求CM 的最小值．【例2】如图，在矩形ABCD 中，AB =20cm ，BC =10cm ．若在AC ，AB 上各取一点M ，N ，使BM +MN 的值最小，求这个最小值．（北京市竞赛试题）ADMN解题思路：作点B 关于AC 的对称点B ′，连结B ′M ，B ′A ，则BM = B ′M ，从而BM +MN = B ′M +MN ．要使BM +MN 的值最小，只需使B ′M 十MN 的值最小，当B ′，M ，N 三点共线且B ′N ⊥AB 时，B ′M +MN 的值最小．【例3】如图，已知□ABCD ，AB =a ，BC =b (b a >)，P 为AB 边上的一动点，直线DP 交CB 的延长线于Q ．求AP +BQ 的最小值． （永州市竞赛试题）PDA BQ解题思路：设AP =x ，把AP ，BQ 分别用x 的代数式表示，运用不等式以ab b a 222≥+或a +b ≥2ab（当且仅当a =b 时取等号）来求最小值． 【例4】阅读下列材料：问题 如图1，一圆柱的底面半径为5dm ，高AB 为5dm ，BC 是底面直径，求一只蚂蚁从A 点出发沿圆柱表面爬行到C 点的最短路线． 小明设计了两条路线：图2图1摊平沿AB 剪开ACBBAC路线1：侧面展开图中的线段AC ．如图2所示．设路线l 的长度为l 1，则l 12 =AC 2=AB 2 +BC 2 =25+(5π) 2=25+25π2． 路线2：高线AB 十底面直径BC ．如图1所示．设路线l 的长度为l 2，则l 22 = (BC +AB )2=(5+10)2 =225．∵l 12 – l 22 = 25+25π2－225=25π2－200=25(π2－8)，∴l 12 ＞l 22 ，∴ l 1＞l 2 ． 所以，应选择路线2．(2)请你帮小明继续研究：在一般情况下，当圆柱的底面半径为r ，高为h 时，应如何选择上面的两条路线才能使蚂蚁从点A 出发沿圆柱表面爬行到C 点的路线最短．解题思路：本题考查平面展开一最短路径问题．比较两个数的大小，有时比较两个数的平方比较简便．比较两个数的平方，通常让这两个数的平方相减．【例5】如图，已知边长为4的正方形钢板，有一个角锈蚀，其中AF =2，BF =1．为了合理利用这块钢板，将在五边形EABCD 内截取一个矩形块MDNP ，使点P 在AB 上，且要求面积最大，求钢板的最大利用率． （中学生数学智能通讯赛试题）NME DAB解题思路：设DN =x ，PN =y ，则S =xy ．建立矩形MDNP 的面积S 与x 的函数关系式，利用二次函数性质求S 的最大值，进而求钢板的最大利用率．能力训练A 级1．如图，将两张长为8、宽为2的矩形纸条交叉，使重叠部分是一个菱形．容易知道当两张纸条垂直时，菱形的周长有最小值，那么菱形周长的最大值是 ． （烟台市中考试题）2．D 是半径为5cm 的⊙O 内一点，且OD =3cm ，则过点O 的所有弦中，最短的弦AB = cm ．3．如图，有一个长方体，它的长BC =4，宽AB =3，高BB 1=5．一只小虫由A 处出发，沿长方体表面爬行到C 1，这时小虫爬行的最短路径的长度是 ．DD 1第1题图 第3题图 第4题图 第5题图4．如图，在△ABC 中，AB =10，AC =8，BC =6，经过点C 且与边AB 相切的动圆与CB ，CA 分别相交于点E ，F ，则线段EF 长度的最小值是( )A ．42B ．4.75C ．5D ．4.85．如图，圆锥的母线长OA =6，底面圆的半径为2．一小虫在圆锥底面的点A 处绕圆锥侧面一周又回到点A ，则小虫所走的最短距离为( ) A ．12B ．4πC ．62D ．636．如图，已知∠MON = 40°，P 是∠MON 内的一定点，点A ，B 分别在射线OM ，ON 上移动，当△P AB 周长最小时，∠APB 的值为( ) A ．80° B ．100° C ．120° D ．140° 7．如图， ⌒AD 是以等边三角形ABC 一边AB 为半径的四分之一圆周，P 为AD 上任意一点．若AC =5，则四边形ACBP 周长的最大值是( ) A ．15B ．20C ．15+52D ．15+55NNMOBCBA BA E第6题图 第7题图 第8题图 8．如图，在正方形ABCD 中，AB =2，E 是AD 边上一点（点E 与点A ，D 不重合），BE 的垂直平分线交AB 于M ，交DC 与N ．(1) 设AE=x，四边形ADNM的面积为S，写出S关于x的函数关系式．(2) 当AE为何值时，四边形ADNM的面积最大？最大值是多少？9．如图，六边形ABCDEF内接于半径为r的⊙O，其中AD为直径，且AB=CD=DE=F A．BC的长；(1) 当∠BAD=75°时，求⌒(2) 求证：BC∥AD∥FE；(3) 设AB=x，求六边形ABCDEF的周长l关于x的函数关系式，并指出x为何值时，l取得最大值．10．如图，已知矩形ABCD的边长AB=2，BC=3，点P是AD边上的一动点（P异于A、D）．Q是BC边上任意一点．连结AQ，DQ，过P作PE∥DQ交于AQ于E，作PF//AQ交DQ于F．(1) 求证：△APE∽△ADQ；(2) 设AP的长为x，试求△PEF的面积S△PEF关于x的函数关系式，并求当P在何处时，S△PEF取得最大值？最大值为多少？(3) 当Q在何处时，△ADQ的周长最小？（须给出确定Q在何处的过程或方法，不必证明）FEB Q11．在等腰△ABC中，AB=AC=5，BC=6．动点M，N分别在两腰AB，AC上(M不与A，B重合，N不与A，C重合)，且MN∥BC．将△AMN沿MN所在的直线折叠，使点A的对应点为P．(1)当MN为何值时，点P恰好落在BC上？(2)设MN=x，△MNP与等腰△ABC重叠部分的面积为y，试写出y与x的函数关系式，当x为何值时，y的值最大，最大值是多少？NMB CB 级1．已知凸四边形ABCD 中，AB +AC +CD = 16，且S 四边彤ABCD =32，那么当AC = ，BD = 时，四边形ABCD 面积最大，最大值是 ．2．如图，已知△ABC 的内切圆半径为r ，∠A =60°，BC =23，则r 的取值范围是 ．（江苏省竞赛试题）yxr COFE EDF O BC A OBCAABP D GAB第2题图 第3题图 第4题图 第5题图3．如图⊙O 的半径为2，⊙O 内的一点P 到圆心的距离为1，过点P 的弦与劣弧⌒AB 组成一个弓形，则此弓形面积的最小值为 ．4．如图，△ABC 的面积为1，点D ，G ，E 和F 分别在边AB ，AC ，BC 上，BD ＜DA ，DG ∥BC ，DE ∥AC ，GF ∥AB ，则梯形DEFG 面积的最大可能值为 ．5．已知边长为a 的正三角形ABC ，两顶点A ，B 分别在平面直角坐标系的x 轴，y 轴的正半轴上滑动，点C 在第一象限，连结OC ，则OC 的最大值是 ．6．已知直角梯形ABCD 中，AD ∥BC ，AB ⊥BC ，AD =2，BC =DC =5，点P 在BC 上移动，则当P A + PD 取最小值时，△APD 中边AP 上的高为( )A ．17172B ．17174C ．17178D ．3QADBCA BDCPP第6题图 第7题图 第8题图7．如图，正方形ABCD 的边长为4cm ，点P 是BC 边上不与点B ，C 重合的任意一点，连结AP ，过点P 作PQ ⊥AP 交DC 于点Q ．设BP 的长为x cm ，CQ 的长为y cm ． (1) 求点P 在BC 上运动的过程中y 的最大值；(2) 当y =41cm 时，求x 的值．8．如图，y 轴正半轴上有两点A (0，a )，B (0，b )，其中a >b >0．在x 轴上取一点C ，使∠ACB 最大，求C 点坐标．9．如图，正方形ABCD 的边长为1，点M ，N 分别在BC ，CD 上，使得△CM N 的周长为2．求： (1) ∠MAN 的大小；(2) △MAN 的面积的最小值．10，如图，四边形ABCD 中，AD = CD ，∠DAB =∠ACB =90°，过点D 作DE ⊥AC 于F ，DE 与AB 相交于点E ．(1) 求证：AB ·AF =CB ·CD ； (2)已知AB =15cm ，BC =9cm ，P 是射线DE 上的动点，设DP =x cm(x >0)，四边形BCDP 的面积为y cm 2． ①求y 关于x 的函数关系式；②当x 为何值时，△PBC 的周长最小？求出此时y 的值．MNExCB第6题图 第7题图 第8题图 第9题图11．如图，已知直线l ：k kx y 42-+=(k 为实数)．(1) 求证：不论k 为任何实数，直线l 都过定点M ，并求点M 的坐标；(2) 若直线l 与x 轴、y 轴的正半轴交于A ，B 两点，求△AOB 面积的最小值．（太原市竞赛试题）。

几何最值的解题方法1. 引言几何最值问题是数学中常见的一类问题，它涉及到在给定的几何形状或空间中寻找某个特定量的最大值或最小值。

在解决这类问题时，我们需要运用几何知识和数学分析方法，结合具体情境进行推理和计算。

本文将介绍几何最值问题的解题方法，并通过实例进行说明。

2. 几何最值问题的分类几何最值问题可以分为两类：平面几何中的最值问题和立体几何中的最值问题。

2.1 平面几何中的最值问题在平面几何中，我们常常需要求解线段、角度、面积等量的最大值或最小值。

例如，求一个给定周长的矩形的面积最大，或者求一个给定半径的圆形内接三角形的面积最大。

为了解决这类问题，我们可以使用以下方法：2.1.1 导数法当需要求解平面图形上某个量（如面积）取得极大或极小值时，我们可以通过对该量进行微分，并令导数等于零来求得临界点。

通过判断临界点处导数符号变化来确定极大或极小值。

例如，对于矩形的面积最大问题，我们可以设矩形的长为x，宽为y，则矩形的面积为S=xy。

根据周长固定的条件，可以得到2x+2y=常数。

将这个条件代入面积公式S=xy中，可以得到只含有一个变量x的函数表达式S(x)，然后对S(x)求导，并令导数等于零，即可求得临界点。

2.1.2 直观法直观法是一种通过观察和推理来解决几何最值问题的方法。

在解决一些简单的几何最值问题时，我们可以通过直观地找出一些特殊情况或者利用几何图形的性质来确定最值。

例如，在求解一个给定周长的矩形面积最大问题时，我们可以发现正方形是具有相同周长下面积最大的矩形，因而答案是正方形。

2.2 立体几何中的最值问题在立体几何中，我们常常需要求解体积、表面积等量的最大值或最小值。

例如，求一个给定表面积的圆柱体体积最大，或者求一个给定体积的圆柱体表面积最小。

为了解决这类问题，我们可以使用以下方法：2.2.1 导数法与平面几何中的导数法类似，我们可以通过对体积或表面积进行微分，并令导数等于零来求得临界点。

例析平面几何中的最值问题某平面几何元素在给定条件下变动时求某几何量的最大值或最小值问题称为平面几何中这类试题综合性强，通常根据“两点之间线段最短”、“垂线段最短”、“三角形的三边关系”或者“利用隐形圆”等方法，找出最长（短）位置，求出最大（小）值．1.利用对称求最值例1: 菱形OABC在平面直角坐标系中的位置如图所示，已知A（5，0），E （0，2），OB＝4，点P是对角线OB上的一个动点，当△EPC周长最小时，则点P的坐标为．解：如图连接AC，AE，分别交OB于G、P′，作BD⊥OA于D．∵四边形OABC是菱形，∴AC⊥OB，GC＝AG，OG＝BG＝2，A、C关于直线OB对称，∴P′C+P′D＝P′A+P′E＝EA，∴P点在P′时PC+PE+CE最短，在RT△AOG中，AG＝＝＝，∵OA•BD＝•AC•OB，∴BD＝4，AD＝＝3，∴点B坐标（8，4），∴直线OB解析式为y＝x，直线AD解析式为y＝﹣x+2，由解得，∴点P坐标（，）．2：利用两点之间距离最短求最值例2：如图，菱形ABCD的边长为2，∠ABC＝60°，点E、F在对角线BD 上运动，且EF＝2，连接AE、AF，则△AEF周长的最小值是（）A．4 B．4+ C．2+2 D．6解：如图作AH∥BD，使得AH＝EF＝2，连接CH交BD于F，则AE+AF的值最小，即△AEF的周长最小．∵AH＝EF，AH∥EF，∴四边形EFHA是平行四边形，∵FA＝FC，∴AE+AF＝FH+CF＝CH，∵菱形ABCD的边长为2，∠ABC＝60°，∴AC＝AB＝2，∵四边形ABCD是菱形，∴AC⊥BD，∵AH∥DB，∴AC⊥AH，∴∠CAH＝90°，在Rt△CAH中，CH＝，∴AE+AF的最小值4，∴△AEF的周长的最小值＝4+2＝6，3：利用垂线段最短求最值例3：如图，矩形ABCD中，AB＝4，AD＝2，E为AB的中点，F为EC上一动点，P为DF中点，连接PB，则PB的最小值是（）A．2 B．4 C． D．解：如图：当点F与点C重合时，点P在P1处，CP1＝DP1，当点F与点E重合时，点P在P2处，EP2＝DP2，∴P1P2∥CE且P1P2＝CE当点F在EC上除点C、E的位置处时，有DP＝FP由中位线定理可知：P1P∥CE且P1P＝CF∴点P的运动轨迹是线段P1P2，∴当BP⊥P1P2时，PB取得最小值∵矩形ABCD中，AB＝4，AD＝2，E为AB的中点，∴△CBE、△ADE、△BCP1为等腰直角三角形，CP1＝2∴∠ADE＝∠CDE＝∠CP1B＝45°，∠DEC＝90°∴∠DP2P1＝90°∴∠DP1P2＝45°∴∠P2P1B＝90°，即BP1⊥P1P2，∴BP的最小值为BP1的长在等腰直角BCP1中，CP1＝BC＝2∴BP1＝2∴PB的最小值是24：利用三边关系求最值例4：:如图，D是等边三角形ABC外一点．若BD＝8，CD＝6，连接AD，则AD的最大值与最小值的差为．解：如图，以CD为边向外作等边△CDE，连接BE，∵△CDE和△ABC是等边三角形，∴CE＝CD，CB＝CA，∠ECD＝∠BCA＝60°，∴∠ECB＝∠DCA，在△ECB和△DCA中，，∴△ECB≌△DCA（SAS），∴BE＝AD，∵DE＝CD＝6，BD＝8，∴在△BDE中，BD﹣DE＜BE＜BD+DE，即8﹣6＜BE＜8+6，∴2＜BE＜14，∴2＜AD＜14．则当B、D、E三点共线时，可得BE的最大值与最小值分别为14和2．∴AD的最大值与最小值的差为14﹣2＝12．5：利用隐圆求最值例5：如图，菱形ABCD边长为4，∠A＝60°，M是AD边的中点，N是AB边上一动点，将△AMN沿MN所在的直线翻折得到△A′MN，连接A′C，则A′C的最小值是（）A．2 B． +1 C．2﹣2 D．3解：如图所示：∵MA′是定值，A′C长度取最小值时，即A′在MC上时，过点M作MH⊥DC于点H，∵在边长为4的菱形ABCD中，∠A＝60°，M为AD中点，∴2MD＝AD＝CD＝4，∠HDM＝60°，∴∠HMD＝30°，∴HD＝MD＝1，∴HM＝DM×cos30°＝，∴MC＝＝2，∴A′C＝MC﹣MA′＝2﹣2；第6页（共6页）。

平面几何最值问题的解法平面几何的最值问题多为在存在动点或者不确定的位置关系的情况下求最值，有两种解题思路，一个是通过几何图形的性质实现对位置的确定，另一个是通过数量关系实现最值问题的解答. 一、利用对称性质，实现问题简单化图形经过某一点或者轴对称之后，就会有很多固有的由对称产生的等量关系，不同的对称性(如中心对称、轴对称等)也有独特的对称性质.合理地利用相应的性质会使问题得到简化，这会给解题带来很大的帮助.例1 在如图所示的平面直角坐标系中，在:轴的正半轴上有一点A ，B 的坐标为，点C 的坐标为1(,0)2，三点构成直角三角形OAB ，斜边OB 上有一个动点P ，求PA PC +的最小值.解析 我们利用对称的性质，会使解题息路得到转化.如右图所示，以OB 为轴，作点A 的对称点D ，连接AD 交OB 于点M .有AP DP =恒成立.利用三角形关系中两边之和大于第三边可得出当P 在DC连线上时取得最小值，即为图中所示的情形，只要求出CD 的长即可.根据B 点坐标可求出AB =，OB =由三角形面积不同求法间的等量关系可得出32AM =.故1322AN AD ==，由C 点坐标可求出1CN =.由勾股定理可求出2DC =，此值即为所求PA PC +的最小值. 点拨 本题中是作直线的对称点，实现直线同侧点到异侧点的转化，这是我们在解题中常遇到的情况以及常见的解题方法.对称性的应用注重于问题的解题技巧，目的是通过对称性使复杂的问题简单化. 二、构造不等关系，巧用基本不等式对于平面几何问题，不等关系的构造是离不开几何图形本身的数量关系的.想要利用基本不等式求解，学生需要在图形中找出满足不等式的条件，这不光对于学生的平面几何知识有考查，还要学生深入理解不等式的相关知识.例 2 已知四边形ABCD ，O 点为对角线AC 与BD 的交点，4AOB S =V ，9COD S =V ，求四边形ABCD 的面积S 的最小值解析 题中的四边形为不规则图形，没有直接求此类图形的公式，我们需要将其拆分成几个三角形进行分别求解.题中给出了两个三角形的面积，我们再表示出另两个三角形的面积就可以了.四边形按照此种分解后求面积，我们发现有很多等高的三角形，出现此类三角形，其面积比就只与底的长度有关，这时就可利用此关系计算.即有AOD CODAOB BOCS S S S =V V V V ，设AOD S a =V ，BOC S b =V ，整理得36ab =.又有131325S a b =++≥=，故最小值为25.点拨 本题中对于三角形知识的考察非常深入，将三角形面积间的关系转化为长度关系进行解答是最为关键的步骤，学生要有思维模式的转化才会想出这一解决方法，而后结合不等式知识解题，否则盲目地求面积是不能实现的.三、化为二次函数，列出方程再求解二次函数是初中数学中最重要的一类函数，此处并不是像压轴题那样对二次函数进行全面的考察，而是将所求的量转化为二次函数的形式，利用二次函数的相关性质解题，更加注重于对问题的分析转化能力.例3 有一三角形ABC ，底边120BC =，高80AD =，如图所示。

Ｌ y
-
1 4
Ｆ Ｏ Ｐ Ａ x
Ｂ Ｂ′ Ｐ′
图３
２ ， ２ （ （ ） 得ｋ ＋ ２ ｋ） １－ ） Ｓ－４ ｋ＋４＝０． ｋ ２ ） （ ， 由 Δ＝ （ 舍去 ） ２ Ｓ－４ －１ ６≥０ 得 Ｓ≥４ 或 Ｓ≤０ 此时 △Ａ Ｏ Ｂ 的最小面积为Ｓ＝４．
２ 由ｋ ＋４ ｋ＋４＝０ 得 ｋ＝－２，
中学教学参考
解题方法与技巧
平面解析几何中几种求最值的方法
） 甘肃会宁县第二中学 （ ７ ３ ０ ７ ０ ０ 吴国顺
一般先根据条件中 解平面解析几何中的最 值 问 题 ， 然后根据函数关系式的 列出的所求目标函数的关系 式 ， 特征选用判别式法 、 不等式的 性 质 以 及 数 形 结 合 等 方 法 求出它的最大值和最小值 ． 一、 判别式法求最值 数学解题中判别式是一 种 重 要 的 角 色 ， 当解析几何 判别式就能发挥其特殊 的量可转化为二次方程问题 时 ， 作用 ． 【 】 例１ 过 点 Ｍ（ １， ２） 如 图 １， ， 、 作直线 Ｌ Ｌ 与 ｘ 轴 ｙ 轴 的 正 半 轴 当 △Ａ 的交点为 Ａ 、 Ｂ． Ｏ Ｂ 的 面 积Ｓ 为最小值时 ， 求直线 Ｌ 的方程 ． 解： 设直线 Ｌ 的方程为ｙ－２＝ ）， 则 Ａ、 ｋ（ ｘ－１ Ｂ 的坐标分别为（ １ ２ ） １ （ － ， ０， ０， ２－ ｋ） ． Ｓ△ＡＯＢ ＝ （ ２－ ｋ ２ 图１
Ｏ y Ｃ Ｐ x
（ ） ， 故所求直线 Ｌ 的方程为ｙ－２＝－２ ｘ－１ 即２ ｘ＋ｙ－４＝０． 二、 应用平面几何知识求最值 把平面解析 几 何 中 的 最 值 问 题 转 化 为 平 面 几 何 中 能 充 分 利 用 平 面 几 何 技 巧 性 强， 运算量小 的最 值 问 题， 的特点 ． 【 例 ２】 平面上有两 如 图 ２， 、 ， 点 Ａ（ －１， ０） Ｂ（ １， ０） Ｍ 为圆（ ｘ

中考数学专题复习—几何最值问题一、知识点睛在平面几何的动态问题中，当某几何元素在给定条件变动时，求某几何量（如线段的长度、图形的周长或面积、角的度数以及它们的和与差）的最大值或最小值问题，称为几何最值问题。

解决平面几何最值问题的常用的方法有：（1）应用两点间线段最短的公理（含应用三角形的三边关系）求最值；（2）应用垂线段最短的性质求最值；（3）应用轴对称的性质求最值；（4）应用二次函数求最值；（5）应用其它知识求最值。

一般处理方法：常用定理：两点之间，线段最短（已知两个定点时）垂线段最短（已知一个定点、一条定直线时）三角形三边关系（已知两边长固定或其和、差固定时）二、考点剖析，分类探究（一）线段之和最小问题P A+PB 最小， 需转化， 使点在线异侧B l1. （2014年贵州南州）在如图所示的平面直角坐标系中，点P是直线y=x上的动点，A(1,0)，B(2,0)是x轴上的两点，则PA+PB的最小值为_____ 。

（二）线段之差最大问题2.（2013年江苏省宿迁市）在平面直角坐标系xoy中，已知点A（0,1），B（1,2），点P在x轴上运动，当点P到A、B两点距离之差的绝对值最大时，点P的坐标是_____ 。

（三）应用垂线段最短求最值问题3.（2014年葫芦岛）如图，矩形ABCD中，点M是CD的中点，点P是AB上的一动点，若AD=1，AB=2，则PA+PB+PM的最小值是_____ 。

（四）图形周长最值问题4. (2015年盘锦）如图，菱形ABCD的边长为2，∠DAB=60°，E为BC的中点，在对角线AC上存在一点P，使△PBE的周长最小，则△PBE的周长的最小值为_____ 。

（五）表面展开最值问题5. 如图,一圆锥的底面半径为2,母线PB的长为6,D为PB的中点.一只蚂蚁从点A出发,沿着圆锥的侧面爬行到点D,则蚂蚁爬行的最短路程为_____ 。

（六）图形面积的最值问题6.（2014年湖北省十堰市）如图，扇形OAB中，∠AOB=60°，扇形半径为4，点C在弧AB上，CD⊥OA，垂足为点D，当△OCD的面积最大时，求图中阴影部分的面积。