4 微分方程建模实例——Malthus模型与Logistic模型
- 格式:ppt
- 大小:1.82 MB
- 文档页数:8

实验目的[1] 学习由实际问题去建立数学模型的全过程;[2] 训练综合应用数学模型、微分方程、函数拟合和预测的知识分析和解决实际问题; [3] 应用matlab 软件求解微分方程、作图、函数拟合等功能,设计matlab 程序来求解其中的数学模型;[4] 提高论文写作、文字处理、排版等方面的能力;通过完成该实验,学习和实践由简单到复杂,逐步求精的建模思想,学习如何建立反映人口增长规律的数学模型,学习在求解最小二乘拟合问题不收敛时,如何调整初值,变换函数和数据使优化迭代过程收敛。
应用实验(或综合实验)一、实验内容从1790—1980年间美国每隔10年的人口记录如表综2.1所示:表综2.1年 份 1790 1800 1810 1820 1830 1840 1850 人口(×106)3.9 5.3 7.2 9.6 12.9 17.1 23.2 年 份 1860 1870 1880 1890 1900 1910 1920 人口(×106)31.4 38.6 50.2 62.9 76.0 92.0 106.5 年 份 193019401950196019701980人口(×106)123.2 131.7 150.7 179.3 204.0 226.5用以上数据检验马尔萨斯(Malthus)人口指数增长模型,根据检验结果进一步讨论马尔萨斯人口模型的改进,并利用至少两种模型来预测美国2010年的人口数量。
二、问题分析1:Malthus 模型的基本假设是:人口的增长率为常数,记为 r 。
记时刻t 的人口为x (t ),(即x (t )为模型的状态变量)且初始时刻的人口为x 0,于是得到如下微分方程:⎪⎩⎪⎨⎧==0)0(d d x x rxtx2:阻滞增长模型(或Logistic 模型) 由于资源、环境等因素对人口增长的阻滞作用,人口增长到一定数量后,增长率会下降,假设人口的增长率为x 的减函数,如设r(x)=r(1-x/x m ),其中r 为固有增长率(x 很小时),x m 为人口容量(资源、环境能容纳的最大数量),于是得到如下微分方程:⎪⎩⎪⎨⎧=-=0)0()1(d d xx x x rx t xm三、数学模型的建立与求解根据Malthus 模型的基本假设,和Logistic 模型,我们可以分别求得微分方程的解析解,y1=x0*exp(r*x);y2= xm/(1+x0*exp(-r*x))对于1790—1980年间美国每隔10年的人口记录,分别用matlab 工具箱中非线性拟合函数的命令作一般的最小二乘曲线拟合,可利用已有程序lsqcurvefit 进行拟合,检验结果进一步讨论模型的改进,预测美国2010年的人口数量。

Malthus模型和Logistic 模型随着社会的发展,人口问题与经济、资源、环境、社会的冲突日益成为制约国家发展的瓶颈,了解了人口增长函数,也就掌握了人口的发展动态和发展规律,这对国家的发展有重要意义。
1798年.英国人口学家和政治经济学家马尔萨斯以两个假设为前提:第一,食物为人类生存所必须;第二,人的性本能几乎无法限制,提出了闻名于世的人口指数增长模型,即Malthus人口模型:人口总数为p(t),人口的出生率为b,死亡率为d。
任取时段【t, t + dt ],在此时段中的出生人数为b p(t)dt ,死亡人数为d p(t)dt。
假设出生数及死亡数与p(t)及dt均成正比,而且以矩形取代了曲边梯形的面积。
在时段【t, t+dt ]中,人口增加量为p(t dt)- p(t)〜d p(t), 它应等于此时段中的出生人数与死亡人数之差,即d p(t) =b p(t) dt —d p(t) dt = a p(t) dt,其中a=b—d称为人口的净增长率。
于是p(t)满足微分方程^=ap(t). (1)dt若已知初始时刻t=t0时的人口总数为P0,那么p(t)还满足初始条件t=t0 时,p(t) =p0. (2)可以求得微分方程(1)满足初始条件⑵ 的解为(设a是常数) p(t)=p c e a(t _t0), ⑶即人口总数按指数增长。
模型参数的意义和作用:t0为初始时刻(初始年度),P0为初始年度t0的人口总数,a为每年的人口净增长率,b为人口出生率,d 为人口死亡率。
Malthus 人口模型所说的人口并不一定限于人,可以是认可一个生物群体,只要满足类似的性质即可。
现在讨论模型的应用和正确性。
例如,根据统计数据知在1961 年全世界人口为30.6 亿,1951 年-1961 年十年每年人口净增长率约为0.02。
取t o=1961, p o=3.06*109和a =0.02,就有9 0.02(t-t0)p(t)=3.06*10 *e ,用这个公式倒计算全世界在1700-1961 年间的人口总数,并把计算结果与实际统计数据作比较可以发现它们是比较符合的。


关键字:人口数平衡点方程模型运动预测曲线稳定增长人口一题目:请在人口增长的简单模型的基础上。
" (1)找到现有的描述人口增长,与控制人口增长的模型;" (2)深入分析现有的数学模型,并通过计算机进行仿真验证;" (3)选择一个你们认为较好的数学模型,并应用该模型对未来20年的某一地区或国家的人口作出有关预测;" (4)就人口增长模型给报刊写一篇文章,对控制人口的策略进行论述。
二摘要:本次建模是依照已知普查数据,利用Logistic模型,对中国人口的增长进行预测。
首先假设人口增长符合Logistic模型,即引入常数,用来表示自然环境条件所能容许的最大人口数。
并假设净增长率为,即净增长率随着人口数N(t)增长而减小,当N(t) 时,净增长率趋于零。
按照这个假设,。
用参数=3.0,r=0.0386, =1908, =14.5。
画出N=N(t)的图像,作为人口增长模型的一种近似。
做微分方程解的定性分析,求出N=N(t)的驻点和拐点,按照函数作图方法列出定性分析表,作出相轨迹的运动图。
当初始人口<时,方程的解单调递增到地趋向,这意味着如果使用Logistic模型描述人口增长,则人口发展地总趋势是渐增到最大人口数,因此可作为人口的预测值,也称谓平衡点。
用导数做稳定分析,为判断平衡点是否为稳定,可在平面上绘制f(x)的图象,然后像函数绘图那样,用导数进行定性分析,通过图看出人口数N(t)按时间是递增的,当人口数未达到饱和状态的时候,将逐渐地趋向,这意味着是稳定的平衡点。
按该模型,未来人口的数量将随着时间的演化,从初始状态出发达到极限状态,这样就给出了人口的未来预测。
三问题的提出1. Malthus模型英国统计学家Malthus(1766-1834)发现人口增长率是一个常数。
设t时刻人口为N(t),因为人口总数很大,可近似把N(t)当作连续变量处理。
Malthus的假设是:在人口的自然增长过程中,净相对增长率(出生率减去死亡率)是常数,即单位时间内人口的增长量与人口总数成正比。
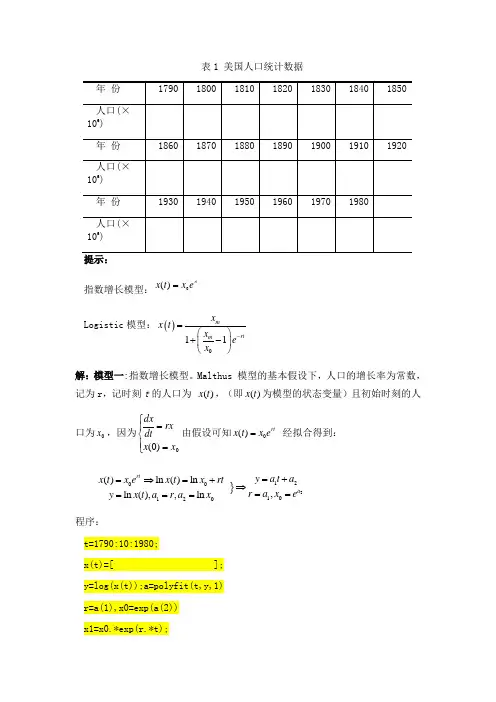
表1 美国人口统计数据指数增长模型:rt e x t x 0)(=Logistic 模型:()011mrtm x x t x e x -=⎛⎫+- ⎪⎝⎭解:模型一:指数增长模型。
Malthus 模型的基本假设下,人口的增长率为常数,记为r ,记时刻t 的人口为 )(t x ,(即)(t x 为模型的状态变量)且初始时刻的人口为0x ,因为⎪⎩⎪⎨⎧==0)0(x x rxdt dx由假设可知0()rt x t x e = 经拟合得到:}2120010120()ln ()ln ,ln (),,ln rt a y a t a x t x e x t x rt r a x ey x t a r a x =+=⇒=+⇒=====程序:t=1790:10:1980;x(t)=[ ]; y=log(x(t));a=polyfit(t,y,1) r=a(1),x0=exp(a(2)) x1=x0.*exp(r.*t);plot(t,x(t),'r',t,x1,'b') 结果:a =r= x0=所以得到人口关于时间的函数为:0.02140()t x t x e =,其中x0 = , 输入:t=2010;x0 = ;x(t)=x0*exp*t)得到x(t)= 。
即在此模型下到2010年人口大约为 610⨯。
模型二:阻滞增长模型(或 Logistic 模型) 由于资源、环境等因素对人口增长的阻滞作用,人口增长到一定数量后,增长率会下降,假设人口的增长率为 x 的减函数,如设)/1()(m x x r x r -=,其中 r 为固有增长率 (x 很小时 ) ,m x 为人口容量(资源、环境能容纳的最大数量), 于是得到如下微分方程:⎪⎩⎪⎨⎧=-=0)0()1(xx x x rx dt dxm 建立函数文件function f=curvefit_fun2 (a,t)f=a(1)./(1+(a(1)/*exp(-a(2)*(t-1790))); 在命令文件中调用函数文件 % 定义向量(数组) x=1790:10:1990; y=[ 76 ... 92 204 ];plot(x,y,'*',x,y); % 画点,并且画一直线把各点连起来 hold on;a0=[,1]; % 初值% 最重要的函数,第1个参数是函数名(一个同名的m 文件定义),第2个参数是初值,第3、4个参数是已知数据点 a=lsqcurvefit('curvefit_fun2',a0,x,y); disp(['a=' num2str(a)]); % 显示结果 % 画图检验结果 xi=1790:5:2020; yi=curvefit_fun2(a,xi); plot(xi,yi,'r'); % 预测2010年的数据 x1=2010;y1=curvefit_fun2(a,x1) hold off 运行结果: a= y1 =其中a(1)、a(2)分别表示()011mrtm x x t x e x -=⎛⎫+- ⎪⎝⎭中的m x 和r ,y1则是对美国美国2010年的人口的估计。

人口增长的微分方程模型通常基于Malthusian或Logistic增长模型。
以下是这两种常见的人口增长模型:
1. **Malthusian模型**:
Malthusian模型是人口增长的最简单模型之一,它基于以下假设:
- 人口的增长率与当前人口数量成正比。
- 增长率是恒定的,不受其他因素的影响。
用数学符号表示,Malthusian模型可以写成如下的微分方程:
\(\frac{dP}{dt} = rP\)
其中,\(P\) 表示人口数量,\(t\) 表示时间,\(r\) 表示增长率。
这个方程的解是指数函数,人口数量会随时间指数增长。
2. **Logistic模型**:
Logistic模型更贴近实际情况,考虑了人口增长的有限性。
它基于以下假设:- 人口的增长率与当前人口数量成正比,但随着人口接近一个上限,增长率会减小。
- 人口增长率的减小是受到资源限制或竞争的影响。
Logistic模型的微分方程如下:
\(\frac{dP}{dt} = rP(1 - \frac{P}{K})\)
其中,\(P\) 表示人口数量,\(t\) 表示时间,\(r\) 表示初始增长率,\(K\) 表示人口的上限或最大承载能力。
这个方程的解是S形曲线,人口数量会在接近\(K\) 时趋于稳定。
需要注意的是,实际的人口增长受到多种复杂因素的影响,包括出生率、死亡率、移民等。
因此,上述模型是简化的描述,用于理论分析和初步估算。
实际人口增长的模拟需要更复杂的模型和更多的参数考虑。
此外,这些模型还可以扩展,以包括更多的因素,如年龄结构、性别比例和社会因素等。


常微分方程在数学建模中的应用这里介绍几个典型的用微分方程建立数学模型的例子. 一、人口预测模型由于资源的有限性,当今世界各国都注意有计划地控制人口的增长,为了得到人口预测模型,必须首先搞清影响人口增长的因素,而影响人口增长的因素很多,如人口的自然出生率、人口的自然死亡率、人口的迁移、自然灾害、战争等诸多因素,如果一开始就把所有因素都考虑进去,则无从下手.因此,先把问题简化,建立比较粗糙的模型,再逐步修改,得到较完善的模型.例1( 马尔萨斯 (Malthus ) 模型) 英国人口统计学家马尔萨斯(1766—1834)在担任牧师期间,查看了教堂100多年人口出生统计资料,发现人口出生率是一个常数,于1789年在《人口原理》一书中提出了闻名于世的马尔萨斯人口模型,他的基本假设是:在人口自然增长过程中,净相对增长(出生率与死亡率之差)是常数,即单位时间内人口的增长量与人口成正比,比例系数设为r ,在此假设下,推导并求解人口随时间变化的数学模型.解 设时刻t 的人口为)(t N ,把)(t N 当作连续、可微函数处理(因人口总数很大,可近似地这样处理,此乃离散变量连续化处理),据马尔萨斯的假设,在t 到t t ∆+时间段内,人口的增长量为t t rN t N t t N ∆=-∆+)()()(,并设0t t =时刻的人口为0N ,于是⎪⎩⎪⎨⎧==.,00)(d d N t N rN t N这就是马尔萨斯人口模型,用分离变量法易求出其解为)(00e )(t t r N t N -=,此式表明人口以指数规律随时间无限增长.模型检验:据估计1961年地球上的人口总数为91006.3⨯,而在以后7年中,人口总数以每年2%的速度增长,这样19610=t ,901006.3⨯=N ,02.0=r ,于是)1961(02.09e1006.3)(-⨯=t t N .这个公式非常准确地反映了在1700—1961年间世界人口总数.因为,这期间地球上的人口大约每35年翻一番,而上式断定34.6年增加一倍(请读者证明这一点).但是,后来人们以美国人口为例,用马尔萨斯模型计算结果与人口资料比较,却发现有很大的差异,尤其是在用此模型预测较遥远的未来地球人口总数时,发现更令人不可思议的问题,如按此模型计算,到2670年,地球上将有36 000亿人口.如果地球表面全是陆地(事实上,地球表面还有80%被水覆盖),我们也只得互相踩着肩膀站成两层了,这是非常荒谬的,因此,这一模型应该修改.例2(逻辑Logistic 模型) 马尔萨斯模型为什么不能预测未来的人口呢?这主要是地球上的各种资源只能供一定数量的人生活,随着人口的增加,自然资源环境条件等因素对人口增长的限制作用越来越显著,如果当人口较少时,人口的自然增长率可以看作常数的话,那么当人口增加到一定数量以后,这个增长率就要随人口的增加而减小.因此,应对马尔萨斯模型中关于净增长率为常数的假设进行修改.1838年,荷兰生物数学家韦尔侯斯特(Verhulst)引入常数m N ,用来表示自然环境条件所能容许的最大人口数(一般说来,一个国家工业化程度越高,它的生活空间就越大,食物就越多,从而m N 就越大),并假设将增长率等于⎪⎪⎭⎫⎝⎛-m N t N r )(1,即净增长率随着)(t N 的增加而减小,当m N t N →)(时,净增长率趋于零,按此假定建立人口预测模型.解 由韦尔侯斯特假定,马尔萨斯模型应改为00d 1d ()m N N r N t N N t N ⎧⎛⎫=-⎪ ⎪⎨⎝⎭⎪=⎩,, 上式就是逻辑模型,该方程可分离变量,其解为,)(00e 11)(t t r m mN N N t N --⎪⎪⎭⎫ ⎝⎛-+=.下面,我们对模型作一简要分析.(1)当∞→t ,m N t N →)(,即无论人口的初值如何,人口总数趋向于极限值m N ; (2)当m N N <<0时,01d d >⎪⎪⎭⎫ ⎝⎛-=N N N r t N m ,这说明)(t N 是时间t 的单调递增函数;(3)由于N N N N N r t N m m ⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=211d d 222,所以当2m N N <时,0d d 22>t N ,t N d d 单增;当2m N N >时,0d d 22<t N ,t N d d 单减,即人口增长率tNd d 由增变减,在2m N 处最大,也就是说在人口总数达到极限值一半以前是加速生长期,过这一点后,生长的速率逐渐变小,并且迟早会达到零,这是减速生长期;(4)用该模型检验美国从1790年到1950年的人口,发现模型计算的结果与实际人口在1930年以前都非常吻合,自从1930年以后,误差愈来愈大,一个明显的原因是在20世纪60年代美国的实际人口数已经突破了20世纪初所设的极限人口.由此可见该模型的缺点之一是m N 不易确定,事实上,随着一个国家经济的腾飞,它所拥有的食物就越丰富, m N 的值也就越大;(5)用逻辑模型来预测世界未来人口总数.某生物学家估计,029.0=r ,又当人口总数为91006.3⨯时,人口每年以2%的速率增长,由逻辑模型得⎪⎪⎭⎫⎝⎛-=m N N r t N N 1d d 1, 即 ⎪⎪⎭⎫ ⎝⎛⨯-=m N 91006.31029.002.0, 从而得 91086.9⨯=m N ,即世界人口总数极限值近100亿.值得说明的是:人也是一种生物,因此,上面关于人口模型的讨论,原则上也可以用于在自然环境下单一物种生存着的其他生物,如森林中的树木、池塘中的鱼等,逻辑模型有着广泛的应用.二、市场价格模型对于纯粹的市场经济来说,商品市场价格取决于市场供需之间的关系,市场价格能促使商品的供给与需求相等(这样的价格称为(静态)均衡价格).也就是说,如果不考虑商品价格形成的动态过程,那么商品的市场价格应能保证市场的供需平衡,但是,实际的市场价格不会恰好等于均衡价格,而且价格也不会是静态的,应是随时间不断变化的动态过程.例3 试建立描述市场价格形成的动态过程的数学模型解 假设在某一时刻t ,商品的价格为)(t p ,它与该商品的均衡价格间有差别,此时,存在供需差,此供需差促使价格变动.对新的价格,又有新的供需差,如此不断调节,就构成市场价格形成的动态过程,假设价格)(t p 的变化率tpd d 与需求和供给之差成正比,并记),(r p f 为需求函数,)(p g 为供给函数(r 为参数),于是()()[]⎪⎩⎪⎨⎧=-=,,0)0(,d d p p p g r p f tpα 其中0p 为商品在0=t 时刻的价格,α为正常数.若设b ap r p f +-=),(,d cp p g +=)(,则上式变为⎪⎩⎪⎨⎧=-++-=,,0)0()()(d d p p d b p c a t pαα ① 其中d c b a ,,,均为正常数,其解为ca db c a d b p t p t c a +-+⎪⎭⎫ ⎝⎛+--=+-)(0e)(α.下面对所得结果进行讨论:(1)设p 为静态均衡价格 ,则其应满足0)(),(=-p g r p f ,即d p c b p a +=+-,于是得ca db p +-=,从而价格函数)(t p 可写为 p p p t p t c a +-=+-)(0e )()(α , 令+∞→t ,取极限得p t p t =+∞→)(lim这说明,市场价格逐步趋于均衡价格.又若初始价格p p =0,则动态价格就维持在均衡价格p 上,整个动态过程就化为静态过程;(2)由于t c a c a p p tp)(0e )()(d d +-+-=αα , 所以,当p p >0时,0d d <t p ,)(t p 单调下降向p 靠拢;当p p <0时, 0d d >tp ,)(t p 单调增加向p 靠拢.这说明:初始价格高于均衡价格时,动态价格就要逐步降低,且逐步靠近均衡价格;否则,动态价格就要逐步升高.因此,式①在一定程度上反映了价格影响需求与供给,而需求与供给反过来又影响价格的动态过程,并指出了动态价格逐步向均衡价格靠拢的变化趋势.三、混合溶液的数学模型 例 4 设一容器内原有100L 盐,内含有盐10kg,现以3L/min 的速度注入质量浓度为0.01kg/L 的淡盐水,同时以2L/min 的速度抽出混合均匀的盐水,求容器内盐量变化的数学模型.解 设t 时刻容器内的盐量为)(t x kg,考虑t 到t t d +时间内容器中盐的变化情况,在dt 时间内容器中盐的改变量=注入的盐水中所含盐量-抽出的盐水中所含盐量容器内盐的改变量为x d ,注入的盐水中所含盐量为t d 301.0⨯,t 时刻容器内溶液的质量浓度为tt x )23(100)(-+,假设t 到t t d +时间内容器内溶液的质量浓度不变(事实上,容器内的溶液质量浓度时刻在变,由于t d 时间很短,可以这样看).于是抽出的盐水中所含盐量为t tt x d 2)23(100)(-+,这样即可列出方程t txt x d 1002d 03.0d +-=,即txt x +-=100203.0d d . 又因为0=t 时,容器内有盐10kg,于是得该问题的数学模型为d 20.03d 100(0)10x x t tx ⎧+=⎪+⎪⎨⎪⎪=⎩,, 这是一阶非齐次线性方程的初值问题,其解为24)100(109)100(01.0)(t t t x +⨯++=. 下面对该问题进行一下简单的讨论,由上式不难发现:t 时刻容器内溶液的质量浓度为34)100(10901.0100)()(t t t x t p +⨯+=+=, 且当+∞→t 时,01.0)(→t p ,即长时间地进行上述稀释过程,容器内盐水的质量浓度将趋于注入溶液的质量浓度.溶液混合问题的更一般的提法是:设有一容器装有某种质量浓度的溶液,以流量1V 注入质量浓度为1C 的溶液 (指同一种类溶液,只是质量浓度不同),假定溶液立即被搅匀,并以2V 的流量流出这种混合溶液,试建立容器中质量浓度与时间的数学模型.首先设容器中溶质的质量为)(t x ,原来的初始质量为0x ,t =0时溶液的体积为2V ,在d t 时间内,容器内溶质的改变量等于流入溶质的数量减去流出溶质的数量,即t V C t V C x d d d 2211-=,其中1C 是流入溶液的质量浓度, 2C 为t 时刻容器中溶液的质量浓度,,tV V V xC )(2102-+=于是,有混合溶液的数学模型11220d d (0)xC V C V tx x ⎧=-⎪⎨⎪=⎩,. 该模型不仅适用于液体的混合,而且还适用于讨论气体的混合.四、振动模型振动是生活与工程中的常见现象.研究振动规律有着极其重要的意义.在自然界中,许多振动现象都可以抽象为下述振动问题.例5 设有一个弹簧,它的上端固定,下端挂一个质量为m 的物体,试研究其振动规律. 解 假设(1)物体的平衡位置位于坐标原点,并取x 轴的正向铅直向下(见图4).物体的平衡位置指物体处于静止状态时的位置.此时,作用在物体上的重力与弹性力大小相等,方向相反;(2)在一定的初始位移0x 及初始速度0v 下,物体离开平衡位置,并在平衡位置附近作没有摇摆的上下振动;(3)物体在t 时刻的位置坐标为)(t x x =,即t 时刻物体偏离平衡位置的位移;(4)在振动过程中,受阻力作用.阻力的大小与物体速度成正比,阻力的方向总是与速度方向相反,因此阻力为txhd d -,h 为阻尼系数;(5)当质点有位移)(t x 时,假设所受的弹簧恢复力是与位移成正比的,而恢复力的方向总是指向平衡位置,也就是总与偏离平衡位置的位移方向相反,因此所受弹簧恢复力为kx -,其中k 为劲度系数;(6)在振动过程中受外力)(t f 的作用.在上述假设下,根据牛顿第二定律得)(d d d d 22x f kx t xh tx m +--= , ①这就是该物体的强迫振动方程.由于方程①中, )(t f 的具体形式没有给出,所以,不能对式 ①直接求解.下面我们分四种情形对其进行讨论.1. 无阻尼自由振动在这种情况下,假定物体在振动过程中,既无阻力、又不受外力 作用.此时方程①变为0d d 22=+kx txm ,令2ω=mk,方程变为 0d d 222=+x tx ω,特征方程为 022=+ωλ, 特征根为ωλi 2,1±=,通解为 t C t C x ωωcos sin 21+=,或将其写为⎪⎪⎭⎫ ⎝⎛++++=t C C C t C C C C C x ωωcos sin 22212222112221图4()t t A ωϕωϕcos sin sin cos +=,)sin(ϕω+=t A 其中 2221C C A +=,22212sin CC C +=ϕ,22211cos CC C +=ϕ.这就是说,无阻尼自由振动的振幅2221C C A +=,频率mk=ω均为常数. 2.有阻尼自由振动在该种情况下,考虑物体所受到的阻力,不考虑物体所受的外力.此时,方程①变为0d d d d 22=++kx t xh tx m ,令2ω=m k ,δ2=mh,方程变为 0d d 2d d 222=++x t xtx ωδ, 特征方程为0222=++ωδλλ,特征根 222,1ωδδλ-±-=.根据δ与ω的关系,又分为如下三种情形:(1)大阻尼情形, δ>ω.特征根为二不等实根,通解为ttC C x )(2)(12222eeωδδωδδ-+--+-+=(2)临界阻尼情形,ωδ=.特征根为重根,通解为tt C C x δ-+=e)(21这两种情形,由于阻尼比较大,都不发生振动.当有一初始扰动以后,质点慢慢回到平衡位置,位移随时间t 的变化规律分别如图5和图6所示.图5 图6(3)小阻尼情形,δ<ω.特征根为共轭复根,通解为)sin C sinC (e 222221t t x t δωδωδ-+-=-将其简化为)sin(e 22ϕδωδ+-=-t A x t其中,cos ,sin ,22211222122221C C C C C C C C A ++=+=ϕϕ振幅A tδ-e 随时间t 的增加而减小.因此,这是一种衰减振动.位移随时间t 的变化规律见图7.3.无阻尼强迫振动在这种情形下,设物体不受阻力作用,其所受外力为简谐力pt m t f sin )(=,此时,方程①化为pt m kx t xm sin d d 22=+,pt x tx sin d d 222=+ω, 根据p i 是否等于特征根ωi ,其通解分为如下两种情形:(1)当ω≠p 时,其通解为 图7t C t C pt px ωωωcos sin sin 12122++-=, 此时,特解的振幅221p -ω为常数,但当p 接近于ω时,将会导致振幅增大,发生类似共振的现象;(2)当ω=p 时,其通解为t C t C pt t px ωωcos sin cos 2121++-=, 此时,特解的振幅t p21随时间t 的增加而增大,这种现象称为共振,即当外力的频率p 等于物体的固有频率ω时,将发生共振.4.阻尼强迫振动在这种情形下,假定振动物体既受阻力作用,又受外力pt m x f sin )(=的作用,并设ωδ<,方程①变为pt x t xtx sin d d 2d d 222=++ωδ ,特征根0,i 22≠-±-=δδωδλ,则p i 不可能为特征根,特解为pt B pt A x cos sin *+=,其中22222224)(p p p A δωω+--=,222224)(2pp pB δωδ+--=, 还可将其化为*22222221[()sin 2cos ]()4x w p pt p pt w p pδδ=---+, 由此可见,在有阻尼的情况下,将不会发生共振现象,不过,当ω=p 时,pt px cos 21*δ-=, 若δ很小,则仍会有较大的振幅;若δ比较大,则不会有较大的振幅.。


种群增长率的计算公式1.离散型增长模型:离散型增长模型适用于种群数量在离散的时间段内发生变化的情况,其中最常用的模型是Malthus模型和Logistic模型。
1.1 Malthus模型:Malthus模型是由Thomas Robert Malthus在18世纪末提出的,他认为种群数量的增长速度与种群数量成正比。
该模型可以用以下公式表示:N(t) = N(0) * e^(rt)其中,N(t)表示时间t时刻的种群数量,N(0)表示初始种群数量,e是自然对数的底,r是每一单位时间内的增长率。
1.2 Logistic模型:Logistic模型在Malthus模型的基础上考虑了资源有限的情况,种群数量的增长速度受到资源限制的影响。
该模型可以用以下公式表示:N(t) = K / [1 + (K/N(0) - 1) * e^(-rt)]其中,N(t)、N(0)和r的含义与Malthus模型中相同,K表示环境的承载能力。
2.连续型增长模型:连续型增长模型适用于种群数量在连续的时间段内发生变化的情况,其中最常用的模型是Logistic模型和Verhulst模型。
2.1 Logistic模型:在离散型增长模型中已经介绍过Logistic模型的公式。
2.2 Verhulst模型:Verhulst模型是对Logistic模型的一种改进,它考虑了种群数量在资源有限条件下的波动。
该模型可以用以下微分方程表示:dN(t)/dt = r * N(t) * [1 - (N(t)/K)]其中dN(t)/dt表示时间t时刻种群数量的增长率,其值等于种群数量关于时间的导数,r表示每一单位时间内的增长率,K表示环境的承载能力。
数学建模平时作业班级:0820862 学号:09姓名:武彩霞一、 Maltlhus 模型: 模型假设:记t 时刻人口的数量为)(t x ,假设人口是连续发生变化的,人口的增长率是常数 r ,如果不考虑环境资源和社会因素对人口的限制,和人口的迁入、迁出,试建立人口数量的变化规律。
已知;150)100(;100)0(==x x 求)150(x ,并图示模型曲线。
建立模型::rx dtdx= , 100)0(=x 由Matlab 软件容易解出这个方程:>> % Malthus 模型 syms x x0 rdsolve('Dx=r * x','x(0)=100') ans =100*exp(r*t) 即: rt e t x 100)(=由已知条件,利用Matlab 软件可以求出r ,>> syms rsolve('150=100*exp(r*100)') ans =1/100*log(3/2)然后 t=150 ,可以计算出 )150(x 。
利用Matlab 软件可以求出解: >> syms t f y>> f=100*exp(1/100*log(3/2)*t); >> subs(f,t,150)ans =183.7117即: )150(x =183.7117。
用Matlab 软件中的“plot ”命令画出图形:>> x=[0:1:100];>> y=100*exp(1/100*log(3/2)*x); >> plot(x,y,'-b')01002003004005006007008009001000100020003000400050006000xy指数增长模型拟合图形Logistic 模型: 模型假设:如果考虑环境资源和社会因素对人口的限制,考虑人口的迁入、迁出,试建立人口数量的变化规律。