电磁感应习题、答案及解法
- 格式:doc
- 大小:495.50 KB
- 文档页数:9

【物理】高中物理电磁感应经典习题(含答案)题一题目:一个导线截面积为$2.5\times10^{-4}m^2$,长度为$0.3m$,放在磁感应强度为$0.5T$的均匀磁场中,将导线两端连接到一个电阻为$2\Omega$的电阻器上,求电阻器中的电流。
解析:根据电磁感应定律,导线中的感应电动势与导线长度、磁感应强度以及导线的运动速度有关。
在此题中,导线不运动,所以感应电动势为零。
因此,电路中的电流完全由电源提供,根据欧姆定律,可以使用$U=IR$求解电流。
答案:电路中的电流为0A。
题二题目:一个充满磁感应强度为$1T$的磁场的金属环,直径为$0.2m$,环的厚度可以忽略不计。
当磁场方向垂直于环的平面并向上时,将环从磁场中抽出后,环中的磁场强度变为多少?解析:根据法拉第电磁感应定律,当闭合回路中的磁通量发生变化时,环中会产生感应电动势导致感应电流的产生。
在此题中,环被抽出磁场后,磁通量减小,从而产生感应电动势。
根据安培环路定理和比奥-萨伐尔定律,感应电动势的方向与磁场的变化方向相反,因此感应电流会生成一磁场。
根据安培定律和环形线圈的磁场公式,可以计算出环中的新的磁场强度。
答案:环中的新磁场强度需要通过计算得出。
具体计算过程请参考相关物理教材或参考书籍。
题三题目:一根长度为$0.5m$的直导线与一个磁场相垂直,导线两端的电动势为$2V$,导线的电阻为$4\Omega$,求导线在磁场中运动的速度。
解析:根据电磁感应定律,导线中的感应电动势与导线长度、磁场强度以及导线的运动速度有关。
在此题中,导线的电动势和电阻已知,可以使用欧姆定律$U=IR$解出电流,并使用感应电动势的公式$E=Bvl$解出运动速度。
答案:导线在磁场中的运动速度需要通过计算得出。
具体计算过程请参考相关物理教材或参考书籍。
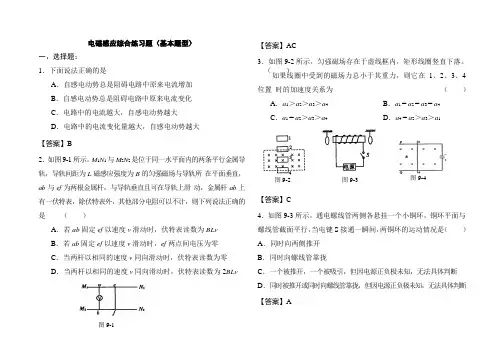
电磁感应综合练习题(基本题型)一、选择题: 1.下面说法正确的是( )A .自感电动势总是阻碍电路中原来电流增加B .自感电动势总是阻碍电路中原来电流变化C .电路中的电流越大,自感电动势越大D .电路中的电流变化量越大,自感电动势越大【答案】B2.如图9-1所示,M 1N 1与M 2N 2是位于同一水平面内的两条平行金属导轨,导轨间距为L 磁感应强度为B 的匀强磁场与导轨所 在平面垂直,ab 与ef 为两根金属杆,与导轨垂直且可在导轨上滑 动,金属杆ab 上有一伏特表,除伏特表外,其他部分电阻可以不计,则下列说法正确的是 ( ) A .若ab 固定ef 以速度v 滑动时,伏特表读数为BLvB .若ab 固定ef 以速度v 滑动时,ef 两点间电压为零C .当两杆以相同的速度v 同向滑动时,伏特表读数为零D .当两杆以相同的速度v 同向滑动时,伏特表读数为2BLv【答案】AC3.如图9-2所示,匀强磁场存在于虚线框内,矩形线圈竖直下落。
如果线圈中受到的磁场力总小于其重力,则它在1、2、3、4位置 时的加速度关系为 ( ) A .a 1>a 2>a 3>a 4 B .a 1 = a 2 = a 3 = a 4C .a 1 = a 2>a 3>a 4D .a 4 = a 2>a 3>a 1【答案】C4.如图9-3所示,通电螺线管两侧各悬挂一个小铜环,铜环平面与螺线管截面平行,当电键S 接通一瞬间,两铜环的运动情况是( ) A .同时向两侧推开 B .同时向螺线管靠拢C .一个被推开,一个被吸引,但因电源正负极未知,无法具体判断D .同时被推开或同时向螺线管靠拢,但因电源正负极未知,无法具体判断 【答案】 A图9-2图9-3图9-4图9-15.如图9-4所示,在U形金属架上串入一电容器,金属棒ab在金属架上无摩擦地以速度v向右运动一段距离后突然断开开关,并使ab停在金属架上,停止后,ab不再受外力作用。

电磁感应练习50题(含答案)1、如图所示,在匀强磁场中有一倾斜的平行金属导轨,导轨间距为L=0.2m,长为2d,d=0.5m,上半段d导轨光滑,下半段d导轨的动摩擦因素为μ=,导轨平面与水平面的夹角为θ=30°.匀强磁场的磁感应强度大小为B=5T,方向与导轨平面垂直.质量为m=0.2kg的导体棒从导轨的顶端由静止释放,在粗糙的下半段一直做匀速运动,导体棒始终与导轨垂直,接在两导轨间的电阻为R=3Ω,导体棒的电阻为r=1Ω,其他部分的电阻均不计,重力加速度取g=10m/s2,求:(1)导体棒到达轨道底端时的速度大小;(2)导体棒进入粗糙轨道前,通过电阻R上的电量q;(3)整个运动过程中,电阻R产生的焦耳热Q.答案分析:(1)研究导体棒在粗糙轨道上匀速运动过程,受力平衡,根据平衡条件即可求解速度大小.(2)进入粗糙导轨前,由法拉第电磁感应定律、欧姆定律和电量公式结合求解电量.(3)导体棒在滑动时摩擦生热为Q f=2μmgdcosθ,再根据能量守恒定律求解电阻产生的焦耳热Q.解答:解:(1)导体棒在粗糙轨道上受力平衡:由 mgsin θ=μmgcos θ+BIL得:I=0.5A由BLv=I(R+r)代入数据得:v=2m/s(2)进入粗糙导轨前,导体棒中的平均电动势为: ==导体棒中的平均电流为: ==所以,通过导体棒的电量为:q=△t==0.125C(3)由能量守恒定律得:2mgdsin θ=Q电+μmgdcos θ+mv2得回路中产生的焦耳热为:Q电=0.35J所以,电阻R上产生的焦耳热为:Q=Q电=0.2625J答:(1)导体棒到达轨道底端时的速度大小是2m/s;(2)导体棒进入粗糙轨道前,通过电阻R上的电量q是0.35C;(3)整个运动过程中,电阻R产生的焦耳热Q是0.2625J.点评:本题实质是力学的共点力平衡与电磁感应的综合,都要求正确分析受力情况,运用平衡条件列方程,关键要正确推导出安培力与速度的关系式,分析出能量是怎样转化的.2、如图所示,两平行金属导轨间的距离L=0.40m,金属导轨所在的平面与水平面夹角θ=37º,在导轨所在平面内,分布着磁感应强度B=0.50T、方向垂直于导轨所在平面的匀强磁场。

高三物理电磁感应试题答案及解析1.电磁感应现象在生活及生产中的应用非常普遍,下列不属于电磁感应现象及其应用的是【答案】 C【解析】试题分析: 发电机是利用线圈在磁场中做切割磁感线运动从而产生电流---电磁感应现象来工作的,所以A属于电磁感应现象及其应用;动圈式话筒是利用说话时空气柱的振动引起绕在磁铁上的线圈做切割磁感线运动,从而产生随声音变化的电流,利用了电磁感应现象,所以B属于电磁感应现象及其应用;电动机是利用通电线圈在磁场中受力转动的原理来工作的,所以C不属于电磁感应现象及其应用;变压器是利用电磁感应现象的原理来改变交流电压的,所以D属于电磁感应现象及其应用,故选C。
【考点】电磁感应2.在倾角为θ足够长的光滑斜面上,存在着两个磁感应强度大小相等的匀强磁场,磁场方向一个垂直斜面向上,另一个垂直斜面向下,宽度均为L,如图所示。
一个质量为m、电阻为R、边长也为L的正方形线框在t=0时刻以速度v0进入磁场,恰好做匀速直线运动,若经过时间t,线框ab边到达gg′与ff′中间位置时,线框又恰好做匀速运动,则下列说法正确的是()A.当ab边刚越过ff′时,线框加速度的大小为gsinθB.t时刻线框匀速运动的速度为C.t时间内线框中产生的焦耳热为D.离开磁场的过程中线框将做匀速直线运动【答案】BC【解析】当ab边进入磁场时,有E=Blv0,I=E/R,mgsinθ=BIl,有B2l2v/R=mgsinθ.当ab边刚越过f′时,线框的感应电动势和电流均加倍,则线框做减速运动,有4B2I2v/R=4mgsinθ,加速向上为3gsinθ,A错误;t0时刻线框匀速运动的速度为v,则有4B2I2v/R=mgsinθ,解得v=v/4,B正确;线框从进入磁场到再次做匀速运动过程,沿斜面向下运动距离为3l/2,则由功能关系得线框中产生的焦耳热为Q=3mglsinθ/2+(mv02/2-mv2/2)=3mgls inθ/2+15mv2/32,C正确;线框离开磁场时做加速运动,D错误。

高一物理电磁感应现象练习题及答案练习题一:1. 一根导线以速度v穿过磁感应强度为B的均匀磁场,导线长度为L,角度θ为导线与磁场方向的夹角。
求导线在时间Δt内所受到的感应电动势。
答案:感应电动势E = B * v * L * sinθ2. 一根导线以速度v进入磁感应强度为B的均匀磁场,导线的长度为L。
当导线完全进入磁场后,突然停止不动。
求此过程中导线两端之间的电势差。
答案:电势差V = B * v * L3. 一个长度为L的导线以速度v匀速通过磁感应强度为B的均匀磁场,当导线通过时间Δt后,磁场方向突然发生改变。
求导线两端之间产生的感应电动势。
答案:感应电动势E = 2 * B * v * L4. 一根长度为L的导线以速度v与磁感应强度为B的均匀磁场垂直相交,导线所受到的感应电动势大小为E,如果将导线切成长度为L/2的两段导线,两段导线所受感应电动势的大小分别是多少?答案:每段导线所受感应电动势的大小都是E练习题二:1. 一台电动机的转子有60个磁极,额定转速为3000转/分钟。
求转子在额定转速下的转子导线所受的感应电动势大小。
答案:转子导线所受感应电动势的大小为ω * Magnetic Flux,其中ω为角速度,Magnetic Flux为磁通量。
转速为3000转/分钟,转速ω =2π * 3000 / 60。
由于转子有60个磁极,每转所经过的磁通量为60 * Magnetic Flux。
因此,转子导线所受感应电动势的大小为60 * 2π * 3000 / 60 * Magnetic Flux。
2. 一根长度为L的导线以角速度ω绕通过导线轴线的磁感应强度为B的磁场旋转。
求导线两端之间的电势差大小。
答案:电势差V = B * ω * L3. 一根输电线路的电阻为R,长度为L,电流为I。
如果在电力系统中,磁感应强度为B的磁场垂直于导线方向,求输电线路两端之间的感应电动势。
答案:感应电动势E = B * L * I4. 一块矩形线圈有N匝,每匝的边长为a和b,磁通量为Φ,求矩形线圈所受到的感应电动势。

初中电磁感应专题练习(含详细答案)
一、选择题
1. 一个导线在磁场中匀速向右移动,感应电动势的方向如何?
A. 由左向右
B. 由右向左
C. 没有感应电动势
D. 无法确定
答案:B
2. 带电粒子在磁场中匀速运动,运动轨迹如何?
A. 直线运动
B. 圆形运动
C. 抛物线运动
D. 双曲线运动
答案:B
二、计算题
1. 一个弯曲的导线长为10cm,导线中有一个电流I=2A,若在
导线处有一个磁感应强度为B=3T的磁场,求电动势的大小为多少?
解答:
$\mathcal{E}=Blv=\frac{1}{2}Blv=\frac{1}{2}Blsin\theta=\frac{1}{2} \times 3 \times 0.1 \times 2=\frac{3}{20}$V。
三、简答题
1. 什么是电磁感应?
电磁感应是指导体中的电子受到磁场的作用从而在导体两端产
生的电动势。
2. 什么是法拉第电磁感应定律?
法拉第电磁感应定律指出,当导体中的磁力线发生变化时,沿
着导体的任意闭合回路中就会产生感应电动势,其大小与磁通量的
变化率成正比,方向满足楞次定律。
3. 什么是楞次定律?
楞次定律指出,当导体内有感应电流时,该电流所发出的磁场的方向是这样的,即它所引起的磁通量的变化总是阻碍引起这种变化的原因。
4. 什么情况下会产生感应电流?
当导体在磁场中发生运动或被磁场线穿过而发生变化时,就会在导体中产生感应电流。

电磁感应习题及答案一、 选择题1.如图1所示,两根无限长平行直导线载有大小相等、方向相反的电流I ,并都以dtdI的变化率增长,一圆形金属线圈位于导线平面内,则()A 线圈中无感应电流 ()B 线圈中感应电流为顺时针方向()C 线圈中感应电流为逆时针方向 ()D 线圈中感应电流方向不确定[ B ]解: 由楞次定律,可判断出感应电流方向为顺时针。
2.如图2所示,一载流螺线管的旁边有一圆形线圈,欲使线圈产生图示方向的感应电流i ,下列哪一种情况可以做到?()A 载流螺线管向线圈靠近 ()B 载流螺线管离开线圈()C 载流螺线管中电流减小 ()D 抽出载流螺线管中的铁心[ A]解:由楞次定律,可判断出必须增加线圈中的电流或将线圈想右移动。
3.一边长为l 的正方形线框,置于均匀磁场中,线框绕OO ’轴以匀角速度ω旋转(如图3所示)。
设0t =时,线框平面处于纸面内,则任一时刻感应电动势的大小为()A t B l ωcos 22 ()B B l 2ω ()C t B l ωωcos 212 ()D t B l ωωcos 2()E t B l ωωsin 2[ D ]解:t B l ωφsin 2= t B l dtd ωωφεcos 2=-=Oω图1 图2 图34.如图所示,导体棒AB 在均匀磁场B中绕通过C 点的垂直于棒长且磁场沿磁场方向的轴OO ’转动(角速度与B同方向),BC 的长度为棒长的41,则()A A 点比B 点电势高 ()B A 与B 点电势相等 ()C A 点比B 点电势低 ()D 稳恒电流从A 点流向B 点[A]()04144321214342224342434434〉=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛====•⨯=⎰⎰⎰----L LL L LL L L BL L L B Bl Bldl vBdl l d B v ωωωωε5.如图5所示,长度为l 的直导线CD 在均匀磁场B 中以速度υ移动,直导线CD 中的电动势为()A υBl ()B θυsin Bl ()C θυ cos Bl ()D 0[D]解: ()02cos sin ==•⨯=πθεvBL L B v6.如图6所示,M 、N 为水平面内两根平行金属导轨,ab 与cd 为垂直于导轨并可在其上自由滑动的两根直裸导线,外磁场垂直水平面向下,当外力使ab 向右平移时,cd()A 不动 ()B 转动 ()C 向左移动 ()D 向右移动[D]7.对于单匝线圈取自感系数的定义为I L φ=.当线圈的几何形状、大小及周围磁介质分布不变,切无铁磁性质时,若线圈中的电流强度变大,则线圈的自感系数L()A 变大,与电流成正比关系 ()B 变大,但与电流不成反比关系 ()C 变小,与电流成反比关系 ()D 不变 [D]8.如图7所示,一导体棒ab 在均匀磁场中沿金属导轨向左作匀加速运动,磁场方向垂直导轨所在平面,若导轨电阻忽略不计,并设铜心磁导率为常数,则达到稳定后在电容器的C 极板上会()A 带有一定量的正电荷 ()B 带有一定量的负电荷 ()C 带有越来越多的正电荷 ()D 带有越来越多的负电荷[A]9.在圆柱形空间内有一磁感应强度为B 的匀强磁场,如图所示。

电磁感应现象习题综合题含答案解析一、高中物理解题方法:电磁感应现象的两类情况1.如图,水平面(纸面)内同距为l 的平行金属导轨间接一电阻,质量为m 、长度为l 的金属杆置于导轨上,t =0时,金属杆在水平向右、大小为F 的恒定拉力作用下由静止开始运动.0t 时刻,金属杆进入磁感应强度大小为B 、方向垂直于纸面向里的匀强磁场区域,且在磁场中恰好能保持匀速运动.杆与导轨的电阻均忽略不计,两者始终保持垂直且接触良好,两者之间的动摩擦因数为μ.重力加速度大小为g .求(1)金属杆在磁场中运动时产生的电动势的大小; (2)电阻的阻值.【答案】0F E Blt g m μ⎛⎫=- ⎪⎝⎭ ; R =220B l t m【解析】 【分析】 【详解】(1)设金属杆进入磁场前的加速度大小为a ,由牛顿第二定律得:ma=F-μmg ① 设金属杆到达磁场左边界时的速度为v ,由运动学公式有:v =at 0 ②当金属杆以速度v 在磁场中运动时,由法拉第电磁感应定律,杆中的电动势为:E=Blv ③ 联立①②③式可得:0F E Blt g m μ⎛⎫=-⎪⎝⎭④ (2)设金属杆在磁场区域中匀速运动时,金属杆的电流为I ,根据欧姆定律:I=ER⑤ 式中R 为电阻的阻值.金属杆所受的安培力为:f BIl = ⑥ 因金属杆做匀速运动,由牛顿运动定律得:F –μmg–f=0 ⑦联立④⑤⑥⑦式得: R =220B l t m2.如图所示,两平行长直金属导轨(不计电阻)水平放置,间距为L ,有两根长度均为L 、电阻均为R 、质量均为m 的导体棒AB 、CD 平放在金属导轨上。
其中棒CD 通过绝缘细绳、定滑轮与质量也为m 的重物相连,重物放在水平地面上,开始时细绳伸直但无弹力,棒CD 与导轨间的动摩擦因数为μ,最大静摩擦力等于滑动摩擦力,忽略其他摩擦和其他阻力,导轨间有一方向竖直向下的匀强磁场1B ,磁场区域的边界满足曲线方程:sin(0y L x x L Lπ=≤≤,单位为)m 。

高中物理电磁感应现象习题知识点及练习题及答案一、高中物理解题方法:电磁感应现象的两类情况1.如图所示,足够长且电阻忽略不计的两平行金属导轨固定在倾角为α=30°绝缘斜面上,导轨间距为l =0.5m 。
沿导轨方向建立x 轴,虚线EF 与坐标原点O 在一直线上,空间存在垂直导轨平面的磁场,磁感应强度分布为1()00.60.8()0T x B x T x -<⎧=⎨+≥⎩(取磁感应强度B垂直斜面向上为正)。
现有一质量为10.3m =kg ,边长均为l =0.5m 的U 形框cdef 固定在导轨平面上,c 点(f 点)坐标为x =0。
U 形框由金属棒de 和两绝缘棒cd 和ef 组成,棒de 电阻为10.2R =Ω。
另有一质量为20.1=m kg ,长为l =0.5m ,电阻为20.2R =Ω的金属棒ab 在离EF 一定距离处获得一沿斜面向下的冲量I 后向下运动。
已知金属棒和U 形框与导轨间的动摩擦因数均为33μ=。
(1)若金属棒ab 从某处释放,且I =0.4N·s ,求释放瞬间金属棒ab 上感应电流方向和电势差ab U ;(2)若金属棒ab 从某处释放,同时U 形框解除固定,为使金属棒与U 形框碰撞前U 形框能保持静止,求冲量I 大小应满足的条件。
(3)若金属棒ab 在x =-0.32m 处释放,且I =0.4N·s ,同时U 形框解除固定,之后金属棒ab 运动到EF 处与U 形框发生完全非弹性碰撞,求金属棒cd 最终静止的坐标。
【答案】(1)感应电流方向从b 到a ;0.1V;(2)0.48N ⋅s ;(3)2.5m 【解析】 【分析】 【详解】(1)金属棒获得冲量I 后,速度为24m/s Iv m == 根据右手定则,感应电流方向从b 到a ; 切割磁感线产生的电动势为1E B lv =其中11B =T ;金属棒ab 两端的电势差为12120.1V ab B lvU R R R ==+(2)由于ab 棒向下运动时,重力沿斜面的分力与摩擦力等大反向,因此在安培力作用下运动,ab 受到的安培力为2212212B l v F m a R R ==+做加速度减小的减速运动;由左手定则可知,cd 棒受到安培力方向沿轨道向上,大小为21212B B l v F R R =+安其中21T B =;因此获得冲量一瞬间,cd 棒受到的安培力最大,最容易发生滑动 为使线框静止,此时摩擦力沿斜面向下为最大静摩擦力,大小为11cos sin m f m g m g μαα==因此安培力的最大值为12sin m g θ; 可得最大冲量为()12122122sin 0.48m m g R R I B B lα+==N·s (3)当I =0.4N·s 时,金属棒获得的初速度为04/v m s =,其重力沿斜面分力与摩擦力刚好相等,在安培力作用下做加速度减小的减速,而U 形框在碰撞前始终处于静止; 设到达EF 时速度为1v ,取沿斜面向下为正,由动量定理得22212012B l vtm v m v R R -=-+ 其中0.32m vt x == 解得12m/s v =金属棒与U 形线框发生完全非弹性碰撞,由动量守恒得()11122m v m m v =+因此碰撞后U 形框速度为20.5m/s v =同理:其重力沿斜面的分力与滑动摩擦力等大反向,只受到安培力的作用,当U 形框速度为v 时,其感应电流为12de ab B lv B lvI R R -=+其中,de B ,ab B 分别为de 边和ab 边处的磁感应强度,电流方向顺时针,受到总的安培力为()2212deab de abB B l vF B Il B Il R R -=-=+其中,,0.8cd ab B B kl k -== 由动量定理得()24122120k l vtm m v R R -=-++ 因此向下运动的距离为()()12212242m m m v R R s k l ++==此时cd 边的坐标为x =2.5m2.如图,光滑金属轨道POQ 、´´´P O Q 互相平行,间距为L ,其中´´O Q 和OQ 位于同一水平面内,PO 和´´P O 构成的平面与水平面成30°。

四. 知识要点:第一单元电磁感应现象楞次定律(一)电磁感应现象1. 产生感应电流的条件:穿过闭合电路的磁通量发生变化.2. 磁通量的计算(1)公式Φ=BS此式的适用条件是:①匀强磁场;②磁感线与平面垂直。
(2)如果磁感线与平面不垂直,上式中的S为平面在垂直于磁感线方向上的投影面积.即其中θ为磁场与面积之间的夹角,我们称之为“有效面积”或“正对面积”。
(3)磁通量的方向性:磁通量正向穿过某平面和反向穿过该平面时,磁通量的正负关系不同。
求合磁通时应注意相反方向抵消以后所剩余的磁通量。
(4)磁通量的变化:可能是B发生变化而引起,也可能是S发生变化而引起,还有可能是B和S同时发生变化而引起的,在确定磁通量的变化时应注意。
3. 感应电动势的产生条件:无论电路是否闭合,只要穿过电路的磁通量发生变化,这部分电路就会产生感应电动势。
这部分电路或导体相当于电源。
(二)感应电流的方向1. 右手定则当闭合电路的部分导体切割磁感线时,产生的感应电流的方向可以用右手定则来进行判断。
右手定则:伸开右手,使大拇指跟其余四指垂直,并且都跟手掌在一个平面内,让磁感线垂直穿入手心,大拇指指向导体运动方向,那么伸直四指指向即为感应电流的方向。
说明:伸直四指指向还有另外的一些说法:①感应电动势的方向;②导体的高电势处。
2. 楞次定律(1)内容感应电流具有这样的方向:就是感应电流的磁场总是阻碍引起感应电流的磁通量的变化。
注意:①“阻碍”不是“相反”,原磁通量增大时,感应电流的磁场与原磁通量相反,“反抗”其增加;原磁通量减小时,感应电流的磁场与原磁通量相同,“补偿”其减小,即“增反减同”。
②“阻碍”也不是阻止,电路中的磁通量还是变化的,阻碍只是延缓其变化。
③楞次定律的实质是“能量转化和守恒”,感应电流的磁场阻碍过程,使机械能减少,转化为电能。
(2)应用楞次定律判断感应电流的步骤:①确定原磁场的方向。
②明确回路中磁通量变化情况。
③应用楞次定律的“增反减同”,确定感应电流磁场的方向。
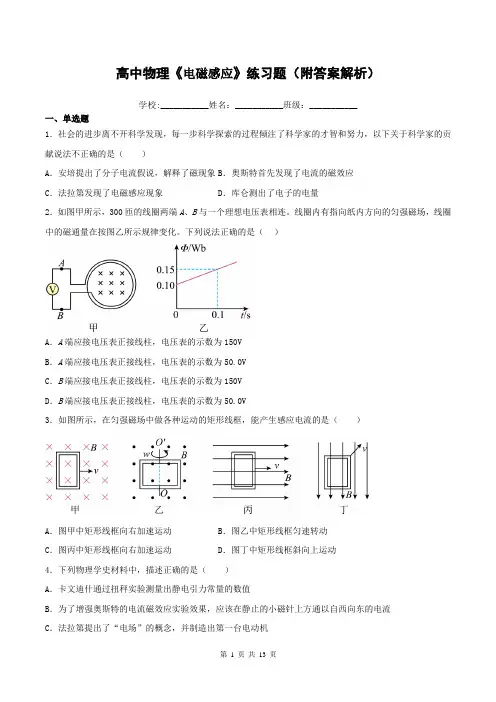
高中物理《电磁感应》练习题(附答案解析)学校:___________姓名:___________班级:___________一、单选题1.社会的进步离不开科学发现,每一步科学探索的过程倾注了科学家的才智和努力,以下关于科学家的贡献说法不正确的是()A.安培提出了分子电流假说,解释了磁现象B.奥斯特首先发现了电流的磁效应C.法拉第发现了电磁感应现象D.库仑测出了电子的电量2.如图甲所示,300匝的线圈两端A、B与一个理想电压表相连。
线圈内有指向纸内方向的匀强磁场,线圈中的磁通量在按图乙所示规律变化。
下列说法正确的是()A.A端应接电压表正接线柱,电压表的示数为150VB.A端应接电压表正接线柱,电压表的示数为50.0VC.B端应接电压表正接线柱,电压表的示数为150VD.B端应接电压表正接线柱,电压表的示数为50.0V3.如图所示,在匀强磁场中做各种运动的矩形线框,能产生感应电流的是()A.图甲中矩形线框向右加速运动B.图乙中矩形线框匀速转动C.图丙中矩形线框向右加速运动D.图丁中矩形线框斜向上运动4.下列物理学史材料中,描述正确的是()A.卡文迪什通过扭秤实验测量出静电引力常量的数值B.为了增强奥斯特的电流磁效应实验效果,应该在静止的小磁针上方通以自西向东的电流C.法拉第提出了“电场”的概念,并制造出第一台电动机D.库仑通过与万有引力类比,在实验的基础上验证得出库仑定律5.如图所示,将一个闭合铝框放在蹄形磁铁的两个磁极之间,铝框可以绕竖直轴OO'自由转动,蹄形磁铁在手摇的控制下可以绕竖直轴OO'转动。
初始时,铝框和蹄形磁铁均是静止的。
现通过不断手摇使蹄形磁铁转动起来,下列关于闭合铝框的说法正确的是()A.铝框仍保持静止B.铝框将跟随磁极同向转动且一样快C.铝框将跟随磁极同向转动,转速比磁铁小D.铝框将朝着磁极反向转动,转速比磁铁小6.如图所示,a、b是用同种规格的铜丝做成的两个同心圆环,两环半径之比为2:3,其中仅在a环所围成区域内有垂直于纸面向里的匀强磁场。
《大学物理》电磁感应练习题及答案解析一、选择题1. 圆铜盘水平放置在均匀磁场中,B 的方向垂直盘面向上,当铜盘绕通过中心垂直于盘面的轴沿图示方向转动时.( D )(A) 铜盘上有感应电流产生,沿着铜盘转动的相反方向流动。
(B) 铜盘上有感应电流产生,沿着铜盘转动的方向流动。
(C) 铜盘上没有感应电流产生,铜盘中心处电势最高。
(D) 铜盘上没有感应电流产生,铜盘边缘处电势最高。
2.在尺寸相同的铁环和铜环所包围的面积中穿过相同变化率的磁通量,则两环中( C )A.感应电动势相同,感应电流相同;B.感应电动势不同,感应电流不同;C.感应电动势相同,感应电流不同;D.感应电动势不同,感应电流相同。
3.两根无限长的平行直导线有相等的电流但电流的流向相反如右图,而电流的变化率均大于零,有一矩形线圈与两导线共面,则( B )A.线圈中无感应电流;B.线圈中感应电流为逆时针方向;C.线圈中感应电流为顺时针方向;D.线圈中感应电流不确定。
4.如图所示,在长直载流导线下方有导体细棒,棒与直导线垂直且共面。
(a)、(b)、(c)处有三个光滑细金属框。
今使以速度向右滑动。
设(a)、(b)、(c)、(d)四种情况下在细棒中的感应电动势分别为ℇa、ℇb、ℇc、ℇd,则( C )A.ℇa =ℇb =ℇc <ℇd B.ℇa =ℇb =ℇc >ℇdC.ℇa =ℇb =ℇc =ℇd D.ℇa >ℇb <ℇc <ℇd5.一矩形线圈,它的一半置于稳定均匀磁 场中,另一半位于磁场外,如右图所示, 磁感应强度B的方向与纸面垂直向里。
欲使线圈中感应电流为顺时针方向则(A ) A .线圈应沿x 轴正向平动; B .线圈应沿y 轴正向平动;C .线圈应沿x 轴负向平动D .线圈应沿y 轴负向平动6.在圆柱形空间内有一磁感强度为B 的均匀磁场,如图所示,B 的大小以速率dtdB变化,在磁场中有A 、B 两点,其间可以放置一直导线和一弯曲的导线,则有下列哪种情[ D ] (A) 电动势只在直导线中产生(B) 电动势只在弯曲的导线产生 (C) 电动势在直导线和弯曲的导线中都产生, 且两者大小相等(D)直导线中的电动势小于弯曲导线中的电动势 知识点:电动势 类型:A7、关于感生电场和静电场下列哪一种说法正确.( B )(A) 感生电场是由变化电场产生的.(B) 感生电场是由变化磁场产生的,它是非保守场. (C) 感生电场是由静电场产生的(D) 感生电场是由静电场和变化磁场共同产生的1D 2C 3B 4C 5A6D7B二、填空题1.如图所示,AB 、CD 、为两均匀金属棒,长均为0.2m ,放在磁感应强度 B=2T 的均匀磁场中,磁场的方向垂直于屏面向里,AB 和CD 可以在导轨上自由滑动,当 CD 和AB 在导轨上分别以s m v /41=、s m v /22=速率向右作匀速运动时,在CD 尚未追上AB 的时间段内ABDCA 闭合回路上动生电动势的大小______________ 方向 _____________________.1电动势的大小 0.8V 方向 顺时针方向2.一匝数的线圈,通过每匝线圈的磁通量,则任意时刻线圈感应电动势的大小 ______________ . 感应电动势的大小 t ππ10cos 1057⨯ 3.感生电场产生的原因_ 变化的磁场产生感生电场4.动生电动势的产生的原因是:___电荷在磁场中运动受到洛伦兹力___ 5 。
1
B.
2
如图所示,两根平行金属导轨置于水平面内,导轨之间接有电阻
中的感应电流逐渐减小
3
时,线圈中的电流改变方向
一个周期内,线圈产生的热量为
4
、总电阻为的正
边与磁场边界平行,如图(a)所示,已知导线框一直向右做匀速
时刻进入磁场.线框中感应电动势随时间变化的图线如图(b)所示(感
左转轴上侧绝缘漆挂掉,右转轴下侧的绝缘漆刮掉左转轴上下两侧绝缘漆都挂掉,右转轴下侧的绝缘漆刮掉
5
D.
和.圆形匀强磁场的边缘恰好与线圈重合,则穿6
7
磁场的方向;
答案B.
1
A 2
中的感应电流逐渐减小3
时,线圈中的电流改变方向
一个周期内,线圈产生的热量为
,所以线圈平面平行于磁感线,故A正确;
和,故B错误;
C.在交变电流产生的过程当中,磁通量最大时,感应电动势以及感应电流最小,故C 4
5
左转轴上侧绝缘漆挂掉,右转轴下侧的绝缘漆刮掉
左转轴上下两侧绝缘漆都挂掉,右转轴下侧的绝缘漆刮掉
6
D.
7
磁场的方向;
考点
开关接后,开始向右加速运动,速度达到最大值时,设上的感应电动势为,有
⑥
依题意有⑦
设在此过程中的平均电流为,上受到的平均安培力为,有
⑧
由动量定理,有
⑨
又⑩
联立⑤⑥⑦⑧⑨⑩式得
⑪
电磁感应
涡流、电磁阻尼和电磁驱动。
电磁感应现象习题综合题及答案解析一、高中物理解题方法:电磁感应现象的两类情况1.如图所示,两根光滑、平行且足够长的金属导轨倾斜固定在水平地面上,导轨平面与水平地面的夹角37θ=︒,间距为d =0.2m ,且电阻不计。
导轨的上端接有阻值为R =7Ω的定值电阻和理想电压表。
空间中有垂直于导轨平面斜向上的、大小为B =3T 的匀强磁场。
质量为m =0.1kg 、接入电路有效电阻r =5Ω的导体棒垂直导轨放置,无初速释放,导体棒沿导轨下滑一段距离后做匀速运动,取g =10m/s 2,sin37°=0.6,求:(1)导体棒匀速下滑的速度大小和导体棒匀速运动时电压表的示数; (2)导体棒下滑l =0.4m 过程中通过电阻R 的电荷量。
【答案】(1)20m/s 7V (2)0.02C 【解析】 【详解】(1)设导体棒匀速运动时速度为v ,通过导体棒电流为I 。
由平衡条件sin mg BId θ=①导体棒切割磁感线产生的电动势为E =Bdv ②由闭合电路欧姆定律得EI R r=+③ 联立①②③得v =20m/s ④由欧姆定律得U =IR ⑤联立①⑤得U =7V ⑥(2)由电流定义式得Q It =⑦由法拉第电磁感应定律得E t∆Φ=∆⑧B ld ∆Φ=⋅⑨由欧姆定律得EI R r=+⑩ 由⑦⑧⑨⑩得Q =0.02C ⑪2.如图所示,光滑的长平行金属导轨宽度d=50cm ,导轨所在的平面与水平面夹角θ=37°,导轨上端电阻R=0.8Ω,其他电阻不计.导轨放在竖直向上的匀强磁场中,磁感应强度B=0.4T .金属棒ab 从上端由静止开始下滑,金属棒ab 的质量m=0.1kg .(sin37°=0.6,g=10m/s 2)(1)求导体棒下滑的最大速度;(2)求当速度达到5m/s 时导体棒的加速度;(3)若经过时间t ,导体棒下滑的垂直距离为s ,速度为v .若在同一时间内,电阻产生的热与一恒定电流I 0在该电阻上产生的热相同,求恒定电流I 0的表达式(各物理量全部用字母表示).【答案】(1)18.75m/s (2)a=4.4m/s 2(3222mgs mv Rt【解析】【分析】根据感应电动势大小与安培力大小表达式,结合闭合电路欧姆定律与受力平衡方程,即可求解;根据牛顿第二定律,由受力分析,列出方程,即可求解;根据能量守恒求解;解:(1)当物体达到平衡时,导体棒有最大速度,有:sin cos mg F θθ= , 根据安培力公式有: F BIL =, 根据欧姆定律有: cos E BLv I R Rθ==, 解得: 222sin 18.75cos mgR v B L θθ==; (2)由牛顿第二定律有:sin cos mg F ma θθ-= ,cos 1BLv I A Rθ==, 0.2F BIL N ==, 24.4/a m s =;(3)根据能量守恒有:22012mgs mv I Rt =+ , 解得: 202mgs mvI Rt-=3.如图所示,在倾角30o θ=的光滑斜面上,存在着两个磁感应强度大小相等、方向分别垂直斜面向上和垂直斜面向下的匀强磁场,两磁场宽度均为L 。
电磁感应练习题及解答电磁感应练习题及解答电磁感应是物理学中的一个重要概念,涉及到电磁场的变化过程中电场和磁场相互作用产生的现象。
它在日常生活和科学研究中都有广泛的应用。
下面是一些电磁感应练习题及解答,供大家进行练习。
1. 一根长导线以速度v从北向南方向通过均匀磁场B,该导线的两端分别连接一个电阻为R的电灯泡。
求当导线通过磁场过程中,电灯泡亮起的时间。
解答:根据法拉第电磁感应定律,导线通过磁场时产生感应电动势,导致电流流过电灯泡。
所以,在导线通过磁场期间,电灯泡会一直亮起。
因此,电灯泡亮起的时间等于导线通过磁场的时间。
2. 一个长方形线圈的边长为a和b,放置在匀强磁场B中,使得长方形线圈的法线与磁场方向垂直。
求长方形线圈在匀强磁场中的磁通量。
解答:根据法拉第电磁感应定律,在匀强磁场中,线圈的磁通量可以通过以下公式计算:Φ = B * A * cosθ,其中B表示磁场强度,A表示线圈的面积,θ表示磁场方向与线圈法线方向之间的夹角。
由于线圈的法线与磁场方向垂直,θ为0,所以磁通量Φ = B * A。
3. 在一个闭合导线中有一个直径为d的圆环,该圆环的电阻为R。
当一个恒定的磁场B垂直于圆环平面时,求圆环上感应的电动势。
解答:根据法拉第电磁感应定律,当磁场的变化导致一个闭合回路中的磁通量发生改变时,会在回路中产生感应电动势。
在这个问题中,磁场是恒定的,所以不会产生感应电动势。
4. 一个导线带有电流I,在该导线旁边有另一条导线,它们平行。
第二条导线的长度为L,并且距离第一条导线的距离为d。
求第二条导线中感应的电动势。
解答:当电流从第一条导线中流过时,会在周围产生磁场。
第二条导线因为位于磁场中,所以会感受到这个磁场产生的磁通量的改变。
根据法拉第电磁感应定律,第二条导线中的感应电动势可以通过以下公式计算:ε = -dΦ/dt,其中Φ表示磁通量的变化率。
在这个问题中,需要计算第二条导线中的磁通量的变化率,并由此得出感应电动势。
电磁感应班级 姓名一、楞次定律的含义及基本应用(需要判断感应电流的方向)应用楞次定律判断感应电流方向的步骤:一原二变三感四螺旋(1)确定原磁场方向;(2)明确闭合回路(研究对象)中磁通量变化的情况;(3)应用楞次定律的“增反减同”,确定感应电流的磁场的方向.(4)应用安培定则,【例1】如图所示,在磁感应强度大小为B 、方向竖直向上的匀强磁场中,有一质量为m 、阻值为R 的闭合矩形金属线框abcd 用绝缘轻质细杆悬挂在O 点,并可绕O 点摆动.金属线框从右侧某一位置由静止开始释放,在摆动到左侧最高点的过程中,细杆和金属线框平面始终处于同一平面,且垂直纸面.则线框中感应电流的方向是( )A .a →b →c →d →aB .d →c →b →a →dC .先是d →c →b →a →d ,后是a →b →c →d →aD .先是a →b →c →d →a ,后是d →c →b →a →d二、楞次定律拓展含义的应用(不需要判断感应电流的方向)当回路中的磁通量发生变化时,感应电流的效果是阻碍原磁通量的变化. 闭合回路位置变化(B ):即“来拒去留”.闭合回路形状变化(S ):即“增缩减扩”闭合回路发生转动(θ)【例2】 如图8所示,粗糙水平桌面上有一质量为m 的铜质矩形线圈.当一竖直放置的条形磁铁从线圈中线AB 的正上方等高快速经过时,若线圈始终不动,则关于线圈受到的支持力FN 及在水平方向上的运动趋势的判断正确的是( )A .F N 先小于mg 后大于mg ,运动趋势向左B .F N 先大于mg 后小于mg ,运动趋势向左C .F N 先小于mg 后大于mg ,运动趋势向右D .F N 先大于mg 后小于mg ,运动趋势向右三、楞次定律、右手定则、左手定则、安培定则的综合应用3.相互联系(1)应用楞次定律,必然要用到安培定则;(2)感应电流受到安培力,有时可以先用右手定则确定电流的方向,再用左手定则确定安培力的方向,有时也可以直接应用楞次定律的推论确定安培力的方向.【例3】 如图所示,水平放置的两条光滑轨道上有可自由移动的金属棒PQ 、MN ,当PQ 在外力作用下运动时,MN 在磁场力的作用下向右运动,则PQ 所做的运动可能是( )A .向右加速运动B .向左加速运动C .向右减速运动D .向左减速运动【例4】 如图所示,固定的水平长直导线中通有电流I ,矩形线框与导线在同一竖直平面内,且一边与导线平行.线框由静止释放,在下落过程中( )A .穿过线框的磁通量保持不变B .线框中感应电流方向保持不变C .线框所受安培力的合力为零D .线框的机械能不断增大四、对法拉第电磁感应定律的理解及应用1.感应电动势E =n ΔΦΔt,决定感应电动势大小的因素是穿过这个回路的磁通量的变化率,而不是磁通量Φ的大小,也不是磁通量变化量ΔΦ的大小.2.下列是几种常见的产生感应电动势的情况,请写出对应的计算公式,其中线圈的匝数为n.(1)线圈面积S 不变,磁感应强度B 均匀变化; E =n ΔB Δt·S (2)磁感应强度B 不变,线圈的面积S 均匀变化: E =nB·ΔS Δt【例5】.如图(a)所示,面积S =0.2 m 2、匝数n =630匝、总电阻r =1.0 Ω的线圈处在变化的磁场中,磁感应强度B 随时间t 按图(b)所示规律变化,方向垂直线圈平面.图(a)中的传感器可看成一个纯电阻R ,并标有“3V 0.9 W ”,滑动变阻器R 0上标有“10 Ω 1 A ”,试回答下列问题:(1)设磁场垂直纸面向外为正方向,试判断通过电流表的电流方向;(2)为了保证电路的安全,求电路中允许通过的最大电流;(3)若滑动变阻器触头置于最左端,为了保证电路的安全,图(b)中的t 0最小值是多少?(1)向右 (2)0.3 A (3)40 s五、导体切割磁感线产生感应电动势的计算导体切割磁感线产生E 感,可分为平动切割和转动切割,在有些情况下要考虑有效切割的问题.试计算下列几种情况下的感应电动势,并总结其特点及E 感的计算方法.1.平动切割:如图(a),在磁感应强度为B 的匀强磁场中,棒以速度v 垂直切割磁感线时,感应电动势E =Blv.2.转动切割:如图(b),在磁感应强度为B 的匀强磁场中,长为l 的导体棒绕一端为轴以角速度ω匀速转动,此时产生的感应电动势E =12B l 2ω.3.有效切割长度:即导体在与v 垂直的方向上的投影长.试分析图中的有效切割长度.甲图中的有效切割长度为:cdsin θ;乙图中的有效切割长度为:l =MN ;丙图中的有效切割长度为:沿v 1的方向运动时,l =2R ;沿v 2的方向运动时,l =R.【例6】 如图所示,磁感应强度B =0.2 T 的匀强磁场中有一折成30°角的金属导轨aOb ,导轨平面垂直磁场方向.一条直导线MN 垂直Ob 方向放置在导轨上并接触良好.当MN 以v =4 m/s 的速度从导轨O 点开始向右沿水平方向匀速运动时,若所有导线单位长度的电阻r =0.1 Ω/m ,求:(1)经过时间t 后,闭合回路的感应电动势的瞬时值;(2)时间t 内,闭合回路的感应电动势的平均值;(3)闭合回路中的电流大小和方向.(1)1.84t V (2)0.92t V (3)1.69 A ,逆时针方向【例7】.如图12所示,导体棒AB 长2R ,绕O 点以角速度ω沿逆时针方向匀速转动,OB 为R ,且OBA 三点在一直线上,有一匀强磁场磁感应强度为B ,充满转动平面且与转动平面垂直,那么AB 两端的电势差大小为( )A.32BωR 2 B .2BωR 2 C .4BωR 2 D .6BωR 2六、通电自感与断电自感的比较1如图甲、乙所示电路中,电阻R 和电感线圈L 的电阻都很小.接通S ,使电路达到稳定,灯泡A 发光,则( )A .在电路甲中,断开S ,A 将渐渐变暗B .在电路甲中,断开S ,A 将先变得更亮,然后渐渐变暗C .在电路乙中,断开S ,A 将渐渐变暗D .在电路乙中,断开S ,A 将先变得更亮,然后渐渐变暗2.如图所示,小金属环和大金属环重叠在同一平面内,两环相互绝缘,小环有一半面积在大环内,当大环接通电源的瞬间,小环中感应电流的情况是( ).(A )无感臆电流 (B )有顺时针方向的感应电流(C )有逆时针方向的感应电流 (D )无法确定3 如图所示,通电螺线管置于闭合金属环a 的轴线上,当螺线管中电流I 减小时( )A .环有缩小的趋势以阻碍原磁通量的减小B .环有扩大的趋势以阻碍原磁通量的减小C .环有缩小的趋势以阻碍原磁通量的增大D .环有扩大的趋势以阻碍原磁通量的增大4.(2011·宿迁模拟)如图15所示是一种延时开关.S 2闭合,当S 1闭合时,电磁铁F 将衔铁D 吸下,将C 线路接通.当S 1断开时,由于电磁感应作用,D 将延迟一段时间才被释放,则( )A .由于A 线圈的电磁感应作用,才产生延时释放D 的作用B .由于B 线圈的电磁感应作用,才产生延时释放D 的作用C .如果断开B 线圈的电键S 2,无延时作用D .如果断开B 线圈的电键S 2,延时将变长5.如图所示,在匀强磁场中放置一个电阻不计的平行金属导轨,导轨跟大线圈M 相连,导轨上放一根导线ab ,磁感线垂直于导轨所在平面,欲使M 所包围的小闭合线圈N 产生顺时针方方的感应电流,则导线的运动情况可能是( ).(A )匀速向右运动 (B )加速向右运动(C )减速向右运动 (D )加速向左运动6.如图所示,要使金属环C 向线圈A 运动,导线AB 在金属导轨上应( )(A )向右作减速运动 (B )向左作减速运动(C )向右作加速运动 (D )向左作加速运动7.如图所示,线圈内有理想边界的磁场,开关闭合,当磁感应强度均匀减小时,有一带电微粒静止于水平放置的平行板电容器中间,若线圈的匝数为n ,平行板电容器的板间距离为d ,粒子的质量为m ,带电荷量为q ,线圈面积为S ,则下列判断中正确的是( )A .带电微粒带负电B .线圈内磁感应强度的变化率为mgd nqSC .当下极板向上移动时,带电微粒将向上运动D .当开关断开时带电微粒将做自由落体运动8金属棒和三根电阻线按图15所示连接,虚线框内存在均匀变化的匀强磁场,三根电阻丝的电阻大小之比R1∶R 2∶R 3=1∶2∶3,金属棒电阻不计.当S 1、S 2闭合,S 3断开时,闭合回路中的感应电流为I ,当S 2、S 3闭合,S 1断开时,闭合回路中的感应电流为9I ,当S 1、S 2闭合,S 2断开时,闭合回路中的感应电流是( )A .0B .3 IC .7ID .12I9.均匀导线制成的单匝正方形闭合线框abcd ,边长为L ,总电阻为R ,总质量为m.将其置于磁感强度为B 的垂直于纸面向里的匀强磁场上方h 处,如图16所示.线框由静止自由下落,线框平面保持在竖直平面内,且cd 边始终与磁场的水平边界面平行.当cd 边刚进入磁场时,(1)求线框中产生的感应电动势大小;(2)求cd 两点间的电势差大小;(3)若此时线框加速度恰好为零,求线框下落的高度h 所应满足的条件. (1)BL 2gh (2)34BL 2gh (3)m 2gR 22B 4L 4。
中考物理电磁感应历年真题及答案解析一、选择题1.某导体电阻是R,将导体两端连接在电动机输出电压为U的线圈上,如果将导体弯曲成半径减小为原来的一半,则此时导体上的电阻是原来的多少倍?解析:由于导体电阻R与导体长度、材料有关,与导体的形状无关,故弯曲导体后电阻仍然是R。
2.如图所示,导体棒AB与金属块之间是活动接触,导体棒自由滑动,金属块垂直地从右边直线运动进入导体棒AB所在位置,那么在这个过程中,导体棒AB上的感应电流的方向是:解析:根据楞次定律可知,当金属块进入导体棒AB的磁感线圈内时,磁感线圈中的磁场发生变化,产生感应电流,根据右手螺旋定则可知,感应电流应该是逆时针方向。
3.电动机是一种什么器件?A.电源B.发电机C.电磁感应器解析:电动机是一种将电能转化为机械能的器件,故选B.发电机。
4.如图所示,AB是一台交流电动机,$N$是定子磁极,它的磁极数目比转子$S$多。
那么当以$P$的方向用力使转子转动时,该电动机的旋转方向是()。
解析:根据左手螺旋定则可知,当以$P$的方向用力使转子转动时,电动机的旋转方向应该与$N$相反。
二、解答题1.近年来的中考题中,经常出现有关电磁感应的题目,请你简述电磁感应的基本原理。
解析:根据法拉第电磁感应定律,当导线或导体在磁场中发生相对运动时,导体中会感应出电动势,产生感应电流。
电磁感应的基本原理是磁场与导体之间的相对运动会产生感应电动势。
2.如图所示,一根闭合的金属导线框住曲柄触头,曲柄触头与导线连接,曲柄被转到其最大位置,此时磁场只是沿$y$轴的正方向,磁感应强度$B$是随时间变化的。
如图所示,导线周围的磁场是由在导线中的积极电流产生的,则最佳写出下面让推动机械工作的主要电路。
解析:根据楞次定律可知,随着磁感应强度$B$的增大,导线中将会产生一个感应电流。
由于曲柄触头与导线连接,故可以将导线上产生的感应电流作为电源连接到机械上,即可推动机械工作。
三、综合题一电动机是如何实现电能转化为机械能的?分析其中涉及的物理原理。
电磁感应习题及答案一、 选择题1.如图1所示,两根无限长平行直导线载有大小相等、方向相反的电流I ,并都以dtdI的变化率增长,一圆形金属线圈位于导线平面内,则()A 线圈中无感应电流 ()B 线圈中感应电流为顺时针方向()C 线圈中感应电流为逆时针方向 ()D 线圈中感应电流方向不确定[ B ]解: 由楞次定律,可判断出感应电流方向为顺时针。
2.如图2所示,一载流螺线管的旁边有一圆形线圈,欲使线圈产生图示方向的感应电流i ,下列哪一种情况可以做到?()A 载流螺线管向线圈靠近 ()B 载流螺线管离开线圈()C 载流螺线管中电流减小 ()D 抽出载流螺线管中的铁心[ A]解:由楞次定律,可判断出必须增加线圈中的电流或将线圈想右移动。
3.一边长为l 的正方形线框,置于均匀磁场中,线框绕OO ’轴以匀角速度ω旋转(如图3所示)。
设0t =时,线框平面处于纸面内,则任一时刻感应电动势的大小为()A t B l ωcos 22 ()B B l 2ω ()C t B l ωωcos 212 ()D t B l ωωcos 2()E t B l ωωsin 2[ D ]解:t B l ωφsin 2= t B l dtd ωωφεcos 2=-=Oω图1 图2 图34.如图所示,导体棒AB 在均匀磁场B ρ中绕通过C 点的垂直于棒长且磁场沿磁场方向的轴OO ’转动(角速度与B ρ同方向),BC 的长度为棒长的41,则()A A 点比B 点电势高 ()B A 与B 点电势相等 ()C A 点比B 点电势低 ()D 稳恒电流从A 点流向B 点[A]()04144321214342224342434434〉=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛====•⨯=⎰⎰⎰----L LL L LL L L BL L L B Bl Bldl vBdl l d B v ωωωωερρρ 5.如图5所示,长度为l 的直导线CD 在均匀磁场B 中以速度υ移动,直导线CD 中的电动势为()A υBl ()B θυsin Bl ()C θυ cos Bl ()D 0[D]解: ()02cos sin ==•⨯=πθεvBL L B v ρρρ6.如图6所示,M 、N 为水平面内两根平行金属导轨,ab 与cd 为垂直于导轨并可在其上自由滑动的两根直裸导线,外磁场垂直水平面向下,当外力使ab 向右平移时,cd()A 不动 ()B 转动 ()C 向左移动 ()D 向右移动[D]7.对于单匝线圈取自感系数的定义为I L φ=.当线圈的几何形状、大小及周围磁介质分布不变,切无铁磁性质时,若线圈中的电流强度变大,则线圈的自感系数L()A 变大,与电流成正比关系 ()B 变大,但与电流不成反比关系 ()C 变小,与电流成反比关系 ()D 不变 [D]8.如图7所示,一导体棒ab 在均匀磁场中沿金属导轨向左作匀加速运动,磁场方向垂直导轨所在平面,若导轨电阻忽略不计,并设铜心磁导率为常数,则达到稳定后在电容器的C 极板上会()A 带有一定量的正电荷 ()B 带有一定量的负电荷 ()C 带有越来越多的正电荷 ()D 带有越来越多的负电荷[A]9.在圆柱形空间内有一磁感应强度为B 的匀强磁场,如图所示。
B 的大小以速率dt d B 变化。
现将同一根导线放在磁场中ab 和a ’b ’两个不同的位置上,则()A 电动势只在ab 位置上产生 ()B 电动势只在a ’b ’位置上产生()C 电动势在ab 和a ’b ’位置上都产生,且两者大小相等 ()D ab 位置上产生的电动势小于a ’b ’位置上产生的电动势[D]解:dtdBSdt d -==φε- dt dB S dt d dt dB S dt d O b a O O b a O b a OabO OabO ab ''''''-==〈-==φεφε-- 10.真空中两只长直螺线管1和2的长度相等,单层密绕匝数相同,直径之比4121=d d 。
当它们通以相同的电流时,两螺线管储存的磁能力之比()A 116: ()B 161: ()C 14: ()D 41:[B]解:nIS 0μ=Φ nS I nIS I L 00μμ==Φ=221LI W = 1614144212122212221222121201*********=⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=======d d S S nS nS L L I L I L W W φφφπφπμμ 二、 填空题1. 半径为r 的无限长直螺线管1和2的长度相等,单位长度上的匝数为n ,通以交变电流t cos i m ωI =,则围在管外的同轴回形回路(半径为R )上的感生电动势为t I r n m ωωπμεsin 20=()t I r n t I r n dtddt d m m ωωπμωπμφεsin cos -2020=-==2. 一导线被弯成回路如图所示,形状,abc 是半径为R 的二分之一圆弧,直线Oa 长为R ,若此导线放在匀强磁场B 中,B 的方向垂直图面向内,导线以角速度ω在图面内绕O 点匀速运动,则此导线中的感生电动势=ε229BR ω- 电势最高的点是O 点 。
()()()[]29032121302223023030〈-=--=-=-=-=•⨯=⎰⎰⎰RR RR BR R B Bl Bldl vBdl l d B v ωωωωερρρ3. 长为L 的金属直导线在垂直于均匀磁场的平面内以角速度ω转动。
如果转轴在导线上的位置是在导线端点,整个导线上的电动势为最大;如果转轴在导线上的位置是在导线中点,整个导线上的电动势为最小。
()()()[]021021212220200〉=-====•⨯=⎰⎰⎰LL LL BL L B Bl Bldl vBdl l d B v ωωωωερρρ()⎰⎰⎰----=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛====•⨯=222222222220222121L LL L LL L L L L B Bl Bldl vBdl l d B v ωωωερρρ 4. 金属圆板在均匀磁场中以角速度ω绕中心轴转动,均匀磁场的方向平行于转轴,如图所示,这时板中由中心至同一边缘点的不同曲线上总R感应电动势的大小为_221R B ω,方向沿曲线由外指向中心。
()()()[]2102121222020〈-=--==-=-=•⨯=⎰⎰⎰RR RR BR R B Bl Bldl vBdl l d B v ωωωωερρρ5. 一线圈中通过的电流I 随时间t 变化的曲线如图11所示。
试定性画出自感电动势L ε随时间变化的曲线。
(以I 的正向作为L ε的正向)6. 自感系数H L 4.0=的螺线管中通以A I 10=的电流时,螺线管存储的磁场能量=W_20 J ___. 参考答案:()()J 20104.0212122=⨯⨯==LI W7. 有两个长直密绕螺线管,长度及线圈匝数均相同,半径为1r 和2r ,管内充满均匀介质,其磁导率分别为1μ和2μ,设2121=r r ,1221=μμ,当将两只螺线管串联在电路中通电稳定后,其自感系数之比为21L L 为_1:2_,磁能2m 1m W W 为_1:2_参考答案:212121222211221122011021222121======r r S S nS nS L L I L I L W W πμμπμμμμμμ 8. 平行板电容器的电容F C μ0.10=,两板上的电压变化率为()15100.2-⋅⨯=s V dtdU,则该平行板电容器中的位移电流为_2 A _. 参考答案:U Q C = ()A 0.2100.2100.1056=⨯⨯⨯===-dtdUC dt dQ I D9. 在感应电场中电磁感应定律可写成t l E LK d d d φ-=•⎰ρρ,式中为感应电场的电场强度。
此表明在感应电场中_不能_(填“能”或“不能”)像对电场那样引入电势概念。
三、 计算题1. 如图所示,一条平行长直导线和一个矩形导线框共面,且导线框的一个边与长直导线平行,它到长直导线的距离为d ,已知导线中电流为t sin m ωI I =,其中m I 和ω为常数, t为时间。
导线框长为a ,宽为b ,求导线框中的感应电动势的大小。
解:规定顺时针方向为回路正方向。
在t 时刻通过整个矩形框面积S 的B ρ通量为t dbd a I adx x I m bd dωπμπμφφsin ln 22d 00+===⎰⎰+ 感应电动势为 t d b d a I t d b d a I dt d m m ωπωμωπμφεcos ln 2sin ln 2dt d 00i +-=⎥⎦⎤⎢⎣⎡+-=-=2. 如图所示,用一根硬导线弯成半径为r 的一个半圆,使这根半圆形导线在磁感应强度为B ρ的匀强磁场中以角速度ω旋转,整个电路的电阻为R 。
求感应电流的表达式。
解: t 时刻半圆环的磁通量为:t B r ωπϕcos 212⎪⎭⎫ ⎝⎛=t 时刻半圆环的产生的电动势为:t B r t B r dt d dt d ωωπωπϕεsin 21cos 2122⎪⎭⎫⎝⎛-=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-=-= t 时刻回路中的产生的电流为:t R r B R I ωωπεsin 22⎪⎪⎭⎫⎝⎛-==3. 如图所示,一根无限长的直导线载有电流I ,长度为b 的金属杆CD 与导线共面且垂直, CD 杆以速度v ρ平行直线电流运动,求CD 杆中的感应电动势,并判断C 、D 两端那端电势高?解: D 点电势高在CD 上取任意一线元dx则dx 上的电动势为: ()dx xIvl d B v d i πμε20-=•⨯=ρρρ所以整个导体的电动势为:()aba Iv dx x Iv l d B v db a a L i +-=-=•⨯==⎰⎰⎰+ln2200L i πμπμεερρρ 4. 如图所示,在匀强磁场B ρ中,a ==EF OE ,0135=∠OEF ,OEF 整体可绕O 点在垂直于磁场的平面内逆时针转动,若转动角速度为ω,则 (1) 求OE 间电势差OE U ; (2) 求OF 间电势差OF U ;(3) 指出O 、E 、F 三点中那点电势最高。
解: (1)()200L OE 21Ba rBdr vBdr l d B v d a a L ωωεε===•⨯==⎰⎰⎰⎰ρρρ(2)()()()()2220220L OF 223Ba rBdr vBdr l d B v d a a Lωωεε+===•⨯==⎰⎰⎰⎰++ρρρ (3)O 点电势高。