【同步练习】人教版2018年 九年级数学上册 二次函数图象性质 一 课堂检测卷(含答案)

22.1 二次函数的图象和性质1．抛物线y=－3x 2上两点A （x ，－27），B （2，y ），则x= ，y= ．2．抛物线y=－4x 2－4的开口向 ，当x= 时，y 有最 值，y = ． 3．当m= 时，y=（m －1）xmm +2－3m 是关于x 的二次函数．4．当m= 时，抛物线y=（m ＋1）x mm +2＋9开口向下，对称轴是 ．在对称轴左侧，y 随x 的增大而 ；在对称轴右侧，y 随x 的增大而 ． 5．抛物线y=3x 2与直线y=kx ＋3的交点为（2，b ），则k= ，b= ．6．已知抛物线的顶点在原点，对称轴为y 轴，且经过点（－1，－2），则抛物线的表达式为．7．在同一坐标系中，图象与y=2x 2的图象关于x 轴对称的是（ ）A ．y=21x 2B ．y=－21x 2C ．y=－2x 2D ．y=－x 28．抛物线，y=4 x 2，y=－2x 2的图象，开口最大的是（ ）A ．y=41x 2B ．y=4x 2C ．y=－2x 2D ．无法确定9．对于抛物线y=31x 2和y=－31x 2在同一坐标系里的位置，下列说法错误的是（ ）A ．两条抛物线关于x 轴对称B ．两条抛物线关于原点对称C ．两条抛物线关于y 轴对称D ．两条抛物线的交点为原点10．二次函数y=ax 2与一次函数y=ax ＋a 在同一坐标系中的图象大致为（ ）错误!未找到引用源。

11．已知函数y=ax 2的图象与直线y=－x ＋4在第一象限内的交点和它与直线y=x 在第一 象限内的交点相同，则a 的值为（ ）A ．4 B ．2 C ．21D ．4112．求符合下列条件的抛物线y=ax 2的表达式：（1）y=ax 2经过（1，2）； （2）y=ax 2与y=21x 2的开口大小相等，开口方向相反；（3）y=ax 2与直线y=21x ＋3交于点（2，m ）．13已知错误!未找到引用源。

是二次函数，且当错误!未找到引用源。

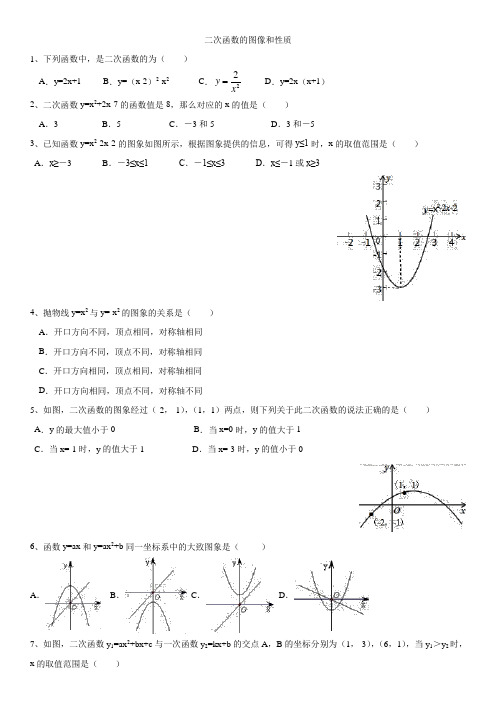
二次函数的图像和性质1、下列函数中，是二次函数的为（ ） A ．y=2x+1 B ．y=（x-2）2-x 2 C ．22x yD ．y=2x （x+1） 2、二次函数y=x 2+2x-7的函数值是8，那么对应的x 的值是（ ） A ．3 B ．5 C ．－3和5 D ．3和－53、已知函数y=x 2-2x-2的图象如图所示，根据图象提供的信息，可得y≤1时，x 的取值范围是（ ） A ．x≥－3 B ．－3≤x≤1 C ．－1≤x≤3 D ．x≤－1或x≥34、抛物线y=x 2与y=-x 2的图象的关系是（ ） A ．开口方向不同，顶点相同，对称轴相同 B ．开口方向不同，顶点不同，对称轴相同 C ．开口方向相同，顶点相同，对称轴相同 D ．开口方向相同，顶点不同，对称轴不同5、如图，二次函数的图象经过（-2，-1），（1，1）两点，则下列关于此二次函数的说法正确的是（ ） A ．y 的最大值小于0 B ．当x=0时，y 的值大于1 C ．当x=-1时，y 的值大于1 D ．当x=-3时，y 的值小于06、函数y=ax 和y=ax 2+b 同一坐标系中的大致图象是（ ）A ．B ．C ．D ．7、如图，二次函数y 1=ax 2+bx+c 与一次函数y 2=kx+b 的交点A ，B 的坐标分别为（1，-3），（6，1），当y 1＞y 2时，x 的取值范围是（ ）A．1＜x＜6 B．x＜1或x＞6 C．-3＜x＜1 D．x＜-3或x＞18、已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下结论：①a＞0．②该函数的图象关于直线x=1对称．③方程ax2+bx+c=0的两根是－1和3．④x＜1时，y随x的增大而增大．其中正确结论的个数是（）A．3 B．2 C．1 D．09、当a 时，函数y=（a－1）x2+bx+c是二次函数．10、已知y=是y关于x的二次函数，则m= ，此函数图象与x轴的交点坐标是，其图象的对称轴是．11、如图是二次函数y1=ax2+bx+c（a≠0）和一次函数y2=mx+n（m≠0）的图象，当y2＞y1，x的取值范围是．12、把函数y=3-4x-2x2写成y=a（x+m）2+k的形式，并写出函数图象的开口方向、顶点坐标和对称轴．13、抛物线y=-x2+（m-1）x+m与y轴交于（0，3）点．（1）求出m的值并画出这条抛物线；（2）求它与x轴的交点和抛物线顶点的坐标；（3）x取什么值时，抛物线在x轴上方？（4）x取什么值时，y的值随x值的增大而减小？14、函数y=（m+2）是关于x的二次函数，求：（1）满足条件的m值；（2）m为何值时，抛物线有最低点？求出这个最低点．这时，当x为何值时，y随x的增大而增大？（3）m为何值时，函数有最大值？最大值是多少？这时，当x为何值时，y随x的增大而减小．15、根据下面的条件列出函数解析式，并判断列出的函数是否为二次函数：（1）如果两个数中，一个比另一个大5，那么，这两个数的乘积p是较大的数m的函数；（2）一个半径为10cm的圆上，挖掉4个大小相同的正方形孔，剩余的面积S（cm2）是方孔边长x（cm）的函数；（3）有一块长为60m、宽为40m的矩形绿地，计划在它的四周相同的宽度内种植阔叶草，中间种郁金香，那么郁金香的种植面积S（cm2）是草坪宽度a（m）的函数．16、已知函数y=21x 2+2x+1，解答下列问题： （1）写出抛物线的开口方向，顶点坐标及对称轴；（2）作出函数图象，并观察图象，写出x 为何值时，y 随x 的增大而增大？x 为何值时，y 随x 的增大而减小？ （3）函数的最值是多少？ 参考答案1、D2、D3、C4、A5、D6、C7、B8、A9、10、11、12、13、14、15、解：（1）这两个数的乘积p与较大的数m的函数关系为：p=m（m-5）=m2-5m，是二次函数；（2）剩余的面积S（cm2）与方孔边长x（cm）的函数关系为：S=100π-4x2，是二次函数；（3）郁金香的种植面积S（cm2）与草坪宽度a（m）的函数关系为：S=（60-2a）（40-2a）=4a2-200a+2400，是二次函数．16、。

22.1.3 二次函数c ax y +=2的图象与性质(一)知识点：函数)0(2≠+=a c ax y 的图象是一条 ，对称轴是 ，顶点是 ，当0>a ，抛物线开口 ，顶点是抛物线的 ，当0<a ，抛物线开口 ，顶点是抛物线的 。

一．选择题1.抛物线122+=x y 的顶点坐标是（ ）A.(0，1)B. (0，-1)C. (1，0)D. (-1，0)2.抛物线)0(2≠+=a b ax y 与x 轴有两个交点，且开口向下，则b a ,的取值范围分别是（ ）A.0,0>>b aB.0,0<>b aC.0,0<<b aD.0,0><b a 3.如图，小芳在某次投篮中，球的运动路线是抛物线y ＝－15x 2＋3.5的一部分，若命中篮圈中心，则他与篮底的距离l 是（ ）A ．3.5mB ．4mC ．4.5mD ．4.6m4.将抛物线322-=x y 平移后得到抛物线22x y =，平移的方法可以是（ ） 第3题A.向下平移3个单位长度B. 向上平移3个单位长度C.向下平移2个单位长度D.向下平移2个单位长度5.抛物线122+-=x y 的对称轴是（ ）A ．直线21=x B ．直线21-=x C ．y 轴 D ．直线2=x 6.抛物线42-=x y 与x 轴交于B,C 两点，顶点为A ，则ABC ∆的周长为（ ）A ．54B ．454+C ．12D ．452+7.在同一平面直角坐标系中，一次函数c ax y +=和二次函数c ax y +=2的图象大2.53.05lxyO致所示中的（ ）A B ． C ． D ．二．填空题1．抛物线322--=x y 的开口 ,对称轴是 ,顶点坐标是 ,当x时, y 随x 的增大而增大, 当x 时, y 随x 的增大而减小.2．二次函数c ax y +=2()0≠a 中，若当)(,2121x x x x x ≠取时，函数值相等，则当x 取21x x +时，函数值等于 。

人教版九年级上册数学22.1.4 二次函数y=ax²+bx+c的图象
和性质同步练习
一、单选题
解析式为，则，的值为（ ）
A ．，
B ．，
C ．，
D ．，
8．已知二次函数的图象大致如图所示．下列说法正确的是（ ）
A ．
B ．当时，
C ．
D ．若在函数图象上，当时，二、填空题
y =23x bx c ++b c 6b =1c =-18b =-23
c =6b =5c =-18b =-29
c =()20y ax bx c a =++≠20
a b -=13x -<<0
y <0
a b c ++>()()1122,,,x y x y 12x x <12
y y <
配方得：y ＝
当x ＜－1时，y 随x 增大而 ；
当x ＝－1时，y 最大值为 ；
当x ＞－1时，y 随x 增大而 ．
18．求出下列抛物线的开口方向，对称轴和顶点坐标．
（1）
(1)求这个二次函数的表达式；
(2)点是直线下方抛物线上的顶点，求2241y x x =--+2245
y x x =-+P BC
20．如图，二次函数的图象与轴交于，两点，
与
轴交于点，为抛物线的顶点．
(1)求此二次函数的解析式；
(2)求的面积；
(3)在其对称轴右侧的抛物线上是否存在一点，使是等腰三角形？若存在，请直接写出点的坐标；若不存在，请说明理由．
()20y ax bx c a =++≠x ()1,0A -()3,0B y ()0,3C D CDB △P PDC △P
参考答案：。

人教版九年级数学上册22.1 二次函数的图象和性质同步训练一、选择题1. 二次函数y＝2x2，y＝－2x2，y＝12x2的共同性质是()A．其图象开口都向上B．其图象的对称轴都是y轴C．其图象都有最高点D．y随x的增大而增大2. 若y＝ax2＋bx＋c，则由表格中的信息可知y与x之间的函数解析式是()A.y＝x2－4x＋3 B．y＝x2－3x＋4C．y＝x2－3x＋3 D．y＝x2－4x＋83. 若二次函数y＝x2＋mx的对称轴是x＝3，则关于x的方程x2＋mx＝7的解为()A. x1＝0，x2＝6B. x1＝1，x2＝7C. x1＝1，x2＝－7D. x1＝－1，x2＝74. 已知二次函数y＝－x2＋2bx＋c，当x＞1时，y的值随x值的增大而减小，则实数b的取值范围是()A．b≥－1 B．b≤－1C．b≥1 D．b≤15. 二次函数y＝2x2－3的图象是一条抛物线，下列关于该抛物线的说法，正确的是()A. 抛物线开口向下B. 抛物线经过点(2，3)C. 抛物线的对称轴是直线x＝1D. 抛物线与x轴有两个交点6. 将函数y＝x2的图象用下列方法平移后，所得的图象不经过点A(1，4)的是() A．向左平移1个单位长度B．向右平移3个单位长度C．向上平移3个单位长度D．向下平移1个单位长度7. 已知抛物线y＝2x2＋bx＋c的顶点坐标是(－1，－2)，则b与c的值分别为() A．－1，－2 B．4，－2C．－4，0 D．4，08. 已知二次函数y＝x2＋bx＋c与x轴只有一个交点，且图象过A(x1，m)、B(x1＋n，m)两点，则m、n的关系为()A. m＝12n B. m＝14n C. m＝12n2 D. m＝14n2二、填空题9. 某抛物线的形状、开口方向与抛物线y＝12x2－4x＋3相同，顶点坐标为(－2，1)，则该抛物线的函数解析式为________________．10. 已知抛物线y＝2(x－1)2上有两点(x1，y1)，(x2，y2)，且1＜x1＜x2，则y1与y2的大小关系是________．11. 抛物线y＝－8x2的开口向________，对称轴是________，顶点坐标是________；当x＞0时，y随x的增大而________，当x＜0时，y随x的增大而________．12. 已知二次函数的图象经过原点及点(－12，－14)，且图象与x轴的另一交点到原点的距离为1，则该二次函数的解析式为________________．13. 如图，抛物线y＝ax2＋bx＋c(a>0)的对称轴是过点(1，0)且平行于y轴的直线，若点P(4，0)在该抛物线上，则4a－2b＋c的值为________．14. 顶点坐标是(2，0)，且与抛物线y＝－3x2的形状、开口方向都相同的抛物线的解析式为________．15. 如图，抛物线y＝ax2＋bx＋c与x轴相交于点A，B(m＋2，0)，与y轴相交于点C，点D在该抛物线上，坐标为(m，c)，则点A的坐标是________．16. 如图，在平面直角坐标系xOy中，已知抛物线y＝ax2＋bx(a＞0)的顶点为C，与x轴的正半轴交于点A，它的对称轴与抛物线y＝ax2(a＞0)交于点B.若四边形ABOC是正方形，则b的值是________．三、解答题17. 已知抛物线y＝ax2经过点A(－2，－8)．(1)求此抛物线的解析式；(2)判断点B(－1，－4)是否在此抛物线上；(3)求出抛物线上纵坐标为－6的点的坐标．18. 在平面直角坐标系xOy中，抛物线y＝ax2＋bx＋2过B(－2，6)，C(2，2)两点．(1)试求抛物线的解析式；(2)记抛物线顶点为D，求△BCD的面积；(3)若直线y＝－12x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点，求b的取值范围．19. 如图，等腰直角三角形ABC的直角边与正方形MNPQ的边长均为10 cm，边CA与边MN在同一直线上，开始时点A与点M重合，△ABC沿MN方向以1 cm/s 的速度匀速运动，当点A与点N重合时，停止运动．设运动的时间为t s，运动过程中△ABC与正方形MNPQ重叠部分的面积为S cm2.(1)试写出S关于t的函数关系式，并指出自变量t的取值范围；(2)当MA＝2 cm时，重叠部分的面积是多少？20. 设函数y＝(x－1)[(k－1)x＋(k－3)](k是常数)．(1)当k取1和2时的函数y1和y2的图象如图所示，请你在同一直角坐标系中画出当k取0时函数的图象；(2)根据图象，写出你发现的一条结论；(3)将函数y2的图象向左平移4个单位，再向下平移2个单位，得到函数y3的图象，求函数y3的最小值．人教版九年级数学上册22.1 二次函数的图象和性质同步训练-答案一、选择题1. 【答案】B2. 【答案】A[解析] ∵x ＝1时，ax 2＝1，∴a ＝1.将(－1，8)，(0，3)分别代入y ＝x 2＋bx ＋c ，得⎩⎨⎧1－b ＋c ＝8，c ＝3，解得⎩⎨⎧b ＝－4，c ＝3.∴y 与x 之间的函数解析式是y ＝x 2－4x ＋3.故选A.3. 【答案】D【解析】∵二次函数y ＝x 2＋mx 的对称轴为x ＝－m2＝3，解得m ＝－6，则关于x 的方程为x 2－6x ＝7，解得，x 1＝－1，x 2＝7.4. 【答案】D [解析] 先根据抛物线的性质得到其对称轴为直线x ＝b ，且当x ＞b 时，y 的值随x 值的增大而减小．因为当x ＞1时，y 的值随x 值的增大而减小，所以b≤1.5. 【答案】D【解析】本题考查了二次函数的性质，由于2>0，所以抛物线的开口向上，所以A 选项错误；由于当x ＝2时，y ＝8－3＝5，所以B 选项错误；由于y ＝2x 2－3的对称轴是y 轴，所以C 选项错误；由2x 2－3＝0得b 2－4ac ＝24>0，则该抛物线与x 轴有两个交点，所以D 选项正确．6. 【答案】D [解析] A ．将函数y ＝x 2的图象向左平移1个单位长度得到函数y ＝(x ＋1)2的图象，它经过点(1，4)；B.将函数y ＝x 2的图象向右平移3个单位长度得到函数y ＝(x －3)2的图象，它经过点(1，4)；C.将函数y ＝x 2的图象向上平移3个单位长度得到函数y ＝x 2＋3的图象，它经过点(1，4)；D.将函数y ＝x 2的图象向下平移1个单位长度得到函数y ＝x 2－1的图象，它不经过点(1，4)．故选D.7. 【答案】D8. 【答案】D【解析】因为二次函数y ＝x 2＋bx ＋c 的图象与x 轴只有一个交点，∴b 2－4c ＝0，即c ＝b 24，由题意知，点A ，B 关于抛物线的对称轴对称，∴12AB＝|n|2＝－b 2－x 1，b ＝－|n|－2x 1, ∴c ＝（－|n|－2x 1）24＝|n|2＋4|n|x 1＋4x 214，∵A(x 1，m)在y ＝x 2＋bx ＋c 上，∴m ＝x 21＋bx 1＋c ，∴ m ＝x 21＋(－|n|－2x 1)· x 1＋|n|2＋4|n|x 1＋4x 214，化简整理得m ＝14n 2，故选D .二、填空题9. 【答案】y ＝12(x ＋2)2＋1 [解析] 已知抛物线的顶点坐标，可以设顶点式y ＝a(x －h)2＋k.又因为该抛物线的形状、开口方向与抛物线y ＝12x 2－4x ＋3相同，所以a ＝12，所以该抛物线的函数解析式是y ＝12(x ＋2)2＋1.10. 【答案】y 1<y 2[解析] ∵抛物线的解析式是y ＝2(x －1)2，∴其对称轴是直线x ＝1，抛物线的开口向上， ∴在对称轴右侧，y 随x 的增大而增大．又∵抛物线y ＝2(x －1)2上有两点(x 1，y 1)，(x 2，y 2)，且1＜x 1＜x 2，∴y 1<y 2.11. 【答案】下y 轴 (0，0) 减小 增大12. 【答案】y ＝x 2＋x 或y ＝－13x 2＋13x 【解析】依题意，所求函数有可能经过(－1，0)，(－12，－14) 或(1，0)，(－12，－14) .设所求函数解析式为y ＝ax 2＋bx ＋c ，图象经过原点，则c ＝0，当图象经过(－1，0)，(－12，－14)时，代入可求得a ＝b ＝1，即所求解析式为y ＝x 2＋x ; 当图象经过(1，0)，(－12，－14)时，代入可求得a ＝－13，b ＝13，即所求解析式为y ＝－13x 2＋13x .综上所述，所求函数的解析式为y＝x 2＋x 或y ＝－13x 2＋13x .13. 【答案】0 【解析】设抛物线与x 轴的另一个交点是Q ，∵抛物线的对称轴是过点(1，0)的直线，与x 轴的一个交点是P(4，0)，∴与x 轴的另一个交点Q(－2，0)，把(－2，0)代入解析式得：0＝4a －2b ＋c ，∴4a －2b ＋c ＝0.14. 【答案】y ＝－3(x －2)215. 【答案】(－2，0)【解析】如解图，过D 作DM ⊥x 轴于点M ，∴M(m ，0)，又B(m ＋2，0)，∴MB ＝2，由C(0，c)，D(m ，c)知：OC ＝DM ，即点C 、D 关于对称轴对称，故点O 、M 也关于对称轴对称，∴OA ＝MB ＝2，∴A(－2，0)．16. 【答案】－2 [解析] 抛物线y ＝ax 2＋bx 的顶点C 的坐标为(－b 2a ，－b 24a)．把x ＝－b 2a 代入y ＝ax 2，得点B 的坐标为(－b 2a ，b 24a )．在y ＝ax 2＋bx 中，令y ＝0，则ax 2＋bx ＝0，解得x 1＝0，x 2＝－b a ，∴A(－ba ，0)．∵四边形ABOC 为正方形，∴BC ＝OA ，∴2·b 24a ＝－b a ，即b 2＋2b ＝0.解得b ＝－2或b ＝0(不符合题意，舍去)．三、解答题17. 【答案】解：(1)∵抛物线y ＝ax 2经过点A(－2，－8)，∴4a ＝－8，解得a ＝－2，∴此抛物线的解析式为y ＝－2x 2.(2)当x ＝－1时，y ＝－2，∴点B(－1，－4)不在此抛物线上．(3)把y ＝－6代入y ＝－2x 2，得－2x 2＝－6，解得x ＝±3，∴抛物线上纵坐标为－6的点的坐标为(3，－6)，(－3，－6)．18. 【答案】解：(1)把B(－2，6)，C(2，2)代入抛物线的解析式得： ⎩⎨⎧6＝a·（－2）2＋b·（－2）＋22＝a·22＋b·2＋2，(1分)解得⎩⎪⎨⎪⎧a ＝12b ＝－1，(2分)∴抛物线的解析式为y ＝12x 2－x ＋2.(3分)(2)抛物线解析式化为顶点式：y ＝12(x －1)2＋32，则抛物线顶点D(1，32)，(4分) 如解图①所示，过点B 、D 、C 分别向x 轴作垂线，垂足分别为点M 、N 、H ，则有：S △BCD ＝S 梯形BMHC －S 梯形BMND －S 梯形DNHC ＝12(6＋2) ×4－12(6＋32)×3－12(32＋2) ×1 ＝3.(6分)解图①解图② (3)如解图②所示，连接BC ，∵直线BC 斜率k BC ＝2－62－（－2）＝－1＜－12，∴过点C 作直线MN 与直线y ＝－12x 平行，设直线MN 的解析式为y ＝－12x ＋b 1，代入C(2，2)， ∴b 1＝3.(7分)作直线EF 与抛物线相切，且与直线y ＝－12x 平行， 设直线EF 的解析式为y ＝－12x ＋b 2，联立抛物线解析式得， ⎩⎪⎨⎪⎧y ＝12x 2－x ＋2y ＝－12x ＋b 2， ∴x 2－x ＋4－2b 2＝ 0， ∵直线EF 与抛物线相切，∴b 2－4ac ＝0，即(－1)2－4(4－2b 2)＝0，(9分)∴b 2＝158，(11分) ∴158＜b ≤3.(12分)注：斜率知识为高中知识，但常渗透于中考压轴题，与二次函数相结合考查，做题时注意其性质的应用．19. 【答案】解：(1)设AB 与MQ 交于点R.∵△ABC 是等腰直角三角形，四边形MNPQ 是正方形， ∴△AMR 是等腰直角三角形． 由题意知，AM ＝MR ＝t ，∴S ＝S △AMR ＝12t·t ＝12t 2(0≤t≤10)．(2)当MA ＝2 cm ，即t ＝2时，重叠部分的面积是12×2×2＝2(cm 2)．20. 【答案】解：(1)当k ＝0时，y ＝－(x －1)(x ＋3)，所画图象如解图所示．(2分)(2)①k 取0和2时的函数图象关于点(0，2)中心对称，②函数y ＝(x －1)[(k －1)x ＋(k －3)](k 是常数)的图象都经过(1，0)和(－1，4)．(5分)(3)由题意可得y 2＝(x －1)[(2－1)x ＋(2－3)]＝(x －1)2，平移后的函数y 3的表达式为y 3＝(x －1＋4)2－2＝(x ＋3)2－2， 所以当x ＝－3时，函数y 3的最小值是－2.(8分)。

《22.1.2二次函数的图象和性质》（1）一、选择题1．抛物线y=﹣2（x﹣1）2+的顶点坐标为（）A．（﹣1，）B．（1，）C．（﹣1，﹣）D．（1，﹣）2．关于y=2（x﹣3）2+2的图象，下列叙述正确的是（）A．顶点坐标为（﹣3，2）B．对称轴为直线y=3C．当x≥3时，y随x增大而增大D．当x≥3时，y随x增大而减小3．若将抛物线y=x2向右平移2个单位，再向上平移3个单位，则所得抛物线的表达式为（）A．y=（x+2）2+3 B．y=（x﹣2）2+3 C．y=（x+2）2﹣3 D．y=（x﹣2）2﹣34．抛物线y=﹣2（x+1）2﹣2可由抛物线y=﹣2x2平移得到，则下列平移过程正确的是（）A．先向右平移1个单位，再向上平移2个单位B．先向右平移1个单位，再向下平移2个单位C．先向左平移1个单位，再向上平移2个单位D．先向左平移1个单位，再向下平移2个单位5．如图，把抛物线y=x2沿直线y=x平移个单位后，其顶点在直线上的A处，则平移后的抛物线解析式是（）A．y=（x+1）2﹣1 B．y=（x+1）2+1 C．y=（x﹣1）2+1 D．y=（x﹣1）2﹣16．设A（﹣1，y1）、B（1，y2）、C（3，y3）是抛物线y=﹣上的三个点，则y1、y2、y3的大小关系是（）A．y1＜y2＜y3B．y2＜y1＜y3C．y3＜y1＜y2D．y2＜y3＜y17．若二次函数y=（x﹣m）2﹣1．当x≤l时，y随x的增大而减小，则m的取值范围是（）A．m=l B．m＞l C．m≥l D．m≤l8．二次函数y=a（x+m）2+n的图象如图，则一次函数y=mx+n的图象经过（）A．第一、二、三象限 B．第一、二、四象限C．第二、三、四象限 D．第一、三、四象限二、填空题：9．抛物线y=﹣2（x+3）2﹣1的对称轴是______，顶点坐标是______；当x______时，y随x的增大而增大，当x______时，y随x的增大而减小，当x______时，y取最______值为______．10．抛物线y=4（x+h）2+k的顶点在第三象限，则有h，k满足h______0，k______0．11．已知点A（x1，y1）、B（x2，y2）在二次函数y=（x﹣1）2+1的图象上，若x1＞x2＞1，则y1______y2（填“＞”、“＜”或“=”）．12．抛物线的顶点坐标为P（2，3），且开口向下，若函数值y随自变量的x增大而减小，那么x 的取值范围为______．13．在平面直角坐标系中，点A是抛物线y=a（x﹣3）2+k与y轴的交点，点B是这条抛物线上的另一点，且AB∥x轴，则以AB为边的等边三角形ABC的周长为______．14．将抛物线y=﹣x2先沿x轴方向向______移动______个单位，再沿y轴方向向______移动______个单位，所得到的抛物线解析式是y=﹣（x﹣3）2+1．15．将抛物线y=x2+1先向左平移2个单位，再向下平移3个单位，那么所得抛物线的函数关系式是______．16．将抛物线y=﹣2（x+1）2+1绕其顶点旋转180°后得到抛物线的解析式为______；将抛物线y=﹣2（x+1）2+1绕原点旋转180°后得到抛物线的解析式为______．17．抛物线y=a（x﹣h）2+k的顶点为（3，﹣2），且与抛物线y=﹣的形状相同，则a=______，h=______，k=______．18．如图，抛物线y1=a（x+2）2﹣3与y2=（x﹣3）2+1交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于点B，C．则以下结论：①无论x取何值，y2的值总是正数；②a=1；③当x=0时，y2﹣y1=4④2AB=3AC．其中正确结论是______．三、解答题：19．若二次函数图象的顶点坐标为（﹣1，5），且经过点（1，2），求出二次函数的解析式．20．若抛物线经过点（1，1），并且当x=2时，y有最大值3，则求出抛物线的解析式．21．已知：抛物线y=（x﹣1）2﹣3．（1）写出抛物线的开口方向、对称轴；（2）函数y有最大值还是最小值？并求出这个最大（小）值；（3）设抛物线与y轴的交点为P，与x轴的交点为Q，求直线PQ的函数解析式．22．在直角坐标系中，二次函数图象的顶点为A（1、﹣4），且经过点B（3，0）（1）求该二次函数的解析式；（2）当﹣3＜x＜3时，函数值y的增减情况；（3）将抛物线怎样平移才能使它的顶点为原点．23．如图是二次函数y=（x+m）2+k的图象，其顶点坐标为M（1，﹣4）（1）求出图象与x轴的交点A、B的坐标；（2）在二次函数的图象上是否存在点P，使S△PAB=S△MAB？若存在，求出点P的坐标；若不存在，请说明理由．《22.1.2二次函数的图象和性质》（1）参考答案与试题解析一、选择题1．抛物线y=﹣2（x﹣1）2+的顶点坐标为（）A．（﹣1，）B．（1，）C．（﹣1，﹣）D．（1，﹣）【解答】解：抛物线y=﹣2（x﹣1）2+的顶点坐标为（1，），故选：B．2．关于y=2（x﹣3）2+2的图象，下列叙述正确的是（）A．顶点坐标为（﹣3，2）B．对称轴为直线y=3C．当x≥3时，y随x增大而增大D．当x≥3时，y随x增大而减小【解答】解：顶点坐标为（3，2），故A选项错误；对称轴为x=3，故选项B错误；因为二次项系数为2＞0，故函数图象开口向上对称轴为x=3，故当x≥3时，y随x增大而增大，故C选项正确；D选项错误，故选C．3．若将抛物线y=x2向右平移2个单位，再向上平移3个单位，则所得抛物线的表达式为（）A．y=（x+2）2+3 B．y=（x﹣2）2+3 C．y=（x+2）2﹣3 D．y=（x﹣2）2﹣3【解答】解：将抛物线y=x2向右平移2个单位可得y=（x﹣2）2，再向上平移3个单位可得y=（x ﹣2）2+3，故选：B．4．抛物线y=﹣2（x+1）2﹣2可由抛物线y=﹣2x2平移得到，则下列平移过程正确的是（）A．先向右平移1个单位，再向上平移2个单位B．先向右平移1个单位，再向下平移2个单位C．先向左平移1个单位，再向上平移2个单位D．先向左平移1个单位，再向下平移2个单位【解答】解：抛物线y=﹣2x2的顶点坐标为（0，0），抛物线y=﹣2（x+1）2﹣2的顶点坐标为（﹣1，﹣2），因为点（0，0）先向左平移1个单位，再向下平移2个单位得到点（﹣1，﹣2），所以把抛物线y=﹣2x2先向左平移1个单位，再向下平移2个单位可得抛物线y=﹣2（x+1）2﹣2．故选D．5．如图，把抛物线y=x2沿直线y=x平移个单位后，其顶点在直线上的A处，则平移后的抛物线解析式是（）A．y=（x+1）2﹣1 B．y=（x+1）2+1 C．y=（x﹣1）2+1 D．y=（x﹣1）2﹣1【解答】解：∵A在直线y=x上，∴设A（m，m），∵OA=，∴m2+m2=（）2，解得：m=±1（m=﹣1舍去），m=1，∴A（1，1），∴抛物线解析式为：y=（x﹣1）2+1，故选：C．6．设A（﹣1，y1）、B（1，y2）、C（3，y3）是抛物线y=﹣上的三个点，则y1、y2、y3的大小关系是（）A．y1＜y2＜y3B．y2＜y1＜y3C．y3＜y1＜y2D．y2＜y3＜y1【解答】解：∵此函数的对称轴为x=，且开口向下，∴x＞时，是减函数，∵A（﹣1，y1）对应A′（2，y1），∴y3＜y1＜y2，故选：C．7．若二次函数y=（x﹣m）2﹣1．当x≤l时，y随x的增大而减小，则m的取值范围是（）A．m=l B．m＞l C．m≥l D．m≤l【解答】解：二次函数y=（x﹣m）2﹣1的对称轴为直线x=﹣m，∵当x≤l时，y随x的增大而减小，∴m≥1，故选C．8．二次函数y=a（x+m）2+n的图象如图，则一次函数y=mx+n的图象经过（）A．第一、二、三象限 B．第一、二、四象限C．第二、三、四象限 D．第一、三、四象限【解答】解：∵抛物线的顶点在第四象限，∴﹣m＞0，n＜0，∴m＜0，∴一次函数y=mx+n的图象经过二、三、四象限，故选C．二、填空题：9．抛物线y=﹣2（x+3）2﹣1的对称轴是直线x=﹣3 ，顶点坐标是（﹣3，﹣1）；当x ＜﹣3 时，y随x的增大而增大，当x ＞﹣3 时，y随x的增大而减小，当x =﹣3 时，y 取最大值为﹣1 ．【解答】解：抛物线y=﹣2（x+3）2﹣1的对称轴是直线x=﹣3，顶点坐标是（﹣3，﹣1）；当x ＜﹣3时，y随x的增大而增大，当x＞﹣3时，y随x的增大而减小，当x=﹣3时，y取最大值为﹣1．故答案为：直线x=﹣3，（﹣3，﹣1），＜﹣3，＞﹣3，=﹣3，大，﹣1．10．抛物线y=4（x+h）2+k的顶点在第三象限，则有h，k满足h ＞0，k ＜0．【解答】解：∵抛物线y=4（x+h）2+k的顶点坐标为（﹣h，k），∴﹣h＜0，k＜0，∴h＞0，k＜0．故答案为：＞，＜．11．已知点A（x1，y1）、B（x2，y2）在二次函数y=（x﹣1）2+1的图象上，若x1＞x2＞1，则y1＞y2（填“＞”、“＜”或“=”）．【解答】解：∵a=1＞0，∴二次函数的图象开口向上，由二次函数y=（x﹣1）2+1可知，其对称轴为x=1，∵x1＞x2＞1，∴两点均在对称轴的右侧，∵此函数图象开口向上，∴在对称轴的右侧y随x的增大而增大，∵x1＞x2＞1，∴y1＞y2．故答案为：＞．12．抛物线的顶点坐标为P（2，3），且开口向下，若函数值y随自变量的x增大而减小，那么x 的取值范围为x＞2 ．【解答】解：∵抛物线的顶点坐标为P（2，3），且开口向下，若函数值y随自变量的x增大而减小，∴x＞2．故答案为：x＞2．13．在平面直角坐标系中，点A是抛物线y=a（x﹣3）2+k与y轴的交点，点B是这条抛物线上的另一点，且AB∥x轴，则以AB为边的等边三角形ABC的周长为18 ．【解答】解：∵抛物线y=a（x﹣3）2+k的对称轴为x=3，且AB∥x轴，∴AB=2×3=6，∴等边△ABC的周长=3×6=18．故答案为：18．14．将抛物线y=﹣x2先沿x轴方向向右移动 3 个单位，再沿y轴方向向上移动 1 个单位，所得到的抛物线解析式是y=﹣（x﹣3）2+1．【解答】解：抛物线y=﹣x2的顶点坐标为（0，0），抛物线y=﹣（x﹣3）2+1的顶点坐标为（3，1），因为点（0，0）先向右平移3个单位，再向上平移1个单位得到点（3，1），所以把抛物线y=﹣x2先向右平移3个单位，再向上平移1个单位可得抛物线y=﹣（x﹣3）2+1．故答案为右，3；上，1．15．将抛物线y=x2+1先向左平移2个单位，再向下平移3个单位，那么所得抛物线的函数关系式是y=（x+2）2﹣2 ．【解答】解：抛物线y=x2+1的顶点坐标为（0，1），向左平移2个单位，向下平移3个单位后的抛物线的顶点坐标为（﹣2，﹣2），所以，平移后的抛物线的解析式为y=（x+2）2﹣2．故答案为：y=（x+2）2﹣2．16．将抛物线y=﹣2（x+1）2+1绕其顶点旋转180°后得到抛物线的解析式为y=2（x+1）2+1 ；将抛物线y=﹣2（x+1）2+1绕原点旋转180°后得到抛物线的解析式为y=2（x﹣1）2﹣1 ．【解答】解：抛物线y=﹣2（x+1）2+1的顶点坐标为（﹣1，1），由于抛物线y=﹣2（x+1）2+1绕其顶点旋转180°后抛物线的顶点坐标不变，只是开口方向相反，则所得抛物线解析式为y=2（x+1）2+1；抛物线y=﹣2（x+1）2+1的顶点坐标为（﹣1，1），由于抛物线y=﹣2（x+1）2+1绕原点旋转180°后抛物线的顶点坐标为（1，﹣1），并且开口方向相反，则所得抛物线解析式为y=2（x﹣1）2﹣1．故答案为y=2（x+1）2+1；y=2（x﹣1）2﹣1．17．抛物线y=a（x﹣h）2+k的顶点为（3，﹣2），且与抛物线y=﹣的形状相同，则a= ﹣，h= 3 ，k= ﹣2 ．【解答】解：∵抛物线y=a（x﹣h）2+k的顶点为（3，﹣2），且与抛物线y=﹣的形状相同，∴a=﹣，h=3，k=﹣2．故答案为：﹣，3，﹣2．18．如图，抛物线y1=a（x+2）2﹣3与y2=（x﹣3）2+1交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于点B，C．则以下结论：①无论x取何值，y2的值总是正数；②a=1；③当x=0时，y2﹣y1=4④2AB=3AC．其中正确结论是①④．【解答】解：①∵抛物线y2=（x﹣3）2+1开口向上，顶点坐标在x轴的上方，∴无论x取何值，y2的值总是正数，故本小题正确；②把A（1，3）代入，抛物线y1=a（x+2）2﹣3得，3=a（1+2）2﹣3，解得a=，故本小题错误；③由两函数图象可知，抛物线y1=a（x+2）2﹣3解析式为y1=（x+2）2﹣3，当x=0时，y1=（0+2）2﹣3=﹣，y2=（0﹣3）2+1=，故y2﹣y1=+=，故本小题错误；④∵物线y1=a（x+2）2﹣3与y2=（x﹣3）2+1交于点A（1，3），∴y1的对称轴为x=﹣2，y2的对称轴为x=3，∴B（﹣5，3），C（5，3）∴AB=6，AC=4，∴2AB=3AC，故本小题正确．故答案为：①④．三、解答题：19．若二次函数图象的顶点坐标为（﹣1，5），且经过点（1，2），求出二次函数的解析式．【解答】解：∵二次函数的图象顶点为（﹣1，5）∴设二次函数的解析式为y=a（x+1）2+5又∵图象过点（1，2）∴a（1+1）2+5=2 解得a=﹣∴．20．若抛物线经过点（1，1），并且当x=2时，y有最大值3，则求出抛物线的解析式．【解答】解：∵x=2时函数y取得最大值3，∴设抛物线解析式为y=a（x﹣2）2+3，又∵抛物线经过点（1，1），∴a（1﹣2）2+3=1，解得a=﹣2，∴y=﹣2（x﹣2）2+321．已知：抛物线y=（x﹣1）2﹣3．（1）写出抛物线的开口方向、对称轴；（2）函数y有最大值还是最小值？并求出这个最大（小）值；（3）设抛物线与y轴的交点为P，与x轴的交点为Q，求直线PQ的函数解析式．【解答】解：（1）抛物线y=（x﹣1）2﹣3，∵a=＞0，∴抛物线的开口向上，对称轴为直线x=1；（2）∵a=＞0，∴函数y有最小值，最小值为﹣3；（3）令x=0，则y=（0﹣1）2﹣3=﹣，所以，点P的坐标为（0，﹣），令y=0，则（x﹣1）2﹣3=0，解得x1=﹣1，x2=3，所以，点Q的坐标为（﹣1，0）或（3，0），当点P（0，﹣），Q（﹣1，0）时，设直线PQ的解析式为y=kx+b（k≠0），则，解得，所以直线PQ的解析式为y=﹣x﹣，当P（0，﹣），Q（3，0）时，设直线PQ的解析式为y=mx+n，则，解得，所以，直线PQ的解析式为y=x﹣，综上所述，直线PQ的解析式为y=﹣x﹣或y=x﹣．22．在直角坐标系中，二次函数图象的顶点为A（1、﹣4），且经过点B（3，0）（1）求该二次函数的解析式；（2）当﹣3＜x＜3时，函数值y的增减情况；（3）将抛物线怎样平移才能使它的顶点为原点．【解答】解：（1）∵二次函数的图象顶点为A（1，﹣4），∴设二次函数的解析式为y=a（x﹣1）2﹣4，又∵二次函数图象过点B（3，0）∴a（3﹣1）2﹣4=0解得a=1，∴y=（x﹣1）2﹣4（2）∵抛物线对称轴为直线x=1，开口向上，∴当﹣3＜x＜1时，y随x的增大而减小，当1≤x＜3，y随x的增大而增大，（3）将抛物线y=（x﹣1）2﹣4向左平移1个单位，再向上平移4个单位即可实现抛物线顶点为原点．23．如图是二次函数y=（x+m）2+k的图象，其顶点坐标为M（1，﹣4）（1）求出图象与x轴的交点A、B的坐标；（2）在二次函数的图象上是否存在点P，使S△PAB=S△MAB？若存在，求出点P的坐标；若不存在，请说明理由．【解答】解：（1）∵抛物线解析式为y=（x+m）2+k的顶点为M（1，﹣4）∴令y=0得（x﹣1）2﹣4=0解得x1=3，x2=﹣1∴A（﹣1，0），B（3，0）（2）∵△PAB与△MAB同底，且S△PAB=S△MAB，∴，即y P=±5又∵点P在y=（x﹣1）2﹣4的图象上∴y P≥﹣4∴∴存在合适的点P，坐标为（4，5）或（﹣2，5）．。

22.1.3 二次函数2)(h x a y -=的图象和性质（二）知识点：抛物线2)(h x a y -=的特点有：(1)当0>a 时，开口向 ；当0<a 时，开口向 。

(2)对称轴是 ，顶点坐标是 。

(3)当0>a 时，在对称轴的左侧（h x <），y 随x 的 ，在对称轴的右侧（h x >），y 随x 的 ；当0<a 时，在对称轴的左侧（h x <），y 随x 的 ，在对称轴的右侧（h x >），y 随x 的 。

(4)当x 时，函数y 的值最大（或最小），是 。

一．选择题1.把二次函数2x y =的图象向右平移3个单位长度，得到新的图象的函数表达式是（ ）A. 32+=x yB. 32-=x yC. 2)3(+=x yD. 2)3(-=x y2.抛物线2)3(2--=x y 的顶点坐标和对称轴分别是（ ）A.3),0,3(-=-x 直线B. 3),0,3(=x 直线C. 3),3,0(-=-x 直线D. 3),3,0(-=x 直线3.已知二次函数2)1(3+=x y 的图象上有三点 ),2(),,2(),,1(321y C y B y A - ，则321,,y y y 的大小关系为（ ）A.321y y y >>B. 312y y y >>C. 213y y y >>D. 123y y y >>4.把抛物线2)1(6+=x y 的图象平移后得到抛物线26x y =的图象，则平移的方法可以是（ ）A.沿y 轴向上平移1个单位长度B.沿y 轴向下平移1个单位长度C.沿x 轴向左平移1个单位长度D.沿x 轴向右平移1个单位长度5.若二次函数12+-=mx x y 的图象的顶点在x 轴上，则m 的值是（ ） A. 2 B. 2- C.0 D. 2±6.对称轴是直线2-=x 的抛物线是（ ）A.22+-=x yB.22+=x yC.2)2(21+=x y D.2)2(3-=x y 7.对于函数2)2(3-=x y ，下列说法正确的是（ ）A. 当0>x 时，y 随x 的增大而减小B. 当0<x 时，y 随x 的增大而增大C. 当2>x 时，y 随x 的增大而增大D. 当2->x 时，y 随x 的增大而减小8.二次函数132+=x y 和2)1(3-=x y ，以下说法：①它们的图象都是开口向上；②它们的对称轴都是y 轴，顶点坐标都是原点（0,0）；③当0>x 时，它们的函数值y 都是随着x 的增大而增大；④它们的开口的大小是一样的.其中正确的说法有（ ）A.1个B.2个C.3个D.4个二．填空题1.抛物线2)1(3--=x y 的开口向 ，对称轴是 ，顶点坐标是 。

2018年九年级数学上册二次函数图象性质一、选择题：1.下列关于二次函数y=-x2图象的说法：①图象是一条抛物线；②开口向下；③对称轴是y轴；④顶点(0，0).其中正确的有( )A．1个B．2个C．3个D．4个2.在平面直角坐标系中，二次函数y=a(x﹣h)2（a≠0）的图象可能是（）3.将二次函数y=x2﹣2x+3化为y=(x﹣h)2+k的形式，结果为（）A．y=(x+1)2+4 B．y=(x+1)22+2 C．y=(x-1)2+4 D．y=(x-1)22+24.下表是满足二次函数y=ax2+bx+c的五组数据，x1是方程ax2+bx+c=0的一个解，则下列选项的正确是（）A．C．5.抛物线y=x2+bx+c图象向右平移2个单位再向下平移3个单位,所得图象的解析式为y=x2﹣2x﹣3，则b、c的值为（）A．b=2，c=2 B．b=2，c=0 C．b=﹣2，c=﹣1 D．b=﹣3，c=26.已知一个函数图象经过（1，﹣4），（2，﹣2）两点，在自变量x的某个取值范围内，都有函数值y随x的增大而减小，则符合上述条件的函数可能是（）A．正比例函数B．一次函数C．反比例函数D．二次函数7.抛物线y=3x2+2x﹣1向上平移4个单位长度后的函数解析式为（）．A．y=3x2+2x﹣5 B．y=3x2+2x﹣4C．y=3x2+2x+3 D．y=3x2+2x+48.若二次函数y=x2＋bx的图象的对称轴是经过点(2，0)且平行于y轴的直线，则关于x的方程x2＋bx=5的解为( )A．x1=0，x2=4 B．x1=1，x2=5 C．x1=1，x2=-5 D．x1=-1，x2=59.在同一坐标系下,抛物线y=﹣x2+4x和直线y2=2x的图象如图,那么不等式﹣x2+4x＞2x的解集是（）1A．x＜0 B．0＜x＜2 C．x＞2 D．x＜0或 x＞210.如图，在直角坐标系中，正△AOB的边长为2，设直线x=t（0≤t≤2）截这个三角形所得位于此直线左方的图形的面积为y，则y关于t的函数图象大致是（）11.抛物线的形状、开口方向与y=12x2-4x+3相同,顶点在(-2,1),则关系式为A．y=12(x-2)2+1 B．y=12(x+2)2-1; C．y=12(x+2)2+1 D．y=-12(x+2)2+112.若t为实数，关于x的方程x2－4x＋t－2=0的两个非负实数根为a、b，则代数式(a2－1)(b2－1)的最小值是( )A．－15 B．－16 C．15 D．16二、填空题:13.把抛物线y=4x2向左平移3个单位．再向下平移2个单位，得到的抛物线对应的函数关系式为．14.抛物线y=x2+mx+n可以由抛物线y=x2向下平移2个单位，再向右平移3个单位得到，则mn值为．15.已知二次函数y=x2+2x+m的最小值为1，则m的值是．16.如图,点A是抛物线y=x2﹣4x对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO′,当O′恰好落在抛物线上时,点A的坐标为．17.如图，是抛物线y=ax2+bx+c（a≠0）图象的一部分，已知抛物线的对称轴是直线x=2，与x轴的一个交点是（-1，0），有下列结论：①abc＜0，②4a+b=0，③抛物线与x轴的另一个交点是（5,0），④若点（﹣2,y1），（5,y2）都在抛物线上,则有y1＜y2，请将正确选项的序号都填在横线上．18.已知二次函数y=ax2+bx+c的图象如图所示，有以下结论：①abc＞0；②a﹣b+c＜0；③2a=b；④4a+2b+c ＞0；⑤若点（﹣2，y1）和（﹣，y2）在该图象上，则y1＞y2．其中正确的结论是（填入正确结论的序号）．三、解答题:19.已知二次函数图象的对称轴是x=1,且函数有最大值为2,图象与x轴的一个交点是(-1,0),求这个二次函数的解析式.20.根据下列条件,求二次函数的解析式:抛物线的对称轴是直线x=1,与x轴的一个交点为（-2,0）,与y轴交于点（0,12）21.已知二次函数的解析式是y=x2-2x-3.(1)在直角坐标系中,用五点法画出它的图象；(2)当x为何值时,函数值y=0？(3)当-3<x<3时,观察图象直接写出函数值y的取值的范围.22.如图，已知抛物线y=ax2＋bx＋c与x轴交于点A(1，0)，点B(3，0)，且过点C(0，－3).(1)求抛物线的函数表达式和顶点坐标；(2)请你写出一种平移的方法，使平移后抛物线的顶点落在直线y=－x上，并写出平移后抛物线的函数表达式.23.在坐标系中,已知抛物线y=x2﹣2x+n﹣1与y轴交于点A,其对称轴与x轴交于点B．（1）当△OAB是等腰直角三角形时,求n的值；（2）点C的坐标为（3,0），若该抛物线与线段OC有且只有一个公共点,结合函数的图象求n的取值范围．24.已知二次函数y=﹣x2+2x+m．（1）如果二次函数的图象与x轴有两个交点，求m的取值范围；（2）如图，二次函数的图象过点A（3，0），与y轴交于点B，直线AB与这个二次函数图象的对称轴交于点P，求点P的坐标．（3）根据图象直接写出使一次函数值大于二次函数值的x的取值范围．25.已知函数y=ax2+x+1的图象与x轴只有一个公共点．（1）求这个函数关系式；（2）如图所示，设二次函数y=ax2+x+1图象的顶点为B，与y轴的交点为A，P为图象上的一点，若以线段PB 为直径的圆与直线AB相切于点B，求P点的坐标；（3）在(2)中，若圆与x轴另一交点关于直线PB的对称点为M，试探索点M是否在抛物线y=ax2+x+1上，若在抛物线上，求出M点的坐标；若不在，请说明理由．参考答案1.D2.D3.D4.C5.B6.D7.C8.D9.D10.C11.A；12.A.13.答案为：y=4(x+3)2﹣2．14.答案是：66．15.答案为：2．16.答案为：（2，﹣1）或（2，2）．17.答案为：②③．18.答案为：②④．19.解：设所求二次函数的解析式为∵图象的对称轴是,且函数有最大值为2 ∴∵图象与x轴的一个交点是(-1,0)∴∴∴所求二次函数的解析式为20.21.解：(1) 已知二次函数的解析式是=(2) 令,解得∴当x = -1或3时,函数值y =0(3) 观察图象知：-4≤y＜1222.解：(1)∵抛物线与x轴交于点A(1，0)，点B(3，0)，∴可设抛物线表达式为y=a(x－1)(x－3)，把C(0，－3)的坐标代入，得3a=－3，解得a=－1，故抛物线表达式为y=－(x－1)(x－3)，即y=－x2＋4x－3.∵y=－x2＋4x－3=－(x－2)2＋1，∴抛物线的顶点坐标为(2，1)；(2)答案不唯一，如：先向左平移2个单位，再向下平移1个单位，得到的抛物线的解析式为y=－x2，平移后抛物线的顶点为(0，0)，落在直线y=－x上.23.解：（1）二次函数的对称轴是x=﹣1，则B的坐标是（1，0），当△OAB是等腰直角三角形时，OA=OB=1，则A的坐标是（0，1）或（0，﹣1）．抛物线y=x2﹣2x+n﹣1与y轴交于点A的坐标是（0，n﹣1）．则n﹣1=1或n﹣1=﹣1，解得n=2或n=0；（2）①当抛物线的顶点在x轴上时，△=（﹣2）2﹣4（n﹣1）=0，解得：n=2；②当抛物线的顶点在x轴下方时，如图，由图可知当x=0时，y＜0；当x=3时，y≥0，即，解得：﹣2≤n＜1，综上，﹣2≤n＜1或n=2．24.解：（1）∵二次函数的图象与x轴有两个交点，∴△=22+4m＞0∴m＞﹣1；（2）∵二次函数的图象过点A（3，0），∴0=﹣9+6+m∴m=3，∴二次函数的解析式为：y=﹣x2+2x+3，令x=0，则y=3，∴B（0，3），设直线AB的解析式为：y=kx+b，∴，解得：，∴直线AB的解析式为：y=﹣x+3，∵抛物线y=﹣x2+2x+3，的对称轴为：x=1，∴把x=1代入y=﹣x+3得y=2，∴P（1，2）．(3) x＜0或x＞325.解：（1）当a = 0时，y = x+1，图象与x轴只有一个公共点,当a≠0时,△=1- 4a=0,a = ，此时，图象与x轴只有一个公共点．∴函数的解析式为：y=x+1 或`y=x2+x+1（2）设P为二次函数图象上的一点，过点P作PC⊥x轴于点C．∵是二次函数，由（1）知该函数关系式为：y=x2+x+1，则顶点为B（-2，0），图象与y轴的交点坐标为A（0，1）∵以PB为直径的圆与直线AB相切于点B ∴PB⊥AB 则∠PBC=∠BAO∴Rt△PCB∽Rt△BOA ∴，故PC=2BC，设P点的坐标为(x，y)，∵∠ABO是锐角，∠PBA是直角，∴∠PBO是钝角，∴x<-2∴BC=-2-x，PC=-4-2x，即y=-4-2x， P点的坐标为(x，-4-2x)∵点P在二次函数y=x2+x+1的图象上，∴-4-2x=x2+x+1解之得：x1=-2，x2=-10∵x<-2 ∴x=-10，∴P点的坐标为：(-10，16)（3）点M不在抛物线上由（2）知：C为圆与x 轴的另一交点，连接CM，CM与直线PB的交点为Q，过点M 作x轴的垂线，垂足为D，取CD的中点E，连接QE，则CM⊥PB，且CQ=MQ∴QE∥MD，QE=MD，QE⊥CE∵CM⊥PB，QE⊥CE PC⊥x 轴∴∠QCE=∠EQB=∠CPB∴tan∠QCE= tan∠EQB= tan∠CPB =CE=2QE=2×2BE=4BE，又CB=8，故BE=，QE=∴Q点的坐标为(-，)可求得M点的坐标为(，)∵=≠∴C点关于直线PB的对称点M不在抛物线上。

二次函数的图象一 、选择题（本大题共10小题）1.由二次函数，可知（ ）A ．其图象的开口向下B ．其图象的对称轴为直线C ．其最小值为1D ．当时，y 随x 的增大而增大2.把抛物线2y x =-向左平移1个单位，然后向上平移3个单位，则平移后抛物线的解析式为（ ）A ．()213y x =---B ．()213y x =-+-C ．()213y x =--+D ．()213y x =-++3.二次函数2365y x x =--+的图象的顶点坐标是（ ）A ．（1-，8）B ．（1，8）C ．（1-，2）D ．（1，4-）4.二次函数()212y x =-+的最小值是（ ）A ．2-B ．2C ．1-D ．15.已知二次函数的图象(03x ≤≤)如图所示．关于该函数在所给自变量取值范围内，下列说法正确的是( )A ．有最小值0，有最大值3B ．有最小值1-，有最大值0C ．有最小值1-，有最大值3D ．有最小值1-，无最大值6.下列函数中，y 随x 增大而增大的是（ ） A.xy 3-= B. 5+-=x y1)3(22+-=x y 3-=x 3<xC. x y 21-= D. )0(212<=x x y 7.二次函数21y ax x =++的图象必过点（ ）A ．()0,aB ．()1,a --C ．()1,a -D ．()0,a -8.二次函数2y ax bx c =++的图象如图所示，则一次函数24y bx b ac =+-与反比例函数a b c y x++=在同一坐标系内的图象大致为（ ）9.抛物线2(2)3y x =+-的图象可以看作是由抛物线2y x =平移得到,则下列平移过程正确的是( )A.先向左平移2个单位,再向上平移3个单位B.先向左平移2个单位,再向下平移3个单位C.先向右平移2个单位,再向下平移3个单位D.先向右平移2个单位,再向上平移3个单位10.已知二次函数2y ax bx c =++的图象如图所示，有以下结论：①0a b c ++<；②1a b c -+>；③0abc >；④420a b c -+<；⑤1c a ->ABCD其中所有正确结论的序号是（ ）A ．①②B ．①③④C ．①②③⑤D ．①②③④⑤二 、填空题（本大题共5小题）11.函数241y x =-的图象可以看做是函数245y x =+的图象向 平移个单位得到的。