正余弦函数图象知识讲解

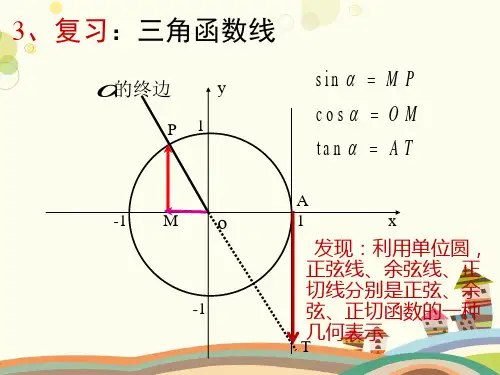
5.4.1 正弦函数、余弦函数的图象一、正弦函数、余弦函数图象的画法1．描点法：按照列表、描点、连线三步法作出正弦函数、余弦函数图象的方法． 2．几何法：利用三角函数线作出正弦函数和余弦函数在]2,0[π内的图象，再通过平移得到x y sin =和cos y x =的图象．3．五点法：先描出正弦曲线和余弦曲线的波峰、波谷和三个平衡位置这五个点，再利用光滑曲线把这五点连接起来，就得到正弦曲线和余弦曲线在一个周期内的图象．在确定正弦函数x y sin =在]2,0[π上的图象时，关键的五点是：)0,2(),1,23(),0,(),1,2(),0,0(ππππ-【注意】（1）若x R ∈，可先作出正弦函数、余弦函数在]2,0[π上的图象，然后通过左、右平移可得到x y sin =和cos y x =的图象．（2）由诱导公式cos sin()2y x x π==+，故cos y x =的图象也可以将x y sin =的图象上所有点向左平移2π个单位长度得到． 二、正（余）弦函数的图象 函数y ＝sin xy ＝cos x图象图象画法五点法五点法关键五点 (0,0),π(,1)2,(,0)π,3π(,1)2-,(2,0)π (0,1),π(,0)2,(,1)π-,3π(,0)2,(2,1)π正（余）弦曲线正（余）弦函数的图象叫做正（余）弦曲线三、用三角函数图象解三角不等式的方法1、作出相应正弦函数或余弦函数在[0,2π]上的图象；2、写出适合不等式在区间[0,2π]上的解集；3、根据公式一写出不等式的解集．题型一 五点法作三角函数的图象【例1】用“五点法”作y ＝2sin2x 的图象，首先描出的五个点的横坐标是（ ） A ．30,,,,222ππππ B ． 30,,,,424ππππ C ．0,,2,3,4ππππD ．20,,,,6323ππππ【答案】B【解析】由“五点法”作图知：令2x ＝0，2π，π，32π，2π，解得x ＝0，4π，2π，34π，π，即为五个关键点的横坐标，故选：B.【变式1-1】用“五点法”作函数cos 1y x =-，[]0,2x π∈的大致图像，所取的五点是______．【答案】(0,0)，,12π⎛⎫- ⎪⎝⎭，(,2)π-，3,12π⎛⎫- ⎪⎝⎭，(2,0)π【解析】由“五点法”作函数cos 1y x =-，[0x ∈，2]π的图象时的五个点分别是(0,0)，,12π⎛⎫- ⎪⎝⎭，(,2)π-，3,12π⎛⎫- ⎪⎝⎭，(2,0)π．【变式1-2】用“五点法”画出下列函数的简图：（1）cos 1y x =-，[],x ππ∈-； （2）sin y x =，3,22x ππ⎡⎤∈-⎢⎥⎣⎦； （3）sin y x =-，[]0,2x π∈．【答案】（1）见解析；（2）见解析；（3）见解析 【解析】（1）按五个关键点列表xπ-2π-2ππcos x1-0 11cos 1x -2- 1- 01- 2-（2）按五个关键点列表x2π-0 2ππ32πsin x1- 011-描点并将它们用光滑的曲线连接起来如下图（3）按五个关键点列表x0 2ππ32π2πsin x11-sin x -0 1-0 1 0【变式1-3】用“五点法”作下列函数的简图. （1）2sin ([0,2])y x x π=∈；（2）5sin()([,])222y x x πππ=-∈. （3）2sin(2)3y x π=-(x ∈R ).【答案】（1）图象答案见解析；（2）图象答案见解析；（3）图象答案见解析. 【解析】（1）列表如下：x2ππ 32π2π 2sin x 02 0 -2 0描点连线如图：（2）列表如下：x2ππ 32π2π 52πsin()2x π-0 1 0 -1 0（3）函数π2sin 23y x ⎛⎫=- ⎪⎝⎭在长为一个周期π的区间上的图象，列表如下：x6π512π23π1112π76π23x π-0 2ππ32π2πy 02 0 -2 0再向左右两边扩展，其图象如下：题型二 含绝对值的三角函数【例2】函数y ＝|cos x |的一个单调增区间是（ ）A ．,22ππ⎡⎤-⎢⎥⎣⎦B ．[0，π]C ．3,2ππ⎡⎤⎢⎥⎣⎦D ．3,2π2π⎡⎤⎢⎥⎣⎦【答案】D【解析】将y ＝cos x 的图像位于x 轴下方的图像关于x 轴对称翻折到x 轴上方，x 轴上方(或x 轴上)的图像不变，即得y ＝|cos x |的图像根据各选项判断只有D 选项正确. 故选：D.【变式2-1】作出函数2sin sin y x x =+，[],x ππ∈-的大致图像． 【答案】图见解析【解析】函数[][]3sin ,0,2sin sin sin ,,0x x y x x x x ππ⎧∈⎪=+=⎨-∈-⎪⎩， 其图如下所示：【变式2-2】作出函数sin ||,[2,2]=∈-y x x ππ的大致图像. 【答案】图象见解析 【解析】列表x0 2ππ32π2πsin ||y x =1 0 -1 0作图：先作出(]0,2π的图像，又原函数是偶函数,图像关于y 轴对称， 即可作出[)2,0π-的图像.【变式2-3】作函数3sin 2y x π⎛⎫=+ ⎪⎝⎭的图象.【答案】图象见解析.【解析】3sin cos 2y x x π⎛⎫=+= ⎪⎝⎭ cos 22,Z 223cos 22,Z 22x k x k k x k x k k ππππππππ⎧⎛⎫-+≤≤+∈ ⎪⎪⎪⎝⎭=⎨⎛⎫⎪-+<<+∈ ⎪⎪⎝⎭⎩故|cos |y x =的图象是cos y x =的图象在x 轴下方的部分翻折到x 轴上方后得到的图象，如图题型三 三角函数识图问题【例3】函数1sin =+y x x的大致图象是（ ）A ．B ．C ．D ．【答案】A【解析】函数1sin =+y x x是定义域(,0)(0,)-∞+∞上的奇函数∴其图象关于原点对称，排除选项D ；当(0,)x π∈时，sin 0x >，此时1sin 0x x+>，∴当(0,)x π∈时，()f x 的图象在x 轴上方，排除选项B ； 当32x π=时，322sin 10233πππ+=-+<，()f x 的图象在x 轴下方，排除选项C ；综上所述，函数1sin =+y x x的大致图象为选项A .故选：A .【变式3-1】函数2sin 2xy x =-的图象大致是（ ）A ．B ．C ．D ．【答案】A【解析】令0x =，则02sin 01y =-=，排除C 、D ；令1x =-，则()112sin 2sin 202y -=--=+>，排除B.故选：A【变式3-2】已知函数()y f x =的图象如图所示，则此函数可能是（ ）A ．()sin ln ||f x x x =⋅B ．()sin ln ||f x x x =-⋅C ．()sin ln f x x x =⋅D ．()|sin ln |f x x x =⋅ 【答案】A【解析】图象关于原点对称，为奇函数，CD 中定义域是0x >，不合，排除，AB 都是奇函数，当(0,1)x ∈时，A 中函数值为负，B 中函数值为正，排除B ．故选：A ．【变式3-3】已知函数()f x 的部分图象如图所示，则()f x 的解析式可能为（ ）A ．()sin πf x x x =B ．()(1)sin πf x x x =-C ．[]()cos π(1)f x x x =+D ．()(1)cos πf x x x =- 【答案】B【解析】对于A ，()()sin πsin π()f x x x x x f x -=--==，所以函数()sin πf x x x =为偶函数，故排除A ； 对于D ，()010f =-≠，故排除D ；对于C ，[]()cos π(1)cos πf x x x x x =+=-，则()()cos πf x x x f x -==-， 所以函数[]()cos π(1)f x x x =+为奇函数，故排除C.故选：B.题型四 利用图象解三角不等式【例4】不等式2sin ,(0,2)2xx π∈的解集为（ ） A ．,62ππ⎡⎤⎢⎥⎣⎦ B ．3,44ππ⎡⎤⎢⎥⎣⎦ C ．423,ππ⎡⎤⎢⎥⎣⎦ D ．,64ππ⎡⎤⎢⎥⎣⎦【答案】B 【解析】2sin ,(0,2)2xx π∈ sin y x =函数图象如下所示：∴344ππ≤≤x ，∴不等式的解集为：3,44ππ⎡⎤⎢⎥⎣⎦．故选：B ．【变式4-1】在()0,2x π∈上，满足cos sin x x >的x 的取值范围（ ）A ．5,44ππ⎛⎫ ⎪⎝⎭B ．0,4π⎛⎫ ⎪⎝⎭C ．50,,244πππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭ D ．5,24ππ⎛⎫⎪⎝⎭【答案】C【解析】作出sin y x =和cos y x =在()0,2x π∈的函数图象，根据函数图象可得满足cos sin x x >的x 的取值范围为50,,244πππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭.故选：C.【变式4-2】在[]0,2π内，不等式3sin x < ） A ．(0，π) B ．3,34ππ⎛⎫ ⎪⎝⎭C ．45,33ππ⎛⎫ ⎪⎝⎭ D ．5,23ππ⎛⎫⎪⎝⎭【答案】C【解析】画出y ＝sin x ，[]0,2x π∈的草图如下．[]0,2x π∈内，令3sin x =43x π=或53x π=，结合图象可知不等式3sin x <的解集为45,33ππ⎛⎫ ⎪⎝⎭．故选：C ．【变式4-3】若函数()2sin13f x x π=- ）A ．56,622k k ππππ⎡⎤++⎢⎥⎣⎦（k ∈Z ） B ．156,622k k ⎡⎤++⎢⎥⎣⎦（k ∈Z ）C ．56,644k k ππππ⎡⎤++⎢⎥⎣⎦（k ∈Z ） D ．156,644k k ⎡⎤++⎢⎥⎣⎦（k ∈Z ） 【答案】B【解析】要使函数有意义，则2sin103x π-≥，即1sin32x π≥， 即522636k x k πππππ+≤≤+，k ∈Z ，得156622k x k +≤≤+，k ∈Z ， 即函数的定义域为156,622k k ⎡⎤++⎢⎥⎣⎦（k ∈Z ）.故选：B【变式4-4】已知()f x 的定义域是3⎡-⎢⎣⎦，则(sin 2)f x 的定义域为（ ） A ．2,36k k ππππ⎡⎤-++⎢⎥⎣⎦，k Z ∈ B ．,63k k ππππ⎡⎤++⎢⎥⎣⎦，k Z ∈C ．22,236k k ππππ⎡⎤-++⎢⎥⎣⎦，k Z ∈ D ．2,263k k ππππ⎡⎤++⎢⎥⎣⎦，k Z ∈【答案】A 【解析】()f x 的定义域是3⎡-⎢⎣⎦，故由31sin 2x -≤≤解得()422233k x k k Z ππππ-+≤≤+∈， ()236k x k k Z ππππ∴-+≤≤+∈ 因此，函数(sin 2)f x 的定义域为()22,236k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦.故选：A.【变式4-5】函数y 12log sin x________． 【答案】{}22,x k x k k Z πππ<<+∈ 【解析】由1122log sin 0log 1x ≥=知，0sin 1x <≤，由正弦函数图象特征知，22,k x k k Z πππ<<+∈． 故定义域为{}22,x k x k k Z πππ<<+∈. 故答案为：{}22,x k x k k Z πππ<<+∈.题型五 与正余弦函数有关的零点【例5】函数sin y x =，[]0,2πx ∈的图像与直线23y =-的交点的个数为（ ） A ．0 B ．1 C ．2 D ．3 【答案】C【解析】在同一平面直角坐标系内，先画函数sin y x =，[]0,2πx ∈的图像，再画直线23y =-，可知所求交点的个数为2．故选：C ．【变式5-1】已知函数f (x )=12x⎛⎫⎪⎝⎭-sin x ，则f (x )在区间[0，2π]上的零点个数为（ ）A ．1B ．2C ．3D ．4 【答案】B【解析】令sin 01()2xf x x ⎛⎫-=⎪⎝⎭= ，则1()sin 2x x =， 在同一坐标系中，作出1(),sin 2xy y x ==，如下图所示：由图知，f (x )在区间[0，2π]上的零点个数为2个.故选：B.【变式5-2】()f x 是定义在R 上的偶函数，且()()11f x f x -=+，[]1,0x ∈-时，()sin 2f x x ππ⎛⎫=+⎪⎝⎭，则函数()()e x g x f x -=-在区间[]2021,2022-上零点的个数为（ ）A ．2021B ．4043C ．2020D ．4044 【答案】B 【解析】(1)(1)f x f x -=+，()(2)f x f x ∴=+，即函数()f x 的周期为2，当[]1,0x ∈-时，()sin()sin()22f x x x πππ=+=-，则当[]0,1x ∈时，()()sin()sin()22f x f x x x ππ=-=--=， 由此可作出函数()f x 与函数e -=xy 的大致图象如下，由图象可知，每个周期内有两个交点， 所以函数((e))xg x f x -=-在区间[]2021,2022-上零点的个数为2021214043⨯+=个．故选：B ．【变式5-3】函数()sin 3|sin |,[0,2]f x x x x π=+∈的图象与直线y k =有且仅有两个不同的交点，则k 的取值范围是（ ）A ．[2,2]-B ．(1,0)(0,3)-C ．(2,4)D ．(1,4) 【答案】C【解析】当[0,]x π∈时，()sin 3sin 4sin f x x x x =+=，当(],2x ππ∈时，()sin 3sin 2sin f x x x x =+=-， 所以函数()f x 的图像如图所示，所以函数()f x 的图象与直线y k =有且仅有两个不同的交点时，(2,4)k ∈.故选：C【变式5-4】已知函数()1sin ,0,21cos ,0,2x x f x x x ⎧+<⎪⎪=⎨⎪+≥⎪⎩若()f x 在区间3,2a π⎡⎤-⎢⎥⎣⎦上至少有5个零点，()f x 在区间[],a π-上至多有5个零点，则正数a 的取值范围是（ ）A ．138,63ππ⎡⎤⎢⎥⎣⎦ B ．1310,63ππ⎡⎫⎪⎢⎣⎭ C ．1910,63ππ⎡⎫⎪⎢⎣⎭ D ．819,36ππ⎡⎤⎢⎥⎣⎦【答案】B【解析】因为方程1sin 2x =-在[),0π-上的解为56π-，6π-， 所以当()f x 在区间[],a π-上至多有5个零点时，100.3a π<<因为方程1cos 2x =-在30,2π⎡⎤⎢⎥⎣⎦上的解为23π，43π， 所以当()f x 在区间3,2a π⎡⎤-⎢⎥⎣⎦上至少有5个零点时，136a π-≤-，即136a π≥综上，正数a 的取值范围是1310,63ππ⎡⎫⎪⎢⎣⎭，故选：B。

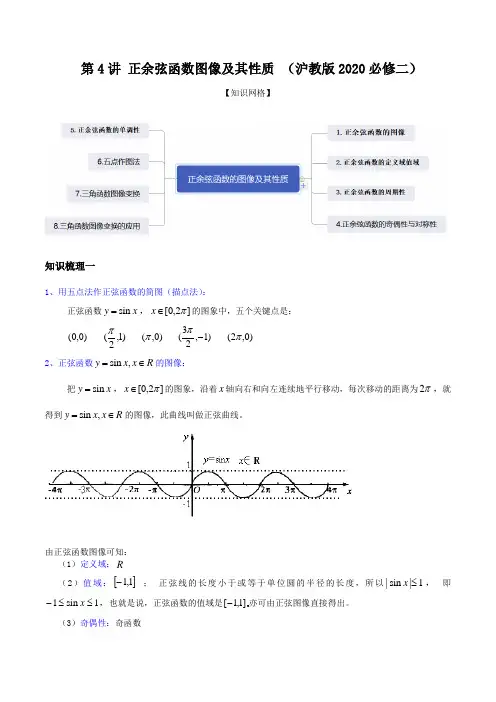
第4讲 正余弦函数图像及其性质 （沪教版2020必修二）【知识网格】知识梳理一1、用五点法作正弦函数的简图（描点法）：正弦函数x y sin =，]2,0[π∈x 的图象中，五个关键点是：)0,0( )1,2(π)0,(π )1,23(-π )0,2(π2、正弦函数R x x y ∈=,sin 的图像：把x y sin =，]2,0[π∈x 的图象，沿着x 轴向右和向左连续地平行移动，每次移动的距离为π2，就得到R x x y ∈=,sin 的图像，此曲线叫做正弦曲线。

由正弦函数图像可知：（1）定义域：R（2）值域：[]1,1- ； 正弦线的长度小于或等于单位圆的半径的长度，所以1|sin |≤x ， 即1sin 1≤≤-x ，也就是说，正弦函数的值域是1,1[-亦可由正弦图像直接得出。

（3）奇偶性：奇函数由x x sin )sin(-=-可知：x y sin =为奇函数，正弦曲线关于原点O 对称 （4）单调递增区间：z k k k ∈⎥⎦⎤⎢⎣⎡+-,22,22ππππ； （5）单调递减区间：z k k k ∈⎥⎦⎤⎢⎣⎡++,232,22ππππ； （6）对称中心：（0,πk ）； （7）对称轴：2ππ+=k x（8）最值：当且仅当,22ππ+=k x y 取最大值1max =y ；当且仅当,232ππ+=k x y 取最小值1min -=y 。

（9）最小正周期：π2=T一般地，对于函数)(x f ，如果存在一个非零常数T ，使得当x 取定义域内的每一个值时，都有)()(x f T x f =+，那么函数)(x f 就叫做周期函数，非零常数T 叫做这个函数的周期由此可知)0(2,,4,2,2,4,≠∈--k z k k 且πππππ 都是这两个函数的周期对于一个周期函数)(x f ，如果在它所有的周期中存在一个最小的正数，那么这个最小正数就叫做)(x f 的最小正周期根据上述定义，可知：正弦函数、余弦函数都是周期函数，)0(2≠∈k z k k 且π都是它的周期，最小正周期是π2 注意：1.周期函数定义域M x ∈，则必有M T x ∈+, 且若0>T ，则定义域无上界；0<T 则定义域无下界；2.“每一个值”只要有一个反例，则)(x f 就不为周期函数;3.T 往往是多值的（如x y sin =中 ,4,2,2,4,ππππ--都是周期）周期T 中最小的正数叫做)(x f 的最小正周期（有些周期函数没有最小正周期） 5、余弦函数R x x y ∈=,cos 的图像：（1）定义域：R （2）值域：[]1,1- （3）奇偶性：偶函数（4）单调递增区间：[]πππk k 2,2-，Z k ∈ （5）单调递减区间：[]Z k k k ∈+,2,2πππ （6）对称中心：（0,2ππ+k ）（7）对称轴：πk x =（8）最值：当且仅当,2πk x =y 取最大值1max =y ； 当且仅当,2ππ+=k x y 取最小值1min -=y 。

5.4.1 正弦函数、余弦函数的图像（基础知识+基本题型）知识点一 正弦函数的图象 1.正弦曲线的几何作法正弦函数sin ,y x x R 的图象如图，我们把正弦函数的图象叫做正弦曲线.如图，在直角坐标系的x 轴上取一点1O ，以1O 为圆心，单位长为半径作圆，从圆1O 与x 轴的交点A 起，把圆1O 分成12等份（份数越多，画出的图象越精确）.过圆1O 上各分点作x 轴的垂线，得到对应于0,,,,,2632等角的正弦线，相应地，再把x 轴上从0到2这一段分成12等份，把角x 的正弦线向右平移，使它的起点与x 轴上的点x 重合，再把这些正弦线的终点用光滑曲线连接起来，即得sin ,[0,2]y x x 的图象.2.用“五点法”作sin ,[0,2]y x x 的简图在函数sin ,[0,2]y x x 的图象上，起关键作用的点有五个：(0,0)，(,1)2，(,0)，3(,1)2，(2,0). 一般地，在精确度要求不高时，我们常常先找出这五个关键点，再用光滑的曲线将它们连接起来，就得到正弦函数在[0,2]上的简图.这种方法叫“五点法”.【提示】（1）“五点法”作三角函数图象的实质是分别找到函数图象的最高点、最低点及三个平衡点，这五个点大致确定了函数图象的位置与形状.（2）用“五点法”作sin ,[0,2]y x x 的图象后，将其向左右平移(每次2个单位长度)，可得出sin ,y x x R 的图象.知识点二 余弦函数的图象 1.利用图象变换作余弦函数的图象 由诱导公式六，有cos sin()2y x x .因此，将正弦函数sin ,y x x R 的图象向右平移2个单位长度，就得到函数sin()cos ,2y x x x R 的图象. 我们把余弦函数cos ,y x x R 的图象叫做余弦曲线，如图所示.2.用“五点法”作cos ,[0,2]y x x 的简图在函数cos ,[0,2]y x x 的图象上，起关键作用的点是它与x 轴的交点、函数图象的最高点和最低点，它们的坐标依次为：(0,1)，(,0)2，(,1)，3(,0)2，(2,1).用光滑的曲线将它们连接起来，就得到余弦函数在[0,2]上的简图.【提示】（1）作余弦函数图象时，可通过正弦函数的图象平移得到，但要注意平移的单位长度. （2）作x R 的余弦函数图象，可由cos ,[0,2]y x x 的图象左右平移得到，也可由 sin ,y x x R 的图象向左平移2个单位长度得到.考点一 通过图象变换作函数的图象 【例1】作函数32sin y x π⎛⎫=+⎪⎝⎭的图象. 解：3sin |cos |2y x x π⎛⎫=+= ⎪⎝⎭cos 22,Z 22,3cos 22,Z .22x k x k k x k x k k ππππππππ⎧⎛⎫-+≤≤+∈ ⎪⎪⎪⎝⎭=⎨⎛⎫⎪-+<<+∈ ⎪⎪⎝⎭⎩故|cos |y x =的图象实际就是cos y x =的图象在x 轴下方的部分翻折到x 轴上方后得到的图象，如图由于余弦函数的图象是利用诱导公式依据图象变换画出的，故掌握利用诱导公式化简三角函数式也是画三角函数图象的切入点。

三角函数正弦函数余弦函数的图象xx年xx月xx日•引言•正弦函数图像•余弦函数图像目录•正弦与余弦函数图像的对比•应用•结论01引言三角函数是数学中的基础知识正弦函数和余弦函数是三角函数的重要组成部分图象是数学中重要的表达方式之一课程背景研究目的和意义理解正弦函数和余弦函数的图象及性质掌握函数图象的绘制方法理解函数图象在实际问题中的应用本文将分为以下几个部分：正弦函数和余弦函数的定义、正弦函数和余弦函数的图象及性质、函数图象的绘制方法以及实际应用案例分析我们将通过观察图象来理解正弦函数和余弦函数的性质，并通过绘制函数图象来解决实际问题本文结构02正弦函数图像正弦函数sin(x)表示直角三角形中一个锐角的对边与斜边的比值。

定义域实数集，即x∈(-∞,∞)。

值域[-1,1]，即sin(x)∈[-1,1]。

1 2 3正弦函数的图像呈现出一种波动或振荡的形状，以原点为中心，左右对称。

图像形状正弦函数是周期性的，即对于任意的x∈(-∞,∞)，都有sin(x+2kπ)=sin(x)，其中k为任意整数。

周期性正弦函数的振幅为1，即正弦函数的取值范围在-1到1之间。

振幅奇偶性正弦函数是奇函数，即对于任意的x∈(-∞,∞)，都有sin(-x)=-sin(x)。

最大值最小值正弦函数的最小正周期为2π，即在2π的时间内完成一次完整的波动。

在每个周期内，正弦函数达到最大值1和最小值-1。

导数求导得sin&#39;(x)=cos(x)。

01020303余弦函数图像余弦定理c² = a² + b² - 2ab cos(C)余弦函数图像以y轴为对称轴，以原点为对称中心，取一段区间，可以是[0,π]或[-π/2,π/2]或[π/2,3π/2]等余弦函数cos(x) = 邻边/斜边 = (b²+c²-a²)/(2bc)余弦函数的图像是在y轴上，以原点为中心，向左右两侧同时对称延长的。