立体几何选择填空专练

立体几何选择填空压轴题专练A 组一、选择题1．如图，矩形ABCD 中， 2AB AD =， E 为边AB 的中点，将ADE ∆沿直线DE翻转成1A DE ∆（1A ∉平面ABCD ）．若M 、O 分别为线段1A C 、DE 的中点，则在ADE ∆翻转过程中，下列说法错误的是（ ）A. 与平面1A DE 垂直的直线必与直线BM 垂直B. 异面直线BM 与1A E 所成角是定值C. 一定存在某个位置，使DE MO ⊥D. 三棱锥1A ADE -外接球半径与棱AD 的长之比为定值 【答案】C【解析】取CD 的中点F ，连BF,MF,如下图：可知面MBF// 1A DE ,所以A 对。

取1A D 中点G,可知//EG BM ，如下图，可知B 对。

点A 关于直线D E 的对为F,则DE ⊥面1A AF ，即过O 与DE 垂直的直线在平面1A AF 上。

故C 错。

三棱锥1A ADE -外接球的球心即为O 点，所以外接球半径为22AD 。

故D 对。

选C 2．一个几何体的三视图如图所示，已知这个几何体的体积为103，则h =（ ）A ．32B ．3C ．33D ．53 【答案】B 【解析】由三视图可知该几何体是三棱锥，其中底面是矩形，边长为6，5，高为h ，所以体积15610333V h h =⨯⨯⨯=∴=3．如图，矩形ABCD 中,AB=2AD,E 为边AB 的中点，将△ADE 沿直线DE 翻折成△A 1DE ．若M 为线段A 1C 的中点，则在△ADE 翻折过程中，下面四个命题中不正确的是A ．｜BM ｜是定值B ．点M 在某个球面上运动C ．存在某个位置，使DE ⊥A 1 CD ．存在某个位置，使MB//平面A 1DE 【答案】C 【解析】取CD 中点F ，连接MF ，BF ，则MF//A 1D 且MF=21A 1D,FB//ED 且FB=ED 所以DE A MFB 1∠=∠，由余弦定理可得MB 2=MF 2+FB 2-2MF •FB •cos ∠MFB 是定值，所以 M 是在以B 为圆心，MB 为半径的球上，可得①②正确．由MF//A 1D 与 FB//ED 可得平面MBF ∥平面A 1DE ，可得④正确；A 1C 在平面ABCD 中的射影为AC ，AC 与DE 不垂直，可得③不正确．故答案为：①②④．4．如图，正四面体D ABC -的顶点A 、B 、C 分别在两两垂直的三条射线Ox ， Oy ，Oz 上，则在下列命题中，错误的是( ) A. O ABC -是正三棱锥B. 直线OB 与平面ACD 相交C. 直线CD 与平面ABC 所成的角的正弦值为32D. 异面直线AB 和CD 所成角是90︒ 【答案】C【解析】①如图ABCD 为正四面体， ∴△ABC 为等边三角形， 又∵OA 、OB 、OC 两两垂直， ∴OA ⊥面OBC ，∴OA ⊥BC ，过O 作底面ABC 的垂线，垂足为N ， 连接AN 交BC 于M ，由三垂线定理可知BC ⊥AM ， ∴M 为BC 中点，同理可证，连接CN 交AB 于P ，则P 为AB 中点， ∴N 为底面△ABC 中心，∴O ﹣ABC 是正三棱锥，故A 正确．②将正四面体ABCD 放入正方体中，如图所示，显然OB 与平面ACD 不平行． 则B 正确，③由上图知：直线CD 与平面ABC 6,则C 错误 ④异面直线AB 和CD 所成角是90︒，故D 正确. 二、填空题 5．（2017全国1卷理）如图，圆形纸片的圆心为O ，半径为5 cm ，该纸片上的等边三角形ABC 的中心为O 。

高三数学立体几何专项练习题及答案一、选择题1. 下列哪个几何体的所有面都是三角形？A. 正方体B. 圆柱体C. 正六面体D. 球体答案：C2. 一个有8个面的多面体，其中6个面是正方形，另外2个面是等边三角形，它的名字是？A. 正八面体B. 正十二面体C. 正二十面体D. 正二十四面体答案：C3. 空间中任意一点到四个角落连线的垂直距离相等的四棱锥称为？A. 正四棱锥B. 圆锥台C. 四棱锥D. 无法确定答案：C4. 任意多面体的面数与顶点数、棱数的关系是？A. 面数 + 顶点数 = 棱数 + 2B. 面数 + 棱数 = 顶点数 + 2C. 顶点数 + 棱数 = 面数 + 2D. 顶点数 + 面数 = 棱数 + 2答案：A5. 求下列多面体的棱数：（1）正六面体（2）正八面体（3）正十二面体答案：（1）正六面体的棱数为 12（2）正八面体的棱数为 24（3）正十二面体的棱数为 30二、填空题1. 下列说法正确的是：一棱锥没有底面时，它的底面是一个______。

答案：点2. 铅垂线是指从一个多面体的一个顶点到与它相对的棱上所作的垂线，它与该棱垂足的连线相交于该多面体的______上。

答案：中点3. 对正八面体，下列说法不正确的是：_____条对角线与_____两两垂直。

答案：六，相邻面三、计算题1. 一个棱锥的底面是一个边长为6cm的正三角形，其高为8cm。

求棱锥体积。

解答：底面积 S = (1/2) ×底边长 ×高 = (1/2) × 6 × 8 = 24 cm²棱锥体积 V = (1/3) × S ×高 = (1/3) × 24 × 8 = 64 cm³所以，棱锥的体积为64 cm³。

2. 一个正四棱锥的底面是一个边长为10cm的正方形，其高为12cm。

求四棱锥的体积。

解答：底面积 S = 边长² = 10² = 100 cm²四棱锥体积 V = (1/3) × S ×高 = (1/3) × 100 × 12 = 400 cm³所以，四棱锥的体积为400 cm³。

高中数学立体几何专项练习题及答案一、选择题1. 下面哪个选项不是描述柱体的特点？A. 体积恒定B. 底面形状不限C. 侧面是矩形D. 顶面和底面平行答案：A2. 如果一个四面体的一个顶点的对边垂直于底面，那么这个四面体是什么类型？A. 正方形四面体B. 倒立四面体C. 锥体D. 正方锥体答案：C3. 以下哪个选项正确描述了一个正方体的特点？A. 全部面都是正方形B. 12 条棱长度相同C. 8 个顶点D. 6 个面都是正方形答案：D4. 若长方体的高度是 6cm，底面积是 5cm²，底面对角线长为 a cm，那么 a 的值为多少？A. √11B. √29C. √31D. √41答案：C二、填空题1. 一个正方体的棱长为 4cm，它的体积是多少？答案：64cm³2. 一个球的表面积是100π cm²，那么它的半径是多少？答案：5cm3. 一个圆柱体的底面半径为 3cm，高度为 8cm，它的体积是多少？答案：72π cm³4. 一个圆锥的底面半径为 6cm，高度为 10cm，它的体积是多少？答案：120π cm³三、计算题1. 一个四棱锥的底面是边长为 5cm 的正方形，高度为 8cm，它的体积是多少？答案：单位为 cm³，计算过程如下：首先计算底面积：5cm * 5cm = 25cm²再计算体积：25cm² * 8cm / 3 = 200cm³2. 一个圆柱体的底面直径为 12cm，高度为 15cm，它的体积是多少？答案：单位为 cm³，计算过程如下：首先计算底面半径：12cm / 2 = 6cm再计算底面积：π * 6cm * 6cm = 36π cm²最后计算体积：36π cm² * 15cm = 540π cm³3. 一个球的直径为 8cm，它的体积是多少？答案：单位为 cm³，计算过程如下：首先计算半径：8cm / 2 = 4cm再计算体积：4/3 * π * 4cm * 4cm * 4cm = 268.08π cm³4. 一个圆锥的底面半径为 10cm，高度为 20cm，它的体积是多少？答案：单位为 cm³，计算过程如下：首先计算底面积：π * 10cm * 10cm = 100π cm²最后计算体积：100π cm² * 20cm / 3 = 2000π cm³四、解答题1. 若一个长方体的长度、宽度、高度分别为 a、b、c，它的表面积为多少？答案：单位为 cm²，计算过程如下：首先计算侧面积：2 * (a * b + a * c + b * c)再计算底面积：a * b最后计算表面积：2 * (a * b + a * c + b * c) + a * b2. 一个四棱锥的底面为边长为 a 的正三角形，高度为 h，求这个四棱锥的体积。

选填训练4答案一、单选题（本大题共8小题，共40.0分。

在每小题列出的选项中，选出符合题目的一项） 1. 如图，在四面体O −ABC 中，G 是底面△ABC 的重心，且OG ⃗⃗⃗⃗⃗⃗ =x OA ⃗⃗⃗⃗⃗ +y OB ⃗⃗⃗⃗⃗⃗ +z OC ⃗⃗⃗⃗⃗ ，则log 3|xyz|等于 ( )A. −3B. −1C. 1D. 3【答案】A 解：连结AG ，OG ⃗⃗⃗⃗⃗⃗ =OA ⃗⃗⃗⃗⃗ +AG ⃗⃗⃗⃗⃗ =OA ⃗⃗⃗⃗⃗ +13(AC ⃗⃗⃗⃗⃗ +AB ⃗⃗⃗⃗⃗ )=OA ⃗⃗⃗⃗⃗ +13(OC ⃗⃗⃗⃗⃗ −OA ⃗⃗⃗⃗⃗ +OB ⃗⃗⃗⃗⃗⃗ −OA ⃗⃗⃗⃗⃗ )=13OA ⃗⃗⃗⃗⃗ +13OB ⃗⃗⃗⃗⃗⃗ +13OC ⃗⃗⃗⃗⃗ =x OA ⃗⃗⃗⃗⃗ +y OB ⃗⃗⃗⃗⃗⃗ +z OC ⃗⃗⃗⃗⃗ ，∴x =y =z =13， 则log 3|xyz|=log 3127=−3．2. 在△ABC 中A =30°，AC =4，BC =a ，若△ABC 仅一个解时，则a 的取值范围是( )A. a ≥4B. a =2C. a ≥4或a =2D. 无法确定【答案】C解：当a =ACsin30°=4×12=2时，以C 为圆心，以a =2为半径画弧，与射线AD 只有唯一交点， 此时符合条件的三角形只有一个，当a ⩾4时，以C 为圆心以a 为半径画弧时，在从垂足到A 点之间得不到交点，交点只能在垂足外侧，三角形也是唯一的， ∴a ≥4或a =2，故选C ．3. 设两个向量e 1⃗⃗⃗ ，e 2⃗⃗⃗ 满足|e 1⃗⃗⃗ |=2，|e 2⃗⃗⃗ |=1，e 1⃗⃗⃗ ，e 2⃗⃗⃗ 之间的夹角为60°，若向量2t e 1⃗⃗⃗ +7e 2⃗⃗⃗ 与向量e 1⃗⃗⃗ +t e 2⃗⃗⃗ 的夹角为钝角，则实数t 的取值范围是( )A. (−7,−12)B. (−7,−√142)∪(−√142,−12) C. (−7,−√142)D. (−√142,−12)【答案】B解：由题意知(2t e 1⃗⃗⃗ +7e 2⃗⃗⃗ )·(e 1⃗⃗⃗ +t e 2⃗⃗⃗ )<0，即2t 2+15t +7<0，解得−7<t <−12．又由2t ·t −7≠0，得t ≠±√142，∴t ∈(−7,−√142)∪(−√142,−12). 故选B ．4. 已知向量a ⃗ =(1,2)，a ⃗ ·b ⃗ =10，|a ⃗ +b ⃗ |=5√2，b ⃗ 方向上的单位向量为e⃗ ，则向量a ⃗ 在 向量b ⃗ 上的投影向量为( ) A. 12e ⃗ B. 2e ⃗ C.125e⃗ D. 52e⃗ 【答案】B解：由a ⃗ =(1,2)可得：|a ⃗ |=√12+22=√5，由|a ⃗ +b|⃗⃗⃗ =5√2两边平方得：|a ⃗ |2+2a ⃗ ·b ⃗ +|b⃗ |2=(5√2)2=50，即：5+2×10+|b⃗ |2=50，解得：|b ⃗ |=5， 设a ⃗ 和b ⃗ 的夹角为θ，则cosθ=a⃗ ·b ⃗|a ⃗ |·|b⃗ |=10√5×5=2√55， 所以向量a ⃗ 在向量b ⃗ 上的投影向量为：|a ⃗ |cosθ·b⃗ |b ⃗ |=√5×2√55e ⃗ =2e ⃗ ．故选B ．5. 如图所示，在直三棱柱ABC −A 1B 1C 1中，AB ⊥AC ，AB =3,AC =AA 1=4，一只蚂蚁由顶点A 沿棱柱侧面经过棱BB 1爬到顶点C 1，蚂蚁爬行的最短距离为( )A. 4B. 4C.D.+【答案】B解：如图所示，把侧面展开，矩形对角线即为蚂蚁爬行的最短距离，∵AB ⊥AC ，AB =3，AC =AA 1=4，∴BC =√AB 2+AC 2=√32+42=5，由题已知AA 1=CC 1=4，∴蚂蚁爬行的最短距离=√(AB +BC )2+(CC 1)2=√(3+5)2+42=4√5，所以最小值为4√5，故选B ．6.在四棱锥P−ABCD中，侧面PAD为正三角形，底面ABCD为正方形，侧面PAD⊥底面ABCD,M为底面ABCD内的一个动点，且满足MP=MC，则点M在正方形ABCD内的轨迹为( )A. B. C. D.【答案】A解：根据题意可知PD=DC，则点D符合“M为底面ABCD内的一个动点，且满足MP=MC”，设AB的中点为N，因为侧面PAD⊥底面ABCD，侧面PAD∩底面ABCD=AD，AB⊥AD，AB⊂底面ABCD，所以AB⊥侧面PAD，又PA⊂侧面PAD，所以AB⊥PA，根据题目条件可知△PAN≌△CBN，∴PN=CN，点N也符合“M为底面ABCD内的一个动点，且满足MP=MC”，故动点M的轨迹肯定过点D和点N，而到点P与到点C的距离相等的点为线段PC 的垂直平分面，线段PC的垂直平分面与平面ABCD的交线是一直线.故选A．7.如图，直角梯形ABCD，AB//CD，∠ABC=90°，CD=2，AB=BC=1，E是边CD中点，△ADE沿AE翻折成四棱锥D′−ABCE，则点C到平面ABD′距离的最大值为( )A. 12B. √3−1 C. √22D. √63【答案】C解：直角梯形ABCD ，AB//CD ，∠ABC =90°，CD =2，AB =BC =1，E 是边CD 中点，△ADE 沿AE 翻折成四棱锥D′−ABCE ，当D′E ⊥CE 时，点C 到平面ABD′距离取最大值，∵D′E ⊥AE ，CE ∩AE =E ，CE ，AE ⊂平面ABCE ，∴D′E ⊥平面ABCE ， 以E 为原点，EC 为x 轴，EA 为y 轴，ED′为z 轴，建立空间直角坐标系，则A(0,1,0)，C(1,0,0)，D′(0,0,1)，B(1,1,0)， AB ⃗⃗⃗⃗⃗ =(1,0,0)，AC ⃗⃗⃗⃗⃗ =(1,−1,0)，AD′⃗⃗⃗⃗⃗⃗⃗ =(0,−1,1)， 设平面ABD′的法向量n⃗ =(x,y,z)，则{n ⃗ ⋅AB ⃗⃗⃗⃗⃗ =x =0n ⃗ ⋅AD′⃗⃗⃗⃗⃗⃗⃗ =−y +z =0，取y =1，得n ⃗ =(0,1,1)，∴点C 到平面ABD′距离的最大值为d =|AC ⃗⃗⃗⃗⃗ ⋅n ⃗⃗ ||n ⃗⃗ |=1√2=√22．故选C ．8. 在△ABC 中，有正弦定理：asinA =bsinB =csinC =定值，这个定值就是△ABC 的外接圆的直径．如图所示，△DEF 中，已知DE =DF ，点M 在直线EF 上从左到右运动(点M 不与E 、F 重合)，对于M 的每一个位置，记△DEM 的外接圆面积与△DMF 的外接圆面积的比值为λ，那么( )A. λ先变小再变大B. 仅当M 为线段EF 的中点时，λ取得最大值C. λ先变大再变小D. λ是一个定值【答案】D解：设△DEM 的外接圆半径为R 1，△DMF 的外接圆半径为R 2，则由题意，πR 12πR 22=λ，点M 在直线EF 上从左到右运动(点M 不与E 、F 重合)，对于M 的每一个位置，由正弦定理可得R 1=12×DE sin∠DME，R 2=12×DFsin∠DMF ，又DE =DF ，sin∠DME =sin∠DMF ， 可得R 1=R 2，可得λ=1．故选D ．二、多选题（本大题共4小题，共20.0分。

已知A1B1C1-ABC为直三棱柱，D为AC中点，O为BC中点，E在CC1上，
∠ACB=90°，AC=BC=CE=2，AA1=6.
（1）证明平面BDE∥AO；
（2）求二面角A-EB-D的大小；
（3）求三棱锥O-AA1D体积.
立测试001
ቤተ መጻሕፍቲ ባይዱ答案
一．选择题：(每题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
10．在一个 的二面角的一个平面内有一条直线与二面角的棱成角 ，则此直线与二面角的另一个平面所成角的大小为 ( )
Ａ． Ｂ． Ｃ． Ｄ．
11. 如图,E, F分别是正方形SD1DD2的边D1D,DD2的中点,
沿SE,SF,EF将其折成一个几何体,使D1,D,D2重合,记作
D.给出下列位置关系:①SD⊥面DEF; ②SE⊥面DEF;
由 ， ， ， ，
易得 ， ， ，
，
所以
18．解：（1） 在平面 上的射影 在 上， 面 。
故斜线 在平面 上的射影为 。
又 ， ，又 ，
面
（2）过 作 ，交 于 。
面 ， ， 面 故 的长就是点 到平面 的距离
， 面
在 中， ；
在 中，
在 中，由面积关系，得
（3）连结 ， 面 ， 是 在平面 的射影
其中所有真命题的序号是_______________。
三.解答题:（共74分，写出必要的解答过程）
17．(本小题满分10分)
如图，已知直棱柱 中，
， ， ， ， 是 的中点。
求证：
18．（本小题满分12分）
如图，在矩形 中， ， ，沿对角线 将 折起，使点 移到 点，且 在平面 上的射影 恰好在 上。

专题10立体几何选择填空题1．【2019年新课标3文科08】如图，点N 为正方形ABCD 的中心，△ECD 为正三角形，平面ECD ⊥平面ABCD ，M 是线段ED 的中点，则（ ）A ．BM ＝EN ，且直线BM ，EN 是相交直线B ．BM ≠EN ，且直线BM ，EN 是相交直线C ．BM ＝EN ，且直线BM ，EN 是异面直线D ．BM ≠EN ，且直线BM ，EN 是异面直线2．【2019年新课标2文科07】设α，β为两个平面，则α∥β的充要条件是（）A．α内有无数条直线与β平行B．α内有两条相交直线与β平行C．α，β平行于同一条直线D．α，β垂直于同一平面3．【2018年新课标2文科09】在正方体ABCD﹣A1B1C1D1中，E为棱CC1的中点，则异面直线AE与CD 所成角的正切值为（）A．B．C．D．4．【2018年新课标1文科05】已知圆柱的上、下底面的中心分别为O1，O2，过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为（）A．12πB．12πC．8πD．10π5．【2018年新课标1文科09】某圆柱的高为2，底面周长为16，其三视图如图．圆柱表面上的点M在正视图上的对应点为A，圆柱表面上的点N在左视图上的对应点为B，则在此圆柱侧面上，从M到N的路径中，最短路径的长度为（）A．2B．2C．3 D．26．【2018年新课标1文科10】在长方体ABCD﹣A1B1C1D1中，AB＝BC＝2，AC1与平面BB1C1C所成的角为30°，则该长方体的体积为（）A．8 B．6C．8D．87．【2018年新课标3文科03】中国古建筑借助榫卯将木构件连接起来．构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是（）A．B．C． D．8．【2018年新课标3文科12】设A，B，C，D是同一个半径为4的球的球面上四点，△ABC为等边三角形且面积为9，则三棱锥D﹣ABC体积的最大值为（）A．12B．18C．24D．549．【2018年北京文科06】某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为（）A．1 B．2 C．3 D．410．【2017年新课标1文科06】如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是（）A．B．C．D．11．【2017年新课标2文科06】如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为（）A．90πB．63πC．42πD．36π12．【2017年新课标3文科09】已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为（）A．πB．C．D．13．【2017年新课标3文科10】在正方体ABCD﹣A1B1C1D1中，E为棱CD的中点，则（）A．A1E⊥DC1B．A1E⊥BD C．A1E⊥BC1D．A1E⊥AC14．【2017年北京文科06】某三棱锥的三视图如图所示，则该三棱锥的体积为（）A．60 B．30 C．20 D．1015．【2019年天津文科12】已知四棱锥的底面是边长为的正方形，侧棱长均为．若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点，另一个底面的圆心为四棱锥底面的中心，则该圆柱的体积为．16．【2019年新课标3文科16】学生到工厂劳动实践，利用3D打印技术制作模型．如图，该模型为长方体ABCD﹣A1B1C1D1挖去四棱锥O﹣EFGH后所得的几何体，其中O为长方体的中心，E，F，G，H分别为所在棱的中点，AB＝BC＝6cm，AA1＝4cm.3D打印所用原料密度为0.9g/cm3．不考虑打印损耗，制作该模型所需原料的质量为g．17．【2019年新课标1文科16】已知∠ACB＝90°，P为平面ABC外一点，PC＝2，点P到∠ACB两边AC，BC的距离均为，那么P到平面ABC的距离为．18．【2019年北京文科12】某几何体是由一个正方体去掉一个四棱柱所得，其三视图如图所示．如果网格纸上小正方形的边长为l，那么该几何体的体积为．19．【2019年北京文科13】已知l，m是平面α外的两条不同直线．给出下列三个论断：①l⊥m；②m∥α；③l⊥α．以其中的两个论断作为条件，余下的一个论断作为结论，写出一个正确的命题：．20．【2018年新课标2文科16】已知圆锥的顶点为S，母线SA，SB互相垂直，SA与圆锥底面所成角为30°．若△SAB的面积为8，则该圆锥的体积为．21．【2018年天津文科11】如图，已知正方体ABCD﹣A1B1C1D1的棱长为1，则四棱锥A1﹣BB1D1D的体积为．22．【2017年新课标2文科15】长方体的长、宽、高分别为3，2，1，其顶点都在球O的球面上，则球O 的表面积为．23．【2017年新课标1文科16】已知三棱锥S﹣ABC的所有顶点都在球O的球面上，SC是球O的直径．若平面SCA⊥平面SCB，SA＝AC，SB＝BC，三棱锥S﹣ABC的体积为9，则球O的表面积为．24．【2017年天津文科11】已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18，则这个球的体积为．1．【2019年湖北省武汉市高考数学(5月份)模拟】已知长方体全部棱长的和为36，表面积为52，则其体对角线的长为（）A．4B C．D．2．【湖北省黄冈中学2019届高三第三次模拟】已知正方体1111ABCD A B C D -的棱长为1，在对角线1A D 上取点M ，在1CD 上取点N ，使得线段MN 平行于对角面11A ACC ，则||MN 的最小值为（ ）A ．1BC ．2D ．33．【广东省2019届高考适应性考试】平面四边形ABCD 中，AD AB ==CD CB ==AD AB ⊥，现将ABD ∆沿对角线BD 翻折成A BD '∆，则在A BD '∆折起至转到平面BCD 的过程中，直线A C '与平面BCD 所成最大角的正切值为（ ）A ．2B ．12C D ．34．【山东省淄博市部分学校2019届高三5月阶段性检测】在正方体1111ABCD A B C D -中，点P 在侧面11BCC B 及其边界上运动，并且保持1AP BD ⊥，则动点P 的轨迹为 （ ）A ．线段1BC B ．线段1BCC ．1BB 的中点与1CC 的中点连成的线段D ．BC 的中点与11B C 的中点连成的线段5．【四川省名校联盟2019届高考模拟信息卷（一)】已知一个几何体的三视图如图所示，其中俯视图是一个边长为2的正方形，则该几何体的表面积为（ ）A ．223B ．20C ．20+D ．20+6．【山东省淄博市部分学校2019届高三5月阶段性检测】如图，在正方体1111ABCD A B C D -中，点F 是线段1BC 上的动点，则下列说法错误．．的是（ ）A ．当点F 移动至1BC 中点时，直线1A F 与平面1BDC 所成角最大且为60B ．无论点F 在1BC 上怎么移动，都有11A F BD ⊥C ．当点F 移动至1BC 中点时，才有1A F 与1BD 相交于一点，记为点E ，且12A EEF= D ．无论点F 在1BC 上怎么移动，异面直线1A F 与CD 所成角都不可能是307．【山东省栖霞市2019届高三高考模拟卷】已知P ，A ，B ，C ，D 是球O 的球面上的五个点，四边形ABCD 为梯形，//AD BC ，2AB DC AD ===，4BC PA ==，PA ⊥面ABCD ，则球O 的体积为（ ）A ．3B ．3C ．D ．16π8．【广东省东莞市2019届高三第二学期高考冲刺试题】如图画出的是某几何体的三视图，网格纸上小正方形的边长为1，则该几何体的体积为（ ）A ．253πB ．263πC ．223πD ．233π9．【河南省百校联盟2019届高三考前仿真试卷】阳马，中国古代算数中的一种几何形体，是底面长方形，两个三角面与底面垂直的四棱锥体，在阳马P ABCD -中，PC 为阳马P ABCD -中最长的棱，1,2,3AB AD PC ===，若在阳马P ABCD -的外接球内部随机取一点，则该点位阳马内的概率为（ ） A ．127πB ．427πC ．827πD ．49π10．【湖南省长沙市湖南师范大学附属中学2019届高三高考模拟（二)】已知平面α平面β=直线l ，点A 、C α∈，点B 、D β∈，且A 、B 、C 、D l ∉，点M 、N 分别是线段AB 、CD 的中点，则下列说法正确的是（ ）A ．当2CD AB =时，M 、N 不可能重合B ．M 、N 可能重合，但此时直线AC 与l 不可能相交 C ．当直线AB 、CD 相交，且//AC l 时，BD 可与l 相交 D ．当直线AB 、CD 异面时，MN 可能与l 平行11．【山东省临沂市2019届高三模拟考试（三模)】如图是某几何体的三视图，则过该几何体顶点的所有截面中，最大截面的面积是（ ）A ．2BC D ．112．【江西省抚州市临川第一中学2019届高三下学期考前模拟】已知如图正方体1111ABCD A B C D -中，P 为棱1CC 上异于其中点的动点，Q 为棱1AA 的中点，设直线m 为平面BDP 与平面11B D P 的交线，以下关系中正确的是（ ）A ．1//m D QB ．1m Q B ⊥C ．//m 平面11BD QD ．m ⊥平面11ABB A13．【山东省日照市2019届高三5月校际联合考试】如图，三棱锥A BCD -的项点,,,A B C D 都在同一球面上，BD 过球心O ，BD ABC =∆是边长为4的等边三角形，点,P Q 分别为线段BC AO ,上的动点（不含端点），且AP CQ =，则三棱锥P QOC -体积的最大值为______．14．【天津市和平区2018-2019学年度第二学期高三年级第三次质量调查】已知两条不重合的直线m ，n ，两个不重合的平面α，β，有下列四个命题： ①若m n ∥，α⊂m ，则n α∥； ②若n α⊥，m β⊥，且m n ∥，则αβ；③若α⊂m ，n α⊂，β∥m ，n β∥，则αβ；④若αβ⊥，m αβ=，且n β⊂，n m ⊥，则n α⊥．其中所有正确命题的序号为______．15．【安徽省黄山市2019届高三毕业班第三次质量检测】连接正方体每个面的中心构成一个正八面体，则该八面体的外接球与内切球体积之比为______．16．【江苏省七市2019届高三第三次调研】已知直角梯形ABCD 中，AB ∥CD ，AB ⊥BC ，AB=3 cm ，BC=1 cm ，CD=2 cm ．将此直角梯形绕AB 边所在的直线旋转一周，由此形成的几何体的体积为____cm 3．17．【山东省威海市2019届高三二模考试】直三棱柱111ABC A B C -中，190,2BC A A A ︒∠==，设其外接球的球心为O ，已知三棱锥O ABC -的体积为1，则球O 表面积的最小值为__________．18．【湖南省岳阳市第一中学2019届高三第一次模拟】记{}()min ,()a ab a b b a b ≤⎧=⎨>⎩，已知矩形ABCD 中，AB=2AD ，E 是边AB 的中点，将ADE 沿DE 翻折至A D E '''△（A '∉平面BCD ），记二面角A BC D '--为α，二面角A CD E '--为β，二面角A DE C '--为γ，二面角A BE D '--为θ，则{}min ,,,αβγθ=____.19．【四川省成都七中2019届高三5月高考模拟测试】如图所示，正方体1111ABCD A B C D -的边长为2，过1BD 的截面的面积为S ，则S 的最小值为_______．20．【四川省内江市2019届高三第三次模拟】如图所示，在中，，在边上任取一点，并将沿直线折起，使平面平面，则折叠后两点间距离的最小值为__________．1．两个半径都是2的球O 1和球O 2相切，且它们与直二面角α﹣l ﹣β的两个半平面都相切，另有一个半径为r 的小球O 与这个二面角的两个半平面均相切，同时与球O 1和球O 2都相切，则r 的值为 ．2．已知（a1，a2，a3），（b1，b2，b3），且||＝3，||＝4，12，则3．如图，在正方体ABCD﹣A1B1C1D1中，点O为线段BD的中点．设点P在线段CC1上，直线OP与平面A1BD所成的角为α，则sinα的取值范围是．4．记min{a，b}，已知矩形ABCD中，AB＝2AD，E是边AB的中点，将△ADE沿DE翻折至△A'D'E'（A'∉平面BCD），记二面角A'﹣BC﹣D为α，二面角A'﹣CD﹣E为β，二面角A'﹣DE﹣C为γ，二面角A'﹣BE﹣D为θ，则min{α，β，γ，θ}＝．5．如图，直线l⊥平面α，垂足为O，已知△ABC中，∠ABC为直角，AB＝2，BC＝1，该直角三角形做符合以下条件的自由运动：（1）A∈l，（2）B∈α．则C、O两点间的最大距离为．。

立体几何考察试题及答案一、选择题1. 若直线l与平面α垂直，则直线l与平面α内任意直线的关系是（）。

A. 相交B. 平行C. 异面D. 垂直答案：D2. 已知一个正四面体的棱长为a，求其体积。

A. \( \frac{a^3 \sqrt{2}}{12} \)B. \( \frac{a^3 \sqrt{2}}{6} \)C. \( \frac{a^3 \sqrt{3}}{12} \)D. \( \frac{a^3 \sqrt{3}}{6} \)答案：C二、填空题1. 已知一个长方体的长、宽、高分别为a、b、c，则其对角线的长度为 \( \sqrt{a^2 + b^2 + c^2} \)。

2. 一个球的半径为r，则其表面积为 \( 4\pi r^2 \)。

三、解答题1. 已知一个圆锥的底面半径为r，高为h，求其体积。

解：圆锥的体积公式为 \( V = \frac{1}{3}\pi r^2 h \)。

答：圆锥的体积为 \( \frac{1}{3}\pi r^2 h \)。

2. 已知一个圆柱的底面半径为r，高为h，求其侧面积。

解：圆柱的侧面积公式为 \( A = 2\pi rh \)。

答：圆柱的侧面积为 \( 2\pi rh \)。

四、证明题1. 证明：若直线l与平面α内的两条直线m和n都垂直，则直线l与平面α垂直。

证明：设直线m和n在平面α内的交点为O，由于直线l与m、n都垂直，根据直线与平面垂直的判定定理，直线l与平面α垂直。

答：直线l与平面α垂直。

2. 证明：若两个平面α和β的交线为l，直线m在平面α内且与l平行，直线n在平面β内且与l平行，则直线m与直线n平行。

证明：设直线m与直线n的交点为P，由于m在平面α内且与l平行，n在平面β内且与l平行，根据平面与平面平行的性质，直线m与直线n平行。

答：直线m与直线n平行。

立体几何试题一、选择题： 1．下列命题中正确命题的个数是（ ）⑴ 三点确定一个平面 ⑵ 若点P 不在平面α内，A 、B 、C 三点都在平面α内,则P 、A 、B 、C 四点不在同一平面内⑶ 两两相交的三条直线在同一平面内 ⑷ 两组对边分别相等的四边形是平行四边形A.0B.1C.2 D 。

3 答案：A 2．已知异面直线a 和b 所成的角为︒50，P 为空间一定点，则过点P 且与a 、b 所成的角都是︒30的直线条数有且仅有 （ ） A 。

1条 B 。

2条 C 。

3条 D 。

4条 答案：B 3．已知直线⊥l 平面α,直线⊂m 平面β，下列四个命题中正确的是 （ ） （1) 若βα//，则m l ⊥ (2） 若βα⊥,则m l //（3） 若m l //，则βα⊥ （4) 若m l ⊥,则βα//A.（3)与（4）B.（1)与（3）C.（2）与(4)D.（1）与(2) 答案:B 4．已知m 、n 为异面直线，⊂m 平面α，⊂n 平面β，l =βα ，则l （ ）A.与m 、n 都相交B.与m 、n 中至少一条相交C.与m 、n 都不相交D.至多与m 、n 中的一条相交答案：B5．设集合A=｛直线}，B=｛平面}，B A C =，若A a ∈，B b ∈，C c ∈,则下列命题中的真命题是（ ) A. c a b a b c ⊥⇒⎭⎬⎫⊥// B.c a c b b a //⇒⎭⎬⎫⊥⊥C. c a b c b a //////⇒⎭⎬⎫ D 。

c a b c b a ⊥⇒⎭⎬⎫⊥//答案：A6．已知a 、b 为异面直线,点A 、B 在直线a 上，点C 、D 在直线b 上，且AC=AD,BC=BD,则直线a 、b所成的角为 ( ） A 。

︒90 B 。

︒60 C 。

︒45 D 。

︒30 答案：A7．下列四个命题中正确命题的个数是（ )有四个相邻侧面互相垂直的棱柱是直棱柱各侧面都是正方形的四棱柱是正方体底面是正三角形，各侧面都是等腰三角形的三棱锥是正三棱锥A.1个B.2个C.3个D 。

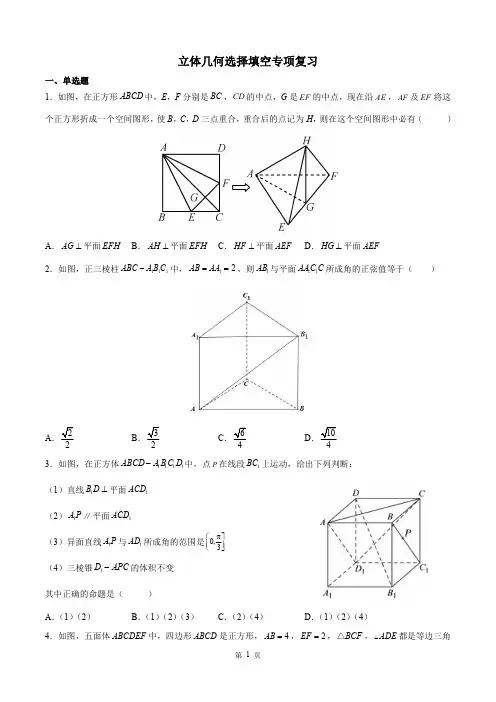
立体几何选择填空专项复习一、单选题1．如图，在正方形ABCD 中，E ，F 分别是BC ，CD 的中点，G 是EF 的中点，现在沿AE ，AF 及EF 将这个正方形折成一个空间图形，使B ，C ，D 三点重合，重合后的点记为H ，则在这个空间图形中必有（）A ．AG ⊥平面EFHB ．AH ⊥平面EFHC ．HF ⊥平面AEFD ．HG ⊥平面AEF2．如图，正三棱柱111ABC A B C -中，12AB AA ==，则1AB 与平面11AAC C 所成角的正弦值等于（）A 22B ．32C ．4D ．1043．如图，在正方体1111ABCD A B C D -中，点P 在线段1BC 上运动，给出下列判断：（1）直线1B D ⊥平面1ACD （2）1A P ∥平面1ACD （3）异面直线1A P 与1AD 所成角的范围是π0,3⎛⎤⎥⎝⎦（4）三棱锥1D APC -的体积不变其中正确的命题是（）A ．（1）（2）B ．（1）（2）（3）C ．（2）（4）D ．（1）（2）（4）4．如图，五面体ABCDEF 中，四边形ABCD 是正方形，4AB =，2EF =，BCF △，ADE 都是等边三角形，则五面体ABCDEF 的体积为（）AB C D ．5．如图，矩形ABCD 是圆柱12O O 的轴截面，2AB =，3AD =，点E 在上底面圆周上，且 2ECDE =，则异面直线AE 与2O C 所成角的余弦值为（）A B ．1920C ．4950D ．15二、多选题6．如图，在矩形ABCD 中，3AB =，4=AD ，将ABC 沿对角线AC 进行翻折，得到三棱锥B ACD -，则下列说法正确的是（）A ．在翻折过程中，三棱锥B ACD -的体积最大为245B ．在翻折过程中，三棱锥B ACD -的外接球的表面积为定值C ．在翻折过程中，存在某个位置使得BC AD ⊥D ．在翻折过程中，存在某个位置使得BD AC⊥7．如图，正方体1111ABCD A B C D -的棱长为a ，线段11B D 上有两个动点E ，F ，且22EF a =.则下列结论正确的是（）A ．当E 与1D 重合时，异面直线AE 与BF 所成的角为3πB ．三棱锥B AEF -的体积为定值C ．EF 在平面11ABB A 内的射影长为12aD ．当E 向1D 运动时，二面角A EF B --的平面角保持不变8．如图，正方体1111ABCD A B C D -的棱长为2，,,E F G 分别为11,,BC CC BB 的中点．则下列结论正确的是（）A ．直线1DB 与平面AEF 垂直B ．直线1A G 与平面AEF 平行C ．三棱锥D AEF -的体积为23D ．点D 到平面AEF 的距离为439．如图，正方体1111ABCD A B C D -的棱长为1，,E F 分别为11,BACC 上的动点，且11||||A E C FEB FC = ，则（）A ．直线//EF 平面ABCDB ．二面角E CF D --为定值C ．直线EF 与平面1A DC 所成角最小为30°D ．三棱锥1D DEF -的体积为定值10．如图，在四棱锥A BCED -中，已知4EC BC AC ===，1BD =，且AC EC ⊥，AC BC ⊥，BC EC ⊥，BC BD ⊥.取BC 的中点O ，过点O 作OQ DE ⊥于点Q ，则（）A ．OD OE ⊥B ．四棱锥A BCED -的体积为40C ．BQ ⊥平面ACQD ．AQ BQ⊥11．如图，正方体1111ABCD A B C D -中，E ，F 分别为11B C ，1BB 的中点，G 为侧面11ADD A 内一点，且满足11C GD BGA ∠=∠，则下列说法正确的是（）A ．1D F CE⊥B ．1EF B G⊥C ．存在点G ，使平面EFG //平面1ACD D ．三棱锥1B EFG -的体积为定值12．在四边形ABCD 中(如图1所示)，AB AD =，45ABD ∠=︒，2BC BD CD ===，将四边形ABCD 沿对角线BD 折成四面体A BCD '(如图2所示)，使得90A BC '∠=︒，E ，F ，G 分别为棱BC ，A D '，A B '的中点，连接EF ，CG ，则下列结论正确的是()A ．A C BD'⊥B ．直线EF 与CG 45C ．C ，E ，F ，G 四点共面D ．四面体A BCD '外接球的表面积为8π三、双空题13．如图，在四棱锥P ABCD -中，底面ABCD 为正方形，PA ⊥底面ABCD ，2PA AB ==，E 为线段PB 的中点，F 为线段BC 上的动点，平面AEF 与平面PBC ____________（填“垂直”或“不垂直”）；AEF 的面积的最大值为_____________．四、填空题14．如图，在正方体1111ABCD A B C D -中，过点A 且与直线1BD 垂直的所有面对角线的条数为___________.15．如图，在边长为2的正方体1111ABCD A B C D -中，E 、F 分别为棱CD 、1DD 的中点，则平面BEF 截该正方体所得截面的面积为__________.16．如图，四边形ABCD是边长为2的正方形，ED⊥平面ABCD，FC⊥平面ABCD，ED＝2FC＝2，则异面直线AE与BF所成角的余弦值为________.参考答案：1．B 【详解】解：根据折叠前后,AH HE AH HF ⊥⊥不变，可得AH ⊥平面EFH ，故B 正确；因为过点A 只有一条直线与平面EFH 垂直，故A 不正确；因为,,AG EF EF GH AG GH G ⊥⊥= ，所以EF ⊥平面HAG ，又EF ⊂平面AEF ，所以平面HAG ⊥平面AEF ，过点H 作直线垂直于平面AEF ，该直线一定在平面HAG 内，故C 不正确；因为HG 不垂直于AG ，所以HG ⊥平面AEF 不正确，故D 不正确.故选：B ．2．C 【详解】取11AC 中点D ，连接1B D ，AD ，在正三棱柱111ABC A B C -中，底面111A B C 是正三角形，∴111B D A C ^，又∵1CC ⊥底面111A B C ，∴11CC B D ⊥，又1111CC AC C ⋂=，∴1B D ⊥平面11AAC C ，∴1B AD Ð为1AB 与平面11AAC C所成角，由题意，1B D ==1AB ==1Rt B AD △中，111sin B D B AD AB ∠=故选：C 3．D 【详解】对于选项A ，连接BD ,根据正方体的性质，∵1BB ⊥ABCD ,且AC ⊂面ABCD ，∴1BB AC ⊥,又∵BD AC ⊥,∴AC ⊥面1BB D ,∴1AC B D ⊥,连接1A D ,根据正方体的性质，∵11A B ⊥11A D DA ,且1AD ⊂面11A D DA ，∴111A B AD ⊥;又∵11AD A D ⊥,∴1AD ⊥面11A B D ,∴11AD B D ⊥,∴直线1B D ⊥平面1ACD 故（1）正确；对于选项B 中，连接111,A B AC ，在正方体中，∵AC ∥11AC ,且AC ⊂平面1ACD ，11A C ⊂/平面1ACD ，∴11A C ∥平面1ACD ，同理可证1BC ∥平面1ACD ,又∵11A C 、1BC ⊂平面11BAC ，且1111=AC BC C ,∴平面11//BA C 平面1ACD ，又∵1A P ⊂平面11BAC ，∴1//AP 平面1ACD ，故（2）正确；对于选项C ，当P 与线段1BC 的B 端重合时，异面直线1A P 与1AD 所成角为11A BC ∠,∵△11A BC 为等边三角形，∴11π3BC A =∠；当P 与线段1BC 的1C 端重合时，异面直线1A P 与1AD 所成角为11AC B ∠,∵△11A BC 为等边三角形，∴11π3AC B ∠=；∴当P 与线段1BC 的中点重合时，1A P 与1AD 所成角取最大值,∴11A PC ∠为异面直线1A P 与1AD 所成角，又∵111A B AC =,且P 为线段1BC 的中点，∴11π2A PC ∠=,故1A P 与1AD 所成角的范围是ππ,32⎡⎤⎢⎥⎣⎦，故（3）错误；对于选项D 中，11D APC P ACD V V --=，∵1BC ∥1AD ,且1BC ⊂/平面1AD C ,1AD ⊂平面1AD C ∴1BC ∥平面1AD C ，∴点P 到平面1ACD 的距离不变，且1ACD △的面积不变，所以三棱锥1P ACD -的体积不变，故（4）正确；综上（1）（2）（4）正确.故选：D.4．B 【详解】如图，过点F 作FH AB ⊥于点H ，FS CD ⊥于点S ，过点E 作EG AB ⊥于点G ，EQ CD ⊥于点Q ，连接HS ，CQ ，则2ABCDEF F BCSH HSF GQE V V V --=+五面体四棱锥三棱柱.根据五面体的结构特征，将五面体的体积转化为两个相同的四棱锥和一个三棱柱的体积之和过点F 作FM HS ⊥于点M ，则易知FM ⊥平面ABCD ，22222211FM FH HM FB HB HM =-=--=，∴FM =1411433F BCSH V -=⨯=四棱锥，1422HSF GQE V -=⨯=三棱柱，故811201133ABCDEF V =+=五面体.故选：B 5．B 【详解】根据题意可以2O 为坐标原点，2O B ，21O O 所在直线分别为y ，z 轴建立如图所示的空间直角坐标系，则()20,0,0O ，()0,1,0A -，()0,1,3C ，31,322E ⎛⎫- ⎪ ⎪⎝⎭，故31,,322AE ⎛⎫= ⎪ ⎪⎝⎭ ，()20,1,3O C = ，故22219192cos ,20AE O CAE O C AE O C+⋅==⋅，故异面直线AE 与2O C 所成角的余弦值为1920，故选：B.6．AB 【详解】解：由题知，当平面BAC ⊥平面ACD 时，三棱锥B ACD -的体积最大，此时111224343255B ACD V -=⨯⨯⨯⨯=，故选项A 正确.取AC 的中点E ，连接BE ，DE ，则52DE AE CE BE ====，所以三棱锥B ACD -的外接球是以点E 为球心，52为半径的球，则该三棱锥外接球的表面积254π25π2S ⎛⎫=⨯= ⎪⎝⎭，故选项B 正确.假设BC AD ⊥，又BC AB ⊥，AB AD A ⋂=，,AB AD ⊂平面BAD ，所以BC ⊥平面BAD .又BD ⊂平面BAD ，所以BC BD ⊥，则在Rt BCD 中，斜边CD 的长度要大于4，这与3CD =矛盾，故选项C 错误.假设BD AC ⊥，过点D 作DF AC ⊥于点F ，连接BF .由于BD DF D =I ，,BD DF ⊂平面BDF ，所以AC ⊥平面BDF .又BF ⊂平面BDF ，所以AC BF ⊥，所以125BF DF ==.又CF CF =，90CFB CFD ∠=∠=︒，所以BCF △≌DCF ，所以BC CD =，这与4BC =，3CD =矛盾，故选项D 错误.故选：AB7．BCD 【详解】A ：当E 与1D 重合时，因为22EF a =，此时F 为11B D 的中点，记BD 中点为O ，连接1D O ，由正方体性质可知，11//,BO D F BO D F =，所以四边形1BOD F 为平行四边形，所以1//D O BF ，又22126()22a a D O a =+=，1AD 2a =，22a AO =，所以222132322cos 26222a a a AD O a a+-∠==⨯⨯，错误；B ：B AEF A BEF V V --=，易知点A 到平面11BB D D 的距离和点B 到直线11B D 的距离为定值，所以三棱锥A BEF -的体积为定值，正确；C ：易知1114A B D π∠=，EF 在平面11ABB A 内的射影在11A B 上，所以射影长为2cos 242a aπ⨯=，正确；D ：二面角A EF B --，即为二面角11A B D B --，显然其平面角不变，正确.故选：BCD8．BCD 【详解】如图，以D 点为坐标原点，以DA 为x 轴，以DC 为y 轴，以1DD 为z 轴，建立空间直角坐标系，则11(0,0,0),(2,2,2),(2,0,0),(1,2,0),(0,2,1),(2,0,2),(2,2,1)D B A E F A G ,对于A,1(2,2,2),(1,2,0),(2,2,1)DB AE AF ==-=-,设平面AEF 的法向量为(,,)n x y z = ，则20220n AE x y n AF x y z ⎧⋅=-+=⎨⋅=-++=⎩，可取(2,1,2)n =，而1(2,2,2)DB = ，与(2,1,2)n = 不平行，故直线1DB 与平面AEF 不垂直，故A 错；对于B ，1(0,2,1)AG =- ,平面AEF 的法向量为(2,1,2)n = ,()()10,2,12,1,20AG n ⋅=-⋅= ,1A G 不在平面AEF 内,故直线1A G 与平面AEF 平行，故B 正确；对于C ，11122213323D AEF F DAE DAE V V S FC --==⨯=⨯⨯⨯⨯= ,故C 正确；对于D ，(2,0,0)DA = ,平面AEF 的法向量为(2,1,2)n = ,,故点D 到平面AEF的距离为||23||n DA d n ⋅===，故D 正确，故选：BCD 9．ACD 【详解】对于A ，连接1BC 、11AC 、AC ，并取1BC 上一点H ，使得H 满足111||||||A E C F C H EB FC HB == ，从而可知//HF BC ,11//HE AC ,又11//AC AC，所以//HE AC ，又HE HF H = ,AC BC C = ,,HE HF ⊂平面EHF ,,AC BC ⊂平面ABCD ,所以平面//EHF 平面ABCD ，又EF ⊂平面EHF ，所以直线//EF 平面ABCD ，故A 正确；对于B 、C ，建立如下图所示的空间直角坐标系，并设正方体的棱长为1，则(0,0,0)D ，(1,1,0)B ，(0,1,0)C ，1(1,0,1)A ，1(0,1,1)C ，由11||||A E C F EB FC = ，令11||||||||BE CF t BA CC == （其中(0,1]t ∈），可得(1,1,)E t t -，(0,1,)F t ，则(1,,0)EF t =- ，(0,0,)CF t = ，(0,1,0)DC = ，1(1,0,1)DA = ，设平面ECF 的法向量111(,,)m x y z = ，则有11100x ty z -+=⎧⎨=⎩，可取(,1,0)m t = ，设平面1A DC 的法向量222(,,)n x y z = ，则有22200y x z =⎧⎨+=⎩，可取(1,0,1)n =- ，设平面ECF 与平面1A DC 的法向量的夹角为α，则有2cos ||||21m n m n t α⋅=⨯⨯+ B 不正确；设直线EF 与平面1A DC 所成角θ，则2211sin |cos ,|2122n EF t t θ=〈〉==⨯++ 显然当1t =时，sin θ有最小值12，此时直线EF 与平面1A DC 所成角最小，为30°，故C 正确；对于D ，易知11112DD F DCC D S S = 正方形为定值，1//A B 平面11DCC D ，所以点E 到平面11DCC D 的距离也为定值，因此11D DEF E DD F V V --=为定值，故D 正确.故选：ACD10．ACD【详解】如图建立空间直角坐标系，则(0,2,0),(0,4,1),(0,0,4),(0,4,0),(4,0,0),(0,0,0)O D E B A C ,则(0,4,3)DE →=-,(0,2,1),(0,2,4)OD OE →→==-,设(0,4,3)DQ λDE λλ→→==-,则(0,44,13)Q λλ-+,故(0,24,13)OQ λλ→=-+OQ DE ⊥ ，0OQ DE →→∴⋅=,0816390λλ∴-+++=，解得15λ=，即168(0,,)55Q ,48168(0,,(4,,5555BQ AQ →→∴=-=-,002(2)140OD OE →→⋅=⨯+⨯-+⨯= ,OD OE ∴⊥，故A 正确；因为直角梯形BCED 的面积()(41)41022EC BD CB S +⋅+⨯===，,,AC CE AC BC CE BC C ⊥⊥⋂=,可得AC ⊥面BCE ，四棱锥高4h AC ==，所以四棱锥体积1140410333V hS ==⨯⨯=，故B 不正确；48(4,0,0)(0,,)055CA BQ →→⋅=⋅-= ,168486464(0,,)(0,,055552525CQ BQ →→⋅=⋅-=-+=,,BQ CA BQ CQ ∴⊥⊥,又CA CQ C = ,BQ ∴⊥平面ACQ ,故C 正确；16848(4,,(0,,)05555AQ BQ →→⋅=-⋅-= ,AQ BQ →→∴⊥,即AQ BQ ⊥，故D 正确.故选：ACD 11．ABD 【详解】因为11C GD BGA ∠=∠，又11,C D BA ⊥面11ADD A ，连接1D G ，AG ，所以11111tan tan C D BA C GD BGA D G AG∠===∠，而11C D BA =，故1D G =AG ，所以G 在1AD 的垂直平分线上，即线段1A D 上，A ：由题设，若正方体各棱长为2，构建如下空间坐标系，则1(0,0,2)D ，(2,2,1)F ，(1,2,2)E ，(0,2,0)C ，所以1(2,2,1)D F =- ，(1,0,2)CE = ，故10D F CE ⋅= ，即1D F CE ⊥，正确；B ：如下图，由正方体的性质易知：11BC CB ⊥且CD ⊥面11BCC D ，1BC ⊂面11BCC D ，所以1CD BC ⊥，又1CD CB C ⊥=且1,CD CB ⊂面11DCB A ，故1BC ⊥面11DCB A ，而1B G ⊂面11DCB A ，则1BC ⊥1B G ，又1//BC EF ，故1EF B G ⊥，正确；C ：要使平面EFG //平面1ACD ，则平面EFG //平面11BAC ，而G 在线段1AD 上，显然1A D 上不存在G 使平面EFG //平面11BAC ，错误；D ：由11G EFB B EFG V V --=，而面1//EFB 面11ADD A ，又1A D ⊂面11ADD A ，G ∈1A D ，故G 到面1EFB 的距离为定值，所以三棱锥1B EFG -的体积为定值，正确.故选：ABD.12．AB 【详解】如图，取BD 的中点O ，连接OA '，OC .对于A ，∵A BD 'V 为等腰直角三角形，BCD △为等边三角形，∴A D A B ''==OA BD '⊥，OC BD ⊥，∵OA OC O '⋂=，∴BD ⊥平面OA C '，∴A C BD '⊥，故A 正确；对于B ，设BC a = ，BD b = ，BA c '= ，则12CG c a =- ，1()2EF b c a =+- ，0a c ⋅= ，2a b b c ⋅=⋅= ，||2CG = ，||EF == ，∴11()222EF CG b c a c a ⎛⎫⋅=+-⋅-= ⎪⎝⎭ ，cos ,15||||EF CG EF CG EF CG ⋅<>== ，故B 正确.对于C ，连接GF ，GF ∥BD ，∴GF 和CE 显然是异面直线，∴C ，E ，F ，G 四点不共面，故C 错误.对于D ，易证△A CB A CD ''△≌△，∴90A DC A BC ''∠=∠=︒.取A C '的中点Q ，则QA QB QC QD '===，即Q 为四面体A BCD '外接球的球心，∴该外接球的半径12R A C '==，从而可知该球的表面积6S π=，故D 错误.故选：AB.13．垂直PA ⊥底面ABCD ，BC ⊂平面ABCD ，所以PA BC ⊥，又底面ABCD 为正方形，所以AB BC ⊥，又AB PA A ⋂=，,AB PA ⊂平面PAB ，所以BC ⊥平面PAB ，因为AE ⊂平面PAB ，所以BC AE ⊥，又2PA AB ==，所以PAB △为等腰直角三角形，且E 为线段PB 的中点，所以AE PB ⊥，又BC PB B ⋂=，,BC PB ⊂平面PBC ，所以AE ⊥平面PBC ，因为AE ⊂平面AEF ，所以平面AEF ⊥与平面PBC .因为AE ⊥平面PBC ，EF ⊂平面PBC ，所以AE EF ⊥，所以当EF 最大时，AEF 的面积的最大，当F 位于点C 时，EF 最大且EF ==AEF 的面积的最大为12=14．2【详解】由正方体性质：1BB ⊥面1111D C B A ，11AC ⊂面1111D C B A ，则1BB ⊥11AC ，又1111B D A C ⊥，1BB ⋂111B D B =，所以11AC ⊥面11BB D ，又1BD ⊂面11BB D ，故11A C ⊥1BD ，即面1111D C B A 上的面对角线11A C ⊥1BD ；同理，可得面对角线1111,,,,DA DC AB CB AC 都垂直于1BD .所以一共6条面对角线与1BD 垂直，其中过A 点的有2条.故答案为：2.15．92##4.5【详解】连接1CD 、1AB 、1A F ，如下图所示：在正方体1111ABCD A B C D -中，11//BC A D 且11BC A D =，故四边形11A BCD 为平行四边形，所以，11//A B CD ，E 、F 分别为CD 、1DD 的中点，则1//EF CD 且112EF CD ==1//EF A B ∴，因为平面11//AA B B 平面11CC D D ，平面BEF I 平面11CC D D EF =，设平面BEF I 平面11AA B B l =，则//l EF ，因为B 为平面BEF 与平面11AA B B 的一个公共点，且1//A B EF ，B l ∈，故直线1A B 与直线l 重合，且1A B =1A BEF 为截面BEF 截正方体1111ABCD A B C D -所得截面，过点E 、F 在平面1A BEF 内作1EG A B ⊥，1FH A B ⊥，垂足点分别为G 、H ，因为BE =1A F =1A BEF 为等腰梯形，因为1BE A F =，1EBG FA H ∠=∠，190BGE A HF ∠=∠= ，则1BGE A HF △≌△，所以，1BG A H =，在平面1A BEF 内，//EF HG ，1FH A B ⊥，1EG A B ⊥，则//EG FH ，故四边形EFHG 为矩形，所以，GH EF ==，则1122A B GH BG A H -===，2EG ∴=，因此，截面面积为()1922EF A B EGS+⋅==.故答案为：92.16．31010##31010【详解】因为ED⊥平面ABCD，FC⊥平面ABCD，所以ED∥FC.取ED的中点为G，连接AG，FG，如图，因为ED＝2FC，所以DG＝FC，且DG∥FC，所以四边形CDGF为平行四边形，则FG∥CD且FG＝CD.又四边形ABCD为正方形，所以CD∥AB，CD＝AB，所以FG∥AB且FG＝AB，所以四边形ABFG为平行四边形，则BF∥AG，所以∠EAG是AE与BF所成的角.由正方形ABCD的边长为2，ED＝2FC＝2，可得22,5,1AE AG EG===，在△AEG中，由余弦定理得222581310cos2102225AG AE EGEAGAE AG+-+-∠===⋅⨯⨯.故答案为：31010。

立体几何选择填空问题集班级______姓名________一． 选择题1．定点P 不在△ABC 所在平面内，过P 作平面α，使△ABC 的三个顶点到α的距离相等，这样的平面共有（ ） （Ａ）１个 （Ｂ）２个 （Ｃ）３个 （Ｄ）４个2．P 为矩形ABCD 所在平面外一点，且PA ⊥平面ABCD ，P 到B ，C ，D 三点的距离分别是5，17，13，则P 到A 点的距离是（ ） （Ａ）１（Ｂ）２（Ｃ）3（Ｄ）４3．直角三角形ABC 的斜边AB 在平面α内，直角顶点C 在平面α外，C 在平面α内的射影为C 1，且C 1 AB ，则△C 1AB 为 （ ） （Ａ）锐角三角形（Ｂ）直角三角形（Ｃ）钝角三角形（Ｄ）以上都不对4．已知四点，无三点共线，则可以确定( ) A.1个平面B.4个平面C.1个或4个平面D.无法确定5． 已知球的两个平行截面的面积分别为5π和8π，它们位于球心的同一侧且相距是1，那么这个球的半径是( ) A.4B.3C.2D.56．球面上有3个点，其中任意两点的球面距离都等于大圆周长的61，经过3个点的小圆的周长为4π，那么这个球的半径为( ) A.43 B.23 C.2 D. 37．棱长为1的正方体ABCD －A 1B 1C 1D 1被以A 为球心，AB 为半径的球相截，则被截形体的表面积为（ ） A ．45π B ．87π C ．π D ．47π 8．某刺猬有2013根刺，当它蜷缩成球时滚到平面上，任意相邻的三根刺都可支撑住身体，且任意四根刺的刺尖不共面，问该刺猬蜷缩成球时，共有（ ）种不同的支撑身体的方式。

A ．2013 B ．4022 C ．4024 D ．4026图－1ESF CB A命题①空间直线a ，b ，c ，若a∥b，b∥c 则a∥c ②非零向量c 、b 、a ，若a ∥b ，b ∥c 则a ∥c ③平面α、β、γ若α⊥β，β⊥γ，则α∥γ ④空间直线a 、b 、c 若有a⊥b，b⊥c，则a∥c⑤直线a 、b 与平面β，若a⊥β，c⊥β，则a∥c 其中所有真命题的序号是（ ） A ．①②③ B．①③⑤ C．①②⑤ D．②③⑤ 9．在正三棱锥中，相邻两侧面所成二面角的取值范围是（ ）A 、3ππ（，） B 、23ππ（，） C 、（0，2π） D 、23ππ（，）3 10．以正方体的任意三个顶点为顶点作三角形，从中随机地取出两个三角形，则这两个三角形不共面的概率为 （ ） A ．367385 B ． 376385 C ．192385 D ．18385二．填空题11．在三棱锥P —ABC 中，底面是边长为2 cm 的正三角形，PA ＝PB ＝3 cm，转动点P 时，三棱锥的最大体积为 ．12．P 为ABC ∆所在平面外一点，PA 、PB 、PC 与平面ABC 所的角均相等，又PA 与BC 垂直，那么ABC ∆的形状可以是 。

A．若侧棱的长小于底面的变长，则 的取值范围为
B．若侧棱的长小于底面的变长，则 的取值范围为
C若侧棱的长大于底面的变长，则 的取值范围为
D若侧棱的长大于底面的变长，则 的取值范围为
二、填空题
36、在长方形 中， ， ， 为 的中点， 为线段 （端点除外）上一动点．现将 沿 折起，使平面 平面 ．在平面 内过点 作 ， 为垂足．设 ，则 的取值范围是．(1/2,1)
A．πB. 2πC.3πD.
6、如果四棱锥的四条侧棱都相等，就称它为“等腰四棱锥”，四条侧棱称为它的腰，以下4个命题中，假命题是B
A．等腰四棱锥的腰与底面所成的角都相等
B．等腰四棱锥的侧面与底面所成的二面角都相等或互补
C．等腰四锥的底面四边形必存在外接圆D．等腰四棱锥的各顶点必在同一球面上
7、给出下列四个命题:
50、在正方体ABCD－A1B1C1D1中，M，N分别是AB1，BC1上的点，且满足AM＝BN，有下列4个结论：①MN⊥AA1；②MN∥AC；③MN∥平面A1B1C1D1；④MN⊥BB1D1D。其中正确的结论的序号是_________
A． B． C． D．
9、过球的一条半径的中点，作垂直于该半径的平面，则所得截面的面积与球的表面积的比为A
（A）(B)(C)(D)
10、如图，平面α⊥平面β，A∈α，B∈β，AB与两平面α、β所成的角分别为和，过A、B分别作两平面交线的垂线，垂足为A′、B′，则AB∶A′B′＝A
（A）2∶1（B）3∶1（C）3∶2（D）4∶3
44、已知正三棱柱 的底面边长为1，高为8，一质点自 点出发，沿着三棱柱的侧面绕行两周到达 点的最短路线的长为.
45、若一条直线与一个正四棱柱各个面所成的角都为 ,则 =______√6/3

高考立体几何选择填空专练班别：__________ 姓名：_________ 一、选择题：（只有一个选项是正确） 1、表面积为23 的正八面体的各个顶点都在同一个球面上，则此球的体积为AA ．23πB ．13πC ．23π D ．223π 2、平面α的斜线AB 交α于点B ，过定点A 的动直线l 与AB 垂直，且交α于点C ，则动点C 的轨迹是A（A ）一条直线 （B ）一个圆（C ）一个椭圆 （D ）双曲线的一支3、过平行六面体ABCD-A 1B 1C 1D 1任意两条棱的中点作直线,其中与平面DBB 1D 1平行的直线有DA.4条B.6条C.8条D.12条4、棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图1, 则图中三角形(正四面体的截面)的面积是CA.22B.322 3 5、过半径为2的球O 表面上一点A 作球O 的截面，若OA 与该截面所成的角是60°则该截面的面积是AA ．π B. 2π C. 3π D. π326、如果四棱锥的四条侧棱都相等，就称它为“等腰四棱锥”，四条侧棱称为它的腰，以下4个命题中，假命题．．．是B A ．等腰四棱锥的腰与底面所成的角都相等B ．等腰四棱锥的侧面与底面所成的二面角都相等或互补C ．等腰四棱锥的底面四边形必存在外接圆D ．等腰四棱锥的各顶点必在同一球面上7、给出下列四个命题:①垂直于同一直线的两条直线互相平行. ②垂直于同一平面的两个平面互相平行. ③若直线12,l l 与同一平面所成的角相等,则12,l l 互相平行.④若直线12,l l 是异面直线,则与12,l l 都相交的两条直线是异面直线.其中假．命题的个数是D (A)1 (B)2 (C)3 (D)48、已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则这个球的表面积是CA ．16πB ．20πC ．24πD ．32π9、过球的一条半径的中点，作垂直于该半径的平面，则所得截面的面积与球的表面积的比为A（A ）316 (B )916 (C )38 (D )93210、如图，平面α⊥平面β，A ∈α，B ∈β，AB 与两平面α、β所成的角分别为π4和π6，过A 、B 分别作两平面交线的垂线，垂足为A ′、B ′，则AB ∶A ′B ′＝A（A ）2∶1 （B ）3∶1 （C ）3∶2 （D ）4∶311、已知平面α外不共线的三点A,B,C 到α的距离都相等,则正确的结论是DA.平面ABC 必平行于αB.平面ABC 必与α相交C.平面ABC 必不垂直于αD.存在△ABC 的一条中位线平行于α或在α内12、若空间中有四个点，则“这四个点中有三点在同一直线上”是“这四个点在同一平面上”的 A（A ）充分非必要条件；（B ）必要非充分条件；（C ）充要条件；（D ）非充分非必要条件13、已知球O 的半径是1，A 、B 、C 三点都在球面上，A 、B 两点和A 、C 两点的球面距离都是4π，B 、C 两点的球面距离是3π，则二面角B OA C --的大小是C （A ）4π B ）3π （C ）2π （D ）23π 14、正四棱锥P ABCD -底面的四个顶点,,,A B C D 在球O 的同一个大圆上，点P 在球面上，如果163P ABCD V -=，则球O 的表面积是D （A ）4π （B ）8π （C ）12π （D ）16π15、对于任意的直线l 与平同α , 在平面a 内必有直线m , 使m 与l C(A)平行 （B ）相交 (C)垂直 (D)互为异面直线16、正三棱柱ABC -A 1B 1C 1的侧棱长与底面边长相等，则AB 1与面ACC 1A 1所成角的正弦等于A(A) 4 (B)4 (C) 2 (D) 217、已知三棱锥的侧棱长的底面边长的2倍，则侧棱与底面所成角的余弦值等于AA B C ．2 D 18、设n m l ,,均为直线,其中n m ,在平面α内，则“l ⊥α”是“l m l n ⊥⊥且”的A (A)充分不必要条件 (B)必要不充分条件(C)充分必要条件(D)既不充分也不必要条件19、把边长为2的正方形ABCD 沿对角线AC 折成直二面角, 折成直二面角后, 在A ,B ,C ,D 四点所在的球面上, B 与D 两点之间的球面距离为 C (A)22π (B)π (C)2π (D)3π 20、半径为1的球面上的四点D C B A ,,,是正四面体的顶点，则A 与B 两点间的球面距离为C（A ）)33arccos(- （B ）)36arccos(- （C ）)31arccos(-（D ）)41arccos(- 21、棱长为1的正方体1111ABCD A B C D -的8个顶点都在球O 的表面上，E F ，分别 是棱AA ，1DD 的中点，则直线EF 被球O 截得的线段长为DA ．2 B ．1 C ．12+ D 22、正方体1AC 的棱长为1，过点A 作平面1A BD 的垂线，垂足为H ，则下列命题中错误．．的命D A ．点H 是1A BD △的垂心 B ．AH 垂直平面11CB DC ．AH 的延长线经过点1CD ．直线AH 和1BB 所成角为4523、四面体ABCD 的外接球球心在CD 上，且2CD =，AB =A B ，间的球面距离是CA ．π6B ．π3C ．2π3D ．5π624、在棱长为1的正方体ABCD －A 1B 1C 1D 1中，E 、F 分别为棱AA 1、BB 1的中点，G 为棱A 1B 1上的一点，且A 1G =λ（0≤λ≤1），则点G 到平面D 1EF 的距离为DA.3B.22C.32λ D.5525、一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱.这个四棱锥的底面为正方形，且底面边长与各侧棱长相等，这个三棱锥的底面边长与各侧棱长也都相等．设四棱锥、三棱锥、三棱柱的高分别为h 1，h 2，h 3，则h 1:h 2:h 3= BA ．3:1:1B ．3:2:2C ．3:2:2D ．3:2:326、已知三棱锥S ABC -的各顶点都在一个半径为r 的球面上，球心O 在AB 上，SO ⊥底面ABC ，2AC r =，则球的体积与三棱锥体积之比是DA ．πB ．2πC ．3πD ．4π 27、若三个平面两两相交，且三条交线互相平行，则这三个平面把空间分成CA ．5部分 B.6部分 C.7部分 D.8部分28、设球O 的半径是1，A 、B 、C 是球面上三点，已知A 到B 、C 两点的球面距离都是2π，且二面角B OA C --的大小是3π，则从A 点沿球面经B 、C 两点再回到A 点的最短距离是C （A ）76π （B ）54π （C ）43π （D ）32π 29、一个正三棱锥的四个顶点都在半径为1的球面上，其中底面的三个顶点在该球的一个大圆上，则该正三棱锥的体积是C（A ）433 (B)33 (C) 43 (D) 123. 30、已知二面角α-l -β为60 ，动点P 、Q 分别在面α、β内，P 到β3Q 到α的距离为23P 、Q 两点之间距离的最小值为C(A) (B)2 (C) 23 (D)431、在半径为3的球面上有C B A 、、三点，ABC ∠=90°，BC BA =, 球心O 到平面ABC 的距离是223，则C B 、两点的球面距离是B A. 3π B. π C. π34 D.2π 32、正六棱锥P －ABCDEF 中，G 为PB 的中点，则三棱锥D －GAC 与P －GAC 体积之比为C （A ）1：1 (B) 1：2 (C) 2：1 (D) 3：2 33、如果把地球看成一个球体，则地球上的北纬060纬线长和赤道长的比值为C（A ）0.8 （B ）0.75 （C ）0.5 （D ）0.2534、已知二面角l αβ--的大小为050，P 为空间中任意一点，则过点P 且与平面α和平面β所成的角都是025的直线的条数为BA ．2B ．3C ．4D ．535、在正四棱柱1111ABCD A B C D -中，顶点1B 到对角线1BD 和到平面11A BCD 的距离分别为h 和d ，则下列命题中正确的是CA ．若侧棱的长小于底面的变长，则h d的取值范围为(0,1) B ．若侧棱的长小于底面的变长，则h d的取值范围为223()23 C 若侧棱的长大于底面的变长，则h d 的取值范围为23(2)3 D 若侧棱的长大于底面的变长，则h d 的取值范围为23()3+∞二、填空题36、在长方形ABCD 中，2AB =，1BC =，E 为DC 的中点，F 为线段EC （端点除外）上一动点．现将AFD ∆沿AF 折起，使平面ABD ⊥平面ABC ．在平面ABD 内过点D 作DK AB ⊥，K 为垂足．设AK t =，则t 的取值范围是 ．(1/2,1)37、直三棱柱111ABC A B C -的各顶点都在同一球面上，若12AB AC AA ===,120BAC ∠=︒，则此球的表面积等于 。

2022年近三年高考数学立体几何选择、填空题汇编一．选择题（共36小题）A ．8πB ．8π3C ．2πD ．4π3 2．如图，“十字歇山”是由两个直三棱柱重叠后的景象，重叠后的底面为正方形，直三棱柱的底面是顶角为120°，腰为3的等腰三角形，则该几何体的体积为（ ）A ．23B ．24C ．26D ．27A ．点PB ．点BC ．点RD ．点Q 4．某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：cm 3）是（ ）A ．22πB ．8πC ．22π3D ．16π3A ．3π4B ．πC ．2πD ．3πA ．[18，814]B ．[274，814]C ．[274，643]D ．[18，27]A ．13B ．12C ．D ．8．如图，网格纸上绘制的是一个多面体的三视图，网格小正方形的边长为1，则该多面体的体积为（）A．8 B．12 C．16 D．20A．平面B1EF⊥平面BDD1B．平面B1EF⊥平面A1BDC．平面B1EF∥平面A1AC D．平面B1EF∥平面A1C1D10．甲、乙两个圆锥的母线长相等，侧面展开图的圆心角之和为2π，侧面积分别为S甲和S乙，体积分别为V甲和V乙．若=2，则=（）A．100πB．128πC．144πD．192πA ．0B ．2C ．4D ．12A ．3πB ．4πC ．9πD ．12πA ．26%B ．34%C ．42%D ．50%A ．20+12√3B ．28√2C ．563 D ．16．某四面体的三视图如图所示，该四面体的表面积为（）17．某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm3）是（）A ．直线A 1D 与直线D 1B 垂直，直线MN∥平面ABCDB ．直线A 1D 与直线D 1B 平行，直线MN⊥平面BDD 1B 1C ．直线A 1D 与直线D 1B 相交，直线MN∥平面ABCDD ．直线A 1D 与直线D 1B 异面，直线MN⊥平面BDD 1B 1A ．2B ．2√2C ．4D ．4√2A ．B ．C ．D ．A ．π2 B ．π3 C ．π4 D ．π6A．12πB．24πC．36πD．144π•25．某三棱柱的底面为正三角形，其三视图如图所示，该三棱柱的表面积为（）A．6+√3B．6+2√3C．12+√3D．12+2√3A．6+4√2B．4+4√2C．6+2√3D．4+2√327．在棱长为10的正方体ABCD-A 1B 1C 1D 1中，P 为左侧面ADD 1A 1上一点，已知点P 到A 1D 1的距离为3，P 到AA 1的距离为2，则过点P 且与A 1C 平行的直线交正方体于P 、Q 两点，则Q 点所在的平面是（ ）A ．AA 1B 1B B ．BB 1C 1C C ．CC 1D 1D D ．ABCDA ．EB ．FC ．GD ．H29．某几何体的三视图（单位：cm ）如图所示，则该几何体的体积（单位：cm 3）是（ ）A ．73B ．143C ．3D ．6A．64πB．48πC．36πD．32πA．α≤β≤γB．β≤α≤γC．β≤γ≤αD．α≤γ≤βA．AB=2ADB．AB与平面AB1C1D所成的角为30°C．AC=CB1D．B1D与平面BB1C1C所成的角为45°A．20°B．40°C．50°D．90°35．已知△ABC是面积为的等边三角形，且其顶点都在球O的球面上．若球O的表面积为16π，则O到平面ABC的距离为（）A．2x+y-z+2=0 B．2x+y+z-6=0 C．2x+y+z-4=0 D．2x+y-z-3=0 二．填空题（共24小题）37．在正三棱柱ABC-A1B1C1中，AB=1，AA1=，则异面直线AB1与BC1所成角的大小为．39．三棱锥P-ABC中，PA⊥底面ABC，且PA=3，AB=CB=2，AC=2√2，则侧面PBC的面积是．40．已知圆柱的底面圆半径为1，高为2，AB为上底面圆的一条直径，C是下底面圆周上的一个动点，则△ABC 的面积的取值范围为．41．已知一个圆锥的底面半径为6，其体积为30π，则该圆锥的侧面积为．42．以图①为正视图，在图②③④⑤中选两个分别作为侧视图和俯视图，组成某个三棱锥的三视图，则所选侧视图和俯视图的编号依次为（写出符合要求的一组答案即可）．43．已知圆柱的底面半径为1，高为2，则圆柱的侧面积为．44．在空间直角坐标系中，已知点A（1，0，2），B（1，1，-1），则经过点A且与直线AB垂直的平面方程为．45．已知正方体ABCD-A1B1C1D1的棱长为2，M、N分别为BB1、AB的中点，则三棱锥A-NMD1的体积为．46．已知圆锥的侧面积（单位：cm2）为2π，且它的侧面展开图是一个半圆，则这个圆锥的底面半径（单位：cm）是．47．如图，六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的．已知螺帽的底面正六边形边长为2cm,高为2cm,内孔半径为0.5cm,则此六角螺帽毛坯的体积是cm3．48．如图，在三棱锥P-ABC的平面展开图中，AC=1，AB=AD=√3，AB⊥AC，AB⊥AD，∠CAE=30°，则cos∠FCB= ．49．已知圆锥的底面半径为1，母线长为3，则该圆锥内半径最大的球的体积为．50．已知平面α截球O的球面所得圆的面积为π，O到α的距离为3，则球O的表面积为．51．已知四棱锥的底面是边长为√2的正方形，侧棱长均为√5．若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点，另一个底面的圆心为四棱锥底面的中心，则该圆柱的体积为．52．已知l,m是平面α外的两条不同直线．给出下列三个论断：①l⊥m；②m∥α；③l⊥α．以其中的两个论断作为条件，余下的一个论断作为结论，写出一个正确的命题：．53．如图，长方体ABCD-A1B1C1D1的体积是120，E为CC1的中点，则三棱锥E-BCD的体积是．54．学生到工厂劳动实践，利用3D打印技术制作模型．如图，该模型为长方体ABCD-A1B1C1D1挖去四棱锥O-EFGH后所得的几何体，其中O为长方体的中心，E，F，G，H分别为所在棱的中点，AB=BC=6cm,AA1=4cm.3D打印所用原料密度为0.9g/cm3．不考虑打印损耗，制作该模型所需原料的质量为g.55．中国有悠久的金石文化，印信是金石文化的代表之一．印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”（图1）．半正多面体是由两种或两种以上的正多边形围成的多面体．半正多面体体现了数学的对称美．图2是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1．则该半正多面体共有个面，其棱长为．58．已知向量则的夹角为．。

立体几何（选择题、填空题）1.【2020年高考全国Ⅰ卷理数】埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥，以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为（）515 1 5 1 5 1A. B. C. D.4 2 4 2【答案】C【解析】【分析】1设C D a,PE b，利用P O2 CD PE 得到关于a,b的方程，解方程即可得到答案.22a【详解】如图，设C D a,PE b，则P O PE 2 2 2 ，OE b41 a2 1 b b由题意P O2 ab，即b 2 ab，化简得4() 2 210，2 4 2 a ab1 5解得（负值舍去）.a 4故选：C.【点晴】本题主要考查正四棱锥的概念及其有关计算，考查学生的数学计算能力，是一道容易题.2.【2020年高考全国I I卷理数】如图是一个多面体的三视图，这个多面体某条棱的一个端点在正视图中对应的点为M ，在俯视图中对应的点为N ，则该端点在侧视图中对应的点为（）A. EB. FC.GD.H【答案】A【解析】【分析】根据三视图，画出多面体立体图形，即可求得M 点在侧视图中对应的点.【详解】根据三视图，画出多面体立体图形，D D B C上的点在俯视图中对应的点为N,3 4上的点在正视图中都对应点M,直线1 4∴在正视图中对应M ,在俯视图中对应N 的点是D4,线段D D,上的所有点在侧试图中都对应E ,∴点3 4D4在侧视图中对应的点为E .故选：A【点睛】本题主要考查了根据三视图判断点的位置，解题关键是掌握三视图的基础知识和根据三视图能还原立体图形的方法，考查了分析能力和空间想象，属于基础题.A, B,C 为球O 的球面上的三个点，⊙O为 A B C的外接圆，若⊙O3. 【2020 年高考全国Ⅰ卷理数】已知11的面积为 4π ， AB BC AC OO ，则球O的表面积为（）1A. 64πB. 48πC. 36πD. 32π【答案】A 【解析】 【分析】由已知可得等边 AB C 的外接圆半径，进而求出其边长，得出O O的值，根据球的截面性质，求出球的半 1径，即可得出结论. 【详解】设圆O半径为 ，球的半径为 R ，依题意， r 14,r 2 ， A B C为等边三角形，得r2由正弦定理可得 AB 2rsin 60 2 3 ，O O AB 2 3 ，根据球的截面性质O O 平面 ABC ， 11 O O O A ,R OA O O2 O A 2 OO 1 2 r 4 ， 21 1 1 1 O 球2 的表面积 S 4R 64 .故选：A【点睛】本题考查球的表面积，应用球的截面性质是解题的关键，考查计算求解能力，属于基础题. 4. 【2020 年高考全国Ⅲ理数】下图为某几何体的三视图，则该几何体的的表面积是（ ）A.6+4 2B.4+4 2C.6+2 3D.4+2 3【答案】C【解析】【分析】根据三视图特征，在正方体中截取出符合题意的立体图形，求出每个面的面积，即可求得其表面积.【详解】根据三视图特征，在正方体中截取出符合题意的立体图形1根据立体图形可得：S△ABC S△AD C S△C DB 22 22根据勾股定理可得：AB A D DB 2 2△A DB是边长为22的等边三角形根据三角形面积公式可得：1 1 3S △A D B AB AD s in60(22) 2 2 32 2 2该几何体的表面积是：3223623.故选：C.【点睛】本题主要考查了根据三视图求立体图形的表面积问题，解题关键是掌握根据三视图画出立体图形，考查了分析能力和空间想象能力，属于基础题. 5. 【2020 年高考全国 I I 卷理数】已知△ABC 是面积为若球 O 的表面积为 16π，则 O 到平面 ABC 的距离为（ 3 9 34的等边三角形，且其顶点都在球 O 的球面上. ）3 A. 3 B.C. 1D.22【答案】C 【解析】 【分析】根据球O 的表面积和 ABC 的面积可求得球O 的半径 R 和 AB C 外接圆半径 ，由球的性质可知所求距r 离 2 2 .d R r 【详解】设球O 的半径为 R ，则 4 R 16 ，解得： R 2 . 2 设 AB C 外接圆半径为 ，边长为 a，r 9 3ABC是面积为 的等边三角形， 41 3 9 32 a 22 9 a 2 ，解得： a 3，r a 2 93 ， 2 24 3 4 3 4球心 O 到平面 ABC 2 2 的距离d R r 43 1.故选：C.【点睛】本题考查球的相关问题的求解，涉及到球的表面积公式和三角形面积公式的应用；解题关键是明 确球的性质，即球心和三角形外接圆圆心的连线必垂直于三角形所在平面.6. 【2019 年高考全国Ⅰ卷理数】已知三棱锥 P −AB C 的四个顶点在球 O 的球面上，PA=PB=P C ，△ABC 是边 长为 2 的正三角形，E ，F 分别是 PA ，AB 的中点，∠CEF =90°，则球 O 的体积为A ．8 6B ． 4 6 D ． 6C ． 2 6 【答案】D【解析】解法一： PA P B PC, ABC 为边长为 2 的等边三角形，P ABC为正三棱锥，△ PB AC ，又 E ， F 分别为 PA ， AB 的中点，EF ∥PB ，EF AC ，又 EF CE ，C E AC C,EF 平面 PAC ，∴ PB 平面 PAC ，APB PA PB PC 2 ，P ABC 为正方体的一部分， 2R 2 2 2 6 ，即6 4 4 6 68 R, V R 3 π 6，故选 D ． P A, AB 2 3 3解法二：设 PA PB PC 2x ，E, F 分别为 的中点， 1EF ∥PB ，且 EF PB x ，△ABC 为边长为 2 的等边三角形，C F 3 ，21 又 CEF 90，CE 3 x 2, AE PA x ， 2 x 243 x 22 x2△AEC 中，由余弦定理可得 cos EAC作 PD AC 于 D ，，A D 1 x 2 4 3 x 4x 21PA PC \ D AC cos EAC ， ， 为 的中点， ，PA 2x 2x1 2 2x 2 1 2，x 2，x ，PA PB PC 2 ，2 2又 AB=B C=A C=2 ， PA , PB , PC 两两垂直，6 2R 2 2 2 6 ，R，24 4 6 68 V R 3 6 ，故选 D. 3 3【名师点睛】本题主要考查学生的空间想象能力，补体法解决外接球问题．可通过线面垂直定理，得到 三棱两两互相垂直关系，快速得到侧棱长，进而补体成正方体解决．7. 【2019 年高考全国Ⅱ卷理数】设α，β为两个平面，则α∥β的充要条件是 A ．α内有无数条直线与β平行 C ．α，β平行于同一条直线 【答案】BB ．α内有两条相交直线与β平行 D ．α，β垂直于同一平面【解析】由面面平行的判定定理知： 内两条相交直线都与 平行是∥的充分条件，由面面平行性质定理知，若∥，则必要条件，故选 B ．内任意一条直线都与 平行，所以平行是∥内两条相交直线都与的【名师点睛】本题考查了空间两个平面的判定与性质及充要条件，渗透直观想象、逻辑推理素养，利用 面面平行的判定定理与性质定理即可作出判断．面面平行的判定问题要紧扣面面平行判定定理，最容易 犯的错误为定理记不住，凭主观臆断，如：“若 a ,b ,a b ，则 ∥ ∥”此类的错误．8. 【2019 年高考全国Ⅲ卷理数】如图，点 N 为正方形 AB C D 的中心，△EC D 为正三角形，平面 EC D ⊥平 面 ABC D ，M 是线段 E D 的中点，则A ．B M =E N ，且直线 B M ，EN 是相交直线 B ．B M ≠EN ，且直线 B M ，E N 是相交直线C ．B M =E N ，且直线 B M ，E N 是异面直线D ．B M ≠EN ，且直线 B M ，EN 是异面直线 【答案】B【解析】如图所示，作 EO C D 于O ，连接O N ，B D ，易得直线 B M ，E N 是三角形 EB D 的中线，是 相交直线.过 M 作 MF OD 于 F ，连接 BF ，AB C D ，E O C D, E O 平面C DE ，EO平面C D E 平面 平面 ABC D ， M F 平面 AB C D ，△MFB 与△EO N 均为直角三角 形 ． 设 正 方 形 边 长 为 2 ， 易 知 E O 3,ON 1,EN 2 ，3 5M F,BF ,BM 7 ，B M EN ，故选 B ．2 2【名师点睛】本题考查空间想象能力和计算能力，解答本题的关键是构造直角三角形.解答本题时，先利 用垂直关系，再结合勾股定理进而解决问题．9. 【2018 年高考全国Ⅰ卷理数】某圆柱的高为 2，底面周长为 16，其三视图如图．圆柱表面上的点 M 在正 视图上的对应点为 A ，圆柱表面上的点 N 在左视图上的对应点为 B ，则在此圆柱侧面上，从 M 到 N 的路径中，最短路径的长度为A ． 2 17B ． 2 5 D ．2C ．3 【答案】B【解析】根据圆柱的三视图以及其本身的特征，知点 M 在上底面上，点 N 在下底面上，且可以确定点 M 和点 N 分别在以圆柱的高为长方形的宽，圆柱底面圆周长的四分之一为长的长方形的对角线的端点处， 所以所求的最短路径的长度为 ，故选 B ．【名师点睛】该题考查的是有关几何体的表面上两点之间的最短距离的求解问题，在解题的过程中，需 要明确两个点在几何体上所处的位置，再利用平面上两点间直线段最短，所以处理方法就是将面切开平 铺，利用平面图形的相关特征求得结果.10. 【2018 年高考全国Ⅰ卷理数】已知正方体的棱长为 1，每条棱所在直线与平面所成的角都相等，则截此正方体所得截面面积的最大值为3 342 3 3 A ．C ．B ．D ．3 2 43 2【答案】A【解析】根据相互平行的直线与平面所成的角是相等的，AB C D A B C D 中，1所以在正方体 1 1 1AB D AA , A B , A D 所成的角是相等的，11 11 1平面 与线 1 1AB D 所以平面 与正方体的每条棱所在的直线所成角都是相等的，11 C BD 1同理，平面 也满足与正方体的每条棱所在的直线所成角都是相等的，AB D C BD要求截面面积最大，则截面的位置为夹在两个面与1中间，且过棱的中点的正六边形，且1 12边长为，223 2 3 34所以其面积为S 6，故选A.4 2【名师点睛】该题考查的是有关平面被正方体所截得的截面多边形的面积问题，首要任务是需要先确定截面的位置，之后需要从题的条件中找寻相关的字眼，从而得到其为过六条棱的中点的正六边形，利用六边形的面积的求法，应用相关的公式求得结果.即首先利用正方体的棱是3组每组有互相平行的4条棱，所以与12条棱所成角相等，只需与从同一个顶点出发的三条棱所成角相等即可，从而判断出面的位置，截正方体所得的截面为一个正六边形，且边长是面的对角线的一半，应用面积公式求得结果.11.【2018年高考全国Ⅲ卷理数】中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是【答案】A【解析】本题主要考查空间几何体的三视图.由题意知，俯视图中应有一不可见的长方形，且俯视图应为对称图形.故选A．12.【2018年高考全国Ⅲ卷理数】设A ，，，是同一个半径为的球的球面上四点，△A B C 为等边三B C D 4角形且其面积为A．12 3，则三棱锥D ABC 体积的最大值为9 3B．18 3D．54 3C．24 3【答案】B【解析】如图所示，设点 M 为三角形 ABC 的重心，E 为 AC 中点，当点 D 在平面 ABC 上的射影为 M 时，三棱锥 D ABC 的体积最大，此时，O D OB R 4，3 S △AB CAB 9 3 ，AB 6 ,点 M 为三角形 ABC 的重心，2 4 2B M BE 2 3 ，3 Rt △OB M 中，有O M OB 2 2 2，D M O D O M 4 2 6，B M1V DABCm ax9 36 18 3 ，故选 B. 3【名师点睛】本题主要考查三棱锥的外接球，考查了勾股定理，三角形的面积公式和三棱锥的体积公 式，判断出当点 D 在平面 ABC 上的射影为三角形 AB C 的重心时，三棱锥 DABC 体积最大很关键，2由 M 为三角形 ABC 的重心，计算得到 B M BE 2 3 ，再由勾股定理得到 O M ，进而得到结果， 3属于较难题型.13. 【2018 年高考全国Ⅱ卷理数】在长方体 AB C D A B C D 中，AB BC 1，AA 3 ，则异面直线 A D 与 1 1 1 1 11 D B 所成角的余弦值为1 1 A ．5 5 B ． D ．6 5 2 C ．52【答案】C【解析】方法一：用一个与原长方体相同的长方体拼到原长方体的前面，B P ∥A D D B DP= 5B P 2，，则11如图，则 1，连接 DP ，易求得 1 DB P A D DB与所成的角，11是异面直线1 D B2 1 B P 2 DP 25 4 5 5 由余弦定理可得cos DB P 1. 12DB PB 4 5 5 1 1故选 C.方法二：以 D 为坐标原点，DA,D C,D D 所在直线分别为 x ,y ,z 轴建立空间直角坐标系， 1D 0, 0, 0, A 1, 0, 0,B 1, 1, 3,D 0, 0, 3A D1, 0, 3 ,DB 1, 1, 3 ,则 ,所以 1 1 1 1cos AD , DB A D DB A D DB 1 3 2 5 5 1 1因为 ， 1 15 1 15 A D DB 所以异面直线 与 所成角的余弦值为 1，故选 C. 15【名师点睛】先建立空间直角坐标系，设立各点坐标，利用向量数量积求向量夹角，再根据向量夹角 与线线角相等或互补关系求结果.利用法向量求解空间线面角的关键在于“四破”：第一，破“建系关”， 构建恰当的空间直角坐标系；第二，破“求坐标关”，准确求解相关点的坐标；第三，破“求法向量关”， 求出直线的方向向量或平面的法向量；第四，破“应用公式关”. ABC A B C 中， ABC 120 BC CC 1，AB 2 ，，113. 【2017 年高考全国Ⅱ卷理数】已知直三棱柱1 1 1 AB BC 所成角的余弦值为1则异面直线 与 13 15 5 A ．B ．D ．2 103 C ． 53【答案】CAB C D A B C D ，1【解析】如图所示，补成直四棱柱 1 1 1则所求角为 BC D,BC 2, BD 2 21 221cos 60 3,C D AB 5 ，11 1 1 BC12 5105 易得 C D 12 BD 2BC 12 ，因此cos BC D，故选 C ． 1C D1【名师点睛】平移法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面问题化归为 共面问题来解决，具体步骤如下：①平移：平移异面直线中的一条或两条，作出异面直线所成的角； ②认定：证明作出的角就是所求异面直线所成的角； ③计算：求该角的值，常利用解三角形；④取舍：由异面直线所成的角的取值范围是(0,]，当所作的角为钝角时，应取它的补角作为两条异面2直线所成的角．求异面直线所成的角要特别注意异面直线之间所成角的范围．14.【2017年高考全国Ⅰ卷理数】某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形，这些梯形的面积之和为A．10 B．12D．16C．14【答案】B【解析】由题意该几何体的直观图是由一个三棱锥和三棱柱构成，如下图，则该几何体各面内只有两个相同的梯形，则这些梯形的面积之和为12(24)212，故选．B2【名师点睛】三视图往往与几何体的体积、表面积以及空间线面关系、角、距离等问题相结合，解决此类问题的关键是由三视图准确确定空间几何体的形状及其结构特征并且熟悉常见几何体的三视图.15.【2017年高考全国Ⅱ卷理数】如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为A．90 C．42B．63 D．36【答案】B【解析】由题意，该几何体是一个组合体，下半部分是一个底面半径为3，高为4的圆柱，其体积V 32 436，上半部分是一个底面半径为，高为的圆柱的一半，其体积3 611 V (3 26) 27，故该组合体的体积V V V36 27 63．21 2 2故选 B ．【名师点睛】在由三视图还原为空间几何体的实际形状时，要从三个视图综合考虑，根据三视图的规 则，空间几何体的可见轮廓线在三视图中为实线，不可见轮廓线在三视图中为虚线．在还原空间几何 体实际形状时，一般是以正视图和俯视图为主，结合侧视图进行综合考虑．求解以三视图为载体的空 间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系，利用 相应体积公式求解．16. 【2017 年高考全国Ⅲ卷理数】已知圆柱的高为 1，它的两个底面的圆周在直径为 2 的同一个球的球面上，则该圆柱的体积为3π π A ．C ．B ．D ．4 π π24【答案】B【解析】绘制圆柱的轴截面如图所示：21 1 3 由题意可得： AC 1, AB ，结合勾股定理，底面半径 r 1 2，2 2 223 3由圆柱的体积公式，可得圆柱的体积是V πr 2h π 1 π ，故选 B.2 4【名师点睛】（1）求解空间几何体体积的关键是确定几何体的元素以及线面的位置关系和数量关系， 利用相应体积公式求解；（2）若所给几何体的体积不能直接利用公式得出，则常用等积法、分割法、 补形法等方法进行求解.17. 【2020 年高考全国 I I 卷理数】设有下列四个命题： p ：两两相交且不过同一点的三条直线必在同一平面内.1p ：过空间中任意三点有且仅有一个平面.2p ：若空间两条直线不相交，则这两条直线平行.3p ：若直线 l 平面α，直线 m ⊥平面α，则 m ⊥l . 4则下述命题中所有真命题的序号是__________.p p p p p ppp③④122334① ② 1 4【答案】①③④【解析】【分析】p p2利用两交线直线确定一个平面可判断命题的真假；利用三点共线可判断命题的真假；利用异面直线可1p p4判断命题的真假，利用线面垂直的定义可判断命题的真假.再利用复合命题的真假可得出结论.3p1l1l2【详解】对于命题，可设与相交，这两条直线确定的平面为；l l若与相交，则交点A 在平面内，3 1l l同理，与的交点B 也在平面内，3 2所以，AB ，即l3，命题为真命题；p1p2对于命题，若三点共线，则过这三个点的平面有无数个，p命题为假命题；2p对于命题，空间中两条直线相交、平行或异面，3p命题为假命题；3p4，若直线m 平面，对于命题m 垂直于平面则内所有直线，直线l 平面，直线m 直线，lp命题为真命题.4综上可知，，为真命题，，为假命题，p p p p为假命题，1 2为真命题，1 4p p p p为真命题.3 4为真命题，2 3故答案为：①③④.【点睛】本题考查复合命题的真假，同时也考查了空间中线面关系有关命题真假的判断，考查推理能力， 属于中等题.18. 【2020 年高考全国Ⅲ理数】已知圆锥的底面半径为 1，母线长为 3，则该圆锥内半径最大的球的体积为_________． 2 【答案】 3【解析】 【分析】将原问题转化为求解圆锥内切球的问题，然后结合截面确定其半径即可确定体积的值. 【详解】易知半径最大球为圆锥的内切球，球与圆锥内切时的轴截面如图所示，B C 2, AB AC 3 其中 ，且点 M 为 BC 边上的中点，设内切圆的圆心为O ，1由于A M 3 2 1 22 2 ，故 S △ABC2 2 2 2 2 ， 2r设内切圆半径为 ，则：1 1 1 S △AB C S △A O B S △BO C S △A O C AB r BC r AC r2 2 21 3 3 2r2 2 ，22 4 2解得： r =，其体积：V r 3 . 2 3 32故答案为：. 3【点睛】与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的 位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于 球的直径.19. 【2019 年高考全国Ⅲ卷理数】学生到工厂劳动实践，利用 3D 打印技术制作模型.如图，该模型为长方体AB C D A B C D 挖去四棱锥 O —EF G H 后所得的几何体，其中 O 为长方体的中心，E ，F ，G ，H 分11 1 1AB = BC = 6 cm, AA = 4 cm 别为所在棱的中点， ，3D 打印所用原料密度为 0.9 g/cm 3，不考虑打印 1损耗，制作该模型所需原料的质量为___________g .【答案】118.81【解析】由题意得， S 46 4 23 12cm 2 ，四边形EF G H2 1∵四棱锥 O −EF G H 的高为 3cm ， ∴V O EF G H 123 12cm 3 ．3AB C D A B C D V 466 144cm，3又长方体 的体积为 1 1 1 1 2 所以该模型体积为 VV V144 12 132cm 3 ，其质量为 0.9132 118.8g ．OEF G H2 【名师点睛】本题考查几何体的体积问题，理解题中信息联系几何体的体积和质量关系，从而利用公式 求解．根据题意可知模型的体积为长方体体积与四棱锥体积之差进而求得模型的体积，再求出模型的质 量即可.20. 【2019 年高考全国Ⅱ卷理数】中国有悠久的金石文化，印信是金石文化的代表之一．印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”（图 1）.半正多面体是 由两种或两种以上的正多边形围成的多面体．半正多面体体现了数学的对称美．图 2 是一个棱数为 48 的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为 1．则该半正多面体共 有________个面，其棱长为_________．（本题第一空 2 分，第二空 3 分．）【答案】26，21【解析】由图可知第一层（包括上底面）与第三层（包括下底面）各有9个面，计18个面，第二层共有8个面，所以该半正多面体共有18826个面．x如图，设该半正多面体的棱长为，则AB BE x，延长CB与FE 的延长线交于点G，延长BC交正方体的棱于H ，由半正多面体对称性可知，△BG E 为等腰直角三角形，2 2BG GE C H x,G H 2x x(21)x1，2 21x21，21即该半正多面体的棱长为21．【名师点睛】本题立意新颖，空间想象能力要求高，物体位置还原是关键，遇到新题别慌乱，题目其实很简单，稳中求胜是关键．立体几何平面化，无论多难都不怕，强大空间想象能力，快速还原图形．721.【2018年高考全国I I卷理数】已知圆锥的顶点为S，母线SA，SB 所成角的余弦值为，SA与圆锥8 底面所成角为45°，若△SAB 的面积为515，则该圆锥的侧面积为__________．【答案】402π7 15 8【解析】因为母线 SA ， SB 所成角的余弦值为 ，所以母线 SA ， SB 所成角的正弦值为，因为 81 15 8 △SAB 的面积为5 15 ，设母线长为l ,所以l 2 25 15 ,l80 ， 2π 2因为 SA 与圆锥底面所成角为 45°，所以底面半径为 r l cosl , 4 22 因此圆锥的侧面积为 πr lπl 40 2π. 22【名师点睛】本题考查线面角、圆锥的侧面积、三角形面积等知识点，考查学生空间想象与运算能力. 先根据三角形面积公式求出母线长，再根据母线与底面所成角得底面半径，最后根据圆锥侧面积公式 求结果.22. 【2017 年高考全国 I 卷理数】如图，圆形纸片的圆心为 O ，半径为 5 c m ，该纸片上的等边三角形 ABC 的中心为 O.D ，E ，F 为圆 O 上的点，△DB C ，△ECA ，△FA B 分 别是以 BC ，CA ，AB 为底边的等腰三角形.沿虚线剪开后，分别以 BC ，CA ，AB 为折 痕折起△DB C ，△ECA ，△FAB ，使得 D ，E ，F 重合，得到三棱锥.当△ABC 的边长变 化时，所得三棱锥体积（单位：cm 3）的最大值为 【答案】 4 15.【解析】如下图，连接 DO 交 BC 于点 G ，设 D ，E ，F 重合于 S 点，正三角形的边长为 x(x>0)，则 1 3 3O G x x. 3 2 63FG SG 5x ， 6223 3x3x， SO h SG2GO2 5 x 556 631 1 3 3 15 3 三棱锥的体积V S △ABC h x2 5 5 x 4 x 5 . 5x3 34 3 1233 5 3 设 n x 5x 4x 5 ，x>0，则 n x 20x 3 x 4， 3 3x 4 n x 0 ，即 4x 30，得 ，易知 n x 在 令 处取得最大值. x 4 3x 4 3 3 15∴V max 48 5 4 4 15 .12【名师点睛】对于三棱锥最值问题，需要用到函数思想进行解决，本题解决的关键是设好未知量，利用图形特征表示出三棱锥体积.当体积中的变量最高次是2次时可以利用二次函数的性质进行解决，当变量是高次时需要用到求导的方式进行解决.。

CBAC 1B 11高三立体几何习题一、 填空题1.已知AB 是球O 的一条直径，点1O 是AB 上一点，若14OO =，平面α过点1O 且垂直AB ，截得圆1O ，当圆1O 的面积为9π时，则球O 的表面积是 ．【答案】1002.把一个大金属球表面涂漆，共需油漆2.4公斤．若把这个大金属球熔化制成64个大小都相同的小金属球， 不计损耗，将这些小金属球表面都涂漆，需要用漆 公斤．【答案】9.63.已知球的表面积为64π2cm ，用一个平面截球，使截面圆的半径为2cm ，则截面与球心的距离是 cm【答案】234.一个圆锥与一个球体积相等且圆锥的底面半径是球半径的2倍，若圆锥的高为1，则球的表面积为 ．【答案】45.一个底面置于水平面上的圆锥，若主视图是边长为2的正三角形，则圆锥的侧面积为 ．【答案】46.如图所示：在直三棱柱111ABC A B C -中，AB BC ⊥，1AB BC BB ==，则平面11A B 与平面ABC 所成的二面角的大小为 ． 【答案】4π二、选择题1.如图，已知圆锥的底面半径为10r =，点Q 为半圆弧AB 的中点， 点P 为母线SA 的中点．若PQ 与SO 所成角为4π，则此圆锥的 全面积与体积分别为（ ）A ．100051006,ππ B ．10005100(16),ππ+C ．100031003,ππD ．10003100(13),ππ+【答案】B2.如图，取一个底面半径和高都为R 的圆柱，从圆柱中挖去一个以圆柱的上底面为底面，下底面圆心为顶点的圆锥，把所得的几何体与一个半径为R 的半球放在同一水平面α上．用一平行于平面α的平面去截这两个几何体，截面分别为圆面和圆环面（图中阴影部分）．设截面面积分别为S 圆和S 圆环，那么（ ） A ．S 圆＞S 圆环 B ．S 圆＜S 圆环 C ．S 圆=S 圆环 D ．不确定3.如图所示，PAB ∆所在平面α和四边形ABCD 所在的平面β互相垂直，且AD α⊥，BC α⊥，4AD =，8BC =，6AB =，若tan 2tan 1ADP BCP ∠-∠=，则动点P在平面α内的轨迹是（ ） A.线段 B.椭圆的一部分 C.抛物线 D.双曲线的一部分PSA Q OB βαP BA DC【答案】D4.在空间中，下列命题正确的是（ ）A ．若两直线,a b 与直线l 所成的角相等，那么//a bB ．空间不同的三点A 、B 、C 确定一个平面C. 如果直线//l 平面α且//l 平面β，那么//αβ D ．若直线a 与平面M 没有公共点，则直线//a 平面M 【答案】D5.如图，已知直线l ⊥平面α，垂足为O ，在ABC △中，2,2,BC AC AB ===P 是边AC 上的动点.该三角形在空间按以下条件作自由移动：(1)A l ∈，(2)C α∈.则OP PB+的最大值为( ) (A) 2. (B) 1【答案】C6.平面α上存在不同的三点到平面β的距离相等且不为零，则平面α与平面β的位置关系为（ ）)(A 平行 )(B 相交)(C 平行或重合 )(D 平行或相交 【答案】D7.a b c 、、表示直线，α表示平面，下列命题正确的是（ ）A ．若//,//αa b a ，则//αbB ． 若,α⊥⊥a b b ，则α⊥aC ．若,⊥⊥a c b c ，则//a bD ．若,αα⊥⊥a b ，则//a b 【答案】D8.下列命题中，正确的个数是【 】① 直线上有两个点到平面的距离相等，则这条直线和这个平面平行； ② a 、b 为异面直线，则过a 且与b 平行的平面有且仅有一个； ③ 直四棱柱是直平行六面体；④ 两相邻侧面所成角相等的棱锥是正棱锥．A 、0B 、1C 、2D 、3 【答案】B9.在四棱锥ABCD V -中，1B ，1D 分别为侧棱VB ，VD 的中点，则四面体11CD AB 的体积与四棱锥 ABCD V -的体积之比为（ ）A ．6:1B ．5:1C ．4:1D ．3:1【答案】C三、解答题1.（本题满分14分）本题共有2小题，第(1)小题满分6分，第(2)小题满分8分． 如图，在长方体1111ABCD A B C D -中，11AD AA ==，2AB =，点E 在棱AB 上移动． （1）证明：11D E A D ⊥；（2）AE 等于何值时，二面角1D EC D --的大小为4π． 【答案】解：（1）在如图所示的空间直角坐标系中，1A 设(1,,0)([0,2])E y y ∈ 则11(1,,1),(1,0,1)D E y DA =-=…… （2）方法一：设(,,)n u v w =为平面1D CE 的一个法向量 由1100n CD n D E ⎧⋅=⎪⎨⋅=⎪⎩，得200v w u yv w -+=⎧⎨+-=⎩，所以(2)2u y v w v =-⎧⎨=⎩…xABl CαNPO因为二面角1D EC D --的大小为4π，所以22222cos ||42(2)5u v wy π===++-+ 又[0,2]y ∈，所以23y =-，即当23AE =-时二面角1D EC D --的大小为4π2.（本题满分14分）本题共有2小题，第(1)小题满分6分，第(2)小题满分8分．如图，在长方体1111ABCD A B C D -中，11AD AA ==，2AB =，点E 在棱AB 上移动． （1）当E 为AB 的中点时，求四面体1E ACD -的体积； （2）证明：11D E A D ⊥． 【答案】解：（1）1122ACE S AE BC ∆=⋅=… 因为1D D ACE ⊥平面，所以1111136E ACD D ACE ACE V V S D D --∆==⋅=… （2）正方形11ADD A 中，11A D AD ⊥……因为11AB ADD A ⊥平面，所以1AB A D ⊥…所以11A D AD E ⊥平面…所以11D E A D ⊥……3.三棱柱111C B A ABC -中，它的体积是315，底面ABC ∆中，090=∠BAC ，3,4==AC AB ,1B 在底面的射影是D ，且D 为BC 的中点．（1）求侧棱1BB 与底面ABC 所成角的大小；(7分) （2）求异面直线D B 1与1CA 所成角的大小．(6分)【答案】解：（1）依题意，⊥D B 1面ABC ，BD B 1∠就是侧棱1BB 与底面ABC 所成的角θ 2分111111431532ABC A B C ABC V S B D B D -∆=⋅=⨯⨯⨯=4分1532B D =5分计算25=BD ，θθtan 25tan 1==BD D B ， tan 3,3πθθ=∴= 7分 （2）取11C B 的中点E ，连E A EC 1,，则1ECA ∠（或其补角）为所求的异面直线的角的大小 9分 ⊥D B 1面ABC ，D B 1‖CE ，面ABC ‖面111C B A ⊥∴CE 面111C B A ，E A CE 1⊥∴ 11分33325tan 251===∠EC AE CE A 12分 所求异面直线D B 1与1CA 所成的角6π13分 4.在如图所示的几何体中，四边形CDPQ 为矩形，四边形ABCD 为直角梯形，且90BAD ADC ∠=∠=，平面CDPQ ⊥平面ABCD ，112AB AD CD ===，2PD =.（1）若M 为PA 的中点，求证：AC //平面DMQ ；（2）求平面PAD 与平面PBC 所成的锐二面角的大小.D 1C 1A 1A ED B 1BC1A A BCQP DM(第20题图）D 1C 1B 1BCDA 1A【答案】解：（1）如图，设CP 与M 的交点为N ，连接MN ．易知点N 是CP 的中点，又M 为PA 的中点，故//AC MN ．…4分 于是，由MN ∉平面DMQ ，得//AC 平面DMQ ．……………6分 （2）如图，以点D 为原点，分别以DA DB DC 、、为x 轴，y 轴，z 轴，建立空间直角坐标系，则(0,0,0),(1,0,0),(1,1,0),(0,2,0),D A B C P ．易知1(0,1,0)n =为平面PAD 的一个法向量，设2(,,)n x y z =为平面PBC 的一个法向量．则22020n BC x y n PC y ⎧=-+=⎪⎨=-=⎪⎩x y z =⎧⎪⇒⎨=⎪⎩，令1y =，得2(1,1n =．…………………10分 设平面PAD 与平面PBC 所成的锐二面角为θ，则12121cos 2n n n n θ==，…………………12分 故平面PAD 与平面PBC 所成的锐二面角的大小为3π．………………………………………14分5.(本题满分14分) 本题共2个小题，第1小题6分，第2小题8分. 在如图所示的直四棱柱1111ABCD A B C D -中，底面ABCD 是边长为2的 菱形，且60,BAD ∠=︒1 4.AA =（1）求直四棱柱1111ABCD A B C D -的体积； （2）求异面直线11AD BA 与所成角的大小．【答案】解：（1）因菱形ABCD 的面积为2sin60AB ⋅︒=……2分故直四棱柱1111ABCD A B C D -的体积为：14ABCD S AA ⋅==底面……6分（2）连接111BC A C 、，易知11//BC AD ，故11A BC ∠等于异面直线11AD BA 与所成角. ……8分由已知，可得1111A B BC AC === ……10分 则在11A BC ∆中，由余弦定理，得222111111117cos .210A B BC AC A BC A B BC +-∠==⋅……12分 故异面直线11AD BA 与所成角的大小为7cos.10arc……14分 6.（本题满分12分）本题共2小题，第1小题满分6分，第2小题满分6分.在长方体1111ABCD A B C D -中，2AB BC ==，13AA =，过11,,A C B 三点的平面截去长方体的一个角后，得到如下所示的几何体111ABCD AC D -.（1）若11A C 的中点为1O ，求求异面直线1BO 与11A D 所成角的大小（用反三角函数值表示）； （2）求点D 到平面11A BC 的距离d ．【答案】解：(1)按如图所示建立空间直角坐标系．由题知，可得点D(0,0,0)、(2,2,0)B 、1(0,0,3)D 、1(2,0,3)A 、1(0,2,3)C ．由1O 是11A C 中点，可得1(1,1,3)O .于是，111(1,1,3),(2,0,0)BO A D =--=-． 设异面直线1BO 与11A D 所成的角为θ，ABCD 1A 1C 1D则111111cos ||||2BO A DBO A D θ⋅===因此，异面直线1BO 与11A D 所成的角为arccos 11． (2)设(,,)nx y z =是平面ABD 的法向量． ∴110,0.n BA n BC ⎧⋅=⎪⎨⋅=⎪⎩ 又11(0,2,3),(2,0,3)BA BC =-=-，∴230,230.y z x z -+=⎧⎨-+=⎩ 取2z =， 可得3,3,2.x y z =⎧⎪=⎨⎪=⎩即平面11BA C的一个法向量是(3,3,2)n =． ∴||n DB d n ⋅==． 7.(本题满分12分)本题共有2个小题，第1小题满分6分，第2小题满分6分．在长方体1111ABCD A B C D -中，2AB BC ==，13AA =，过1A 、1C 、B 三点的平面截去长方体的 一个角后，得到如下所示的几何体111ABCD AC D -．（1）求几何体111ABCD AC D -的体积，并画出该几何体的左视图(AB 平行主视图投影所在的平面)； （2）求异面直线1BC 与11A D 所成角的大小（结果用反三角函数值表示）． 【答案】解：2AB BC ==，13AA =，左视图如右图所示． (2)依据题意，有11,A D AD AD BC ，即11A D BC ．∴1C BC ∠就是异面直线1BC 与11A D 所成的角． 又1C C BC ⊥，∴113tan 2C C C BC BC ∠==．∴异面直线1BC 与角是3tan2arc ． 8. (本题满分12分)本题共有2个小题，第1小题满分4分，第2小题满分8分．如图，在直三棱柱111C B A ABC -中，已知21===AB BC AA ，AB ⊥BC ． （1）求四棱锥111A BCC B -的体积； （2）求二面角111C C A B --的大小．【答案】解：（1）因为AB ⊥BC ，三棱柱111C B A ABC -是直三棱柱，所以从而11A B 是四棱锥111A BCC B -的高. ……………………………………2分 四棱锥111A BCC B -的体积为1822233V =⨯⨯⨯=…………………………4分 （2）如图（图略），建立空间直角坐标系．则A （2，0，0），C （0，2，0），A 1（2，0，2），B 1（0，0，2），C 1（0，2，2）， 设AC 的中点为M ，,,1CC BM AC BM ⊥⊥)0,1,1(11=⊥∴C ，C A BM 即平面是平面A 1C 1C 的一个法向量．设平面A 1B 1C 的一个法向量是),,(z y x n =，)0,0,2(),2,2,2(11-=--=B A AC …8分 令z=1，解得x=0，y=1．)1,1,0(=∴， …………………………………………9分 设法向量n 与BM 的夹角为ϕ，二面角B 1—A 1C —C 1的大小为θ，显然θ为锐角．ABCD1C 1D A1A 1111.3B AC Cπ∴--二面角的大小为………………………………………………12分9. (本题满分12分)本题共有2个小题，第1小题满分4分，第2小题满分8分．如图，在正三棱柱111CBAABC-中，已知16AA=，三棱柱111CBAABC-（1）求正三棱柱111CBAABC-的表面积；（2）求异面直线1BC与1AA所成角的大小.【答案】解：（1）因为三棱柱的体积为16AA=，从而2ABCS∆==因此BC=. ………………………2分该三棱柱的表面积为2+ABCS S S∆=⋅=全侧………4分（2）由（1）可知BC=因为1CC//1AA.所以1BC C∠为异面直线1BC与1AA所成的角，………8分在Rt1BC C∆中，1tan63BC C∠==，所以1BC C∠=6π.异面直线1BC与1AA所成的角6π……………………………………………12分10.如图，已知圆锥的底面半径为10r=，点Q为半圆弧AB的中点，点PPQ与SO所成的角为4π，求此圆锥的表面积．【答案】解：取OA的中点M,连接PM,又点P为母线SA的中点所以//PM OS，故MPQ∠为PQ与SO所成的角． (2)在Rt MPQ△中，4MPQπ∠=，PM QM=，………………………4分由点Q为半圆弧AB的中点知OQ AB⊥，在Rt MOQ△中，10,5OQ OM MQ==⇒=故PM=，所以OS=SA所以2S100rππ==底，10S r SAππ=⋅=⨯⨯=侧………………10分100100(1S S Sππ=+=+=+全底侧．…………………………………12分11.（本大题共有2个小题，满分14分）第（1）小题满分7分，第（2）小题满分7分．如图，在四棱锥P ABCD-中，底面正方形ABCD为边长为2，PA⊥底面ABCD，E为BC的中点，PC与平面PAD所成的角为．（1）求异面直线AE与PD所成角的大小（结果用反三角函数表示）；（2）求点B到平面PCD的距离．【答案】解：方法１,（1）因为底面ABCD为边长为2的正方形，⊥PA底面ABCD,则⊥⇒⎪⎭⎪⎬⎫=⊥⊥CDAPAADPACDADCD平面PAD，所以CPD∠就是CP与平面PAD所成的角．………………2分PAB CD在CDP Rt ∆中，由22tan ==∠PD CD CPD ，得22=PD，…………………………3分 在PAD Rt ∆中，2=PA ．分别取AD 、PA 的中点M 、N ，联结MC 、NC 、MN ， 则NMC ∠异面直线AE 与PD 所成角或补角．……………4分 在MNC ∆中，2=MN ，MC =，3NC =，由余弦定理得，2223cos 10NMC +-∠==-， 所以NMC π∠=-，………6分 即异面直线AE 与PD 所成角的大小为1010arccos ．……7分（2）设点B 到平面PCD 的距离为h ，因为BCD P PCD B V V --=，…………………………9分 所以，11113232CD PD h BC CD PA ⨯⋅⋅=⨯⋅⋅，得h =14分 方法２，（1） 如图所示，建立空间直角坐标系，同方法１，得2=PA ，……………3分 则有关点的坐标分别为()0,0,0A ，()2,1,0E ，()0,2,0D ，()2,0,0P 所以()2,1,0AE =，()2,2,0-=．设θ为异面直线AE 与PD 所成角， 则()101085202102cos =⨯-⨯+⨯+⨯=θ，所以，1010arccos =θ，即异面直线AE 与PD 所成角的大小为1010arccos（2）因为()2,2,0-=PD ，()0,0,2=CD ，()0,2,0=BC ，设()w v u n ,,=， 则由⎩⎨⎧==⇒⎪⎩⎪⎨⎧==⋅=-=⋅w v u u w v 002022，………………………………………………11分 可得()1,1,0=，所以2n BC d n⋅===14分 12.（本题共有2个小题，满分14分）；第（1）小题满分7分，第（2）小题满分7分. 如图，在四棱锥ABCD P -中，底面ABCD 为边长为2的正方形， ⊥PA 底面ABCD , 2=PA ．（1）求异面直线PC 与BD 所成角的大小； （2）求点A 到平面PBD 的距离．【答案】解：（1）联结AC 与BD 交于点M ，取PA 的中点N ，联结MN ，则CP MN //，P ABCD MNyPABCD所以NMB ∠为异面直线PC 与BD 所成角或补角．……………………2分 在BMN ∆中，由已知条件得，5=BN ，2=BM ，3=MN ，…………5分所以222MN BM BN +=，2π=∠BMN ，所以异面直PC 与BD 所成角为2π．…7分 （或用线面垂直求异面直线PC 与BD 所成角的大小）（2）设点A 到平面PBD 的距离为h ，因为ABD P PBD A V V --=，……………9分所以，11113232BD PM h BC CD PA ⨯⋅⋅=⨯⋅⋅，得332=h ．（或在MAN Rt ∆中求解）………14分 13.(本题满分14分)本题共有2个小题，第1小题满分6分，第2小题满分8分． 在正方体1111-ABCD A B C D 中，E 是棱1DD 的中点．（1）求直线BE 与平面11ABB A 所成的角的大小（结果用反三角函数值表示）； （2）在棱11C D 上是否存在一点F ，使得1//B F 平面1A BE ，若存在，指明点F 的位置；若不存在，说明理由．【答案】解：（1）以A 为坐标原点，以射线1AB AD AA 、、分别为x y z 、、轴，建立空间 直角坐标系，如图所示.不妨设正方体1111ABCD A B C D -的棱长为a （0a >），则(,0,0),(0,,)2aB a E a ，于是(,,)2a BE a a =- 3分 根据正方体的性质，可知11DA ABB A ⊥平面,故11AD ABB A 是平面的一个法向量且AD =(0,,0)a 4分设直线BE 与平面11ABB A 所成的较为θ，则22sin 0332BE AD a BE ADa a θ===>⨯ 5分 所以2arcsin3θ=，故直线BE 与平面11ABB A 所成的角的大小为2arcsin 3. 6分（2）假设在棱11C D 上是存在一点F ,使得11//B F A BE 平面,设(,,)F x a a （其中0x a ≤≤）111(,0,0),(0,0,),(,0,),(,,0)B a A a BA a a B F x a a =-=- 8分根据（1）可知，(,,)2aBE a a =- 9分设(,,)n x y z =平面1A BE 的一个法向量，则100n BA n BE ⎧=⎪⎨=⎪⎩，即002ax az aax ay z -=⎧⎪⎨--=⎪⎩， 10分 取2z =，则(2,1,2)n =，由于直线11//B F A BE 平面,所以10B F n = 11分即(,,0)(2,1,2)0x a a -=，化简得2()0x a a -+=，解得2ax = 12分故在棱11C D 上是存在一点F ，使得11//B F A BE 平面,且点F 是棱11C D 的中点. 14分NPAB DMy14.在正方体1111-ABCD A B C D 中，E 是棱1DD 的中点． 求直线BE 与11B A 所成的角的大小（结果用反三角函数值表示）； 【答案】解：设正方体的棱长为a ，根据正方体的性质可得： 四棱锥E ABCD -的底面积2ABCD S a =，高2aED =2分21143323ABCD a V S ED a =⨯⨯=⨯=，解得2a = 5分因为11//AB A B ,所以ABE ∠即为异面直线BE 与11B A 所成角 或其补角， 8分在ABE中，2,3AB AE BE ===,由余弦定理可得4952cos 02233ABE +-∠==>⨯⨯，即2arccos 3ABE ∠= 11分所以异面直线BE 与11B A 所成的较的大小为2arccos 3ABE ∠=. 12分15.(本题满分12分) 本题共有2个小题，第1小题满分6分，第2小题满分6分． 如图，在Rt AOB ∆中，6OAB π∠=，斜边4AB =，D 是AB 的中点．现将Rt AOB ∆以直角边AO 为轴旋转一周得到一个圆锥，点C 为圆锥底面圆周上的一点，且2BOC π∠=．（1）求该圆锥的全面积；（2）求异面直线AO 与CD 所成角的大小．（结果用反三角函数值表示）【答案】解：（1）在Rt AOB ∆中，2OB =，即圆锥底面半径为2圆锥的侧面积8S rl ππ==侧………………..4’故圆锥的全面积=+8+412S S S πππ==全侧底……………….6’（2）解法一：如图建立空间直角坐标系．则(0,0,(2,0,0),A C D(0,0,23),(AO CD ∴=-=-………………..8’设AO 与CD 所成角为θ，则cos 42AO CD AO CDθ⋅===-⋅∴异面直线AO 与CD 所成角为arc ..12’ 解法二：过D 作//DM AO 交BO 于M ，连CM则CDM ∠为异面直线AO 与CD 所成角………………..8’在Rt AOB ∆中，AO =DM ∴=D 是AB 的中点 M ∴是OB 的中点 1OM ∴=CM ∴=在Rt CDM ∆中，tan CDM ∠==，………………..10’CDM ∴∠=AO 与CD 所成角的大小为……………….12’ 16.在棱长为1的正方体1111ABCD A B C D -中，点E 是棱BC 的中点，点F 是棱CD 上的动点.（1）试确定点F 的位置，使得1D E ⊥平面1AB F ;ED 1C 1A 1B 1CDBA1A 1D 1C 1B（2）当1D E ⊥平面1AB F 时，求二面角1C EF A --的大小（结果用反三角函数表示）. 【答案】解：（1）如图建系，设 ),10(≤≤=x x DF 1分 则)0,1,()0,21,1()1,1,0()1,0,1(),0,1,0(),0,0,1(),0,0,0(11x F E D B D B A 2分)0,1,(),1,0,1(),1,21,1(11x AF AB E D ==--=∴, 3分1111,011AB E D AB E D ⊥∴=-=⋅ 4分 由AF E D F AB E D ⊥∴⊥111,平面 5分21,01=⇒=⋅∴x AF E D 6分)0,1,21(F ∴，即F 为CD 中点时F AB E D 11平面⊥。

全国通用2020_2022三年高考数学真题分项汇编：05 立体几何（选择题、填空题）（文科专用）1．【2022年全国甲卷】如图，网格纸上绘制的是一个多面体的三视图，网格小正方形的边长为1，则该多面体的体积为（）A．8 B．12 C．16 D．20【答案】B【解析】【分析】由三视图还原几何体，再由棱柱的体积公式即可得解.【详解】由三视图还原几何体，如图，×2×2=12.则该直四棱柱的体积V=2+42故选：B.2．【2022年全国甲卷】在长方体ABCD−A1B1C1D1中，已知B1D与平面ABCD和平面AA1B1B 所成的角均为30°，则（）A．AB=2AD B．AB与平面AB1C1D所成的角为30°C．AC=CB1D．B1D与平面BB1C1C所成的角为45°【答案】D【解析】【分析】根据线面角的定义以及长方体的结构特征即可求出． 【详解】 如图所示：不妨设AB =a,AD =b,AA 1=c ，依题以及长方体的结构特征可知，B 1D 与平面ABCD 所成角为∠B 1DB ，B 1D 与平面AA 1B 1B 所成角为∠DB 1A ，所以sin30∘=cB 1D=b B 1D，即b =c ，B 1D =2c =√a 2+b 2+c 2，解得a =√2c ．对于A ，AB =a ，AD =b ，AB =√2AD ，A 错误；对于B ，过B 作BE ⊥AB 1于E ，易知BE ⊥平面AB 1C 1D ，所以AB 与平面AB 1C 1D 所成角为∠BAE ，因为tan ∠BAE =c a=√22，所以∠BAE ≠30∘，B 错误；对于C ，AC =√a 2+b 2=√3c ，CB 1=√b 2+c 2=√2c ，AC ≠CB 1，C 错误； 对于D ，B 1D 与平面BB 1C 1C 所成角为∠DB 1C ，sin ∠DB 1C =CDB 1D=a2c =√22，而0<∠DB 1C<90∘，所以∠DB 1C =45∘．D 正确． 故选：D ．3．【2022年全国甲卷】甲、乙两个圆锥的母线长相等，侧面展开图的圆心角之和为2π，侧面积分别为S 甲和S 乙，体积分别为V 甲和V 乙．若S 甲S 乙=2，则V 甲V 乙=（ ）A ．√5B ．2√2C ．√10D ．5√104【答案】C 【解析】 【分析】设母线长为l ，甲圆锥底面半径为r 1，乙圆锥底面圆半径为r 2，根据圆锥的侧面积公式可得r 1=2r 2，再结合圆心角之和可将r 1,r 2分别用l 表示，再利用勾股定理分别求出两圆锥的高，再根据圆锥的体积公式即可得解. 【详解】解：设母线长为l ，甲圆锥底面半径为r 1，乙圆锥底面圆半径为r 2，则S 甲S 乙=πr 1l πr 2l =r1r 2=2， 所以r 1=2r 2， 又2πr 1l +2πr 2l=2π，则r 1+r 2l=1，所以r 1=23l,r 2=13l ，所以甲圆锥的高ℎ1=√l 2−49l 2=√53l ，乙圆锥的高ℎ2=√l 2−19l 2=2√23l ， 所以V 甲V 乙=13πr 12ℎ113πr 22ℎ2=49l 2×√53l 19l ×2√23l =√10.故选：C.4．【2022年全国乙卷】在正方体ABCD −A 1B 1C 1D 1中，E ，F 分别为AB,BC 的中点，则（ ） A ．平面B 1EF ⊥平面BDD 1 B ．平面B 1EF ⊥平面A 1BD C ．平面B 1EF//平面A 1AC D ．平面B 1EF//平面A 1C 1D【答案】A 【解析】 【分析】证明EF ⊥平面BDD 1，即可判断A ；如图，以点D 为原点，建立空间直角坐标系，设AB =2，分别求出平面B 1EF ，A 1BD ，A 1C 1D 的法向量，根据法向量的位置关系，即可判断BCD. 【详解】解：在正方体ABCD −A 1B 1C 1D 1中， AC ⊥BD 且DD 1⊥平面ABCD ， 又EF ⊂平面ABCD ，所以EF ⊥DD 1， 因为E,F 分别为AB,BC 的中点， 所以EF ∥AC ，所以EF ⊥BD ， 又BD ∩DD 1=D ， 所以EF ⊥平面BDD 1， 又EF ⊂平面B 1EF ，所以平面B 1EF ⊥平面BDD 1，故A 正确； 对于选项B ，如图所示，设11A BB E M =，EF BD N =，则MN 为平面1B EF 与平面1A BD 的交线，在BMN △内，作BP MN ⊥于点P ，在EMN △内，作GP MN ⊥，交EN 于点G ，连结BG ，则BPG ∠或其补角为平面1B EF 与平面1A BD 所成二面角的平面角，由勾股定理可知：222PB PN BN +=，222PG PN GN +=， 底面正方形ABCD 中，,E F 为中点，则EF BD ⊥， 由勾股定理可得222NB NG BG +=，从而有：()()2222222NB NG PB PN PG PN BG +=+++=， 据此可得222PB PG BG +≠，即90BPG ∠≠， 据此可得平面1B EF ⊥平面1A BD 不成立，选项B 错误； 对于选项C ，取11A B 的中点H ，则1AHB E ，由于AH 与平面1A AC 相交，故平面1B EF 平面1A AC 不成立，选项C 错误；对于选项D ，取AD 的中点M ，很明显四边形11A B FM 为平行四边形，则11A MB F ，由于1A M 与平面11AC D 相交，故平面1B EF 平面11AC D 不成立，选项D 错误；故选：A.5．【2022年全国乙卷】已知球O的半径为1，四棱锥的顶点为O，底面的四个顶点均在球O 的球面上，则当该四棱锥的体积最大时，其高为（）A．13B．12C．√33D．√22【答案】C【解析】【分析】先证明当四棱锥的顶点O到底面ABCD所在小圆距离一定时，底面ABCD面积最大值为2r2，进而得到四棱锥体积表达式，再利用均值定理去求四棱锥体积的最大值，从而得到当该四棱锥的体积最大时其高的值.【详解】设该四棱锥底面为四边形ABCD，四边形ABCD所在小圆半径为r，设四边形ABCD对角线夹角为α，则S ABCD=12⋅AC⋅BD⋅sinα≤12⋅AC⋅BD≤12⋅2r⋅2r=2r2（当且仅当四边形ABCD为正方形时等号成立）即当四棱锥的顶点O到底面ABCD所在小圆距离一定时，底面ABCD面积最大值为2r2又r2+ℎ2=1则V O−ABCD=13⋅2r2⋅ℎ=√23√r2⋅r2⋅2ℎ2≤√23√(r2+r2+2ℎ23)3=4√327当且仅当r2=2ℎ2即ℎ=√33时等号成立，故选：C6．【2021年甲卷文科】在一个正方体中，过顶点A的三条棱的中点分别为E，F，G．该正方体截去三棱锥A EFG后，所得多面体的三视图中，正视图如图所示，则相应的侧视图是（）A ．B ．C ．D ．【答案】D 【解析】 【分析】根据题意及题目所给的正视图还原出几何体的直观图，结合直观图进行判断. 【详解】由题意及正视图可得几何体的直观图，如图所示，所以其侧视图为故选：D7．【2021年乙卷文科】在正方体1111ABCD A B C D 中，P 为11B D 的中点，则直线PB 与1AD 所成的角为（ ）A ．π2B ．π3C ．π4D ．π6【答案】D 【解析】 【分析】平移直线1AD 至1BC ，将直线PB 与1AD 所成的角转化为PB 与1BC 所成的角，解三角形即可. 【详解】如图，连接11,,BC PC PB ，因为1AD ∥1BC ， 所以1PBC ∠或其补角为直线PB 与1AD 所成的角，因为1BB ⊥平面1111D C B A ，所以11BB PC ⊥，又111PC B D ⊥，1111BB B D B ⋂=， 所以1PC ⊥平面1PBB ，所以1PC PB ⊥， 设正方体棱长为2，则111112BC PC D B === 1111sin 2PC PBC BC ∠==，所以16PBC π∠=. 故选：D8．【2021年甲卷文科】已知一个圆锥的底面半径为6，其体积为30π则该圆锥的侧面积为________. 【答案】39π 【解析】 【分析】利用体积公式求出圆锥的高，进一步求出母线长，最终利用侧面积公式求出答案. 【详解】∵216303V h ππ=⋅=∴52h =∴132 l==∴136392S rlπππ==⨯⨯=侧.故答案为：39π.9．【2021年乙卷文科】以图①为正视图，在图②③④⑤中选两个分别作为侧视图和俯视图，组成某个三棱锥的三视图，则所选侧视图和俯视图的编号依次为_________（写出符合要求的一组答案即可）．【答案】③④（答案不唯一）【解析】【分析】由题意结合所给的图形确定一组三视图的组合即可.【详解】选择侧视图为③，俯视图为④，如图所示，长方体1111ABCD A B C D -中，12,1AB BC BB ===，,E F 分别为棱11,B C BC 的中点，则正视图①，侧视图③，俯视图④对应的几何体为三棱锥E ADF -. 故答案为：③④. 【点睛】三视图问题解决的关键之处是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系.。

四川省2019届高三数学理一轮复习典型题专项训练立体几何一、选择、填空题1、（2018全国III 卷高考）中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫棒头，凹进部分叫卯眼，图中木构件右边的小长方体是棒头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是（ ）2、（2017全国III 卷高考）已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为（） A ．πB ．3π4C ．π２D ．π43、（2016全国III 卷高考）如图，网格纸上小正方形的边长为1，粗实现画出的是某多面体的三视图，则该多面体的表面积为（A ）18365+ （B ）54185+ （C ）90 （D ）814、（成都市2018届高三第二次诊断）已知m ，是空间中两条不同的直线，α，β为空间中两个互相垂直的平面，则下列命题正确的是（ ）A ．若m α⊂，则m β⊥B ．若m α⊂，n β⊂，则m n ⊥C ．若m α⊄，m β⊥，则//m αD ．若m αβ=，n m ⊥，则n α⊥5、（成都市2018届高三第三次诊断）在正三棱柱111ABC A B C - (底面是正三角形,侧棱垂直于底面的棱柱)中，所有棱长之和为定值a .若正三棱柱111ABC A B C -的顶点都在球O 的表面上，则当正三棱柱侧面积取得最大值24时，该球的表面积为（ ） A ．43π B ．323π C ．12π D ．643π6、（达州市2017届高三第一次诊断）如图某几何体的三视图是直角边长为1的三个等腰直角三角形，则该几何体的外接球的表面积为（ ） A ．32π B ．3π C ．32π D ．3π7、（德阳市2018届高三二诊考试）如图所示的三视图表示的几何体的体积为323，则该几何体的外接球的表面积为（ ）A ．12πB ．24πC ．36πD ．48π8、（广元市2018届高三第一次高考适应性统考）设,m n 是两条不同的直线，,αβ是两个不同的平面，且,m n αβ⊂⊂，下列命题中正确的是（ ）A ．若αβ⊥，则m n ⊥B ．若//αβ，则//m nC ．若m n ⊥，则αβ⊥D ．若n α⊥，则αβ⊥9、（泸州市2018届高三第二次教学质量诊断）设a ，b 是两条不同的直线，α、β是不重合的两个平面，则下列命题中正确的是A ．若a b ⊥，a α⊥，则//b αB ．若//a α，αβ⊥，则//a βC ．若//a α，//a β，则//αβD ．若//a b ，a α⊥，b β⊥，则//αβ10、（南充市2018届高三第二次高考适应性考试）某三棱锥的三视图如图所示，则该三棱锥的表面积为( )A ．23472++B ．1072+ C. 710+ D ．3412+11、（仁寿县2018届高三上学期零诊）如图，正方体ABCD ﹣A 1B 1C 1D 1的棱长为1，E 为棱DD 1上的点，F 为AB 的中点，则三棱锥B 1﹣BFE 的体积为12、（遂宁市2018届高三三诊考试）在一圆柱中挖去一圆锥所得的机械部件的三视图如图所示，则此机械部件的表面积为A ．π)27(-B ．π)27(+C ．π)26(+D ．π)37(-13、（雅安市2018届高三下学期三诊）某几何体的三视图如图所示，其中，正视图、俯视图都是矩形，侧视图是直角三角形，则该几何体的体积等于（ ）A ．1B ．2C ．3D ．414、（资阳市2018届高三4月模拟考试（三诊））如图，二面角BC αβ--的大小为6π，AB CD αβ⊂⊂，，且2AB =，243BC CD ABC BCD ππ==∠=∠=，，，则AD 与β所成角的大小为A ．π4B ．π3 C.π6D ．π1215、（成都市石室中学高2018届高三下期二诊模拟）一个底面为正方形的四棱锥，其三视图如图所示，若这个四棱锥的体积为2 ，则此四棱锥最长的侧棱长为 .23A.11B .13C .10D16、（成都市2018届高三第二次诊断）《九章算术》中将底面为长方形，且有一条侧棱与底面垂直的四棱锥称之为“阳马”.现有一阳马，其正视图和侧视图是如图所示的直角三角形.若该阳马的顶点都在同一个球面上，则该球的体积为（ ）A ．863π B ．86π C ．6π D ．24π 17、（2016全国III 卷高考）在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球，若AB BC ⊥，6AB =，8BC =，13AA =，则V 的最大值是（A ）4π （B ）92π（C ）6π （D ）323π二、解答题1、（2018全国III 卷高考）如图，边长为2的正方形ABCD 所在平面与半圆弧CD 所在平面垂直，M是CD 上异于C ，D 的点．⑴证明：平面AM D ⊥平面BMC ；⑵当三棱锥M ABC -体积最大时，求面MAB 与面MCD 所成二面角的正弦值．2、（2017全国III 卷高考）如图，四面体ABCD 中，△ABC 是正三角形，△ACD 是直角三角形．ABDCBD ??，AB BD =．（1）证明：平面ACD ^平面ABC ；（2）过AC 的平面交BD 于点E ，若平面AEC 把四面体ABCD 分成体积相等的两部分．求二面角D AE C --的余弦值．DABCE3、（2016全国III 卷高考）如图，四棱锥P ABC -中，PA ⊥地面A B C D ，ADBC ，3AB AD AC ===，4PA BC ==，M 为线段AD 上一点，2AM MD =，N 为PC 的中点．（I ）证明MN平面PAB ；（II ）求直线AN 与平面PMN 所成角的正弦值.4、（成都市2018届高三第二次诊断）如图，D 是AC 的中点，四边形BDEF 是菱形，平面BDEF ⊥平面ABC ，60FBD ∠=，AB BC ⊥，2AB BC ==.（1）若点M 是线段BF 的中点，证明：BF ⊥平面AMC ； （2）求平面AEF 与平面BCF 所成的锐二面角的余弦值.5、（成都市2018届高三第三次诊断）如图①,在等腰梯形ABCD 中，已知AB ∥CD ，60ABC ∠=，2CD =，4AB =，点E 为AB 的中点；现将三角形BEC 沿线段EC 折起，形成直二面角P EC A --,如图②，连接,PA PD 得四棱锥P AECD -，如图③.（I ）求证：PD EC ⊥；（Ⅱ）求平面PEC 与平面PAD 所成的锐二面角的余弦值.6、（达州市2017届高三第一次诊断）如图在棱锥P ABCD -中，ABCD 为矩形，PD ⊥面ABCD ，2PB =，PB 与面PCD 成045角，PB 与面ABD 成030角.（1）在PB 上是否存在一点E ，使PC ⊥面ADE ，若存在确定E 点位置，若不存在，请说明理由； （2）当E 为PB 中点时，求二面角P AE D --的余弦值.7、（德阳市2018届高三二诊考试）如图，在四棱锥P ABCD -中，底面ABCD 为边长为2的菱形，60DAB ∠=，90ADP ∠=，面ADP ⊥面ABCD ，点F 为棱PD 的中点.（1）在棱AB 上是否存在一点E ，使得//AF 面PCE ，并说明理由； （2）当二面角D FC B --的余弦值为14时，求直线PB 与平面ABCD 所成的角.8、（广元市2018届高三第一次高考适应性统考）如图，ABC ∆是以ABC ∠为直角的三角形，SA ⊥平面,2,4,,ABC SA BC AB M N ===分别是,SC AB 的中点. （1）求证：MN AB ⊥；（2）D 为线段BC 上的点，当二面角S ND A --的余弦值为66时，求三棱锥D SNC -的体积.9、（泸州市2018届高三第二次教学质量诊断）如图，三棱锥A BCD -的侧面ABD △是等腰直角三角形，90BAD ∠=，BD DC =，120BDC ∠=，且2AC AB =． （I ）求证：平面ABD ⊥平面BCD ； （II ）求二面角B AC D --的余弦值．DCBA10、（南充市2018届高三第二次高考适应性考试）如图，四棱锥ABCD P -中，底面ABCD 是边长为2的菱形，PB PA ABC ⊥︒=∠，660,2=PC . (Ⅰ)求证：平面⊥PAB 平面 ABCD ；(Ⅱ)若PB PA =,求二面角D PC A --的余弦值.11、（仁寿县2018届高三上学期零诊）如图，直角梯形ABCD 与等腰直角三角形ABE 所在的平面互相垂直，AB ∥CD ，AB ⊥BC ，AB=2CD=2BC ，EA ⊥EB （1）求证：EA ⊥平面EBC ； （2）求二面角C ﹣BE ﹣D 的余弦值．12、（遂宁市2018届高三三诊考试）如图所示的几何体中，111C B A ABC -为三棱柱，且⊥1AA 平面ABC ，四边形ABCD 为平行四边形，︒=∠=60,2ADC CD AD ．（1）若AC AA =1，求证：1AC ⊥平面CD B A 11； （2）若12,CD AA AC λ==，二面角11C A D C --的余弦值为24，求三棱锥11C ACD -的体积．13、（雅安市2018届高三下学期三诊）如图，在四棱锥S ABCD -中，SD ⊥底面ABCD ，M 为SD 的中点，底面ABCD 为直角梯形，AB AD ⊥，//AB CD ，且222CD AB AD ===.（1）求证：//AM 平面SBC ，平面SBC ⊥平面SDB ； （2）若SB 与平面SDC 所成角的正弦值为33，求二面角A SB C --的余弦值.14、（资阳市2018届高三4月模拟考试（三诊））如图，三棱柱111ABC A B C -的各棱长均相等，1AA ⊥底面ABC ，E ，F 分别为棱1AA BC ，的中点．（1）过1FA 作平面α，使得直线BE //平面α，若平面α与直线1BB 交于点H ，指出点H 所在的位置，并说明理由；（2）求二面角1B FH A --的余弦值．15、（成都市石室中学高2018届高三下期二诊模拟）如图，在多面体ABCDEF 中，矩形BDEF 所在平面与正方形ABC D 所在平面垂直，点M 为AE 的中点. （1）求证：BM //平面EFC（2）若DE AB =，求直线AE 与平面BDM 所成角的正弦值.参考答案： 一、选择、填空题 1、A 2、【答案】B【解析】由题可知球心在圆柱体中心，圆柱体上下底面圆半径2213122r ⎛⎫=-= ⎪⎝⎭，则圆柱体体积23ππ4V r h ==，故选B.3、B4、C5、【答案】D【解析】设正三棱柱111ABC A B C -底面边长为x ，侧棱为y ，则63x y a +=，三棱柱111ABC A B C -侧面积3S xy =.所以2216336224x y a S xy +⎛⎫=≤= ⎪⎝⎭，当且仅当632a x y ==，即,126a a x y ==时，等号成立，所以24a =，2x =，4y =.所以正三棱柱111ABC A B C -的外接球的球心O 到顶点A 的距离为443434+=，所以该球的表面积为643π.故选D.6、D7、C8、D9、D 10、B 11、11212、B 13、B 14、C 15、C 16、C 17、【答案】B 【解析】试题分析：要使球的体积V 最大，必须球的半径R 最大．由题意知球的与直三棱柱的上下底面都相切时，球的半径取得最大值32，此时球的体积为334439()3322R πππ==，故选B ．二、解答题1、解答：（1）∵正方形ABCD ⊥半圆面CMD ，∴AD ⊥半圆面CMD ，∴AD ⊥平面MCD .∵CM 在平面MCD 内，∴AD CM ⊥，又∵M 是半圆弧CD 上异于,C D 的点，∴CM MD ⊥.又∵AD DM D =I ，∴CM ⊥平面ADM ，∵CM 在平面BCM 内，∴平面BCM ⊥平面ADM .（2）如图建立坐标系： ∵ABC S ∆面积恒定，∴MO CD ⊥，M ABC V -最大.(0,0,1)M ，(2,1,0)A -，(2,1,0)B ，(0,1,0)C ，(0,1,0)D -,设面MAB 的法向量为111(,,)m x y z =u r ，设面MCD 的法向量为222(,,)n x y z =r， (2,1,1)MA =--，(2,1,1)MB =-，(0,1,1)MC =-，(0,1,1)MD =--，11111120(1,0,2)20x y z m x y z --=⎧⇒=⎨+-=⎩， 同理(1,0,0)n =，， ∴15cos 55θ==，∴ 25sin 5θ=.2、【解析】⑴取AC 中点为O ，连接BO ，DO ；ABC ∆为等边三角形∴BO AC ⊥∴AB BC =AB BC BD BDABD DBC =⎧⎪=⎨⎪∠=∠⎩ABD CBD ∴∆≅∆. ∴AD CD =,即ACD ∆为等腰直角三角形，ADC ∠ 为直角又O 为底边AC 中点 ∴DO AC ⊥令AB a =，则AB AC BC BD a ==== 易得：22OD a =，32OB a = ∴222OD OB BD +=由勾股定理的逆定理可得2DOB π∠=即OD OB ⊥OD ACOD OB AC OB O AC ABC OB ABC⊥⎧⎪⊥⎪⎪=⎨⎪⊂⎪⊂⎪⎩平面平面OD ABC ∴⊥平面 又∵OD ADC ⊂平面由面面垂直的判定定理可得ADC ABC ⊥平面平面 ⑵由题意可知V V D ACE B ACE --= 即B ,D 到平面ACE 的距离相等 即E 为BD 中点以O 为原点，OA 为x 轴正方向，OB 为y 轴正方向，OD 为z 轴正方向，设AC a =，建立空间直角坐标系，则()0,0,0O ，,0,02a A ⎛⎫ ⎪⎝⎭，0,0,2a D ⎛⎫ ⎪⎝⎭，30,,02B a ⎛⎫ ⎪ ⎪⎝⎭，30,,44a E a ⎛⎫ ⎪ ⎪⎝⎭ 易得：3,,244a a AE a ⎛⎫=- ⎪ ⎪⎝⎭，,0,22a a AD ⎛⎫=- ⎪⎝⎭，,0,02a OA ⎛⎫= ⎪⎝⎭ 设平面AED 的法向量为1n ，平面AEC 的法向量为2n ， 则110AE n AD n ⎧⋅=⎪⎨⋅=⎪⎩，解得()13,1,3n =DABC EODABCEyxOz220AE n OA n ⎧⋅=⎪⎨⋅=⎪⎩，解得()20,1,3n =- 若二面角D AE C --为θ，易知θ为锐角，则12127cos 7n n n n θ⋅==⋅ 3、设),,(z y x n =为平面PMN 的法向量，则⎪⎩⎪⎨⎧=⋅=⋅00PN n PM n ，即⎪⎩⎪⎨⎧=-+=-0225042z y x z x ，可取)1,2,0(=n ，于是2558|||||||,cos |=⋅=><AN n AN n AN n .4、解：（1）连接MD ，FD .∵四边形BDEF 为菱形，且60FBD ∠=，∴DBF ∆为等边三角形.∵M 为BF 的中点，∴DM BF ⊥.∵AB BC ⊥，2AB BC ==，又D 是AC 的中点， ∴BD AC ⊥. ∵平面BDEF平面ABC BD =，平面ABC ⊥平面BDEF ，AC ⊂平面ABC ，∴AC ⊥平面BDEF .又BF ⊂平面BDEF ，∴AC BF ⊥. 由DM BF ⊥，AC BF ⊥，DM AC D =，∴BF ⊥平面AMC.（2）设线段EF 的中点为N ，连接DN .易证DN ⊥平面ABC .以D 为坐标原点，DB ，DC ，DN 所在直线分别为轴，y 轴，轴建立如图所示的空间直角坐标系.则(0,1,0)A -，13(,0,)22E -，13(,0,)22F ，(1,0,0)B ，(0,1,0)C . ∴13(,1,)22AE =-，(1,0,0)EF =，13(,0,)22BF =-，(1,1,0)BC =-.设平面AEF ，平面BCF 的法向量分别为111(,,)m x y z =，222(,,)n x y z =.由00AE m EF m ⎧⋅=⎪⎨⋅=⎪⎩111113022102x y z x ⎧-++=⎪⎪⇒⎨⎪=⎪⎩.解得1132y z =-.取12z =-，∴(0,3,2)m =-.又由00BC n BF n ⎧⋅=⎪⎨⋅=⎪⎩2222013022x y x z -+=⎧⎪⇒⎨-+=⎪⎩解得223y z =. 取21z =，∴(3,3,1)n =. ∵cos ,m n <>m n m n⋅=11777==⋅.∴平面AEF 与平面BCF 所成的锐二面角的余弦值为17.5、 【解析】6、1)法一：要证明PC ⊥面ADE ，易知AD ⊥面PDC ，即得AD ⊥PC ，故只需0DE PC ⋅=即可， 所以由()00||1DP PE PC DP PC PE PC PE +⋅=⇒⋅+⋅=⇒=,即存在点E 为PC 中点 …6分 法二：建立如图所示的空间直角坐标系D －XYZ ， 由题意知PD ＝CD ＝1， 2CE =，设PE PB λ=， (2,1,1)PE PB λλ∴==-，(0,1,1)PC =-由()(0,1,1)(2,,1)0PC DE PC DP PE λλλ⋅=⋅+=-⋅-=，得12λ=， 即存在点E 为PC 中点。