当前位置：文档之家 › 测试系统动态特性

测试系统动态特性

  • 格式：ppt
  • 大小：2.09 MB
  • 文档页数：55

下载文档原格式

  / 55

合集下载

3 测试系统的基本特性 (动态识别、不失真)

3 测试系统的基本特性 (动态识别、不失真)

ξ
ζ = ζ = ζ = ζ = ζ = ζ =
0 .0 5 0 .1 0 0 .1 5 0 .2 5 0 .5 0 1 .0 0
3
η = ω /ω
n
位移共 振频率
ω r = ω n 1 − 2ζ
2
精确求法：
A(ω r ) 1 = 2 A(0) 2ζ 1 − 2ζ
ωn ζ
测 试 系 统 动 态 特 性 的 识 别
利用半功率法求
ζ
ω 2－ω1 ζ＝ 2ω n
适合阻尼比较小。
测 （二）阶跃响应法 试 系 统 阶跃响应法是以阶跃信号作为测试 动 态 系统的输入，通过对系统输出响应的测 特 试，从中计算出系统的动态特性参数。 性 的 这种方法实质上是一种瞬态响应法。即 识 别 通过研究瞬态阶段输出与输入之间的关
系找到系统的动态特性参数。
u (t )
t
y u (t ) = 1 − e
动 态 传 递 特 性 的 时 域 描 述
结论：一阶系统在单位阶跃激励下稳态输出 的理论误差为零，并且，进入稳态的时间
t→∞。但是，当t =4τ时，y(4τ)=0.982；误
差小于2%；当t =5τ时，y(5τ)=0.993,误差小 于1%。所以对于一阶系统来说，时间常数τ越小 越好。
3.3.3 测试系统动态特性参数的识别
频率响应法是以一组频率可调的标准正弦信号作为 系统的输入，通过对系统输出幅值和相位的测试，获得 系统的动态特性参数。
测 试 系 统 动 态 特 性 的 识 别
系统特性识别试验原理框图
测 试 系 统 动 态 特 性 的 识 别
一阶系统
A(ω ) =
A( ϖ) 1.0 0.8 0.6 0.4 0.2 0 0.707

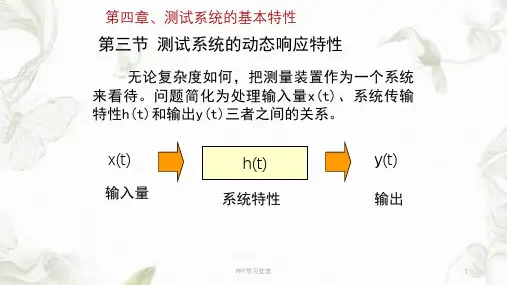
测试系统的动态响应特性ppt课件

测试系统的动态响应特性ppt课件
第四章、测试系统的基本特性
第三节 测试系统的动态响应特性
无论复杂度如何，把测量装置作为一个系统 来看待。问题简化为处理输入量x(t)、系统传输 特性h(t)和输出y(t)三者之间的关系。
x(t)
h(t)
y(t)
输入量
系统特性
输出
PPT学习交流
1
第三节 测试系统的动态响应特性
测试系统的动态特性 :是指输入量随时间变化时， 其输出随输入而变化的关系
PPT学习交流
15
3.3 测试系统的动态响应特性
小结:
系统特性在时域可以用脉冲响应函数 h( t )
来描述，
在频域可以用频率响应函数 来描述，
H()
在复数域可以用传递函数 来描述
H(s)
PPT学习交流
16
3.3 测试系统的动态响应特性
四、环节的串联和并联
串联 :由两个传递函数分别为 H1(s) 和 H2(s) 的 环节经串联后组成的测试系统
PPT学习交流
7
3.3 测试系统的动态响应特性---频响函数
频响函数:直观的反映了测试系统对不同频率成分输 入信号的扭曲情况。
A
PPT学习交流
8
3.3 测试系统的动态响应特性---频响函数
频响函数的测量(正弦波法)
依据：频率保持性
若
x(t)=Acos(ωt+φx)
则
y(t)=Bcos(ωt+φy)
令 H(s) 中 s 的实部为零，即 s=jω ，便可以求 得频率响应函数 H(ω)
在测得输入 x(t) 和输出 y(t) 后，由其傅里叶
变换 X(S) 和 Y(S) 可求得频率响应函数 H(ω)
A ( )H (j )RH (e j )[2 ]Im H (j )[2]

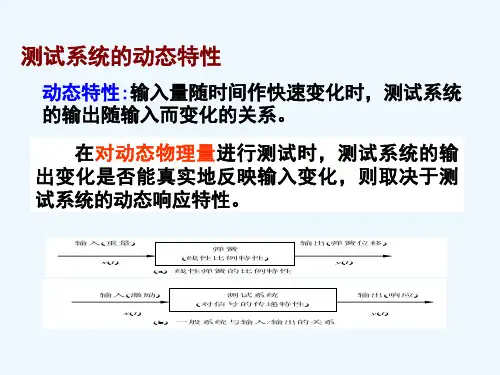
第二章 测试系统的基本特性-动态特性

第二章 测试系统的基本特性-动态特性

练习
0
( t ) 0 . 5 cos 10 t 0 . 2 cos( 100 t 45 ) 求周期信号 x
通过传递函数为
1 H (s ) 0 .005 s 1
的装置后得到的稳态响应?
一阶系统在典型输入下的响应
• 脉冲响应
x(t) (t) 其拉氏变换：X(s) 1 1 t / 一阶系统的响应： y(t) e
2 2 4 2
a r c t a n ( ) a r c t a5 . 2 3 1 0 ) 9 1 9 5 0
4 o
练习
一温度传感器为一阶系统，其时 间常数τ=0.001s，求当测量频率 f=100Hz信号时的幅值误差和相位误差。
1
1 () 1
2
≤0.05
1 ( ) ≤ 2 1 0 . 1 0 8 0 . 9 5
0 .00052
1 1 1 1 1 1 1 0 . 9 8 6 8 1 . 3 2 % ( )1 ( 2 f )1 ( 2 5 0 5 . 2 3 1 0 )1
n
n 2
1 4
22 2 n n
1
2
2 n ( ) arctg 2 1 n
二阶系统的幅相频特性
1) 、ω/ω A(ω) 近似水平直线， φ(ω) =-180º 4)、当 ω=ω 时， A(ω)=1/(2ξ) ， φ(ω) =-90º ， 。 n>2 n， 幅值剧增，共振。
m m 1
频率响应函数是传递函数的特例。
Y ( j ) X ( j ) H ( j )
传递函数H(s)是在复数域中描述和考察系统的 特性；频率响应函数H(ω)是在频域中描述和 考察系统特性。

简述系统动态特性及其测定方法

简述系统动态特性及其测定方法

简述系统动态特性及其测定方法系统的特性可分为静态特性和动态特性。

其中动态特性是指检测系统在被测量随 时间变化的条件下输入输出关系。

一般地，在所考虑的测量范围内，测试系统都 可以认为是线性系统，因此就可以用一定常线性系统微分方程来描述测试系统以 及和输入x(t)、输出y(t)之间的关系。

1)微分方程：根据相应的物理定律(如牛顿定律、能量守恒定律、基尔霍夫电 路定律等)，用线性常系数微分方程表示系统的输入 x 与输出y 关系的数字 方程式。

n 二 m m J d y dy , d , d x , dx , n … 印一，a °y 二 *——m - bm J —m 」’J 一 ’ b °X dt dt dt dt dta i 、b i (i=0,1, •:系统结构特性参数，常数，系统的阶次由输出量最高微分 阶次决定。

2)通过拉普拉斯变换建立其相应的“传递函数”，该传递函数就能描述测试装 置的固有动态特性，通过傅里叶变换建立其相应的“频率响应函数”，以此来描述测试系统的特性。

定义系统传递函数 H(S)为输出量与输入量的拉普拉斯变换之比，即 Y(s) _ b m s m •…• ds • b o H (s ) - - n nj X(s) a n s +a n 』s + …^a^+a 。

式中S 为复变量，即j ■传递函数是一种对系统特性的解析描述。

它包含了瞬态、稳态时间响应和频 率响应的全部信息。

传递函数有一下几个特点：(1)H(s)描述系统本身的动态特性，而与输入量x(t)及系统的初始状态无 关。

(2) H(S)是对物理系统特性的一种数学描述，而与系统的具体物理结构无 关。

H(S)是通过对实际的物理系统抽象成数学模型后，经过拉普拉斯变换后 所得出的，所以同一传递函数可以表征具有相同传输特性的不同物理系统。

(3) H(S)中的分母取决于系统的结构，而分子则表示系统同外界之间的联系，如输入点的位置、输入方式、被测量以及测点布置情况等。

04第四部分 测试系统的特性2_动态特性

04第四部分 测试系统的特性2_动态特性
– 通过测试系统后，输出信号中各频率成分的相移与该频 率成正比，且各频率成分的时移是同一个量
– 实际中，很难满足不失真测量条件，只能在某一频率范 围内近似符合不失真测量条件，该频率段称为测试系统 的工作频率范围
– 如果测试部分作为反馈环节，成为控制系统的一部分， 则应注意由于相移可能导致控制系统的稳定性被破坏了
– 实际应用中，首先，选用合适的测试装备，在测量范围 内，满足或接近满足不失真测量条件；其次，对输入信 号进行前置滤波，将非测量频带内的高频信号滤掉
– 另外，对具体的测量情况应具体分析，例如进行振动测 量时，只关心其幅值谱和振动强度，此时应重点考虑使 测试系统满足幅值不失真条件；相反，如果对延迟时间 关心，则应重点考虑相位不失真条件
– 一阶系统不失真条件分析
• 时间常数越小，满足不失真 测量的频带越宽
G(s) k Ts 1
A()
1
(T)2 1
() arctan(T)
北京航空航天大学宇航学院 王可东
5/35
测试信号处理技术
Sensor Technology & Measurement Systems
A0e jt0
H ()
A0
o

北京航空航天大学宇航学院 王可东
o
()

1/35
测试信号处理技术
Sensor Technology & Measurement Systems
§4.2 不失真测量的条件
• 不失真测量的条件
– 输出信号的频率与输入信号的频率相同
– 通过测试系统后，输出信号中各频率成分的幅值是输入 信号中相应频率成分的常数倍
北京航空航天大学宇航学院 王可东

第三章测试系统特性3-动态特性

第三章测试系统特性3-动态特性

2）传递函数
3）频率响应函数 4）阶跃响应函数等
航海学院
传感器与测试技术
第3章 测试系统的特性
1、动态特性的数学描述
1）线性微分方程 微分方程是最基本的数学模型，求解微分方程， 就可得到系统的动态特性。
对于一个复杂的测试系统和复杂的测试信号，
求解微分方程比较困难，甚至成为不可能。为此， 根据数学理论，不求解微分方程，而应用拉普拉斯 变换求出传递函数、频率响应函数等来描述动态特 性。
dy(t ) y (t ) Sx(t ) dt
取S＝1
1 H ( s) s 1
H ( j ) 1 j 1
A( )
1 1 ( )
2
() arctg( )
航海学院
传感器与测试技术
第3章 测试系统的特性
幅 频 和 相 频 曲 线
伯 德 图
H ( j) Y ( j) / X ( j) 或 H () Y () / X ()
当系统的初始条件为零时，对微分方程进行傅 立叶变换，可得频率响应函数为
Y ( j ) bm ( j ) m bm1 ( j ) m1 b1 ( j ) b0 H ( j ) X ( j ) an ( j ) n an 1 ( j ) n 1 a1 ( j ) a0
频率响应特性
模A()反映了线性时不变系统在正弦信号激励 下，其稳态输出与输入的幅值比随频率的变化， 称为系统的幅频特性； 幅角()反映了稳态输出与输入的相位差随频 率的变化，称为系统的相频特性。
航海学院
传感器与测试技术
第3章 测试系统的特性
频率响应特性的图形描述： 直观地反映了测试系统对不同频率成分输入信号 的扭曲情况——输出与输入的差异。

测试系统动态特性


高效数据处理
采用高效的数据处理算法和架构，确保测试数据的准确性和实时性。
提高测试系统的稳定性
冗余设计
关键部件采用冗余设计，提高系统的可靠性和稳定性。
自适应调整
根据测试过程中的实际情况，自动调整系统的参数和性能， 确保测试结果的准确性。
故障诊断与恢复
具备故障诊断和恢复功能，能够在系统出现故障时快速定位 并恢复。
降低测试系统的噪声
噪声抑制技术
采用先进的噪声抑制技术，降低测试系统内部和外部噪声的影响。
滤波算法
应用合适的滤波算法对测试数据进行处理，去除噪声干扰，提高测 试结果的准确性。
环境控制
对测试环境进行严格的控制，减少环境因素对测试结果的干扰。
06 结论
研究成果总结
测试系统的动态特性对于确 保其稳定性和可靠性至关重
激振试验的优点在于可以人为控制激励信号的频率、幅值和波形等参数， 以便于对系统的不同动态特性进深入研究。
激振试验的局限性在于它只能模拟特定条件下的动态特性，无法完全模拟 实际运行中的复杂情况。
振动台试验
01
振动台试验是一种利用振动台 模拟实际运行中的振动环境， 对测试对象进行振动试验的方 法。
02
测试系统动态特性
目 录
• 引言 • 测试系统动态特性概述 • 测试系统动态特性分析方法 • 测试系统动态特性测试技术 • 测试系统动态特性优化与改进 • 结论
01 引言
目的和背景
确定测试系统的性能指标
通过对测试系统的动态特性进行评估，可以了解测试系统的性能指标，如响应时间、稳定性、可 靠性等。
动态特性对于故障诊断和预测具有重要意义
通过对测试系统的动态特性进行分析，可以及时发现系统潜在的问题和故障，并对其进行诊断和预测。 这对于预防故障发生、减少系统维护成本和提高系统可靠性具有重要意义。

测试系统特性(第2讲)


输出关系是一条理想的直线，斜率
为常数。
但是实际测试系统并非是理想定常线性系统，输入、输出曲线并不是理想的直线 ，式实际上变成
测试系统的静态特性就是在静态测量情况下描述实际测试装置与理想定常线性系 统的接近程度。下面用定量指标来研究实际测试系统的静态特性。
• 动态特性：当被测量随时间迅速变化时， 输出量与输入量之间的关系称为动态特 性，可以用微分方程表示。
3、系统特性的划分：
静态特性：当被测量不随时间变化或变化缓慢时，输出量
测 试
与输入量之间的关系称为静态特性，可以用代数方程 表示。
在式（1.1）描述的线性系统中，当系统的输入
（常数），即输
系
入信号的幅值不随时间变化或其随时间变化的周期远远大于测试
统
时间时，式（1.1）变成：
概
念
也就是说，理想线性系统其输出与输入之间是呈单调、线性比例的关系，即输入、
测试系统的动态特性是指输入量随时间变化时，其输 出随输入而变化的关系。一般地，在所考虑的测量范 围内，测试系统都可以认为是线性系统，因此就可以 用式(1.1)这一定常线性系统微分方程来描述测试系统 以及和输入x(t)、输出y(t)之间的关系，通过拉普拉斯 变换建立其相应的“传递函数”，该传递函数就能描 述测试装置的固有动态特性，通过傅里叶变换建立其 相应的“频率响应函数”，以此来描述测试系统的特 性。
• 传递函数
• 定义系统的传递函数H(s)为输出量和输入量的拉普拉斯变换之比，即
• • 式中s是复变量，即s =σ+jω。
• 传递函数是一种对系统特性的解析描述。它包含了瞬态、稳态时间响 应和频率响应的全部信息。传递函数有一下几个特点：
• （1）H(s)描述了系统本身的动态特性，而与输入量x(t)及系统的初

测试系统的动态特征

9
组合系统的传递函数
（1）串联系统
H(s)
X(s)
Z(s)
Y(s)
H1(s)
H2(s)
H (s) = H1 (s) H 2 (s)
10
（2）并联系统
X(s)
H(s)
Y1(s)
H1(s)
Y(s)
H2(s)
Y2(s)
n
∑ H (s) = H i (s) i =1
（3）反馈系统
X1(s) +
Y(s) HA(s)
拉普拉斯变换（简称拉氏变换）为
∫ L( f (t)) = F (s) = ∞f (t)e d -st 0
s — 复变量（复频率），s = σ + jω
f（t）— F（s）的原函数 F（s） — f（t）的象函数
F(s)=L[f(t)]
6
（2）传递函数(Transfer function)
定义传递函数是输出信号与输入信号之比。
测试系统的动态特征
第一节 测量系统在瞬变参数测量中的动态特性 第二节 测量系统的动态响应 第三节 测量系统的动态标定
1
第一节 测量系统在瞬变参数测量中的动态特性
传感器
调理电路
数据采集系统
CPU
现代测试系统方框图
测量系统的基本特性：测量系统与其输入、输出的关系。
显示
分类
静态特性 输入信号x(t)不随时间变化 动态特性 输入信号x(t) 随时间变化
➢ 不说明被描述系统的物理结构，不论是电路 结构还是机械结构，只要动态特性相似均可 用 同一类传递函数来描述。
➢ 传递函数的分母取决于系统的结构（输入方 式、被测量及测点布置等）
热能与动力机械测试技术

测试系统的动态特性

有时也用信号电压和噪声电压来 表示信噪比，信噪比SNR（以dB为 单位）为
SNR 20 lg Vs Vn
18
案例：物料配重自动测量系统的静态参数测量
灵敏度=△y/△x
回程误差=(hmax/A)×100%
非线性度=B/A×100% 测量范围：
19
第3章、测试系统特性
（三）测试系统的动态特性
测试系统的动态特性是指输入 量随时间变化时，其输出随输入而 变化的关系。
an y n (t) an1 y n1 (t) ...a1 y(t) a0 bm x m (t) bm1x m1 (t) ...b1x(t) b0
一般在工程中使用的测试装置都是线性系统。
5
线性系统性质： an y n (t) an1 y n1 (t) ...a1 y(t) a0
y b0 x Sx a0
静态测量时，测试装置表现出的响应特 性称为静态响应特性。
a)灵敏度
当测试装置的输入x有一增量△x,引起输出y发 生相应变化△y时,定义: S=△y/△x
y
△y △x
x
12
b)非线性度
标定曲线与拟合直线的偏离程度就是非线性度。
=B/A×100% y B
非线性度
y
A
Bi
定度曲线
(ansn an1sn1 a1s a0 )Y (s)
L[ f (n) (t)] sn F (s)
an y n (t) an1 y n1(t) ...a1 y(t) a0 bm xm (t) bm1xm1(t) ...b1x(t) b0
(bm sm bm1sm1 b1s b0 ) X (s) 输出量和输入量的拉普拉斯变换 Y (,s) X (s)
若系统的输入为某一频率的谐波信号，则系统
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一个测量系统的频率特性为W j ，它要执行的功能 用理想频率特性表示为WN j时，二者之间存在的误
差。动态幅值误差ε表示为：
W j WN j 100% WN j
动态相位绝对误差为：
N
Xi’an Jiaotong University
系统动态误差与信号频率的关系
（2）典型环节的动态误差：
Xi’an Jiaotong University
测试系统的数学模型
A，常系数线性微分方程
d n y t
d n1y t
an dt n an1 dt n1
d m x t
d m1x t
bm dt m bm1 dt m1
a1
dy t
dt
a0
y
t
b1
dx t
dt
b0
x
t
B，传递函数：当t≤0时，x(t)=0，y(t)=0
arctan
1
1 2
20 lg A / dB
0 -3 -10
0° －20°
－40° －60° －80°
-20 0.1
1.0
0.1 10
1.0
10
Xi’an Jiaotong University
测试系统的动态特性参数
20lg A / dB 0
-3
-10
-20 0.1/τ
1/τ
由图可见：
10/τ
Ti
duo dt
uo
ui
x ky b dy dt
令 b / k, K 1/ k dy y Kx
dt
Xi’an Jiaotong University
常见测试系统的数学模型
（二）、二阶系统微分方程通式——振荡环节
a2 a0
d 2 y(t) dt 2
a1 a0
dy(t) dt
y(t)
系统动态误差与信号频率的关系
Xi’an Jiaotong University
系统动态误差与信号频率的关系
信号频率与一些系统转折频率之比（ / ＝ f / f ）
与动态幅值误差ε的关系计算如下：
f / f
ε (%)
0.1 0.2 0.3 0.4 0.5 0.6 0.7 1.0 -0.5 -1.9 -4.2 -7.1 -10.5 -14 -18 -29
t
e0t
1 2
sin dt
arctan
1 2
令
t
t
0，可求得t p
d
，将t
代入上式得
p
tp
e e / 1 2
0t p
（推导）
从而可求得
ln tp
2 ln
tp
2
0
tp
1 2
Xi’an Jiaotong University
系统动态误差与信号频率的关系
（1）动态误差：
现代检测技术
系统动态特性
精勤求学 敦笃励志 果毅力行 忠恕任事
系统动态特性
❖ 对理想的测试系统，输出与输入具有相同时间函数。
▪ 对于测量动态信号的测试系统，要求能够迅速而准确的测 出信号的大小并真实再现信号的波形变化，但是在实际系 统中，由于存在弹簧、阻尼、质量（惯性）等元件，只能 在一定频率范围内、对应一定动态误差条件下保持输出与 输入一致。
幅频特性：
A() H
1
1
0
2 2
2
0
2
相频特性：
2
arctan
0
1
0
2
Xi’an Jiaotong University
测试系统的动态特性参数
L 20 lg A / dB
10
0
ζ小
-10 ζ大
-20
0.1
1
10
/0
0
ζ小
-90° ζ大
-180°
测试系统的动态特性参数
二阶系统阶跃响应特性参数——时域指标
Xi’an Jiaotong University
测试系统的动态特性参数
• 延迟时间 td：输出由零上升到稳态值的一 半所需的时间。
• 上升时间 tr：输出由稳态值的10%上升到 稳态值的90%所需的时间。
•
峰值时间
t
：输出由零上升到第一个峰值
测试系统的动态特性参数
1临界阻尼情况：（推导）
y t KA 1 1 0t e0t y t KA 单调衰减项，无振荡。
1 过阻尼情况：（推导）
y t
1
2
1 e
2 1 0t
1 e 2
2 1 0t
2 2 1
2 2 1
无振荡，近似按一阶系统对待。
Xi’an Jiaotong University
测试系统的数学模型
一阶系统频 率响应特性
Xi’an Jiaotong University
测试系统的数学模型
Xi’an Jiaotong University
测试系统的数学模型
❖ 任何高阶系统均可以视为多个一阶、二阶系统的并联或串联。
Xi’an Jiaotong University
常见测试系统的数学模型
-20 0.1/τ
1/τ
10/τ
c， 当 1 , A() 0.7073dB, 45 ，称 1
为转折频率或截止角频率。因此τ越小转折频率越
大，系统的动态范围越宽。
Xi’an Jiaotong University
测试系统的动态特性参数
（2） 二阶系统频率特性与图示：令K＝1
1 d 2 y 2 dy y Kx 02 dt2 0 dt
Xi’an Jiaotong University
测试系统的数学模型
H Y / X A e j
幅频特性：表示输出与输入幅值比随ω的变化
A
Y X
H
对数幅频特性： L 20lg A
相频特性：表示输出与输入相位差随ω的变化
arg H
Xi’an Jiaotong University
由 dA() d
0可得，当0
0.707，存在谐振频率n
0
1 2 2，
n时，幅频特性曲线达到峰值,A(n ) 2
1。
1 2
当 0时，系统发生共振，A(n ) 。 当 0.707时，系统无共振，A()随增大而减小。
Xi’an Jiaotong University
测试系统的动态特性参数
a） 一阶系统的动态误差 执行传递信号功能的一阶系统的理想频率特性的模为
WN j const W 0 由于 W j H K , W 0 K
1 2
所以一阶系统动态幅值误差表达式为：
1
1 100%
1
1 100%
1 2
1 / 2
相位误差表达式为： arctan
Xi’an Jiaotong University
反映系统的响应速度，通常Tr 4 称为响应时间。
Xi’an Jiaotong University
测试系统的动态特性参数
•τ的测量
Z O
△Z △t
t
e
1
y t
t
A
t
Z
ln 1
y t
A
t
Z
Xi’an Jiaotong University
测试系统的动态特性参数
• 输出终值 y 实时快速测定
C，频率响应：
H
j
Y j X j
bm an
j m bm1 j m1 j n an1 j n1
b1 j b0 a1 j a0
频率响应函数是传递函数的特例，可以由傅立
叶变换得到。频率响应函数反映的是系统处于稳态 输出阶段的输入输出特性，传递函数则反映了激励 所引起的系统固有的瞬态输出特性和对应该激励的 稳态输出特性。
❖ 通过时间响应、频率响应和系统动态特性的关系，可以：
▪ 根据信号频率范围和测量误差要求确立测量系统； ▪ 已知系统动态特性，估算可测信号的频率范围与对应的动
态误差。
Xi’an Jiaotong University
主要内容
测试系统的数学模型 常见测试系统的数学模型 测试系统的动态特性参数 系统动态误差与信号频率的关系 实现系统不失真测试的条件
y(t)
uu23 u1
0 △t △t
将一阶微分方程改为差分方程
A
U2 U1 t
U2
A
(1)
U3 U2 t
U3
A
(2)
A y
U
2 2
U1U 3
t
2U2 U3 U1
Xi’an Jiaotong University
测试系统的动态特性参数
(4) 二阶系统阶跃响应特性与特性参数
Xi’an Jiaotong University
（一）一阶系统微分方程通式：
a 1 dy y b0 x
a0 dt
a0
dy y Kx
dt
式中： y ——系统输出
x ——系统输入
a 1 ——时间常数 K b0 ——静态灵敏度（放大倍数）
a0
a0
传递函数：
H
s
Y X
s s
K
1 s
频率特性：
H
Y X
K
1 j
Xi’an Jiaotong University
a，当ω<1/τ时， A(接) 近于1，输入输出几乎相等，
L 20lg A() 0
b，当ω增大时，
A( )减小，
A
10
1 10
A
1
，工作