信息光学 常用函数

信息光学公式 1·矩形函数⎪⎩⎪⎨⎧≤-=⎪⎭⎫ ⎝⎛-其它,021,100a x x a x x rectF { a sinc(a x ) } = rect(f /a )F ⎪⎭⎫ ⎝⎛Λ=b f b 1(bx)}{sinc22·inc s 函数()()a x x a x x a 000sin x x sinc --=⎪⎭⎫ ⎝⎛-ππ 3·三角形函数 ⎪⎩⎪⎨⎧≤-=⎪⎭⎫ ⎝⎛Λ其它,0,1a x a xa x4·符号函数()⎪⎩⎪⎨⎧<-=>=0,10,00,1sgn x x x x5·阶跃函数()⎩⎨⎧<>=0,00,1x x x step6·圆柱函数⎪⎩⎪⎨⎧<+=⎪⎪⎭⎫⎝⎛+其它,0,12222ayx a y x circ极坐标内⎩⎨⎧><=⎪⎭⎫ ⎝⎛ar o a r a r ,,1circ7·δ函数的定义 普通函数形式的定义()()⎪⎪⎭⎪⎪⎬⎫=⎩⎨⎧==∞≠≠=∞∞-⎰⎰1,0,0,0,0,dxdy y x y x y x y x δδ广义函数形式的定义()()()0,0,,φφδ=∞∞-⎰⎰dxdy y x y x其中()y x ,φ在原点处连续 δ函数的性质设函数()y x f ,在()00,y x 点出连续，则有 筛选性质()()()y x f dxdy y y x x y x f ,,,00=--∞∞-⎰⎰δ坐标缩放性质 ()()y x abby ax ,1,δδ=可变性 ()()()y x y x δδδ=, 8·梳状函数性质()()()∑∑∞-∞=∞∞-=-=m nx j m x x πδ2exp comb()∑∞∞-∆-∆=⎪⎭⎫ ⎝⎛∆x m x x x x δcomb()∑∞-∞=⎪⎭⎫⎝⎛∆-∆=∆m xm x x δ1xx comb ()()ξcomb x comb −−→←ℑ()ξx comb x x comb ∆∆−−→←⎪⎭⎫ ⎝⎛∆ℑx ()()()y x comb comb y x,comb =9·傅里叶变换()()(){}dxdy y x j y x f F ηξπηξ+-=∞∞-⎰⎰2exp ,, ()()()[]ηξηξπηξd d y x j F y x f +=∞∞-⎰⎰2exp ,,10·阶跃函数step(x)的傅里叶变换(){}(){}()⎭⎬⎫⎩⎨⎧-=+=ℑℑπξξδj 21x sgn 121x step11·卷积的定义()()()()()x h x f d x h f x g *=-=⎰∞∞-ααα定义()x f 和()x h 的二维卷积：()()()()()y x h y x f d d y x h f y x g ,*,,,,=--=⎰⎰∞∞-βαβαβα卷积的几个重要性质： 线性性质：{),(),(),(),(),()},(),(y x g y x bh y x g y x af y x g y x bh y x af *+*=*+卷积符合交换律：,(),(),(),(y x f y x h y x h y x f *=*卷积符合结合律：[][]),(),(),(),(),(),(y x g y x h y x f y x g y x h y x f **=**卷积的坐标缩放：若),(),(),(y x g y x h y x f =*，则),(1),(),(by ax g abby ax h by ax f =*（a,b 均不等于0）卷积位移不变性：若),(),(),(),(y x f y x h y x h y x f *=*，则),(),(),(),(),(000000y y x x g y y x x h y x f y x h y y x x f --=--*=*--函数),(y x f 与δ函数的卷积： ),(),(),(0000y y x x f y y x x y x f --=--*δ12·米尔对称性()()ηξηξ--=*,,FF13·卷积定理()()()x rect x rect *=Λx(){}(){}(){}()ξ2sinc x rect x rect ==Λℑℑℑx()(){}()()()ξξξrect rect rect sin x sinc ==*ℑx c()()(){}()x sinc rect sinc sinc 1==*-ℑξx x14·线性平移不变系统()()()()()y x h y x f d d y x h f y x g ,,,,,*=--=∞∞-⎰⎰βαβαβα15·函数变换输入函数 ()()y x y x f 002cos ,ηξπ+= 其频谱函数()()()[]0000,,21,ηηξξδηηξξδηξ-++--=F16·单色光波场的复振幅复振幅 ()()r k j ra P U *=exp 0光强 *==UU UI 217·X 方向的空间频率的相关公式等相线位方程 c kx =αcos λπ2=k αλc o s =X X 方向的空间频率λαξcos 1==X 18·整个空间的空间频率()()[]z y x j a Z Y X U ζηξπ++=2exp ,, 221λζηξ=++2219·泰伯效应()()jkz d n c n nG exp ⎪⎭⎫ ⎝⎛-=∑∞-∞=ξδξ 泰伯距离 λ22dz T =20·相干截止频率 f D λρ2c =非相干截止频率 f D λρρ22c oc == 21·相干面积 ()()SSC A Z A Ω≈=λλ2第二章2·1夫琅禾费近似()()()()⎥⎦⎤⎢⎣⎡+-⎥⎦⎤⎢⎣⎡+=y y x x z k j y x z k j zj jkz y x y x h 002200exp 2exp exp ,,λ； 2·2菲涅尔衍射()()()()()0020200002exp ,exp ,dy dx z y y x x jk y x U zj jkz y x U ⎥⎥⎦⎤⎢⎢⎣⎡-+-=∞∞-⎰⎰λ傅里叶变换()()()()()()00002020000222exp 2exp ,2expexp1,dy dx y y xx z jy x z k j y x Uy x z k j jkz zj y x U ⎥⎦⎤⎢⎣⎡+-⨯⎥⎦⎤⎢⎣⎡+⨯⎥⎦⎤⎢⎣⎡+=∞∞-⎰⎰λπλ2·3透镜系统（1）输入平面位于透镜前焦面 这时f d =0得 ()()000000exp ,,dy dx f y y x x jk y x t c y x U ⎪⎪⎭⎫⎝⎛+-'=∞∞-⎰⎰ （2）输入面紧贴透镜 这时00=d 得 ()()00000022exp ,2exp ,dy dx q y y x x jk y x t qy x jk c y x U ⎪⎪⎭⎫ ⎝⎛+-⎪⎪⎭⎫ ⎝⎛+'=∞∞-⎰⎰ （3）物在透镜后方()()()0000000022exp ,2exp ,dy dx d q y y x x jk y x t d q y x jk c y x U ⎪⎪⎭⎫⎝⎛-+-⎥⎦⎤⎢⎣⎡-+'=∞∞-⎰⎰ 4·1希尔伯特变换可看成是一个线性平移不变系统，该系统的脉冲响应为t t h π1)(-= 而 )()()(t u t j t t u r *⎥⎦⎤⎢⎣⎡+=πδ脉冲响应对应的传递函数为()()νπνn j t F H sg 1=⎭⎬⎫⎩⎨⎧-=4·2互相干函数时间的平均值⎰-∞→=TTT dt t f Tt f )(21lim)(光场的互相干函数())(,),(),(),(12**2*12211ττΓ=+--t P u t P u t t P u t t P u *＝光场的自相干函数)(),(),(111*1ττΓ+＝t P u t P u复相干度()()()()()21122/122111212]00[I I τττγΓ=ΓΓΓ=Q 点的光强为()()()()(){}τγ122121Re 2)(I Q I Q I Q I Q I Q ++=干涉条纹的可见度为min ma x m i n m a x I I I I +-=V ()()()()()τγ1221212Q I Q I Q I Q I +=Imax 和Imin 是Q 点附近干涉条纹的极大值和极小值()()()()()()()()Q I Q I Q I Q I I Q I Q I Q I Q I I 2121min 2121max 22-+=++=光源的光谱密度分布 ()()()()⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡=∞→∞→2T 2T2*,lim ,,lim v P v P v P v T T TTT U U UG相干时间vc ∆=1τ 相干长度c c c l τ= 时间延迟t ＝2h/c4·3确定像点坐标：i z 为正表示发散球面波，i z 为负表示会聚球面波1012121-⎪⎪⎭⎫ ⎝⎛±=z z z z r p i λλλλ p pi r i i i x z zx z z x z z x +±=2120012λλλλp pi r i i i y z z y z z y z z y +±=2120120λλλλ4.4)⎪⎪⎭⎫⎝⎛--=-±-⎰∞∞-A B AC A dx C Bx Ax 22exp 2exp π积分公式：4·5 范西泰特——策尼克定理()()()()[]()()()()βαβαβαβαλπβαψd d I d d y x z j I j y x I y x I y xy x y xy x J u ,2exp ,exp ,,,;,,;,221122112211∞∞-∞∞-⎰⎰⎰⎰⎥⎦⎤⎢⎣⎡∆+∆-==4·6 傅里叶透镜的截止频率、空间带宽积和视场 1. 截止频率 传播方向角u 最大为 ()()fD D fD D u 22211-=-≈相应的空间频率 f D D uuλλλξ2sin 1-=≈=传播方向角u 最小为 ()()fD D f D D v 22211+=+≈相应的空间频率 fD D v vλλλξ2sin 1+=≈=2.空间带宽积δξξ单频线宽频带宽度信息容道∆=NfD D λξξ12-==∆11D =δξ SW N =∆=δξξSW 就是空间带宽积3.视场 21DD =4正弦条件 ηλf u f h ==sin。

信息光学复习提纲信息光学的特点Ch1. 线性系统分析1.矩形函数：①定义②图像③作用④傅里叶变换谱函数2.sinc函数：①定义②图像③作用④傅里叶变换谱函数3.三角函数：①定义②图像③作用④傅里叶变换谱函数4.符号函数：①定义②图像③作用④傅里叶变换谱函数5.阶跃函数：①定义②图像③作用④傅里叶变换谱函数6.余弦函数：①定义②图像③作用④傅里叶变换谱函数7. 函数：①三种定义②四大性质③作用8.梳状函数：①定义②图像③作用④傅里叶变换谱函数9.高斯函数：①定义②图像③作用④傅里叶变换谱函数10.傅里叶变换（常用傅里叶变换对）11.卷积：四大步骤，两大效应12.互相关、自相关的定义、物理意义13.傅里叶变换的基本性质和有关定理14.线性系统理论15.线性不变系统的输入输出关系，脉冲响应函数，传递函数16.抽样定理求抽样间隔Ch2. 标量衍射理论1. 标量衍射理论成立的两大条件2.平面波及球面波表达式:exp[(cos cos cos )]A ik x y z αβγ++（求平面波的空间频率）)](2exp[]exp[22y x zik ikz z A + 3.惠更斯——菲涅耳原理：()⎰⎰∑=dsrikr K P U cQ U )exp()()(0θ 4.基尔霍夫衍射理论： ⎰⎰∑-=dsrikr r n r n r ikr a j Q U )exp(]2),cos(2),cos([)exp(1)(0000λ令()()θλK rikr j Q P h )exp(1,=所以()⎰⎰∑=ds Q P hP UQ U ,)()(0当光源足够远，且入射光在孔径平面上各点的入射角都不大时，(),1,cos 0≈r n(),1,cos ≈r n ().1≈∴θK故()z ikr j Q P h )exp(1,λ=，]})()[(211{20020zy y z x x z r -+-+≈ 5. 菲涅耳衍射——近场衍射：0000202000022)](2exp[)](2exp[),()](2exp[)exp(),(dy dx yy xx zj y x z jk y x U y x zjkz j jkz y x U +-++=⎰⎰∞∞-λπλ6. 夫琅禾费衍射——远场衍射：（根据屏函数求衍射光强分布）000000022)](2exp[),()](2exp[)exp(),(dy dx yy xx zj y x U y x zjkz j jkz y x U +-+=⎰⎰∞∞-λπλ 7.衍射的角谱理论：（角谱的传播，求角谱分布）Ch.3 光学成像系统的频率特性1.透镜的傅里叶变换性质： ①相位变换作用：)](2exp[),(),(22y x f jky x p y x t +-=（二次位相因子）②透镜的傅里叶变换特性：（满足条件？什么情况下实现准确傅立叶变换） a. 物在透镜前b.物在透镜后 2. 衍射受限系统的点扩散函数：⎰⎰∞∞--+--=--yd x d y y y x x x j y d x d P d K y y x x h i i i i ii i ~~]}~)~(~)~[(2exp{)~,~()~,~(002200πλλλ 光瞳相对于i d λ足够大时，理想情况：点物成点像)~,~()~,~(22o i o i i o i o i y y x x d K y y x x h --≅--δλ3. 相干照明下衍射受限系统的成像规律：),(),(~),(i i g i i i i i y x U y x h y x U *=其中，)]~,~([),(~y d x d P F y x h i i i i λλ=，),(1),(0My M x U M y x U i i i i g =4.衍射受限系统的相干传递函数（CTF ）：()()ηλξληξi i d d P H ,,=（坐标轴反演）5. 截止频率：圆形光瞳：o c oc i c d DM d D λρρλρ2,2=== 正方形光瞳：不同方向的截止频率不同，45度时最大)22max ic d aλρ= 6. 衍射受限系统的非相干传递函数（OTF ） 7. OTF 与CTF 的关系Ch.4 光学全息1. 普通照相与全息照相的比较2. 全息照相的核心：波前记录和再现①方法：干涉法（标准方法，即将空间相位调制→空间强度调制） ②特点：全息图实际上就是一幅干涉图 ③全息图的分类：a 。

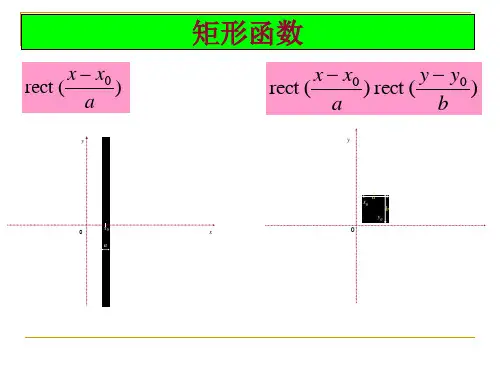
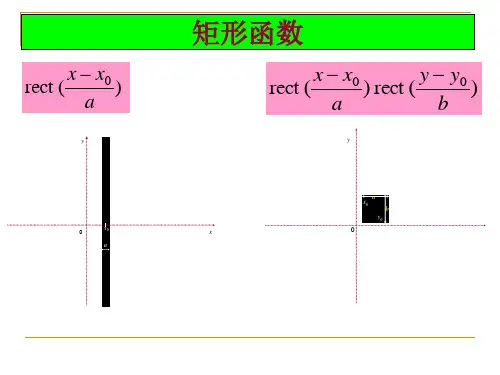
[]{}{}{}{}{}{}),(),(),(),(),(),(),(),()2()()]()([212sin )](exp[)](exp[)]()([212cos )()()()(),()](2exp[)(sin )(sin )()(1),()(sin )(sin )()()](2exp[),()()(),()()(11)()(),(),(),(),()(),(1),(),(),(),(1),(000),(1)2(),()(),(01)(exp ),(exp 01)()(),()()(sin sin Sinc )()(),(021)(11110002222000220000000000222212222212222222222000200ηεηεηεηερπρδδπππδδπδπδπδτδτδτττδδδδδδδδδδδππππππG b F a bG aF y x g b y x f a y x bg y x af J r circ f f f f jx f f f y x f f f f xf f comb f comb y comb x comb f f f f y f x f j f c f c y tri x tri y x f c f c y rect x rect b f a f j b y a x y Comb x Comb y x Comb n x n x x Comb y x y x y y x x y x f y y x x xy f y x abby ax y x f dxdy y y x x y x f dxdy y x y x y x y x y x N J N y x f y x N Circ N y x f a y x a y x Circ y x N N y x f a x a x Gaus ax a x a x a x Tir Ny Sinc Nx Sinc N y x f a x x ax x a x x c Ny rect Nx rect N y x f a x x a x x rect x x y x x x y x b y a x b a y x y x y x n n N NN N N ---∞-∞=∞-∞=∞+∞-∞+∞-+=++=+---+-+--+---++---=-=-=⎪⎭⎫ ⎝⎛=--=--==--⎪⎩⎪⎨⎧=≠≠=++=+=⎪⎩⎪⎨⎧≤+=++-=⎥⎦⎤⎢⎣⎡-=⎪⎩⎪⎨⎧≤-=∧==--=-=⎪⎩⎪⎨⎧≤-=-∑∑⎰⎰⎰⎰F F FF F F 频谱函数原函数频谱函数原函数，梳状函数：分离性质：相乘性质：比例性质：筛选性质：函数的定义及性质：贝塞尔函数：，其它）（）（圆域函数：，）（）（高斯函数：其它）（）（三角函数：，）（函数：，其它矩形函数：线性关系。

光学信息一、基本概念:1. 傅里叶变换，傅里叶逆变换；正变换 dx πux j x g u G ⎰∞∞--=]2[exp )()( 逆变换u ux j u x g d ]2exp[)G()(⎰∞∞-=πμ，ν— 空间频率 G(μ，ν) — 频谱 ，傅里叶谱，角谱物理意义： 1.一个空间函数 g(x ，y) ，可视为向前传播的一列光波。

2.它可分解为无穷多个传播方向不同的平面波。

3.某一方向传播的平面波可视为一个空间单频信号。

4.每个空间单频信号可看作原函数 g(x ，y) 的傅里叶分量，其振幅是该频率的函数 G(μ，ν)。

5.原函数 g(x ，y) 可看作是所有傅里叶分量的加权的迭加， G(μ，ν) 是其权重 。

2.频谱, 空间频率；空间频率：沿某一特定方向传播的平面波具有单一的空间频率 。

定义为:其中:cos α 、cos β为平面波的方向余弦。

空间频谱 ：一般情况下可视为各平面波分量的振幅分布函数，高频分量的振幅较小，低频分量的振幅较大。

3.脉冲响应，传递函数传递函数 ：改写为：()()()νμνμνμ,,,,,0H z A z A z ∙=其中()]cos cos 1exp[,22βανμ--=jkz H 表征光的传播在频域中的特性。

脉冲响应：惠更斯—菲涅尔原理：普通光源可看作若干个单个球面波照明的集合。

h 称为脉冲响应函数它表示当P 处有一点源时，在观察点Q 处接收到的复振幅分布。

y ) 也称为 点扩展函数。

4. 空间滤波, 高通滤波, 低通滤波, 带通滤波，振幅滤波, 位相滤波；空间滤波：利用透镜的傅里叶变换特性，把透镜作为频谱分析仪，改变物体的频谱结构从而改变像的结构。

高通滤波： 通高频信号阻低频信号，滤除频谱中的低频部分，增强模糊图像的边缘，提高对图像的识别能力，实现衬度反转；能量损失较大，输出结果一般较暗。

低通滤波：通低频信号阻高频信号，用于消除图像中的高频噪声和周期性网格。

带通滤波：利用信号能量集中的频带不同，选择某些频谱分量通过，阻挡另一些分量。

Rect函数物理意义：用来描述无限大不透明屏上矩形孔的透过率。

Sine函数：与矩形函数（单缝、矩孔的透过率）之间的这种紧密联系，致使他们在傅里叶光学中经常被用到。

阶跃函数：描述光学直边（或刀口）的透过率。

符号函数：描述孔径的复振幅透过率。

三角形函数：表示一个光瞳为矩形的非相干成像系统的光学传递函数。

高斯函数：在统计学领域内经常遇到。

在光学领域小，描述激光器发出的高斯光束，有时也用于光学信息处理中的“切趾术”。

圆域函数：描述无限大不透明屏上圆孔的透过率。

§函数:在物理学和工程技术中常用来描述一个极限状态，描述脉冲状态这一类的物理现象。

互相关是两个信号间存在多少相似性或关联性的量度。

自相关是两个相同函数图像重叠程度的量度。

位相调制作用：不改变振幅，只改变位相。

相干、非相干成像系统是广场复振幅变换的线性空间不变系统。

F(/v , f y ) = F{/(x, y)} = J L /(x, y)e~l27r(flX+f )y)dxdy基尔霍夫积分定理:X ））= 士"咕云仏 +九）.才｛“ 3，x ）｝5诂你唱-嚎心已 cos(n, &)一 cos(〃, ©)菲涅尔衍射积分公式:夫琅禾费衍射公式:卷积物理意义:光学系统像平面上的光强分布是物的光强分布与单位强度点光源对应的像强度分布的卷积。

几何意义：1、置换变量：将f(X)与h (x) >p的自变量X换成积分变量;2、折叠：将h ()绕轴旋转180度，构成对称于纵轴的镜像h (-)；3、位移：将曲线h (-) 移动距离x,得到h(X-)；4、相乘：将位移后的函数h (x-)乘以f (),得到f ()h(x-)；5、积分：f () h (x-)曲线下的面积即为给定于x值得卷积值。

线性系统：设函数于= 代表对系统的激励，函数/=!果在激励与响应之间成立关系匕(兀2，丿2)=必(坷」)}'&(%2，)‘2)= £纟心2』2)代表系统相应的响应，勺是任意复常数，(p{ }表示系统算符。

信息光学复习重要知识点1.常用的非初等函数：矩形函数、Sinc函数、三角形函数、符号函数、阶跃函数、圆柱函数。

2.δ函数的定义：a.类似普通函数定义b.序列极限形式定义c.广义函数形式定义δ函数的性质：a.筛选性质b.坐标缩放性质c.可分离变量性d.与普通函数乘积性质4.卷积，性质：线性性质、交换律、平移不变性、结合律、坐标缩放性质5.互相关，两个函数f(x,y）和g(x,y)的互相关定义为含参变量的无穷积分6.惠更斯-菲涅尔原理：光场中任意给定曲面上的诸面元可以看作是子波源，如果这些子波源是相干的，则在波继续传播的空间上任意一点处的光振动都可看作是子波源各自发出的子波在该点相干叠加的结果。

7.基尔霍夫理论：在空域中光的传播，把孔径平面上的光场看作点源的集合，观察平面上的场分布则等于他们所发出的带有不同权重的因子的球面子波的相干叠加。

8.角谱理论：孔径平面和观察平面上的光场分布都可以分别看成是许多不同方向传播的单色平面波分量的线性组合。

9.点扩散函数：面元的光振动为单位脉冲即δ函数时，这个像场分布函数叫做~。

10.菲涅尔衍射成立的充分条件：传递函数：11.泰伯效应：当用单色平面波垂直照明一个具有周期性透过率函数的图片时，发现在该透明片后的某些距离上出现该周期函数的现象，这种不用透镜就可以对周期物体成像的现象称为~。

12.夫琅禾费衍射：13.衍射受限系统：不考虑系统的几何像差，仅仅考虑系统的衍射限制。

14.单色信号的复表示：去掉实信号的负频成分，加倍实信号的正频成分。

多色信号的复表示：16.如果两点处的光扰动相同，两点间的互相干函数将变成自相干函数。

18.光学全息：利用干涉原理，将物体发出的特定光波以干涉条纹的形式记录下来，使物光波前的全部信息都储存在记录介质中，做记录的干涉条纹图样被称为“全息图”，当用光波照射全息图时，由于衍射原理能能重现出原始物光波，从而形成与原物体逼真的三维像，这个波前记录和重现的过程成为~19.+1级波（虚像），-1级波（实像），±1级波（赝像）20.从物光与参考光的位置是否同轴考虑：同轴全息、离轴全息。