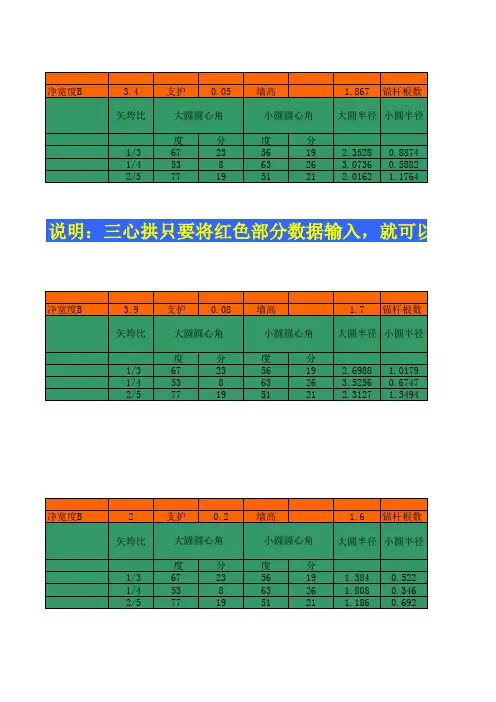
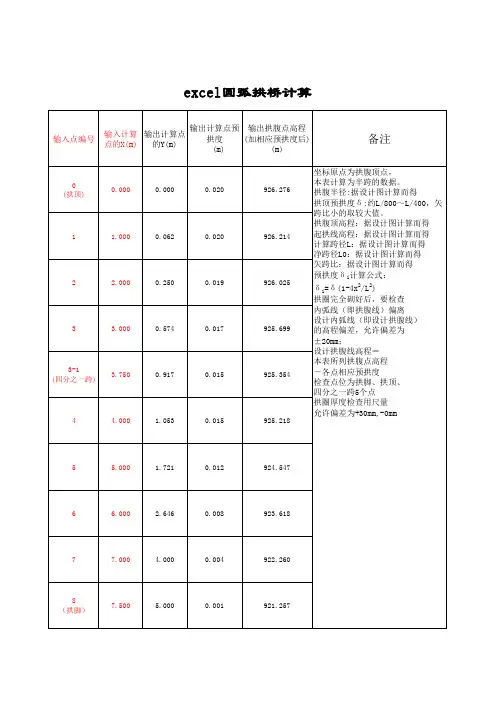
交岔点、三心拱及圆弧拱excel计算表格
- 格式:xls
- 大小:2.12 MB
- 文档页数:4

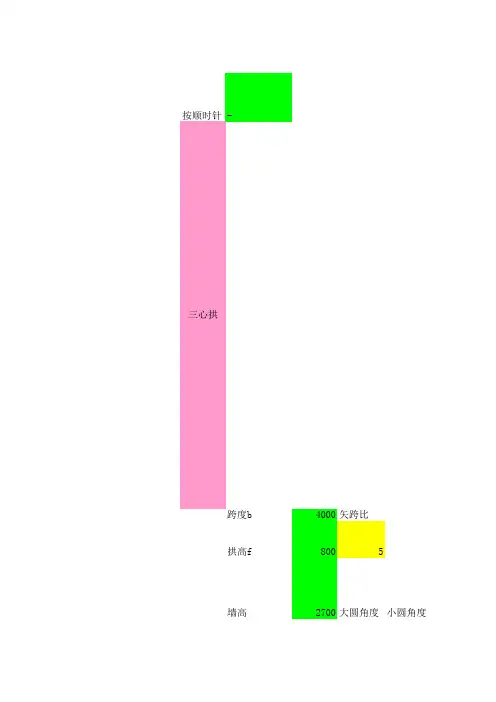
定义所谓“三心拱”,即拱形由三段相内切的圆弧构成。
三段圆弧则有三个圆心,故称三心拱。
编辑本段特性任意三心拱,是指三心拱的拱宽和拱高可以任意指定,但拱形本身必须具备下列特点:1.拱作为受力结构的主要特性,是要将覆在其上的载荷作用所产生的内应力,沿拱上任意点的切线方向传递至拱(或墙脚),而拱上任意点的径向应力(拉或压应力)为0,这在理论上就必须要求拱的三段圆弧上的任意点的切线均应垂直通过该点的圆弧半径,包括大小三段弧相切之切点的切线必须垂直大小圆弧半径的重合点。
不具备这一特性,则不是一个标准的拱形。
一心拱即半圆拱和弧形拱具备这一特性,仅是三心拱的特例。
2.大拱的顶部圆弧之圆心在拱的对称轴线上,而两侧小圆弧之圆心的联线被对称轴线垂直平分。
3.拱之大小圆弧相内切,通过其切点的切线垂直大小圆弧半径之重合线。
编辑本段任意三心拱的作法已知三心拱的净高h和净宽w,作三心拱。
步骤:1.作直线ab=w,作ab的中垂线cf=h;2.分别过c点和a点作cf和ab的垂线,并交于d点,连接ca;3.分别过c点和a点作角dca和角dac的角平分线,并交于e点;4.过e点作ac的垂线,与ab交于o2点,与cf的延长线交于o1点;5.以o1为圆心,co1为半径作弧,过c、e两点;以o2为圆心,eo2为半径作弧,过e、a两点;6.然后将弧aec以cf为对称轴镜像,得到完整的三心拱,如图所示。
o1、o2和o3即为一个大圆和两个小圆的圆心。
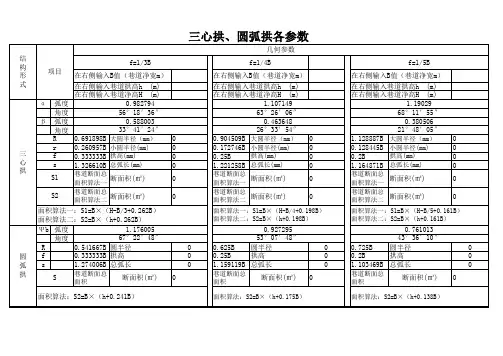
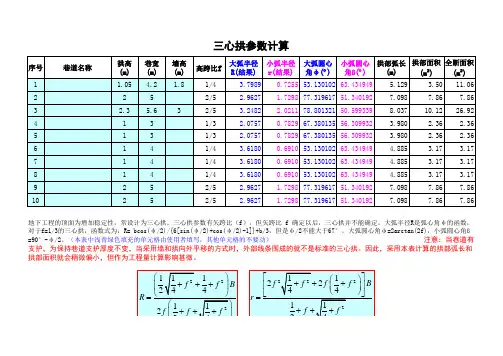
二、三分之一的三心拱的大小圆半径1、大圆半径为R=0.692B(B为巷道宽度)2、小圆半径为r=0.262B(B为巷道宽度)3、大圆圆心角a=67°22′4、小圆圆心角a=56°19′5、1/3三心拱面积为0.264B²三、1/4三心拱1、大圆半径为R=0.904B(B为巷道宽度)2、小圆半径为r=0.173B(B为巷道宽度)3、大圆圆心角a=53°08′4、小圆圆心角a=63°26′5、1/3三心拱面积为0.198B²四、2/5三心拱1、大圆半径为R=0.593B(B为巷道宽度)2、小圆半径为r=0.346B(B为巷道宽度)3、大圆圆心角a=77°19′4、小圆圆心角a=51°21′5、1/3三心拱面积为0.315B²五、1/3圆弧拱1、大圆半径为R=0.542B(B为巷道宽度)2、弧心至拱基线高为r=0.209B(B为巷道宽度)3、大圆圆心角a=134°46′4、面积为0.241B²六、1/4圆弧拱1、大圆半径为R=0.625B(B为巷道宽度)2、弧心至拱基线高为r=0.371B(B为巷道宽度)3、大圆圆心角a=106°16′4、面积为0.175B²七、2/5圆弧拱1、大圆半径为R=0.512B(B为巷道宽度)2、弧心至拱基线高为r=0.110B(B为巷道宽度)3、大圆圆心角a=154°38′4、面积为0.298B²。
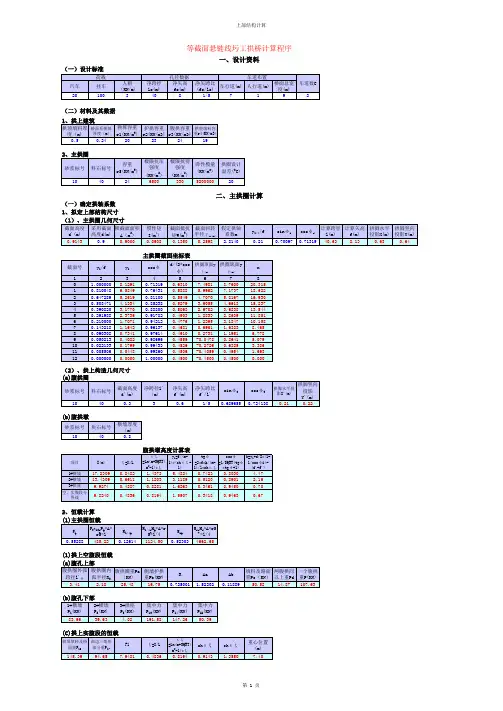
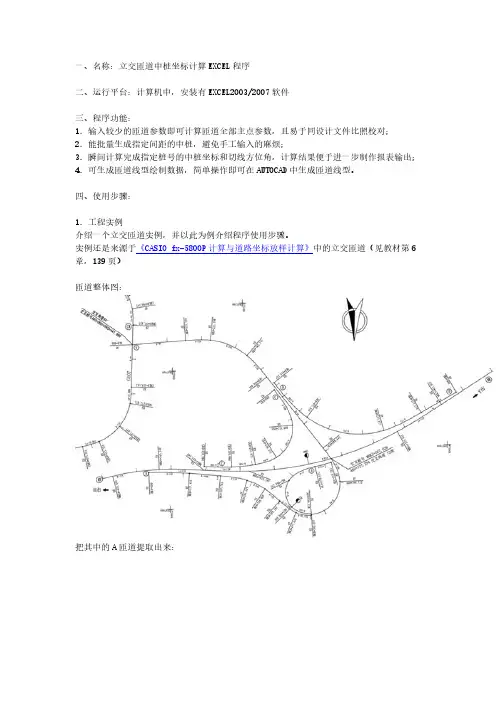
一、名称:立交匝道中桩坐标计算EXCEL程序二、运行平台:计算机中,安装有EXCEL2003/2007软件三、程序功能:1.输入较少的匝道参数即可计算匝道全部主点参数,且易于同设计文件比照校对;2.能批量生成指定间距的中桩,避免手工输入的麻烦;3.瞬间计算完成指定桩号的中桩坐标和切线方位角,计算结果便于进一步制作报表输出;4.可生成匝道线型绘制数据,简单操作即可在AUTOCAD中生成匝道线型。
四、使用步骤:1.工程实例介绍一个立交匝道实例,并以此为例介绍程序使用步骤。
实例还是来源于《CASIO fx-5800P计算与道路坐标放样计算》中的立交匝道(见教材第6章,139页)匝道整体图:把其中的A匝道提取出来:A匝道相关的参数表也提取出来:.2.打开EXCEL计算程序,输入A匝道的相关参数图中浅绿色部分是输入的原始数据部分。
这里原始数据的输入是难点和关键,一定要准确验证,否则后面的工作全是无用功。
这里就数据输入作详细解读如下:(1)第一行,“匝道”后面的单元格可输入匝道编号,这个不参与计算,仅作提示,使界面清晰明了。
(2)数据第一列,是节点栏,“节点”是我起的名字,含义是两种不同线元交界的点,如ZH、ZY、HZ、GQ、YZ等特征点都是节点,匝道的起、终点也是节点,注意QZ不是节点。
这一栏就填节点的名称,注意不要漏了。
(3)节点桩号栏。
这个在设计文件上可以找到,需要强调的是输入时按数字输入,如输入153.194,回车后会自动显示为K0+153.194格式,千万不可按桩号格式K**+***的格式输入,否则会出错。
(4)半径1、半径2两栏。
节点除匝道起、终点外,都是对前后两个线元起承接作用的点,一般情况下,其曲率半径是连续的,但也有例外,如ZY点,节点前承直线终点,半径无穷大,后接圆曲线,半径为R。
因此,在节点处曲率半径连续的情况下,就在半径1中填写半径值,半径2中空着就行(当然填一个与半径1一样的值也没事),而当节点出曲率半径不连续的情况下,就分别在半径1和半径2中相应填写两个不同的半径值。
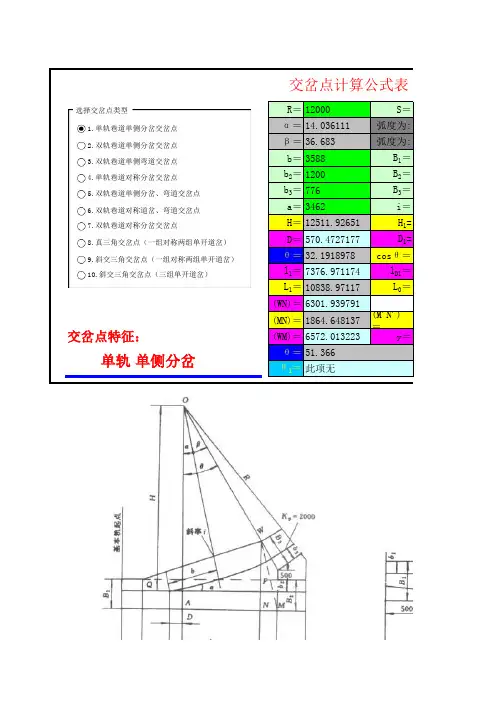
R=12000S=1α=14.036111弧度为:β=36.683弧度为:b=3588B 1=b 2=1200B 2=b 3=776B 3=a=3462i=H=12511.92651H 1=D=570.4727177D 1=θ=32.1918978cos θ=l 1=7376.971174l D1=L 1=10838.97117L 0=(WN)=6301.939791(M N)=1864.648137(M'N')=(WM)=6572.013223y=θ=θ1=此项无单轨单侧分岔交岔点计算公式表交岔点特征:51.366选择交岔点类型1.单轨巷道单侧分岔交岔点2.双轨巷道单侧分岔交岔点3.双轨巷道单侧弯道交岔点4.单轨巷道对称分岔交岔点5.双轨巷道单侧分岔、弯道交岔点6.双轨巷道对称道岔、弯道交岔点7.双轨巷道对称分岔交岔点8.真三角交岔点(一组对称两组单开道岔)9.斜交三角交岔点(一组对称两组单开道岔)10.斜交三角交岔点(三组单开道岔)1.单轨单侧分岔3.双轨单侧弯道5.双轨单侧分岔弯道6.双轨对7.双轨对称分岔9.斜三角(一组对称二组单开)0α1=142100.244976α1=14.03611111弧度为:0.2449760.64023914213500α=2β=56284010493500β1=0.3β2=此项无β1=此项无β3=此项无此项无β2=此项无γ=此项无0.846269θ1=此项无cos θ1=此项无此项无l 2=此项无P=此项无9339.799L=此项无n=此项无m=此项无n 1=此项无m 1=此项无n 2=-365.476m 2=m 3=β3=γ=此项无表此项无此项无此项无°°′′″″°′″2.双轨单侧分岔4.单轨对称分岔6.双轨对称道岔8.真三角(一组对称二组单开)10.斜三角(三组单开)。

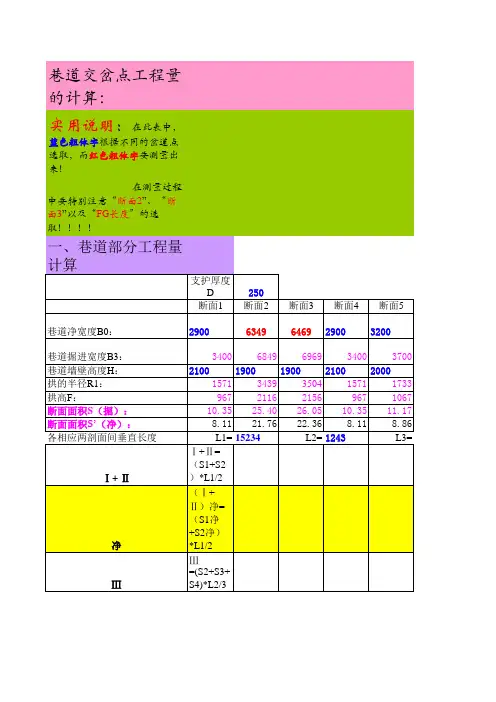
巷道断面、周长计算公式巷道断面三心拱:S=B(0.26B+h2)圆弧拱:S=B(0.24B+h2)半圆拱:S=B (0.39B+h2)梯形断面:S=( B1+B2) / 2 *h巷道周长三心拱:p=2.33B+2 h2圆弧拱:p=2.27B+2 h2半圆拱:p=2.57B+2 h2梯形断面:S=B1+B2 +( 2 h2/sina)以上:B——巷道的净宽度h ——从道渣面起巷道的净高度h2——从道渣面起巷道的墙度B1——巷道的上净宽B2——巷道的下净宽sina——一般取80度17三心拱画法、参数、巷道面积计算公式三心拱的画法:;拱形巷道参数表:;L——拱弧长f——拱高;B——巷道宽度α——小圆角度β——大圆角度R——;巷道断面面积计算公式:三心拱面积公式1:S=B(;S=B(h+0.241B)——f=B/3S=B(;注:式中B为巷道净宽,h为墙高,f为拱高三心拱面;S=B×(H-B/3+0.262B)——f=B/;注:式中B为巷道净宽,H为巷道净高,f为拱高;三心拱的画法:拱形巷道参数表:L——拱弧长 f——拱高1B——巷道宽度α——小圆角度β——大圆角度 R ——大圆半径 r ——小圆半径ψ——圆心角巷道断面面积计算公式:三心拱面积公式1:S=B(h+0.262B) —— f=B/3 S=B(h+0.198B) —— f=B/4S=B(h+0.161B) —— f=B/5 圆弧拱面积公式:S=B(h+0.241B) —— f=B/3 S=B(h+0.175B) —— f=B/4 S=B(h+0.138B) —— f=B/5 半圆拱:S=B(h+0.39B)注:式中B为巷道净宽,h为墙高,f为拱高三心拱面积公式2:S=B ×(H-B/3+0.262B)—— f=B/3 S=B ×(H-B/4+0.198B)—— f=B/4注:式中B为巷道净宽,H为巷道净高,f为拱高。