无风险利率和股市收益率表

什么是股权溢价之谜进一步，又对其他发达国家1947—1998年的数据分析发现同样存在不同程度的溢价。

金融理论将风险资产超过无风险利率的超额期望收益率解释为风险的数量乘以风险价格。

在Rubinstein(1976)．Lucas(1978)等人所研究的标准消费资产定价模型中．当风险的价格是一个代表性代理人的相对风险厌恶系数时，股市风险数量根据股票超额收益率与消费增长的协方差来测量。

股票收益率高．而无风险利率低．意味着股票的期望超额收益率高即股票溢价高。

但是消费的平滑性使得股票收益率与消费的协方差较低。

所以股票溢价只能由非常高的风险厌恶系数来解释。

Mehra和Prescott(1985)将此问题称为”股票溢价之谜”。

Kandel和Stambaugh{1991)等一些作者对股票溢价之谜提出了另外的看法他们认为风险厌恶实际比传统认为的高。

但是这会导致Well(1989)提出的无风险利率之谜”为了跟我们观察到的低实际利率相适应．我们必须假定投资者是非常具有忍耐力的他们的偏好给予未来消费几乎跟当前消费一样的权重．或者甚至更大的权童。

换言之．他们有着低的或者甚至负的时间偏好率。

负的时间偏好率是不可能的．因为人们偏好于更早的效用。

股权溢价之谜的解释有关股权溢价之谜的解释也层出不穷,经典理论由于无法合理解释市场上的高股权溢价现象,后来的研究人员对经典理论进行了一系列的修正,并提出了各种各样的解释。

股权溢价之谜的古典理论解释(一)在完全理性的基础上引入更加复杂的效用函数1.“无风险利率之谜”。

由于在Mehra—Prescott模型中要解决风险溢价难题，相对风险厌恶系数必须很高，而这显然是不可能的，因此Weil(1989)l率先对投资者的期望效用函数进行修正来解释股权溢价之谜，在这种效用函数下，投资者的消费跨期替代弹性是一个常数，并且与投资者的相对风险厌恶系数无关，然而这种模型的最终的结果却显示Weil不仅没有解决股权溢价之谜，反而提出了一个“无风险利率之谜”，即市场中的无风险利率水平与理论值相比，明显偏低。

如何计算股票的 Beta 系数Beta 系数是特定股票相对整个股票市场波动率的波动率，或称风险程度。

Beta 系数是衡量特定股票风险程度的指标，可用于计算股票的预期收益率。

Beta 系数是股票分析师们在选择资产组合中的股票时要考虑的基本因素之一，其他因素包括市盈率、股东权益、资本负债比率等。

本文介绍如何计算 Beta 系数及如何使用 Beta 系数来计算预期收益率。

方法1使用简单公式计算 Beta 系数1 确定无风险利率。

这是投资者在无风险投资上预期可获得的收益率，例如以美元投资的美国国库券，以欧元交易和投资的德国政府债券等。

该数字通常以百分比表示。

2 分别确定股票收益率、市场（或代表性指数）收益率。

这些数字也以百分比表示。

通常情况下，需要使用若干个月的时段数据计算收益率。

上述二值或其中之一均可能为负数，表示投资股票或市场（指数）整体在该期限内出现亏损。

如果 2 个收益率中只有 1 项为负数，则 Beta 系数将为负数。

3 用股票的收益率减去无风险利率。

如果股票的收益率为 7%，无风险利率为2%，则二者的差为 5%。

4 用市场（或指数）收益率减去无风险利率。

如果市场或指数收益率为 8%，无风险利率仍为 2%，则二者的差为 6%。

5 用股票收益率减无风险利率的差除以市场（或指数）收益率减无风险利率的差。

得出的即为 Beta 系数，通常用小数表示。

在上例中，Beta 系数为 5除以 6，得到 0.833。

从定义上可以得出，市场或其代表性指数本身的 Beta 系数为 1.0，这是因为市场与其自身作比较的话，任何非零数除以本身结果都等于 1。

Beta 系数小于 1 表示股票比市场整体的波动率低，Beta 系数大于 1 表示股票比市场整体的波动率高。

Beta 系数可以小于零，表示投资该股票出现亏损，但市场整体盈利（此可能性较大）；或者投资该股票盈利，但市场整体亏损（此可能性较小）。

在计算 Beta 系数时，通常（尽管不是必需的）要使用待计算股票所处市场的代表性指数。

二、银行间拆借利率和 债券回购利率缺乏无风险特 征
另有一些学者采用银行间 拆借利率和债券回购利率作为 无风险利率的替代， 笔者也认为 不合适。理由是： 银行间拆借利率是指银行 在保证自身资金流动性前提下 为加速资金流转而进行的同业
!"
广西金融研究
!""#$%
证券 市场
间拆借资金利率， 它可以反映一 定的金融商品收益率， 但从根本 上讲它隐含了一种银行自身的 经营风险在内。在现阶段国有商 业银行、 民营银行、 股份制银行 和外资银行并存的情况下， 拆借 利率由大家共同决定， 而银行各 自的风险管理能力各不相同， 将 拆借利率当成无风险利率是不 合适的。 债券回购利率是指投资者 在卖出债券时， 同意在将来某个 约定时间以约定价格购回该债 券， 借以获得资金上的融通的利 率。在我国， 交易所债券市场受 股市影响太大， 回购利率和债券 价格被股票价格走势所引导。由 于股票一、 二级市场一直存在较 大的价差， 认购新股的收益远远 高于社会平均利润率， 而且风险 较小，因此吸引了全社会的资 金。但根据政策， 金融机构中只 有证券 经营机 构才可 以认购 新 股 ， 于 是 ， 其他金 融机构 提供资 金给券 商 ，然 后大家分享利润。这样一来， 国 债回购市场理所当然成为了资 金融通的桥梁。有关的分析显 示： 交易所回购市场的利率大幅 波动与新股发行在时间上出现 强相关关系。 !""# 年上海证券交 易所债券价格平均年波动幅度 为 $% ，远远高 于 一 般 发 达 国 家 项目 Y 日期 表!
# 年期贷款年利率 ( 个月存款年利率
注：加权平均后 #HHR 年贷款利率 H&’I ，存款利率 !&’’ ， #HH’ 年贷款利率 R&*$ ，存款利率 !&’I ， #HHH 年 贷 款 利 率 存款利率 !&(I 。 $&"H ， 根据中经网数据中心数据整理 ［ !""I 年 $ 月 (" 日］

中国股票市场β和收益关系的实证分析资本资产定价模型（CAPM）已经在资本市场资本成本的估计，基金管理绩效的度量等方面得到广泛的应用。

但对于CAPM的有效性，即β和收益的关系问题，一直存在着很大的争议。

Fama和French（1992）根据对美国的股票市场的研究，得出β和收益不存在明显的关系。

Pettengill（1995）提出β和收益这种弱关系的原因，由于我们使用的是事后收益率，因此我们必须考虑条件关系，并利用剩余市场收益模型和两阶段回归方法进行检验，得出β和收益间存在显著的条件关系，这种条件关系就是我们根据市场收益和无风险收益的比较，把样本分成两部分，市场收益大于无风险收益时，我们成为上市场，当市场收益小于无风险收益时，我们称之为下市场。

则应该有，当市场收益大于无风险收益时，β和收益正相关，而当市场收益小于无风险收益时，β和收益负相关。

否则，低β股票将无人持有。

本文利用Pettengill的剩余收益模型和Fama的两阶段回归方法，对中国的股票市场进行实证分析，检验中国股票市场β和收益的条件关系。

①市场均衡条件下，Black推导出0-βCAPM公式。

E（R i）=γ0+γ1β1，i=1，…，N，（38-1）式中：E（R i）为资产i的预期收益；βi=cov（R i，R m）/Var（R m）为资产i的β；γ0是与市场投资组合0协方差的投资组合的预期收益；γ1是市场投资组合预期风险溢价。

CAPM表明高β对应高收益，β和收益应该正相关。

它隐含的条件假设是风险溢价γ1大于0。

但是当我们考虑风险溢价γ1小于零时，理论上高β对应低收益，β和收益应该负相关。

②两阶段回归方法。

Fama和French利用两阶段回归方法对美国股票市场进行了实证研究，得出结论，美国股票市场β和收益间并不存在明显的关系。

也就是CAPM定价是无效的。

他采用的方法是：第一阶段，利用R it=αi+βi R mt+εit（38-2）估计βi。

市场风险溢价计算思路
研究方法选择
历史数据法是当前研究中国股权风险溢价的最佳方法。
计算中国市场股权风险溢价思路图
年度无风险资产收益 名义收益下的溢价
年度股票投资收益
年度无风险资产收益 实际收益下的溢价 年度股票投资收益
年度通货膨胀率
周期的确定
1995年2月~2002年12月是一个比较好的周期选择。
--------------------------------------------------------------------rp3 不考虑交易成本的实际收益溢价 0.0692755 rp4 考虑交易成本的实际收益溢价 0.0571228 ---------------------------------------------------------------------
计算市场投资收益
市场投资收益数据采用Resset/DB数据库中的市场年持有期收益数据。数 据集名为Yrretm 。 不考虑交易成本的市场投资收益使用表Yrretm中的“流通市值加权平均 市场年收益率”Yrettmv。 考虑交易成本的市场投资收益使用表Yrretm中的“流通市值加权平均市 场年收益率_考虑交易成本”Yret_tcctmv。 data yrretm; set resdat.yrretm; where Exchflg='0' and Mktflg='A' and 1995<=year(date)<=2005; year=year(date); keep year yrettmv yret_tcctmv; run;
实际收益下的溢价
股票实际收益=(1+股票名义收益率)/(1+通货膨胀率)-1； 无风险资产实际收益率=（1+无风险资产名义收益率） /(1+通货膨胀率)-1;

3
CAPM之假设 CAPM之假设 1、投资者的行为可以用平均数─变异数(Mean─Variance)准 则来描述，投资者效用受期望报酬率与变异数两项影响，假设 投资人为风险规避者(效用函数为凹性)，或假定证券报酬率的 分配为常态分配。 2、证券市场的买卖人数众多，投资人为价格接受者(Price taker)。 3、完美市场假设：交易市场中，没有交易成本、交易税…等， 且证券可无限制分割。 4、同构型预期：所有投资者对各种投资标的之预期报酬率和 风险的看法是相同的。 5、所有投资人可用无风险利率无限制借贷，且存款利率＝贷 款利率＝无风险利率。 6、所有资产均可交易，包括人力资本(Human Capital)。 7、对融券放空无限制。 4
7
β系数系数是同行业股票收益率与整个证券市场收益率的关 系，常用预测方法有： 在资本市场发达的国家，目前已有专门机构通过收集、整理 证券市场的有关数据、资料，计算各种证券的β系数，以便出 售给需要的投资者。 估测证券β系数的历史值。用历史值代替下一时期证券的β 值。历史的β值可以用某一段时期内证券价格与市场指数之间 的协方差对市场指数的方差的比值来估算。 用回归分析法估测β值。假定某年度的β系数与上一年度的 β系数之间存在着线性关系，即βt=α0＋α1βt－1。通过许 多年度β值的积累和回归，便可估计出上式中的α0和α1，这 样就能计算出下一年度证券的β值，即：βt＋1=α0＋α1βt。
2
CAPM：资本资产定价模型
Capital Asset Pricing Model(CAPM) 市场均衡时，证券要求报酬率与证券的市场风险( 市场均衡时，证券要求报酬率与证券的市场风险(系 统性风险)间的线性关系，而市场风险系数是用β 统性风险)间的线性关系，而市场风险系数是用β值 来衡量。 美国财务学家Treynor(1961) Treynor(1961)， 来衡量。 美国财务学家Treynor(1961)，W. Sharpe(1964)， Lintner(1965)， Sharpe(1964)，J. Lintner(1965)，J. Mossin(1966) 等人于1960年代发展而来。 1960年代发展而来 等人于1960年代发展而来。 Ra=Rf+Ba(Rm-Rf) 其中： 其中：Ra — 股票期望回报率 Rf — 无风险收益率 无风险收益率（长期国债收益率） Ba — 股票的 股票的Beta系数 系数（常采用周综合收益率） 系数 Rm-Rf — 市场风险溢价 市场风险溢价（参考国际标准以及国内市 场历史回报率，取风险溢价为7.5%）

理论与实践Theory&Practice保险公司无风险利率预测量化模型应用研究张佳余诚汪越王玲焱安永（中国)企业咨询有限公司精算与风险管理团队对于保险行业而言，无风险利率是同时 影响资产端和负债端的重要因素，它既是保 险产品定价利率的锚，也是资产端投资收益 率的基石，其未来变动趋势会在很大程度上 影响保险公司的关键经营业绩和指标。

利 率风险，是保险公司尤其是人身险公司传统 上面临的最重要的风险之一。

若对利率未来走势缺乏科学合理的预测，保险公司就无法对未来利率风险提前进行研判。

在我国劳动力人口增速下滑和全球高债务背景下，无风险利率中枢震荡下移，很可能会导致保险公司出现利差损的风险。

本文将与行业同仁共同探讨和研究如何采用量化模型的方式对未来利率水平进行预测，从而支持保险业负债端产品策略、资产端配置策略以及资产负债匹配管理策略的制定。

一、保险业的发展与无风险利率从历史经验看，保险业的发展与无风险利率有着非常深刻的关联。

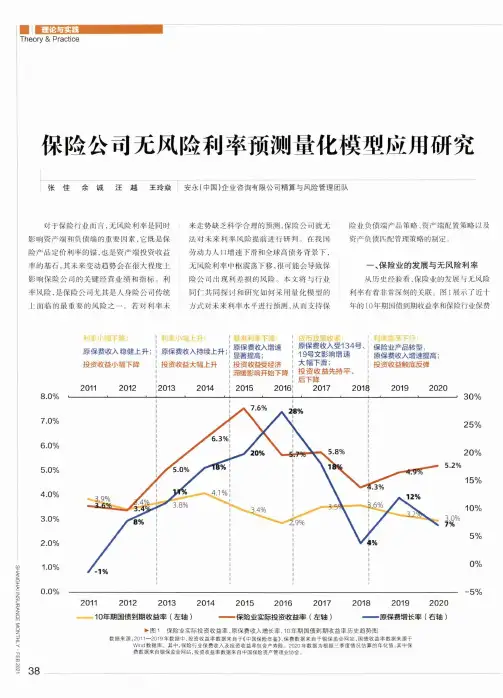
图1展示了近十年的10年期国债到期收益率和保险行业保费8.0% 7.0% 6.0% 5.0% 4.0% 3.0% 2.0% 1.0% 0.0%2011201220132014 10年期国债到期收益率（左轴）201520162017-保险业实际投资收益率（左轴）201820192020-----原保费增长率（右轴）►图1保险业实际投资收益率、原保费收入增长率、10年期国债到期收益率历史趋势图数据来源:2011 —2019年数据中，投资收益率数据来自于《中国保险年鉴》，保费数据来自于银保监会网站，国债收益率数据来源于W i n d数据库。

其中，保险行业保费收入及投资收益率包含产寿险。

2020年数据为根据三季度情况估算的年化值.其中保费数据来自银保监会网站,投资收益率数据来自中国保险资产管理业协会。

38收人增长、保险行业投资收益率的变化趋势 及相关性。

根据图1所示，10年期国债到期收益率 (黄色趋势线）与原保险保费收人增长率(蓝 色趋势线）在大部分情况下呈负相关关系，主要原因为保险产品在宏观经济相对不好 的情况下相比传统金融产品存在一定优势，也符合保险产品负凸性的特征。

资本资产定价模型(CAPM)在我国股市的适用性研究资本资产定价模型(CAPM)在我国股市的适用性研究摘要：本文主要探讨了资本资产定价模型(CAPM)在我国股市的适用性，并通过实证分析的方法对其进行了验证。

研究结果表明，虽然CAPM作为一个经典的投资理论模型，具有一定的适用性，但在我国股市中存在一定的局限性。

因此，在使用CAPM进行投资决策时，需要结合其他因素进行综合考虑。

1. 引言资本资产定价模型(CAPM)是投资领域中最重要的理论模型之一，在投资组合的选择和定价上起着关键作用。

该模型是根据风险投资的基本原理和市场均衡理论基础上发展起来的，旨在通过考虑风险和回报之间的关系，提供一种合理的投资参考。

然而，CAPM模型的适用性一直备受争议，尤其是在我国股市的背景下。

本文将从理论和实证两个方面，对CAPM模型在我国股市中的适用性进行深入研究。

2. CAPM模型理论基础2.1 市场均衡理论市场均衡理论是CAPM模型的理论基础，它认为所有投资者都是追求效用最大化的理性决策者，在完全竞争的市场中，资产价格将通过供需关系来确定。

基于这一理论，CAPM模型假设所有的风险投资者都对风险敏感，并且会通过配置资产来在风险与回报之间寻求平衡。

2.2 风险和收益之间的关系CAPM模型认为，风险与回报呈正相关关系，即投资组合的预期收益率是风险无关部分与风险部分的线性组合。

该模型量化了风险与收益之间的关系，通过计算投资组合的无风险回报与风险溢价之间的关系，提供了一种衡量资产的合理回报率的方法。

3. CAPM模型的适用性研究3.1 实证分析方法本文利用我国股市的实证数据，运用回归分析方法，对CAPM 模型的适用性进行验证。

具体而言，我们选择了一组具有代表性的股票样本，收集相关数据，包括每只股票的收益率、市场风险溢价、无风险利率等指标。

3.2 实证结果分析根据回归分析的结果，我们发现CAPM模型在我国股市中具有一定的适用性，但也存在一些局限性。

2、证券市场的买卖人数众多，投资人为价格接受者(Price taker)。
3、完美市场假设：交易市场中，没有交易成本、交易税…等， 且证券可无限制分割。
4、同构型预期：所有投资者对各种投资标的之预期报酬率和 风险的看法是相同的。
5、所有投资人可用无风险利率无限制借贷，且存款利率＝贷 款利率＝无风险利率。
的现金流量及残余价值，利用折现法折现成目前的价值。
预测未来数年所有现金流，必须把资产负债表、损益表
和现金流量表数据全部预测。依成长率的差别及时间的长短
可分为：
固定成长折现模型
二阶段折现模型
三阶段折现模型
➢ 现金流折现方式一般分为：
股利折现
股权自由现金流量（FCF）折现
加权平均资本成本（WACC）折现
17
ROC：资本报酬率Return on Capital、Return on Invested Capital 。 计算一段时间内，公司运用长期资本创造利润的能力， 在此所指的“资本”为股东权益加上长期负债。 ROC=税后净利／运用资本。（运用资本 = 股东权益 ＋ 长期负债）
18
使用：一般而言，判断公司创造利润的能力指针为 总资产报酬率(ROA)及股东权益报酬率(ROE)，而 资本报酬率(ROC)则是判断公司运用长期资本创造 获利的指针。
8
❖β的使用：资产的预期报酬率会受到风险因子的影响，导致实 现的报酬不稳定，而这些因子主要可分成系统风险与非系统风险。 非系统风险是可以利用多角化来分散殆尽以达到投资效率，因此， 对投资人来说，他只需观察对于整个市场具有威胁性的风险，如 物价指数、货币供给额成长等等，也就是所谓的「系统风险」。
❖以股市投资而言，在一段特定时间内，当贝他值等于1时，代 表个股之风险等于指数之风险；当贝他值小于1时，代表个股变 动的幅度低于指数(亦即风险较低)；当贝他值大于1时，代表个股 变动的幅度高于指数(亦即风险较高)。

2024年银行存款利率表(完整版)2024年银行存款利率表完整版国有六大行：中国银行：三个月1.15%，半年1.35%，一年1.45%，二年1.65%，三年1.95%，五年2.0%。

工商银行：三个月1.15%，半年1.35%，一年1.45%，二年1.65%，三年1.95%，五年2.0%。

建设银行：三个月1.15%，半年1.35%，一年1.45%，二年1.65%，三年1.95%，五年2.0%。

农业银行：三个月1.15%，半年1.35%，一年1.45%，二年1.65%，三年1.95%，五年2.0%。

邮政银行：三个月1.15%，半年1.36%，一年1.48%，二年1.65%，三年1.95%，五年2.0%。

交通银行：三个月1.15%，半年1.35%，一年1.45%，二年1.65%，三年1.95%，五年2.0%。

12家全国性股份制商业银行：招商银行：三个月1.15%，半年1.35%，一年1.45%，二年1.65%，三年1.95%，五年2.0%。

华夏银行：三个月1.20%，半年1.45%，一年1.65%，二年1.80%，三年2.00%，五年2.05%。

兴业银行：三个月1.20%，半年1.45%，一年1.65%，二年1.80%，三年2.00%，五年2.05%。

光大银行：三个月1.20%，半年1.45%，一年1.65%，二年1.80%，三年2.00%，五年2.05%。

中信银行：三个月1.20%，半年1.45%，一年1.65%，二年1.70%，三年2.00%，五年2.05%。

民生银行：三个月1.20%，半年1.45%，一年1.65%，二年1.75%，三年2.00%，五年2.05%。

浦发银行：三个月1.20%，半年1.45%，一年1.65%，二年1.80%，三年2.00%，五年2.05%。

平安银行：三个月1.20%，半年1.45%，一年1.65%，二年1.90%，三年2.00%，五年2.05%。

恒丰银行：三个月1.20%，半年1.45%，一年1.65%，二年1.90%，三年2.30%，五年2.30%。

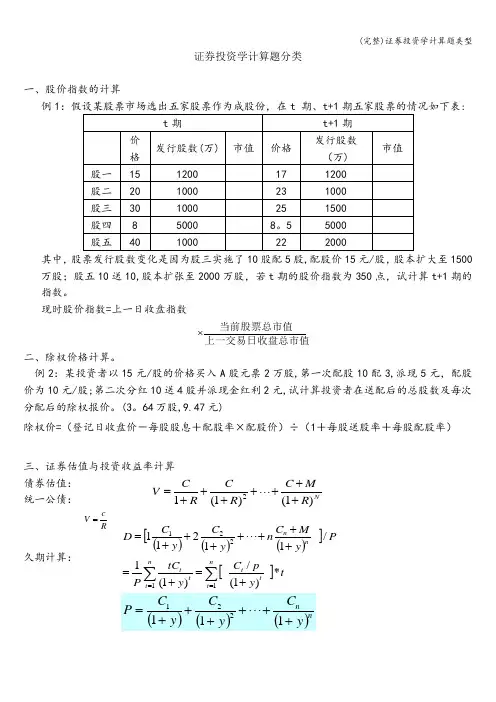
证券投资学计算题分类一、股价指数的计算例1:其中，股票发行股数变化是因为股三实施了10股配5股,配股价15元/股，股本扩大至1500万股；股五10送10,股本扩张至2000万股，若t 期的股价指数为350点，试计算t+1期的指数。

现时股价指数=上一日收盘指数二、除权价格计算。

例2：某投资者以15元/股的价格买入A 股元票2万股,第一次配股10配3,派现5元，配股价为10元/股;第二次分红10送4股并派现金红利2元,试计算投资者在送配后的总股数及每次分配后的除权报价。

(3。

64万股,9.47元)除权价=（登记日收盘价－每股股息＋配股率×配股价）÷（1＋每股送股率＋每股配股率）三、证券估值与投资收益率计算 债券估值： 统一公债：久期计算：上一交易日收盘总市值当前股票总市值⨯)1()1(12NR MC R C R C V +++⋅⋅⋅++++=Rc V =[()()()][]ty p C y tC P Py M C n y C y C D nt tt n t t tnn *)1(/)1(1/1121111221∑∑==+=+=+++++++=股票价值计算：四、资本市场理论1、均值——方差模型单种证券的预期收益率与风险∑-==j j j p r r Var 22)()(μσ两种证券的预期收益率与风险一般意义下的两证券最小风险组合:y D y y D P P ∆-=⎪⎪⎭⎫ ⎝⎛+∆-=∆+⨯='11到期收益率到期收益率变化久期价格变化的百分比∑∞=+=++++++=1332210)1()1()1()1(t tt R D R D R D R D P ,)1()1(1110∑-=++=-g R D R g D P tt ∑∑=∞+=-++++=Tt T t tt t T R D R g D P 111110)1()1()1( )1()1(10∑=+++=nt nnn t t R E M R D P ∑==jj j j p r r E )(μ212222]..)1(2)1([)1(B A AB A A B A A A P BA A A P x x x x x x σσρσσσμμμ-+-+=-+=210RDR D P ∆+=当相关系数=1，0，-1时的最小方差组合。

3.4483
18.8115
100003.IB
10附息国债03
3.4332
20.1667
150021.IB
15附息国债21
3.4250
15.7268
070006.IB
07国债06
3.4156
17.3770
019319.SH
13国债19
3.4071
23.7104
130009.IB
13附息国债09
3.3635
3.7000
28.8087
019547.SH
16国债19
3.6958
26.6421
140025.IB
14附息国债25
3.6614
24.8224
150017.IB
15附息国债17
3.6473
25.5710
130019.IB
13附息国债19
3.6386
23.7104
019508.SH
15国债08
3.6302
17.3770
090025.IB
09附息国债25
4.2646
19.7896
019208.SH
12国债08
4.2493
42.3770
101208.SZ
国债1208
4.2493
42.3770
019310.SH
13国债10
4.2393
43.3852
101310.SZ
国债1310
4.2393
43.3852
101427.SZ
12国债13
4.1181
22.5874
101213.SZ
国债1213
4.1181
22.5874

2018 年 11 月（同花顺）
月初
月初开 月末收 月涨跌
月末收
年 月份
月收益率 开盘
盘指数 盘指数 幅度
盘价
价
201 7 1965.99 1993.8 1.41% 6.57% 3.5 3.73
3
2098.3
8 2000.82
4.88% 18.13% 3.75 4.43
8
2174.6
9 2104.09
4
8
月平 3013.56 3024.1
0.66%
均
9
87
2.08%
8.9866 8.99881
14Biblioteka 注：表中上证 A 综合指数涨跌幅度为月初收盘指数减去开 盘指数的值除以开盘指数计算所得，中国高科股票月收益率为
月初收盘价减开盘价的值除以开盘价计算所得。
189
经济纵横
2019 年第 02 期（总第 218 期）
数据及来源： （1）2013 年 7 月至 2018 年 10 月上证综合指数每月月初开盘 指数与每月月末收盘指数（网易财经网站 2018 年 11 月 10 日） （2）2013 年 7 月至 2018 年 10 月中国高科股票每月月初开盘 股价与每月月末收盘股价（同花顺官官方网站 2018 年 11 月 10 日） （3）不包含 2014 年 3 月至 2014 年 7 月数据（中国高科此时 间段停牌） 通过以上数据计算（利用 excel 回归分析函数）可得： 相 关 系 数 R＝0.4594，R2 ＝0.21，趋 势 线 可 表 示 为 ：Y= 1.4128X+0.0116，其中中国高科月收益率为 Y,同期上海 A 股综 合指数涨跌幅度为 X。 β = 相 关 系 数 * 该 股 票 收 益 标 准 差/上 证 指 数 标 准 差 ＝ 0.4594*0.2063/0.0671＝1.41 上证 A 股综合指数标准差（stdev 函数）＝0.0671 中国高科收益率标准差（stdev 函数）＝0.2063 利用资本定价模型可知中国高科预期月收益率＝Rf +β* （Rm- Rf）＝4.27%/12+1.41*（0.66%-4.27%/12）=0.7847% 其中： Rf－为 2018 年 11 月 10-11 月 19 日发行的五年期凭证式国 债票面年利率为 4.27% Rm－为上表上证 A 股综合指数月平均涨跌幅度 0.66% 中国高科预期名义年化收益率（POWER 函数）＝9.8336% 考虑到通货膨胀率的影响，中国高科预期实际收益率＝ （1+预期名义年化收益率）（/ 1+通货膨账率）-1＝（1+9.8336%）/ （1+2%）-1＝7.68%。 中国高科的 β 值为 1.41，大于 1，说明中国高科的股票收益 率与整个市场回报率高度敏感，也就是说，如上海证券交易所 整个市场回报率上升，中国高科的预期收益率会有更高的涨 幅，如上海证券交易所整个市场回报率下降，中国高科预期收 益率会有比较大的跌幅 二是资本定价模型分析的局限性： （1）运用资本定价模型分析中的依赖历史数据，中国高科 自 2017 年 6 月以来通过并购以教育培训为主业的新三板广西 英腾教育股份有限公司实施战略转型，由此前的房地产行业转 向教育行业，资本密集型的房地产行业与轻资产互联网教育培 训行业与系统风险的敏感度有比较大的差异，因此，以中国高 科历史数据得出的 β 值估计能否适用于的转型后的中国高科股 票预期收益率分析，存在不确定性。 （2）影响系统风险的经济环境的不确定性增加和不断变 化，自 2018 年 3 月 23 日，美国总统签署对华贸易备忘录后，中美 贸易战正式开打，至 2018 年 11 月尚未有明显停战的迹象，使得 总体经济形势不确定性继续存在，据央行 2018 年 11 月 13 日发 布数据，10 月份 M2 增速、新增社会融资规要模与同期增带相比 骤降，信托贷款、委托贷款皆为 2016 年 7 月份以来新低，社会融 资规模、广义货币和狭义货币同时新低，整个市场信心不足，对 降准降息预期增大，在国内外经济形势发生较大变化的情况 下，系统风险水平必然有所改变，依据历史数据估算出来的 β 值 的指导作用则减弱。

一、引言1952年，马科威茨（Markowitz）发表了《投资组合选择》这篇具有里程碑意义的论文，标志着现代投资组合理论的开端。

在此基础上，夏普（William Sharp）、林特纳（John Lintner）和默森（Jan Mossin）等经济学家推导出了资本资产定价模型（CAPM）。

首先，CAPM建立在严格的前提假设的基础之上：假设1所有资产均为责任有限的，即对任何资产其期末价值总是大于等于零。

假设2市场是完备的，即不存在交易成本和税收，而且所有资产均为无限可分割的。

假设3市场上有足够多的投资者使得他们可以按市场价格买卖他们所想买卖的任何数量的任何交易资产。

假设4资本市场上的借贷利率相等，且对所有投资者都相同。

假设5所有投资者均为风险厌恶者，同时具有不满足性，即对任何投资者，财富越多越好。

假设6所有投资者都追求期末财富的期望效用极大化。

假设7所有投资者均可免费获得信息，市场上的信息是公开的、完备的。

假设8所有投资者对未来具有一致性的预期，都正确的认识到所有资产的收益服从联合的正态分布。

假设9对于任何风险资产，投资者对其评价有两个主要“指标”：风险资产收益率的预期和方差。

预期代表收益，方差（或标准差）代表风险。

假设1～4是关于资本市场的一种理想化，概括起来实质是认为一个理想的市场应该是完备的，无摩擦的，从而对资源的配置是有效的。

当然，这种理想的市场在现实中是不存在的，但可以对这些条件进行放松，并发现放松后对原来的结果影响不是根本的，即这些理想的假说抓住了主要矛盾，结果也就十分有意义。

同时，随着科学技术尤其是信息技术的发展，现实中的资本市场也正一步一步地向这一理想市场靠近。

假设5、6、8、9是关于投资者的假设，风险厌恶的假设是有代表性的，当然，我们并不否认存在风险偏好的投资者，同时这些假设对投资者的选择标准也给了说明，而假设7则是一个有效市场假设。

基于以上假设，CAPM模型可以表达为以下的形式：E(Rp)=Rf+i=Cov(Ri，Rm)/Var(Rm)，E(Rp)表示投资组合的期望收益率，Rf为无风险报酬率，E(RM)表示市场组合期望收益率，之间的正相关关系成立。

CAPM模型在股市中的运用我国股市发展至今，制度逐渐完善，市场逐渐成熟，但仍存在诸多问题。

风险和收益的关系是投资者重点关注的问题。

CAPM模型作为国际上研究风险与收益关系的主流理论，主要研究证券市场中风险资产与资产的预期收益率之间的关系，以及均衡价格是如何形成的。

据此，本文拟基于CAPM模型，对中国股市风险与收益的关系进行测度，验证CAPM模型的有效性。

一、研究背景2012年开始，中国金融行业过于追求与经济周期不匹配的高收益率，却没有能够为市场风险、信用风险正确定价。

这种定价机制的扭曲，推动了2016年金融市场各类资产价格的大幅波动（刘煜辉，2017）。

综上，如何度量我国股票市场的金融风险，怎样评价收益和风险的关系已成为广大股票投资者日益关注的紧迫问题。

资本资产定价理论是目前国际上关于证券投资收益和风险相关性研究的主流金融理论。

应用CAPM模型对我国股市收益和风险进行研究，有助于进一步明确收益和风险的关系。

CAPM模型主要研究证券市场中资产的预期收益率与风险资产之间的关系，以及均衡价格是如何形成的，是现代金融市场价格理论的支柱。

CAPM模型将股票市场假设为一个理想化的、被简化的、抽象的市场。

CAPM模型假设股票市场是有效的，这要求市场信息是被充分披露的，信息的获取是没有成本的，投资者是理性投资者能及时的对市场信息做出反应。

然而我国股市建立较晚，虽然股市制度被逐渐完善，但是我国股市依然存在诸多问题，导致我国股市可能并非是个有效的市场。

同时CAPM模型认为非系统性风险可以通过投资组合而分散，我国股市未必能满足这一假设。

我国股市发展至今，规模日益扩大、制度不断完善，市场逐渐成熟，资本资产定价模型在我国股票市场的适用性是否得到了改善？需要我们对CAPM模型在我国股市适用性进行相关问题研究。

研究CAPM模型在我国股市的适用性，会对资产的定价提供一定的参考意义，也有助于CAPM模型在我国的实证研究与发展。

二、CAPM模型具体介绍CAPM模型主要研究均衡市场上资产预期收益与风险资产的相关性问题和证券均衡价格形成过程。

2024各大银行利息表最新公布（含不同产品的利率）2024各大银行利息表最新公布(含不同产品的利率)一.中国工商银行：工商银行定期存款利率：1.整存整取：三个月年利率1.25%、半年年利率1.45%，一年年利率1.65%、二年年利率2.15%、三年年利率2.6%、五年年利率2.65%。

2.零存整取、整存零取、存本取息：一年年利率1.25%、三年年利率1.45%，五年年利率1.45%。

3.定活两便：按一年以内定期整存整取同档次利率打6折。

协定存款利率：年利率0.9%。

通知存款利率：一天年利率为0.45%，七天年利率为1%。

二.中国农业银行：农业银行1.整存整取：三个月1.25%、六个月1.45%、1年1.65%、2年2.15%、3年2.6%、5年2.65%。

2.零存整取、整存零取、存本取息：1年1.25%、3年1.45%、5年1.45%。

3.定活两便：按一年以内定期整存整取同档次利率打六折执行。

4.协定存款：0.9%。

5.通知存款：1天0.45%，七天1%。

三.中国建设银行建设银行定期存款利率：1.整存整取：三个月1.25%、六个月1.45%，一年1.65%、二年2.15%、三年2.6%，五年2.65%。

2.零存整取、整存零取、存本取息：一年1.25%、三年1.45%、五年1.45%。

3.定活两便：按一年以内定期整存整取同档次利率打六折执行。

4.通知存款：一天0.45%、七天1.00%。

四.中国银行中国银行定期存款利率：1.整存整取：三个月1.25%、六个月1.45%、一年1.65%、二年2.15%、三年2.60%、五年2.65%。

2.零存整取、整存零取、存本取息：一年1.25%、三年1.45%、五年1.45%。

3.定活两便：按一年以内定期整存整取同档次利率打6折。

协定存款利率：0.90%。

通知存款利率：一天0.45%、七天1.00%。

五.交通银行交通银行定期存款利率：1.整存整取：三个月1.25%、六个月1.45%、一年1.65%、二年2.15%、三年2.60%、五年2.65%。

股市特质风险与股票收益率相关关系的实证研究熊伟;陈浪南;柯忠义【摘要】Based on traditional asset pricing models,idiosyncratic risks can be well-diversified through portfolio selection,and only systematic risk is priced.However,idiosyncratic risks might not be fully diversified as there are frictions and imperfect information in the market.Researchers have different views on the effect of idiosyncratic risks on stockreturns,depending on model specifications for measuring idiosyncratic risks as well as sample data.In this paper,we examine the relationship between idiosyncratic risks and stock market return by incorporating idiosyncratic risks as a source of systematic risks un-captured by beta coefficients in China's stock market.First,we estimate idiosyncratic volatility as a standard deviation of daily residuals in the regression timessquare root of number of days based on the Fama-French by employing a sample data from Shanghai Stock Exchange for the period from 3 January 1996 to 31 December 2011.We construct different portfolios based on idiosyncratic volatility and use the difference of the weigh average rate of return of the portfolio with high volatility and that of the portfolio with low volatility as a systematic risk-based factor IVF.We allocate stocks into two portfolios by size based on whether their month of end market equity is above or below the median market equity.Further,we construct six size-idiosyncratic volatility portfolios with two dimensions of size and idiosyncratic volatility.Second,we examine the ability of systematic idiosyncratic riskfactors in predicting future market return and future market variance by utilizing a regime switching model.We find that IVF can be used to forecast future market return or volatility.The idiosyncratic risk-based factor is positively correlated to stock market return,and is also positively correlated to stock market variance in the high variance regime.Third,we examine to what extent cross-sectional differences in return for portfolio sorted by idiosyncratic volatility and size can be explained by differences in exposure to the computed systematic idiosyncratic risk factor.Betas are first estimated using the variance-covariance method with a rolling window of 24 months.Afterwards,we examine the extent to which exposure to the systematic idiosyncratic risk factor is priced in a cross section of portfolios via cross-sectional regressions of asset returns against estimated betas.We find that IVF can be used as a risk factor in the cross section.The higher the correlation between stock returns and IVF,the higher the risk premium demanded by the investors.The sensitivity of investors to the idiosyncratic risk factor is higher for the high idiosyncratic volatility portfolio.%本文将股票特质风险以系统性风险因子形式引入资产定价过程,实证检验了中国股票市场特质波动率与股票收益率的关系.本文按照股票特质波动率的大小构造投资组合,将高特质波动率组合的加权平均收益率与低特质波动率组合的加权平均收益率之差作为特质风险因子IVF.实证结果表明:(1)特质风险因子对股票市场有一定的预测作用.特质风险因子越高,预期股票市场收益率越高;高波动市场环境下的预期股票市场波动率也越高. (2)特质风险因子可以解释股票收益的截面差异.股票收益与特质风险因子IVF之间的相关性越大,投资者要求的风险溢酬越高,股票期望收益率就越高.【期刊名称】《管理工程学报》【年(卷),期】2017(031)002【总页数】7页(P170-176)【关键词】特质波动率;系统性风险;资产定价【作者】熊伟;陈浪南;柯忠义【作者单位】中山大学岭南学院,广东广州510275;惠州学院数学系,广东惠州516000【正文语种】中文【中图分类】F832.5传统资产定价模型认为投资者可以通过构造投资组合来充分分散化股票特质风险，影响资产均衡价格的因素只有系统性风险。