电动力学第二章
- 格式:pdf
- 大小:426.81 KB
- 文档页数:61



第二章一、选择题1、 静电场的能量密度等于( ) A ρϕ21 B E D ⋅21 C ρϕ D E D ⋅ 2、下列函数(球坐标系a 、b 为非零常数)中能描述无电荷区电势的是( )A a 2rB a b r +3C ar(2r +b)D b ra + 3、真空中两个相距为a 的点电荷1q 和2q ,它们之间的相互作用能是( ) A a q q 0218πε B a q q 0214πε C a q q 0212πε D aq q 02132πε 4、电偶极子p 在外电场e E 中所受的力为( )A (∇⋅P )e EB —∇(⋅P e E )C (P ⋅∇)e ED (eE ⋅∇)P5、电导率为1σ和2σ,电容率为1ε和2ε的均匀导电介质中有稳恒电流,则在两导电介质面上电势的法向微商满足的关系为( ) A n n ∂∂=∂∂21ϕϕ B σϕεϕε-=∂∂-∂∂n n 1122 C nn ∂∂=∂∂2211ϕσϕσ D n n ∂∂=∂∂122211σσϕσ 6. 用点像法求接静电场时,所用到的像点荷___________ 。
A) 确实存在;B) 会产生电力线;C) 会产生电势;D) 是一种虚拟的假想电荷。
7.用分离变量法求解静电场必须要知道__________ 。
A) 初始条件;B) 电场的分布规律;C) 边界条件;D) 静磁场。
8.设区域V 内给定自由电荷分布)(x ρ,S 为V 的边界,欲使V 的电场唯一确定,则需要给定( )。
A. S φ或S n ∂∂φB. S QC. E 的切向分量D. 以上都不对9.设区域V 内给定自由电荷分布()ρx ,在V 的边界S 上给定电势s ϕ或电势的法向导数s n ϕ∂∂,则V 内的电场( )A . 唯一确定 B. 可以确定但不唯一 C. 不能确定 D. 以上都不对10.导体的静电平衡条件归结为以下几条,其中错误的是( )A. 导体内部不带电,电荷只能分布于导体表面B. 导体内部电场为零C. 导体表面电场线沿切线方向D. 整个导体的电势相等11.一个处于x ' 点上的单位点电荷所激发的电势)(x ψ满足方程( )A. 2()0x ψ∇=B. 20()1/x ψε∇=-C. 201()()x x x ψδε'∇=-- D. 201()()x x ψδε'∇=-12.对于均匀带电的球体,有( )。



郭硕鸿《电动力学》课后答案第 2 页电动力学答案第一章 电磁现象的普遍规律1. 根据算符∇的微分性与向量性,推导下列公式:B A B A A B A B B A )()()()()(∇⋅+⨯∇⨯+∇⋅+⨯∇⨯=⋅∇ A A A A )()(221∇⋅-∇=⨯∇⨯A 解:(1))()()(cc A B B A B A ⋅∇+⋅∇=⋅∇B A B A A B A B )()()()(∇⋅+⨯∇⨯+∇⋅+⨯∇⨯=cc c c B A B A A B A B )()()()(∇⋅+⨯∇⨯+∇⋅+⨯∇⨯=(2)在(1)中令B A =得:AA A A A A )(2)(2)(∇⋅+⨯∇⨯=⋅∇,所以 A A A A A A )()()(21∇⋅-⋅∇=⨯∇⨯ 即 A A A A )()(221∇⋅-∇=⨯∇⨯A2. 设u 是空间坐标z y x ,,的函数,证明:u u f u f ∇=∇d d )( , u u u d d )(A A ⋅∇=⋅∇, uu u d d )(AA ⨯∇=⨯∇ 证明: (1)z y x z u f y u f x u f u f e e e ∂∂+∂∂+∂∂=∇)()()()(zy x zuu f y u u f x u u f e e e ∂∂+∂∂+∂∂=d d d d d du uf z u y u x u u f z y x ∇=∂∂+∂∂+∂∂=d d )(d d e e e(2)z u A y u A x u A u z y x ∂∂+∂∂+∂∂=⋅∇)()()()(A zuu A y u u A x u u A z y x ∂∂+∂∂+∂∂=d d d d d du z u y u x u u A u A u A z y x z z y y x x dd)()d d d d d d (e e e e e e ⋅∇=∂∂+∂∂+∂∂⋅++=第 3 页(3)u A u A u A zu y u x u uu z y x zy x d /d d /d d /d ///d d ∂∂∂∂∂∂=⨯∇e e e Azx y y z x x y z yu u A x u u A x u u A z u u A z uu A y u u A e e e )d d d d ()d d d d ()d d d d (∂∂-∂∂+∂∂-∂∂+∂∂-∂∂=zx y y z x x y z yu A x u A x u A z u A z u A y u A e e e ])()([])()([])()([∂∂-∂∂+∂∂-∂∂+∂∂-∂∂=)(u A ⨯∇=3. 设222)'()'()'(z z y y x x r -+-+-=为源点'x 到场点x 的距离,r 的方向规定为从源点指向场点。

第二章 习题1. 有导体存在时的唯一性定理是说: 若给出介质中自由电荷的分布,给定每个导体上的_______或每个导体上的______,以及(包围所有导体的)界面S 上sn s ∂∂ϕϕ或,则S 内静电场E被唯一确定. 2. 无导体存在时的静电学问题的唯一性定理为: 设空间区域V 可以分为若干小区域i V ,每个小区域i V 充满均匀介质i ε,若给出V 内自由电荷的分布,同时给出V 的界面S上的__ _ ___或_ __ ____,则V 内静电场E被唯一确定.3. 半径为0R 的接地导体球置于均匀外电场0E 中,导体球外为真空.试用分离变量法,求导体球外的电势、场强和导体球面上的自由电荷面密度σ.4. 半径为0R 的接地导体球置于均匀外电场0E中,球外真空, 试用分离变量法,求电势、导体面上的电荷面密度及场强.5. 半径为R 的空心带电球面,面电荷密度为θσσcos 0=f (0σ为常量),球外充满介电常数为ε的均匀介质,求球内外的电势、场强.6. 在两个互相垂直的接地导体平面所围成的直角空间内有一点电荷Q ,它到两个平面的距离为a 和b ,其坐标为)0,,(b a ,那么当用镜像法求空间的电势时,其镜像电荷的数目为______,这时所围成的直角空间内任意点),,(z y x 的电势为______.7. 两个无穷大的接地导体平面分别组成一个450、600、900两面角,在两面角内与两导体平面等距离处置一点电荷Q ,则在这三种情形下,像电荷的个数分别为 ______,______,______.8. 一电量为q 的点电荷在两平行接地导体平面中间,离两板距离均为a ,则像电荷的个数为_______.9.有两个电量为q的点电荷A和B,相距2b,在它们的联线的中点放一半径为a的接地导体球(b>a),则每一个点电荷受力大小为_______.10.电荷分布为ρ,体积为V的带电体系在外电场(电势为eϕ)中的能量为_______.11.两个同心带电球面(内、外半径分别为a、b)均匀地带有相同的电荷Q,则这两个带电球面之间的相互作用能为_________;系统的总静电能为_________.12.半径为R的接地导体球外有一点电荷q,它离球心的距离为a,则他们的相互作用能为_______.。

习题二1.将一个位于真空中的带电导体球切成两半,求它们之间的排斥力.设球的半径为0R ,球的电势为0V .答案: .ˆ2200z eV F πε= 解:0004R q V πε=,0004V R q πε=,.000R V εσ=z z e V e R F ˆ2ˆ22002002πεπεσ=⋅=2.内外半径分别为a 和b 的无限长圆柱形电容器,单位长度荷电为f λ,板间填充电导率为σ的非磁性物质.⑴证明在介质中任何一点传导电流与位移电流严格抵消.因此内部无磁场.⑵求f λ随时间的衰减规律.⑶求与轴相距为r 的地方的能量耗散功率密度.⑷求长度为l 的一段介质总的能量耗散功率,并证明它等于这段的静电能减少率. ⑵;0tf eεσλλ-=⑶22⎪⎪⎭⎫⎝⎛r f πελσ; ⑷.ln222ab l f πελσ解:⑴r f e r D ˆ2πλ=,.ˆ2r f e rDE πελε==.ˆ2r f f e r E J πεσλσ== .ˆ21r fD e tr t D J ∂∂=∂∂=λπ对两式求散度,并且由f D ρ=⋅∇ ,0=∂∂+⋅∇tJ ff ρ得f f tλεσλ-=∂∂,所以0=∂∂+tD J f。
因为介质是非磁性的,即H Bμ=,故任意一点,任意时刻有000=⎪⎪⎭⎫⎝⎛∂∂+=⨯∇=⨯∇t D J H B fμμ ⑵由f f tλεσλ-=∂∂,解这个微分方程得()tf et εσλλ-=0⑶()222/r E E J p f f πελσσ==⋅=⑷长度为l 的一段介质耗散的功率为.ln 222222a bl rldr r f baf πελσππελσ=⎪⎪⎭⎫ ⎝⎛⎰能量密度()22/,21r tw D E w f πελσ-=∂∂⋅=长度为l 的一段介质内能量减少率为 .ln2222ab l rldr tw f baπελσπ⎰=∂∂-3.一很长的直圆筒,半径为R ,表面上带有一层均匀电荷,电荷量的面密度为σ.在外力矩的作用下,从0=t 时刻开始,以匀角加速度α绕它的几何轴转动,如图所示.⑴试求筒内的磁感应强度B;⑵试求筒内接近内表面处的电场强度E和玻印廷矢量S ;⑶试证明:进入这圆筒长为l 一段的S 的通量为⎪⎪⎭⎫ ⎝⎛2022B l R dt d μπ. 答案: ⑴ωσμR B 0=;⑵ωασμe eRr E r ˆˆ210⨯= ; r er R S ˆ212320ασμ-= .解:⑴单位面电流ωσσπR lT Rl i ==2ωσμμR ei B z 00ˆ== ⑵在圆筒的横截面内,以轴线为心,r 为半径作一圆,通过这圆面积的磁通量为 ωσμπR r S d B s02=⋅=Φ⎰由法拉第定律,得 .21210d td Rrdtd r E ωσμπ-=Φ-=因为t αω= 所以ασμrR E 021-=考虑到方向,则有z r e erR E ˆˆ210⨯=ασμ 在筒内接近表面处,z r e eR E ˆˆ2120⨯=ασμ 该处的能流密度为 ()()z z r R R R e R e eR H E S ˆˆˆ2120ωσασμ⨯⨯=⨯=r et R ˆ212320ασμ-= 负号表明,S 垂直于筒表面指向筒内。


电动力学A 刘克新
第二章
静电场
本章主要内容
§1、静电势和Poisson方程,唯一性定理§2、微分方程分离变量法
§3、镜像法
§4、Green函数法
§5、电多极矩及其与外场作用
§1、静电势和Poisson方程,唯一性定理¾1、静电势
¾2、静电势的方程和边值关系
¾3、唯一性定理
¾4、静电场的能量
§2、微分方程分离变量法
¾1、从Poisson方程到Laplace方程¾2、分离变量法
¾3、举例
0=2)
2
j
x )][][sin()()]kz
kz
k k n n A e B e A n B con n ρϕϕ−++第一类n 阶贝塞尔函数第二类贝塞尔函数
§3、镜像法
¾1、平面边界
¾2、接地导体球¾3、不接地导体球
(2) 在z < 0 的半无限空间
导体表面上的电荷在上半平面产生的电势,相当于像电荷-q在上半平面的产生的电势。
根据对称性,
导体表面上的电荷在下半平面产生的电势,相当于上面的-q在下半平面的产生的电势。
上面的-q和原有的q相加为0,
因此下半个空间中的电势为0。
思考题:当上半平面充满介电常数为ε 的均匀电介质时,情况如何?
§4、Green函数法
¾1、Green函数
¾2、利用Green函数解边值问题¾3、几种特殊Green函数的表达式¾4、应用举例
§5、电多极矩及其与外场作用
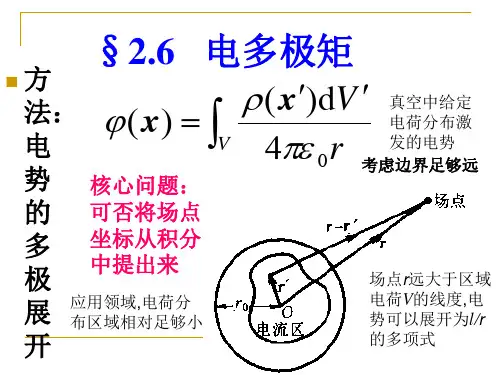
¾1、电势的多极展开
¾2、电多极矩
¾3、电荷体系在外电场中的能量
¾4、电偶极子在外场中受到的作用力和力矩。