大学物理2-212章习题详细答案
- 格式:doc
- 大小:1.24 MB
- 文档页数:16


题1-3图第一章 流体力学1.概念(3)理想流体:完全不可压缩又无黏性的流体。
(4)连续性原理:理想流体在管道中定常流动时,根据质量守恒定律,流体在管道内既不能增 多,也不能减少,因此单位时间内流入管道的质量应恒等于流出管道的质量。
(6)伯努利方程:C gh v P =++ρρ221(7)泊肃叶公式:LPR Q ηπ84∆=2、从水龙头徐徐流出的水流,下落时逐渐变细,其原因是( A )。
A. 压强不变,速度变大; B. 压强不变,速度变小;C. 压强变小,流速变大;D. 压强变大,速度变大。
3、 如图所示,土壤中的悬着水,其上下两个液面都与大气相同,如果两个页面的曲率半径分别为R A 和R B (R A <R B ),水的表面张力系数为α,密度为ρ,则悬着水的高度h 为___)11(2BA R R g -ρα__。
(解题:BB A A A B R P P R P P gh P P ααρ2,2,00-=-==-) 4、已知动物的某根动脉的半径为R, 血管中通过的血液流量为Q , 单位长度血管两端的压强差为ΔP ,则在单位长度的血管中维持上述流量需要的功率为____ΔPQ ___。
5、城市自来水管网的供水方式为:自来水从主管道到片区支管道再到居民家的进户管道。
一般说来,进户管道的总横截面积大于片区支管的总横截面积,主水管道的横截面积最小。
不考虑各类管道的海拔高差(即假设所有管道处于同水平面),假设所有管道均有水流,则主水管道中的水流速度 大 ,进户管道中的水流速度 小 。
10、如图所示,虹吸管的粗细均匀,略去水的粘滞性,求水流速度及A 、B 、C 三处的压强。
221.2 理想流体的定常流动'2gh v C =∴222121'CC D D v P v gh P ρρρ+=++0,0≈==D C D v P P P 练习5:如图,虹吸管粗细均匀,略去水的粘滞性,求管中水流流速及A 、B 、C 三处的压强。

Pd L0dxxθxydEd θ习题1212-3.如习题12-3图所示,真空中一长为L 的均匀带电细直杆,总电量为q ,试求在直杆延长线上到杆的一端距离为d 的点P 的电场强度。
[解] 建立如图所示坐标系ox ,在带电直导线上距O 点为x 处取电荷元x Lqq d d =,它在P 点产生的电电场强度度为()()x x d L Lq x d L qE d 41d 41d 2020-+=-+=πεπε则整个带电直导线在P 点产生的电电场强度度为()()d L d qx x d L Lq E L+=-+=⎰002041d 41πεπε故()i E d L d q+=04πε12-4.用绝缘细线弯成的半圆环,半径为R ,其上均匀地带有正电荷Q ,试求圆心处点O 的场强。
[解] 将半圆环分成无穷多小段,取一小段dl ,带电量l RQ q d d π=dq 在O 点的电场强度20204d 4d d RlR Q R qE πεππε== 从对称性分析,y 方向的电场强度相互抵消,只存在x 方向的电场强度l RQ E E d sin 4sin d d 302x ⋅=⋅=θεπθ θd d R l =θεπθd 4sin d 202x R Q E =2020202x x 2d 4sin d R QR Q E E E επθεπθπ====⎰⎰ 方向沿x 轴正方向 12-5. 如习题12-5图所示,一半径为R 的无限长半圆柱面形薄筒,均匀带电,沿轴向单位长度上的带电量为λ,试求圆柱面轴线上一点的电场强度E 。
[解]θd 对应的无限长直线单位长带的电量为θπλd d =q 它在轴线O 产生的电场强度的大小为RRq E 0202d 2d d επθλπε==因对称性y d E 成对抵消RE E 02x 2d cos cos d d επθθλθ=⋅=d θRR E E 02202x 2d cos 2d επλεπθθλπ===⎰⎰ 12-6.一半径为R 的半球面,均匀地带有电荷,电荷面密度为σ,求球心点O 处的场强。

第一章质点运动学1、(习题1.1):一质点在xOy 平面内运动,运动函数为2x =2t,y =4t 8-。
(1)求质点的轨道方程;(2)求t =1 s t =2 s 和时质点的位置、速度和加速度。
解:(1)由x=2t 得,y=4t 2-8 可得: y=x 2-8 即轨道曲线 (2)质点的位置 : 22(48)r ti t j =+- 由d /d v r t =则速度: 28v i tj =+ 由d /d a v t =则加速度: 8a j =则当t=1s 时,有 24,28,8r i j v i j a j =-=+= 当t=2s 时,有 48,216,8ri j v i j a j =+=+=2、(习题1.2): 质点沿x 在轴正向运动,加速度kv a -=,k 为常数.设从原点出发时速度为0v ,求运动方程)(t x x =.解:kv dtdv-= ⎰⎰-=t vv kdt dv v 001 tk e v v -=0t k e v dtdx-=0 dt ev dx tk tx-⎰⎰=000)1(0t k e kv x --=3、一质点沿x 轴运动,其加速度为a = 4t (SI),已知t = 0时,质点位于x 0=10 m 处,初速度v 0 = 0.试求其位置和时间的关系式. 解:=a d v /d t 4=t d v 4=t d t⎰⎰=vv 0d 4d tt t v 2=t 2v d =x /d t 2=t 2t t x txx d 2d 020⎰⎰= x 2= t 3 /3+10 (SI)4、一质量为m 的小球在高度h 处以初速度0v 水平抛出,求:(1)小球的运动方程;(2)小球在落地之前的轨迹方程; (3)落地前瞬时小球的d d r t ,d d v t ,tv d d . 解:(1) t v x 0= 式(1)2gt 21h y -= 式(2) 201()(h -)2r t v t i gt j =+(2)联立式(1)、式(2)得 22v 2gx h y -=(3)0d -gt d rv i j t = 而落地所用时间 gh2t = 所以0d -2g h d r v i j t =d d v g j t =- 2202y 2x )gt (v v v v -+=+= 2120212202)2(2])([gh v gh g gt v t g dt dv +=+=5、 已知质点位矢随时间变化的函数形式为22r t i tj =+,式中r 的单位为m ,t 的单位为s .求:(1)任一时刻的速度和加速度;(2)任一时刻的切向加速度和法向加速度。
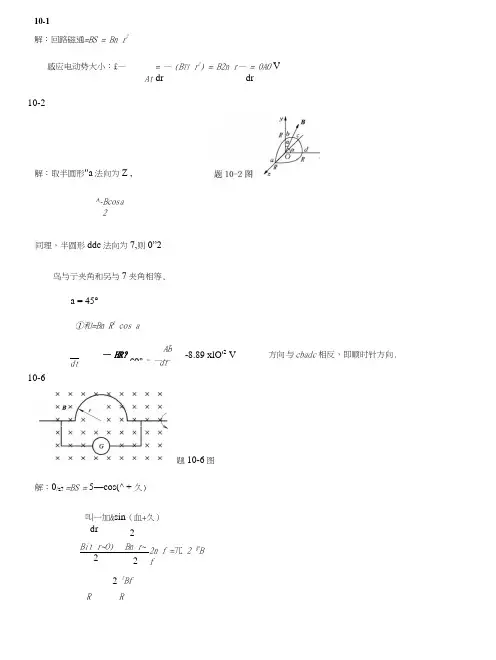
解:回路磁通=BS = Bn r 2感应电动势大小:£— = — (B TI r 2) = B2n r — = 0A0 V At dr dr10-2^-Bcosa2同理,半圆形ddc 法向为7,则0”2鸟与亍夹角和另与7夹角相等,a = 45°①和=Bn R 2 cos a10-6解:0/z? =BS = 5—cos(^ + 久)叫一加&sin (血+久)dr _2Bit r~O) Bn r~2 _ 2 2 2Bf2n f =兀 2『BfR R 解:取半圆形"a 法向为Z ,dt — HR? ABcos a —— dt -8.89 xlO'2V方向与cbadc 相反,即顺时针方向. 题10-6图(1)在Ob 上取尸T 尸+ dr 一小段71 同理•• • r 1 9 % - 3 ca^BAr = 一 Bco, °"」) 18 1 2 1 , £ab - £aO +% =(一花' + 石)广=(2)・・・£ah >0即U a -U h <0 :.b 点电势高.10-11在金属杆上取dr 距左边直导线为r ,则(2) |nj 理, £dc = 碇・d7>0U d -U c v0即 / >U d10-15 设长直电流为/ ,其磁场通过正方形线圈的互感磁通为%蓄绘/警5210-16Q)见题10-16图Q),设长直电流为/,它产生的磁场通过矩形线圈的磁通为丛(丄+丄)d- I 2龙 r 2a-r •:实际上感应电动势方向从g T A , 即从图中从右向左,71 a-b10-14•d5 知, 此吋E 旋以。
为中心沿逆时针方向.(1) V ab 是直径,在〃上处处E 旋与ab m§E 旋• d7 = 0• • £亦也 U Q =Ub心 2n r 2TI 由样旋• M -/z 0/v a + b71 a-b(a (b12-4解:⑴由0 =—,务=£_知,各级条纹向棱边方 2/ 2向移动,条纹间距不变;(2)各级条纹向棱边方向移动,H.条纹变密. 12 5解:工件缺陷是凹的.故各级等厚线(在缺陷附近的)向棱边方向弯曲・按题意,每一条纹弯曲部分的顶点恰与左邻的直线部分连线相切,说明弯曲部分相当于条纹2向棱边移动了一条,故相应的空气隙厚度差为Ae = -,这也是工件缺陷的程度.2 12-6 ・・・ A/ = ^^- = A^^ln2 = 2.8xlO~6 H1 2JI(b)・・•长直电流磁场通过矩形线圈的磁通*2 = 0,见题10-16图(b)・・・ M = O10-17如图10-17图所示,取dS = /dr①二U(如+ ^_炖=做 广「丄)做(In 厶-In 丄) 2〃r 2兀(d-r)2兀 “ r r-d 2K a d-a = ^Il_Xn d-a_7i a:.L / =如1门上£I TI a10-18•・•顺串时厶=厶+厶2 +2M反串联时//二厶+厶2-2M・•・ L_L f = 4MM = --------- = 0.15 H 412-1 y 不变,为波源的振动频率;A,n =— 变小;u = A n v 变小. n 12- 2由心=三久知,(1)条纹变疏;(2)条纹变密;(3)条纹变密;(4)零级明纹在屏幕上作相反方向的上下移动;(5)零 a级明纹向下移动.12- 3解:不同媒质若光程相等,则其儿何路程定不相冋其所需吋间相同,为&€・因为△中已经将光在介质中的路程折算为光在真空中所走的路程。

* *(1)题2-2图由①、②式消去t ,得1 2 g sin2v 2当t = 2 s 时质点的 ⑴位矢;(2)速度.7aym 16m习题二1 一个质量为P 的质点,在光滑的固定斜面(倾角为 )上以初速度V o 运动, 斜面底边的水平线 AB 平行,如图所示,求这质点的运动轨道. 解:物体置于斜面上受到重力 mg ,斜面支持力N .建立坐标:取V 0方向为X v 0的方向与,平行斜面与X 轴垂直方向为Y 轴•如图2-2. X 方向: F x x V o t Y 方向:F ymg sinma yv yy ^gsint 2x 22 质量为16 kg 的质点在 xOy 平面内运动,受一恒力作用,力的分量为6 N , f y =-7 N ,当 t = 0 时,x y0 , v x = -2 m s -1V y = 0 .解:a xm6 16* *1⑶质点停止运动时速度为零,即 t *,23v xv x0 0 a x dt2 8 227 7v yv y00 a y dt2 —168于是质点在2s 时的速度5 7 .v i j m s 4 8(v °t 1 a x t 2)i1 a.2 .y t J 221 31 7 (2 2 — —4)i -()4J2 82 1613.7 .i j m48v v 0ex vdt: v 0e^dt3 质点在流体中作直线运动,受与速度成正比的阻力 kv (k 为常数)作用,t =0时质点的速度为v o ,证明(1) t 时刻的速度为v = v 0e m ; (2) 由0到t 的时间内经过的距离为d )tx =(一二)[1- e m ]; (3)停止运动前经过的距离为 k mv o 代);⑷证明当t mk 时速答:⑴••• kv amdvdt分离变量,得 dv kdt v vdv v 0vm t kdtln — v °In kte扁故有xkt mv0v0e m dt0k⑷当t= m时,其速度为kV k mv°e m^ v°e 1v e1即速度减至V。

第二章 牛顿运动定律一、填空题1、考察直线运动,设加速度为()a t ,初速度为00v =,则由dv a dv adt dt =⇒= 两边定积分,即 00v t v dv adt =⎰⎰ 得质点在任意时刻t 的速度为 110()()t v t a t dt =⎰ (2-1)再由ds v ds vdt dt =⇒= 两边定积分,即 00s t s ds vdt =⎰⎰ 得质点在任意时刻t 的路程为 0220()t s s s v t dt ∆=-=⎰ 把(2-1)式代入上式,得211200()tt s a t dt dt ∆=⎰⎰依题设可知两物体必做直线运动,设某时刻两物体间作用力为F ,则两物体的加速度分别为11F a m = 和 22F a m = 所以两物体在相同时间内发生的路程分别为:2221111121211200000011()1()()tt tt t t F t s a t dt dt dt dt F t dt dt m m ∆===⎰⎰⎰⎰⎰⎰ 2221221121211200000022()1()()t t t t t t F t s a t dt dt dt dt F t dt dt m m ∆===⎰⎰⎰⎰⎰⎰所以 11222111s m m s m m ∆==∆ 此即为所求。
2、箱子在最大静摩擦力的作用下,相对地面具有的最大加速度为2max 0max 00.49.8 3.92()F mg a g m s m mμμ-====⨯=⋅ (1)若设箱子相对卡车静止,即物体相对地面的加速度2max 2a m s a -=⋅<表明箱子与卡车底板间是静摩擦,摩擦力的大小为40280()F ma N ==⨯=(2)依然设箱子相对卡车静止,即物体相对地面的加速度2max 4.5a m s a -=⋅>表明箱子与卡车底板间是滑动摩擦,摩擦力的大小为0.25409.898()F mg N μ==⨯⨯=3、如图2-1(a)所示建立直角坐标系,再分析滑块的受力情况,如图2-1(b)所示,滑块受到三个力的作用,分别是地球施加的重力mg ,斜面对它的支持力1N 和滑动摩擦力1f ,并设其加速度为a 。

大学物理第二章习题答案# 大学物理第二章习题答案开始部分在解答大学物理的习题之前,我们需要对第二章的物理概念和公式有一个清晰的理解。
本章通常涵盖了经典力学的基础知识,包括牛顿运动定律、功和能量等概念。
习题1:牛顿运动定律的应用问题描述:一个物体在水平面上受到一个恒定的力F=10N,求物体的加速度a。
解答:根据牛顿第二定律,\[ F = ma \],其中m是物体的质量。
设物体的质量为m,我们可以解出加速度a:\[ a = \frac{F}{m} = \frac{10}{m} \, \text{m/s}^2 \]注意,这里我们假设物体的质量m是已知的。
习题2:斜面上的物体问题描述:一个质量为m=5kg的物体放在一个倾斜角度为30°的斜面上,求物体受到的重力分量。
解答:物体受到的重力分量可以分解为两个方向的力:平行于斜面的分量和垂直于斜面的分量。
垂直分量为:\[ F_{垂直} = mg \sin(30°) = 5 \times 9.8 \times 0.5 = 24.5 \, \text{N} \]平行分量为:\[ F_{平行} = mg \cos(30°) = 5 \times 9.8 \times\frac{\sqrt{3}}{2} \approx 49.04 \, \text{N} \]习题3:功和能量问题描述:一个物体从高度h=10m的平台上自由落体,求物体落地时的动能。
解答:首先,我们需要计算物体在自由落体过程中重力做的功W,它等于物体的重力势能变化:\[ W = mgh = 5 \times 9.8 \times 10 \]根据能量守恒定律,这个功将转化为物体的动能:\[ KE = W = 5 \times 9.8 \times 10 = 490 \, \text{J} \]结束部分在解答物理习题时,重要的是理解每个物理量的含义以及它们之间的关系。
通过逐步分析问题,应用适当的物理定律和公式,我们可以找到正确的答案。


大学物理学第二版下册习题解答第一章:力学1.1 力学基本概念1.1.1 力的概念问题:什么是力?力的种类有哪些?解答:力是物体之间相互作用导致的物体运动或形变的原因。
力可以分为以下几种:•接触力:当两个物体接触时产生的力,如弹簧力、摩擦力等。
•引力:天体之间由于引力而产生的力,如地球引力、行星引力等。
•重力:地球上物体受到的引力,是一种特殊的引力。
•弹力:当物体被弹性体拉伸或压缩时,物体回复原状所产生的力。
•阻力:物体在流体中运动时受到的阻碍力,如空气阻力、水阻力等。
1.1.2 力的合成与分解问题:什么是力的合成与分解?如何进行力的合成与分解?解答:力的合成是指将多个力按照一定的规律合成为一个力的过程。
力的分解是指将一个力按照一定的规律分解为多个力的过程。
力的合成可以使用力的三角法进行。
假设有两个力F₁、F₂,其方向分别为α₁、α₂,大小分别为|F₁|、|F₂|,则合力F的大小可以通过以下公式计算:F = √(F₁² + F₂² + 2F₁F₂cos(α₁-α₂))合力F的方向则可以通过以下公式计算:tan(θ) = (F₂sin(α₁-α₂))/(F₁+F₂cos(α₁-α₂))力的分解可以使用力的正弦法和余弦法进行。
假设有一个力F,其大小为|F|,方向为α,要将该力分解为水平方向的力F x和竖直方向的力F x,可以通过以下公式计算:Fₓ = |F|cosα, Fᵧ = |F|sinα1.2 牛顿定律与惯性1.2.1 牛顿第一定律问题:什么是牛顿第一定律?牛顿第一定律适用于哪些情况?解答:牛顿第一定律,也称为惯性定律,指的是:物体在没有受到外力或受到的合外力为零时,物体保持静止或匀速直线运动的状态。
牛顿第一定律适用于只有一个物体或多个物体之间相互独立运动的情况。
当物体受到外力时,按照该定律,物体会发生运动或停止运动。
1.2.2 牛顿第二定律问题:什么是牛顿第二定律?如何计算物体所受合外力和加速度的关系?解答:牛顿第二定律指的是:物体所受合外力等于物体的质量乘以加速度。

题1第⼀一章流体⼒力力学1、基本概念(3)理理想流体:完全不不可压缩,没有粘滞性的流体。
(4)连续性原理理:流管上⼀一节流速与截⾯面积的乘积是⼀一个常量量,截⾯面⼤大的流速⼩小,反之⼤大(6)伯努利利⽅方程:P 1+12ρv 12+ρg h 1=P 2+12ρv 22+ρg h 2=c(7)泊肃叶公式:2、从⽔水⻰龙头徐徐流出的⽔水流,下落时逐渐变细,其原因是(A )。
A.压强不不变,速度变⼤大; B.压强不不变,速度变⼩小;C.压强变⼩小,流速变⼤大;D.压强变⼤大,速度变⼤大。
3、如图所示,⼟土壤中的悬着⽔水,其上下两个液⾯面都与⼤大⽓气相同,如果两个⻚页⾯面的曲率半径分别为R A 和R B (R A <R B ),⽔水的表⾯面张⼒力力系数为α,密度为ρ,则悬着⽔水的⾼高度h 为_____。
4、已知动物的某根动脉的半径为R,⾎血管中通过的⾎血液流量量为Q ,单位⻓长度⾎血管两端的压强差为ΔP ,则在单位⻓长度的⾎血管中维持上述流量量需要的功率为ΔPQ 。
5、城市⾃自来⽔水管⽹网的供⽔水⽅方式为:⾃自来⽔水从主管道到⽚片区⽀支管道再到居⺠民家的进户管道。
⼀一般说来,进户管道的总横截⾯面积⼤大于⽚片区⽀支管的总横截⾯面积,主⽔水管道的横截⾯面积最⼩小。
不不考虑各类管道的海海拔⾼高差(即假设所有管道处于同⽔水平⾯面),假设所有管道均有⽔水流,则主⽔水管道中的⽔水流速度⼤大,进户管道中的⽔水流速度⼩小。
6、如图所示,虹吸管的粗细均匀,略略去⽔水的粘滞性,求⽔水流速度及A 、B 、C 三处的压强。
题1-10图解:在管外液⾯面上任选⼀一点D ,CD 两点:BC两点:AC两点:7、⼀一开⼝口容器器截⾯面积为S1,底部开⼀一截⾯面积为S2的孔。
当容器器内装的液体⾼高度为h时,液体从孔中喷出的速度为多⼤大?设液体为理理想流体且作定常流动。
解:由于液体为理理想流体且作定常流动,根据连续性原理理,有根据伯努利利⽅方程,有从上两式联⽴立解得8、⼀一圆筒中的⽔水深为H=0.70m,底⾯面积S1=0.06m2,桶底部有⼀一⾯面积为1.0×10-4m2的⼩小孔。
大学物理(二)练习册 参考解答第12章 真空中的静电场一、选择题1(A),2(C),3(C),4(A),5(C),6(B),7(C),8(D),9(D),10(B), 二、填空题(1). 电场强度和电势,0/q F E=,l E q W U aa⎰⋅==00d /(U 0=0).(2). ()042ε/q q +, q 1、q 2、q 3、q 4 ;(3). 0,λ / (2ε0) ; (4). σR / (2ε0) ; (5). 0 ; (6).⎪⎪⎭⎫ ⎝⎛-π00114r r qε ; (7). -2³103V ; (8).⎪⎪⎭⎫ ⎝⎛-πb a r r q q 11400ε(9). 0,pE sin α ; (10). ()()j y x i xy40122482+-+-- (SI) ;三、计算题1. 将一“无限长”带电细线弯成图示形状,设电荷均匀分布,电荷线密度为λ,四分之一圆弧AB 的半径为R ,试求圆心O 点的场强.解:在O 点建立坐标系如图所示. 半无限长直线A ∞在O 点产生的场强:()j i R E -π=014ελ半无限长直线B ∞在O 点产生的场强:()j i R E +-π=024ελ四分之一圆弧段在O 点产生的场强:()j i R E +π=034ελ由场强叠加原理,O 点合场强为: ()j i RE E E E +π=++=03214ελBA∞O BA∞∞2. 实验表明,在靠近地面处有相当强的电场,电场强度E垂直于地面向下,大小约为100N/C ;在离地面1.5 km 高的地方,E也是垂直于地面向下的,大小约为25 N/C .(1) 假设地面上各处E都是垂直于地面向下,试计算从地面到此高度大气中电荷的平均体密度;(2) 假设地表面内电场强度为零,且地球表面处的电场强度完全是由均匀分布在地表面的电荷产生,求地面上的电荷面密度.(已知:真空介电常量0ε=8.85³10-12 C 2²N -1²m -2)解:(1) 设电荷的平均体密度为ρ,取圆柱形高斯面如图(1)(侧面垂直底面,底面∆S 平行地面)上下底面处的 场强分别为E 1和E 2,则通过高斯面的电场强度通量为:⎰⎰E²S d =E 2∆S -E 1∆S =(E 2-E 1) ∆S高斯面S 包围的电荷∑q i =h ∆S ρ由高斯定理(E 2-E 1) ∆S =h ∆S ρ /ε 0∴() E E h1201-=ερ=4.43³10-13C/m 3(2) 设地面面电荷密度为σ.由于电荷只分布在地表面,所以电力线终止于地面,取高斯面如图(2) 由高斯定理⎰⎰E²S d =∑i1qε-E ∆S =S ∆σε01∴ σ =-ε 0 E =-8.9³10-10C/m 33. 带电细线弯成半径为R 的半圆形,电荷线密度为λ=λ0sin φ,式中λ0为一常数,φ为半径R 与x 轴所成的夹角,如图所示.试求环心O 处的电场强度.解:在φ处取电荷元,其电荷为d q =λd l = λ0R sin φ d φ它在O 点产生的场强为R R qE 00204d sin 4d d εφφλεπ=π= 在x 、y 轴上的二个分量d E x =-d E cos φ, d E y =-d E sin φ 对各分量分别求和⎰ππ=000d cos sin 4φφφελR E x =0 RRE y 000208d sin 4ελφφελ-=π=⎰π∴ j Rj E i E E y x008ελ-=+=(2)2(1)4. 一“无限长”圆柱面,其电荷面密度为: σ = σ0cos φ ,式中φ 为半径R 与x 轴所夹的角,试求圆柱轴线上一点的场强.解:将柱面分成许多与轴线平行的细长条,每条可视为“无限长”均匀带电直线,其电荷线密度为λ = σ0cos φ R d φ, 它在O 点产生的场强为:φφεσελd s co 22d 000π=π=R E它沿x 、y 轴上的二个分量为: d E x =-d E cos φ =φφεσd s co 220π-d E y =-d E sin φ =φφφεσd s co sin 20π 积分:⎰ππ-=2020d s co 2φφεσx E =2εσ0)d(sin sin 2200=π-=⎰πφφεσy E∴ i i E E x02εσ-==5. 一半径为R 的带电球体,其电荷体密度分布为4πRqr =ρ (r ≤R ) (q 为一正的常量)ρ = 0 (r >R )试求:(1) 带电球体的总电荷;(2) 球内、外各点的电场强度;(3) 球内、外各点的电势.解:(1) 在球内取半径为r 、厚为d r 的薄球壳,该壳内所包含的电荷为 d q = ρd V = qr 4πr 2d r /(πR 4) = 4qr 3d r/R 4 则球体所带的总电荷为 ()q r r Rq V Q rV===⎰⎰34d /4d ρ(2) 在球内作一半径为r 1的高斯球面,按高斯定理有4041241211d 414Rqr r r Rqr E r r εε=π⋅π=π⎰得402114R qr E επ=(r 1≤R),1E方向沿半径向外.在球体外作半径为r 2的高斯球面,按高斯定理有 0222/4εq E r =π得22024r q E επ=(r 2 >R ),2E方向沿半径向外.(3) 球内电势⎰⎰∞⋅+⋅=RR r r E r E U d d 2111⎰⎰∞π+π=RRr r rq r Rqrd 4d 4204021εε40310123Rqr R qεεπ-π=⎪⎪⎭⎫ ⎝⎛-π=3310412R r R qε ()R r ≤1 球外电势 2020224d 4d 22r q r rq r E U r Rr εεπ=π=⋅=⎰⎰∞()R r >26. 如图所示,一厚为b 的“无限大”带电平板 , 其电荷体密度分布为ρ=kx (0≤x ≤b ),式中k 为一正的常量.求: (1) 平板外两侧任一点P 1和P 2处的电场强度大小;(2) 平板内任一点P 处的电场强度; (3) 场强为零的点在何处?解: (1) 由对称分析知,平板外两侧场强大小处处相等、方向垂直于平面且背离平面.设场强大小为E .作一柱形高斯面垂直于平面.其底面大小为S ,如图所示.按高斯定理∑⎰=⋅0ε/d q S E S,即22d d 12εερεkSbx x kSx S SE bb===⎰⎰得到 E = kb 2/ (4ε0) (板外两侧) (2) 过P 点垂直平板作一柱形高斯面,底面为S .设该处场强为E ',如图所示.按高斯定理有()022εεk S b x d x kSSE E x==+'⎰得到 ⎪⎪⎭⎫ ⎝⎛-='22220b x k E ε (0≤x ≤b ) (3) E '=0,必须是0222=-bx , 可得2/b x =7. 一“无限大”平面,中部有一半径为R 的圆孔,设平面上均匀带电,电荷面密度为σ.如图所示,试求通过小孔中心O 并与平面垂直的直线上各点的场强和电势(选O 点的电势为零).解:将题中的电荷分布看作为面密度为σ的大平面和面密度为-σ的圆盘叠加的 结果.选x 轴垂直于平面,坐标原点O在圆盘中心,大平面在x 处产生的场强为i xx E012εσ='圆盘在该处的场强为i x R x x E⎪⎪⎭⎫ ⎝⎛+--=2202112εσ ∴ i xR xE E E 220212+=+=εσ该点电势为 ()220222d 2xR R xR x x U x+-=+=⎰εσεσ8.一真空二极管,其主要构件是一个半径R 1=5³10-4m 的圆柱形阴极A 和一个套在阴极外的半径R 2=4.5³10-3 m 的同轴圆筒形阳极B ,如图所示.阳极电势比阴极高300 V ,忽略边缘效应. 求电子刚从阴极射出时所受的电场力.(基本电荷e =1.6³10-19C)解:与阴极同轴作半径为r (R 1<r <R 2 )的单位长度的圆柱形高斯面,设阴极上电荷线密度为λ.按高斯定理有 2πrE = λ/ ε0得到 E = λ / (2πε0r ) (R 1<r <R 2) 方向沿半径指向轴线.两极之间电势差⎰⎰π-=⋅=-21d 2d 0R R B A B A rr r E U U ελ120ln 2R R ελπ-= 得到()120/ln 2R R UUAB-=πελ, 所以 ()rR R UUE AB1/ln 12⋅-=在阴极表面处电子受电场力的大小为()()11211/c R R R U U e R eE F A B ⋅-===4.37³10-14N 方向沿半径指向阳极.四 研讨题1. 真空中点电荷q 的静电场场强大小为 241rq E πε=式中r 为场点离点电荷的距离.当r →0时,E →∞,这一推论显然是没有物理意义的,应如何解释?参考解答:点电荷的场强公式仅适用于点电荷,当r →0时,任何带电体都不能视为点电荷,所以点电荷场强公式已不适用.若仍用此式求场强E ,其结论必然是错误的.当r →0时,需要具体考虑带电体的大小和电荷分布,这样求得的E 就有确定值.2. 用静电场的环路定理证明电场线如图分布的电场不可能是静电场.参考解答:证:在电场中作如图所示的扇形环路abcda .在ab 和cd 段场强方向与路径方向垂直.在bc 和da 段场强大小不相等(电力线疏密程度不同)而路径相等.因而0d d d ≠⋅'-⋅=⋅⎰⎰⎰cb a d l E l E l E按静电场环路定理应有0d =⋅⎰l E,此场不满足静电场环路定理,所以不可能是静电场.3. 如果只知道电场中某点的场强,能否求出该点的电势?如果只知道电场中某点的电势,能否求出该点的场强?为什么?参考解答:由电势的定义: ⎰⋅=零势点场点l E U d式中E为所选场点到零势点的积分路径上各点的场强,所以,如果只知道电场中某点的场强,而不知道路径上各点的场强表达式,不能求出该点的电势。
题1-3图第一章 流体力学1.概念(3)理想流体:完全不可压缩又无黏性的流体。
(4)连续性原理:理想流体在管道中定常流动时,根据质量守恒定律,流体在管道内既不能增 多,也不能减少,因此单位时间内流入管道的质量应恒等于流出管道的质量。
(6)伯努利方程:C gh v P =++ρρ221(7)泊肃叶公式:LPR Q ηπ84∆=2、从水龙头徐徐流出的水流,下落时逐渐变细,其原因是( A )。
A. 压强不变,速度变大; B. 压强不变,速度变小;C. 压强变小,流速变大;D. 压强变大,速度变大。
3、 如图所示,土壤中的悬着水,其上下两个液面都与大气相同,如果两个页面的曲率半径分别为R A 和R B (R A <R B ),水的表面张力系数为α,密度为ρ,则悬着水的高度h 为___)11(2BA R R g -ρα__。
(解题:BB A A A B R P P R P P gh P P ααρ2,2,00-=-==-) 4、已知动物的某根动脉的半径为R, 血管中通过的血液流量为Q , 单位长度血管两端的压强差为ΔP ,则在单位长度的血管中维持上述流量需要的功率为____ΔPQ ___。
5、城市自来水管网的供水方式为:自来水从主管道到片区支管道再到居民家的进户管道。
一般说来,进户管道的总横截面积大于片区支管的总横截面积,主水管道的横截面积最小。
不考虑各类管道的海拔高差(即假设所有管道处于同水平面),假设所有管道均有水流,则主水管道中的水流速度 大 ,进户管道中的水流速度 小 。
10、如图所示,虹吸管的粗细均匀,略去水的粘滞性,求水流速度及A 、B 、C 三处的压强。
221.2 理想流体的定常流动'2gh v C =∴222121'CC D D v P v gh P ρρρ+=++0,0≈==D C D v P P P 练习5:如图,虹吸管粗细均匀,略去水的粘滞性,求管中水流流速及A 、B 、C 三处的压强。
题1第⼀一章流体⼒力力学1、基本概念(3)理理想流体:完全不不可压缩,没有粘滞性的流体。
(4)连续性原理理:流管上⼀一节流速与截⾯面积的乘积是⼀一个常量量,截⾯面⼤大的流速⼩小,反之⼤大(6)伯努利利⽅方程:P 1+12ρv 12+ρg h 1=P 2+12ρv 22+ρg h 2=c(7)泊肃叶公式:2、从⽔水⻰龙头徐徐流出的⽔水流,下落时逐渐变细,其原因是(A )。
A.压强不不变,速度变⼤大; B.压强不不变,速度变⼩小;C.压强变⼩小,流速变⼤大;D.压强变⼤大,速度变⼤大。
3、如图所示,⼟土壤中的悬着⽔水,其上下两个液⾯面都与⼤大⽓气相同,如果两个⻚页⾯面的曲率半径分别为R A 和R B (R A <R B ),⽔水的表⾯面张⼒力力系数为α,密度为ρ,则悬着⽔水的⾼高度h 为_____。
4、已知动物的某根动脉的半径为R,⾎血管中通过的⾎血液流量量为Q ,单位⻓长度⾎血管两端的压强差为ΔP ,则在单位⻓长度的⾎血管中维持上述流量量需要的功率为ΔPQ 。
5、城市⾃自来⽔水管⽹网的供⽔水⽅方式为:⾃自来⽔水从主管道到⽚片区⽀支管道再到居⺠民家的进户管道。
⼀一般说来,进户管道的总横截⾯面积⼤大于⽚片区⽀支管的总横截⾯面积,主⽔水管道的横截⾯面积最⼩小。
不不考虑各类管道的海海拔⾼高差(即假设所有管道处于同⽔水平⾯面),假设所有管道均有⽔水流,则主⽔水管道中的⽔水流速度⼤大,进户管道中的⽔水流速度⼩小。
6、如图所示,虹吸管的粗细均匀,略略去⽔水的粘滞性,求⽔水流速度及A 、B 、C 三处的压强。
题1-10图解:在管外液⾯面上任选⼀一点D ,CD 两点:BC两点:AC两点:7、⼀一开⼝口容器器截⾯面积为S1,底部开⼀一截⾯面积为S2的孔。
当容器器内装的液体⾼高度为h时,液体从孔中喷出的速度为多⼤大?设液体为理理想流体且作定常流动。
解:由于液体为理理想流体且作定常流动,根据连续性原理理,有根据伯努利利⽅方程,有从上两式联⽴立解得8、⼀一圆筒中的⽔水深为H=0.70m,底⾯面积S1=0.06m2,桶底部有⼀一⾯面积为1.0×10-4m2的⼩小孔。
大学物理教程课后习题答案 第二章 2.1 两根轻弹簧与物体连接方式如题图 2.1,物体质量为m ,弹簧劲度系数为1k 和2k ,水平面光滑.证明系统可作简谐振动,并求振动的固有频率. 题图2.1 解 以物体m 的平衡位置为原点,建立坐标轴Ox 水平向右.设m 位于x 时,两弹簧分别伸长1x 和2x ,则12x x x =+.因两弹簧弹性力相等,所以物体m 所受合力1122F k x k x ==.设由两弹簧组合而成的“组合弹簧”的劲度系数为k ,于是12121212()()k k F F F kx k x x k kF k k k k +==+=+= 由此求得“组合弹簧”的劲度系数1212k k k k k =+为常量,可见物体m 所受合力为线性回复力,所以系统作简谐振动,振动的固有频率12121122()k k k m m k k νππ==+ 2.2 两根轻弹簧与物体连接方式如题图2.2,物体质量为m ,弹簧劲度系数为1k 和2k ,水平面光滑,物体静止时两弹簧均处于自由伸张状态.证明系统可作简谐振动,并求振动的圆频率和周期. 题图2.2 解 以物体m 的平衡位置为原点,建立坐标轴Ox 水平向右.m 位于x 时,弹簧1被拉长,弹簧2被压缩,m 所受合力1212()F kx k x k x k k x ==+=+由此求得“组合弹簧”的劲度系数12k k k =+为常量,可见物体m 所受合力为线性回复力,所以系统作简谐振动,振动的圆频率和周期分别为120k k m ω+= , 122m T k k π=+ 2.3 弹簧振子的质点质量为42.510kg -⨯,运动学方程为0.06cos(5)(m)x t π=+.求:(1)振幅和周期;(2)质点的初始位置;(3)质点位于初始位置时所受合力;(4)质点在s t π=时的位置、速度和加速度.解 (1)由运动学方程可见,振幅006m A .=,05ω=,周期0204(s)126(s)T ..ππω===(2)由运动学方程可见,0t =时,质点的初始位置0006cos 006(m)x ..π==-.(3)对运动学方程求时间导数可得d 0.3sin(5)d x x v t tπ==-+ d 1.5cos(5)d x x v a t t π==-+ 0t =时0 1.5cos 1.5x a π=-=,根据牛顿第二定律可知质点位于初始位置时所受合力440025101537510(N)x F ma ...--==⨯⨯=⨯(4)把t π=代入运动学方程和(3)中求得的x v 、x a 表达式,即可求得质点在t π=时的位置、速度和加速度分别为006cos(5+)006(m)x ..ππ==03sin(5)0(m )x v .ππ=-+=215cos(5) 1.5(m )x a .ππ=-+=-2.4 一质点作简谐振动,振幅为0.02m ,速度幅为0.03m s ,取速度为最大值时为0t =.求:(1)周期;(2)加速度幅;(3)运动学方程. 解 设运动学方程为00cos()002cos()x A t .t ωϕωϕ=+=+,则00002sin()x v .t ωωϕ=-+200002cos()x a .t ωωϕ=-+(1)由m 0002003v ..ω==,可知000315002...ω==,所以周期为 022419(s)15T ..ππω=== (2) 222m 0002002150045(m s )a ....ω==⨯=(3)由已知条件0t =时00x =、0m x v v =,可知0002cos .ϕ=、m m sin v v ϕ=-,即cos =0ϕ ,sin =1ϕ- 由以上二式求出2πϕ=-,所以运动学方程为002cos(15)2x ..t π=-2.5 一水平放置的弹簧振子,质点质量为0.1kg ,振幅为0.01m ,质点运动的最大加速度为20.04m s .求:(1)系统的机械能;(2)质点通过平衡位置时的动能;(3)以0.01m x =时为0t =,动能与势能相等的时刻.解 根据001m A .=和22m 0004m s a A .ω==,可以求出00040012..ω==. 由0k m ω=,可知2001404k m ..ω==⨯=.(1)系统的机械能2251104001210(J)22E kA ..-==⨯⨯=⨯ (2)通过平衡位置时0x =,势能p 0E =,所以动能5k 210(J)E E -==⨯.(3)由已知条件0t =时0001m x .=、00x v =,可知cos 1ϕ= , sin 0ϕ=由以上二式求出0ϕ=.于是2252k 01sin ()210sin 22E kA t t ωϕ-=+=⨯ 2252p 01cos ()210cos 22E kA t t ωϕ-=+=⨯ 动能与势能相等的时刻,k p E E =,即22sin 2cos 2t t =可求出2(21)244t kk πππ=+=+ , 0123k ,,,...= 所以(21)8t k π=+,0123k ,,,...=2.6 题图2.6所示为振幅与频率相同的两个简谐振动的x t -图.求:(1)两个简谐振动的运动学方程;(2)哪个简谐振动的相位超前?超前多少? 题图2.6解 由x t -图可见01m A .=、4s T =,可知0205.Tπωπ==. 对振动(1),1101cos (05)x ..t πϕ=+,当0t =时101005201cos x ..ϕ== , 101005sin 0x v .πϕ=-<可知14πϕ=.运动学方程为 101cos(05)4x ..t ππ=+ 振动(2),2201cos (05)x ..t πϕ=+,当0t =时 202005201cos x ..ϕ== , 202005sin 0x v .πϕ=->可知24πϕ=-.运动学方程为101cos(05)4x ..t ππ=- 两个简谐振动的的相位差 122πϕϕϕ∆=-=说明振动(1)比振动(2)超前2π. 2.7 有两个同方向同频率的简谐振动,它们的运动学方程分别为130.05cos(10)4x t π=+和210.05cos(10)4x t π=+(国际制单位).求:(1)合振动的振幅和初相位;(2)若另有一振动30.08cos(10)x t ϕ=+,ϕ为何值13x x +的振幅最大?ϕ为何值13x x +的振幅最小?(利用旋转矢量图解题)解 (1)分别作与0t =时刻的1x 和2x 对应的旋转矢量1A 和2A ,如题解图2.7.由旋转矢量图可见合矢量12A A +的长度为0.052,与Ox 轴夹角为90ο.于是可知合振动的振幅0.052m A =,初相位12ϕπ=合. 题解图2.7(2)1x 和3x 同相,即34ϕπ=时,13x x +的振幅最大;1x 和3x 反相,即14ϕπ=-时,13x x +的振幅最小.2.8 有两个同方向同频率的简谐振动,其合振动的振幅为0.02m ,合振动与第一个分振动的相位差为30ο,第一个分振动的振幅为0.013m .求:(1)第二个分振动的振幅;(2)两个分振动的相位差.(利用旋转矢量图解题)解 根据已知条件作旋转矢量图,如题解图2.8.(1)由图可见,第二个分振动的振幅20.01m A =.(2)由图可见,两个分振动的相位差2190ϕϕο-=. 题解图2.82.9 现在力学的学习暂时告一段落,请读者总结一下有何收获和体会?(牛顿质点力学的理论结构、数学和物理的关系、学习了哪些方法……)*2.10 某阻尼振动(弱阻尼状态)的振幅经一“周期”后变为原来的13,求振动的“周期”为振动系统固有周期的几倍.解 弱阻尼振动()e cos t x A 't βωϕ-=+,由题意()e 1e 3e et T 't T'T'A A ββββ--+-=== lne ln3T'T 'ββ==所以22ln 3'T 'ππβω==根据'ω=0ω== 于是0022T ''T 'ωπωπωω===1015.= *2.11 质量为3310kg m -=⨯的质点,挂在劲度系数21.210N m k -=⨯的弹簧下端,沿Ox 轴运动.质点除线性回复力外,还受策动力0cos 2t(N)x F F =和阻力rx x F v γ=-作用.求当阻力系数γ增为原来的3倍时,质点稳态振幅减为原来的几分之几?解 根据已知条件,22312104310k .m ω--⨯===⨯,2ω=.故弱阻尼受迫振动的稳态振幅004f A β== 由于00F f m =和2mγβ=,所以 002F A γ=当3'γγ=,00001263F F A A γγ'===',因此当阻力系数γ增为原来的3倍时,质点稳态振幅减为原来的三分之一.*2.12 为什么说牛顿力学是“确定性”的?混沌的基本特征是什么?。
P习题1212-3.如习题12-3图所示,真空中一长为L 的均匀带电细直杆,总电量为q ,试求在直杆延长线上到杆的一端距离为d 的点P 的电场强度。
[解] 建立如图所示坐标系ox ,在带电直导线上距O 点为x 处取电荷元x Lq q d d =,它在P 点产生的电电场强度度为()x x d L Lq x d L qE d 41d 41d 2020-+=-+=πεπε则整个带电直导线在P 点产生的电电场强度度为()d L d qx x d L Lq E L+=-+=⎰002041d 41πεπε故()i E d L d q+=04πε12-4.用绝缘细线弯成的半圆环,半径为R ,其上均匀地带有正电荷Q ,试求圆心处点O 的场强。
[解] 将半圆环分成无穷多小段,取一小段dl dq 在O点的电场强度20204d 4d d RlR Q R qE πεππε== 从对称性分析,y场强度l R Q E E d sin 4sin d d 302x ⋅=⋅=θεπθ θd d R l =θεπθd 4sin d 202x RQ E =2020202x x 2d 4sin d R QR Q E E E επθεπθπ====⎰⎰ 方向沿x 轴正方向12-5. 如习题12-5图所示,一半径为R 的无限长半圆柱面形薄筒,均匀带电,沿轴向单位长度上的带电量为,试求圆柱面轴线上一点的电场强度E 。
[解] θd 对应的无限长直线单位长带的电量为θπλd d =q 它在轴线O 产生的电场强度的大小为RRq E 0202d 2d d επθλπε==因对称性y d E 成对抵消RE E 02x2d cos cos d d επθθλθ=⋅=RR E E 02202x 2d cos 2d επλεπθθλπ===⎰⎰ 12-6.一半径为R 的半球面,均匀地带有电荷,电荷面密度为,求球心点O 处的场强。
d θ[解] 将半球面分成无限多个圆环,取一圆环半径为r ,到球心距离为x ,所带电量绝对值l r q d 2d πσ=。
在O 点产生的电场强度(利用圆环轴线电场强度公式)()23220x 4d d rx q x E +=πε带电半球壳在O 点的总电场强度()()⎰⎰⎰+=+==2322023220x x 424d d rx rdlx rx q x E E πεπσπε由于 θcos R x =,θsin R r =,θd d R l = 所以()0200202x 42cos 82d 2sin 8d cos sin 2εσθεσθθεσθθθεσπππ=⎪⎭⎫ ⎝⎛-==⋅==⎰⎰E E 方向沿x 轴负向12-7.如习题12-7图所示,A 、B 为真空中两个平行的“无限大”均匀带电平面,已知两平面间的电场强度为E 0,两平面外侧电场强度大小都是03E ,方向如图。
求两平面A 、B 上的面电荷密度A和B。
[解] 无限大平面产生的电场强度为dl xθOr E 0/3E 0/3E 0AB2εσ=E 则 0A A 2εσ=E 0BB 2εσ=E ⎪⎪⎩⎪⎪⎨⎧=+=-322220A 0B 0A0B E E εσεσεσεσ 解得 00A 32E εσ-= 00B 34E εσ=12-8.一半径为R 的带电球体,其体电荷密度分布为=Ar (r ≤R ),0=ρ (r >R ),A为常量。
试求球内、外的场强分布。
[解] 在带电球体内外分别做与之同心的高斯球面。
应用高斯定理有024επqr E =⋅q 为高斯球面内所包围的电量。
设距球心r 处厚度为d r 的薄球壳所带电量为d qr Ar r r q d 4d 4d 32ππρ=⋅=r ≤R 时 403d 4Ar r Ar q rππ==⎰解得 024εAr E =(r ≤R ) (或24Ar ε=r E e )r >R 时高斯面内包围的是带电体的总电量Q4030d 4d AR r Ar q Q RR ππ===⎰⎰应用高斯定理024επQr E =⋅2044r AR E ε=(r >R ) (或r E 2044r AR ε=) 当A >0时,电场强度方向均径向向外;当A <0时,电场强度方向均指向球心。
12-9.有一带电球壳,内、外半径分别为R 1和R 2,体电荷密度r A =ρ,在球心处有一点电荷Q ,求当A 取什么值时,球壳区域内(R 1<r<R 2)的场强E 的大小与r 无关。
[解] 以同心球面为高斯面,电通量为24d επ∑⎰⎰==⋅q E r SS E()Q R r A Q dr r q r R +-=+=⎰⎰⎰∑21220202d sin d 1πθθϕππ()2021242rQR r A E πεπ+-=当212R QA π=时 02εA E =与r 无关。
因此得证。
12-10.一球体内均匀分布着体电荷密度为ρ的正电荷,若保持电荷分布不变,在该球体内挖去半径为r 的一个小球体,球心为O ,两球心间距离OO d '=,如习题12-10图所示。
求:(1)在球形空腔内,球心O 处的电场强度O 'E;(2)在球体内点P 处的电场强度E 。
设O 、O 、P 三点在同一直径上,且OP =d 。
[解] 在空腔内分别填上密度为ρ+的电荷和密度为ρ-的电荷。
(1) O '处的电场强度是密度为ρ的大球和ρ-的小球所产生的电场强度的叠加。
大球产生电场强度:在球体内做半径为d 的同心高斯球面,应用高斯定理32344επρπd d E ⋅=⋅ 03ερdE =而小球产生电场强度由于对称性为0 因此O '点的电场强度 i E 0O 3ερd='(2)P 点的电场强度也是两球电场强度的叠加。
同理大球产生的电场强度 i E 03ερd-=小球产生的电场强度 0323444επρπr dE =⋅' i E 20312dr ερ='合电场强度 i i E ⎪⎪⎭⎫⎝⎛--=⎪⎪⎭⎫ ⎝⎛+-=2302030P 43123d r d d r d ερερερ12-11.一半径为R 的带电球体,其体电荷密度分布为 4R qrπρ=(r ≤R )0=ρ (r >R )试求:(1)带电球体的总电量;(2)球内外各点的场强;(3)球内外各点的电势。
[解] (1)带点球体的总电量:q r r Rqrq Q RR===⎰⎰0240d 4d ππ (2)在带电球体内外分别做与之同心的高斯球面。
应用高斯定理有024επ内q r E =⋅内q 为高斯球面内所包围的电量。
设距球心r 处厚度为d r 的薄球壳所带电量为d qr r Rq r r q d 4d 4d 342=⋅=πρ r ≤R 时 44034d 4r Rq r r R q q r==⎰内 解得 4024R qr E πε= (r ≤R ) (或2404qr Rπε=rE e ) r >R 时高斯面内包围的是带电体的总电量q应用高斯定理024επqr E =⋅204r q E πε=(r >R ) 方向沿径向 (或204q r πε=r E e )当q >0时,电场强度方向均径向向外;当q<0时,电场强度方向均指向球心。
(3))( 412)( d 4d 4d 330 R 20 402 R r R r R q R r r rq r R qr r E U Rrr ≤⎪⎪⎭⎫⎝⎛-=>+==⎰⎰⎰∞∞πεπεπε)( 4)( d 4d 0 r20 R r rq R r r r q r E U r >=>==⎰⎰∞∞πεπε12-12.如习题12-12图所示,在Oxy 平面内有与y 轴平行、位于2a x =和a x 21-=处的两条无限长平行均匀带电直线,电荷线密度分别为+和。
求z 轴上任一点的电场强度。
[解] 无限长带电直线在线外任一点的电电场强度度 rE 02πελ=所以 P 点的电场强度 21220λ42⎪⎪⎭⎫ ⎝⎛+=+z a E πελ21220λ42⎪⎪⎭⎫ ⎝⎛+=-z a E πελ由对称性知合电场强度的z 方向分量为零,x 方向分量θcos 2λx E E =而 212242cos ⎪⎪⎭⎫ ⎝⎛+=z a a θ所以 ()220λ42cos 2z a a E E +==πελθ 方向指向x 轴负方向12-13.如习题12-13图所示,在半径为R ,体电荷密度为ρ的均匀带电球体内点O '处放一个点电荷q 。
试求:点O 、P 、N 、M 处的场强 (O '、O 、P 、N 、M 在一条直线上)。
[解] 由电场叠加原理2O O 0q O 4'=+=r qE E E πε球20OO 4q rπε'=O E i0OM 2NO 02ON 03OM2N O 0q N 344344ερπεπεπρπεr r qr r r q E E E -=-=-=''球E -λ-λa/2xyz -a/2O+λPE xE +λOM 20O N 0()43r qr ρπεε'=-N E i 0OP 2P O 02OP 03OP2P O 0q P 344344ερπεπεπρπεr r qr r r q E E E -=-=+=''球OPP 20O P()43r qr ρπεε'=-E i 2OM 032N O 02OM 032M O 0q M 344344r R r q r R r q E E E ερπεπεπρπε-=+=+=''球3M 220O N 0OM()43q R r r ρπεε'=-E i 12-14.如习题12-14图所示一环形薄片由细绳悬吊着,环的外半径R ,内半径为R/2,并有电量Q 均匀分布在环面上。
细绳长3R ,也有电量Q 均匀分布在绳上,试求圆环中心处的电场强度(圆环中心在细绳的延长线上)。
【解】:以悬点为坐标原点,建立竖直向下为x 轴的正方向,在x 位置处任取一微元dx ,在圆环中处的电场强度为()()122001d 1d d 44434qQE x R x R R x πεπε==--则这个细绳上的电荷在圆心处产生的电场强度为()33200011d 412434RRQ QE x R R x R R x πεπε==---⎰32000112416RQQR R x R πεπε=-=-R3R2/R环形薄片上的电荷在圆心处产生的电场强度为零,因此所有电荷在环心处产生的电场强度为20=16Q E R πε总方向竖直向下12-15.电量q 均匀分布在长为2l 的细杆上,端距离为a 的点P 的电势(以无穷远为零电势点)。