2016.7高二数学(文科)暑假作业 主观题部分

第14天 正弦定理、余弦定理、解三角形课标导航：1.把握正弦定理、余弦定理并能解决简单的三角气宇问题；2.能运用正弦定理、余弦定理等知识与方式解决一些与测量和几何计算有关的实际问题.一、选择题1. 在△ABC 中，若sin 2A ＋sin 2B ＜sin 2C ，则△ABC 的形状是 ( )A ．钝角三角形B ．直角三角形C ．锐角三角形D ．不能确信 2. 在Rt △ABC 中，∠C ＝90°，AC ＝4，则AB →·AC →等于（ ）A ．－16B ．－8C ．8D ．163. 在△ABC 中，“C b B c cos cos =”是“△ABC 是等腰三角形”的 （ ） A.«Skip Record If...»充分没必要要条件 B.«Skip Record If...»必要不充分条件 C.«Skip Record If...»充分必要条件 D.«Skip Record If...»既不充分也没必要要条件4. 若是等腰三角形的周长是底边长的5倍，那么它的顶角的余弦值为 （ ）A ．185B ．43 C ．23 D ．875. △ABC 的三个内角A 、B 、C 所对的边别离为,,a b c ，且2sin sin cos a A B b A +=，则«Skip Record If...»（ ） A.«Skip Record If...» «Skip Record If...» B.«Skip Record If...» «Skip Record If...» C.«Skip Record If...» «Skip Record If...» D.«Skip Record If...»«Skip Record If...» 6. 若△ABC 的内角，,,A B C 知足«Skip Record If...»，则cos B = （ ）A B ．34C D ．11167. 在△ABC 中，内角A 、B 、C 的对边别离是,,a b c ，若22a b -=，，则A （ ） A.«Skip Record If (30)B.«Skip Record If (60)C.«Skip RecordIf (120)D.«Skip Record If (150)8. 在△ABC 中，AC ，BC ＝2，B ＝60°，则BC 边上的高等于( )二、填空题9. 在ABC ∆中，角A 、B 、C 所对的边别离为a b c 、、，若1,3a c C π===，则A = ;10. 在△ABC 中，已知最长边23=AB ，3=BC ，∠A =30︒，则∠C = ; 11. 若P ，Q 是等腰直角三角形ABC 斜边AB 的三等分点，则=∠PCQ tan ;12. 某船在A 处看灯塔S 在北偏东30︒方向，它以每小时30海里的速度向正北方向航行，通过40分钟航行到B处，看灯塔S 在北偏东75︒方向，则此刻该船到灯塔S 的距离约为 海里（精准到海里）．三、解答题13.已知在ABC ∆中，,,a b c 别离为角,,A B C 的对边，60B =,b =，3a =(1)求cos A 的值； (2) 求cos(2)61cos 2A Aπ--的值.14. 在△ABC 中，角A ，B ，C 的对边别离为,,a b c ，且4cos 5C =，2cos c b A =． （1）求证：A B =； （2）若△ABC 的面积152S =，求c 的值.15. 已知A 、B 、C 是△ABC的三个内角，向量(1,(cos ,sin )m n A A ==，且1m n ⋅=- （1）求角A ； （2）若sin cos 3,tan sin cos B BC B B+=-求的值16. 如图，渔船甲位于岛屿A 的南偏西60方向的B 处，且与岛屿A 相距12海里，渔船乙以10海里/小时的速度从岛屿A 起身沿正北方向航行，若渔船甲同时从B 处起身沿北偏东α的方向追赶渔船乙，恰好用2小时追上.（1）求渔船甲的速度； （2）求sin α的值．ABC东南 西北【链接高考】设△ABC 是锐角三角形，a ，b ，c 别离是内角A ，B ，C 所对边长，而且sin 2A ＝sin 3B π⎛⎫+⎪⎝⎭sin 3B π⎛⎫- ⎪⎝⎭＋sin 2B . (1) 求角A 的值；(2) 若AB →·AC →＝12，a ＝，求b ，c (其中b ＜c )．第14天1~8 ADAD DDAB ；9. 6π; 10. 135︒; 11. 43;12. ; 13.（1）cos 3A ==；（2）cos(2)61cos 2A A π-=-. 14.（1）证明：略；（2）c =15.（1）3A π=；（2）tan C ==60α16.«Skip Record If...»（1）渔船甲的速度为14海里/小时；（2）sin 的值为14A＝π3；(2) c＝6，b＝4.。

【KS5U 】2015-2016下学期高二数学暑假作业七本套试卷的知识点：集合与简易逻辑 基本初等函数 数列 三角函数 平面向量 不等式 空间几何体 圆锥曲线与方程 导数及其应用 概率 统计第I 卷（选择题）1.已知集合{}21<-=x x A ，集合{}0ln >=x x B ，则集合=⋂B A ( ) A. )3,1( B. )3,0( C. )3,1(- D. )1,1(-2.复数+５１２i 的共轭复数为A 51033i --B ．51033i -+ C. 12i + D.12i -3.设∆ABC 的内角A,B ，C 所对边的长分别为a,b,c ，若b+c= 2a,.3sinA=sinB ，则角C= ( )A ．3πB ．23πC ．34π D.56π4.已知平面向量(3,1)a = ，(,3)b x =- ，且a b ⊥ ，则x =（ ）A ．3-B ．1-C ．1D ．35.设实数x ，y 满足，则xy 的最大值为（ ）A ．B ．C ．12D ．166.一个几何体的三视图如图所示，则这个几何体的表面积等于( )7.某程序框图如图所示，该程序运行后输出的k 的值是( )A ．4B ．5C ．6D ．78.已知双曲线22221(0,0)x y a b a b -=>>的左焦点)0)(0,(>-c c F ，过点F 作圆：4222b y x =+的切线，切点为E ，延长FE 交双曲线右支于点P ，若EP FE =，则双曲线的离心率为（ ）A. 10B. 5C.210 D. 259.如图，EFGH 是以O 为圆心，1为半径的圆的内接正方形，将一颗豆子随机地掷到圆内，用A 表示事件“豆子落在正方形EFGH 内”，B 表示事件“豆子落在扇形HOE （阴影部分）内”，则P （B|A ）=（ ）A ．41 B ．31 C ．8π D ．4π10.如果关于x 的方程213ax x+=正实数解有且只有一个，那么实数a 的取值范围为（ ）A. 0a ≤B. 0a ≤或 2a =C. 0a ≥D. 0a ≥或 2a =-第II 卷（非选择题）11.如图为甲、乙两名篮球运动员每场比赛得分情况的茎叶图，则甲和乙得分的中位数的和是12.几何体ABCDEF 如图所示，其中AC ⊥AB, AC=3，AB=4，AE 、CD 、BF 均垂直于面ABC ，且AE=CD=5，BF=3，则这个几何体的体积为 .13.已知ABC ∆为锐角三角形，且满足1tan ,1tan -=+=t B t A ，则实数t 的取值范围是_________．14. （2016新课标高考题）设等比数列{}n a 满足a 1+a 3=10，a 2+a 4=5，则a 1a 2鬃?a n 的最大值为 . 15.（本小题满分12分）医生的专业能力参数K 可有效衡量医生的综合能力，K 越大，综合能力越强，并规定: 能力参数K 不少于30称为合格，不少于50称为优秀．某市卫生管理部门随机抽取300名医生进行专业能力参数考核,得到如图所示的能力K 的频率分布直方图: （Ⅰ）求出这个样本的合格率、优秀率；（Ⅱ）现用分层抽样的方法从中抽出一个样本容量为20的样本,再从这20名医生中随机选出2名．①求这2名医生的能力参数K 为同一组的概率；②设这2名医生中能力参数K 为优秀的人数为X ,求随机变量X 的分布列和期望．16.（本小题满分14分）已知椭圆C ：()222210x y a b a b+=>>的两焦点与短轴的一个端点的连线构成等腰直角三角形，直线01=++y x 与以椭圆C 的右焦点为圆心，以椭圆的长半轴长为半径的圆相切. （1）求椭圆的方程；（2）设P 为椭圆上一点，若过点)0,2(M 的直线l 与椭圆E 相交于不同的两点S 和T ,且满足OP t OT OS =+(O 为坐标原点)，求实数t 的取值范围.17.（本小题满分13分）已知多面体ABCDE 中，AB ⊥平面ACD ，DE ⊥平面ACD ，AC = AD = CD = DE = 2， AB = 1，F 为CD 的中点．（Ⅰ）求证：AF ⊥平面CDE ；（Ⅱ）求直线AC 与平面CBE 所成角正弦值； （Ⅲ）求面ACD 和面BCE 所成锐二面角的大小．【KS5U】2015-2016下学期高二数学暑假作业七试卷答案1.A2.C3.B4.C5.A【考点】简单线性规划．【专题】不等式的解法及应用．【分析】作出不等式组对应的平面区域，利用基本不等式进行求解即可．【解答】解：作出不等式组对应的平面区域如图；由图象知y≤10﹣2x，则xy≤x（10﹣2x）=2x（5﹣x））≤2（）2=，当且仅当x=，y=5时，取等号，经检验（，5）在可行域内，故xy的最大值为，故选：A【点评】本题主要考查线性规划以及基本不等式的应用，利用数形结合是解决本题的关键．6.A7.A【考点】程序框图．【专题】算法和程序框图．【分析】根据流程图所示的顺序，逐框分析程序中各变量、各语句的作用可知：该程序的作用是计算满足S=≥100的最小项数【解答】解：根据流程图所示的顺序，程序的运行过程中各变量值变化如下表：是否继续循环 S K循环前/0 0第一圈是 1 1第二圈是 3 2第三圈是 11 3第四圈是 2059 4第五圈否∴最终输出结果k=4故答案为A【点评】根据流程图（或伪代码）写程序的运行结果，是算法这一模块最重要的题型，其处理方法是：①分析流程图（或伪代码），从流程图（或伪代码）中既要分析出计算的类型，又要分析出参与计算的数据（如果参与运算的数据比较多，也可使用表格对数据进行分析管理）⇒②建立数学模型，根据第一步分析的结果，选择恰当的数学模型③解模．8.B9.A10.B11.58【考点】茎叶图．【专题】计算题；概率与统计．【分析】由茎叶图可知甲得分数据共有13个，出现在中间第7位的数据是32，乙得分的中位数是32．乙得分数据共有13个，出现在中间第7位的数据是26，乙得分的中位数是26，即可得出结论．【解答】解：由茎叶图可知甲得分数据共有13个，出现在中间第7位的数据是32，乙得分的中位数是32．乙得分数据共有13个，出现在中间第7位的数据是26，乙得分的中位数是26．两数之和32+26=58故答案为：58．【点评】本题考查茎叶图和中位数，本题解题的关键是看清所给的数据的个数，计算中位数时，看清是有偶数个数字还是奇数个数字，选择出中位数． 12.26 13.2>t14. 【答案】64考点：等比数列及其应用 15.（1）合格率是：10.021010.20.8-⨯=-=优秀率是：0.015100.010100.005100.3⨯+⨯+⨯= …………3分 （2）由题意知，这20名医生中，有4人，有6人，有4人，有3人，有2人，有1人①222224643222031190C C C C C p C ++++== …………7分 ②优秀的人数为：3+2+1＝6人0,1,2x =112146142*********(0),(1)19095C C C p x p x C C ======，26220153(2)19038C p x C ====x ∴的分布列是：故x 的期望是()5795E x =…………12分 16.（1）由题意：以椭圆C 的右焦点为圆心，以椭圆的长半轴长为半径的圆的方程为222)(a y c x =+-,∴圆心到直线01=++y x 的距离=d a c =+21∵椭圆)0(1:2222>>=+b a by a x C 的两焦点与短轴的一个端点的连线构成等腰直角三角形， b=c, c b a 22==代入*式得b=c=1 ∴22==b a故所求椭圆方程为.1222=+y x 5分 （Ⅱ）由题意知直线L 的斜率存在，设直线L 方程为)2(-=x k y ，设()00,y x p 将直线方程代入椭圆方程得：()028*******=-+-+k x k x k ………… 6分 ∴()()081628214642224>+-=-+-=∆k k k k ∴212<k 7分 设()11,y x S ,()22,y x T 则222122212128,218kk x x k k x x +-=+=+………………8分 当t=0时，直线l 的方程为y=0,此时t=0，t =+成立，故，t=0符合题意。

安徽省六安市2016年高二数学文暑假作业第18天Word 版含答案-精品课标导航：1.了解数列的概念和几种简单的表示法； 2.了解数列是自变量为整数的一类函数. 一、选择题1. 下面是关于公差d>0的等差数列{a n }的四个命题：p 1：数列{a n }是递增数列； p 2：数列{na n }是递增数列；p 3：数列a nn 是递增数列；p 4：数列{a n ＋3nd}是递增数列，其中的真命题为 ( ) A ．p 1，p 2B ．p 3，p 4C ．p 2，p 3D ．p 1，p 42. 已知数列 ,12,,7,5,3,1-n ，则53是它的（ ）A. 第22项B. 第23项C. 第24项D. 第28项 3. 已知031=--+n n a a ，则数列{}n a 是（ ）A. 递增数列B. 递减数列C. 常数列D. 摆动数列4. 数列{}n a 的通项公式为n n a n 2832-=，则数列{}n a 各项中最小项是（ ）A. 第4项B. 第5项 C . 第6项 D. 第7项5. 数列1,0,1,0,1,0,……的一个通项公式是（ ）A. ()2111+--=n n a B. ()2111+-+=n n a C. ()211--=n na D. ()211nn a ---=6. 已知数列{}n a 满足()nn n n a a a 111-+=--且11=a ，则=35a a（ ） A.1516B.34 C. 158 D. 38 7. 已知()*1133,21N n a a a a n n n ∈+==+，则=n a（ ） A.52+n B.42+n C. 53+n D. 43+n 8. 数列{a n }的通项a n =)(9998N n n n ∈--,则数列{a n }的前30项中最大项是( ) A ．30a B ．10a C ． 9a D ． 1a 二、填空题9. 数列{}n a 满足11=a ，13321++=-+n n a a n n ，根据这个数列的前4项并归纳通项公式得n a = ；10. 设{a n }是首项为1的正项数列，且（n +1）a n +12－na n 2+a n +1a n =0（n ∈N *），则它的通项公式a n =______________;11. 数列{}n a 中，已知()*1221,2,1N n a a a a a n n n ∈-===++，则=2002a ；12. 数列{}n a 满足⎪⎪⎩⎪⎪⎨⎧<≤-<≤=+)121(12)210(21n n n n n a a a a a ,若761=a ，则=8a .三、解答题13.已知数列{}n a 满足q pa a a n n +==+11,1，且15,342==a a ，求q p ,的值．14. 设数列{}n a 的前n 项和为n S ，已知()21nn n ba b S -=-（1）证明：当2b =时，{}12n n a n --⋅是等比数列； （2）求{}n a 的通项公式．15. 已知公差不为0的等差数列{}n a 的前3项和3S ＝9，且125,,a a a 成等比数列. （1）求数列{}n a 的通项公式和前n 项和n S ; (2）设n T 为数列11{}n n a a +的前n 项和，若1n n T a λ+≤对一切n N *∈恒成立，求实数λ的最小值.16. 设同时满足条件：①122++≥+n n n b b b ；②n b M ≤(N n +∈，M 是与n 无关的常数)的无穷数列{}n b 叫“仁风”数列.已知数列{}n a 的前n 项和n S 满足： (1)1n n aS a a =--（a 为常数，且0a ≠，1a ≠）． （1）求{}n a 的通项公式；（2）设21n n n S b a =+，若数列{}n b 为等比数列，求a 的值，并证明此时⎭⎬⎫⎩⎨⎧n b 1为“仁风”数列.【链接高考】[2013·安徽卷] 设数列{a n }满足a 1＝2，a 2＋a 4＝8，且对任意n ∈N *，函数f(x)＝(a n －a n＋1＋a n ＋2)x ＋a n ＋1cos x －a n ＋2sin x 满足'()2f π＝0. (1)求数列{a n }的通项公式； (2)若，求数列{b n }的前n 项和S n .第18天1~8 DBAB BBCB ;9. 3n ; 10.n 1;11. 1-; 12. 75;13．⎩⎨⎧=-=63q p 或⎩⎨⎧==12q p ’14．（1）证明：由题意知12a =，且()21nn n ba b S -=-，()11121n n n ba b S +++-=-两式相减得()()1121nn n n b a a b a ++--=-，即12n n n a ba +=+ ① 当2b =时，由①知122n n n a a +=+，于是()()1122212n n n n n a n a n +-+⋅=+-+⋅()122n n a n -=-⋅又111210n a --⋅=≠，所以{}12n n a n --⋅是首项为1，公比为2的等比数列。

第34天 推理与证明课标导航：1.了解合情推理与演绎推理的含义.2．了解合情推理与演绎推理的联系与区别一、选择题 1. 已知f (x ＋1)＝2()()2f x f x +，f (1)＝1(x ∈N *)，猜想f (x )的表达式为（ ）A ．f (x )＝42x ＋2B ．f (x )＝2x ＋1C ．f (x )＝1x ＋1D ．f (x )＝22x ＋22. 若2sinsin (i)777n n S πππ=+++（n N *∈），则在12100,,...,S S S 中，正数的个数是 （ ）A ．16 B.72 C.86 D.100 3. 函数f (x )＝191||i x n =-∑的最小值为（ ）A ．190 B.171 C ．90 D ．454. 观察下列事实|x|+|y|=1的不同整数解（x,y ）的个数为4 ， |x|+|y|=2的不同整数解（x,y ）的个数为8， |x|+|y|=3的不同整数解（x,y ）的个数为12 ….则|x|+|y|=20的不同整数解（x ，y ）的个数为 （ ）A.76B.80C.86D.92 5. 给出如下三个命题：①四个非零实数a 、b 、c 、d 依次成等比数列的充要条件是ad ＝bc ；②设a ，b ∈R ，且ab ≠0，若a b ＜1，则ba＞1；③若f (x )＝log 2x ，则f (|x |)是偶函数． 其中不正确命题的序号是 （ ）A ．①②B ．②③C ．①③D ．①②③6. 由710>58，911>810，1325>921，…若a >b >0且m >0，则b ＋m a ＋m 与b a 之间大小关系为( )A ．相等B ．前者大C ．后者大D ．不确定7. 观察下列各式：则234749,7343,72401===，…，则20117的末两位数字为（ ）A.01B.43C.07D.498. 正方形ABCD 的边长为1，点E 在边AB 上，点F 在边BC 上，13AE BF ==.动点P 从E 出发沿直线向F 运动，每当碰到正方形的边时反弹，反弹时反射角等于入射角，当点P 第一次碰到E 时，P 与正方形的边碰撞的次数为（ ）A ．8 B.6 C ．4D ．3二、填空题9. 若数列{a n }满足1a n ＋1－1a n ＝d (n ∈N *，d 为常数)，则称数列{a n }为调和数列．已知数列1n x ⎧⎫⎨⎬⎩⎭为调和数列，且x 1＋x 2＋…＋x 20＝200，则x 5＋x 16＝_______; 10. 若数列{}n a 中，12341,35,7911,13151719,.a a a a ==+=++=+++则10____a =。

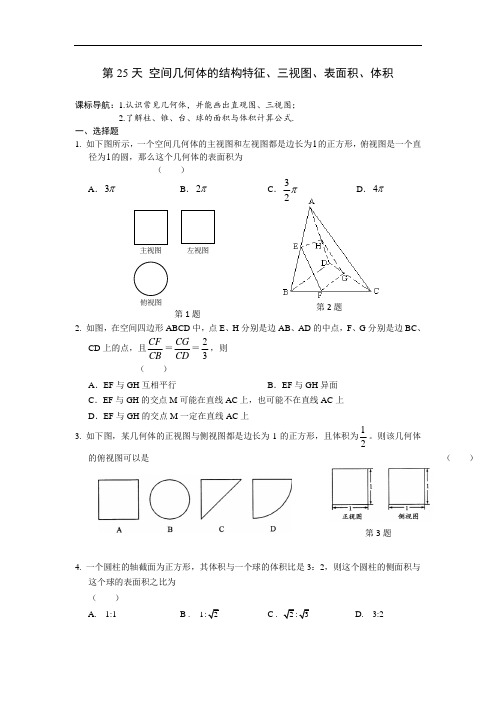
第2题第1题主视图俯视图左视图第25天 空间几何体的结构特征、三视图、表面积、体积课标导航：1.认识常见几何体，并能画出直观图、三视图； 2.了解柱、锥、台、球的面积与体积计算公式. 一、选择题1. 如下图所示，一个空间几何体的主视图和左视图都是边长为1的正方形，俯视图是一个直径为1的圆，那么这个几何体的表面积为 （ ） A ．π3 B ．π2 C ．π23D ．π42. 如图，在空间四边形ABCD 中，点E 、H 分别是边AB 、AD 的中点，F 、G 分别是边BC 、CD 上的点，且CF CB ＝CG CD ＝23，则（ ）A ．EF 与GH 互相平行B ．EF 与GH 异面C ．EF 与GH 的交点M 可能在直线AC 上，也可能不在直线AC 上D ．EF 与GH 的交点M 一定在直线AC 上3. 如下图，某几何体的正视图与侧视图都是边长为1的正方形，且体积为12。

则该几何体的俯视图可以是（ ）4. 一个圆柱的轴截面为正方形，其体积与一个球的体积比是3：2，则这个圆柱的侧面积与这个球的表面积之比为（ ）A. 1:1 B .C .D. 3:25. 某四面体的三视图如图所示，该四面体四个面的面积中最大的是（ ）A ．8B ．C ．10D ．826. 一个四棱锥的三视图如图所示，其左视图是等边三角形，该四棱锥的体积等于（ ）A B ． C ．D ．7. 一个几何体的三视图如图所示，则此几何体的体积是（ ）A ．112 B.80 C.72 D.648. 已知三棱锥S ABC -的所有顶点都在球O 的求面上，ABC ∆是边长为1的正三角形，SC 为球O 的直径，且2SC =；则此棱锥的体积为（ ）A ．6B ．6C ．3 D ．2二、填空题9. 一个空间几何体的三视图及部分数据如下图所示，则这个几何体的体积是 ；第7题10. 某几何体的三视图，其中正视图是腰长为2的等腰三角形,侧视图是半径为1的半圆，则该几何体的表面积是 ；11. 一个几何体的三视图如图所示，则该几何体的体积（单位：3cm ）为 3cm ;12. 一空间几何体的三视图如图所示，则该几何体的体积为 .三、解答题13. 已知四棱锥P ABCD -的三视图如下图所示，其中主视图、侧视图是直角三角形，俯视图是有一条对角线的正方形.E 是侧棱PC 上的动点． （1）求证：BD AE ⊥；（2）若五点,,,,A B C D P 在同一球面上，求该球的体积.第11题CD P E14. 已知某几何体的俯视图是如图所示的矩形，正视图(或称主视图)是一个底边长为8、高为4的等腰三角形，侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形．(1) 求该几何体的体积V ； (2) 求该几何体的侧面积S15. 一个多面体的直观图和三视图如下:(其中N M ,分别是BC AF ,中点)(1) 求证://MN 平面CDEF ; (2) 求多面体CDEF A 的体积.16. 如图，三棱柱ABC －A 1B 1C 1中，侧棱垂直底面，∠ACB=90°，AC=BC=12AA 1，D 是棱AA 1的中点（1）证明：平面BDC 1⊥平面BDC ；（2）平面BDC 1分此棱柱为两部分，求这两部分体积的比.【链接高考】如图，ABCDEFG 为多面体，平面ABED 与平面AGFD 垂直，点O 在线段AD 上，1,2,OA OD ==OAB V ,△OAC ，△ODE ，△ODF 都是正三角形.（1）证明直线BC ∥EF ； （错误！未找到引用源。

第26天 空间中的平行与垂直关系课标导航：1.明白得空间直线、平面位置关系的概念；2.能运用公理、定理和一些结论证明空间图形的位置关系的简单命题.一、选择题1. 已知m ，n ，l 为三条不同的直线，α，β为两个不同的平面，则下列命题中正确的是 （ ）A ．//,,//m n m n αβαβ⊂⊂⇒B ．l l ⇒⊥⊥βαβ,∥αC ．,//m m n n αα⊥⊥⇒D ．α∥,l l βαβ⊥⇒⊥ 2. 设n m l ,,为三条不同的直线，α为一个平面，下列命题中正确的个数是（ ）①若α⊥l ，则l 与α相交②若，，，，n l m l n m ⊥⊥⊂⊂αα则α⊥l ③若l ||m ，m ||n ，α⊥l ，则α⊥n ④若l ||m ，α⊥m ，α⊥n ，则l ||n A ．1B ．2C ．3D ．4 3. 用a ，b ，c 表示三条不同的直线，γ表示平面，给出下列命题：（ ）①若a ∥b ，b ∥c ，则a ∥c ； ②若a ⊥b ，b ⊥c ，则a ⊥c ； ③若a ∥γ，b ∥γ，则a ∥b ； ④若a ⊥γ，b ⊥γ，则a ∥b . 其中真命题的序号是（ ）A ．①②B ．②③C ．①④D ．③④4. 已知m 、n 为两条不同的直线，α、β为两个不同的平面，则下列命题中正确的是 （ ） A ．m ∥n ，m ⊥α⇒n ⊥αB ．α∥β，m ⊂α，n ⊂β⇒m ∥nC ．m ⊥α，m ⊥n ⇒n ∥αD ．m ⊂α，n ⊂α，m ∥β，n ∥β⇒α∥β5．设平面α与平面β相交于直线m ，直线a 在平面α内，直线b 在平面β内，且b m ⊥,则“αβ⊥”是“a b ⊥”的（ ）A ． 充分没必要要条件B ． 必要不充分条件C ． 充要条件D ． 即不充分没必要要条件 6. 到两彼此垂直的异面直线的距离相等的点（ ）A ．只有1个B ．恰有3个C ．恰有4个D ．有无穷多个7. 直三棱柱111ABC A B C -中，若90BAC ∠=︒，1AB AC AA ==，则异面直线1BA 与1AC 所成的角等于( )A ．30°B ．45°C ．60°D ．90°第8题8. 如图，已知六棱锥P-ABCDEF 的底面是正六边形，PA ⊥平面ABC ，PA=2AB ，则下列结论正确的是( )A ．PB ⊥AD B ．平面PAB ⊥平面PBC C ．直线BC ∥平面PAED ．直线PD 与平面ABC 所成角为450二、填空题9. 三棱锥S —ABC 中，SA ⊥底面ABC ，SA=4，AB=3，D 为AB 的中点 ∠ABC=90°，则点D 到面SBC 的距离等于 ； 10. 如图，直线l α⊥平面，垂足为O ，已知ABC ∆中，ABC ∠为直角，AB=2，BC=1，该直角三角形做符合以下条件的自由运动：（1）A l ∈，（2）B α∈.则C 、O 两点间的最大距离为 .11.若四面体«Skip Record If...»的三组对棱别离相等,即«SkipRecord If...»,«Skip Record If...»,«Skip Record If...»,则 .(写出所有正确结论编号)①四面体«Skip Record If...»每组对棱彼此垂直; ②四面体«Skip Record If...»每一个面的面积相等;③从四面体«Skip Record If...»每一个极点起身的三条棱两两夹角之和大于«Skip Record If...»而小于«Skip Record If...»;④连接四面体«Skip Record If...»每组对棱中点的线段互垂直平分;⑤从四面体«Skip Record If...»每一个极点起身的三条棱的长可作为一个三角形的三边长. 12.关于四面体ABCD ，下列命题正确的是________（写出所有正确命题的编号）。

山东省高二暑假作业：文科数学（含答案）解答题17.若函数当时，函数极值(1)求函数的解析式;(2)若函数有3个解，求实数的取值范围.18.(本小题满分12分) 与等腰直角所在平面互相垂直，为的中点，，∥，.(1)求证：平面平面;(2)求证：∥平面;(3)求四面体的体积.19、己知等比数列所有项均为正数，首，且成等差数列.(I)求数列的通项公式;(II)数列的前n项和为，若，求实数的值.20.(本小题满分12分)已知函数.(1)若曲线在和处的切线互相平行，求的值;(2)求的单调区间;(3)设，若对任意，均存在，使得，求的取值范围.2019高二文科数学暑假作业(一)答案1-5 ACABC 6-10 BADBD 11-12BB13. 614. 2i15.1/216.17. (1)所以,.即,由此可解得,(2)所以在处取得极大值,在处取得极小值所以18.(1)∵面面，面面，,面，又∵面，平面平面.(2)取的中点，连结、，则 ,又∵，，四边形是平行四边形，∥，又∵面且面，∥面.(3)∵，面面=，面.就是四面体的高，且=2.∵==2=2，∥，19.(Ⅰ)设数列的公比为，由条件得成等差数列，所以解得由数列的所有项均为正数,则=2数列的通项公式为=(Ⅱ)记,则若不符合条件;若，则，数列为等比数列，首项为，公比为2, 此时又=,所以20.解：.(1)，解得.(3).①当时，，，在区间上，;在区间上，故的单调递增区间是，单调递减区间是.②当时，，在区间和上，;在区间上，故的单调递增区间是和，单调递减区间是.③当时，，故的单调递增区间是.④当时，，在区间和上，;在区间上，故的单调递增区间是和，单调递减区间是. (Ⅲ)由已知，在上有.由已知，，由(Ⅱ)可知，①当时，在上单调递增，故，所以，，解得，故.②当时，在上单调递增，在上单调递减，故.由可知，，，所以，，，综上所述，.这篇山东省高二暑假作业就为大家分享到这里了。

希望对大家有所帮助！。

高二文科数学暑假作业一、选择题（本大题共12小题，共60.0分）1. 设P ={x|y =x 2},Q ={(x,y)|y =x 2}，则P,Q 的关系是( )A. P ⊆QB. P ⊇QC. P =QD. P ∩Q =⌀ 2. 下列命题正确的是( )(1)命题“∀x ∈R ，2x >0”的否定是“∃x 0∈R ，2x 0≤0”； (2)l 为直线，α，β为两个不同的平面，若l ⊥β，α⊥β，则l//α； (3)给定命题p ，q ，若“p ∧q 为真命题”，则¬p 是假命题； (4)“sinα=12”是“α=π6”的充分不必要条件．A. (1)(4)B. (2)(3)C. (3)(4)D. (1)(3)3. 已知命题，函数f(x)=x 2−(m −1)x +1在上为增函数，命题q:若a <b ，则1a >1b ，下列命题为真命题的是( )A. p ∧¬qB. ¬p ∧qC. p ∧qD. ¬p ∧¬q4. 已知函数f(x)={log 2x +x,x >0,4x−2+2,x ≤0,若f(a)=6，则f(a −2)=( )A. 1B. 3C. 1或4D. 3或45. 已知函数f(x)的定义域为(0,+∞)，则函数y =f(x+1)√−x 2−3x+4的定义域是( )A. (−1,1)B. [−1,1]C. [−1,1)D. (−1,1] 6. 设函数f(x)=2x +3,g(x +2)=f(x)，则g(x)=( )A. 2x +1B. 2x −1C. 2x −3D. 2x +77. 函数的值域是( )A.B. {−1,1,3}C. {1,3}D. {−1,3}8. 若函数f(x)=√ax 2+(a +1)x −a −2的值域为，则实数a 的取值范围为( ) A. a ≥0 B. a >0 C. a ≤0 D. a <09. 下列函数中是偶函数且最小正周期为π4的是( )A. y =cos 24x −sin 24xB. y =sin4xC. y =sin2x +cos2xD. y =cos2x10. 在△ABC 中，a ，b ，c 分别为角A ，B ，C 所对的边．若b =2acosC ，则△ABC 的形状一定是( )A. 等腰直角三角形B. 直角三角形C. 等腰三角形D. 等腰或直角三角形11. 函数f(x)=e x −x (e 为自然对数的底数)在区间[−1,1]上的最大值是( ) ．A. 1+1eB. 1C. e +1D. e −112.已知函数f(x)=12x4−2x3+3m，x∈R，若f(x)+9≥0恒成立，则m的取值范围是()A. m≥32B. m>32C. m≤32D. m<32二、填空题（本大题共4小题，共20.0分）13.函数f(x)=x+ln x在点P(1,1)处的切线方程为__________________________________．14.函数f(x)=log4(5−x)+√2x−1的定义域为____．15.设a=log412，b=log515，c=log618，则a，b，c的大小关系为.(用“>”连接)16.已知a，b，c分别为△ABC的内角A，B，C的对边，a=2，且(2+b)(sin A−sin B)=(c−b)sin C，则△ABC面积的最大值为________．三、解答题（本大题共6小题，共72.0分）17.已知a，b，c分别是△ABC内角A，B，C的对边，sin2A+sin2C−23sin Asin C=sin2B．(1)求sin B的值；(2)若b=2，△ABC的面积为√2，求△ABC的周长．18.已知向量m⃗⃗⃗ =(cos x2,−1)，n⃗=(√3sin x2,cos2x2)，设函数f(x)=m⃗⃗⃗ ⋅n⃗+1．(1)求函数f(x)的对称轴方程和对称中心坐标；(2)若关于x的方程f(x)=a在区间[0,π]上有两个实数解，求实数a的取值范围．19.已知函数f(x)=−2√3sin2x+2sinxcosx．(1)求函数f(x)在区间[0,π2]上的值域；(2)设α∈(0,π)，f(α2)=12−√3，求cosα的值．20. 已知f(x)是定义在R 上的偶函数，且x ≥0时，f(x)=log 12(x +1)． (1)求f(0)，f(−1)；(2)求函数f(x)的表达式；(3)已知f(x)在x ∈[0,+∞)单调递减，若f(a −1)−f(3−a)<0，求a 的取值范围．21. 求解下列问题(1)已知函数f(x)=(12)x2−3x+2，求函数f(x)的单调递增区间；(2)已知函数g(x)=(14)x−(12)x+1+2，x ∈[−3,3]，求函数g(x)的值域．22. 设函数f(x)=2x 3+3ax 2+3bx +c 在x =1及x =2时取得极值．(1)求a ，b 的值； (2)若f(x)在上的最大值是9，求f(x)在上的最小值．。

第22天 不等式的概念与性质课标导航：1.不等式的性质及应用；2.利用不等式的性质证明不等关系；3.了解基本不等式的证明过程，会用基本不等式解决简单的最值问题一、选择题 1. 若0a b >>，则( )A ．22()a c b c c R >∈ B ．1b a>C ．lg()0a b ->D ．11()()22ab<2. 若b a c b a >∈,R 、、，则下列不等式成立的是（ ）A ．ba 11< B ．22b a >C ．1122+>+c bc aD ．||||c b c a >3. 已知0<a<b<1，则（ ）A ．3b ＜3aB ．log 3a >log 3bC ．(lga)2<(lgb)2D ．(1e )a <(1e)b4. 如果01a <<，那么下列不等式中正确的是（ ）A ．1132(1)(1)a a ->-B ．(1)log (1)0a a -+>C ．32(1)(1)a a ->+D ．1(1)1aa +->5 若关于x 的不等式m x x ≥-42对任意]1,0[∈x 恒成立，则实数m 的取值范围是（ ）A ．03≥-≤m m 或B ．03≤≤-mC ． 3-≥mD ．3-≤m 6. 定义在R 上的偶函数)(x f 满足)()2(x f x f =-，且在[－3，－2]上是减函数，βα,是钝角三角形的两个锐角，则下列不等式关系中正确的是 （ ）A ．(sin )(cos )f f αβ>B ．(cos )(cos )f f αβ<C ．(cos )(cos )f f αβ>D ．(sin )(cos )f f αβ< 7. 已知ln x π=，5log 2y =，12z e -=，则（ ）A ．x y z <<B ．z x y <<C ．z y x <<D ．y z x <<8. 设 a ＞b ＞1，0c <,给出下列三个结论： ①c a ＞cb；② c a ＜c b ； ③ log ()log ()b a a c b c ->-， 其中所有的正确结论的序号是（ ） A ．① B.①② C.②③D.①②③二、填空题9. 设10<<a ，函数)22(log )(2--=xx a a a x f ，则使0)(<x f 的x 的取值范围是 ；10. 设关于x 的方程22230kx x k --=的两个实根一个大于1，另一个小于1，则实数k的取值范围是 ；11. 若正数,a b 满足3ab a b =++，则ab 的取值范围是 ；12. 若1x 和2x 是方程220x mx --=的两个实根，不等式21253a a x x --≥- 对任意实数[1,1]m ∈-恒成立，则a 的取值范围是 .三、解答题13. 已知,x y 都是正实数，求证：3322x y x y xy +≥+14. 若二次函数y=f(x)的图象经过原点，且1≤f(-1)≤2，3≤f(1)≤4，求f(-2)的范围．15. ,,a b c 为互不相等的正数，222a c bc +=，判断下列关系中可能成立的有哪几个？①．a b c >>；②．b a c >>；③．a c b >> ； ④．b c a >>16. 已知函数()(1)ln 1f x x x x =+-+.（1）若2'()1xf x x ax ≤++，求a 的取值范围；（2）证明：(1)()0x f x -≥ .【链接高考】已知2log 3log a =+2log 9log b =-，3log 2c =,则a,b,c 的大小关系是（ )（A ） a b c =<（B ）a b c => （C ）a b c <<（D ）a b c >>第22天1~8 DCAA DDDD; 9. 3(,log )a -∞; 10. 04k k ><-或; 11. [9,)+∞; 12.(,1][6,)-∞-⋃+∞13.332222()()()()x y x y xy x x y y y x +-+=-+-222()()()()x y x y x y x y =--=-+，∵,x y R +∈，∴2()0,0x y x y -≥+>，∴2()()0x y x y -+≥，∴3322x y x y xy +≥+14. f(-2)的取值范围是[6，10]．15.若a b >，则22222a c b c bc +>+≥，不符合条件，排除①④；又由()222a c c b c -=-，故a c -与b c -同号，排除③；且当b a c >>时，222a c bc +=有可能成立，例如取()(),,3,5,1a b c =，故②可能成立。

高二数学（文）暑假作业(1)编制:杜善鲁 审定:郝学云 20RR/7/8一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（每小题5分，共60分）.1．在回归直线方程表示回归系数中b bx a y ,ˆ+= （ ） A ．当0x =时，y 的平均值B ．当x 变动一个单位时，y 的实际变动量C ．当y 变动一个单位时，x 的平均变动量D ．当x 变动一个单位时，y 的平均变动量2．下面几种推理是类比推理的是 （ ）A ．两条直线平行，同旁内角互补，如果A ∠和B ∠是两条平行直线的同旁内角，则 180=∠+∠B A B ．由平面向量的运算性质，推测空间向量的运算性质C ．某校高二级有20个班，1班有51位团员，2班有53位团员，3班有52位团员，由此可以推测各班都超过50位团员 D ．一切偶数都能被2整除，1002是偶数，所以1002能被2整除 3．若,1a >则1a 1a -+的最小值是 （ ）A ．2B ．aC ．3D ．1a a2- 4．在对分类变量R, R 进行独立性检验时,算得k 2=7有以下四种判断(1) 有99﹪的把握认为R 与R 有关;(2)有99﹪的把握认为R 与R 无关;(3)在假设H 0:R 与R 无关的前提下有99﹪的把握认为R 与R 有关;(4)在假设H 1: R 与R 有关的前提下有99﹪的把握认为R 与R 无关.以上4个判断正确的是 （ ） A ． (1)、(2) B ． (1)、(3) C ． (2)、(4) D ． (3)、(4) 5．不等式0)1)(1(>-+x x 的解集是 （ ）A ．{}10<≤x xB ．{}1,0-≠<x x xC ．{}11<<-x xD ．{}1,1-≠<x x x6．已知c b a <<，且0=++c b a ，则ac b 42-的值 （ ） A ．大于零 B ．小于零 C ．不大于零 D ．不小于零7．把一块边长是a 的正方形铁片的各角切去大小相同的小正方形，再把它的边沿着虚线折转成一个无盖方底的盒子，盒子的容积最大时，切去的正方形边长是 （ ）A ．3aB ．4a C ．5aD ．6a 8．的最小值求且已知y x x a Rb a y x +=+∈+1,y b,,,,（ ）A ．b a +B ．ba 11+ C ．b a +D ． 2)(b a +9．如图，第n 个图形是由正n+2边形“扩展”而来，(n=1、2、3、…)则在第n 个图形中共有（ ）个顶点. （ ）A ．(n+1)(n+2)B ． (n+2)(n+3)C ．2nD ．n 10．在回归分析中，代表了数据点和它在回归直线上相应位置的差异的是 （ ） A ．总偏差平方和 B ．残差平方和 C ．回归平方和 D ．相关指数R211．设()f n 为正整数n （十进制）的各数位上的数字的平方之和，比如()22212312314f =++=.记1()()f n f n =，1()(())k k f n f f n +=，1,2,3...k =， 则2006(2006)f =（ ）A ．20B ．4C ．42D ．14512．某大学的信息中心A 与大学各部门、各院系B ，C ，D ，E ，F ，G ，H ，I 之间拟建立信息联网工程，实际测算的费用如图所示（单位：万元）.请观察图形，可以不 建部分网线，而使得中心与各部门、院系彼此都能连通 （直接或中转），则最少的建网费用（万元）是（ ） A ．12 B ．13C ．14D ．16二、填空题：请把答案填在题中横线上（每小题4分，共1613．R 、R ∈R ，ii y i x315211-=---，则RR=___ ___. 14．不等式42x 1x >++-的解集是______________.15．黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案：则第n 个图案中有白色地面砖_________________块. 16．深圳市的一种特色水果上市时间仅能持续5个月，预测上市初期和后期会因供不应求使价格呈连续上涨态势，而中期又将出现供大于求使价格连续下跌，现有三种价格模拟函数.① xf(x)=p q ⋅；②2f(x)=px +qx+1；③ 2f(x)=x(x-q)+p ；（以上三式中p,q 均为常数，且q>1，x=0表示4月1日，x=1表示5月1日，依次类推）. （1）为准确研究其价格走势，应选_______种价格模拟函数.（2）若f(0)=4，f (2)=6，预测该果品在_________月份内价格下跌. 三、解答题：解答应写出文字说明、证明过程或演算步骤（共76分）. 17．（12分）已知集合A 中的元素由部分实数组成，试求满足以下条件的所有集合A ：①集合A 中的任两元素之和还是集合A 中的元素；②集合A 中的任两元素之积还是集合A 中的元素；③集合A 中的任一元素的n 次幂还是集合A 中的元素.（直接写出答案即可，无需写推理过程）18．（12分）(1)设321,,a a a 均为正数，且m a a a =++321，求证ma a a 9111321≥++；（2）已知a,b 都是正数，R,R ∈R ，且a+b=1，求证：aR 2+bR 2≥(a R+bR)2. 19．（12分）某渔业公司年初用98万元购买一艘捕鱼船，第一年各种费用12万元，以后每年都增加4万元，每年捕鱼收益50万元.（1）问第几年开始获利；（2）若干年后，有两种处理方案：①年平均获利最大时，以26万元出售该渔船；②总纯收入获利最大时，以8万元出售该渔船.问哪种方案最合算.20．（12分）12n 12n 2221212 ,x ,x R ,x x 1,x 1:.1x 111n n x x x x x x n +∈+++=+++≥++++设且求证21．（12分）以下资料是一位销售经理收集来的每年销售额和销售经验年数的关系：（1）依据这些数据画出散点图并作直线^y＝78＋4.2R ，计算∑=101i （R i －^yi ）2；（2）依据这些数据由最小二乘法求线性回归方程，并据此计算∑=-1012^)(i i iy y；（3）比较（1）和（2）中的残差平方和∑=-1012^)(i i iy y的大小.22．（14分）已知函数)(x f 是在),0(+∞上每一点均可导的函数，若)()(/x f x xf >在0>x 时恒成立.（1）求证：函数xx f x g )()(=在),0(+∞上是增函数； （2）求证：当0,021>>x x 时，有)()(2121x x f x x f +>+；（3）请将（2）问推广到一般情况，并用数学归纳法证明你的结论.高二数学（文）暑假作业(2)编制:杜善鲁 审定:郝学云 20RR/7/8一、选择题：本大题共12个小题. 每小题5分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的.1．设全集)}1ln(|{},0)3(|{,--==>--==x y x B x x x A U R ，则图中阴影部分表示的集合为 A ．}0|{>x xB ．}03|{<<-x xC ．}13|{-<<-x xD ．}1|{-<x x2．设函数⎪⎩⎪⎨⎧>-+≤-=,1,2,1,1)(22x x x x x x f 则))2(1(f f 的值为 A ．1615 B ．1627- C ．98 D ．183．设)1,0(∈a ，则函数)1(log -=x y a 的定义域为A ．]2,1(B ．),1(+∞C ．),2[+∞D ．]2,(-∞4．下列函数中，在其定义域内既是奇函数又是增函数的是 A ．)0(log 2>-=x x y B ．)(3R ∈+=x x x y C ．)(3R ∈=x y xD ．)0,(1≠∈-=x x xy R5．函数x xx f -=1)(的图象关于 A ．y 轴对称 B ．直线x y -=对称 C ．坐标原点对称D ．直线x y =对称6．设}3,21,1,1{-∈α，则使函数αx y =的定义域为R 且为奇函数的所有α值为 A ．3,1B ．1,1-C ．3,1-D ．3,1,1-7．复数i 211i 21-++-的虚部是 A ．i 51 B ．51C ．i 51-D ．51-8．给出下列三个类比结论.①n n n b a ab =)(与n b a )(+类比，则有n n n b a b a +=+)(；②y x xy a a a log log )(log +=与)sin(βα+类比，则有βαβαsin sin )sin(=+；③2222)(b ab a b a ++=+与2)(b a +类比，则有.2)(222b b a a b a+∙+=+ 其中结论正确的个数是A ．0B ．1C ．2D ．39．甲、乙、丙、丁四位同学各自对A 、B 两变量的线性相关性作试验，并用回归分析方法分别求得相关系数r 与残差平方和m 如下表：甲乙丙丁r 0.82 0.78 0.69 0.85 m 106 115 124 103则哪位同学的试验结果体现A 、B 两变量更强的线性相关性？ A ．甲 B ．乙 C ．丙 D ．丁10．设曲线2ax y =在点),1(a 处的切线与直线062=--y x 平行，则=aA ．1B ．21C ．21- D ．1-11．当0>x 时，xx x f 4)(+=的单调减区间是A ．),2(+∞B ．)2,0(C ．),2(+∞D ．)2,0( 12．函数23)(23+-=x x x f 在区间]1,1[-上的最大值是A ．－2B ．0C ．2D ．4 二、填空题（每题4分，共16分）13．已知函数269)(,2)(22+-=++=x x bx f a x x x f ，其中b a x ,,R ∈为常数，则=+)(b ax f14．已知向量),sin ,(cos θθ=a 向量)1,3(-=b , 则b a -2的最大值是 ． 15．若函数x a x x f sin )(+=在R 上递增，则实数a 的取值范围为 .16．已知：xxx f -=1)(，设*)1)](([)(),()(111N ∈>==--n n x f f x f x f x f n n n 且，则)(3x f 的表达式为 .三、解答题（本大题共6个小题，其中17—21题每题12分，22题14分，满分74分。