大学物理学11.3 分子平均平动动能统计分布规律(1)-理想气体的性质
- 格式:pdf
- 大小:223.21 KB
- 文档页数:4

理想气体的性质与过程解析理想气体是指在一定温度和压力范围内,分子之间的相互作用可以忽略不计的气体。
它是理想化的模型,用来描述真实气体的一些性质和行为。
以下是关于理想气体的性质和过程的解析:性质:1.粒子间无相互作用:在理想气体中,气体分子之间的相互作用力可以忽略不计。
这意味着理想气体的压力、温度和体积只取决于其分子数,与分子之间的相互作用无关。
2.分子间的容积可以忽略不计:理想气体中,分子的体积与整个气体的体积相比可以忽略不计。
这是因为气体分子的体积相对较小,与气体分子数目相比较小时,分子之间的碰撞几乎没有。
3.分子运动速度分布均匀:理想气体中,气体分子的平均动能与温度成正比。
根据麦克斯韦速度分布律,气体分子的速度呈现高斯分布,也就是说在给定温度下,速度越快的分子数量越少。
4.气体的体积与压力成反比:根据波义耳定律,理想气体的体积和压力成反比。
当温度和分子数目保持不变时,压力增大,则气体的体积减小;压力减小,则气体的体积增大。
过程:1.等温过程:在等温过程中,理想气体的温度保持不变。
根据理想气体状态方程PV=nRT(其中P代表压力,V代表体积,n代表物质的摩尔数,R代表气体常数,T代表温度),等温过程中的压强和体积成反比。
即PV=常数。
2.等容过程:在等容过程中,理想气体的体积保持不变。
根据理想气体状态方程PV=nRT,等容过程中的压强和温度成正比。
即P/T=常数。
3.等压过程:在等压过程中,理想气体的压力保持不变。
根据理想气体状态方程PV=nRT,等压过程中的体积和温度成正比。
即V/T=常数。
4.绝热过程:在绝热过程中,理想气体不与外界交换热量。
根据绝热过程的定义,PV^γ=常数(其中γ为比热容比,γ=Cp/Cv,Cp为定压比热容,Cv为定容比热容),即压强和体积的乘积的γ次方等于常数。
总结:理想气体的性质和过程可以通过理想气体状态方程以及各种过程方程来描述。
理想气体的性质包括分子间无相互作用、分子间的容积可以忽略不计、分子速度分布均匀以及气体体积与压力成反比。



气体平均平动动能公式和分子平均平动动能气体是由大量分子组成的物质,这些分子不断地做无规律的热运动。
在热学中,我们常常关注气体内部的平均平动动能,这对于研究气体性质和行为具有重要意义。
本文将从气体平均平动动能公式和分子平均平动动能两个方面展开讨论。
一、气体平均平动动能公式1.1 动能的定义在物理学中,动能是描述物体运动状态的物理量,它与物体的质量和速度有关。
对于气体内部的分子而言,它们具有的平均平动动能可以通过以下公式来表示:\[KE_{avg} = \frac{3}{2} kT\]其中,\(KE_{avg}\)表示气体分子的平均平动动能,\(k\)是玻尔兹曼常数,\(T\)是气体的绝对温度。
1.2 推导过程这个公式的推导过程可以通过统计力学的方法进行。
由分子动能定理可知,一个分子的平均平动动能大小与温度成正比。
而对于气体而言,由于分子具有三个独立的平动方向,因此气体分子的平均平动动能为3kT。
气体内部所有分子的平均平动动能可以表示为3kT的总和,即\(KE_{avg} = \frac{3}{2} kT\)。
1.3 公式意义这个公式的意义在于,它揭示了气体分子的平均平动动能与温度之间的关系。
从宏观角度来看,气体的温度越高,分子的平均平动动能就越大,这也说明了温度对气体热运动的影响。
二、分子平均平动动能2.1 分子速度的分布气体分子的速度分布是描述气体分子热运动状态的重要物理量。
根据麦克斯韦-玻尔兹曼分布律,气体分子在热平衡状态下的速度分布可以用以下公式来表示:\[f(v) = \sqrt{\frac{m}{2\pi kT}} e^{-\frac{mv^2}{2kT}}\]其中,\(f(v)\)表示速度为\(v\)的分子的概率密度函数,\(m\)为分子的质量,\(k\)为玻尔兹曼常数,\(T\)为气体的绝对温度。
2.2 分子平均平动动能气体分子的平均平动动能可以通过速度分布函数来进行求解。
根据统计力学的理论,气体分子的平均平动动能可以表示为:\[KE_{avg} = \int_0^\infty \frac{1}{2}mv^2 f(v) dv\]将速度分布函数带入上式,可以得到气体分子的平均平动动能。

分子动理论气体分子的运动和理想气体的性质分子动理论: 气体分子的运动和理想气体的性质气体是物质存在的三种基本状态之一,其分子动理论是解释气体性质和行为的重要理论基础。
本文将探讨分子动理论对气体分子的运动和理想气体的性质的解释。
一、分子动理论的基本假设分子动理论基于以下几个基本假设:1. 气体由大量微观粒子组成,这些粒子被称为分子。
2. 分子之间相互独立,它们之间的相互作用力可以忽略不计。
3. 分子具有质量,具有热运动,它们的运动是无规则的,遵循统计规律。
4. 分子之间碰撞时,它们之间的碰撞是弹性碰撞,能量和动量得以守恒。
5. 气体体积与分子体积相比可以忽略。
基于这些假设,分子动理论提供了解释气体性质的理论框架。
二、气体分子的运动根据分子动理论,气体分子的运动是无规则的,并且具有以下几个特点:1. 分子的热运动速度分布是高斯分布,也称作麦克斯韦分布。
即大多数分子的速度接近平均速度,而极端高速和低速分子的数量相对较少。
2. 分子之间碰撞时,它们的碰撞是弹性碰撞。
在碰撞过程中,动能和动量得到守恒,但碰撞后的运动方向和速度可能发生改变。
3. 分子间的相互作用力可以忽略不计。
这是因为气体的分子间距相对较大,在气体的条件下,分子间的吸引或斥力相对较弱。
4. 分子的运动决定了气体的压力。
分子撞击容器壁产生的压力对应于分子的平均动能,而与分子的质量和速度分布有关。
三、理想气体的性质在分子动理论的基础上,我们可以推导出理想气体的性质。
理想气体是指完全符合分子动理论假设的气体,在实际中不存在。
1. 状态方程:理想气体的状态方程可以用理想气体定律描述,即PV = nRT。
其中,P表示气体的压力,V表示气体的体积,n表示气体的物质量,R表示理想气体常数,T表示气体的温度。
2. 温度和压力的关系:根据理想气体定律,温度和压力成正比。
当气体的温度升高时,其压力也会增加。
3. 等温过程和绝热过程:理想气体的等温过程和绝热过程可以用分子动理论解释。


理想气体分子的平均平动动能理想气体分子的平均平动动能是指气体分子在统计力学中的动能。
它是气体分子的内能的一种,用于描述气体分子的运动状态。
它在描述和研究物理系统中起着重要的作用,因此,了解理想气体分子的平均平动动能的知识对工程师、技术人员和学术研究人员都是非常重要的。
一、理想气体分子的平均平动动能的定义理想气体分子的平均平动动能是指单个气体分子在统计力学中的动能。
它是指任何气体分子在一定温度条件下所具有的平均动能,它可以用来描述气体分子的运动状态。
在一般情况下,理想气体分子的平均平动动能可以用下式表示:E_avg=\frac{3RT}{2N_A}其中,E_avg表示理想气体分子的平均平动动能,R表示气体常数,T表示绝对温度,N_A表示气体的分子数。
二、理想气体分子的平均平动动能的计算由于理想气体分子的平均平动动能是描述气体分子的运动状态的一个量,因此,计算理想气体分子的平均平动动能是非常重要的。
1、根据上面的公式,我们可以计算出理想气体分子的平均平动动能:E_avg=\frac{3RT}{2N_A}其中,R=8.314J/mol·K,T为实验温度,N_A表示气体的分子数,由于温度和分子数都是实验可以测量出来的,因此,只需要计算出R的值,就可以计算出理想气体分子的平均平动动能。
2、根据统计力学的定义,理想气体分子的平均平动动能还可以用下式表示:E_avg=\frac{3k_BT}{2}其中,k_B为玻尔兹曼常数,T为绝对温度。
由于玻尔兹曼常数是一个实验常数,因此,只需要计算出绝对温度,就可以计算出理想气体分子的平均平动动能。
三、理想气体分子的平均平动动能的应用1、物理系统的研究理想气体分子的平均平动动能是描述气体分子的运动状态的一个量,它可以用来描述物理系统的运动状态,因此,它在研究物理系统中有着重要的作用。
2、工程应用理想气体分子的平均平动动能也可以用于工程应用。
例如,在燃烧反应的过程中,理想气体分子的平均平动动能可以帮助我们计算出燃烧反应产生的热量,从而帮助我们设计出更好的工程设备。
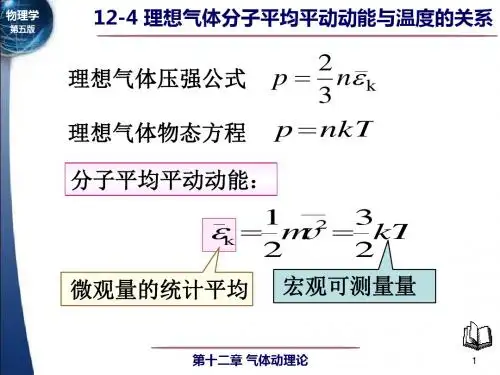

理想气体能量均分定理
理想气体能量均分定理(Equipartition theorem)是统计力学中
的一个重要定理,用于描述分子在热平衡状态下的能量分布。
该定理指出,在平衡态下,每个自由度上的平均能量是相等的。
根据理想气体能量均分定理,一个理想气体的分子具有3个独立的平动自由度和3个独立的转动自由度。
对于每个平动自由度,能量的平均值为kT/2,其中k是玻尔兹曼常数,T是气体的绝对温度。
对于每个转动自由度,能量的平均值也是kT/2。
因此,一个理想气体的总能量等于6kT/2,或者3kT。
这个定理的重要性在于它描述了在热平衡状态下分子能量的分布。
由于气体分子自由度的不同,分子之间的相对运动可以有多种方式,因此它们可以以各种不同的方式存储和传递能量。
理想气体能量均分定理表明,平衡态下每个自由度上的能量平均分布,这又进一步导致了其他热力学性质的计算与预测。
需要注意的是,理想气体能量均分定理是基于统计力学的概率理论基础推导而来的,适用于满足经典力学和统计力学假设的简单系统。
在某些特殊情况下(如低温、高压、低密度等),分子之间的相互作用可能会导致能量的分布不再满足该定律。

理想气体分子的平均平动动能理想气体是一种假想的气态物质,它有以下几个特点:分子大小可以忽略不计,分子表面无相互作用力,分子间无相互作用力,分子速度分布服从Maxwell分布律等。
理想气体分子的平均平动动能是理解理想气体性质的一个重要概念。
在热学中,分子的平动运动是分子达到一个完全混沌状态的必要条件,它是气体压力和气体温度的直接来源。
因此,我们可以通过计算理想气体分子的平均平动动能来推导理想气体压强和温度的关系。
首先,我们需要考虑分子的平均能量。
如果一个分子运动的速度较快,那么其动能也就较大,其运动状态也会更加混沌,在一个相同大小的立方体内碰撞的次数也会更多,因此其平均能量也会更高。
根据理想气体的假设,分子之间的相互作用力可以被忽略,这使得我们可以使用统计物理学的方法来推导理想气体分子的平均平动动能。
具体地说,根据Maxwell分布律,我们可以得到理想气体分子的速度分布函数f(v)。
根据这个分布函数,我们可以计算出速度在v到v+dv范围内的分子数,然后将每个分子的平动动能计算出来,并将这些动能加起来,就能得到所有分子的平均平动动能。
根据统计物理学的理论,理想气体分子速度分布函数f(v)可以写成以下形式:$f(v)=\frac{4\pi(\frac{m}{2\pikT})^\frac{3}{2}v^2e^{-\frac{mv^2}{2kT}}}{N}$其中,m是分子的质量,T是气体的温度,k是玻尔兹曼常数,N是气体中分子的总数。
这个式子实际上描述的是速度为v的分子数目与速度范围的比例。
根据这个分布函数,我们可以计算出速度在v到v+dv范围内的分子数:然后,我们把每个速度范围内的动能计算出来:最后,我们把每个速度范围内的动能加起来,就能得到所有分子的平均平动动能:$<E_{kin}>=\frac{3kT}{2}$这个推导说明了理想气体分子平均平动动能与温度有关,对于理想气体中分子的平均速度,我们可以使用平均平动动能公式,加上分子质量的平方根,然后取平方根:这个公式表明,对于相同温度下的不同分子,质量越大,速度越小,而质量越小,速度越大。

气体分子的平均平动动能气体分子的平均平动动能(Kinetic Energy)是指气体分子在平移运动过程中所具有的能量。
平动动能的大小与气体分子的质量和速度有关,可以用以下公式来表示:E = 1/2 mv²其中,E为气体分子的平均平动动能,m为分子的质量,v为分子的速度。
气体分子的平动动能与温度、气体分子的质量和速度的平方成正比。
这是因为温度的提高会增加气体分子的平均动能,而根据动能定理,平动动能正比于速度的平方。
在宏观上,气体的温度是一种表示气体分子平均平动动能的量度。
温度的单位是开尔文(K)。
绝对零度(0 K)是温度的最低限度,气体分子的平动动能为零。
根据理想气体定律,气体的压力与气体分子的平动动能有关。
理想气体定律可以表示为:PV = nRT其中,P为气体的压力,V为气体的体积,n为气体分子的摩尔数,R为气体常数,T为气体的温度。
可以看出,气体分子的平动动能与气体的温度成正比。
在气体分子的平动动能上,布尔兹曼分布定律起到了重要的作用。
布尔兹曼分布定律描述了分子在不同速度上的分布情况。
根据布尔兹曼分布定律,速度较大的分子数量相对较少,速度较小的分子数量相对较多。
另外,平动动能还与气体分子间的碰撞有关。
当气体分子相互碰撞时,它们会交换动量和能量。
碰撞的频率和能量转移的大小与气体分子的速度有关。
平动动能决定了分子碰撞的速度大小和能量转移的大小。
总的来说,气体分子的平均平动动能与温度、气体分子的质量和速度有关。
平动动能决定了气体的温度、压力和分子碰撞的速度和能量转移的大小。
了解气体分子的平动动能对于理解气体性质和研究气体行为具有重要意义。
分子的平均平动动能公式首先,我们需要了解一些基本概念和假设:1. 分子速度分布函数:它描述了理想气体中分子速度的分布情况。
一般来说,分子速度分布服从麦克斯韦-玻尔兹曼分布,表示为f(v) =4πv^2 * (m/(2πkT))^1.5 * e^(-mv^2/(2kT)),其中v是分子速度,m 是分子质量,k是玻尔兹曼常数,T是气体温度。
2. Maxwell-Boltzmann分布定律:根据这个定律,理想气体中分子的速度分布可以用麦克斯韦-玻尔兹曼分布函数来描述。
3. 分子平动动能的定义:根据动能定理,分子的平动动能E_kin等于分子的质量m乘以速度v的平方再除以2,即E_kin = 1/2 * m * v^2我们现在开始推导分子的平均平动动能公式:1.首先我们假设分子速度在其中一方向上的分布为麦克斯韦-玻尔兹曼分布。
2.为了计算平均平动动能,我们需要对分子速度的分布进行积分。
由于麦克斯韦-玻尔兹曼分布在速度的全部区间上都有定义,所以我们将积分区间确定为从0到无穷大。
3. 我们用E_kin表示分子平动动能的平均值,根据定义,有E_kin = ∫(1/2 * m * v^2 * f(v))dv。
根据麦克斯韦-玻尔兹曼分布函数的表达式,代入并进行积分运算,可以得到E_kin = (3/2) * kT。
4. 由于我们的假设是分子速度在其中一方向上的分布,而分子的运动是三维的,所以我们需要将结果乘以3,即E_total = (3/2) * 3 * kT = 3kT。
所以,分子的平均平动动能公式为E_total = 3kT,其中E_total是分子的总平动动能,k是玻尔兹曼常数,T是气体温度。
这个公式说明了分子平动动能与温度之间的线性关系,说明了当温度升高时,分子的平动动能也会增加。
此外,公式还表明了当温度接近绝对零度时,分子的平动动能接近零,符合经典平衡态的预期。
气体分子的平均平动动能气体分子的平均平动动能可以根据理想气体状态方程和分子动理论进行推导。
首先,我们先来回顾一下理想气体状态方程:PV = nRT其中,P表示气体的压强,V表示气体的体积,n表示气体的物质的量,R为气体常数,T表示气体的温度。
在分子动理论中,气体被认为是由大量微观分子组成的,分子具有质量m和速度v。
根据分子动理论,我们可以得到气体分子的平均平动动能的表达式。
首先,根据动能定理,一个物体的动能可以表示为其质量和速度的平方的乘积的一半。
因此,气体分子的平均平动动能可以表示为:KE_avg = (1/2) m v^2同时,根据分子动理论,气体分子的速度和温度之间存在着直接的关系。
具体来说,根据麦克斯韦尔-玻尔兹曼速率分布定律,分子速度的分布满足麦克斯韦尔-玻尔兹曼速率分布函数:f(v) = 4π (m/2πkT)^(3/2) v^2 exp(-mv^2/2kT)其中,f(v)表示速度为v的分子的比例,m为分子质量,k为玻尔兹曼常数,T为温度。
由于分子速度的平方与动能直接相关,所以我们可以将速率分布函数转化为动能分布函数,得到动能分布函数的表达式。
首先,我们假设动能为E的分子与速度为vE的分子的比例为f(E),则有:f(E) = (4π (m/2πkT)^(3/2) / vE^2) exp(-E/kT)接下来,我们对动能分布函数进行积分,得到分子平均动能的表达式。
KE_avg = ∫ E f(E) dE= ∫ (4π (m/2πkT)^(3/2) / vE^2) E exp(-E/kT) dE= (4π (m/2πkT)^(3/2)) ∫ E^2 exp(-E/kT) dE / ∫ E exp(-E/kT) dE由于上述积分不太好求解,我们可以利用近似方法来简化计算。
一种常用的近似方法是利用玻尔兹曼分布函数的性质,在该分布下,分子动能的平均值与温度成正比,即:KE_avg = (3/2) kT结合理想气体状态方程 PV = nRT,我们可以将分子平均动能表达式进一步转化为:KE_avg = (3/2) (PV/n)通过以上推导,我们得到了气体分子的平均平动动能的表达式。
气体分子的平均平动动能气体是一种非常特殊的物质状态,气体分子在空间中自由运动并且具备能量,这种能量被称为平动能。
平动能是气体分子内部能量的一种表现形式,它是热力学研究的重要基础概念。
在研究气体的热力学过程时需要用到平动能的相关概念和计算公式。
本文将介绍气体分子的平均平动动能的相关参考内容。
1. 气体分子的平均平动动能公式气体分子的平均平动动能可以通过以下公式进行计算:E_k = (3/2) kT其中,E_k 表示气体分子的平均平动动能,k 是玻尔兹曼常数,T 是气体的温度。
平均平动动能的大小是与温度直接相关的,其大小随温度升高而增加。
这个公式表明,对于一定的温度,不同种类的气体分子之间的平均平动动能是相同的。
2. 玻尔兹曼常数的概念玻尔兹曼常数是热力学基本常数之一,通常用符号 k 表示,其数值约为 1.38×10^-23 J/K。
玻尔兹曼常数是一个关键性质,它连接了气体分子的热运动和温度之间的关系。
3. 温度的概念温度是热力学的基本物理量之一,通常用符号 T 表示,其单位是开尔文(K)。
温度是表示物质内部分子热运动强度的物理量,温度越高表示分子的热运动越剧烈。
温度是所有热力学过程中的基本参量之一,它可以用来描述物质的状态和性质。
4. 平均平动动能的性质平均平动动能是气体分子内部的一种动能表现形式,它具备以下性质:(1) 平均平动动能与气体分子的质量成反比例关系。
质量越大的气体分子,其平均平动动能越小,反之亦然。
(2) 平均平动动能与气体分子的速度成平方关系。
速度越高的气体分子,其平均平动动能越大,反之亦然。
(3) 平均平动动能与温度成正比例关系。
温度越高,气体分子的平均平动动能越大,反之亦然。
5. 总结气体分子的平均平动动能是气体内部能量分布的一种表现形式,它可以通过温度和气体分子质量等参数来计算和描述。
平均平动动能的大小和分布可以影响气体的运动和力学性质,因此对热力学过程有着重要的应用价值。