因子分析和主成分分析的方法步骤

报告中的主成分分析与因子提取主题：报告中的主成分分析与因子提取一、主成分分析的背景与概念1.1 主成分分析的起源与发展1.2 主成分分析的基本概念1.3 主成分分析的应用领域二、主成分分析的基本步骤与计算方法2.1 数据预处理2.2 特征值与特征向量的计算2.3 主成分的提取与解释三、主成分分析的评价标准与结果解释3.1 Kaiser准则3.2 解释方差与贡献率3.3 因子载荷与因子解释四、主成分分析在数据降维中的应用4.1 数据降维的概念与方法4.2 主成分分析在特征选择中的应用4.3 主成分分析在图像处理中的应用五、因子提取的背景与基本概念5.1 因子提取与主成分分析的关系与区别5.2 因子提取的基本原理5.3 因子载荷矩阵与因子解释六、因子提取的常用方法与应用6.1 最大方差法6.2 主因子法6.3 最大似然法6.4 因子提取在心理学研究中的应用【正文】一、主成分分析的背景与概念1.1 主成分分析的起源与发展主成分分析(Principal Component Analysis, PCA)是一种多变量分析技术，最早由英国统计学家卡尔·皮尔逊(Karl Pearson)于1901年提出。

在过去的百年里，主成分分析得到了广泛的应用和研究，成为了数据分析领域中不可或缺的工具之一。

1.2 主成分分析的基本概念主成分分析是一种通过线性组合的方式，将原始数据变换到一个新的坐标系中，使得新的坐标中的变量之间无相关性，并且按照方差递减的方式排列。

主成分分析的目标是找到最能代表原始数据信息的主成分，从而实现数据降维和特征提取的目的。

1.3 主成分分析的应用领域主成分分析在各个领域都有广泛的应用，包括金融学、生物学、工程学、心理学等。

在金融学中，主成分分析被用于风险管理和投资组合优化；在生物学中，主成分分析用于基因表达数据的分析；在工程学中，主成分分析用于信号处理和图像处理等。

二、主成分分析的基本步骤与计算方法2.1 数据预处理在进行主成分分析之前，通常需要对原始数据进行标准化或归一化处理，以消除不同变量尺度之间的影响。

主成分分析、因子分析步骤最大收敛性迭代次数：默认25.（3）因子旋转（Rotation）对话框设置因子旋转的方法，常选择“最大方差法”。

“输出”框中的“旋转解”。

（4）因子得分（Scores）对话框设置“保存为变量”，则可将新建立的因子得分储存至数据文件中，并产生新的变量名称。

（5）选项（Options）对话框设置2结果分析（1）KMO及Bartlett’s检验（很、Communalities（称共同度）表示公因子对各个变量能说明的程度，每个变量的初始公因子方差都为1，共同度越大，公因子对该变量说明的程度越大，也就是该变量对公因子的依赖程度越大。

共同度低说明在因子中的重要度低。

一般的基准是<0.4就可以认为是比较低，这时变量在分析中去掉比较好。

（3）解释的总方差至此已经将5个问项降维到两个因子，在数据文件中可以看到增加了2个变量，fac1_1、fac2_1，即为因子得分。

（4）成分矩阵与旋转成分矩阵成分矩阵是未旋转前的因子矩阵，从该表中并无法清楚地看出每个变量到底应归属于哪个因子。

旋转后的因子矩阵，从该表中可清楚地看出每个变量到底应归属于哪个因子。

此表显示旋转后原始的所有变量与新生的2个公因子之间的相关程度。

一般的，因子负荷量的绝对值0.4以上，认为是显着的变量，超过0.5时可以说是非常重要的变量。

如味道与饭量关于因子1的。

=-0.010*X1+0.425*X2-0.038*X3+0.408*X4-0.316*X5因子2的分数=0.447*X1-0.036*X2+0.424*X3+0.059*X4-0.371*X5（6）因子转换矩阵元件转换矩阵元件 1 21 .723 -.6912 .691 .723撷取方法：主体元件分析。

转轴方法：具有Kaiser正规化的最大变异法。

因子转换矩阵是主成分形式的系数。

（7）因子得分协方差矩阵，【得分】：“保存为变量”【方法】：“回归”；再选中“显示因子得分系数矩阵”。

主成分分析 因子分析主成分分析和因子分析是很重要的统计分析方法。

两者都是用于对一组同质或异质的变量进行数据探索研究的技术，它们都可以提供有价值的结论，增强数据有意义的理解。

1. 主成分分析主成分分析（Principal Component Analysis，简称PCA）是从一大组变量中提取具有代表性的正交变量，组成一个新的变量集合。

PCA通过减少变量数量，减少多变量间相关性带来的重复性，从而提升数据分析的准确性和有效性。

注意减少变量数量不是减少观测样本数量，而是把原先高维度的变量合并成一组较低维度的变量。

PCA算法的基本思想是：它分析原始数据集中的变异，并从中提取主要的变量，然后将这些变量的组合（叫做主成分）用推断法来重新构建原来的数据集，最后能够说明原始变量的结构，对被研究的变量结构有系统的解释。

2. 因子分析因子分析（Factor Analysis，简称FA）是一种用来探索相关变量之间潜在关系的统计分析方法。

这一方法注重的是把一系列的变量映射到一个尽可能少的多个隐变量的过程。

其中，这些隐变量就是“因子”，它们是原来变量的代表性变量，且变量之间有因果或相关的结构关系。

FA的基本思想是，将一组变量之间的复杂的相关关系映射到一组基本关系，即因子上。

然后，当每个变量映射到一个或几个因子上后，只需要解释因子就能够完全解释自变量变化的原因。

常用的因子模型有因子旋转、因子分层、因子波动等。

相比较，主成分分析和因子分析都有各自的专业领域，它们都有不同的数据需求和分析方法，在不同的数据处理中也表现出各自的优势和劣势。

主成分分析处理比较复杂的数据，可以根据原始变量的关系构建视图，但不涉及因果关系的推断；而因子分析可以推导出被研究的变量之间的关系，进而探索或验证其原因。

数据分析中的因子分析和主成分分析在数据分析领域，因子分析和主成分分析是两种常用的多变量分析方法。

它们可以用来处理大量的数据，找出数据的内在规律，并将数据简化为更少的变量。

本文将介绍因子分析和主成分分析的定义、应用以及它们在数据分析中的区别和联系。

一、因子分析因子分析是一种用于研究多个变量之间的潜在因素结构及其影响的统计方法。

它通过将多个观测变量转化为少数几个无关的因子，来解释变量之间的相关性。

因子分析的基本思想是将多个相关观测变量归因于少数几个潜在因子，这些潜在因子不能被观测到，但可以通过观测变量的变化来间接地推断出来。

因子分析通常包括两个主要步骤：提取因子和旋转因子。

提取因子是指确定能够解释原始变量方差的主要共性因子，常用的方法有主成分分析法和最大似然估计法。

旋转因子是为了减少因子之间的相关性，使得因子更易于解释。

常用的旋转方法有正交旋转和斜交旋转。

因子分析的应用非常广泛，可以用于市场研究、社会科学调查、心理学、金融等领域。

例如，在市场研究中，因子分析可以用来确定消费者购买行为背后的潜在因素，从而更好地理解市场需求。

二、主成分分析主成分分析是一种通过线性变换将原始变量转化为一组线性无关的主成分的统计方法。

主成分是原始变量的线性组合，具有较大的方差，能够尽可能多地解释原始数据。

主成分分析的主要思想是将原始变量投影到一个新的坐标系中，使得新坐标系上的第一主成分具有最大方差，第二主成分具有次最大方差，以此类推。

通过选择解释原始数据方差较多的前几个主成分，我们可以实现数据的降维和主要信息提取。

主成分分析在数据降维、特征提取和数据可视化等领域有广泛的应用。

例如，在图像处理中，主成分分析可以用来压缩图像数据、提取重要特征，并且可以在保留图像主要信息的同时减少存储空间的需求。

三、因子分析和主成分分析的区别和联系因子分析和主成分分析在某些方面有相似之处，但也存在明显的区别。

首先，因子分析是用于研究多个观测变量之间的潜在因素结构，而主成分分析是通过线性变换将原始变量转化为一组线性无关的主成分。

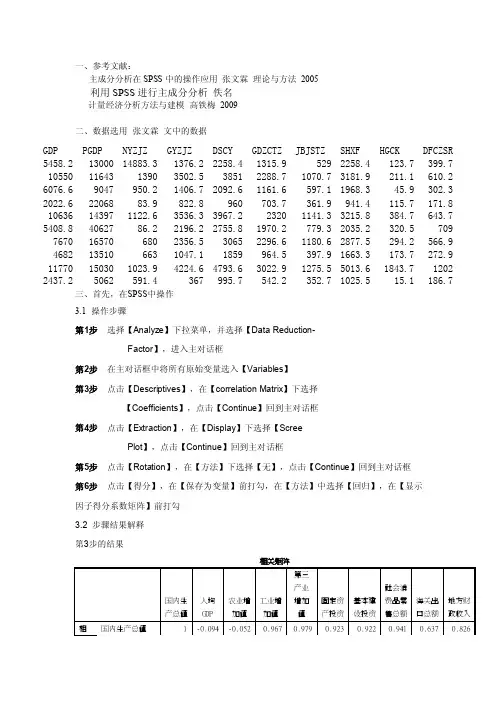
一、参考文献：主成分分析在SPSS中的操作应用张文霖理论与方法2005利用SPSS进行主成分分析佚名计量经济分析方法与建模高铁梅2009二、数据选用张文霖文中的数据GDP PGDP NYZJZ GYZJZ DSCY GDZCTZ JBJSTZ SHXF HGCK DFCZSR 5458.2 13000 14883.3 1376.2 2258.4 1315.9 529 2258.4 123.7 399.7 10550 11643 1390 3502.5 3851 2288.7 1070.7 3181.9 211.1 610.2 6076.6 9047 950.2 1406.7 2092.6 1161.6 597.1 1968.3 45.9 302.3 2022.6 22068 83.9 822.8 960 703.7 361.9 941.4 115.7 171.8 10636 14397 1122.6 3536.3 3967.2 2320 1141.3 3215.8 384.7 643.7 5408.8 40627 86.2 2196.2 2755.8 1970.2 779.3 2035.2 320.5 709 7670 16570 680 2356.5 3065 2296.6 1180.6 2877.5 294.2 566.9 4682 13510 663 1047.1 1859 964.5 397.9 1663.3 173.7 272.9 11770 15030 1023.9 4224.6 4793.6 3022.9 1275.5 5013.6 1843.7 1202 2437.2 5062 591.4 367 995.7 542.2 352.7 1025.5 15.1 186.7三、首先，在SPSS中操作3.1 操作步骤第1步选择【Analyze】下拉菜单，并选择【Data Reduction-Factor】，进入主对话框第2步在主对话框中将所有原始变量选入【Variables】第3步点击【Descriptives】，在【correlation Matrix】下选择【Coefficients】，点击【Continue】回到主对话框第4步点击【Extraction】，在【Display】下选择【ScreePlot】，点击【Continue】回到主对话框第5步点击【Rotation】，在【方法】下选择【无】，点击【Continue】回到主对话框第6步点击【得分】，在【保存为变量】前打勾，在【方法】中选择【回归】，在【显示因子得分系数矩阵】前打勾3.2 步骤结果解释第3步的结果变量之间的存在较强的相关关系，适合作主成分分析是以自变量X 作为被解释变量，对应的公共因子载荷平方之和。

主成分分析和因子分析法一、主成分分析概论主成分分析的工作对象是样本点×定量变量类型的数据表。

它的工作目标，就是要对这种多变量的平面数据表进行最佳综合简化。

也就是说，要在力保数据信息丢失最少的原则下，对高维变量空间进行降维处理。

很显然，识辨系统在一个低维空间要比一个高维空间容易得多。

英国统计学家斯格特（M.Scott ）在1961年对157个英国城镇发展水平进行调查时，原始测量的变量有57个。

而通过主成分分析发现，只需5个新的综合变量（它们是原变量的线性组合），就可以95%的精度表示原数据的变异情况，这样，对问题的研究一下子从57维降到5维。

可以想象，在5维空间中对系统进行任何分析，都比在57维中更加快捷、有效。

另一项十分著名的工作是美国的统计学家斯通(Stone)在1947年关于国民经济的研究。

他曾利用美国1929～1938年各年的数据，得到了17个反映国民收入与支出的变量要素，例如雇主补贴、消费资料和生产资料、纯公共支出、净增库存、股息、利息和外贸平衡等等。

在进行主成分分析后，竟以97.4%的精度，用三个新变量就取代了原17个变量。

根据经济学知识，斯通给这三个新变量要别命名为总收入1F 、总收入变化率2F 和经济发展或衰退的趋势3F （是时间t 的线性项）。

更有意思的是，这三个变量其实都是可以直接测量的。

二、主成分分析的基本思想与理论1、主成分分析的基本思想在对某一事物进行实证研究中，为了更全面、准确地反映出事物的特征及其发展规律，人们往往要考虑与其有关系的多个指标，这些指标在多元统计中也称为变量。

这样就产生了如下问题：一方面人们为了避免遗漏重要的信息而考虑尽可能多的指标，而另一方面随着考虑指标的增多增加了问题的复杂性，同时也由于各指标均是对同一事物的反映，不可避免地造成信息的大量重叠，这种信息有时甚至会抹杀事物的真正特征与内在规律。

基于上述问题，人们就希望在定量研究中涉及的变量较少，而得到的信息量又较多。

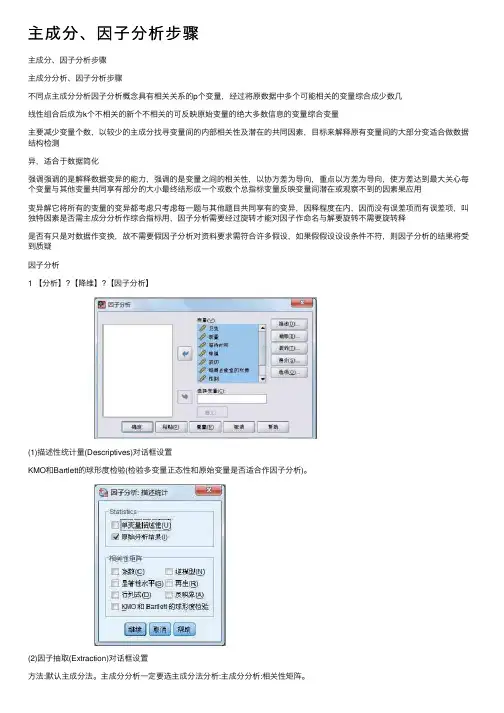
主成分、因⼦分析步骤主成分、因⼦分析步骤主成分分析、因⼦分析步骤不同点主成分分析因⼦分析概念具有相关关系的p个变量，经过将原数据中多个可能相关的变量综合成少数⼏线性组合后成为k个不相关的新个不相关的可反映原始变量的绝⼤多数信息的变量综合变量主要减少变量个数，以较少的主成分找寻变量间的内部相关性及潜在的共同因素，⽬标来解释原有变量间的⼤部分变适合做数据结构检测异，适合于数据简化强调强调的是解释数据变异的能⼒，强调的是变量之间的相关性，以协⽅差为导向，重点以⽅差为导向，使⽅差达到最⼤关⼼每个变量与其他变量共同享有部分的⼤⼩最终结形成⼀个或数个总指标变量反映变量间潜在或观察不到的因素果应⽤变异解它将所有的变量的变异都考虑只考虑每⼀题与其他题⽬共同享有的变异，因释程度在内，因⽽没有误差项⽽有误差项，叫独特因素是否需主成分分析作综合指标⽤，因⼦分析需要经过旋转才能对因⼦作命名与解要旋转不需要旋转释是否有只是对数据作变换，故不需要假因⼦分析对资料要求需符合许多假设，如果假假设设设条件不符，则因⼦分析的结果将受到质疑因⼦分析1 【分析】?【降维】?【因⼦分析】(1)描述性统计量(Descriptives)对话框设置KMO和Bartlett的球形度检验(检验多变量正态性和原始变量是否适合作因⼦分析)。

(2)因⼦抽取(Extraction)对话框设置⽅法:默认主成分法。

主成分分析⼀定要选主成分法分析:主成分分析:相关性矩阵。

输出:为旋转的因⼦图抽取:默认选1.最⼤收敛性迭代次数:默认25.(3)因⼦旋转(Rotation)对话框设置因⼦旋转的⽅法，常选择“最⼤⽅差法”。

“输出”框中的“旋转解”。

(4)因⼦得分(Scores)对话框设置“保存为变量”，则可将新建⽴的因⼦得分储存⾄数据⽂件中，并产⽣新的变量名称。

(5)选项(Options)对话框设置2 结果分析(1)KMO及Bartlett’s检验KMO 和 Bartlett 的检验取样⾜够度的 Kaiser-Meyer-Olkin 度量。