第十章 曲线积分与曲面积分
- 格式:doc
- 大小:1.13 MB
- 文档页数:19

第十章曲线积分与曲面积分【教学目标与要求】1.理解两类曲线积分的概念,了解两类曲线积分的性质及两类曲线积分的关系。
2.掌握计算两类曲线积分的方法.3.熟练掌握格林公式并会运用平面曲线积分与路径无关的条件,会求全微分的原函数.4.了解第一类曲面积分的概念、性质,掌握计算第一类曲面积分的方法。
【教学重点】1。
两类曲线积分的计算方法;2。
格林公式及其应用;3。
第一类曲面积分的计算方法;【教学难点】1。
两类曲线积分的关系及第一类曲面积分的关系;2.对坐标的曲线积分与对坐标的曲面积分的计算;3。
应用格林公式计算对坐标的曲线积分;6.两类曲线积分的计算方法;7.格林公式及其应用格林公式计算对坐标的曲线积分;【参考书】[1]同济大学数学系.《高等数学(下)》,第五版.高等教育出版社。
[2]同济大学数学系.《高等数学学习辅导与习题选解》,第六版.高等教育出版社.[3]同济大学数学系。
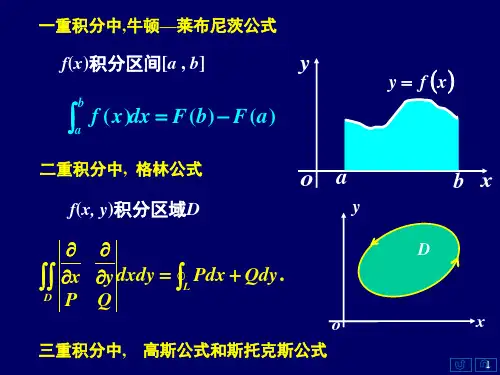
《高等数学习题全解指南(下)》,第六版.高等教育出版社§11.1 对弧长的曲线积分一、对弧长的曲线积分的概念与性质曲线形构件的质量:设一曲线形构件所占的位置在xOy面内的一段曲线弧L上,已知曲线形构件在点(x,y)处的线密度为μ(x,y)。
求曲线形构件的质量.把曲线分成n小段,∆s1,∆s2,⋅⋅⋅,∆s n(∆s i也表示弧长);任取(ξi,ηi)∈∆s i,得第i小段质量的近似值μ(ξi,ηi)∆s i;整个物质曲线的质量近似为;令λ=max{∆s1,∆s2,⋅⋅⋅,∆s n}→0,则整个物质曲线的质量为.这种和的极限在研究其它问题时也会遇到。
定义设函数f(x,y)定义在可求长度的曲线L上,并且有界。
,将L任意分成n个弧段:∆s1,∆s2,⋅⋅⋅,∆s n,并用∆s i表示第i段的弧长;在每一弧段∆s i上任取一点(ξi,ηi),作和;令λ=max{∆s1,∆s2,⋅⋅⋅,∆s n},如果当λ→0时,这和的极限总存在,则称此极限为函数f(x,y)在曲线弧L上对弧长的曲线积分或第一类曲线积分,记作,即.其中f(x,y)叫做被积函数,L叫做积分弧段。

第十章曲线积分与曲面积分§ 1对弧长地曲线积分计算公式:无论是对弧长还是对坐标地曲线积分重要地是写出曲线地参数方程x =x t L :y =y tx = x(t ) L:<y = y(t )"z(t )Lf x,y,z ds - 注意:上限一定要大于下限1.计算下列对弧长地曲线积分<1) \(x 2y 2)2ds ,其中 L 为圆周 x 2y 2=a 2; 解:法一:Q|jx2+y 2)2ds = |J L (a 2)2ds二玄仁 ds =a 4(2二a) =2二a 5法二:_L x =acosv L: 0 心::2二,匸(x 2 y 2)2ds2二 2 2 2 2 2[a cos : a si n ] -asi na cos d :2二 5 . 5ad^ - 2「a<2) \e x yds ,其中L 为圆周x 2■ y 2=a 2,直线y=x 及x 轴在第一象限内所围成地扇形ba 兰t 兰b ,则(f (x, y ps= f a f(x (t ), y(tddbafxt ,y t ,zt解:忆e 拧%s = ( & +廟+ J BO 卅“ ds ,其中故口 e^iyds=e a(2+ — a) -2匕 4<3) L xds ,其中L 为抛物线y =2x 2-1上介于x =0与x=1之间地一段弧;「X =x解:由 L:20<x<1,得、y=2x -1l xds 二 ° x 1亠〔4x 2dx2 3_2(1+16x)2o_17用-1 -32-48<4) L y 2ds ,其中 L 为摆线地一拱 x =a(t - si nt), y =a(1 - cost)(0 — t — 2二); 解: .L y 2ds = :0〔a(1-cost)『」a 1-cost ]2a si nt^dt2TI 5=V2a 3「(1 —cost)2dtx = x x = a cos—— x = x 、2 OA: ,0_x_a ,AB:,0, BO: 0_x a y =0 y =as in 4 y = x 2f e x 旳 ds =『少尺 J 12 +02 dxoA-0aoa二ABey ds 二ABe ds二 e ABds4<或]e x 七ds■AB=[4 e ' 严"巧塔“巧 J (一 a sin 盯 + (acos日 j d 日JI4 e a ad ) 4a 二 BO-a-2-2匸2a 一2 2 -------- ■ 2 e x 2 x 2,12 12dx 0-1 a二5二 迈a 3 : (2sin 2*)2dt =8a 3J6a 3siJI353= 32a 2sin 如-32a」0x 2+y 2+z 2=22 2]x = cosT解:由」 丫,得2X 2+Z2=2,令 < 厂 0兰日兰2兀y = xz = \ 2 sin 71x= cos 日sin 5 -dt <令—-v4 2 256 3a5 3 15<5) “L xyds ,其中L 为圆周x 2 y 2 =a 2 ; 解:利用对称性J |xyds = 4jJxyds ,其中 Lix = a cos 日 0<6y = a sinJI< 一2[xy ds = 4『xy ds = 4 fxyds迟,=4 02 (acos R(asin v) (-asin v)2 (acosv)2dv"a 3jcosrsin=2a 3sin =-2a 3<6)-x 2y 22ds ,其中-为曲线 z 2X =e t cost ,y =e t si nt ,z =e t 上相应于 t 从 0 变到 2 地------ 2 -- 1 ---- 2 ---- cost )]2 +[(£ sin t )]2 +e 2t dte tcost ]亠[d sin t ]亠[d =—fe^dt =^(1 —e‘) 2 02<7)广yds ,其中-为空间圆周:x 2 + y 2 + z 2 =2』=x弧段; 解:故丫: * y = cos日0兰日乞2兀.故z = J2s in。


第十章曲线积分与曲面积分习题简答习题10—11 计算下列对弧长的曲线积分:(1)LIxds ,其中L 是圆221xy中(0,1)A 到11(,)22B 之间的一段劣弧;解:1(1)2.(2)(1)Lx y ds,其中L 是顶点为(0,0),(1,0)O A 及(0,1)B 所成三角形的边界;解:(1)322Lxyds.(3)22Lxy ds,其中L 为圆周22x yx ;解:222Lxy ds.(4)2Lx yzds ,其中L 为折线段ABCD ,这里(0,0,0)A ,(0,0,2),B (1,0,2),C (1,2,3)D ;解:2853Lx yzds .2 求八分之一球面2221(0,0,0)xyzx y z 的边界曲线的重心,设曲线的密度1。
解故所求重心坐标为444,,333.习题10—21 设L 为xOy 面内一直线y b (b 为常数),证明xyz(0,0,0)A (0,0,2)B (1,0,2)C (1,2,3)D xyoABC(,)0LQ x y dy 。
证明:略.2 计算下列对坐标的曲线积分:(1)Lxydx ,其中L 为抛物线2yx 上从点(1,1)A 到点(1,1)B 的一段弧。
解:45Lxydx 。
(2)Ldy y xdx y x 2222)()(,其中L 是曲线x y11从对应于0x 时的点到2x 时的点的一段弧;解34)()(2222Ldyy xdxy x.(3),Lydx xdy L 是从点(,0)A a 沿上半圆周222xya 到点(,0)B a 的一段弧;解0.Lydxxdy(4)22Lxy dyx ydx ,其中L 沿右半圆222xya 以点(0,)A a 为起点,经过点(,0)C a 到终点(0,)B a 的路径;解22Lxy dyx ydx44a 。
(5)3223Lx dx zy dy x ydz ,其中L 为从点(3,2,1)A 到点(0,0,0)B 的直线段AB ;解3223Lx dx zy dy x ydz3187874t dt。


第十章 曲线积分与曲面积分(第六部分)曲面积分习题解答一、对面积的曲面积分1.计算曲面积分⎰⎰∑++dS y x z )342(,其中∑为平面1432=++zy x 在第一卦限中的部分. 分析 因为∑:1432=++z y x ,可恒等变形为∑:y x z 3424--=,又因被积函数y x z 342++与∑形式相同,故可利用曲面方程来简化被积函数,即将4342=++y x z 代入,从而简化计算。
解 平面∑方程的为)321(4yx z --=(如图), ∑在xoy 面上的投影区域xy D :0,0,132≥≥≤+y x yx ;34,2-=∂∂-=∂∂y z x z ,面积元素 dxdy dxdy y z x z dS 361122=⎪⎪⎭⎫⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂+= 从而⎰⎰⎰⎰⋅=++∑xyD dxdy dS y x z 3614)342( 61432213614=⋅⋅⋅=. 2. 计算曲面积分⎰⎰∑+dS y x |)|(,其中∑为1||||||=++z y x .解 由对称性可知,0=⎰⎰∑xd S ,由轮换对称性和代入技巧知,⎰⎰⎰⎰⎰⎰∑∑∑=++=dS dS z y x dS y 31|)||||(|31||,再由曲面积分的几何意义知,34238=⋅=⎰⎰∑dS ,所以,334|)|(=+⎰⎰∑dS y x .y二、对坐标的曲面积分1.计算曲面积分⎰⎰∑dydz x 2.其中∑为球面2222R z y x =++在第一卦限部分的上侧。
分析 由于∑不是封闭曲面,且只是对坐标z y ,的曲面积分,故直接计算即可。
解 因∑:222z y R x --=取前侧,且∑在yoz 面上的投影区域为0 ,0 , :222≥≥≤+z y R z y D yz .于是得 ⎰⎰∑dydz x 2dydz z y R yzD ⎰⎰--=)(222⎰⎰⋅-θ=πRrdr r R d 02220 )(402228141212R r r R Rπ=⎥⎦⎤⎢⎣⎡-π=. 2. 计算曲面积分⎰⎰∑++=ydzdx xdydz zdxdy I .其中∑是柱面122=+y x 被平面0=z 及3=z 所截得的在第一卦限内的部分的前侧。




第十章 曲线积分与曲面积分一.曲线积分的计算 (1)基本计算1.第一类:对弧长线积分的计算(,)Lf x y ds ⎰关键是用曲线L:(),(),x t y t ϕψ=⎧⎨=⎩()t αβ≤≤做变量替换(被积函数,积分变元,积分范围)(,)[(),(,()Lf x y ds f t t βαϕψαβ=<⎰⎰例 L 为圆周221,x y +=则22xy Le ds +=⎰2e π 参数方程,曲线代入解 cos :(02)sin x L y θθπθ=⎧≤≤⎨=⎩ds d θθ==22x y Leds +=⎰202ed e πθπ=⎰例 计算2⎰L x ds ,其中2222:(0)0⎧++=>⎨-=⎩x y z a L a x y . (8分)解 由于 22222222::00⎧⎧++=+=⇒⎨⎨-=-=⎩⎩x y z a x z a L L x y x y 所以L 的参数方程可表示为:(02)sin θθπθ⎧=⎪⎪⎪=≤≤⎨⎪⎪=⎪⎩x L y t z a (3分)θθ==ds ad (2分) 故23222cos 22ππθθ==⎰⎰La a x ds ad(3分) 【例10.22】求⎰,式中L 为圆周22(0)x y ax a +=>解 L 的极坐标方程为:,(),cos 22L ds ad r a θθππθθθθ=⎧-≤≤==⎨=⎩则222cos 2a ad a ππθθ-=⋅=⎰⎰第二类:对坐标的线积分的计算 关键是用曲线L:(),(),x t y t ϕψ=⎧⎨=⎩(:)t αβ→做变量替换(被积函数,积分变元,积分范围)''(,)(,){[(),()]()[(),()]()}LP x y dx Q x y dy P t t t Q t t t dt βαϕψϕϕψψ+=+⎰⎰例 设L 为抛物线2y x =从点()0,0到()2,4一段弧,则()22Lx y dx -=⎰5615-注意微元,及参数方程的形式【例10.17】 求2L ydx xdy x +⎰,其中L 是曲线ln y x =上从点(1,0)到点(,1)e 的一段弧. 解 由ln y x =得1,ydx dy x e x==,故原式=1121002()|y y ydy e dy y e e +=+=⎰⎰⑵ 基本技巧① 利用对称性简化计算;对弧长的线积分,对称性同二重积分 例 计算3222(),Lx y ds L x y R 其中:++=⎰解:33()LLLx y ds xds y ds =+=0+⎰⎰⎰ 第一个L 关于y 对称,第二个L 关于x 对称【例10.15】 求yL xe ds ⎰,其中L 是由cos (0)sin x a ta y a t =⎧>⎨=⎩所表示的曲线上相应于233t ππ≤≤的一段弧.解 (法一)ds adt ==,故 原式=22sin sin 3333cos |0a ta ta t e adt aeππππ⋅⋅==⎰.(法二)容易看出积分弧段关于y 轴对称,而被积函数是关于变量x 的奇函数,故0y Lxe ds =⎰【例10.18】 求2()Lx y ds +⎰,其中L 为圆周222x y a +=.解 由对称性得0Lxyds =⎰,故22222()(2)()2LLLLx y ds x xy y ds x y ds xyds +=++=++⎰⎰⎰⎰2223022LLa ds a ds a a a ππ=+==⋅=⎰⎰对坐标的线积分,对称性为,当平面曲线L 是分段光滑的,关于x 对称,L 在上半平面与下半平面部分的走向相反时,若P 对y 为偶函数,则,0LPdx =⎰奇函数,则12LL Pdx Pdx =⎰⎰。
第十章 曲线积分与曲面积分§10.1 对弧长曲线的积分一、判断题1.若f(x)在(-+∞∞,)内连续,则⎰badx x f )(也是对弧长的曲线积分。
( )2.设曲线L 的方程为x=)(y ϕ在[βα,]上连续可导则⎰⎰'+=Ldyy y y f ds y x f βαϕϕ2)]([1)),((),(( )二、填空题1.将⎰+Lds y x)(22,其中L 为曲线x=a(cost+tsint),y=a(sint-tcost)()20π≤≤t 化为定积分的结果是 。
2.⎰+L ds y x )(= ,其中L 为连接(1,0)和(0,1)两点的直线段。
三、选择题1.⎰+Lds y x )(22=( ),其中L 为圆周122=+y x (A )⎰02πθd (B )⎰πθ2d (C )⎰πθ22d r (D )⎰πθ22d2.⎰Lxds =( ),L 为抛物线2x y =上10≤≤x 的弧段。
(A ))155(121- (B ))155(- (C )121 (D ))155(81-四、计算⎰+Cds y x )(,其中C 为连接点(0,0)、(1,0)、(0,1)的闭折线。
五、计算⎰++L ds z y x )2(22,其中L 为⎩⎨⎧=++=++02222z y x R z y x六、计算⎰+Ln ds y x)(22,L 为上半圆周:)(222N n R y x ∈=+七、计算⎰+Ly x ds e22,其中L 为圆周222a y x =+,直线y=x 和y=0在第一象限内围成扇形的边界。
八、求半径为a ,中心角为ϕ2的均匀圆弧(ρ=1)的重心。
§10.2 对坐标的曲线积分一、判断题1.定积分也是对坐标的曲线积分。
( ) 2.022=+-⎰L y x ydx xdy ,其中L 为圆周122=+y x 按逆时针方向转一周。
( )二、填空题1.ydz x dy y dx x 2233++⎰Γ= ,其中Γ是从点A (1,2,3)到点B (0,0,0)的直线段AB 。
第十章曲线积分与曲面积分一.第一型曲线积分的概念和性质1.金属曲线的质量设有金属曲线L (如图9-1),L 上各点的密度为二元连续函数ρ=ρ(x,y),求这曲线的质量。
把L 分成n 个小弧段:Δs 1,Δs 2,…,Δs n ,其中Δs i (i=1,2,…n )也表示这些小弧段的长度。
在Δs i 上任取一点(ξi ,ηi ),由于线密度函数是连续的,因此当Δs i 很小时,Δs i 的质量∆m i 便可近似地表示为:∆m i ≈ρ(ξi ,ηi )Δs i ,于是整个金属曲线地质量近似于M ≈ni 1=∑ρ(ξi ,ηi )Δs i .记λ=ni ≤≤1max {Δs i },令λ→0取上式和式的极限,得M =0lim →λni 1=∑ρ(ξi ,ηi )Δs i .2.第一型曲线积分(对弧长的曲线积分)的定义定义:设L 为xoy 平面内的曲线弧,),(y x f 是L 上的有界函数,把L 分成n 个小弧段: Δs 1,Δs 2,…,Δs n ,其中Δs i (i=1,2,…n )也表示第i 个小弧段的弧长. 记λ=n i ≤≤1max {Δs i },在每个小弧段Δs i 上任取一点(ξi ,ηi ),作和式ni 1=∑),(i i f ηξΔs i ,如和式极限0lim →λni 1=∑),(i i f ηξΔs i存在,且极限值与L 的分法和点(ξi ,ηi )在Δs i 上的取法无关,则称此极限值为函数ƒ(x,y)在曲线L 上的第一型曲线积分或称为对弧长的线积分,记作⎰Lds y x f ),(,即⎰Li i ds f ),(ηξ=0lim →λni 1=∑),(i i f ηξΔs i 称),(y x f 为被积函数,L 为积分曲线弧.注1:同前面一样,并非任一个函数),(y x f 在L 上的对弧长的曲线积分都是存在的.但若),(y x f 在L 上连续,则其积分是存在的.故以后在不作特别说明的情况下,总假定),(y x f 在L上连续.注2:显然物体M 的质量为:M=⎰Lds y x ),(ρ注3:类似地,我们可定义),,(z y x f 对于空间曲线弧Γ的曲线积分:⎰Γds z y x f ),,(=∑=→∆ni i i i i s f 1),,(limζηξλ注4:若L 为闭曲线,则),(y x f 在L 上的对弧长的曲线积分记为⎰Lds y x f ),(性质1.若⎰Li dsy x f ),((i=1,2…n)存在,Ci(i=1,2,…n)为常数,则⎰∑=L ni i ids y x f c),(=⎰=ni Li i ds y x f c 1),(性质2:如按段光滑曲线L 由曲线L 1,L 2,…,L n 首尾相接而成,且 ⎰iL ds y x f ),((i=1,2,…n)都存在,则⎰Lds y x f ),(=∑⎰=ni L ids y x f 1),(性质3:若⎰Lds y x f ),(,⎰Lds y x g ),(都存在,且在L 上),(y x f ≤),(y x g ,则⎰Lds y x f ),(≤⎰Lds y x g ),(性质4:若⎰Lds y x f ),(存在,则⎰Lds y x f ),(也存在,且有⎰Lds y x f ),(≤⎰Lds y x f ),(性质5:若⎰Lds y x f ),(存在,L 的弧长为S,则存在常数C,使得⎰Lds y x f ),(=CS二.第一型曲线积分的计算法我们可应用下列定理将第一型曲线积分转化为定积分来计算:定理:设曲线L 的方程为:)(t x ϕ=,)(t y φ=,βα≤≤t ,其中)(t ϕ,)(t φ在[]βα,上具有连续的一阶导数, ),(y x f 为L上的连续函数,则有⎰Lds y x f ),(=[][][]⎰'+'βαφϕφϕdt t t t t f 22)()()(),(证:详细的证明书上有,大家自己看,现在我们从另外一方面来说明这个问题:我们用)(t s s =来表示L上的以[]t ,α为取值区间所对应部分的弧长,则有)(t s s ==⎰'+'tdt t t αφϕ22)]([)]([.两边求微分,得dt t t ds 22)]([)]([φϕ'+'=进而: dt t t t t f ds y x f 22)]([)]([)](),([),(φϕφϕ'+'= 又当),(y x 在L 上变化时,相应地t 在[]βα,上取值,故⎰Lds y x f ),(=[][][]⎰'+'βαφϕφϕdt t t t t f 22)()()(),( . (注:并非严格的证明)注1:若L 的方程为)(x y ϕ=,],[βα∈x 则⎰Lds y x f ),(=⎰'+βαϕϕdx x x x f 2)]([1)](,[若L 的方程为)(y x φ=,],[d c y ∈,则⎰Lds y x f ),(=dy y y y f dc⎰'+2)]([1]),([φφ2:若空间曲线Γ的方程为: )(t x ϕ=,)(t y φ=,)(t z ω=,],[βα∈t .则有⎰Lds z y x f ),,(=[][][][]⎰'+'+'βαωφϕωφϕdt t t t t t t f 222)()()()(),(),(3:定理.注1.2中的定积分的上下限,一定满足:下限≤上限.这是因为,在这里的L(或Γ)是无向曲线弧段,因而单从L 的端点看不出上下限究竟是什么.这就要从L(或Γ)的方程的形式来考虑.又)(t s '>0⇒ts t ∆∆→∆0lim >0从而当t ∆很小时,s ∆∆/>0.此时若视s ∆为L 上某一段弧的弧长,应有s ∆>0⇒t ∆>0.这说明此时t 的变化是由小到大的.而这里s ∆正是i s ∆的一般形状,故下限≤上限.第二节对坐标的曲线积分这里讲的是曲线积分的另一种形式.假设一质点受力),(y x F →=),(y x P i +),(y x Q j 的作用沿平面曲线L 运动,求当质点从L 的一端点A 移动到另一端点B 时,力),(y x F →所做的功W.(这里假设),(y x P ,),(y x Q 在L 上连续)首先,对有向曲线L 作分割:用点M 1,M 2,…,M 1-n 与M 0=A,M n =B 将L 分成n 个小段⋂-i i M M 1(i=1,2…n).以i s ∆表示其弧长.记该分割的细度为λ=ni ≤≤1max {Δs i },当i s ∆很小时,有向的小弧段⋂-i i M M 1可用有向的直线段i i M M 1-来代替: ⋂-ii M M 1≈i i M M 1-=i x ∆i +i y ∆j,其中i x ∆=1--i i x x ,i y ∆=1--i i y y .而),(11--i i y x ,),(i i y x 分别为M1-i 与M i 点的坐标.又在⋂-i i M M 1上任取一点(ξi ,ηi )∈⋂-i i M M 1.当i s ∆很小时,由于),(y x P ,),(y x Q 在L 上连续,故可用在(ξi ,ηi )点处的力),(i i F ηξ→=),(i i P ηξi +),(i i Q ηξj 来近似代替⋂-i i M M 1上其它各点的力,因此变力),(y x F →在小弧段⋂-i i M M 1上所作的功i W ∆,就近似地等于常力),(i i F ηξ→沿i i M M 1-所做的功.故有i W ∆≈),(i i F ηξ→.i i M M 1-=),(i i P ηξi x ∆+),(i i Q ηξi y ∆所以 W=∑=∆n i i W 1≈∑=∆+∆ni i i i i i iy Q x P 1]),(),([ηξηξ.且当0→λ时,有W=∑=→∆+∆ni i i i i i iy Q x P 1]),(),([limηξηξλ.2.第二型曲线积分(对坐标的曲线积分)的定义定义:设L 是xoy 面上从点A 到点B 的有向光滑曲线, ),(y x P ,),(y x Q 在L 上有界,把L 分成n 个小弧段Δs 1,Δs 2,…,Δs n ,其中Δs i (i=1,2,…n )也表示第i 个小弧段的弧长.在Δs i (i=1,2,…n)上任取一点(ξi ,ηi ),做和式∑=∆+∆ni i i i i i i y Q x P 1]),(),([ηξηξ,其中i x ∆和i y ∆是i s ∆分别在x 轴和y 轴上的投影.记λ=ni ≤≤1max{Δsi},如果极限∑=→∆+∆ni i i i i i iy Q x P 1]),(),([limηξηξλ存在,且极限值与L 的分法及点(ξi ,ηi )在Δs i 上的取法无关,则称此极限值为函数),(y x P ,),(y x Q 在有向曲线弧L 上的第二型曲线积分或对坐标的曲面积分,记作⎰+Ldy y x Q dx y x P ),(),(即有:⎰+Ldy y x Q dx y x P ),(),(=),(y x P ,),(y x Q其中),(y x P ,),(y x Q 称为被积函数,L 称为积分曲线弧.同理,当),(y x P ,),(y x Q 都在L 上连续时,上述积分才存在.故今后总假定),(y x P ,),(y x Q 在L 上连续注1:完全可以类似地扩到空间曲线Γ上,得⎰Γ++dz z y x R dy z y x Q dx z y x P ),,(),,(),,(2: 当L 为封闭曲线时,常记为:⎰+Ldy y x Q dx y x P ),(),(3:这两类线积分,除了形式上不同之外,还有一关键性区别在于:第一类线积分与L 的方向无关,而第二类线积分与L 的方向有关.(下见性质2) 性质1:若L 由有限有向曲线弧组成,例如L=L 1+L 2,则⎰+Ldy y x Q dx y x P ),(),(=⎰+1),(),(L dy y x Q dx y x P +⎰+2),(),(L dy y x Q dx y x P性质2:设–L 是L 的反向曲线弧,则⎰-+Ldy y x Q dx y x P ),(),(=⎰+-Ldy y x Q dx y x P ),(),(一. 第二型曲线积分的计算法同前面一样,我们可以将对坐标的曲线积分转化为定积分来计算,有下列定理:定理: ),(y x P ,),(y x Q 在有向曲线弧L 上连续,L 的方程为: )(t x ϕ=,)(t y φ=. 当t 由α变动到β时,对应L 上的动点),(y x M 从L 的起点A 变到终点B,)(t ϕ',)(t φ'在],[βα上连续且不全为零,则⎰+Ldy y x Q dx y x P ),(),(=⎰'+'βαφφϕϕφϕdt t t t Q t t t P )}()](),([)()](),([{ (证明略)注1:若L 的方程为)(x y ϕ=,x 在a ,b 之间.且x=a 且x=b 分别为L 的起点和终点,则有⎰+Ldy y x Q dx y x P ),(),(=⎰'+badx x x x Q x x P )())](,())(,([ϕϕϕ同理,若L 的方程为)(y x ϕ=,也有类似的结果.2:设空间曲线Γ的方程为: )(t x ϕ=,)(t y φ=,)(t z ω=,],[βα∈t ,且α=t ,β=t 分别对应于Γ的起点和终点,则有⎰Γ++dz z y x R dy z y x Q dx z y x P ),,(),,(),,(=⎰'+'+'βαωωφϕφωφϕϕωφϕdt t t t t R t t t t Q t t t t P )}()](),(),([)()](),(),([)()](),(),([{3:定理及注1,2中的定积分的上下限分别时参数所对应的参数值,起点对应的值为下限,终点对应的值为上限.二、两类线积分之间的关系直到现在为止,我们已学过两种曲线积分:⎰Lds y x f ),(和⎰+Ldy y x Q dx y x P ),(),(.两者都是转化为定积分计算.那么两者有何联系呢?这两种曲线积分来源于不同的物理原型,有着不同的特性,但在一定的条件下,我们可建立它们之间的联系.设有向曲线弧L 表示成以弧长s 为参数的参数方程: x=x(s),y=y(s), 0≤s ≤ℓ,这里L 由点A 到点B 的方向就是s 增大的方向.又设α,β依次为从x 轴正向,y 轴正向到曲线L 的切线的正向的夹角,则a dsdx cos =,βcos sin ==a dsdy(cos α,cos β也称为有向曲线L 上点(x,y)处的切向量的方向余弦,切向量的指向与曲线L 的方向一致).因此,得⎰+Ldy y x Q dx y x P ),(),(=ds s y s x Q s y s x P l}cos )](),([cos )](),([{0⎰+βα⇒⎰+Ldy y x Q dx y x P ),(),(=⎰+Lds y x Q y x P ]cos ),(cos ),([βα注1: 上式可推广到空间曲线的曲线积分上去,有⎰++Ldz z y x R dy z y x Q dx z y x P ),,(),,(),,(=⎰++Lds z y x R z y x Q z y x P ]cos ),,(cos ),,(cos ),,([γβα其中cos α,cos β,cos γ 是L 上点(x,y,z)处的切向量的方向余弦.第二节 格林公式格林(Green)公式是指出了沿闭曲线的第二型曲线积分与二重积分的关系.下面我们来规定L 的正向:设区域D 是由一条或几条光滑曲线所围成.边界曲线L 的正向规定为:当人沿着L 行走时,区域D 总在他的左边.若与L 的正向相反,就称为负方向.记作–L.定理1 设闭区域D 由分段光滑的闭曲线L 围成,函数),(y x P ,),(y x Q 在D 上具有一阶连续偏导数,则⎰+LQdy Pdx =⎰⎰⎪⎪⎭⎫⎝⎛∂∂-∂∂D dxdy y P x Q (1) 其中左端的闭曲线积分是沿边界曲线L 的正方向.公式(1)称为格林公式.证:(i)首先我们证明一个特殊情况:D 既可表示为X-型区域,也可表示为Y-型区域.由D 可表示为X 型区域,不妨设D={(x,y) : a ≤x ≤b, )(1x ϕ≤y ≤)(2x ϕ} (如图)则⎰⎰∂∂Ddxdy yP =⎰badxdy yy x P x x ⎰∂∂)()(21),(ϕϕ=⎰-badx x x P x x P )]}(,[)](,[{12ϕϕ又⎰LP d x =⎰1L Pdx +⎰2L Pdx =⎰badx x x P )](,[1ϕ +⎰badx x x P )](,[2ϕ=⎰--badx x x P x x P )]}(,[)](,[{12ϕϕ因此有⎰L P d x =⎰⎰∂∂-Ddxdy yP同理,D 可表示为Y-型区域,不难证明:⎰LQdy =⎰⎰∂∂Ddxdy xQ将上面两式相加得⎰+LQdy Pdx =⎰⎰⎪⎪⎭⎫⎝⎛∂∂-∂∂Ddxdy y P xQ . (ii)对于一般的区域D,即如果闭区域D不满足上述条件(既可表示为X-型区域,也可表示为Y-型区域),则可以在D 内引进若干条辅助线把D 分成有限个部分闭区域,使每个部分满足上述条件.在每快小区域上分别运用Green 公式,然后相加即成.如图中D 的边界曲线L,通过作辅助线AE 将L 分为L 1,L 2,同时将区域D 分为D 1,D 2,它们都满足上述条件,于是⎰→++EAL QdyPdx 1=⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂1D dxdy y P x Q ,⎰→++AEL Qdy Pdx 2=⎰⎰⎪⎪⎭⎫⎝⎛∂∂-∂∂Ddxdy y PxQ 上面两式相加,并注意到⎰→+EAL 1=⎰1L +⎰→EA,⎰→+AEL 2=⎰2L +⎰→AE,⎰→AE=⎰→-EA.又L=L 1+L 2, D= D 1+D 2, 于是⎰+LQ d y P d x =⎰⎰⎪⎪⎭⎫⎝⎛∂∂-∂∂D dxdy y P x Q . 注:在Green 公式中,当x Q =, y P -=时,有yP xQ ∂∂-∂∂=1–(–1)=2, 代入公式,得⎰+-Lxdy ydx = ⎰⎰Ddxdy 2=A 2 (其中A 为D 的面积)于是 ⎰-=Ly d x x d y A 21. (2)平面曲线积分与路径无关的条件从前面的讨论,我们看到第二型曲线积分当积分路径起点,终点固定时,它的数值一般与积分曲线有关.如:⎰-++Ldy x y dx y x )()(中,当L 的端点固定在(1,1)点和(4,2)点时,若L取不同的路径,所得到的积分值不一样.这说明积分值与所取的积分路径有关.然而,存在着另一种情况,即积分值与积分路径无关,只与起点和终点有关.亦即对任意两条以A 为起点,B 为终点的曲线1L 和2L ,有⎰+1L Qdy Pdx =⎰+2L Qdy Pdx .本段将讨论曲线积分在什么条件下,其值与路径无关.首先,介绍单连通区域的概念:若对于平面开区域D 内任一条封闭曲线L,均可以D 以外的点而连续收缩于D 中某一点,即L 所围的点全属于D,那么就称D 为单连通区域,通俗地说D 是没有“洞”的区域.否则,称为复(多)连通区域.(如图).定理: 设G是一个单连通的开区域,函数),(y x P ,),(y x Q 在G内具有一阶连续偏导数,则下述命题是等价的 1)yP xQ ∂∂=∂∂在D 内恒成立;2) 0=+⎰LQdy Pdx 对G 内任意闭曲线L 成立;3)⎰+LQdy Pdx 在G 内与积分路径无关;4) 存在可微函数),(y x u u =,使得Qdy Pdx du +=在G 内恒成立. 证 1)⇒2). 已知yP xQ ∂∂=∂∂在G 内恒成立,对G 内任意闭曲线L,设其所包围的闭区域为D,由格林公式=+⎰LQdy Pdx ⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂Ddxdy y P x Q 00==⎰⎰Ddxdy2) ⇒3).已知对G 内任一条闭曲线L,0=+⎰LQdy Pdx . 对G 内任意两点A 和B,设1L 和2L 是G 内从点A 到点B 的任意两条曲线(如图),则-+=21L L L 是G 内一条封闭曲线,从而有⎰+=LQdy Pdx 0=⎰+1L Qdy Pdx +⎰-+2L Qdy Pdx 。