数据分析模型之趋势面模型

趋势面拟合趋势面拟合（Trend Surface Fitting）是一种数据建模方法，用于寻找数据中的趋势和模式。

它广泛应用于地理信息系统、地质勘探、气象预测等领域。

在趋势面拟合中，我们假设数据点的分布在一个平面上，并尝试找到最适合数据点的平面方程。

这个平面方程可以用来预测未知数据点的数值，或者分析数据中的趋势。

趋势面拟合的基础概念是多项式回归。

多项式回归是通过用一个多项式函数近似拟合数据点，来描述数据间的关系。

在趋势面拟合中，我们通常使用二维二次多项式来拟合数据，即：Z = a + bx + cy + dx^2 + exy + fy^2其中Z是数据点的数值，x和y是数据点的坐标，a、b、c、d、e、f是待定参数。

为了找到最适合数据点的参数，我们需要使用优化方法，如最小二乘法。

最小二乘法的目标是最小化实际数据点与拟合曲面之间的残差平方和。

通过求解最小二乘法的优化问题，我们可以得到最佳的参数估计。

对于一组离散点数据，趋势面拟合可以通过以下步骤实现：1. 收集和整理数据，确定数据点的坐标和数值。

2. 创建一个二维空间网格，在网格上均匀采样若干个点。

3. 对于每个网格点，计算其对应的Z值，代入二维二次多项式中。

4. 使用最小二乘法拟合数据点，找到最适合的参数估计。

5. 根据参数估计的方程，预测其他未知数据点的数值。

需要注意的是，趋势面拟合是一种插值方法，只适用于数据点周围的区域。

如果要预测远离数据点的位置，可能需要更复杂的模型和方法。

总结起来，趋势面拟合是一种用于数据建模和预测的方法，可以找到数据中的趋势和模式。

通过拟合一个二维二次多项式，我们可以预测未知数据点的数值，并进行数据分析和预测工作。

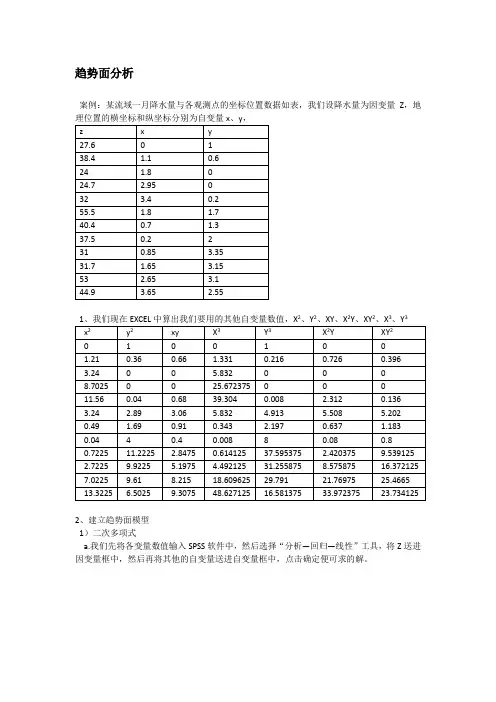
趋势面分析案例：某流域一月降水量与各观测点的坐标位置数据如表，我们设降水量为因变量Z，地2、Y2、XY、X22、X3、Y32、建立趋势面模型1）二次多项式a.我们先将各变量数值输入SPSS软件中，然后选择“分析—回归—线性”工具，将Z送进因变量框中，然后再将其他的自变量送进自变量框中，点击确定便可求的解。

b.运行结果如下图1图1中B列的数据为拟合方程的各系数，根据表中的数值及所对应的常量，我们求得的拟合方程为：Z=5.998+17.438X+29.787Y-3.588X2+0.357XY-8.070Y2图2图2显示该拟合二次趋势面的判定系数R2=0.839，显著性F=6.2322）三次多项式a.方法与二次多项式类似，将所有的变量输入SPSS，选择“分析—回归—线性”工具，将Z 送进因变量框中，然后再将其他的自变量送进自变量框中，点击确定便可求解。

b.运行结果如下图1图1中数列B的数据为拟合方程的各系数，根据表中的数值及所对应的常量，我们求得的拟合方程为：Z=-48.810+37.557X+130.130Y+8.389X2-33.166XY-62.740Y2-4.133X3+6.138X2Y+2.566XY2+9.785Y3图2图2显示，该拟合二次趋势面的判定系数R2=0.965，显著性F=6.0543、检验模型1）趋势面拟合适度检验。

根据两次拟合的输出结果表明，二次趋势面的判定系数为R2=0.839，三次趋势面的判定系数为R2=0.965，可见二者趋势面回归模型的显著性都较高（>0.8），且三次趋势面较二次趋势面具有更高的拟合程度（数值更大）。

2）趋势面适度的显著性检验。

根据两次拟合的输出结果表明，两者趋势面的F值分别为F2=6.236、和F3=6.054，在置信水平a=0.05下，查F分布表得F2a=F0.05(5,6)=4.53，F3a=F0.05(9,2)=19.4，我们得出F2>F2a F3 < F3a，因此我们判定用二次趋势面进行拟合比较合理。

：空间数据．．．．拓扑分析、空间叠加、缓冲分析、网络分析P3数字地面模型(DTM)：数字高程模型(DEM)：不规则三角网(TIN)：地质统计学：是利用空间变量的自相关特征研究空间随机场性质的一种统计理论。

它分为(1)结构分析理论；(2)克立格插值理论（插值理论）；(3)条件模拟理论。

协方差、空间采样理论P9估计误差：是指实测值与真实值之间的误差。

估计方差：是指估计误差的离散程度。

数字高程模型DEM：是描述地面特性空间分布的有序数值阵列，所记地面特性是高程z，它的空间分布由x , y水平坐标系统来描述。

DEM派生信息：以数字地面模型为基础，通过数字地形分析（DTA）手段可提取出用于描述地表不同方面特征的参数，这些参数统称为DEM派生信息。

坡度、坡向、曲率P16地面曲率：地面曲率是对地形表面一点扭曲变化程度的定量化度量因子，地面曲率在垂直和水平两个方向上分量分别称为平面曲率和剖面曲率。

剖面曲率、平面曲率、坡形P18汇流量（汇流面积）：一个栅格单元的汇流量是其上游单元向其输送的水流量的总和。

地形湿度指数：单位等高线上的汇流面积与坡度之比。

通视分析：就是利用DEM判断地形上任意点之间是否可以相互可见的技术方法，分为视线分析和视域分析。

缓冲区：地理空间目标的一种影响范围或服务范围,具体指在点. 线. 面实体周围自动建立的一定宽度的多边形。

叠置分析：是将同一地区的两组或两组以上的要素进行叠置，产生新的特征的分析方法。

合成叠置、统计叠置P30交、并、剪P31 差、识别P32距离分析：用于分析图像上每个点与目标的距离，如有多目标，则以最近的距离作为栅格值。

距离制图、直线距离分析P32密度分析：针对一些点要素（或线要素）的特征值（如人口数）并不是集中在点上（或线上）的特点，对要素的特征值进行空间分配，从而更加真实地反映要素分布。

密度制图：根据输入的要素数据集计算整个区域的数据聚集状况，从而产生一个连续的密度表面。

趋势面拟合的r检验趋势面拟合的r检验是用来评估趋势面拟合模型的拟合程度的统计检验方法。

在统计学中，趋势面拟合是指通过拟合一个二维平面或高维平面来描述数据的趋势和变化规律。

趋势面拟合常用于时间序列分析、经济预测、气候变化等领域。

在进行趋势面拟合的过程中，我们需要将原始数据用一个数学函数进行拟合，常见的函数有多项式函数、指数函数、对数函数等。

然后通过r检验来判断拟合函数与实际数据之间的拟合程度。

r检验是通过计算样本数据与拟合函数的相关系数r来判断两者之间的线性关系的强弱。

相关系数r的取值范围是-1到1，其中1表示完全正相关，-1表示完全负相关，0表示无相关。

当r的绝对值越接近1时，说明拟合函数与实际数据的拟合程度越好。

具体计算r检验的步骤如下：1. 首先，我们需要通过拟合函数获得拟合值，即对于每个自变量的取值，计算出拟合函数的预测值。

2. 然后，计算实际值与拟合值之间的差异，得到残差。

残差是实际值与拟合值之间的偏差，可以用来衡量模型对数据的拟合程度。

3. 使用相关系数公式计算相关系数r。

相关系数r可以通过计算残差的协方差与实际值和拟合值的标准差之积的比值来得到。

4. 计算相关系数的显著性水平。

在r检验中，我们还需要计算相关系数的显著性水平，这是通过对相关系数进行假设检验得到的。

通常，我们会假设相关系数为零，然后计算相关系数的t值，再根据t值和自由度决定相关系数是否显著。

需要注意的是，在进行趋势面拟合和r检验时，我们需要小心拟合模型的选择和数据的处理。

不正确的拟合模型或数据的处理方式可能导致拟合度不准确，从而影响r检验的结果。

总结起来，趋势面拟合的r检验是一种用于评估拟合度的统计检验方法，通过计算相关系数r来判断拟合函数与实际数据之间的线性关系的强弱。

它对于评估和比较不同拟合函数的拟合效果具有重要的意义。

在实际应用中，我们可以通过r 检验来选择最优的拟合模型，并进行相应的分析和预测。

arcmap趋势面法趋势面分析是一种在ArcMap中应用的空间分析方法，它用于描述地理现象随时间变化的趋势。

它可以帮助我们理解和预测自然和人为现象的发展情况，为决策和规划提供科学依据。

趋势面分析可以应用于多个领域和问题。

例如，在自然资源管理中，我们可以使用趋势面分析来研究土地利用变化、森林覆盖率变化、水资源利用变化等。

在城市规划和交通规划中，我们可以使用趋势面分析来研究人口分布变化、交通流量变化、城市扩张趋势等。

在疫情分析和气候变化研究中，趋势面分析可以用来描述疫情传播趋势、气温变化趋势等。

在ArcMap中进行趋势面分析，首先需要准备一系列的时间序列数据。

时间序列数据可以是多个时间点上的栅格数据，也可以是多个时间点上的矢量数据。

在输入数据准备好之后，我们可以通过以下步骤进行趋势面分析。

第一步是数据预处理。

在进行趋势面分析之前，需要先对数据进行预处理，以确保数据的质量和连续性。

这包括数据清洗、数据插值等步骤。

例如，如果时间序列数据中存在缺失值，我们可以使用空间插值方法（如克里金插值）来填补缺失值。

第二步是趋势面建模。

在趋势面分析中，最常用的建模方法是线性回归分析。

线性回归模型假设地理现象的变化是通过时间的线性函数来描述的。

根据具体问题的不同，我们可以选择简单线性回归模型，也可以选择多元线性回归模型。

在ArcMap中，我们可以使用回归分析工具来进行趋势面建模。

首先，我们需要选择需要进行趋势面分析的变量（如土地利用类型、气温等）作为自变量，选择时间作为因变量。

然后，我们可以通过工具的参数设定来选择回归模型的类型和参数。

在进行模型拟合之后，工具会生成模型拟合结果，包括回归系数、拟合优度等信息。

第三步是结果可视化。

在趋势面分析中，可视化是非常重要的，它可以帮助我们更直观地理解和解释分析结果。

在ArcMap中，我们可以使用各种方式来可视化趋势面分析的结果，例如生成趋势面图、制作图表、制作动态图等。

最后，对于趋势面分析的结果，我们可以通过进一步分析和解读来得到更多有用的信息。

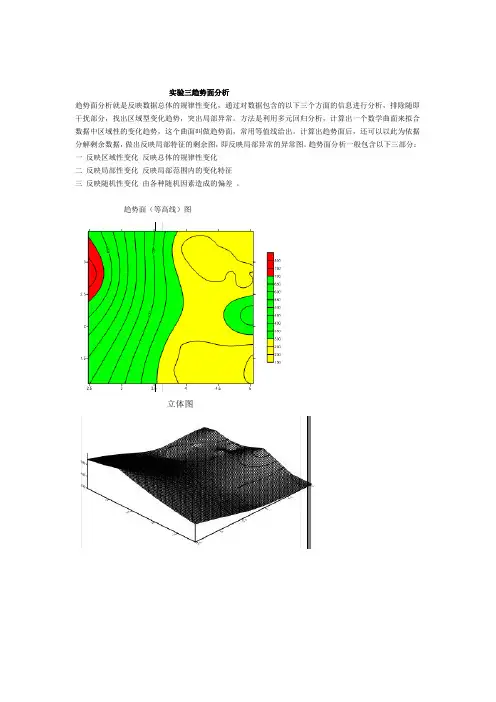
实验三趋势面分析
趋势面分析就是反映数据总体的规律性变化，通过对数据包含的以下三个方面的信息进行分析，排除随即干扰部分，找出区域型变化趋势，突出局部异常。

方法是利用多元回归分析，计算出一个数学曲面来拟合数据中区域性的变化趋势，这个曲面叫做趋势面，常用等值线给出。

计算出趋势面后，还可以以此为依据分解剩余数据，做出反映局部特征的剩余图，即反映局部异常的异常图。

趋势面分析一般包含以下三部分：一反映区域性变化反映总体的规律性变化
二反映局部性变化反映局部范围内的变化特征
三反映随机性变化由各种随机因素造成的偏差。

趋势面（等高线）图
立体图
彩图
地势两边高（图中表现为红色部分），中间低（黄色与红色的过渡部分）右上角有一凹陷（黄色部分）。

截图X 范围3.5-6 Y范围0-4
原始数据如下。

一、趋势面分析法(2007-03-06 14:45:57)转载下面将就趋势面分析、克里金、形函数法三种算法作简单介绍，以后将进一步整理一些资料，介绍更多优秀的实用算法。

一、趋势面分析法趋势面分析法是针对大量离散点信息，从整体插值角度出发，来进行趋势渐变特征分析的最简单的方法。

趋势面分析一般是采取多项式进行回归分析。

趋势面通常应用多项式回归，主要是因为多项式回归的求解比较简单，通常可以得到显示的数学解答。

回归方法采用最小二乘法原理，其本质就是对回归函数在某个区间上的极值求取。

M阶N项多项式趋势面基本可以表示以下形式：要注意在上式中，是参变量，但不是每个参变量都是独立参变量。

在实际分析中，M一般取1，2，3。

一般来说来M不取超过3以上的高阶,主要基于两方面，一是高阶求解相对复杂，二是高级很难赋予物理意义。

N取多参变量在生产实践中是很常见的。

对于任何一组离散型数据，多项式趋势面到底取多少阶和多少个参变量，有一个临界限制：就是不管你取多少阶和多少个参变量，只要待求趋势面中的独立参变量总数小于或者等于已知离散控制点的数量就可以。

事实上，趋势面分析并不限制只取多项式趋势面，可以取任何函数构成的趋势面，如以下形式：上式为任意函数，为待求参变量。

在实际应用中，即使碰到了用一般多项式趋势面解决不了的拟合问题，往往也不采取以上方法，因为其求取复杂和费时。

通常做法是大致估算出其函数形式，将原始数据进行相应转换，然后再采取多项式趋势面方法来进行分析和求解。

在空间分析中，最简单的趋势面分析函数大致有以下一些类型。

1、空间趋势平面模型。

数学函数如下所示：2、简单二次曲面模型。

数学函数如下所示：或3、复杂二次曲面模型。

数学函数如下所示：所谓趋势面，顾名思义只是从趋势上来进行拟合，严格意义说它是平滑函数。

一般趋势面不经过原始数据点，除非趋势面中待求参变量的个数与已知离散控制点所确定的线性不相关方程组的个数相等。

趋势面分析中另一个重要特性就是揭示了分析区域中不同于总趋势的最大偏离部分。