利用数学模型解题——大角夹半角
- 格式:pptx
- 大小:129.57 KB
- 文档页数:8
夹半角模型及应用
方法与技巧:
夹半角问题是通过旋转对除半角外剩余的角进行拼凑,从而产生一组旋转全等和一组轴对称全等来解决。
在实际解题过程中,添加辅助线的方式与截长补短相同。
强化练习:
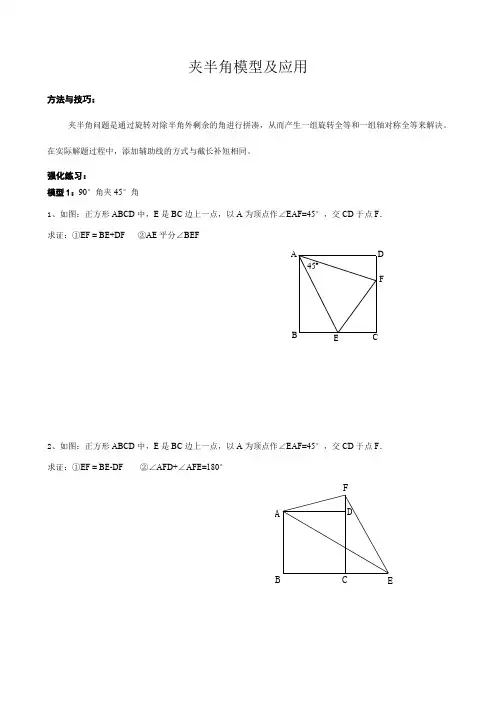
模型1:90°角夹45°角
1、如图:正方形ABCD 中,E 是BC 边上一点,以A 为顶点作∠EAF=45°,交CD 于点F . 求证:①EF = BE+DF ②AE 平分∠BEF
2、如图:正方形ABCD 中,E 是BC 边上一点,以A 为顶点作∠EAF=45°,交CD 于点F . 求证:①EF = BE-DF ②∠AFD+∠AFE=180°
F
A
C
B
D E
45
F
E
D
C B A
模型2: 120°角夹60°角
3、如图:四边形ABCD 中,BC=CD ,∠BCD=120°,E 、F 分别是AB ,AD 上的点,∠ECF=∠A=60°. 求证:①BE+DF=EF ②点C 在∠BAD 的平分线上
模型3: 2a °角夹a °角
4、如图,在四边形ABCD 中, AB =AD ,∠B+∠D=180°, E 、F 分别是边BC 、CD 上的点,且2∠EAF =∠BAD, 求证: ①BE+DF=EF ②CE 平分∠BEF
F
E D
C
B
A。

几何图形之半角模型主题半角模型教学内容教学目标1。
掌握正方形的定义,弄清正方形与平行四边形、菱形、矩形的关系。
2。
掌握正方形的性质定理1和性质定理2。
3.正确运用正方形的性质解题.4。
通过四边形的从属关系渗透集合思想。
5.通过理解四种四边形内在联系,培养学生辩证观点。
知识结构正方形的性质因为正方形是特殊的平行四边形,还是特殊的矩形,特殊的菱形,所以它具有这些图形性质的综合,因此正方形有以下性质(由学生和老师一起总结)。
正方形性质定理1:正方形的四个角都是直角,四条边相等。
正方形性质定理2:正方形的两条对角线相等并且互相垂直平分,每一条对角线平分一组对角。
说明:定理2包括了平行四边形,矩形,菱形对角线的性质,一个题设同时有四个结论,这是该定理的特点,在应用时需要哪个结论就用哪个结论,并非把结论写全。
小结:(1)正方形与矩形,菱形,平行四边形的关系如上图(2)正方形的性质:①正方形对边平行。
②正方形四边相等.③正方形四个角都是直角。
④正方形对角线相等,互相垂直平分,每条对角线平分一组对角.典型例题精讲例1.如图,折叠正方形纸片ABCD ,先折出折痕BD ,再折叠使AD 边与对角线BD 重合,得折痕DG ,使2AD =,求AG .【解析】:作GM ⊥BD ,垂足为M . 由题意可知∠ADG=GDM , 则△ADG ≌△MDG . ∴DM=DA=2. AC=GM 又易知:GM=BM .而BM=BD-DM=22-2=2(2—1), ∴AG=BM=2(2—1).例2 .如图,P 为正方形ABCD 内一点,10PA PB ==,并且P 点到CD 边的距离也等于10,求正方形ABCD 的面积?【解析】:过P 作EF AB ⊥于F 交DC 于E .设PF x =,则10EF x =+,1(10)2BF x =+.由222PB PF BF =+. 可得:222110(10)4x x =++. 故6x =.216256ABCD S ==.例3。

几何图形之半角模型主题半角模型教学内容教学目标1.掌握正方形的定义,弄清正方形与平行四边形、菱形、矩形的关系。
2。
掌握正方形的性质定理1和性质定理2。
3。
正确运用正方形的性质解题。
4。
通过四边形的从属关系渗透集合思想。
5.通过理解四种四边形内在联系,培养学生辩证观点。
知识结构正方形的性质因为正方形是特殊的平行四边形,还是特殊的矩形,特殊的菱形,所以它具有这些图形性质的综合,因此正方形有以下性质(由学生和老师一起总结).正方形性质定理1:正方形的四个角都是直角,四条边相等。
正方形性质定理2:正方形的两条对角线相等并且互相垂直平分,每一条对角线平分一组对角。
说明:定理2包括了平行四边形,矩形,菱形对角线的性质,一个题设同时有四个结论,这是该定理的特点,在应用时需要哪个结论就用哪个结论,并非把结论写全.小结:(1)正方形与矩形,菱形,平行四边形的关系如上图(2)正方形的性质:①正方形对边平行.②正方形四边相等.③正方形四个角都是直角。
④正方形对角线相等,互相垂直平分,每条对角线平分一组对角。
典型例题精讲例1.如图,折叠正方形纸片ABCD ,先折出折痕BD ,再折叠使AD 边与对角线BD 重合,得折痕DG ,使2AD =,求AG .【解析】:作GM ⊥BD ,垂足为M . 由题意可知∠ADG=GDM , 则△ADG ≌△MDG . ∴DM=DA=2. AC=GM 又易知:GM=BM .而BM=BD-DM=22-2=2(2—1), ∴AG=BM=2(2-1).例2 .如图,P 为正方形ABCD 内一点,10PA PB ==,并且P 点到CD 边的距离也等于10,求正方形ABCD 的面积?【解析】:过P 作EF AB ⊥于F 交DC 于E .设PF x =,则10EF x =+,1(10)2BF x =+.由222PB PF BF =+. 可得:222110(10)4x x =++. 故6x =.216256ABCD S ==.例3。


数学故事古典密码术大家经常见到的藏头诗实际是一种加密术,它通过坐标变换的方式隐藏了秘密,这个例子虽然很简单,但它反映出了加密术的本质--变换坐标系。
加密术最早应用于古代战争,当时是靠士兵随身携带的信件来传递情报,但总是免不了被敌方俘虏,从而使情报落入敌手,这对作战部队而言可是生死悠关的大事。
传说当时的凯撒大帝有一个能加密的办法,就在写命令前做一个对应表:明码:A B C D E F....W X Y Z密码:D E F G H I....Z A B C如果他想写BABY,就用EDEB来表示。
当大将收到了EDEB这个密码后,向前推3个字母,就得到了明文。
这个对应表的移位数是3,当然别的数也可以,作战前由凯撒定好后通知大将们。
这种加密方式其实就是把坐标系横移了3格,这种方法非常简单,但同时也很容易被敌方猜到,敌人从1到25推25次,得到25组新编码,必有一种编码是真实的情报内容,把这组编码区别出来非常容易,因为其它24组都是毫无意义的字母组合,只有这一组是有意义的句子,找个识字的人就可以看得出来。
凯撒该怎么办呢?有个聪明人帮他出了个主意,对应表不按字母顺序写,而是搞个乱乎的。
例如A对Q,B对F,随便配对,只要保证26个明密码对里,每个都出现一次就行了。
每次出征前,凯撒都会临时搞个非常乱乎的明密码对应表,然后发给大将。
这招很不错,敌人即使截获了密文,由于不知道明密码对应表,也很难破译出来,这其实也是坐标系的一种变换,这种方法被后人称为“单表系统”。
很多年过去了,有人发现了这种加密方法的漏洞,因为英文字母的出现次数是不同的,例如E出现的次数最多,甚至可以搞出个频次表来,如果一件密文中R出现的次数最多,那这个R会不会就是E呢?这个猜想很合理,即使代表的不是E,那它代表的也应是明文中出现次数较多的字母。
按照这种思路试试吧,My God,密码解开了。
现在又轮到加密方纠结了,他们想,破解方是在拿明密文中字母出现的频次做文章,如果我们能把频次的区别消除掉,他们不就没办法了吗?道理虽然很好,但怎样才能消除这种频次的差别呢,毕竟明文中字母的频次就是不一样,这本身没法改变啊。
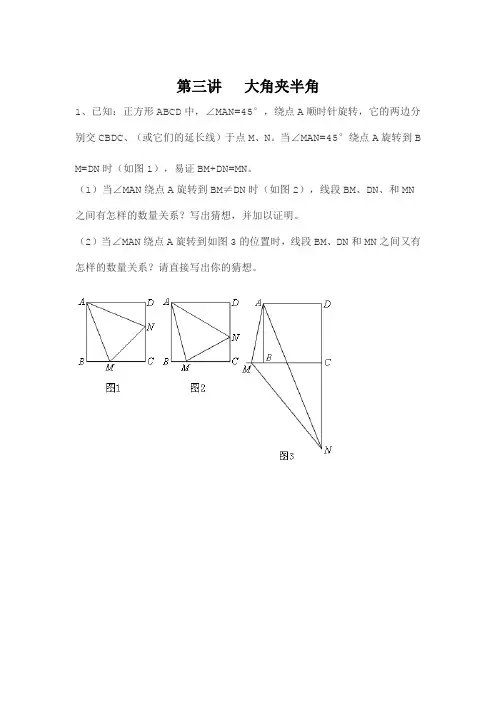
第三讲大角夹半角1、已知:正方形ABCD中,∠MAN=45°,绕点A顺时针旋转,它的两边分别交CBDC、(或它们的延长线)于点M、N。
当∠MAN=45°绕点A旋转到B M=DN时(如图1),易证BM+DN=MN。
(1)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM、DN、和MN 之间有怎样的数量关系?写出猜想,并加以证明。
(2)当∠MAN绕点A旋转到如图3的位置时,线段BM、DN和MN之间又有怎样的数量关系?请直接写出你的猜想。
12、已知四边形ABCD 中,A B A D ⊥,BC CD ⊥,AB BC =,120ABC =∠,60MBN =∠,MBN ∠绕B 点旋转,它的两边分别交AD DC ,(或它们的延长线)于E F ,.当MBN ∠绕B 点旋转到AE CF =时(如图1),易证AE CF EF +=.当MBN ∠绕B 点旋转到AE CF ≠时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,线段AE CF ,,EF 又有怎样的数量关系?请写出你的猜想,不需证明.(图1) A B CDE FM N(图2)A B CDE FM N(图3)A BCDE F MN如图1:在四边形ABCD 中,AB =AD ,∠BAD =120°,∠B =∠ADC =90°.E 、F 分别是BC 、CD 上的点.且∠EAF =60°.探究图中线段BE 、EF 、FD 之间的数量关系. 小王同学探究此问题的方法是,延长FD 到点G ,使DG =BE .连结AG ,先证明△ABE ≌△ADG ,再证明△AEF ≌△AGF ,可得出结论,他的结论应是 EF =BE +DF ;探索延伸:如图2,若在四边形ABCD 中,AB =AD ,∠B +∠D =180°.E 、F 分别是BC 、CD 上的点,且∠EAF =12∠BAD ,上述结论是否仍然成立,并说明理由; 实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O 处)北偏西30°的A 处,舰艇乙在指挥中心南偏东70°的B 处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进.1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E ,F 处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离?11. 如图,ABC ∆是边长为3的等边三角形,BDC ∆是等腰三角形,且0120BDC ∠=,以D 为顶点做一个060角,使其两边分别交AB 于点M ,交AC 于点N ,连接MN ,则A MN ∆的周长为 ;在平面直角坐标系中,O为原点,点A(-2,0),点B(0,2),点E,点F分别为OA,OB的中点。

中考数学必备专题目中考模型解题目系列之大角夹半角模型
【中考数学必备专题】中考模型解题系列之大
角夹半角模型
一、解答题(共1道,每道100分)
1.(2010重庆改编)等边的两边AB、AC所在直线上分别有两点M、N,D为外一点,且,,BD=DC.探究:当M、N 分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系及的周长Q与等边的周长L的关系.
(I)如图1,当点M、N在边AB、AC上,且DM=DN时,BM、NC、MN之间的数量关系是_____________;此时___________;
(II)如图2,点M、N在边AB、AC上,且当DM DN时,猜想(I)问的两个结论还成立吗?写出你的猜想并加以证明;
(III)如图3,当M、N分别在边AB、CA的延长线上时,若AN=,则
Q=_________(用、L表示).。

几何图形之半角模型主题半角模型教学内容教学目标1。
掌握正方形的定义,弄清正方形与平行四边形、菱形、矩形的关系。
2.掌握正方形的性质定理1和性质定理2。
3.正确运用正方形的性质解题。
4.通过四边形的从属关系渗透集合思想.5。
通过理解四种四边形内在联系,培养学生辩证观点.知识结构正方形的性质因为正方形是特殊的平行四边形,还是特殊的矩形,特殊的菱形,所以它具有这些图形性质的综合,因此正方形有以下性质(由学生和老师一起总结)。
正方形性质定理1:正方形的四个角都是直角,四条边相等。
正方形性质定理2:正方形的两条对角线相等并且互相垂直平分,每一条对角线平分一组对角.说明:定理2包括了平行四边形,矩形,菱形对角线的性质,一个题设同时有四个结论,这是该定理的特点,在应用时需要哪个结论就用哪个结论,并非把结论写全。
小结:(1)正方形与矩形,菱形,平行四边形的关系如上图(2)正方形的性质:①正方形对边平行。
②正方形四边相等.③正方形四个角都是直角.④正方形对角线相等,互相垂直平分,每条对角线平分一组对角。
典型例题精讲例1.如图,折叠正方形纸片ABCD ,先折出折痕BD ,再折叠使AD 边与对角线BD 重合,得折痕DG ,使2AD =,求AG .【解析】:作GM ⊥BD,垂足为M . 由题意可知∠ADG=GDM, 则△ADG ≌△MDG . ∴DM=DA=2. AC=GM 又易知:GM=BM .而BM=BD —DM=22—2=2(2—1), ∴AG=BM=2(2—1).例2 .如图,P 为正方形ABCD 内一点,10PA PB ==,并且P 点到CD 边的距离也等于10,求正方形ABCD 的面积?【解析】:过P 作EF AB ⊥于F 交DC 于E .设PF x =,则10EF x =+,1(10)2BF x =+.由222PB PF BF =+. 可得:222110(10)4x x =++. 故6x =.216256ABCD S ==.例 3. 如图,E 、F 分别为正方形ABCD 的边BC 、CD 上的一点,AM EF ⊥,•垂足为M ,AM AB =,则有EF BE DF =+,为什么?【解析】:要说明EF=BE+DF,只需说明BE=EM ,DF=FM 即可,而连结AE 、AF .只要能说明△ABE ≌△AME,△ADF ≌△AMF 即可. 理由:连结AE 、AF .由AB=AM ,AB ⊥BC ,AM ⊥EF,AE 公用, ∴△ABE ≌△AME . ∴BE=ME .同理可得,△ADF ≌△AMF .∴DF=MF .∴EF=ME+MF=BE+DF .例4.如下图E 、F 分别在正方形ABCD 的边BC 、CD 上,且45EAF ︒∠=,试说明EF BE DF =+. 【解析】:将△ADF 旋转到△ABC ,则△ADF ≌△ABG∴AF=AG ,∠ADF=∠BAG,DF=BG∵∠EAF=45°且四边形是正方形, ∴∠ADF ﹢∠BAE=45° ∴∠GAB ﹢∠BAE=45° 即∠GAE=45°∴△AEF ≌△AEG (SAS ) ∴EF=EG=EB ﹢BG=EB ﹢DF例5。

几何图形之半角模型主题半角模型教学内容教学目标1。
掌握正方形的定义,弄清正方形与平行四边形、菱形、矩形的关系。
2。
掌握正方形的性质定理1和性质定理2。
3。
正确运用正方形的性质解题。
4.通过四边形的从属关系渗透集合思想。
5。
通过理解四种四边形内在联系,培养学生辩证观点.知识结构正方形的性质因为正方形是特殊的平行四边形,还是特殊的矩形,特殊的菱形,所以它具有这些图形性质的综合,因此正方形有以下性质(由学生和老师一起总结).正方形性质定理1:正方形的四个角都是直角,四条边相等.正方形性质定理2:正方形的两条对角线相等并且互相垂直平分,每一条对角线平分一组对角.说明:定理2包括了平行四边形,矩形,菱形对角线的性质,一个题设同时有四个结论,这是该定理的特点,在应用时需要哪个结论就用哪个结论,并非把结论写全。
小结:(1)正方形与矩形,菱形,平行四边形的关系如上图(2)正方形的性质:①正方形对边平行。
②正方形四边相等。
③正方形四个角都是直角。
④正方形对角线相等,互相垂直平分,每条对角线平分一组对角.典型例题精讲例1.如图,折叠正方形纸片ABCD ,先折出折痕BD ,再折叠使AD 边与对角线BD 重合,得折痕DG ,使2AD =,求AG .【解析】:作GM ⊥BD,垂足为M . 由题意可知∠ADG=GDM , 则△ADG ≌△MDG . ∴DM=DA=2. AC=GM 又易知:GM=BM .而BM=BD-DM=22—2=2(2-1), ∴AG=BM=2(2-1).例2 .如图,P 为正方形ABCD 内一点,10PA PB ==,并且P 点到CD 边的距离也等于10,求正方形ABCD 的面积?【解析】:过P 作EF AB ⊥于F 交DC 于E .设PF x =,则10EF x =+,1(10)2BF x =+.由222PB PF BF =+. 可得:222110(10)4x x =++. 故6x =.216256ABCD S ==.例3。


几何模型07——半角模型一、正方形中夹半角模型(45°)例1.如图,已知正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°.求证:(1)EF=BE+DF;变式1.如图,已知正方形ABCD的边长为6,E,F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.(1)求证:EF=MF(2)若AE=2,求FC的长.变式2.在四边形ABCD中,AD∥BC(BC>AD),∠A=∠B=90°,AB=BC=20,E是AB上一点,且∠DCE=45°,BE=4,求DE的长.变式3.已知,正方形ABCD,M在CB延长线上,N在DC延长线上,∠MAN=45°.求证:MN=DN﹣BM.变式4.在平面直角坐标系中,已知A(x,y),点A作AB⊥y轴,垂足为B.若在x轴正半轴上取一点M,连接BM并延长至N,以BN为直角边作等腰Rt △BNE,∠BNE=90°,过点A作AF∥y轴交BE于点F,连接MF,设OM =a,MF=b,AF=c,试证明:=.例2.如图所示,过正方形ABCD的顶点A在正方形ABCD的内部作∠EAF=45°,E、F分别在BC、CD上,连接EF,作AH⊥EF于点H求证:AH=AB.变式1.已知△AMN中,∠MAN=45°,AH⊥MN于点H,且MH=3,NH=7,求AH的长.变式2.已知:如图,在正方形ABCD中,M在CB延长线上,N在DC延长线上,∠MAN=45°,AH⊥MN,垂足为H,求证:AH=AB.二、等腰直角三角形中的夹半角模型(45°)例3.已知Rt△ABC中,∠ACB=90°,AC=BC,点D、E在斜边AB上,且∠DCE=45°,证明:DE2=BE2+AD2;.变式1.如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,则MN的长为.变式2.如图,在△ABC中,AB=AC,点E,F是边BC所在直线上与点B,C不重合的两点.∠BAC=90°,∠EAF=135°,证明:EF2=EC2+BF2三、其他半角模型例4.在等边△ABC的两边AB,AC上分别有两点M,N,点D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC,DM≠DN,证明:MN=BM+NC.变式1.如图,在△ABC中,AB=AC,点E,F是边BC所在直线上与点B,C不重合的两点.∠BAC=60°,∠EAF=30°,已知BE=3,CF=5,求线段EF的长度;例5.如图,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD.求证:EF=BE+FD;变式1.如图,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD.求证:EF=BE+FD;变式2.如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=∠BAD.证明:EF=BE﹣FD,变式3.已知,如图,在四边形ABCD中,∠B+∠D=180°,AB=AD,E,F分别是线段BC,CD上的点,且BE+FD=EF.求证:∠EAF=∠BAD.变式4.已知△ABC中,AB=AC,∠BAC=120°.点M在BC上,点N在BC 的上方,且∠MBN=∠MAN=60°,求证:MC=BN+MN;。
夹半角模型夹半角模型是八年级全等三角形这一章中非常重要的模型,在武汉市的期中期末和月考考试中经常出现,他的特征是90°里面夹着45°,120°里面夹着60°,60°里面夹着30°,等等,类似这样的2倍角度或者一半的角度,通常会借助截长补短的方法,构造相等的角度构造全等三角形求解,谢老师通过多年的教学经验总结出以下典型例题供大家巩固提高。
1、如图,四边形ABCD 为正方形,∠MAN=45°,求证:DN+BM=MN解答:延长 CB 到 G,使 BG=DN,连接 AG ,∵AD=AB∠ADN=∠ABG=90°BG=DN ∴△ADN≅△ABG(SAS)∴AG=AN,∠GAB=∠DAN∴∠NAG=∠BAG+∠BAN=∠DAN+∠B AN=90°∴∠MAN=∠GAM=45°,DN=BGAG=AM ∴△AMN≅AGM(SAS)∴MN=GM∴DN+BM=MN2、四边形 ABCD 为正方形,∠MAN=45°,求证:DN-BM=MN解答:在 DN 上截取 DG,使 DG=BM,连接 AG∵AD=AB∠ADG=∠ABM=90°DG=BM ∴△ADG≅△ABM(SAS)∴AG=AM,∠DAG=∠BAM∴∠MAG=∠BAM+∠BAG=∠DAG+∠BAG =∠BAD=90°∠MAN=∠GAN=45°∵AG=AM∴△AMN≅△AGN(SAS)∴MN=GN=DN-BM3、如图,四边形ABCD 为正方形,DN+BM=MN,求证:∠MAN=45°解答:延长 CB 到 G,使 BG=DN,连接 AG ,∵AD=AB ,∠ADN=∠ABG=90°BG=DN∴△ADN≅△ABG(SAS)∴AG=AN,∠GAB=∠DAN∴∠NAG=∠BAG+∠BAN=∠DAN+∠BAN=90°∵DN+BM=MN∴BG+BM=MN=GM在△AMN与AGM中,AG=ANAM=AMMN=GM∴△AMN≅AGM(SSS)∴∠MAN=∠GAM=1/2X90°=45°4、四边形 ABCD 为正方形,DN-BM=MN,,求证:∠MAN=45°解答:在 DN 上截取 DG,使 DG=BM,连接 AG∵AD=AB ,∠ADG=∠ABM=90°DG=BM∴△ADG≅△ABM(SAS)∴AG=AM,∠DAG=∠BAM∴∠ MAG=∠BAM+∠BAG=∠DAG+∠BAG=∠BAD=90°∵DN-BM=MN ∴MN=GN在△AMN与AGM中,AG=AMAN=ANMN=GN∴△AMN≅AGN(SSS)∴∠MAN=∠GAN=1/2X90°=45°练习题:1、△ABD 中AB=AD,∠BAD=120°,∠MAN=60°,△BCD 为等边三角形,求证:DN+BM=MN2、△ABD 中AB=A D,∠BAD=120°,∠MAN=60°,△BCD 为等边三角形,求证:DN-BM=MN3、(2017秋·武昌月考)问题背景:“半角问题”(1)如图:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段EF,BE,FD之间的数量关系.小明同学探究此“半角问题”的方法是:延长FD到点G.使DG =BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是________;(直接写结论,不需证明)探索延伸:当聪明的你遇到下面的问题该如何解决呢?(2)若将(1)中“∠BAD=120°,∠EAF=60°”换为∠EAF=1/2∠BAD.其它条件不变.如图1,试问线段EF、BE、FD具有怎样的数量关系,并证明.(3)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=1/2∠BAD,请直接写出线段EF、BE、FD它们之间的数量关系.(不需要证明)(4)如图3,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=1/2∠BAD,试问线段EF、BE、FD具有怎样的数量关系,并证明.日期:2019/10/8 19:00:07;用户:王小帅;邮箱:*************************;学号:33475答案:1、解答:延长 CB 到 G,使 BG=DN,连接 AG;∵AD=AB ,∠ADN=∠ABG, BG=DN∴△ADN≅△ABG(SAS)∴AG=AN,∠GAB=∠DAN∴∠NAG=∠BAD=120°∴AG=AN,∠MAN=∠GAM=60°∴△AMN≅AGM(SAS)∴MN=GM∴DN+BM=MN2、解答:在 DN 上截取 DG,使 DG=BM,连接 AG ,∵AD=AB ,∠ADG=∠ABM,DG=BM∴△ADG≅△ABM(SAS)∴AG=AM,∠DAG=∠BAM∴∠MAG=∠BAD=120°∴∠MAN=∠GAN=60°∵AG=AM∠MAN=∠GAN=60°∴△AMN≅AGN(SAS)∴MN=GN∴DN-BM=MN3、【解答】(1)答案为:EF=BE+DF;(2)如图1,延长EB到G,使BG=DF,连接AG.∵在△ABG与△ADF中,AB =AD,∠ABG=∠A DF ,BG =DF,∴△ABG≌△ADF(SAS).∴AG=AF,∠1=∠2,∴∠1+∠3=∠2+∠3=1/2∠BAD=∠EAF.∴∠GAE=∠EAF.又AE=AE,易证△AEG≌△AEF.∴EG=EF.∵EG=BE+BG.∴EF=BE+FD(3)(1)中的结论EF=BE+FD仍然成立.理由是:如图2,延长EB到G,使BG=DF,连接AG.∵∠ABC+∠D=180°,∠ABG+∠ABC=180°,∴∠ABG=∠D,∵在△ABG与△ADF中,AB =AD,∠ABG=∠D,BG =DF,∴△ABG≌△ADF(SAS).∴AG=AF,∠1=∠2,∴∠1+∠3=∠2+∠3=∠BAD=∠EAF.∴∠GAE=∠EAF.又AE=AE,∴△AEG≌△AEF.∴EG=EF.∵EG=BE+BG.∴EF=BE+FD(4)结论EF=BE+FD不成立,应当是EF=BE﹣FD.证明:在BE上截取BG,使BG=DF,连接AG.∵∠B+∠ADC=180°,∠ADF+∠ADC=180°,∴∠B=∠ADF.∵在△ABG与△ADF中,AB =AD,∠ABG=∠A DF ,BG =DF,∴△ABG≌△ADF(SAS).∴∠BAG=∠DAF,AG=AF.∴∠BAG+∠EAD=∠DAF+∠EAD=∠EAF=1/2∠BAD.∴∠GAE=∠EAF.∵AE=AE,易证△AEG≌△AEF.∴EG=EF∵EG=BE﹣BG∴EF=BE﹣FD.更多的几何模型学习欢迎扫码加谢老师微信:。
几何图形之半角模型主题半角模型教学内容教学目标1。
掌握正方形的定义,弄清正方形与平行四边形、菱形、矩形的关系。
2。
掌握正方形的性质定理1和性质定理2。
3。
正确运用正方形的性质解题.4.通过四边形的从属关系渗透集合思想.5.通过理解四种四边形内在联系,培养学生辩证观点。
知识结构正方形的性质因为正方形是特殊的平行四边形,还是特殊的矩形,特殊的菱形,所以它具有这些图形性质的综合,因此正方形有以下性质(由学生和老师一起总结)。
正方形性质定理1:正方形的四个角都是直角,四条边相等.正方形性质定理2:正方形的两条对角线相等并且互相垂直平分,每一条对角线平分一组对角。
说明:定理2包括了平行四边形,矩形,菱形对角线的性质,一个题设同时有四个结论,这是该定理的特点,在应用时需要哪个结论就用哪个结论,并非把结论写全。
小结:(1)正方形与矩形,菱形,平行四边形的关系如上图(2)正方形的性质:①正方形对边平行.②正方形四边相等.③正方形四个角都是直角。
④正方形对角线相等,互相垂直平分,每条对角线平分一组对角。
典型例题精讲例1.如图,折叠正方形纸片ABCD ,先折出折痕BD ,再折叠使AD 边与对角线BD 重合,得折痕DG ,使2AD =,求AG .【解析】:作GM ⊥BD ,垂足为M . 由题意可知∠ADG=GDM, 则△ADG ≌△MDG . ∴DM=DA=2. AC=GM 又易知:GM=BM .而BM=BD —DM=22-2=2(2—1), ∴AG=BM=2(2—1).例2 .如图,P 为正方形ABCD 内一点,10PA PB ==,并且P 点到CD 边的距离也等于10,求正方形ABCD 的面积?【解析】:过P 作EF AB ⊥于F 交DC 于E .设PF x =,则10EF x =+,1(10)2BF x =+.由222PB PF BF =+. 可得:222110(10)4x x =++. 故6x =.216256ABCD S ==.例 3. 如图,E 、F 分别为正方形ABCD 的边BC 、CD 上的一点,AM EF ⊥,•垂足为M ,AM AB =,则有EF BE DF =+,为什么?【解析】:要说明EF=BE+DF ,只需说明BE=EM ,DF=FM 即可,而连结AE 、AF .只要能说明△ABE ≌△AME ,△ADF ≌△AMF 即可. 理由:连结AE 、AF .由AB=AM ,AB ⊥BC,AM ⊥EF,AE 公用, ∴△ABE ≌△AME . ∴BE=ME .同理可得,△ADF ≌△AMF .∴DF=MF .∴EF=ME+MF=BE+DF .例4.如下图E 、F 分别在正方形ABCD 的边BC 、CD 上,且45EAF ︒∠=,试说明EF BE DF =+.【解析】:将△ADF 旋转到△ABC ,则△ADF ≌△ABG∴AF=AG,∠ADF=∠BAG,DF=BG∵∠EAF=45°且四边形是正方形, ∴∠ADF ﹢∠BAE=45° ∴∠GAB ﹢∠BAE=45° 即∠GAE=45°∴△AEF ≌△AEG (SAS ) ∴EF=EG=EB ﹢BG=EB ﹢DF例5。
几何图形之半角模型主题半角模型教学内容教学目标1。
掌握正方形的定义,弄清正方形与平行四边形、菱形、矩形的关系.2.掌握正方形的性质定理1和性质定理2。
3.正确运用正方形的性质解题。
4。
通过四边形的从属关系渗透集合思想。
5.通过理解四种四边形内在联系,培养学生辩证观点。
知识结构正方形的性质因为正方形是特殊的平行四边形,还是特殊的矩形,特殊的菱形,所以它具有这些图形性质的综合,因此正方形有以下性质(由学生和老师一起总结)。
正方形性质定理1:正方形的四个角都是直角,四条边相等.正方形性质定理2:正方形的两条对角线相等并且互相垂直平分,每一条对角线平分一组对角。
说明:定理2包括了平行四边形,矩形,菱形对角线的性质,一个题设同时有四个结论,这是该定理的特点,在应用时需要哪个结论就用哪个结论,并非把结论写全。
小结:(1)正方形与矩形,菱形,平行四边形的关系如上图(2)正方形的性质:①正方形对边平行。
②正方形四边相等.③正方形四个角都是直角。
④正方形对角线相等,互相垂直平分,每条对角线平分一组对角。
典型例题精讲例1.如图,折叠正方形纸片ABCD ,先折出折痕BD ,再折叠使AD 边与对角线BD 重合,得折痕DG ,使2AD =,求AG .【解析】:作GM ⊥BD ,垂足为M . 由题意可知∠ADG=GDM, 则△ADG ≌△MDG . ∴DM=DA=2. AC=GM 又易知:GM=BM .而BM=BD-DM=22—2=2(2-1), ∴AG=BM=2(2-1).例2 .如图,P 为正方形ABCD 内一点,10PA PB ==,并且P 点到CD 边的距离也等于10,求正方形ABCD 的面积?【解析】:过P 作EF AB ⊥于F 交DC 于E .设PF x =,则10EF x =+,1(10)2BF x =+.由222PB PF BF =+. 可得:222110(10)4x x =++. 故6x =.216256ABCD S ==.例3。
中考模型解题系列之大角夹半角模型满分100分 答题时间30分钟1.(本小题100分) (2010重庆改编)等边的两边AB 、AC 所在直线上分别有两点M 、N ,D 为外一点,且,,BD=DC.探究:当M 、N 分别在直线AB 、AC 上移动时,BM 、NC 、MN 之间的数量关系及的周长Q 与等边的周长L 的关系.(I )如图1,当点M 、N 在边AB 、AC 上,且DM=DN 时,BM 、NC 、MN 之间的数量关系是_____________;此时___________;(II )如图2,点M 、N 在边AB 、AC 上,且当DM DN 时,猜想(I )问的两个结论还成立吗?写出你的猜想并加以证明;(III )如图3,当M 、N 分别在边AB 、CA 的延长线上时,若AN=,则Q=_________(用、L 表示).核心考点: 全等三角形的判定与性质 旋转的性质单选题(本大题共8小题,共100分)1.(本小题10分)Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD.把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m=()<M<M<M</M<M<M∙ A. 80°∙ B. 120°∙ C. 70°或120°∙ D. 80°或120°核心考点: 旋转的性质2.(本小题10分)如图,在平面直角坐标系中,点A的坐标为(0,2),点C是第二象限内一点,且AC=1,则∠AOC的取值范围是()∙ A. 0°<∠AOC≤60° B. 0°<∠AOC≤30° C. 30°≤∠AOC<90°D. 60°≤∠AOC<90°核心考点: 切线的性质坐标与图形性质3.(本小题10分)如图,在Rt△ABC中,∠C=90°,BC=3,AC=4.点D在BC边上运动(不与点B,C重合),点E是AB边上一点,且DC=DE,则DC的取值范围是()∙ A. B. C. D.核心考点: 直线与圆的位置关系4.(本小题10分)如图,在△ABC中,AB=15,AC=12,BC=9,经过点C且与边AB相切的动圆与CB、CA分别相交于点E、F,则线段EF长度的最小值是( )∙ A. B. C. D.核心考点: 切线的性质垂线段最短5.(本小题15分)如图,已知两点A,B在直线l的异侧,点A到直线l的距离AM=2,点B到直线l的距离BN=6,MN=3,点P在直线l上运动,则的最大值为()∙ A. B. C. D.核心考点: 三角形三边关系定理6.(本小题15分)如图,已知M是平行四边形ABCD中BC边的中点,DM交AC于E,则图中阴影部分的面积与平行四边形ABCD的面积之比是( )∙ A. B. C. D.核心考点: 相似三角形的判定与性质7.(本小题15分)如图,在△ABC中,∠ACB=90°,AC=2,BC=1,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动,在运动过程中,点B到原点O的最大距离为()∙ A. B. C. D. 3核心考点: 三角形任意两边之和大于第三边求最大距离8.(本小题15分)已知:二次函数的图象如图所示,下列结论中:①abc>0;②2a+b<0;③<M(AM+B)(M≠1)<M(AM+B)(M≠1);④(A+C)<B;④;⑤a>1.其中正确的项是( )</B</M(AM+B)(M≠1)<M(AM+B)(M≠1);④(A+C)∙ A. ①⑤ B. ①②⑤ C. ②⑤ D. ①③④核心考点: 二次函数综合题【中考数学必备专题】中考模型解题系列之弦图模型解答题(本大题共2小题,共100分)1.(本小题50分)(湖北襄阳)如图,点P是正方形ABCD边AB上一点(不与点A、B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F,连接BE、DF.(1)求证:∠ADP=∠EPB;(2)求∠CBE的度数;(3)当的值等于多少时,△PFD∽△BFP?并说明理由.核心考点: 相似三角形的判定与性质2.(本小题50分)如图,等腰梯形ABCD中,AD∥BC,AD=3cm,BC=7cm,∠B=60°,P是底边BC上一点(不和B、C重合),连接AP,过P作PE交DC于E,使得∠APE=∠B.(1)求证:△ABP∽△PCE;(2)求AB的长;(3)在底边BC上是否存在一点P,使得DE:EC=5:3?为什么?核心考点: 相似三角形的判定与性质本试卷为中考数学二次函数与几何综合的课后测试题1.(本小题15分)如图所示,在平面直角坐标系中,点B的坐标为(-3,-4),线段OB绕原点逆时针旋转后与x轴的正半轴重合,点B的对应点为点A,经过A,O,B三点的抛物线的解析式为()∙ A. B. C. D.核心考点: 二次函数与几何综合2.(本小题15分)如图所示,在平面直角坐标系中,点B的坐标为(-3,-4),线段OB绕原点逆时针旋转后与x轴的正半轴重合,点B的对应点为点A,在抛物线的对称轴上是否存在点C,使BC+OC的值最小?若存在,点C的坐标为()∙∙ A. 存在, B. 存在, C. 存在, D. 存在,核心考点: 二次函数与几何综合3.(本小题20分)如图所示,在平面直角坐标系中,点B的坐标为(-3,-4),线段OB绕原点逆时针旋转后与x轴的正半轴重合,点B的对应点为点A, 如果点P是抛物线上的一个动点,且在x轴的上方,设点P的横坐标为x,△PAB的面积为S,则S与x之间的函数关系式为(),当x等于()时,S有最大值.A. ,1B. ,2C. ,1∙ D. ,2核心考点: 二次函数与几何综合4.(本小题15分)已知:抛物线的顶点M的坐标为(1,-2)与y轴交于点,与x轴交于A、B两点(A在B的左边).此抛物线的表达式为()∙∙ A. B. C. D.核心考点: 二次函数与几何综合5.(本小题15分)已知:抛物线的顶点M的坐标为(1,-2)与y轴交于点,与x轴交于A、B两点(A在B的左边).点P是线段OB上一动点(不与点B重合),点Q在线段BM上移动且∠MPQ=45°,设线段OP=x,,则与x的函数关系式为()(写出自变量x的取值范围)∙ A. B.∙ C. D.核心考点: 二次函数与几何综合6.(本小题20分)已知:抛物线的顶点M的坐标为(1,-2)与y轴交于点,与x轴交于A、B两点(A在B的左边).在此抛物线的对称轴上是否存在点F,使△BMF是以BM为底边的等腰三角形?若存在,则点F的坐标为()A. (1,2)B.C. (1,0)D.。
半角模型半角模型:指的是一个大角夹着一个度数为它一半的角。
条件:四边形ABCD中,E、F分别在BC、CD(或延长线上),具备下列三个条件:①AB=AD(共顶点等线段);①①BAD=2①EAF;(共顶点的倍半角)①①B+①ADC=180°(或①BAD+①BCD=180°)(对角互补四边形)结论:EF=BE+DF (延长线上为EF=BE-DF);AE平分∠BEF,AF平分∠EFD。
情形一:角内含半角(补短)情形二:角外含半角(截长)模型一:90°夹45°例1、如图,点E、F分别是正方形BC、CD上的点,①EAF=45°,求证:(1)DF+BE=EF;(2)AE平分∠BEF,AF平分∠EFD证明:延长CB至点G,使得BG=DF(在CD上补BE亦可)△ABG≌△ADF(SAS)△AEG≌△AEF(SAS)90°外夹45°例2、如图,在正方形ABCD中,E、F为CB、DC延长线上点,且∠EAF=45°,探究线段EF、BE、DF之间的数量关系,并证明。
类型二、120°角夹60°例3、如图,在四边形ABCD中,AB=AD,∠BAD=120°,E,F分别为BC,CD上的点,∠EAF=∠C=60°,求证(1)EF=BE+DF;(2)点A在∠BCD的平分线上.练习:1.如图,四边形ABCD中,∠A=∠BCD=60°,∠ADC=60°,AB=BC,E、F分别在AD、DC延长线上,且∠EBF=60°,求证:AE=EF+CF例4、在等边△ABC的两边AB、AC所在直线上分别有两点M、N,D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC.探究:当M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系及△AMN的周长Q与等边△ABC的周长L的关系.(1)如图1,当点M、N边AB、AC上,且DM=DN时,BM、NC、MN之间的数量关系是;此时=;(2)如图2,点M、N在边AB、AC上,且当DM≠DN时,猜想(I)问的两个结论还成立吗?若成立请直接写出你的结论;若不成立请说明理由.(3)如图3,当M、N分别在边AB、CA的延长线上时,探索BM、NC、MN之间的数量关系如何?并给出证明.任意角夹半角例5、已知,如图,在四边形ABCD中,∠B+∠D=180°,AB=AD,E,F分别是线段BC,CD上的点,且BE+FD=EF.求证:∠EAF=∠BAD.练习(1)如图,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD 上的点,且∠EAF=∠BAD.求证:EF=BE+FD;(2)如图,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD 上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?(3)如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.例6、(1)如图1,已知正方形ABCD中,∠MAN=45°,猜想线段MN、BM与DN之间有怎样的关系?并证明.(2)如图2,已知四边形ABCD中,AB⊥BC于点B,AD⊥CD于点D,AB=AD,∠BAD =120°,∠MAN=60°,(1)中线段BM与DN之间的关系还成立吗?如果成立,请证明;如果不成立,请说明理由.(3)张大爷有一块五边形的土地,如图3,已知AB=AE=6,BC=4,DE=3,∠BAE =2∠CAD,AB⊥BC于点B,AE⊥DE于点E,请你帮助张大爷计算这块土地的面积.课后练习1.如图,等腰直角三角板的一个锐角顶点与正方形ABCD的顶点A重合,将此三角板绕点A旋转,使三角板中该锐角的两条边分别交正方形的两边BC、DC于点E、F,连结EF.若EF=5,DF=2,则BE的长为.(第1题) (第2题)2.如图,△ABC为等边三角形,BD=CD,∠BDC=120°,BC=2,M、N分别在边AB,AC上,且∠MDN=60°,则△AMN的周长等于.3.在四边形ABCD中,∠B+∠D=180°,CB=CD.以点C为顶点的∠ECF在四边形ABCD 的内部绕点C旋转,角的两边分别与AB、AD交于点E、F,∠ECF=∠BCD.(1)若∠BCD=120°,①如图1,当∠B=90°,∠BCE=30时,求证:EF=BE+DF;②如图2,当∠B≠90时,①中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由;③在∠ECF绕点C旋转的过程中,①中的结论是否仍然成立,请直接写出你的结论;(2)如图3,若∠BCD为任意的一个角(0°<∠BCD<180°),在∠ECF绕点C旋转的过程中,①中的三条线段BE,DF,EF之间的数量关系是否发生变化?若变化,请说明理由;若不变,请直接写出你的结论.4.如图1,四边形ABCD,将顶点为A的∠EAF绕着顶点A顺时针旋转,角的一条边与DC 的延长线交于点F,角的另一边与CB的延长线交于点E,连接EF.(1)如果四边形ABCD为正方形,当∠EAF=45°时,有EF=DF﹣BE.请你思考如何证明这个结论(只需思考,不必写出证明过程);(2)如图2,如果在四边形ABCD中,AB=AD,∠ABC=∠ADC=90°,当∠EAF=∠BAD时,EF与DF、BE之间有怎样的数量关系?请写出它们之间的关系式(3)如图3,如果在四边形ABCD中,AB=AD,∠ABC与∠ADC互补,当∠EAF=∠BAD时,EF与DF、BE之间有怎样的数学关系?请写出它们之间的关系式并给予证明;(4)在(3)中,若BC=4,DC=7,CF=2,求△CEF的周长(直接写出结果即可).5.已知正方形ABCD,一等腰直角三角板的一个锐角顶点与A重合,将此三角板绕A点旋转时,两边分别交直线BC、CD于M、N.(1)当M、N分别在边BC、CD上时(如图1),求证:BM+DN=MN;(2)当M、N分别在边BC、CD所在的直线上时(如图2),线段BM、DN、MN之间又有怎样的数量关系,请直接写出结论;(不用证明)(3)当M、N分别在边BC、CD所在的直线上时(如图3),线段BM、DN、MN之间又有怎样的数量关系,请写出结论并写出证明过程.6.问题背景:如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,探究图中线段BE、EF、FD之间的数量关系.小王同学探究此问题的方法是,延长FD到点G,使DG=BE.连结AG,先证明△ABE ≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;(2)探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,且∠EAF=∠BAD,上述结论是否仍成立,并说明理由;(3)实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(点O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等.接到行动指令后,舰艇甲向正东方向以45海里/时的速度前进,同时,舰艇乙沿北偏东50°的方向以60海里/时的速度前进,2小时后,指挥中心观察到甲、乙两舰艇分别到达E、F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.7.如图,△ABC和△DEF是两个等腰直角三角形,∠BAC=∠DFE=90°,AB=AC,FD =FE,△DEF的顶点E在边BC上移动,在移动过程中,线段DE与线段AB相交于点P,线段EF与线段CA相交于点Q.(1)如图1,当E为BC中点,且BP=CQ时,求证:△BPE≌△CQE;(2)如图2,当ED经过点A,且BE=CQ时,求∠EAQ的度数;(3)如图3,当E为BC中点,连接AE、PQ,若AP=3,AQ=4,PQ=5,求AC的长.11/ 11。
☞半角问题旋转模型图【例1】(1)已知:正方形ABCD 中,45MAN ∠=︒,MAN ∠绕点A 顺时针旋转,它的两边分别交线段CB DC 、于点M N 、.求证BM DN MN +=.全等模型——夹半角(2)已知:正方形ABCD 中,,M N 、分别是线段BC 、CD 边上一点,且BM DN MN +=.求证45MAN ∠=︒.【例2】(1)如图,在四边形ABCD 中,90AB AD B D ∠∠︒=,==,E F 、分别是边BC CD 、上的点,且12EAF =BAD ∠∠.求证:EF BE FD =+;(2)如图,在四边形ABCD 中,180AB AD B +D ∠∠︒=,=°,E F 、分别是边BC CD 、上的点,且12EAF BAD ∠=∠,(1)中的结论是否仍然成立?不用证明.(3)如图,在四边形ABCD 中,AB =AD ,∠B+∠ADC =180°,E 、F 分别是边BC 、CD 延长线上的点,且12EAF BAD ∠=∠,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.【例3】如图,在四边形ABCD 中,180∠+∠=︒=B D AB AD ,,E 、F 分别是线段BC 、CD 上的点,且BE +FD =EF .求证:12∠=∠EAF BAD .【例4】等边ABC ∆的两边AB ,AC 所在直线上分别有两点M N D ,,为ABC ∆外一点,且60MDN ∠=︒,120BDC ∠=︒,BD CD =,探究:当点M N ,分别爱直线AB AC ,上移动时,BM CN MN ,,之间的数量关系及AMN ∆的周长Q 与等边ABC ∆的周长L 的关系.(1)如图①,当点M N ,在边AB AC ,上,且DM DN =时,BM NC MN ,,之间的数量关系式_________;此时QL=__________(2)如图②,当点M N ,在边AB AC ,上,且DM DN ≠时,猜想(1)问的两个结论还成立吗?写出你的猜想并加以证明;(3)如图③,当点M N ,分别在边AB CA ,的延长线上时,若AN x =,则Q =_________(用x L ,表示)【例5】条件:正方形ABCD ,M 在CB 延长线上,N 在DC 延长线上,45MAN ∠=︒.结论:⑴MN DN BM =-;⑵点A 作AH ⊥MN 于点H ,求证:AH AB =.【例6】(1)如图1,点E F 、分别是正方形ABCD 的边BC CD 、上的点,45EAF ∠=︒,连接EF ,则EF BE FD 、、之间的数量关系是:EF BE FD =+.连结BD ,交AE AF 、于点M N 、,且MN BM DN 、、满足222DN BM MN +=,请证明这个等量关系;(2)在ABC 中,AB AC =,点D E 、分别为BC 边上的两点.①如图2,当60BAC ∠=︒,30DAE ∠=︒时,BD DE EC 、、应满足的等量关系是__________________;【例7】如图1,Rt ABC ∆≌Rt EDF ∆,90ACB F ∠=∠= ,30A E ∠=∠= .EDF ∆绕着边AB 的中点D 旋转,DE ,DF 分别交线段AC 于点M ,K .(1)观察:①如图2、图3,当0CDF ∠= 或60 时,AM CK +______MK (填“>”,“<”或“=”).②如图4,当∠CDF =30 时,AM CK +______MK (只填“>”或“<”).(2)猜想:如图1,当0 <∠CDF <60 时,AM CK +______MK ,证明你所得到的结论.(3)如果222MK CK AM +=,请直接写出CDF ∠度数和AMMK的值.图1图2图3图4【题1】E 、F 分别是正方形ABCD 的边BC 、CD 上的点,且45EAF =︒∠,AH EF ⊥,H 为垂足,求证:AH AB =.CHF ED BA【题2】如图所示,在正方形ABCD中,AB =点E 、F 分别在BC 、CD 上,且30BAE ∠=︒,15DAF ∠=︒,求AEF ∆的面积.FED CB A【题3】如图,正方形ABCD 的边长为1,AB 、AD 上各存一点P 、Q ,若APQ ∆的周长为2,求PCQ ∠的度数.【题4】如图,△ABC 是边长为3的等边三角形,△BDC 是等腰三角形,且∠BDC =120°.以D 为顶点作一个60°角,使其两边分别交AB 于点M ,交AC 于点N ,连接MN ,则△AMN 的周长为.【题5】已知如图,在正方形ABCD 中.⑴如果BE +DF =EF ,求证:①∠EAF =45°;②FA 平分∠DFE .⑵如果∠EAF =45°,求证:BE +DF =EF .⑶如果点F 在DC 的延长线上,点E 在CB 的延长线上,当BE 、DF 、EF 满足什么条件时,则⑴中结论仍然成立?A BCDEF【题6】如图,在四边形ABCD 中,180∠+∠=︒B ADC ,AB AD =,E 、F 分别是边BC 、CD 延长线上的点,且12EAF BAD =∠∠,求证:EF BE FD=-【题7】已知:如图,正方形ABCD 的边长为a ,BM ,DN 分别平分正方形的两个外角,且满足45MAN ∠=︒,连结MC ,NC ,MN .猜想线段BM ,DN 和MN 之间的等量关系并证明你的结论.【题8】小辉遇到这样一个问题:如图1,在Rt ABC △中,90BAC ∠︒=,AB AC =,点,E 在边BC 上,45DAE ∠︒=.若3BD =,1CE =,求DE 的长.小辉发现,将绕点A 按逆时针方向旋转90º,得到ACF ,连接EF (如图2),由图形旋转的性质和等腰直角三角形的性质以及45DAE ∠︒=,可证FAE DAE ≌,得FE DE =.解FCE ,可求得EF (即DE )的长.请回答:在图2中,FCE ∠的度数是__________,DE 的长为_______Rt ABC ____.参考小辉思考问题的方法,解决问题:如图3,在四边形ABCD 中,AB AD =,180B D ∠∠︒+=.E F ,分别是边BC CD ,上的点,且12EAF BAD ∠∠=.猜想线段BE EF FD ,,之间的数量关系并说明理由.图1图2图3。