【强烈推荐】梯形面积计算公式的练习题

小学数学梯形的面积练习题下面是一些小学数学的练题，主要涉及梯形的面积计算。

每个练题都有详细说明和解答步骤，供学生进行练和巩固知识。

练题一已知梯形的上底长度为 6 cm，下底长度为 10 cm，高度为 4 cm。

请计算该梯形的面积。

解答步骤：1. 首先，计算梯形的平均底长：（上底长 + 下底长）/ 2 = （6+ 10）/ 2 = 8 cm。

2. 然后，根据梯形面积公式，将平均底长和高度代入：面积 =平均底长 ×高度 = 8 × 4 = 32 cm²。

所以，该梯形的面积为 32 平方厘米。

练题二已知梯形的上底长度为 5 cm，下底长度为 9 cm，面积为 36 平方厘米。

请计算该梯形的高度。

解答步骤：1. 首先，根据梯形面积公式，将上底、下底和高度代入：36 = （5 + 9）/ 2 ×高度。

2. 将公式重组，解出高度：高度 = 36 × 2 / （5 + 9）= 6 cm。

所以，该梯形的高度为 6 厘米。

练题三已知梯形的面积为 63 平方厘米，上底长度为 7 cm，下底长度为 12 cm。

请计算该梯形的高度。

解答步骤：1. 首先，计算梯形的平均底长：（上底长 + 下底长）/ 2 = （7+ 12）/ 2 = 9.5 cm。

2. 然后，根据梯形面积公式，将平均底长和高度代入：63 =9.5 ×高度。

3. 将公式重组，解出高度：高度 = 63 / 9.5 = 6.63 cm。

所以，该梯形的高度约为 6.63 厘米。

通过这些练习题，希望能够加深对梯形面积计算的理解和掌握。

学生们可以使用这些练习题进行反复练习，提高解题能力和速度。

祝愿大家在学习数学的道路上取得更好的成绩！。

《梯形的面积》专项练习题梯形的面积专项练题题目一已知梯形ABCD，底边AB长度为6cm，上底边CD长度为10cm，高为4cm。

求梯形的面积。

解题思路：梯形的面积可以通过底边长度和高来计算。

公式为：面积 = (底边之和乘以高)除以2。

解题步骤：将底边AB和上底边CD长度相加得16cm，将16cm乘以高4cm得64，再将64除以2得32。

所以，梯形ABCD的面积为32平方厘米。

题目二已知等腰梯形EFGH，底边EF长度为8cm，上底边GH长度为12cm，高为5cm。

求梯形的面积。

解题思路：对于等腰梯形，梯形的面积也可以通过底边之和和高来计算。

解题步骤：将底边EF和上底边GH长度相加得20cm，将20cm乘以高5cm得100，再将100除以2得50。

所以，梯形EFGH的面积为50平方厘米。

题目三已知梯形IJKL，底边IJ长度为5cm，上底边KL长度为9cm，面积为36平方厘米。

求梯形的高。

解题思路：可以通过已知的梯形面积和底边长度来求得梯形的高。

公式为：高 = (2乘以面积)除以(底边之和)。

解题步骤：将面积36平方厘米乘以2得72，将底边IJ和上底边KL长度相加得14，将72除以14得5.14。

所以，梯形IJKL的高约为5.14厘米。

题目四已知等腰梯形MNOP，底边MN长度为12cm，上底边OP长度为16cm，面积为96平方厘米。

求梯形的高。

解题思路：与题目三类似，已知等腰梯形的面积和底边长度，可以通过公式求得梯形的高。

解题步骤：将面积96平方厘米乘以2得192，将底边MN和上底边OP长度相加得28，将192除以28得6.86。

所以，等腰梯形MNOP的高约为6.86厘米。

以上是梯形的面积专项练题。

五年级数学上册梯形计算练习题在五年级数学上册中，梯形是一个重要的图形。

它有四条边，其中两条边是平行的，另外两条不平行。

学生们需要学会如何计算梯形的面积和周长。

为了帮助同学们更好地掌握这个内容，下面将给出一些梯形计算的练习题。

练习题1：已知梯形的上底长为8cm，下底长为12cm，高为5cm。

求该梯形的面积和周长。

解答：首先，我们来计算面积。

梯形的面积可通过上底长和下底长以及高来计算。

根据公式，梯形的面积公式为：面积 = （上底长 + 下底长）×高 ÷ 2。

代入已知数据进行计算：面积 = （8cm + 12cm）× 5cm ÷ 2 = 20cm²。

接下来，我们计算周长。

梯形的周长可通过将上底长、下底长和两斜边的长度相加来计算。

代入已知数据进行计算：周长 = 8cm + 12cm + 两斜边长度。

需要注意的是，在这个题目中，我们没有给出两斜边的具体长度，所以无法准确计算周长。

练习题2：已知梯形的上底长为15cm，下底长为10cm，面积为75cm²。

求该梯形的高和周长。

解答：我们先来计算梯形的高。

梯形的面积公式为：面积 = （上底长 + 下底长）×高 ÷ 2，代入已知数据进行计算。

75cm² = （15cm + 10cm）×高 ÷ 2，化简得到 75cm² = 25cm ×高，进一步计算可得高 = 3cm。

接下来，我们计算梯形的周长。

由于已知上底长为15cm，下底长为10cm，我们需要求出两斜边的长度。

根据梯形的定义，两斜边长度相等，可以使用勾股定理进行计算。

根据勾股定理，两斜边的平方和等于梯形的高的平方加上上底长与下底长之差的一半的平方。

设两斜边长度为 x cm，则有：x² + x² = 3² + （15cm - 10cm ÷ 2）²。

梯形面积练习题(优选6篇）（经典版）编制人：__________________审核人：__________________审批人：__________________编制单位：__________________编制时间：____年____月____日序言下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!并且，本店铺为大家提供各种类型的经典范文，如计划总结、合同协议、管理制度、演讲致辞、心得体会、条据书信、好词好句、教学资料、作文大全、其他范文等等，想了解不同范文格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!Moreover, our store provides various types of classic sample essays for everyone, such as plan summaries, contract agreements, management systems, speeches, insights, evidence letters, good words and sentences, teaching materials, complete essays, and other sample essays. If you want to learn about different sample formats and writing methods, please pay attention!梯形面积练习题(优选6篇）梯形面积练习题（1）梯形的面积计算开心预习新课，轻松搞定基础。

小学五年级数学梯形面积练习题梯形是一种常见的四边形，它具有两组平行边，其中一组较长，被称为上底；另一组较短，被称为下底。

本文将为小学五年级的同学们提供一些关于梯形面积的练习题，帮助大家巩固对梯形面积的理解和计算能力。

练习题一：1. 某个梯形的上底长为6cm，下底长为10cm，高为4cm。

请计算该梯形的面积是多少？练习题二：2. 一个梯形的上底长为12cm，下底长为8cm，高为5cm。

请计算该梯形的面积是多少？练习题三：3. 一个梯形的上底长为7cm，下底长为9cm，高为6cm。

请计算该梯形的面积是多少？练习题四：4. 某个梯形的面积为28cm²，上底长为4cm，高为7cm。

请计算该梯形的下底长是多少？练习题五：5. 某个梯形的面积为72cm²，上底长为9cm，高为8cm。

请计算该梯形的下底长是多少？练习题六：6. 某个梯形的面积为45cm²，上底长为5cm，高为9cm。

请计算该梯形的下底长是多少？解答：练习题一：1. 上底长为6cm，下底长为10cm，高为4cm的梯形的面积计算公式为：面积 = (上底长 + 下底长) ×高 ÷ 2将具体数值代入公式，可以得到：面积 = (6 + 10) × 4 ÷ 2 = 16cm²所以该梯形的面积是16cm²。

练习题二：2. 上底长为12cm，下底长为8cm，高为5cm的梯形的面积计算公式为：面积 = (上底长 + 下底长) ×高 ÷ 2将具体数值代入公式，可以得到：面积 = (12 + 8) × 5 ÷ 2 = 50cm²所以该梯形的面积是50cm²。

练习题三：3. 上底长为7cm，下底长为9cm，高为6cm的梯形的面积计算公式为：面积 = (上底长 + 下底长) ×高 ÷ 2将具体数值代入公式，可以得到：面积 = (7 + 9) × 6 ÷ 2 = 48cm²所以该梯形的面积是48cm²。

梯形、平行四边形面积提高练习题1. 梯形ABCD中，AB = 5 cm，CD = 9 cm，高为4 cm。

求梯形的面积。

解答：梯形的面积公式为：面积 = （上底 + 下底）×高 ÷ 2代入已知数值：面积 = （5 + 9）× 4 ÷ 2计算得：面积 = 14 cm²2. 平行四边形EFGH中，边长为6 cm，高为3 cm。

求平行四边形的面积。

解答：平行四边形的面积公式为：面积 = 底边 ×高代入已知数值：面积 = 6 × 3计算得：面积 = 18 cm²3. 梯形PQRS中，上底PQ = 8 cm，下底RS = 12 cm，高为5 cm。

求梯形的面积。

解答：梯形的面积公式为：面积 = （上底 + 下底）×高 ÷ 2代入已知数值：面积 = （8 + 12）× 5 ÷ 2计算得：面积 = 50 cm²4. 平行四边形IJKL中，边长为7 cm，高为4 cm。

求平行四边形的面积。

解答：平行四边形的面积公式为：面积 = 底边 ×高代入已知数值：面积 = 7 × 4计算得：面积 = 28 cm²5. 梯形UVWX中，上底UV = 10 cm，下底WX = 16 cm，高为6 cm。

求梯形的面积。

解答：梯形的面积公式为：面积 = （上底 + 下底）×高 ÷ 2代入已知数值：面积 = （10 + 16）× 6 ÷ 2计算得：面积 = 78 cm²以上是梯形和平行四边形的面积提高练习题示例，希望对你的练习有所帮助。

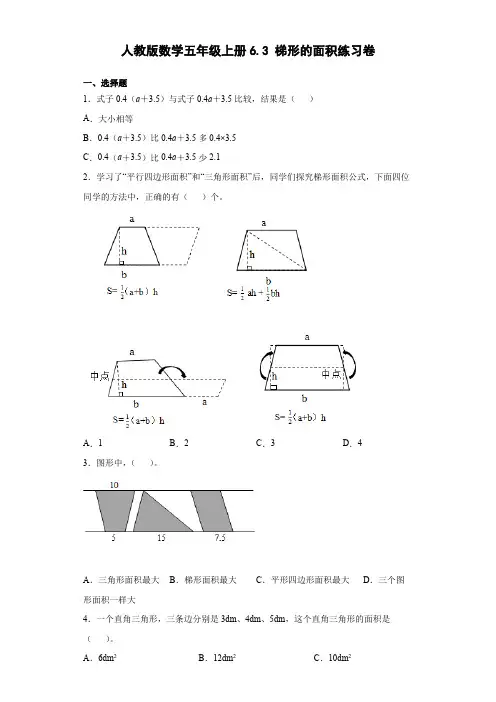
人教版数学五年级上册6.3 梯形的面积练习卷一、选择题1．式子0.4（a＋3.5）与式子0.4a＋3.5比较，结果是（）A．大小相等B．0.4（a＋3.5）比0.4a＋3.5多0.4×3.5C．0.4（a＋3.5）比0.4a＋3.5少2.12．学习了“平行四边形面积”和“三角形面积”后，同学们探究梯形面积公式，下面四位同学的方法中，正确的有（）个。

A．1B．2C．3D．43．图形中，（）。

A．三角形面积最大B．梯形面积最大C．平形四边形面积最大D．三个图形面积一样大4．一个直角三角形，三条边分别是3dm、4dm、5dm，这个直角三角形的面积是（）。

A．6dm2B．12dm2C．10dm25．一个直角梯形，上、下底和是20厘米，两条腰分别长10cm和18cm，求这个梯形的面积，正确的算式是（）A．20×10÷2B．（20+10）×12÷2C．20×12÷26．下列说法正确的有（）个。

①把一个平行四边形拉成一个长方形面积变大了。

①任意两个面积相等的三角形都可以拼成一个平行四边形。

①任意一个平行四边形都可以剪拼成一个长方形。

①两个完全一样的梯形可以拼成一个平行四边形。

A．1B．2C．3D．4二、文字题7．一个梯形面积是48平方厘米，已知上底和高都是6厘米，下底是多少？三、图形计算8．下面的平行四边形中，空白部分的面积是10平方分米，求涂色部分的面积．（单位：分米）四、填空题9．一个三角形的底是6dm，高为3dm，它的面积是( )dm2，和它等底等高的平行四边形的面积是( )dm2。

10．把一个梯形按下图所示的方法拼成一个三角形，这时三角形的底是( )，高是( )。

11．如图所示，正方形ABCD的边长是9cm，正方形DEFH的边长是6cm，HG长2cm．求：（1）直角梯形CEFH的面积是平方厘米．（2）三角形EFG的面积是三角形AHG面积的倍．（3）如果AE=CH，梯形ABCH的周长比三角形ADE的周长长厘米．12．一个等腰直角三角形的面积是100平方厘米，这个三角形的最长边等于厘米．13．计算下面图形的面积_____．(单位：厘米)14．一个直角梯形的上底是5厘米，如果把下底缩短3厘米，它就变成一个正方形，这个梯形的面积是( )平方厘米。

梯形的面积》习题精选4．一条水渠的横截面是一个梯形，渠口宽2.2 米，渠底宽 1.4 米，渠深 1.3 米，横截面面积是多少？圆木共多少根？5．一批同样的圆木，堆成的横截面成梯形．上层是5根，下层是10 根，一共堆 6 层，这批6．比较下面每组图形中两个阴影部分面积的大小，在“○”里画上“>”“<”或“＝”号．2）梯形（3）两个平行四边形高相等1）两个长方形的长和宽分别相等参考答案1．略平方米2．630 平方厘米8.12 平方厘米41403．略4． 2.34 平方米5．45根6．（1）＝（2）＝（3）＝梯形的面积》习题精选一、填空1．0.45 公顷＝（）平方米2．两个完全一样的梯形可以拼成一个（）形．3．一个梯形上底与下底的和是15 厘米，高是8.8 厘米，面积是（）平方厘米．4．平行四边形的底是 2 分米 5 厘米，高是底的 1.2 倍，它的面积是（）平方厘米．5．梯形的上底增加 3 厘米，下底减少 3 厘米，高不变，面积（）．6．有一堆圆木堆成梯形，最上面一层有 3 根，最下面一层有7 根，一共堆了 5 层，这堆圆木共有（）根．、判断题1．平行四边形的面积大于梯形面积．（）2．梯形的上底下底越长，面积越大．（）3．任何一个梯形都可以分成两个等高的三角形．（）4．两个形状相同的三角形可以拼成一个平行四边形．（）、选择1．两个（）梯形可以拼成一个长方形．①等底等高②完全一样③完全一样的直角2．等腰梯形周长是48 厘米，面积是96 平方厘米，高是8厘米，则两腰长是（）．①24厘米②12厘米③18厘米④36 厘米四、应用题1．一条水渠横截面是梯形，渠深0.8 米，渠底宽 1.2 米，渠口宽 2 米，横截面积是多少平方米？2．两个同样的梯形，上底长23厘米，下底长27 厘米，高20厘米．如果把这两个梯形拼成一个平行四边形，这个平行四边形的面积是多少？3．梯形的上底是 3.8 厘米，高是4厘米，已知它的面积是20 平方厘米，下底是多少厘米？参考答案一、填空1．0.45 公顷＝（4500 ）平方米2．两个完全一样的梯形可以拼成一个（平行四边）形．3．一个梯形上底与下底的和是15 厘米，高是8.8 厘米，面积是（66 ）平方厘米．4．平行四边形的底是 2 分米 5 厘米，高是底的 1.2 倍，它的面积是（750 ）平方厘米．5．梯形的上底增加 3 厘米，下底减少 3 厘米，高不变，面积（不变）．6．有一堆圆木堆成梯形，最上面一层有 3 根，最下面一层有7 根，一共堆了 5 层，这堆圆木共有（25 ）根．二、判断题1．平行四边形的面积大于梯形面积．（× ）2．梯形的上底下底越长，面积越大．（× ）3．任何一个梯形都可以分成两个等高的三角形．（√ ）4．两个形状相同的三角形可以拼成一个平行四边形．（√ ）三、选择1．两个（③ ）梯形可以拼成一个长方形．①等底等高②完全一样③完全一样的直角2．等腰梯形周长是48 厘米，面积是96 平方厘米，高是8厘米，则两腰长是① ）．（①24厘米②12厘米③18厘米④36 厘米四、应用题1．（ 1.2 ＋2）× 0.8 ÷ 2＝1.28 （平方米）答：横截面积是 1.28 平方米．2．（23＋27）× 20÷2× 2＝1000（平方厘米）答：这个平行四边形的面积是1000 平方厘米．3．20× 2÷4－3.8 ＝6.2 （厘米）答：下底是 6.2 厘米．例． 学校航空模型小组制作的飞机平面图，是由两个完全相同的梯形组成的，如图所示． 这个平面图的面积是多大？（图中单位：毫米）分析 ：机翼是由两个梯形组成的，所以解法可以是：根据梯形面积公式，求出一个梯形的面积，再乘 2，就得出了这个机翼平面图的面积． 解：（100＋48）× 250÷2×2 ＝ 148× 125÷2×2 ＝ 37000 （平方毫米）答：平面图的面积是 37000平方毫米．例．下图中直角梯形的面积是多少平方厘米？分析 ：要求梯形的面积，先要求出梯形的高，我们可以根据 45°这个角再连出一个梯形的 高，如下图连出的三角形为等腰直角三角形，这就得出梯形的高就是 2 厘米，解决了关键问题． 解：（4＋6）× 2÷ 2＝ 10（平方厘米） 答：直角梯形的面积是 10平方厘米．例．一个梯形，它的高与上底的乘积是15 平方厘米，高与下底的乘积是21 平方厘米，这个梯形的面积是多少平方厘米？分析：根据题意可知：高×上底＝15，高×下底＝21，所以：高×上底＋高×下底＝（上底＋下底）×高⋯⋯乘法分配率又因为（上底＋下底）×高＝梯形面积× 2，即15＋21＝36是梯形面积的 2 倍．解：（15＋21）÷ 2＝18（平方厘米）答：梯形面积是18 平方厘米．例．如图所示，为一直角梯形土地，已知阴影部分的面积为 2145 平方米，若在另一不知 面积的部分上种上水稻，每平方米收得稻谷 1.2 千克．可收水稻多少千克？分析 1：不知面积部分是三角形，已知其底是 60 米，关键是求出它的高．在直角梯形中，它的高就是阴影三角形的高，也是不知道．而已知面积的三角形的底为 78 米，高可求 出来，问题得解．解法 1： 60×（ 2145×2÷78）÷2×1.2＝60×55÷ 2×1.2 ＝3300÷2×1.2 ＝1650×1.2 ＝1980（千克）答：可收水稻 1980 千克．分析 2：可以先求出直角梯形的面积，再减去已知阴影部分的面积，同样可得解． 解法 2： [ （ 60＋ 78）×（ 2145× 2÷ 78）÷ 2－ 2145] × 1.2＝ [138 × 55 ÷ 2－ 2145] ×1.2 ＝（ 3795－ 2145）× 12 ＝1650×1.2 ＝1980（千克）答：可收水稻 1980千克．例．一个直角梯形，若下底增加 1.5 米，则面积就增加 3.15 平方米，上底增加 1.2 米，就得到一个正方形．这个直角梯形的面积是多少平方米？分析：若下底增加 1.5 米，则面积增加一个底为 1.5 米的三角形，已知三角形的面积是 3.15 平方米，底是 1.5 米，就可以求出该三角形的高，也就是梯形的高， 3.15×2÷1.5 ＝4.2 （米）．又知上底延长 1.2 米能得到一个正方形，说明梯形的下底和高相等，并且下底比上底多 1.2 米，这样可以求出梯形的上底， 4.2 － 1.2 ＝3（米），已知梯形上底3米，下底和高都是 4.2 米，可以求出直角梯形的面积．解：（3＋4.2 ）× 4.2 ÷2＝15.12 （平方米）答：这个直角梯形的面积是15.12 平方米．例．一个梯形， 如果它的上底增加 3 米，下底和高都不变， 那么它的面积就增加 9.6 平方米； 如果上底和下底都不变，高增加 3 米，那么它的面积就增加 18.6 米，求原梯形的面积．分析：根据题意，图中有阴影部分的三角形的面积就是 9.6 平方米，此三角形的底为 3 米，解： h ＝9.6 ×2÷3＝6.4 （米）a b18.623 6.2 （米） 原梯形的面积＝abh ＝6.2 × 6.4 ＝ 39.68 (平方米)答：原梯形的面积是 39.68 平方米．ab梯形的面积＝ h ．如果上、下底都不变，高增2ab ab a b(h 3) h 3．22 2从而可以求出高 h ， h 也是梯形的高．3 米，梯形的面积变为由 a 2b 318.6，可得ab 218.6 3 6.2 （米）．问题得解．是三角形的高， 再通过三角形的底和高分别计算甲、 乙的面积， 进而求出甲比乙的面积少多少平方厘米．解： 360× 2÷（ 10＋30）＝ 18（厘米）10×18÷2＝90（平方厘米）30×18÷2＝270（平方厘米） 270－90＝180（平方厘米）分析 2：根据梯形的性质，上底和下底平行，所以甲和乙这两个三角形的高相等．由已知条 件乙三角形的底是甲三角形底的3倍（ 30÷10），所以乙的面积是甲的 3 倍，即乙的面 积比甲多 2 倍．梯形面积一共是 360 平方米，一共分成 4 份，一份是 90 平方米，所以 甲比乙少 90× 2＝180 平方米．解： 30÷10＝3360÷（ 3＋1）×（ 3－1） ＝ 90× 2＝ 180 （平方米） 答：甲的面积比乙少 180 平方厘米．例1．分析 1：已知梯形的面积是 360 平方厘米，又知梯形的上底和下底，可以求出梯形的高，也所得的差．解： 60×28－（ 36＋24）× 10÷2＝ 1680－ 300 ＝ 1380 （平方毫米）答：这个零件横截面的面积是 1380平方毫米．例．已知ABC和EFG 是两个完全一样的直角三角形，BD 4，DF 3，FG 12，求梯形ABDE 的面积．分析：因为ABC和EFG面积相等，从中同时减去EDC ，剩下的面积也一定相等，即：梯形ABDE 与梯形DFGC的面积相等，也就是说，要求梯形ABDE 的面积，只要求出梯形DFGC 的面积就可以了．解：在梯形DFGC 中，DC 12 4 8，DF 3，FG 12（8＋12）× 3÷ 2＝30答：梯形ABDE 的面积是30．。

新版教材五年级梯形的面积练习题
一、计算下列梯形的面积：
1. 梯形ABCD，底边AB = 6 cm，上底CD = 10 cm，高h = 4 cm。

请计算梯形ABCD的面积。

解答：梯形ABCD的面积可以通过以下公式计算：面积 = (底边AB + 上底CD) ×高 ÷ 2。

将给定的数值代入公式中，可以计算得到梯形ABCD的面积：
面积 = (6 cm + 10 cm) × 4 cm ÷ 2 = 16 cm²
2. 梯形EFGH，底边EF = 8 cm，上底GH = 12 cm，高h = 5 cm。

请计算梯形EFGH的面积。

解答：同样地，使用梯形面积公式计算梯形EFGH的面积：面积 = (底边EF + 上底GH) ×高 ÷ 2 = (8 cm + 12 cm) × 5 cm ÷2 = 40 cm²
二、综合练题：
3. 一个梯形的上底比下底大4 cm，高为5 cm。

如果梯形的面积为60 cm²，求该梯形的上底和下底分别是多少？
解答：设梯形的下底为x cm，则上底为(x + 4) cm。

根据梯形面积公式，可以列出方程：
60 cm² = (x + x + 4) cm × 5 cm ÷ 2
解方程得：10x + 20 = 600
解得：x = 58
因此，该梯形的下底为58 cm，上底为62 cm。

以上是新版教材五年级梯形的面积练题。

希望能对你的研究有所帮助。

小学求梯形面积10题
以下是10道适合小学生求解梯形面积的题目：
1.一个梯形的上底是6厘米，下底是10厘米，高是4厘米，求它的面积。

2.一个梯形的面积是65平方厘米，上底是7厘米，下底是13厘米，求它的高。

3.一个梯形的上底是12分米，下底是18分米，高是9分米，求它的面积。

4.一个梯形的面积是144平方厘米，上底是10厘米，下底是16厘米，求它的高。

5.一个梯形的上底是15米，下底是20米，高是8米，求它的面积。

6.一个梯形的面积是210平方厘米，上底是14厘米，下底是20厘米，求它的高。

7.一个梯形的上底是24分米，下底是30分米，高是15分米，求它的面积。

8.一个梯形的面积是448平方厘米，上底是28厘米，下底是42厘米，求它的高。

9.一个梯形的上底是33米，下底是44米，高是20米，求它的面积。

10.一个梯形的面积是770平方厘米，上底是35厘米，下底是49厘米，求它的高。

这些题目旨在帮助学生熟悉梯形面积的计算公式，即面积= (上底+ 下底) ×高÷ 2，并能够根据已知的信息进行计算。

在解答这些题目时，学生需要理解梯形面积的计算公式，并能够正确应用这个公式进行计算。

同时，他们还需要注意单位的正确书写和使用，以及计算的准确性。

梯形的面积练习题
温馨提示：不要忘记梯形的面积=（上底+下底）×高÷2
用字母表示：S=（a+b ）×h ÷2
1、计算梯形的面积。

2、填空
12.5公顷=（ ）平方米 78000平方米=（ ）公顷 680平方厘米=（ ）平方分米 0.75平方米=（ ）平方分米
3、判断，对的在（ ）里面“√”，错的画“×”。

（1）平行四边形的面积一定比梯形面积大。

（ ）
（2）两个面积相等的梯形可以拼成一个平行四边形。

（ ）
（3）梯形的面积等于梯形的上底加下底的和乘高。

（ ）
4、计算下面每个梯形的面积。

（1）上底:2.5m ，下底:3.8m ，高:2m （2）上底:5dm ，下底:4dm,高:3.5dm
56
7、应用题
（1）有一块梯形菜地，上底长15m，下底长28m，高14.7m，如果每平方米疏菜收入36.5元，这块菜地的总收入是多少元？
（2）一个加工厂运来一批钢管。

把它堆成梯形状，最上层有6根，最下层有14根。

从上往下数共有9层。

这批钢管共有多少根？
（3）王大爷在自家墙外围成一个养鸡场（如右图），围鸡场的篱笆的总长是22m，其中一条边是8m，求养鸡场的面积。

（4）一个梯形广告牌，它的上底是8米，下底是12米，高是6米。

如果要给这个广告牌正反两面都涂上油漆，按每平方米花费15元来计算，共要花多少元？
5、在方格纸上画出面积相等的三角形和梯形。

梯形和菱形的面积练习题1. 梯形的面积计算题目：已知梯形的上底长度为10 cm，下底长度为16 cm，高度为8 cm，求该梯形的面积。

已知梯形的上底长度为10 cm，下底长度为16 cm，高度为8 cm，求该梯形的面积。

解答：梯形的面积计算公式为：$$\text{面积} = \frac{{(\text{上底长} + \text{下底长}) \times\text{高度}}}{2}$$代入已知数值，可得：$$\text{面积} = \frac{{(10 + 16) \times 8}}{2} = \frac{{26 \times 8}}{2} = 104 \, \text{cm}^2$$所以，该梯形的面积为104平方厘米。

2. 菱形的面积计算题目：已知菱形的对角线长度分别为12 cm和16 cm，求该菱形的面积。

已知菱形的对角线长度分别为12 cm和16 cm，求该菱形的面积。

解答：菱形的面积计算公式为：$$\text{面积} = \frac{{d_1 \times d_2}}{2}$$其中，$d_1$和$d_2$分别表示菱形的两条对角线长度。

代入已知数值，可得：$$\text{面积} = \frac{{12 \times 16}}{2} = \frac{{192}}{2} = 96 \, \text{cm}^2$$所以，该菱形的面积为96平方厘米。

3. 综合练题题目：画出一个梯形和一个菱形，并计算它们的面积。

画出一个梯形和一个菱形，并计算它们的面积。

解答：首先，画出梯形和菱形如下图所示：_________/ \/ \-------------其中，梯形的上底长度为8 cm，下底长度为12 cm，高度为6 cm；菱形的对角线长度分别为10 cm和8 cm。

梯形的面积计算：$$\text{面积} = \frac{{(8 + 12) \times 6}}{2} = \frac{{20 \times 6}}{2} = 60 \, \text{cm}^2$$菱形的面积计算：$$\text{面积} = \frac{{10 \times 8}}{2} = \frac{{80}}{2} = 40 \,\text{cm}^2$$所以，梯形的面积为60平方厘米，菱形的面积为40平方厘米。

梯形的面积经典例题五年级一、梯形面积基础计算例题。

1. 一个梯形的上底是3厘米，下底是5厘米，高是4厘米。

求这个梯形的面积。

- 解析：根据梯形面积公式S=(a + b)h÷2（其中a为上底，b为下底，h为高）。

这里a = 3厘米，b=5厘米，h = 4厘米。

- 计算：S=(3 + 5)×4÷2=8×4÷2 = 16（平方厘米）。

2. 梯形的上底是4.5分米，下底是6.5分米，高是3分米，它的面积是多少？- 解析：同样运用梯形面积公式，a = 4.5分米，b = 6.5分米，h=3分米。

- 计算：S=(4.5+6.5)×3÷2 = 11×3÷2=16.5（平方分米）。

3. 已知梯形的上底为2米，下底为4米，高为2.5米，求面积。

- 解析：按照公式S=(a + b)h÷2，a = 2米，b = 4米，h = 2.5米。

- 计算：S=(2 + 4)×2.5÷2=6×2.5÷2 = 7.5（平方米）。

二、已知面积求梯形的底或高例题。

4. 一个梯形的面积是20平方厘米，上底是3厘米，高是4厘米，求下底。

- 解析：根据梯形面积公式S=(a + b)h÷2，可推出b = 2S÷h - a。

已知S = 20平方厘米，a = 3厘米，h = 4厘米。

- 计算：b = 2×20÷4-3=10 - 3=7（厘米）。

5. 梯形的面积是18平方分米，下底是5分米，高是3分米，求上底。

- 解析：由S=(a + b)h÷2可得a = 2S÷h - b，这里S = 18平方分米，b = 5分米，h = 3分米。

- 计算：a = 2×18÷3 - 5=12 - 5 = 7（分米）。

6. 已知梯形面积为25平方米，上底是4米，下底是6米，求高。

梯形面积的计算一、复习旧知（一）求出下面图形的面积（二）回忆三角形面积公式的推导过程（演示课件：拼摆三角形）（三）学生讨论：在日常生活中你见过哪些物品是梯形的？二（一）梯形面积公式的推导。

1．小组合作操作讨论（1）用两个完全一样的梯形可以拼成一个形。

（2）这个平行四边形的底等于；高等于。

（3）每一个梯形的面积等于平行四边形面积的。

（4）梯形的面积等于。

3．学生概括总结，归纳公式梯形面积=（+ ）×÷2S= ( + )×÷2(二)教学例1。

例3：我国三峡水电站大坝的横截面的一部分是梯形（如下图），求它的面积。

1．教师提问：已知什么？求什么？怎样解答？（二）计算下面梯形的面积（二）动手测量学具（梯形）的相关数据，并计算梯形学具的面积。

（三）下面是一个水电站拦河坝的横截面图，求它的面积。

【基础知识自主学习】一、填空题.1.两个( )的梯形可以拼成一个( )。

梯形的上底和下底的和等于( )，梯形的高等于( )的高，每个梯形的面积等于拼成的( )的面积的一半，用字母公式表示是( )。

2.求梯形的面积，必须知道( )个条件，它们分别是( )。

3.一个梯形的面积是4.2平方分米，它的下底与一个平行四边形的底边相等，高等于平行四边形的高，这个平行四边形的面积是( )平方分米。

4.一个梯形的面积是76平方厘米，下底是12厘米，上底是8厘米，梯形的高是( )厘米。

5.一个梯形的面积是28平方米，它的高是7米，上底是3米，下底是( )米。

二、计算下面每个梯形的面积(单位：米)【基本能力达标学习】一、判断.(对的打“√”，错的打“×”)1.三角形面积总是平行四边形面积的一半.( )2.正方形和长方形也是平行四边形.( )3.两个梯形可以拼成一个平行四边形.( )4.等底等高的两个三角形面积相等，形状也相同.( )5.平行四边形的面积或梯形面积的大小分别与它们的底和高有关，与它们的形状和位置无关.( )6.两个面积相等、形状一样的梯形，可以拼成一个平行四边形，拼成的平行四边形的面积是梯形面积的2倍.( )二、应用题.1.一个平行四边形和一个梯形的高都是6厘米，梯形上底与平行四边形的上底都是10厘米，梯形上底比下底多3厘米，梯形面积比平行四边形的面积少多少?2.一块木板的面积是2.25平方米，锯成上底是0.6米，下底是0.4米，高是0.5米的梯形，最多可以锯多少块?3.秦王川灌区修了一条水渠，上口宽9米，下口宽6.5米，深5.4米，这条水渠横截面积是多少平方米?4.一块梯形地，上底是30米，下底减少10米变成一个平行四边形，它的面积就是1500平方米，原来梯形的面积是多少?【理解运用探究学习】计算下面每个图形阴影部分的面积。

人教版五年级数学上册梯形的面积练习题五年级数学上册梯形的面积梯形的面积可以用公式 S=(a+b)×h÷2 表示，其中 a 和 b 分别表示上底和下底的长度，h 表示梯形的高。

一、填空1.13.6公顷=xxxxxxx平方米，平方米=0.67公顷，650平方厘米=0.065平方分米，0.48平方米=480平方分米，4.8平方米=480平方分米，62平方厘米=0.0062平方分米，1.2公顷=平方米，1.2平方千米=120公顷，650平方分米=0.065平方米，平方米=3.5公顷。

2.两个相等的梯形可以拼成一个平行四边形，这个平行四边形的底等于两个梯形的上底之和，高等于梯形的高，每个梯形的面积等于拼成的平行四边形面积的一半。

3.这个梯形的面积是 21 平方米。

4.这个梯形的面积是 58.5 平方米。

5.这个梯形的高是 1 平方分米。

6.这个梯形的下底是 16.5 米。

7.这个梯形的面积是 336 平方厘米。

三、判断1.×2.√3.√4.×5.×6.√7.√四、计算梯形面积1.这个梯形的面积是 5.5 平方米。

2.这个梯形的面积是 2.4 平方米。

3.这个梯形的面积是 162 平方米。

4.这个梯形的面积是 18 平方厘米。

五、应用题1.这条水渠的横截面面积是 (2.6+2)×1.5÷2=3.45 平方米。

2.这块梯形菜地的面积是 (16+28)×14.5÷2=406 平方米，总收入是 406×43= 元。

3.这批钢管共有 (5+12)×8÷2=68 根。

4.这个梯形荔枝园的面积是(250+180)×50÷2=7000 平方米，可种荔枝树的棵数是 7000÷5=1400 棵。

5、XXX在自家墙外围成一个养鸡场，围鸡场的篱笆的总长是26m，其中一条边是8m，求养鸡场的面积。

梯形的面积练习题：一、求下面梯形的面积：上底2米下底3米高5米上底4分米下底5分米高2分米上底48米，下底56米，高35米。

上底124米，下底76米，高82米。

上底80米，下底50米，高60米。

上底15分米,下底9分米，高比下底长1分米。

下底24厘米,上底是下底的一半，高1分米。

上底5厘米，下底8厘米,高6厘米上底2。

4分米,下底7.6分米，高8分米二、填空：1、两个完全一样的梯形可以拼成一个（ )形，这个拼成的图形的底等于梯形的（）与（）的和,高等于梯形的（），每个梯形的面积等于拼成的平行四边形面积的（）。

3、梯形的上底是a，下底是b,高是c,则它的面积＝( ）4、一个梯形上底与下底的和是15米,高是4米，面积是( ）平方米。

5、一个梯形的面积是8平方厘米，如果它的上底、下底和高各扩大2倍，它的面积是（ )平方厘米.6、用两个完全一样的梯形拼成一个平行四边形,已知每个梯形的面积是24平方分米，拼成的平行四边形的面积是多少平方分米？三、判断：1、梯形的面积等于平行四边形的面积的一半。

（）2、两个完全相同的直角梯形，可以拼成一个长方形。

（ )3、一个上底是5厘米，下底是8厘米，高是3厘米的梯形，它的面积是12平方厘米。

（）4、一个梯形的上底是３分米，下底是５分米，高是４分米，面积就是32平方分米.(）四、应用题1、一座小型拦河坝,横截面的上底5米,下底131米,高21米。

这座拦河坝的横截面积是多少？2、一块梯形稻田,上底长8米，下底比上底长1.2米,高是上底的2倍。

这块稻田的面积是多少平方米？3、一块梯形草坪的面积是90平方米，上底是6米，下底是12米，高是多少米？4、一块梯形的果园,它的上底是160米，下底是120米,高30米。

如果每棵果树占地10平方米，这个果园共有树多少棵？5、用65米长的篱笆沿墙边围一个直角梯形的鸡舍,梯形的直角边是15米，你能计算出围成的鸡舍的面积吗？6、有一块梯形地，上底长64米，比下底短16米，高50米。

一、基础计算题1. 已知梯形的上底为5厘米，下底为10厘米，高为6厘米，求该梯形的面积。

2. 梯形的上底为8厘米，下底为12厘米，高为5厘米，计算梯形的面积。

3. 一块梯形菜地的上底为3米，下底为6米，高为2米，求菜地的面积。

4. 梯形的上底为4分米，下底为8分米，高为3分米，求梯形的面积。

5. 已知梯形的上底为7厘米，下底为14厘米，面积为84平方厘米，求梯形的高。

二、应用题6. 一块梯形土地的上底为50米，下底为100米，高为40米，求这块土地的面积。

7. 某梯形广告牌的上底为4米，下底为8米，高为3米，求广告牌的面积。

8. 一座梯形水坝的上底为30米，下底为60米，高为20米，求水坝的面积。

9. 一块梯形麦田的上底为200米，下底为400米，高为100米，求麦田的面积。

10. 一块梯形果园的上底为15米，下底为30米，面积为225平方米，求果园的高。

三、拓展题11. 已知等腰梯形的上底为10厘米，下底为20厘米，面积为150平方厘米，求等腰梯形的高。

12. 一块等腰梯形菜地的上底为8米，下底为16米，高为6米，求菜地的面积。

13. 梯形的上底为12厘米，下底为18厘米，面积为90平方厘米，求梯形的高。

14. 一块等腰梯形土地的上底为40米，下底为80米，高为30米，求土地的面积。

15. 已知等腰梯形的上底为6分米，下底为12分米，高为4分米，求等腰梯形的面积。

四、综合运用题16. 一个梯形的上底和下底之和为18厘米，高为6厘米，面积是72平方厘米，求该梯形的上底和下底各是多少厘米。

17. 一个梯形的上底比下底短6厘米，高为4厘米，面积为24平方厘米，求梯形的上底和下底。

18. 两个梯形面积相等，一个梯形的上底为8厘米，下底为12厘米，高为5厘米，另一个梯形的上底为10厘米，下底为14厘米，求另一个梯形的高。

19. 一块梯形草地被分成两个面积相等的部分，已知整个草地的上底为20米，下底为40米，高为10米，求分割线所在的高。