下载文档原格式
第一章 流体及其物理性质1－1 已知油的重度为7800N/m 3，求它的密度和比重。
又，0.2m 3此种油的质量和重量各为多少？已已知知：：γ＝7800N/m 3；V ＝0.2m 3。
解解析析：：(1) 油的密度为 3kg/m 79581.97800===gγρ； 油的比重为 795.01000795OH 2===ρρS (2) 0.2m 3的油的质量和重量分别为 kg 1592.0795=⨯==V M ρ N 15602.07800=⨯==V G γ1－2 已知300L(升)水银的质量为4080kg ，求其密度、重度和比容。
已已知知：：V ＝300L ，m ＝4080kg 。
解解析析：：水银的密度为 33kg/m 13600103004080=⨯==-V m ρ 水银的重度为 3N/m 13341681.913600=⨯==g ργ 水银的比容为 kg /m 10353.7136001135-⨯===ρv1－3 某封闭容器内空气的压力从101325Pa 提高到607950Pa ，温度由20℃升高到78℃，空气的气体常数为287.06J/k g ·K 。
问每kg 空气的体积将比原有体积减少多少？减少的百分比又为多少？已已知知：：p 1＝101325Pa ，p 2＝607950Pa ，t 1＝20℃，t 2＝78℃，R ＝287.06J/k g ·K 。
解解析析：：由理想气体状态方程(1－12)式，得 kg /m 83.0101325)27320(06.2873111=+⨯==p RT v kg /m 166.0607950)27378(06.2873222=+⨯==p RT v kg /m 664.0166.083.0321=-=-v v%80%10083.0166.083.0%100121=⨯-=⨯-v v v每kg 空气的体积比原有体积减少了0.664m 3；减少的百分比为80％。
第一章 绪论1-1．20℃的水2.5m 3，当温度升至80℃时，其体积增加多少？ [解] 温度变化前后质量守恒，即2211V V ρρ= 又20℃时，水的密度31/23.998m kg =ρ 80℃时，水的密度32/83.971m kg =ρ 321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆1-2．当空气温度从0℃增加至20℃时，运动粘度ν增加15%，重度γ减少10%，问此时动力粘度μ增加多少（百分数）？ [解] 原原ρννρμ)1.01()15.01(-+==原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμ此时动力粘度μ增加了3.5%1-3．有一矩形断面的宽渠道，其水流速度分布为μρ/)5.0(002.02y hy g u -=，式中ρ、μ分别为水的密度和动力粘度，h 为水深。
试求m h 5.0=时渠底（y =0）处的切应力。
[解] μρ/)(002.0y h g dydu-=)(002.0y h g dydu-==∴ρμτ 当h =0.5m ，y =0时)05.0(807.91000002.0-⨯⨯=τPa 807.9=1-4．一底面积为45×50cm 2，高为1cm 的木块，质量为5kg ，沿涂有润滑油的斜面向下作等速运动，木块运动速度u=1m/s ，油层厚1cm ，斜坡角22.620 （见图示），求油的粘度。
[解] 木块重量沿斜坡分力F 与切力T 平衡时，等速下滑yu AT mg d d sin μθ== 001.0145.04.062.22sin 8.95sin ⨯⨯⨯⨯==δθμu A mg s Pa 1047.0⋅=μ1-5．已知液体中流速沿y 方向分布如图示三种情况，试根据牛顿内摩擦定律yud d μτ=，定性绘出切应力沿y 方向的分布图。
[解]1-6．为导线表面红绝缘，将导线从充满绝缘涂料的模具中拉过。
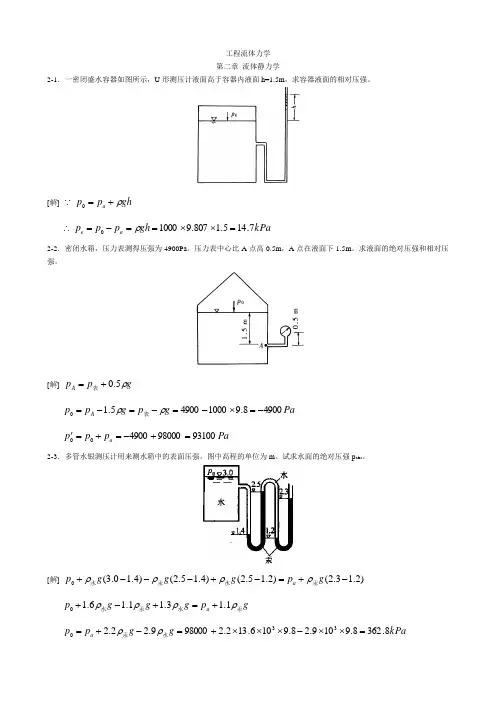
工程流体力学 第二章 流体静力学2-1．一密闭盛水容器如图所示，U 形测压计液面高于容器内液面h=1.5m ，求容器液面的相对压强。
[解] gh p p a ρ+=0kPa gh p p p a e 7.145.1807.910000=⨯⨯==-=∴ρ2-2．密闭水箱，压力表测得压强为4900Pa 。
压力表中心比A 点高0.5m ，A 点在液面下1.5m 。
求液面的绝对压强和相对压强。
[解]g p p A ρ5.0+=表Pa g p g p p A 49008.9100049005.10-=⨯-=-=-=ρρ表 Pa p p p a 9310098000490000=+-=+=' 2-3．多管水银测压计用来测水箱中的表面压强。
图中高程的单位为m 。
试求水面的绝对压强p abs 。
[解])2.13.2()2.15.2()4.15.2()4.10.3(0-+=-+---+g p g g g p a 汞水汞水ρρρρ g p g g g p a 汞水汞水ρρρρ1.13.11.16.10+=+-+kPa g g p p a 8.3628.9109.28.9106.132.2980009.22.2330=⨯⨯-⨯⨯⨯+=-+=水汞ρρ2-4． 水管A 、B 两点高差h 1=0.2m ，U 形压差计中水银液面高差h 2=0.2m 。
试求A 、B 两点的压强差。
（22.736N ／m 2）[解] 221)(gh p h h g p B A 水银水ρρ+=++Pa h h g gh p p B A 22736)2.02.0(8.9102.08.9106.13)(33212=+⨯⨯-⨯⨯⨯=+-=-∴水水银ρρ2-5．水车的水箱长3m,高1.8m ，盛水深1.2m ，以等加速度向前平驶，为使水不溢出，加速度a 的允许值是多少？[解] 坐标原点取在液面中心，则自由液面方程为：x gaz -=0 当m lx5.12-=-=时，m z 6.02.18.10=-=，此时水不溢出 20/92.35.16.08.9s m x gz a =-⨯-=-=∴2-6．矩形平板闸门AB 一侧挡水。
第一章 流体及其物理性质1－1 已知油的重度为7800N/m 3，求它的密度和比重。
又，0.2m 3此种油的质量和重量各为多少？已已知知：：γ＝7800N/m 3；V ＝0.2m 3。
解解析析：：(1) 油的密度为 3kg/m 79581.97800===gγρ； 油的比重为 795.01000795OH 2===ρρS (2) 0.2m 3的油的质量和重量分别为 kg 1592.0795=⨯==V M ρ N 15602.07800=⨯==V G γ1－2 已知300L(升)水银的质量为4080kg ，求其密度、重度和比容。
已已知知：：V ＝300L ，m ＝4080kg 。
解解析析：：水银的密度为 33kg/m 13600103004080=⨯==-V m ρ 水银的重度为3N/m 13341681.913600=⨯==g ργ水银的比容为 kg /m 10353.7136001135-⨯===ρv1－3 某封闭容器内空气的压力从101325Pa 提高到607950Pa ，温度由20℃升高到78℃，空气的气体常数为287.06J/k g ·K 。
问每kg 空气的体积将比原有体积减少多少？减少的百分比又为多少？已已知知：：p 1＝101325Pa ，p 2＝607950Pa ，t 1＝20℃，t 2＝78℃，R ＝287.06J/k g ·K 。
解解析析：：由理想气体状态方程(1－12)式，得 kg /m 83.0101325)27320(06.2873111=+⨯==p RT v kg /m 166.0607950)27378(06.2873222=+⨯==p RT v kg /m 664.0166.083.0321=-=-v v%80%10083.0166.083.0%100121=⨯-=⨯-v v v每kg 空气的体积比原有体积减少了0.664m 3；减少的百分比为80％。
工程流体力学第二版答案工程流体力学 第二章 流体静力学2-1．一密闭盛水容器如图所示，U 形测压计液面高于容器内液面h=1.5m ，求容器液面的相对压强。
[解] gh p p a ρ+=0kPa gh p p p a e 7.145.1807.910000=⨯⨯==-=∴ρ2-2．密闭水箱，压力表测得压强为4900Pa 。
压力表中心比A 点高0.5m ，A 点在液面下1.5m 。
求液面的绝对压强和相对压强。
[解]g p p A ρ5.0+=表Pa g p g p p A 49008.9100049005.10-=⨯-=-=-=ρρ表 Pa p p p a 9310098000490000=+-=+=' 2-3．多管水银测压计用来测水箱中的表面压强。
图中高程的单位为m 。
试求水面的绝对压强p abs 。
[解])2.13.2()2.15.2()4.15.2()4.10.3(0-+=-+---+g p g g g p a 汞水汞水ρρρρg p g g g p a 汞水汞水ρρρρ1.13.11.16.10+=+-+kPa g g p p a 8.3628.9109.28.9106.132.2980009.22.2330=⨯⨯-⨯⨯⨯+=-+=水汞ρρ2-4． 水管A 、B 两点高差h 1=0.2m ，U 形压差计中水银液面高差h 2=0.2m 。
试求A 、B 两点的压强差。
（22.736N ／m 2）[解] 221)(gh p h h g p B A 水银水ρρ+=++Pah h g gh p p B A 22736)2.02.0(8.9102.08.9106.13)(33212=+⨯⨯-⨯⨯⨯=+-=-∴水水银ρρ2-5．水车的水箱长3m,高1.8m ，盛水深1.2m ，以等加速度向前平驶，为使水不溢出，加速度a 的允许值是多少？[解] 坐标原点取在液面中心，则自由液面方程为：x gaz -=0 当m lx5.12-=-=时，m z 6.02.18.10=-=，此时水不溢出 20/92.35.16.08.9s m x gz a =-⨯-=-=∴2-6．矩形平板闸门AB 一侧挡水。
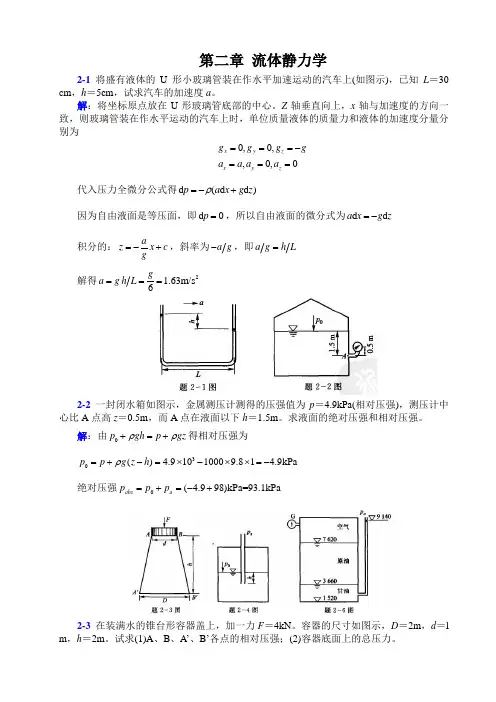
第二章 流体静力学2-1 将盛有液体的U 形小玻璃管装在作水平加速运动的汽车上(如图示)，已知L ＝30 cm ，h ＝5cm ，试求汽车的加速度a 。
解：将坐标原点放在U 形玻璃管底部的中心。
Z 轴垂直向上，x 轴与加速度的方向一致，则玻璃管装在作水平运动的汽车上时，单位质量液体的质量力和液体的加速度分量分别为0,0,,0,0x y z x y z g g g ga a a a ===-===代入压力全微分公式得d (d d )p a x g z ρ=-+因为自由液面是等压面，即d 0p =，所以自由液面的微分式为d d a x g z =- 积分的：a z x c g=-+，斜率为a g -，即a g h L = 解得21.63m/s 6g a g h L ===2-2 一封闭水箱如图示，金属测压计测得的压强值为p ＝4.9kPa(相对压强)，测压计中心比A 点高z ＝0.5m ，而A 点在液面以下h ＝1.5m 。
求液面的绝对压强和相对压强。
解：由0p gh p gz ρρ+=+得相对压强为30() 4.91010009.81 4.9kPa p p g z h ρ=+-=⨯-⨯⨯=-绝对压强0( 4.998)kPa=93.1kPa abs a p p p =+=-+2-3 在装满水的锥台形容器盖上，加一力F ＝4kN 。
容器的尺寸如图示，D ＝2m ，d ＝l m ，h ＝2m 。
试求(1)A 、B 、A ’、B ’各点的相对压强；(2)容器底面上的总压力。
解：(1)02 5.06kPa 4F F p D A π===,由0p p gh ρ=+得：0 5.06kPa A B p p p ===''0 5.06kPa+10009.82Pa 24.7kPa A B p p p gh ρ==+=⨯⨯=(2) 容器底面上的总压力为2'24.7kPa 77.6kN 4A D P p A π==⨯= 2-4 一封闭容器水面的绝对压强p 0＝85kPa ，中间玻璃管两端开口，当既无空气通过玻璃管进入容器、又无水进人玻璃管时，试求玻璃管应该伸入水面下的深度h 。
第一章 绪论1-1．20℃的水2.5m 3，当温度升至80℃时，其体积增加多少？ [解] 温度变化前后质量守恒，即2211V V ρρ= 又20℃时，水的密度31/23.998m kg =ρ 80℃时，水的密度32/83.971m kg =ρ 321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆1-2．当空气温度从0℃增加至20℃时，运动粘度ν增加15%，重度γ减少10%，问此时动力粘度μ增加多少（百分数）？ [解] 原原ρννρμ)1.01()15.01(-+==原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμ此时动力粘度μ增加了3.5%1-3．有一矩形断面的宽渠道，其水流速度分布为μρ/)5.0(002.02y hy g u -=，式中ρ、μ分别为水的密度和动力粘度，h 为水深。
试求m h 5.0=时渠底（y =0）处的切应力。
[解] μρ/)(002.0y h g dydu-=)(002.0y h g dydu-==∴ρμτ 当h =0.5m ，y =0时)05.0(807.91000002.0-⨯⨯=τPa 807.9=1-4．一底面积为45×50cm 2，高为1cm 的木块，质量为5kg ，沿涂有润滑油的斜面向下作等速运动，木块运动速度u=1m/s ，油层厚1cm ，斜坡角22.620 （见图示），求油的粘度。
[解] 木块重量沿斜坡分力F 与切力T 平衡时，等速下滑yu AT mg d d sin μθ== 001.0145.04.062.22sin 8.95sin ⨯⨯⨯⨯==δθμu A mg s Pa 1047.0⋅=μ1-5．已知液体中流速沿y 方向分布如图示三种情况，试根据牛顿内摩擦定律yud d μτ=，定性绘出切应力沿y 方向的分布图。
[解]1-6．为导线表面红绝缘，将导线从充满绝缘涂料的模具中拉过。
工程流体力学课后习题答案(第二版)(总22页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第一章 绪论1-1．20℃的水，当温度升至80℃时，其体积增加多少 [解] 温度变化前后质量守恒，即2211V V ρρ= 又20℃时，水的密度31/23.998m kg =ρ 80℃时，水的密度32/83.971m kg =ρ 321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆1-2．当空气温度从0℃增加至20℃时，运动粘度ν增加15%，重度γ减少10%，问此时动力粘度μ增加多少（百分数）[解] 原原ρννρμ)1.01()15.01(-+==原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμ此时动力粘度μ增加了%1-3．有一矩形断面的宽渠道，其水流速度分布为μρ/)5.0(002.02y hy g u -=，式中ρ、μ分别为水的密度和动力粘度，h 为水深。
试求m h 5.0=时渠底（y =0）处的切应力。
[解] μρ/)(002.0y h g dydu-=)(002.0y h g dydu-==∴ρμτ 当h =，y =0时)05.0(807.91000002.0-⨯⨯=τPa 807.9=1-4．一底面积为45×50cm 2，高为1cm 的木块，质量为5kg ，沿涂有润滑油的斜面向下作等速运动，木块运动速度u=1m/s ，油层厚1cm ，斜坡角 （见图示），求油的粘度。
[解] 木块重量沿斜坡分力F 与切力T 平衡时，等速下滑yu AT mg d d sin μθ== 001.0145.04.062.22sin 8.95sin ⨯⨯⨯⨯==δθμu A mg s Pa 1047.0⋅=μ1-5．已知液体中流速沿y 方向分布如图示三种情况，试根据牛顿内摩擦定律yud d μτ=，定性绘出切应力沿y 方向的分布图。
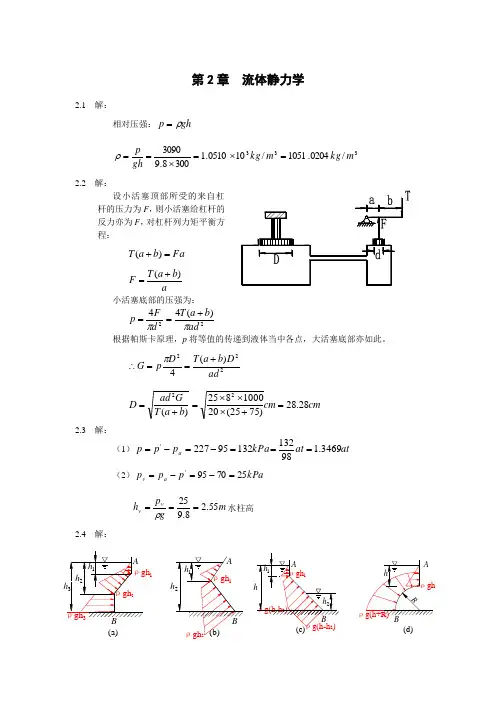
第2章 流体静力学2.1 解：相对压强：gh p ρ=333/0204.1051/100510.13008.93090m kg m kg gh p =⨯=⨯==ρ 2.2 解：设小活塞顶部所受的来自杠杆的压力为F ，则小活塞给杠杆的反力亦为F ，对杠杆列力矩平衡方程：Fa b a T =+)(a b a T F )(+=小活塞底部的压强为：22)(44ad b a T d F p ππ+==根据帕斯卡原理，p 将等值的传递到液体当中各点，大活塞底部亦如此。
222)(4ad D b a T D p G +==∴π cm cm b a T Gad D 28.28)7525(201000825)(22=+⨯⨯⨯=+=2.3 解：（1）at at kPa p p p a 3469.19813213295227'===-=-= （2）kPa p p p a v 257095'=-=-=m g p h v v 55.28.925===ρ水柱高 2.4 解：ρgh 2 ρgh 1ρgh 3ρgh 2ρgh 1h 2h 1 h 1 h 2h 3 (b)(a)BAA Bρg(h-h 2)ρg(h+R)ρghρg(h-h 2) ρgh 1Rhh 2h 1h(d)(c)B AAB2.5 解：1－1为等压面：gh p gH p a ρρ+=+0kPa m N m N m N H h g p p a 94.100/100940/)2.15.1(8.91000/108.9)('22240==-⨯⨯+⨯=-+=ρ kPa p 94.20=2.6 解: kPa gL p c 45.230sin 5.08.9sin =⨯⨯==αρ 2.7 解：如图所示，过1、2、3点的水平面是等压面。
)()()(322341121z z g z z g gh p z z g gh p B B A A ---++=--+ρρρρρ[])()()()(32212341z z g z z z z g h h g p p A B B A ---+-+-=-ρρρ[])()()()(3221234141z z g z z z z g z z g ---+-+-=ρρρ[]{}310)3262(8.0)1862()3253(6.13)5318(8.9-⨯---+-+-⨯=Pa 8085=2.8 解：gh gh p gh p p B B A A ρρρ+-=- ()gh h h g p p p B A B A ρρ+-=-＝()[]gh h g p ρρ++-1＝()[]31036.08.96.13136.08.9-⨯⨯⨯++-＝34.6528kPa2.9 解：如图所示，A 、B 、C 点水平面是等压面。
第一章 绪论1-1．20℃的水2.5m 3，当温度升至80℃时，其体积增加多少？ [解] 温度变化前后质量守恒，即2211V V ρρ= 又20℃时，水的密度31/23.998m kg =ρ 80℃时，水的密度32/83.971m kg =ρ 321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆1-2．当空气温度从0℃增加至20℃时，运动粘度ν增加15%，重度γ减少10%，问此时动力粘度μ增加多少（百分数）？ [解] 原原ρννρμ)1.01()15.01(-+==Θ原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμΘ此时动力粘度μ增加了3.5%1-3．有一矩形断面的宽渠道，其水流速度分布为μρ/)5.0(002.02y hy g u -=，式中ρ、μ分别为水的密度和动力粘度，h 为水深。
试求m h 5.0=时渠底（y =0）处的切应力。
[解] μρ/)(002.0y h g dydu-=Θ)(002.0y h g dydu-==∴ρμτ 当h =0.5m ，y =0时)05.0(807.91000002.0-⨯⨯=τPa 807.9=1-4．一底面积为45×50cm 2，高为1cm 的木块，质量为5kg ，沿涂有润滑油的斜面向下作等速运动，木块运动速度u=1m/s ，油层厚1cm ，斜坡角22.620 （见图示），求油的粘度。
[解] 木块重量沿斜坡分力F 与切力T 平衡时，等速下滑yuATmgddsinμθ==001.0145.04.062.22sin8.95sin⨯⨯⨯⨯==δθμuAmgsPa1047.0⋅=μ1-5．已知液体中流速沿y方向分布如图示三种情况，试根据牛顿内摩擦定律yuddμτ=，定性绘出切应力沿y方向的分布图。
[解]1-6．为导线表面红绝缘，将导线从充满绝缘涂料的模具中拉过。
已知导线直径0.9mm，长度20mm，涂料的粘度μ=0.02Pa．s。
［陈书2-8］容器中盛有密度不同的两种液体，问测压管A 及测压管B 的液面是否和容器中的液面O-O 齐平？为什么？若不齐平，则A 、B 测压管液面哪个高？
［解］依题意，容器内液体静止。
测压管A 与上层流体连通，且上层流体和测压管A 均与大气连通，故A 测压管的液面与液面O-O 齐平。
测压管B 与上下层流体连通，其根部的压强为：
a p gh gh p ++=2211ρρ
其中1h 为上层液体的厚度，2h 为液体分界面到B 管根部的垂向距离，a p 为大气压 因测压管B 与大气连通，其根部的压强又可表示为：
a p gh p +=2ρ
其中h 为B 管内气液界面到B 管根部的垂向距离 所以：gh gh gh 22211ρρρ=+
212
1
22211h h h h h +=+=
ρρρρρ
由此可知：若21ρρ<，B 测压管的液面低于A 测压管的液面和O-O 面；若21ρρ>，B 测压管的液面高A 测压管的液面和O-O 面；若21ρρ=，A 、B 测压管的液面和O-O 面三者平齐。
又因为密度为1ρ的液体稳定在上层，故21ρρ<。
［陈书2-12］容器中有密度为1ρ和2ρ的两种液体，试绘出AB 面上的压强分布图。
［解］令上、下层液体的厚度分别为1h 和2h ，取垂直向下的方向为z 轴的正方向，并将原点设在自由表面上，可写出AB 表面上压强的表达式：
()⎩⎨
⎧+≤<-++≤≤+=21121111 0
h h z h h z g gh p h z gz p p a
a ρρρ 整理得：
()⎩⎨
⎧+≤<+-+≤≤+=2
11212111 0
h h z h gz gh p h z gz p p a a ρρρρ
A
C
B
P 012P g AC g BC
ρρ++01P g AC
ρ+/h m
/P Pa
［陈书2-24］直径D=1.2m ，L=2.5的油罐车，内装密度3
900m kg =ρ的石油，油面高度为h=1m ，以2
2s m a =的加速度水平运动。
试确定油罐车侧盖 A 和B 上所受到的油液的作用
力。
［解］取x 坐标水平向右，y 坐标垂直纸面向内，z 坐标垂直向上，原点定在油罐的中轴线上。
油液受到的体积力为：
a f x -= 0=y f g f z -=
由欧拉方程积分可得：gz ax p p C ρρ--=
根据题意及所选的坐标系，当h z x ==,0时，a p p = 故：gh p p C a ρ-=
gh p p a C ρ+=
所以：()ax z h g p p a ρρ--+=
因大气压的总体作用为零，故上式中可令0=a p 于是：()ax z h g p ρρ--=
左侧盖形心的坐标：0,2
=-
=z L
x 故该处的压强：2
L
a gh p L ρρ+=
左侧盖所受油液的作用力：N D p F L L 7.1252342
==π（取2s m 81.9=g ） 右侧盖形心的坐标：0,2
==
z L
x 故该处的压强：2
L
a gh p R ρρ-=
左侧盖所受油液的作用力：N D p F R R 1.74394
2
==π（取2s m 81.9=g ）
［陈书2-26］盛有水的圆筒形容器以角速度ω绕垂直轴作等速旋转，设原静水深为h ，容器半径为R ，试求当ω超过多少时可露出筒底？
解：非惯性坐标系中相对静止流体满足欧拉方程：()Zdz Ydy Xdx dp ++=ρ 等速旋转时液体所受的质量力为：
θωcos 2r X =，θωsin 2r Y =，g Z -=
将其代入欧拉方程，积分得：
C gz r p +⎪⎭
⎫ ⎝⎛-=2221ωρ
自由表面中心处r=0，a p p =（大气压），再令此处的z 坐标为：C z （令筒底处z=0），代入上式，得：
C gz p C a +-=ρ
所以：C a gz p C ρ+= 所以：C a gz p gz r p ρωρ++⎪⎭
⎫ ⎝⎛-=
2221
等压面的方程：
gz r gz p p C
a -=--222
1
ωρ
ρ 对于自由表面：a p p =，故自由表面的方程为：
gz r gz C
-=-222
1
ωρ
ρ 当筒底刚好露出时，0=C z ，所以自由面方程为：
2
221r g
z ω=
自由面与筒壁相交处的垂向坐标：2
221R g
H ω= 旋转后的水体体积：
4
2424222222
422
2222
2
20
2244221212212R g
R g R g R g R g g R g
H g R g R dz gz
h R dz r H R V H
H ωπωπωπωωωπωπ
ω
πωπωπ
πππ=-=-
=
-=-=-=⎰⎰
将水视为不可压缩流体，根据质量守恒，旋转前后的水体体积应相等，所以：
h R R g
V 2424πωπ
==
所以：gh R
2
=
ω
［陈书2-39］在由贮水池引出的直径D=0.5m 的圆管中安装一蝶阀，h=10m ，蝶阀是一个与管道直径相同的圆板，它能绕通过中心的水平轴回转。
为不使该阀自行转动，问所需施加的力矩应为多大？
［解］将阀门的圆心定为坐标原点，z 轴垂直向上，则压强分布为：
()z h g p -=ρ
由于静水压导致阀门所受的总力矩为：
()⎰⎰⎰⎰
⎰
⎰
⎰
-
---
-----=-⎪⎪⎭⎫ ⎝⎛-=-=-=-==2
224
2
2
242
2
3
32
2
224
2
2
2
3
2
232
222
2cos sin 2cos sin 23cos 2cos sin 2cos sin 2cos sin sin 22ππ
ππππππ
ππππθ
θθρθθθρθρθ
θθρθθθρθθθθρd gR
d gR h gR d gR
d h gR d R h gR dz z R pz pzdA M R R R R
()14cos 8
1
162422cos sin 442
222
2
2
2-=+-=⎪⎪⎭⎫ ⎝
⎛-=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭
⎫ ⎝⎛-=----θθθσ
θσ
θσθσθi i i i i i i i e e e e e e e e
所以：()()m
N gR gR d gR d gR M .08.304
4sin 414114cos 4
1
14cos 81242
242242
24==⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫
⎝⎛--=--=--=---⎰⎰
ρππθρθθρθθρππππππ
［陈书2-43］图示一储水设备，在C 点测得绝对压强为Pa 29430
=p ，h=2m ，R=1m 。
求半球曲面AB 所受到液体的作用力。
［解］建立如图所示的坐标系，其中坐标原点取在球心，z 轴垂直向上。
以C 为参考点，容器内任意点的压强可表达为：
⎪⎭⎫ ⎝
⎛
+-=2h z g p p C ρ
作用在曲面AB 上任意点处的压强均与表面垂直，即压力的作用线通过球心。
简单分析可知，曲面上水平方向的液体合压力为零，液体的曲面的总作用力仅体现在垂直方向，且合力方向向上，且合力作用线通过球心。
球面的外法线方向：
()
k j i n
θϕθϕθsin ,sin cos ,cos cos =
其中θ为纬度角，ϕ为经度角。
曲面AB 上的垂向总液体压力：
⎰
=2
2πθπrRd pn F z z
其中：θsin =z n ，θcos R r = 所以：⎰
=2
2
cos sin 2πθθθπd p R F z
⎪⎭
⎫ ⎝⎛--=⎥⎦⎤⎢⎣⎡⎪⎭⎫
⎝⎛+-=⎥⎦⎤⎢⎣
⎡⎪⎭⎫ ⎝⎛+-=⎰⎰⎰⎰⎰⎰
2020202202022
2cos sin 2cos sin cos sin 2cos sin 2cos sin 2cos sin 22ππππππθθθρθθθρθθθπθθθρθθθπθθθρπd h g d z g d p R d h z g d p R d h z g p R F C C C
z
将θsin R z =和2
1
cos sin 20=⎰πθθθd 代入上式，得：
⎪
⎭
⎫
⎝⎛--=⎪⎭⎫ ⎝⎛--=⎪⎭
⎫ ⎝⎛--=⎪
⎭⎫
⎝⎛--=⎰⎰gh gR p R gh gR p R gh d gR p R gh d gR p R F C C C C z ρρπρρπρθθθρπρθθθρπππ2132413121241cos sin 21241cos sin 212220222022
将Pa 29430=C p ，h=2m ，R=1m ，3m kg 1000=ρ和2
s m 81.9=g 代入，得： N 6.41102=z F。
