同济大学_汽车学院_汽车振动_郭荣_chapter2_作业答案

1.1 试举出振动设计、系统识别和环境预测的实例。

1.2 如果把双轴汽车的质量分别离散到前、后轴上去，在考虑悬架质量和非悬架质量两个离散质量的情况下，画出前轴或后轴垂直振动的振动模型简图，并指出在这种化简情况下，汽车振动有几个自由度?1.3 设有两个刚度分别为1k ，2k 的线性弹簧如图T —1.3所示，试证明：1)它们并联时的总刚度eq k 为：21k k k eq +=2)它们串联时的总刚度eq k 满足：21111k k k eq +=解：1)对系统施加力P ，则两个弹簧的变形相同为x ，但受力不同，分别为：1122P k xP k x=⎧⎨=⎩由力的平衡有：1212()P P P k k x =+=+故等效刚度为：12eq Pk k k x ==+2)对系统施加力P ，则两个弹簧的变形为： 1122Px k Px k ⎧=⎪⎪⎨⎪=⎪⎩，弹簧的总变形为：121211()x x x P k k =+=+故等效刚度为：122112111eq k k P k x k k k k ===++1.4 求图所示扭转系统的总刚度。

两个串联的轴的扭转刚度分别为1t k ，2t k 。

解：对系统施加扭矩T ，则两轴的转角为： 1122t t Tk T k θθ⎧=⎪⎪⎨⎪=⎪⎩系统的总转角为：121211()t t T k k θθθ=+=+，12111()eq t t k T k k θ==+故等效刚度为：12111eq t t k k k =+1.5 两只减振器的粘性阻尼系数分别为1c ，2c ，试计算总粘性阻尼系数eq c1)在两只减振器并联时，2)在两只减振器串联时。

解：1)对系统施加力P ，则两个减振器的速度同为x ，受力分别为：1122P c x P c x =⎧⎨=⎩ 由力的平衡有：1212()P P P c c x =+=+故等效刚度为：12eq P c c c x ==+ 2)对系统施加力P ，则两个减振器的速度为：1122P x c Px c ⎧=⎪⎪⎨⎪=⎪⎩，系统的总速度为：121211()x x x P c c =+=+ 故等效刚度为：1211eq P c x c c ==+1.6 一简谐运动，振幅为0.5cm，周期为0.15s，求最大速度和加速度。

欢迎共阅同济大学汽车实验学题目填空题（45分）1.分析系统动态特性可用时域分析法和频域分析法,在用频域分析法中,通过傅里叶变换,描述系统的特性函数H(f)称为(频响函数),还可以用其对应幅值关系的(幅频函数)和对应相位关系的(相频函数)来描述。

2.一阶动态系统的特征是(时间常数τ)二阶动态系统的特征参数是性补偿的方法由(串联补偿电阻补偿法、推挽补偿法)13.电容式传感器的电容量C与(极板面积大小、极板间距离和介电质常数)等参数有关,其中与变量___的表达式为非线性。

14.噪声测量的客观量有(声压与压级、声强与声强级、声功率和声功率级), 它们是客观描述声音的物理量.而描述声音的主观量是模拟正常人的听力的强度,为(响度和响度级).对噪声的主观评价方法有(纯音噪音和复合音噪音)简答及问答：（40分）1.什么是应变片的横向效应，为什么会产生横向效应？（p.53）由于横向段的存在，感受横向应变而使电阻变化化率减小并降低灵敏度的现象。

原因：理想的电阻应变片输出应该完全是片长方向上的变形，但由于电阻片是制成栅状的，它存在横向段，所以会产生横向效应。

2.电阻位移计出现最大误差的位置在什么地方？其误差的产生与什么因素有关？减小误差的方法是什么？3.简述霍尔效应以及霍尔传感器的基本原理。

霍尔效应:金属或半导体薄片，若在它两端通以控制电流I，并在薄片的垂直方用差动法计算其灵敏度和非线性误差.C=εA/δ,其中δ为电容两极板的距离,A为极板面积,ε为介电常数,C为电容.答：原理及优点：使用两个具有特性方程的装置，使其中一个装置输入端作用一个正变量的输入信号时，另一个装置的输入端作用一个绝对值与前相等的负变量输入信号，其总输出为这两个装置的输出之差；两个优点：（1）输出增加一倍；（2）非线性误差大大减小；2.为测量某轴的转动功率,用测量轴受到的力矩M和轴的转速ω进行间接测量. 测得轴受到的力矩为M1,转速ω1其理想值应为M和ω,试计算转动功率N=Mω的相对误差和绝对误差。

机械振动习题集同济大学机械设计研究所2004．91_简谐运动及其运算1-1 求下列简谐函数的单边复振幅和双边复振幅(1) x 2sin( t )(2) x 4 cos(10 t ) ( 3) x 3 cos(2 t 45 )341-2 通过简谐函数的复数表示，求下列简谐函数之和。

(1)x12sin( t 3)x23sin( t3)(2)x15sin 10 tx 24 cos(10 t4)(3) x 1 4 sin(2 t 30 ) x 2 5 sin( 2 t 60 )x 3 3cos(2 t 45 )x 47cos(2 t38 )x 5 2 cos(2 t 72 )答案：(1) x 124.359 cos( t 6.6)(2) x 12 3.566 cos(10 t 47.52 )(3) x 12345 14.776 cos(2 t9.22 )1-3试计算题 1中 x(t)的一阶对数和二阶导数对应的复振幅，并给出它们的时间历程。

1-4 设 x(t)、 f(t) 为同频简谐函数，并且满足 ax bx cx f(t) 。

试计算下列问题 (1)已知 a 1.5,b 6,c 25,x(t) 10 sin(12 37 ) ，求 f(t)(2)已知 a 3,b 7,c 30, f (t) 25 sin(7 64 )，求 x(t)1-5 简述同向异频简谐振动在不同频率和幅值下合成的不同特点。

1-6 利用“振动计算实用工具” ，通过变换频率和相位总结垂直方向振动合成的特点。

2_单自由度系统振动2-1 请解释有阻尼衰减振动时的固有圆频率d为什么总比自由振动时的固有圆频率n小？答案：因为 d 1 2 n ， <12-2 在欠阻尼自由振动中，把 改成 0.9 的时候，有人说曲线不过 X 轴了，这种说法正确么，请说明理由？答案： <1 为小阻尼的衰减振动，当然过 X 轴2-3 在单自由度自由振动时候，给定自由振动时的固有圆频率n ,阻尼系数 ,初始位移 x 0,以及初始速度 v 0 ,利用本计算工具 ,请计算有阻尼衰减振动时的固有圆频率d .答案：如n =3rad/s, =0.01, x 0 =-1, v 0=0;则 d =2.9985rad/s 2-4 如图 2-1 所示，一小车(重 P )自高 h 处沿斜面滑下，与缓冲器相撞后，随同缓冲器一 起作自由振动。

（一）一、概念解释（选其中１０题，计２０分）１汽车使用性能2 滚动阻力系数3 牵引力与（车轮）制动力4 汽车驱动与附着条件5 汽车动力性及评价指标6 回正力矩7 临界车速8 滑移（动）率9 侧向偏离10 制动距离11 汽车动力因数12 汽车通过性几何参数13 汽车（转向特性）的稳态响应14 汽车前或后轮（总）侧偏角二、写出表达式、画图、计算，并简单说明（选择其中5道题，计２０分）1 用结构使用参数写出汽车功率平衡方程式2 写出ｎ档变速器ｍ档传动比表达式3 画图并说明地面制动力、制动器制动力、附着力三者关系4 简述图解计算燃料消耗量的方法5 写出汽车的后备功率方程式，其对汽车的动力性和燃料经济性有何影响？6 写出可以绘制I曲线方程或方程组三、叙述题（选择其中5道题，计20分）1 从制动侧滑受力分析和试验，可以得出哪些结论？2 写出计算汽车动力因数的步骤，并说明其在计算汽车动力性的用途。

3 写出计算汽车加速性能的步骤。

4 写出制做汽车的驱动力图的步骤？5 如何选择汽车发动机功率？6 画出制动时车轮的受力简图并定义符号。

7 分析汽车紧急制动过程中减速度的变化规律？8 在侧向力的作用下，刚性轮胎和弹性轮胎行驶方向的变化规律（假设驾驶员不对汽车的行驶方向进行干预）？四、分析题（选择其中5道题，计20分）1 如何确定传动系最小传动比2 已知某汽车φ0＝0.4，请利用Ｉ、β、ｆ、γ线，分析φ＝0.5,φ＝0.3以及φ＝0.7时汽车的制动过程。

3 汽车在水平道路上，轮距为B,重心高度为h g,以半径为R做等速圆周运动,汽车不发生侧翻的极限车速是多少?该车不发生侧滑的极限车速又是多少，并导出汽车在该路段的极限车速?4 在划有中心线的双向单车道的本行车道上，汽车以40km/h的初速度实施紧急制动，仅汽车左侧轮胎在路面留下制动拖痕，但是，汽车的行驶方向几乎没有发生变化，请产生分析该现象的各种原因。

5 请分析制动力系数、峰值附着系数、滑动附着系数与滑动率的关系。

汽车空气动力学考试题及参考答案(试验部分)A 卷1. 以下各项为中国汽车工程师协会发表的《汽车工程手册—试验篇》中关于汽车工程试验的类别(部分)，请选出4种与空气动力学有关的、可能在汽车风洞中进行的试验课题(8’)。

1) 动力传动系性能试验2) 操纵稳定性试验3) 振动与噪声试验4) 可靠性试验5) 碰撞安全性试验6) 空气动力特性试验7) 驾驶方便性、合适性和平顺性试验8) 汽车电子电气系统试验9) 环境保护试验10) 车身试验参考答案：3)4)7)10)评分标准：每点答对2分2. 汽车空气动力学试验可以用实车在路面上进行，简称为“路试”，但是更多的空气动力学研发试验在汽车风洞中进行，请简述在汽车风洞中进行试验的主要优点(6’)。

参考答案要点：1) 经济型；2) 试验效率；3) 重复性。

评分标准：回答正确每要点2分。

B 卷3. 某车型正投影面积2.25m 2, 汽车模型风洞试验采用1/4缩比模型，在喷口宽等于2m 、高等于1.6m 的风洞中测量气动阻力系数，请回答：1) 模型在风洞中的阻塞比等于多少？2)速等于多少m/s? 3) ’)0.260.280.300.320.34C d U(m/s)参考答案和评分标准：1) 阻塞比 = 模型投影面积 / 风洞喷口面积 = (2.25*(1/4)^2）/ (2*1.6) = 4.4% (2’)2) Re = νUL ，雷诺数相等，则4L L U U modelfull full model ==,Umodel = 100/3.6*4 = 111m/s (3’) 3) 根据雷诺数试验曲线，20m/s 时阻力系数随雷诺数增大减小明显，阻力系数测量值较真值偏大较多；而50m/s 时，阻力系数随雷诺数变化很小了，可以代表实际结果。

(3’)4. 汽车风洞试验主要设计三个学科方向，请问是哪三个学科方向？(6’)参考答案要点：1) 空气动力学；2) 气动声学；3) 热力学。

第四章（一） 振动学基础解答一、选择题1．D 2．B 3．C 4．C 5．B 6．B 7．D 8．B二、填空题1．振动系统自身的性质；π2秒内的的振动次数；振动系统运动的初始条件；表示振动的幅度或振动的强度；表征计时零点的振动状态。

2．；cm 2 ；4s ；1-s 2π ；π23 )232cos(02.0ππ+t ；m )232s i n (01.0πππ+-t -1s m ⋅；)232cos(201.02πππ+-t -2s m ⋅； ππ或33．0.158 m ； 0.5 s ； 2π4．)41cos(02.0ππ+t m ； )43c o s (02.0ππ+t m5．π326．8T ， T 83 7．ππ232或-8．合力的大小与位移成正比，方向与位移方向相反； 0d d 222=+x tx ω三、计算题1．解：(1) s 638.084.922,s84.9258.0251-======πωπωT mk(2) m/s 17.03sin02.084.9sin ,30-=⨯⨯-=-==πϕωπϕA v (3) )384.9cos(02.0)cos(πϕω+=+=t t A x m2．解：（1）)32cos(3πππϕ-=-=t T A x （2）0=a ϕ，2πϕ=b（3）作振幅矢量图，得到： 6233T Tt a ===ππωπ125223T Tt b =⎪⎭⎫⎝⎛=πππ＋3．解：木块下移时，恢复力 )1(22xgL gxLf -=-=水ρmk =ω , 由（1）式知 2gL k =所以，木块做简谐运动。

在水中的木块未受压而处于平衡时 a gL mg 2水ρ= ，于是可求得ag aL gLm k ===22水ρω ga T πωπ22==振幅：a b A -=4．解：（1）两个同方向、同频率简谐运动的合振动仍为简谐运动，且合振动的频率与分振动的频率相同，即121s 3-＝＝＝ωωω合振动振幅A 和初相0ϕ为 ()cm 52cos 43243cos 22221212221=⨯⨯++=++=πϕϕ－A A A A A︒==+︒+︒=++=--13.5334tg 24cos 3cos024sin 3sin0tgcos cos sin sin tg11-2211221110ππϕϕϕϕϕA A A A即0ϕ在第一象限内。

同济大学汽车试验学考卷考题答案新编HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】同济大学汽车实验学题目填空题（45分）1.分析系统动态特性可用时域分析法和频域分析法,在用频域分析法中, 通过傅里叶变换,描述系统的特性函数H(f)称为(频响函数),还可以用其对应幅值关系的(幅频函数)和对应相位关系的(相频函数)来描述。

2.一阶动态系统的特征是(时间常数τ)二阶动态系统的特征参数是 (系统固有频率ω0、阻尼比ξ)3.如果时域信号为x(t),若满足相应条件,其频域信号X(f),则有：df ef X t x ftj π2)()(-∞∞-⎰= (傅里叶逆变换表达式) 4.信号在时域被压缩,则该信号在频域的(幅值)成分将减小。

5.信号x(t)的输出为y(t),当t=t 0时输出的显示值为y(t 0),由于系统非线性误差的存在,实际的真值应该是A0，此时系统的绝对误差Δ为(X-A 0)相对误差(δ2 =（X-A 0）/X max *100%)6.由于测量的真值无法获得,则在有限次等精度测量中(样本平均值)作为最佳估计值取代测量值,其数学表达式为平均值(X=(x 1+x 2+x 3+…..x n )/n)7.随机误差正态分布具有的特性是(单峰性、对称性、有界性和抵偿性)8.应变片灵敏度应(小于)相同材料单根金属丝的灵敏度.应变片实际灵敏度应由厂家标定,标定的条件是(单向应力状态、贴片方向与主应力方向一致和试件材料的泊松比μ0=）9.根据截面应力分布的特点以及测量值尽可能大的要求,测量正应力的应变片贴片位置在截面的(正面)上,贴片方向与截面方向(相同);测量剪应力的应变片贴片位置在截面的(侧面)处,贴片方向与截面方向(垂直)10.一般情况下电桥的加减特性可采用来(进行温度补偿、提高输出灵敏度以及实现载荷分离)11.霍尔电势UH,是由霍尔元件上运动的带电粒子和磁场的作用产生的(洛伦茨力)以及带电粒子产生的(横向电场力)的瞬时平衡时的电势差12.电位式电阻传感器的空载特性是线性的,而实际特性是非线性的,常用的非线性补偿的方法由(串联补偿电阻补偿法、推挽补偿法)13.电容式传感器的电容量C 与(极板面积大小、极板间距离和介电质常数)等参数有关,其中与变量___的表达式为非线性。

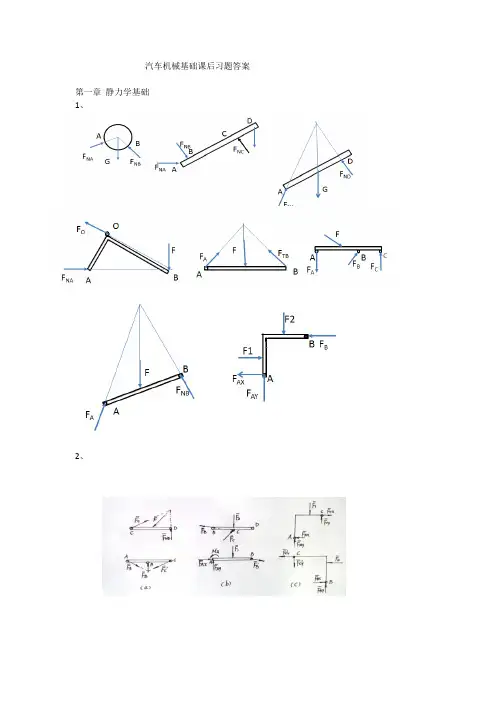
汽车机械基础课后习题答案第一章静力学基础1、2、3、4、解：以滑轮A 为研究对象，画受力图（a ）(b)(a) (b)对（a ）列平衡方程求解KNF KN FG F F F F F F F F AC AB AC T AB Y AC T AB X 75.1507.2030cos 15sin 30sin ,0030sin 15cos 30cos ,0=-=∴⎪⎩⎪⎨⎧=-+-==+--=∑∑对（b ）列平衡方程求解KNF KN FG F F F F F F F AC AB AC T Y AC T AB X 64.3831.22045sin 30cos ,0045cos 30sin ,0==∴⎪⎩⎪⎨⎧=-+-==+--=∑∑5、解：先取滚子B 为研究对象，画受力图（a ）(a) (b)对（a ）列平衡方程有∑=∴=-=ααsin 0sin ,0FF F F FBC BC X再以压块C 为研究对象，画受力图（b ）对（b ）列平衡方程有KN FF F F FCB Y67.5tan 0cos ,011==∴=+-=∑αα增力比：αtan 11=F F ，显然α越小，增力比越大。

第二章 力矩与平面力偶系 1、(a)()FlF M O = (b)()0=F M O (c)()αsin Fl F M O =(d)())(r l F F M O +=(e) ()Fa F M O = (f) ()αsin 22b a F F M O +=2、解：先以杆O 1B 为研究对象，画受力图（a ）(a) (b) 对（a ）用平面力偶系的平衡方程KN F B O F M MAB AB i100,011=∴=⨯-=∑再以杆O 2A 为研究对象，画受力图（b ） 对（b ）用平面力偶系的平衡方程m KN M A O F M M BA i •=∴=⨯+-=∑4030sin ,0222第三章 平面任意力系 1、（a ）解：画杆AB 的受力图分析得属于平面力偶系的平衡KN F F KN F F MNA B NA NA i5.1,5.1062415,0===∴=⨯+-=∑(b)画杆AD 受力图列平面任意力系的平衡方程求解()∑∑∑=∴=-+-==∴=-==∴=⨯-⨯=KNF F F F F KN F F F F B KN F F F F M AYBCAYYAXBCAXXBCBCA10045sin ,020045cos ,0)(22004245sin ,0处约束力的大小此即为支座（c ）画杆AD 受力图列平面任意力系的平衡方程求解()∑∑∑=∴=-==∴=-==∴=⨯-⨯=KNF F F F KN F F F F B KN F F F F M AYAYYAXBCAXXBC BCA100,0200,0)(200445cos 245sin ,0处约束力的大小此即为支座（d ）画杆AD 受力图列平面任意力系的平衡方程求解()∑∑∑=∴=-+-=-=∴=+==∴=⨯-⨯=KNF F F F F KN F F F F B KN F F F F M AYBCAYYAXBCAXXBCBCA10045sin ,020045cos ,0)(22004245sin ,0处约束力的大小此即为支座2、解：以横梁AB 为研究对象，画受力图列平面任意力系的平衡方程求解()∑∑∑=∴=--+==∴=-==∴=⨯-⨯-⨯=KNF G G F F FKN F F F F CD KN F x G l G l F F M AY CD AY YAX CD AX XCD CD A 32530sin ,06370030cos ,0)(3700230sin ,02121 受力的大小此即为拉杆3、解：先以BC 杆为研究对象，画受力图列平面任意力系的平衡方程求解()∑∑∑=∴=-+-==∴=+-==∴=⨯-⨯=KNF G F F F KN F F F F DE KN F G F F M BYDEBYYBXDEBXXDEDEB10045sin ,020045cos ,0)(22002145sin ,0受力的大小此即为拉杆再以AB 杆为研究对象，画受力图列平面任意力系的平衡方程求解()∑∑∑=∴=+-'==∴=--'==∴=⨯'-+⨯=KNF F F F F KN F F F F F mKN M F M F F M AYAYEDBYYAXAXEDBXXABXAEDA10045sin ,00045cos ,0.2005.25.145cos ,0第四章 摩擦1、解：先以车后轮为研究对象，画受力图()d F M d F M F M SB SB O ∑=∴=⨯-=2102,0（1）再以整车为研究对象，画受力图()()∑=⨯+⨯-+⨯-=20240021200,0NB SB A F dF MG F M由（1）和（2）得KN F NB 5.7=KN F F G F FNA NB NA Y27.1073.0sin ,0sin ,0=∴==+-=∑ααKN F F F FSB sB NA X01.7,0cos ,0=∴=-=∑αm kN d F M F F f SB NB SB s .05.12193.05.701.7=====2、解：以梯子为研究对象，画受力图列平面任意力系的平衡方程()⎪⎪⎩⎪⎪⎨⎧=--⨯+⨯==+--==-=∑∑∑060cos 60sin 60cos 60cos 2,00,00,011 l F l F s G l G F M F G G F F F F F SB NB A NA SB Y SA NB X 补充方程NB s SB NA s SA F f F F f F ==,求得l s 456.0=3、（1）解：以料斗为研究对象，设料斗有下滑的趋势画受力图（方向与图示相反）时，当时，当KN F KN F kNF KN FG F F FS T S T S T X51.12549.12270sin 252270sin ,02211-===-==-+=∑（2）解：以料斗为研究对象，画匀速上升与匀速下降的受力图（b ）(c)匀速上升时，对（b ）列平衡方程KNF fF FG F F F G F F T N d N Y d T X 06.26070cos ,0070sin ,0111111==⎪⎩⎪⎨⎧=-==--=∑∑求得补充方程：匀速上升时，对（C ）列平衡方程KNF fF FG F F F G F F T N d N Y d T X 93.20070cos ,0070sin ,0222222==⎪⎩⎪⎨⎧=-==+-=∑∑求得补充方程：第五章 刚体定轴转动1、获得较大的转动惯量，使柴油机在载荷波动时仍能平稳运转。

1.2 如果把双轴汽车的质量分别离散到前、后轴上去，在考虑悬架质量和非悬架质量两个离散质量的情况下，画出前轴或后轴垂直振动的振动模型简图，并指出在这种化简情况下，汽车振动有几个自由度？解：前轴或后轴垂直振动的振动模型简图为图1.2所示，此时汽车振动简化为二自由度振动系统。

2m 为非悬架质量，1m 为悬架质量1. 3设有两个刚度分别为21,k k 的线性弹簧如图T-1.3所示， 试证明：1）它们并联时的总刚度eq k 为：21k k k eq +=2）它们串联时的总刚度eq k 为：21111k k k eq +=证明：1) 如图T-1.3(a)所示，21,k k 两个弹簧受到力的作用，变形相同， 即2211k F k F k F eq ==, 而F F F =+21，故有 F F k kF k k eq eq =+21, 从而 21k k k eq +=2）如图T-1.3(b)所示，21,k k 两个弹簧受到相同的力作用 即∆=∆=∆=eq k k k F 2211 （1）且21∆+∆=∆ （2）由（1）和（2）有：)(21k Fk F k F eq += （3） 由（3）得:21111k k k eq += 1.8证明：两个同频率但不同相角的简谐运动的合成仍是同频率的简谐运动，即)cos()cos(cos θωϕωω-=-+t C t B t A ，并讨论ϕ=0，ππ,2三种特例。

证明：因t B t B t B ωϕωϕϕωsin sin cos cos )cos(+=-从而有t B t B A t B t A ωϕωϕϕωωsin sin cos )cos ()cos(cos ++=-+令 ()ϕϕϕθ222sin cos sin sin B B A B ++=则()[]t t B B A t B t A ωθωθϕϕϕωωsin sin cos cos sin cos )cos(cos 222+++=-+=())cos(sin cos 222θωϕϕ-++t B B A令C=()ϕϕ222sin cos B B A ++，则有 )cos()cos(cos θωϕωω-=-+t C t B t A当ϕ=0时，C=A+B ；当ϕ=2π时，22B A C +=，22BA arcsin +=B θ ；当ϕ=π时，B A -=C ，0=θ1.13汽车悬架减振器机械式常规性能试验台，其结构形式之一如图T-1.13所示。

一、选择题1．关于简谐运动的质点的以下说法正确的是（ ）A ．间隔半个周期的整数倍的两个时刻，物体的振动情况相同B ．做简谐运动的质点在半个周期内物体的动能变化一定为零C ．质点在四分之一周期的时间内的路程一定等于一倍振幅D ．任一时刻加速度和速度方向都相反2．如图所示为单摆在两次受迫振动中的共振曲线，下列说法正确的是（ ）A ．若两次受迫振动分别在月球上和地球上进行，且摆长相等，则图线II 是月球上的单摆共振曲线B ．若两次受迫振动均在地球上同一地点进行的，则两次摆长之比为12:4:25l l =C ．若图线I 的摆长约为1m ，则图线I 是在地球表面上完成的D ．图线II 若是在地球表面上完成的，则该摆摆长约为1m3．“洗”是古代盥洗用的脸盆，多用青铜铸成，现代亦有许多仿制的工艺品。

倒些清水在其中，用手掌摩擦盆耳，盆就会发出嗡嗡声，还会溅起层层水花。

现某同学用双手摩擦盆耳，起初频率非常低，逐渐提高摩擦频率，则关于溅起水花强弱的描述正确的是（ ）A ．溅起水花越来越弱B ．溅起水花越来越强C ．溅起水花先变弱后变强D ．溅起水花先变强后变弱4．某弹簧振子在水平方向上做简谐运动，其位移x 随时间t 变化的函数关系式为sin x A t ω=，振动图像如图所示，下列说法不正确的是（ ）A ．弹簧在第1s 末与第3s 末的长度相同B ．简谐运动的圆频率rad /s 4πω=C ．第3s 末振子的位移大小为22A D ．从第3s 末到第5s 末，振子的速度方向发生变化5．如图所示，两长方体木块A 和B 叠放在光滑水平面上，质量分别为m 和M ，A 与B 之间的最大静摩擦力为0f ，B 与劲度系数为k 的水平轻质弹簧连接构成弹簧振子。

A 和B 在振动过程中始终不发生相对滑动，则（ ）A ．A 受到B 的摩擦力f F 与B 离开平衡位置位移x 总满足f km F x M m =-+ B ．它们的最大加速度不能大于0f M C ．它们的振幅不可能大于0km f M m+ D ．振动过程中，AB 间的摩擦力对A 做正功，对B 做负功6．一弹簧振子振动过程中的某段时间内其加速度的值越来越大，则在这段时间内（ ） A ．振子的速度越来越大B ．振子的振幅越来越大C ．振子的速度方向与回复力方向相反D ．振子正在向平衡位置运动7．如图所示，O 是弹簧振子的平衡位置，小球在B 、C 之间做无摩擦的往复运动，则小球任意两次经过O 点可能不同的物理量是（ ）A ．速度B ．机械能C ．回复力D ．加速度 8．一弹簧振子做简谐运动，周期为T （ ）A ．若t 和（t +△t ）时刻振子运动速度的大小相等、方向相同，则△t 一定是2T 的整数倍B ．若t 和（t +△t ）时刻振子运动位移的大小相等、方向相反，则△t 一定是2T 的整数倍C ．若△t =T ，则t 和（t +△t ）时刻振子运动的加速度一定相等D ．若△t =2T ，则t 和（t +△t ）时刻弹簧的长度一定相等 9．如图，长为l 的细绳下方悬挂一小球a ．绳的另一端固定在天花板上O 点处，在O 点正下方34l 的O 处有一固定细铁钉．将小球向右拉开，使细绳与竖直方向成一小角度（约为2°）后由静止释放，并从释放时开始计时．当小球a 摆至最低位置时，细绳会受到铁钉的阻挡．设小球相对于其平衡位置的水平位移为x ，向右为正．下列图像中，能描述小球在开始一个周期内的x-t 关系的是_____．A ．B ．C ．D．10．如图，细绳一端固定于悬挂点O，另一端系一小球．在悬挂点正下方A点处钉一个钉子．小球从B点由静止释放，摆到最低点C的时间为t1，从C点向右摆到最高点的时间为t2．摆动过程中，如果摆角始终小于5º，不计空气阻力．下列说法正确的是A．t1= t2，摆线碰钉子的瞬间，小球的速率变小B．t1> t2，摆线碰钉子的瞬间，小球的速率变小C．t1> t2，摆线碰钉子的瞬间，小球的速率不变D．t1= t2，摆线碰钉子的瞬间，小球的速率不变11．一弹簧振子做简谐运动，其位移x与时间t的关系曲线如图所示，由图可知：（）A．质点的振动频率是4HzB．t=2s时，质点的加速度最大C．质点的振幅为5cmD．t=3s时，质点所受合力为正向最大12．做简谐运动的物体，下列说法正确的是A．当它每次经过同一位置时，位移可能不同B．当它每次经过同一位置时，速度可能不同C．在一次全振动中通过的路程不一定为振幅的四倍D．在四分之一周期内通过的路程一定为一倍的振幅13．一根自由长度为10cm的轻弹簧，下端固定，上端连一个质量为m的物块P．在P上再放一个质量也是m的物块Q．系统静止后，系统静止后，弹簧长度为6cm，如图所示．如果迅速向上移去Q ．物块P 将在竖直方向做简谐运动．此后，弹簧的最大长度是（ ）A ．8cmB ．9cmC ．10cmD ．11cm14．如图，O 点为弹簧振子的平衡位置，小球在B 、C 间做无摩擦的往复运动．若小球从C 点第一次运动到O 点历时0.1s ，则小球振动的周期为（ ）A ．0.1sB ．0.2sC ．0.3sD ．0.4s15．右图为同一实验中甲、乙两个单摆的振动图象,从图象可知 ( )A ．两摆球质量相等B ．两单摆的摆长相等C ．两单摆相位相差πD ．在相同的时间内,两摆球通过的路程总有s 甲=2s 乙二、填空题16．在用单摆测量重力加速度的实验中，下面的叙述哪些是正确的________？哪些是错误的________？A ．摆线要选择细些的、伸缩性小些的，并且尽可能长一些B ．摆球尽量选择质量大些、体积小些的C ．为了使摆的周期大一些，以方便测量，开始时拉开摆球，使摆角较大D ．用刻度尺测量摆线的长度l ，这就是单摆的摆长E. 释放摆球，从摆球经过平衡位置开始计时，记下摆球做50次全振动所用的时间t ，则单摆周期50t T 17．如图所示为单摆在两次受迫振动中的共振曲线，两个单摆的固有周期之比为T 1：T 2=______；若两次受迫振动是在地球上同一地点进行，则两次摆长之比L Ⅰ：L Ⅱ=______；图线Ⅱ若是在地球上完成的，则该摆摆长约为______（精确到个位数）。