2016届华师一附中招生数学模拟试题

1.(3 分)华师一附中小升初数学模拟试题（一）A.比原来大 2 平方厘米 【分析】观察图形可知：现在图形的表面积比原来长方体的表面积大，增加的表面积是 4× 1× 1－2× 1× 1＝2 （平方厘米）。

【答案】A2.(3 分)一批商品，按期望获得 50％的利润来定价，结果只销售掉 70％的商品，为了尽早销售掉剩 下的商品， 商店决定按定价打八折出售。

这样所获得的全部利润占原来所期望利润的百分比 是 82％3.(3 分)小宏上学骑车去学校，放学步行回家，往返一次需 20 分；如果往返都步行需要 30 分，那么 骑车从家到学校需要 5 分（往返骑车或步行的速度均不变）。

【分析】小宏单程步行需要的时间是：30÷ 2＝15（分），小宏上学骑车，放学步行往返一次用 20 分，所以 小宏单程骑车需要的时间是：20－15＝5（分）。

【答案】A4.(3 分)一个三角形的三个角中最大的角是 89 度，这个三角形是( 锐角三角形)。

试题解析： 【分析】三角形按角分类可以分为三种:锐角三角形、直角三角形、钝角三角形。

最大的角是 89 度＜90 度， 所以是锐角三角形。

【答案】A5.(3 分)按规律排列的一串数：1，2，4，7，11，16，22，29，…，这串数的第 1997 个数是 1993007 。

6.(3 分)甲、乙两地之间的道路分上坡和下坡两种路段，共 24 千米，小明上坡速度为 4 千米/时，下 坡速度为 6 千米/时，去时用了 4.5 小时，则返回时用 小时。

【分析】设去的时候，上坡的时间为 x 小时，这样就有 4x＋6（4.5－x）＝24，解得 x＝1.5（小时），于是 可知上坡的路程是 4× 1.5＝6（千米），下坡的路程是 24－6＝18（千米）。

则返回的时候，上坡的路程是 1 8 千米，下坡的路程是 6 千米，那么返回是所用的时间为 18÷ 4＋6÷ 6＝5.5（小时）。

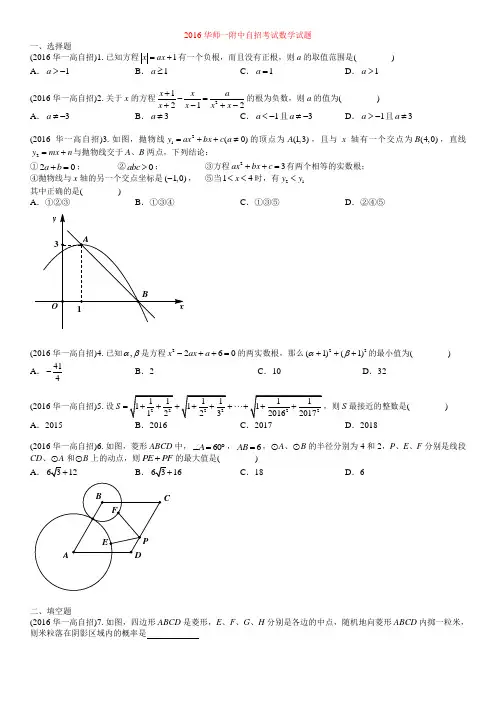
2016华师一附中自招考试数学试题一、选择题(2016华一高自招)1.已知方程1x ax =+有一个负根，而且没有正根，则a 的取值范围是( )A ．1a >-B ．1a ≥C ．1a =D ．1a >(2016华一高自招)2.关于x 的方程21212x x a x x x x +-=+-+-的根为负数，则a 的值为( ) A ．3a ≠-B ．3a ≠C ．1a <-且3a ≠-D ．1a >-且3a ≠(2016华一高自招)3.如图，抛物线21(0)y ax bx c a =++≠的顶点为(1,3)A ，且与x 轴有一个交点为(4,0)B ，直线2y mx n =+与抛物线交于A 、B 两点，下列结论：①20a b +=； ②0abc >； ③方程23ax bx c ++=有两个相等的实数根；④抛物线与x 轴的另一个交点坐标是(1,0)-， ⑤当14x <<时，有21y y <其中正确的是( )A ．①②③B ．①③④C ．①③⑤D ．②④⑤(2016华一高自招)4.已知,αβ是方程2260x ax a -++=的两实数根，那么22(1)(1)αβ+++的最小值为( )A ．414- B ．2C ．10D ．32(2016华一高自招)5.设S =⋅⋅⋅+S 最接近的整数是( ) A ．2015 B ．2016 C ．2017 D ．2018(2016华一高自招)6.如图，菱形ABCD 中，60A ∠=︒，6AB =，⊙A 、⊙B 的半径分别为4和2，P 、E、F 分别是线段CD 、⊙A 和⊙B 上的动点，则PE PF +的最大值是( )A ．12B ．16C ．18D ．6C二、填空题(2016华一高自招)7.如图，四边形ABCD 是菱形，E 、F 、G 、H 分别是各边的中点，随机地向菱形ABCD 内掷一粒米，则米粒落在阴影区域内的概率是GB D (2016华一高自招)8.已知222x y z x y z x y z z y x +--+-++==且0xyz ≠，则()()()x y y z z x xyz+++=(2016华一高自招)9.满足1mx m n +-=的整数对(,)m n 共有 对(2016华一高自招)10.已知22(1)56p q p p q pq ++=⎧⎨+=⎩，则以p 、q 为实数根的一元二次方程为(2016华一高自招)11.函数3max{4,,}y t t t =-+表示对于给定的t 的值，代数式4t -+、t 、3t的值中最大的数，例如当1t =-时，max{5,1,3}5y =--=，当1t =时，max{3,1,3}3y ==，则当t = 时函数y 的值最小(2016华一高自招)12.在平面直角坐标系中，同时满足下列两个条件的点的坐标为(1)直线23y x =-+通过这样的点(2)不论m 取何非零实数值，抛物线2(21)3y mx m x m =+--都不通过这样的点三、解答题(2016华一高自招)13.对于任意实数k ，方程2222(1)2()40k x k a x k k b +-++++=总有一个根是1(1)求实数a 、b(2)求另一个根的范围(2016华一高自招)14.如图，在平面直角坐标系中，直线142y x =+与x 轴交于A 点，与y 轴交于B 点，以AB 为直径作⊙1O ，过B 作⊙1O 的切线交x 轴于点C(1)求C 点的坐标(2)设点D 为BC 延长线上一点，CD BC =，P 为线段BC 上一动点(异于B 、C )，过P 点作x 轴的平行线交AB 于M ，交DA 的延长线于N ，试判断PM PN +是否为定值，如果是，求出这个值，若不是，说明理由(2016华一高自招)15.在四边形ABCD 中，AD ∥BC ，BAC D ∠=∠，点E 在边BC (点C 除外)上运动，点F 在边CD 上运动，且AEF ACD ∠=∠(1)如图1，若AB kBC =(k 为常数)，则AE 与EF 之间是否存在某种确定的数量关系，若存在，请证明，若不存在，请说明理由(2)如图2，若5AB AC ==，2425sin BAC ∠=，BAC ∠为锐角，设EF 的长度为m ，当E 、F 点运动时，求m 的变化范围E B B(2016华一高自招)16.已知抛物线2:24C y x x =-+，其顶点为E ，与y 轴交于点D (1)直线2:(0)l y kx k =>与抛物线C 交于不同两点P 、Q ，并与直线1:28l y x =-+交于点R ，分别过P 、Q 、R 作x 轴的垂线，其垂足依次都1P 、1Q 、1R ，若11111u OP OQ OR +=，求u 的值 (2)若直线31:83l y x =-+与抛物线C 在第一象限交于点B ，交y 轴于点A ，求ABD DBE ∠-∠的值 (3)若13(1,)4F 、(0,8)A ，请在抛物线C 上找一点K ，使得KFA ∆的周长最小，并求出周长的最小值。

湖北省华中师大一附中2016届高三五月适应性考试试题文数试题一、选择题（本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1.已知全集{}U=1,234,5，，，集合{}1,2,3A =，集合{}3,4B =，则()U C A B ⋃=（ ） A ．{}4 B ．{}2,3,4,5 C ．{}3,4,5 D ．{}2,3,4 【答案】C考点：集合的运算.2.计算0000107cos 47cos 17cos 47sin +的结果等于（ ）A ．12-B C D ．12【答案】D 【解析】试题分析: )1747sin()17sin (47cos 17cos 47sin 107cos 47cos 17cos 47sin 0-=-+=+2130sin 0==，故选D. 考点：诱导公式；两角差的正弦公式． 3.已知复数1023z i i=-+（其中i 是虚数单位），则z =（ ）A ．B ．C ．D ．【答案】C 【解析】试题分析: 10232333z i i i i i=-=--=-=+，故选C.考点：复数的运算．4.已知五个数2,,,,8a m b 构成一个等比数列，则圆锥曲线2212x y m +=的离心率为（ ）A B D 【答案】A 【解析】试题分析:由题意得28,4ab m m ⨯==∴=±．当4-=m 时圆锥曲线表示双曲线，2222,4,6,a b c e ==∴=∴=；当4=m 时圆锥曲线表示椭圆， 2224,2,2,a b c e ==∴=∴=．故选A.考点：双曲线的简单几何性质．5.若()xxf x e ae -=+为偶函数，则()211e f x e+-<的解集为（ ）A ．()2,+∞B ．()0,2C ．(),2-∞D ．()(),02,-∞⋃+∞ 【答案】B考点：函数的奇偶性；函数的单调性．6.ABC ∆的外接圆圆心为O ，半径为2，OA AB AC ++为零向量，且OA AB =.则CA 在BC 方向上的投影为（ ）A ．3-B ．．3 D 【答案】B 【解析】试题分析:由题意可得四边形ABOC 为菱形，且边长为2，0120,30A ACB =∴∠=,则CA 在BC 方向上的投影为3)30180cos(00-=-CA ，故选B ． 考点：向量的投影．7.已知函数()()()sin 0,0,62f x x x f f f x ππωωω⎛⎫⎛⎫=>+= ⎪ ⎪⎝⎭⎝⎭在区间,62ππ⎛⎫⎪⎝⎭上单调， 则ω=（ ）A ．2B ．3C ．1D ．5 【答案】A考点：三角函数的性质．8.已知某几何体的三视图如图所示，则该几何体的各侧面中，面积最小值为（ ）A C D ．12【答案】D 【解析】试题分析: 由三视图可得几何体的直观图，平面⊥AED 平面BCDE ,四棱锥的高为1，四边形BCDE 为边长为1的正方形，则255121,222121,211121=⨯⨯==⨯⨯===⨯⨯=ACD ABE ABC AED S S S S ,故该几何体的各侧面中，面积最小的为21，故选D. EDCBA考点：由三视图求面积，体积．【易错点睛】本题主要考查了由三视图求面积，体积．求解有关多面体表面积的问题，关键是找到其特征几何图形，如棱柱中的矩形，棱台中的直角梯形，棱锥中的直角三角形，它们是联系高与斜高、边长等几何元素的桥梁，从而架起侧面积公式中的未知量与条件中已知几何元素的联系．由三视图还原几何体是本题的难点．9.阅读如图所示的程序框图，则输出结果S 的值为（ ）A ．18 B ．12 CD ．116【答案】D 【解析】考点：算法初步；二倍角公式．10.直线y a =分别与曲线2ln ,2y x x y x =-=-交于点P Q 、，则PQ 的最小值为（ ）A ．2BC ．1D 【答案】A 【解析】试题分析: 设),(),,(21a x Q a x P ,则2ln 2ln 12122121+-=∴-=-x x x x x x ,21PQ x x ∴=-2111ln 2x x x =--+,令2ln 2+--=x x x y ,则)0()12)(1(121122'>+-=--=--=x xx x x x x x x y ,函数在)1,0(上单调递减,在),0(+∞上单调递增,1=∴x 时,函数的最小值为2，所以A 选项是正确的. 考点：导数与函数的单调性．11.如图，AB 是平面α外固定的斜线段，B 为斜足，若点C 在平面α内运动，且CAB ∠等于直 线AB 与平面α所成的角，则动点C 的轨迹为（ ）A ．圆B ．椭圆C ．双曲线D ．抛物线 【答案】D 【解析】试题分析：如下图所示，作α⊥AO ,垂足为O ，连结BO ，在α内过O 作BO 的垂线，建立空间直角坐标系，由题意得，设=∴∴==∠=∠AC a B a A y x C a AB CAB ABO ),0,cos ,0(),sin ,0,0(),0,,(,,θθθ()2422222222222222(,,sin ),(0,cos ,sin ),cos cos sin sin cos sin cos (sin )2sin ,cos cos AC AB x y a AB a AC ABx ay aa x y a x a y a a C θθθθθθθθθθθθθθ⋅-=-∴===⇒+=++⇒=+-∴的轨迹是抛物线，故选D.考点：立体几何中的动态问题．【易错点睛】在立体几何中，某些点、线、面依一定的规则运动，构成各式各样的轨迹，探求空间轨迹与平面轨迹类似，就注意几何条件，善于基本轨迹化，对于较为复杂的轨迹，常常要分段考虑，注意特定情况下的动点的位置，然后对任意情形加以分析判定，也可能化为平面问题，也可利用空间直角坐标系求出轨迹方程，即可知其对应的轨迹类型，对每一道轨迹命题特别注意轨迹的纯粹性与完备性． 12.定义在R 上的函数()x f 是减函数，且函数()x f y =的图像关于原点中心对称，若t s 、满足不 等式()()2222t t f s s f --≤-，其中s k t ⋅=，则当42<<s 时，k 的取值范围是（ ）A ．⎥⎦⎤⎢⎣⎡-1,21 B ．()[)+∞⋃∞-,10, C ．⎥⎦⎤⎝⎛-1,21 D ．(][)+∞⋃∞-,10, 【答案】C 【解析】试题分析: 定义在R 上的函数()x f 是减函数,且函数()x f y =的图象关于原点中心对称,故()x f 为奇函数.若t s 、满足不等式()()2222tt f s s f --≤-,其中s k t ⋅=,42<<s .则()()2222f ss f t t -≤-+，2222,2s s t t s t s ∴-≥-+∴-≤≤，0--==s t s t k 表示图中四边形ABCD 及其内部区域内的点与原点O 连线的斜率,故当点),(t s 位于线段AD 上时, k 取得最大值为1,当点),(t s 位于点)2,4(-D 时, k 取得最小值为21-.故k 的取值范围为]1,21(-,所以C 选项是正确的．考点：奇偶性与单调性的综合．【易错点睛】本题综合考查了函数的奇偶性，单调性知识，同时考查由最大值，最小值求取值范围的策略，以及运算能力，属于中档题．另本题还考查了转化与化归思想和数形结合思想．将函数问题转化为简单的线性规划问题是本题的难点，也是关键点，这样方便了不等式的解决．数形结合是解决线性规划问题必要的步骤．第Ⅱ卷（非选择题共90分）二、填空题（本大题共4小题，每题5分，满分20分．）13.若幂函数()()22233--⋅+-=m m xm m x f 的图像不过原点，则m 的值为 .【答案】1m =或2=m考点：幂函数的定义；性质．14.从{}5,4,3,2,1中随机选取一个数为a ，从{}3,2,1中随机选取一个数为b ，则a b >的概率是 . 【答案】51【解析】试题分析:由题意可得如下基本事件：(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),(4,1),(4,2),(4,3),(5,1),(5,2),(5,3)共15个，其中满足a b >的基本事件包括3个，故概率为31155=． 考点：古典概型． 15.在ABC ∆中，10103cos ,21tan ==B A ，若最长为1，则最短边的长为 .【答案】55 【解析】试题分析:由10103cos ,21tan ==B A得sin sin A A B C ===∴=,由最长为1得1=c ，则最短边为,b由正弦定理可得sin sin c b B C =⨯==考点：正弦定理．【易错点睛】解三角形问题的两重性：①作为三角形问题，它必须要用到三角形的内角和定理，正弦、余弦定理及其有关三角形的性质，及时进行边角转化，有利于发现解题的思路；②它毕竟是三角变换，只是角的范围受到了限制，因此常见的三角变换方法和原则都是适用的，注意“三统一”(即“统一角、统一函数、统一结构”)是使问题获得解决的突破口．16.定义在R 上的函数()x f 对任意两个不等的实数21x x 、都()()()()12212211x f x x f x x f x x f x +>+，则称函数()x f 为“Z 函数”，以下函数中为“Z 函数”的序号为 .⎪⎩⎪⎨⎧<+-≥+=⎩⎨⎧=≠=--=+-=0,0,4)4(0,00,ln )3(cos 2sin 23)2(1)1(222x x x x x x y x x x y x x x y x y 【答案】(2)(4)考点：函数的单调性．【易错点睛】本题主要考查了函数的单调性．判断(或证明)函数单调性的主要方法(1)函数单调性的定义；(2)观察函数的图象；(3)利用函数和、差、积、商和复合函数单调性的判断法则；(4)利用函数的导数等．其中(2)(3)一般用于选择、填空题．对初等函数的单调性的判断要依赖于图象，对于分段函数的单调性的判断一定要注意自变量的取值范围．三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17.（本小题满分12分）设等差数列{}n a 的前n 项和为n S ，143,241165==+S a a ，数列{}n b 的 前n 项和为n T ，满足)(211N n a T n a n ∈-=-．（Ⅰ）求数列{}n a 的通项公式及数列⎭⎬⎫⎩⎨⎧+11n n a a 的前n 项和； （Ⅱ）判断数列{}n b 是否为等比数列？并说明理由. 【答案】(I)21n a n =+，69nn +；(II)数列{}n b 不是等比数列．试题解析：(I)设数列{}n a 的公差为d ，由11611143,S a ==613a ∴=. 又5624,a a +=解得511a =，2d =， 因此{}n a 的通项公式是21n a n =+()n N *∈，所以111111()(21)(23)22123n n a a n n n n +==-++++， 从而前n 项的和为1113557(21)(23)n n +++⨯⨯++1111111()235572123n n =-+-++-++ 111()2323n =-+69n n =+. (II)因为13a =，124n a n -=，43n n T =+.当1n =时，17b =；当2n ≥时，1114434n n n n n n b T T ---=-=-=⨯；所以14n n b b +=（2n ≥．若{}n b 是等比数列，则有214b b =，而127,12b b ==，所以与214b b =矛盾， 故数列{}n b 不是等比数列．考点：等差数列的性质；裂项相消数列求和；等比数列的定义．【易错点睛】本题主要考查了等差数列的性质；裂项相消数列求和；等比数列的定义．用裂项相消法求和应注意的问题：利用裂项相消法求和时，应注意抵消后并不一定只剩下第一项和最后一项，也有可能前面剩两项，后面也剩两项，再就是将通项公式裂项后，有时候需要调整前面的系数，使裂开的两项之差与系数相乘后与原项相等．18.（本小题满分12分）如图，在四棱锥ABCD P -中，底面ABCD 为直角梯形，BC AD //，⊥PD 底面ABCD ，Q BC AD ADC ,2,90==∠为AD 的中点，M 为棱PC 的中点.（Ⅰ）证明：//PA 平面BMQ ；（Ⅱ）已知2===AD DC PD ，求点P 到平面BMQ 的距离.【答案】(I)证明见解析；．试题解析： (I)证明 连接AC 交BQ 于N ，连接MN ，因为090ADC ∠=，Q 为AD 的中点，所以N 为AC 的中点，又M 为PC 的中点，故MN ∥PA ，又MN ⊂平面BMQ ，所以PA ∥平面BMQ .考点：直线与平面平行的判定定理；点到平面的距离．19.（本小题满分12分）某校高中三个年级共有学生1800名，各年级男生、女生的人数如下表：高一年级 高二年级 高三年级 男生290 b 344 女生 260 c a已知在高中学生中随机抽取一名同学时，抽到高三年级女生的概率为17.0.（Ⅰ）求a 的值；（Ⅱ）现用分层抽样的方法在全校抽取60名学生，则在高二年级应抽取多少名学生？（Ⅲ）已知200,260≥≥c b ，求高二年级男生比女生多的概率.【答案】（I ）306=a ；(II)20；（Ⅲ）141100)(=A P ．试题解析：（I ）根据题意得高三年级女生抽到的概率为1800a ，所以17.01800=a 所以30617.01800=⨯=a （人）(II)由表格知高二年级的总人数为600)306344()290260(1800=+-+-人， 所以高二年级应抽取的人数为20180060060=⨯（人） （III ）设事件A=“高二年级男生比女生多”，求概率)(A P用b 表示高二年级男生的人数，用c 表示高二年级女生的人数，且600=+c b 则满足200,260≥≥c b 的),(c b 配对的情况为)200,400()339,261(),340,260( ，共有141种情况，而事件A 发生的),(c b 配对的情况为)298,302(),299,301(，)200,400(, 共有100种情况，所以高二年级男生比女生多的概率为141100)(=A P 考点：分层抽样；古典概型．20.（本小题满分12分）已知椭圆)0(1:2222>>=+b a b y a x C 的离心率为21，过右焦点F 且垂直于 x 轴的直线与椭圆C 相交于N M ,两点，且3=MN .（Ⅰ）求椭圆C 的方程；（Ⅱ）设直线l 经过点F 且斜率为k ，l 与椭圆C 相交于,A B 两点，与以椭圆C 的右顶点E 为圆心的圆相 交于,P Q 两点（,,,A P B Q 自下至上排列），O 为坐标原点.95OA OB ⋅=-，且Ap BQ =，求直线l 和圆E 的方程.【答案】（Ⅰ）22143y x +=；0y --=0y +=，()223312100x y -+=．试题解析： （Ⅰ）设(,0)F c ，则由题意得222c a b =-，12c a =，223b a ⋅=，解得2,1a b c ===，∴椭圆C 的方程为22143y x +=． （Ⅱ）由题意，直线l 的斜率k 存在．设l 的方程为()1y k x =-，联立椭圆方程得()22223484120k x k x k +-+-=．设()()1122,,,A x y B x y ，则2122834k x x k +=+，212241234k x x k -=+， ∴2122934ky y k =-+． ∴21212212534kOA OB x x y y k+⋅=+=-+． ∵95OA OB ⋅=-，∴221259534k k +-=-+，解得23k =． 由题意可得，AP BQ =等价于AB PQ =．设圆E 的半径为r ，222121234k x k +-=+，PQ = 将23k =代入AB PQ =解得2331100r =．故所求直线l 的方程为)1y x =-0y -=0y +=；圆E 的方程为()223312100x y -+=．考点：椭圆的简单性质．【易错点睛】本题综合考查了椭圆的标准方程及其简单性质，直线与椭圆相交问题转化为方程联立得到根与系数的关系，向是垂直与数量积的关系等基础知识与基本技能，考查了推理能力和计算能力，属于难题． 本题的难点在于利用一元二次方程与根与系数的关系建立等式，求得23k =，利用圆的有关知识可求得半径．21.（本小题满分12分）设函数()ln ,m f x x m R x=+∈． （Ⅰ）当m e =（e 为自然对数的底数）时，求()f x 的最小值；（Ⅱ）讨论函数()()3x g x f x '=-的零点的个数； （Ⅲ）若对任意()()0,1f b f a b a b a->><-恒成立，求实数m 的取值范围. 【答案】(I)2；(II) 当32>m 时，函数)(x g 无零点，当32=m 或0≤m 时，函数)(x g 有且仅有一个零点，当320<<m 时，函数)(x g 有两个零点；（III ）⎪⎭⎫⎢⎣⎡+∞,41．试题解析：(I)当e m =时，xe x xf +=ln )(，易知函数)(x f 的定义域为),0(+∞，所以221)(xe x x e x xf -=-='，当),0(e x ∈时，0)(<'x f ，此时)(x f 在),0(e 上是减函数；当),(+∞∈e x 时，0)(>'x f ，此时)(x f 在),(+∞e 上是增函数，所以当e x =时， )(x f 取得极小值2ln )(=+=ee e ef (II)因为函数),0(313)()(2>--=-'=x x x m x x x f xg 令0)(=x g ，得),0(313>+-=x x x m 设),0(31)(3>+-=x x x x h 所以),1)(1(1)(2+--=+-='x x x x h 当)1,0(∈x 时，0)(>'x h ，此时)(x h 在)1,0(上为增函数；当),1(+∞∈x 时，0)(<'x h ，此时)(x h 在),1(+∞上为减函数，所以当1=x 时，)(x h 取极大值32131)1(=+-=h ，令0)(=x h ，即0313=+-x x ，解得0=x 或3=x ，由函数)(x h 的图像知： ①当32>m 时，函数m y =和函数)(x h y =无交点； ②当32=m 时，函数m y =和函数)(x h y =有且仅有一个交点； ③当320<<m 时，函数m y =和函数)(x h y =有两个交点； ④当0≤m 时，函数m y =和函数)(x h y =有且仅有一个交点。

湖北省华中师范大学第一附属中学中考提前招生提前招生数学模拟试卷一、选择题1．下列图像中有关量的变化趋势与对应叙述关系正确的是（）A．向一定质量表面生锈的铁片中滴加盐酸至过量 B．向一定质量的稀硫酸中滴加水C．向氢氧化钠和碳酸钠的混合溶液中滴加石灰水至过量 D．加热一定质量的氯酸钾2．现有一包由5.6g铁、7.2g镁、1.0g碳混合而成的粉末，把它加入一定量的CuCl2溶液中。

实验结束后，测得剩余固体中含有三种物质。

则剩余固体的质量不可能是A．26. 2gB．26.6gC．26. 0gD．25. 8g3．固体X可能由氢氧化钠、碳酸钠、氯化钠、硝酸镁、硝酸钡、硫酸钠、硫酸铜中的一种或几种物质组成（提示：以上物质中，只有氢氧化钠和碳酸钠的水溶液显碱性）。

为确定其组成，进行如下实验：①将固体X加入水中充分溶解，得到无色溶液；②测X溶液的pH，pH= 13；③向X的溶液中加入足量的硝酸钡溶液，产生白色沉淀，过滤；④向步骤③所得沉淀中加入足量的稀盐酸，沉淀不溶解；⑤向步骤③所得的滤液中加入过量的稀硝酸，再加入硝酸银溶液，产生白色沉淀。

根据以上实验信息，关于固体X组成的判断有以下几种说法：①不能确定是否有硝酸镁；②硝酸钡、硫酸铜、碳酸钠一定不存在；③硫酸钠和氢氧化钠一定存在；④不能确定是否有氯化钠。

以上说法中正确的个数是A．1个B．2个C．3个D．4个4．已知反应前后分子变化的微观示意图如下所示，下列说法错误．．的是A．反应前后元素种类不变B．A是有机物，C、D是无机物C．点燃前要先检验A的纯度，防止爆炸D．此反应中A和B的化学计量数之比等于1：15．逻辑推理是化学学习中常用的思维方法。

下列推理正确的是A．碱溶液呈碱性，呈碱性的溶液一定是碱溶液B．单质只含一种元素，只含一种元素的纯净物一定是单质C．中和反应生成盐和水，生成盐和水的反应一定是中和反应D．有机化合物都含碳元素，含碳元素的化合物一定是有机化合物6．下图是a、b、c三种物质的溶解度曲线，下列有关叙述正确的( )A．a物质的溶解度大于b物质的溶解度B．降低温度，c物质会从其饱和溶液中析出C．t2℃时30ga物质加入到50g水中不断搅拌，能形成80g溶液。

华中师大一附中2016年高中招生考试数学试题考试时间：80分钟 卷面满分：150分说明：所有答案一律书写在答题卡上，写在试卷上作答无效．一、选择题 (本大题共6小题，每小题7分，共42分．在每小题给出的四个选项中，有且只有一项是正确的．)1.已知方程1x ax =+有一个负根，而且没有正根，则a 的取值范围是( ) A ．1a >- B ．1a ≥C ．1a =D ．1a >2.关于x 的方程21212x x ax x x x +-=+-+-的根为负数，则a 的值为( ) A ．3a ≠-B ．3a ≠C ．1a <-且3a ≠-D ．1a >-且3a ≠3.如图，抛物线21(0)y ax bx c a =++≠的顶点为(1,3)A ，且与x 轴有一个交点为(4,0)B ，直线2y mx n =+与抛物线交于A 、B 两点，下列结论： ①20a b +=；②0abc >；③方程23ax bx c ++=有两个相等的实数根； ④抛物线与x 轴的另一个交点坐标是(1,0)-，⑤当14x <<时，有21y y <．其中正确的是( ) A ．①②③B ．①③④C ．①③⑤D ．②④⑤4.已知,αβ是方程2260x ax a -++=的两实数根，那么22(1)(1)αβ+++的最小值为( ) A ．414-B ．2C ．10D ．325.设S =⋅⋅⋅+，则S 最接近的整数是( ) A ．2015B ．2016C ．2017D ．20186.如图，菱形ABCD 中，60A ∠=︒，6AB =，⊙A 、⊙B 的半径分别为4和2，P 、E 、F 分别是线段CD 、⊙A 和⊙B 上的动点，则PE PF +的最大值是( ) A．12 B．16C ．18D ．6CBD二、填空题(本大题共6小题，每小题7分，共42分)．7.如图，四边形ABCD 是菱形，E 、F 、G 、H 分别是各边的中点，随机地向菱形ABCD 内掷一粒米，则米粒落在阴影区域内的概率是 . 8.已知222x y z x y z x y z z y x +--+-++==且0xyz ≠，则()()()x y y z z x xyz+++= . 9.满足 mn + m −n =1的整数对(,)m n 共有 对.10.已知22(1)56p q p p q pq ++=⎧⎨+=⎩，则以p 、q 为实数根的一元二次方程为 . 11.函数3max{4,,}y t t t =-+表示对于给定的t 的值，代数式4t -+、t 、3t 的值中最大的数，例如当1t =-时，max{5,1,3}5y =--=，当1t =时，max{3,1,3}3y ==，则当t = 时函数y 的值最小.12.在平面直角坐标系中，同时满足下列两个条件的点的坐标为 . (1)直线23y x =-+通过这样的点；(2)不论m 取何非零实数值，抛物线2(21)3y mx m x m =+--都不通过这样的点. 三、解答题(本大题共4小题，共66分．解答应写出文字说明、证明过程和演算步骤) 13. (本小题满分16分)对于任意实数k ，方程2222(1)2()40k x k a x k k b +-++++=总有一个根是1. (1)求实数a 、b ； (2)求另一个根的范围.14. (本小题满分16分)如图，在平面直角坐标系中，直线y ＝－12x ＋4与x 轴交于A 点，与y 轴交于B 点，以AB 为直径作⊙1O ，过B 作⊙1O 的切线交x 轴于点C . (1)求C 点的坐标；(2)设点D 为BC 延长线上一点，CD BC =，P 为线段BC 上的一个动点(异于B 、C )，过P 点作x 轴的平行线交AB 于M ，交DA 的延长线于N ，试判断PM PN +是否为定值，如果是，求出这个值，若不是，说明理由.15. (本小题满分16分)在四边形ABCD 中，AD ∥BC ，BAC D ∠=∠，点E 在边BC (点C 除外)上运动，点F 在边CD 上运动，且AEF ACD ∠=∠.(1)如图1，若AB kBC =(k 为常数)，则AE 与EF 之间是否存在某种确定的数量关系？若存在，请证明，若不存在，请说明理由； (2)如图2，若5AB AC ==，2425sin BAC ∠=，BAC ∠为锐角，设EF 的长度为m ，当E 、F 点运动时，求m 的变化范围.16. (本小题满分16分)已知抛物线2:24C y x x =-+，其顶点为E ，与y 轴交于点D . (1)直线2:(0)l y kx k =>与抛物线C 交于不同两点P 、Q ，并与直线1:28l y x =-+交于点R ，分别过P 、Q 、R 作x 轴的垂线，其垂足依次为1P 、1Q 、1R ，若11111u OP OQ OR +=，求u 的值；(2)若直线31:83l y x =-+与抛物线C 在第一象限交于点B ，交y 轴于点A ，求ABD DBE∠-∠的值； (3)若13(1,)4F 、(0,8)A ，请在抛物线C 上找一点K ，使得KFA ∆的周长最小，并求出周长的最小值.DBB华中师大一附中2016年高中招生考试数学试题参考答案及评分标准考试时间：80分钟卷面满分：150分说明：所有答案一律书写在答题卡上，写在试卷上作答无效．一、选择题(本大题共6小题，每小题7分，共42分．在每小题给出的四个选项中，有且只有一项是正确的．)7．１２8．－1或8(只填对一个只得3分) 9．610．x2－3x＋2=0 (填了x2－2x＋3=0给4分) 11．212．(－3，9)，(1，1)，(3，－3)[(正确答案个数－错误答案个数)×2。

华师一附中高中提前自主招生考试数学训练题华师一附中高中提前自主招生考试数学训练题一、选择题1.如图，四边形48co 中，AC, 80是对角线，△48C 是等边三角形.ZADC= 30°, AO-3, BD-5,则。

的长为(). (A) 3亚B) 4 (C) 2出(D)2.设关于工的方程+(o + 2)x + 9a = 0,有两个不相等的实数根/、A 取值范围是()B C，2，且用〈1〈工2，那么实数。

的 DA^ a < ---- B 、——<a <— C 、a> - D 、 ------------ <11 7 5 5 113 .如图 AC_LBC 于 C, BC=a, CA=b, AB=c, 00 与直线 AB 、B 都相切，则。

的半径为() A a+b-c 口 b+c-a 「a+b+c n a+c-bXXa 2JO ・ 2 lx ・ 2 JLx • 2 4 .如果a 、b 、c 是非零实数，且a+b 十c=0,那么/_ + _L+工 HI 闻 1。

( ) A. 0 B. 1 或-1 C. 2 或-2 D. 0 或- 5.如图线段AB,CD 将大长方形分成四个小长方形，其中\=8,邑=6, §3=5,则S 4=()A 20 n 5 「10 A. —B ・— D ・—3 3 3 za <0 c cC 3题图_+W 的所有可能的值为 \abc\ 2Si s 2A ............... ............R关的S3 )5题图D 一,, 一 C 圆弧，则无阴影部分的两部分的面积之差是() A 、--1 B 、1-- 2 4 C 、--1 D 、1-- 3 6 7.在aABC 中，a 、b 、c 分别为角A 、B 、C 的对边, & --p 若NB = 60° ,则—L +，_的值为( ) A. 1 B.匹 2 2 C. 1 D. y[2 8..已知 a=1999x+2000, b= 1999x4-2001, c=1999x+2002, A. 0 B. 1 C.2 D. 3 9.如图9-2,点E 、F 分别是矩形ABCD 的边AB 、BC 的中点, a+b c+b A则多项式a 2+b 2+c 2-ab-bc-ca 的值为 ( ) 连AF 、CE,设AF 、CE 交于点G,则 D ^FA ES 四边形AGCD 等丁 S 祖形ABCD10 .如图，D 、E 在6c 上，F 、G 分别在AC 、A6上，且DEFG 为正方形,如果 S ACFEM S UGL I, S&BDG =3, S A J 48c 等于( ) (A)6 (B)7 (C)8 (D)911 .如果 4+b+c=0, ! + J+L = _4,那么 ± 上的值 a b c a~b' c~(A)3 (B)8 (C)16 (D) 2012 .如果a. b 是关于x 的方程(x+c)(x+d)=l 的两个根，那么(。

第I 卷（选择题共60分）注意事项：务必将每小题的答案填在答题卡的相应位置.答在试卷上无效.一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的，请将你认为正确的选项代号涂填在选择题的答题卡内.1.已知集合2{|lg()}A x y x x ==-,集合2{|0(0)}B x x cx c =-<>错误！未找到引用源。

,若A B ⊆错误！未找到引用源。

,则c 的取值范围为( ) A.(0,1] B.(0,1) C.[1,)+∞ D.(1,)+∞【答案】C考点：集合的运算 2.复数241iz i+=-错误！未找到引用源。

(i 为虚数单位)在复平面内对应点的坐标为( ) A.(3,3) B.(1,3)- C.(3,1)-D.(2,4)【答案】B 【解析】试题分析：由题化简所给复数根据复数的几何意义判断即可. 因为()()()()2412426131112i i i iz i i i i +++-+====-+--+,所以其在复平面对应的点的坐标为(1,3)-，故选B. 考点：复数的运算及其几何意义3.已知向量(1,2),(2,1)a x b =-=错误！未找到引用源。

，则“0x >”是“a 与b 错误！未找到引用源。

夹角为锐角”的( )A ．充分不必要条件B ．充要条件C ．必要不充分条件D ．既不充分也不必要条件【答案】C 【解析】试题分析：由题(1,2),(2,1),(1,2)(2,1)2x a x b a b x =-=∴⋅=-⋅=，22255cos ,255cos ,a b x x a b x x a b ⋅=-+⨯⨯<>=-+⨯⨯<>，x>0不一定推出向量a 与b 错误！未找到引用源。

夹角为锐角，反之可以得到x>0,所以“0x >”是“a 与b 错误！未找到引用源。

夹角为锐角”的必要不充分条件，故选C 考点：必要条件4..已知定义在R 上的奇函数()f x 满足(1)(1)f x f x +=-,数列{}n a 错误！未找到引用源。

2016年华中师大一附中预录数学模拟试题一、选择题（本大题6个小题，每小题6分，共36分） 1．已知,c b a ,c b a 31110-=++=++那么222111cb a ++的值为（ ） A ．3 B ．6 C ．9 D ．122．若1≠mn ，且有07201652=++m m 及05201672=++n n ，则nm的值为（ ） A ．57 B ．75 C ．52016- D ．72016-3．已知sin αcos α=81，且45°<α<90°，则cos α- sin α的值为（ ）A ．23 B ．43 C ．23- D ．43-4．如图，在正△ABC 中，P 为正三角形内任意一点，过P 作PD⊥BC ，PE ⊥AB ，PF ⊥AC ，连接AP ，BP ，CP ，如果S △APF + S△BPE+ S △CPD =233，那么△ABC 的内切圆的半径为（ ） A ．1 B ．3 C ．2 D ．23 5．如图，在平面直角坐标系中，⊙O 1过原点O ，且与⊙O 2外切，圆心O 1与O 2在x 正半轴上，⊙O 1的半径O 1P 1，⊙O 2的半径O 2P 2都与x 轴垂直，且点P 1、P 2在反比例函数)0(1>=x xy 的图象上，则21y y +的值为（ ）A ．22B ．1C ．23D ．2 6．如图，在△ABC 中，D 、E 是BC 边上的点，BD :DE :EC=3:2:1，M 在AC 边上，CM :MA=1:2，BM 交AD 、AE 于H 、G ，则BH :HG :GM 等于（ ） A ．3:2:1 B ．5:3:1 C ．25:12:5 D ．51:24:10二、填空题（本大题共6个小题，每小题7分，共42分）7．已知0132=+-a a 且3331234=+-++2ama a ma a ,则m 的值为 . 8．记∑=+++=2016122)1(111k k k M ，再记[M]表示不超过M 的最大整数，则[M]为 .9．在平面直角坐标系中，如果直线kx y =与函数⎪⎩⎪⎨⎧>-≤≤-<+=)3(82)33(2)3(42x x x --x x y 的图象恰有3个不同的交点，则k 的取值范围是 . 10.如图，四边形ABHK 是边长为6的正方形，点C 、D 在边AB 上，且AC=BD=1，点P 是线段CD 上的动点，分别以AP 、PB 为边在线段AB 的同侧作正方形AMNP 和正方形BRQP ，E 、F 分别为MN 、QR 的中点，连接EF ，设EF 的中点为G ，则当点P 从点C 运动到点D 时，点G 移动的路径长为 . 11.一位小朋友在粗糙不打滑的“Z ”字形平面轨道上滚动一个半径为10cm 的圆盘，如图所示，AB 与CD 是水平的，BC 与水平面的夹角为60°，其中AB=CD=60cm ，BC=40cm ，请你作出该小朋友将圆盘从A 点滚动到D 点其圆心经过的路线示意图，圆心O 所经过的路线长度为 .12.△ABC 的一边长为5，另两边长分别是二次函数m x x y +-=62与x 轴的交点的横坐标的值，则m 的取值范围为 . 三、解答题（本大题共5个小题，共72分）13.（本题13分）已知⊙O 的面积为4π，△ABC 内接于⊙O ，a 、b 、c 分别是三角形三个内角∠A 、∠B 、∠C 的对边的长，关于x 的方程02)(2=-+-+a c bx x c a 有两个相等的实数根，cosA 、cosB 是二次函数3)]13([)]13([2+-+---=x m x m y 的图象与x 轴的两个交点的横坐标，求△ABC 三边的长.14.（本题13分）已知二次函数8422-+-=m mx x y .(1)若以抛物线8422-+-=m mx x y 的顶点A 为一个顶点作该抛物线的内接正三角形AMN （M 、N 两点在抛物线上）.请问：△AMN 的面积是与m 无关的定值吗？若是，请求出这个定值；若不是，请说明理由.(2)若抛物线8422-+-=m mx x y 与x 轴交点的横坐标均为整数，求整数m 的值.15.（本题15分）已知，在平面直角坐标系中，直线AB 分别交x 轴、y 轴于A 、B 两点，且OB=2OA ，线段AB 绕点B 顺时针旋转90°，得到线段BC.(1)如图①，当OA=3时，求点C 的坐标；(2)如图②，若点A 和点D 关于y 轴对称，直线CD 交y 轴于点E ，连接AE ，求∠DAE 的度数； (3)在(2)的条件下，当△AOE 的面积为29，当点P 从点B 出发，沿y 轴负方向以每秒2个单位的速度匀速运动，设运动时间为t 秒，△PAC 的面积为S （S ≠0），求S 与t 的函数关系式，并写出自变量t 的取值范围.16.（本题13分）已知，如图，直线)0(3>+=k kx y 交x 轴于B 点，交y 轴于A 点，以A 点为圆心，AB 为半径作⊙A 交x 轴于另一点D ，交y 轴于E 、F 两点，交直线AB 于C 点，连结BE 、CE ，∠CBD 的平分线CE 于I. (1)求证：BE=IE ；(2)若AI ⊥CE ，设Q 为上一点，连结DQ 交y 轴于T ，连BQ 并延长交y 轴于G ，求AT ·AG 的值；(3)设P 为线段AB 上的一动点（异于点A 、B ），连接PD 交y 轴于M 点，过P 、M 、B 三点作⊙O 1交y 轴于另一点N ．设⊙O 1的半径为R ，当43=k 时，求出RMN的值.17.（本题满分18分）在平面直角坐标系中，抛物线21212+++-=t tx x y 与x 轴交于A 、B 两点（点A 在点B 的左侧），其顶点M 在直线x y 2=上.(1)求t 的值；(2)如图，C 为线段OM 上一点，过C 作x 轴的平行线交线段BM 于点D ，以CD 为边向上作正方形CDEF ，CF 、DE 分别交此抛物线于P 、Q 两点，是否存在这样的点C ，使得正方形CDEF 的面积和周长恰好被直线PQ 平分?若存在，求点C 的坐标；若不存在，请说明理由；(3)将此抛物线A 、B 之间的部分（含点A 和点Ｂ）向右平移n (n >0)个单位后得到的图象记为G ，同时将直线64+=x y 向下平移n 个单位，请结合图象回答：平移后的直线与图象G 有公共点时，n 的取值范围.参考答案一、选择题1．C 2．A 3．C 4．A 5．D 6．D 二、填空题7．5 8．2016 9．232<<k 10．2 11．3103320160+-π 12．9411<<m 三、解答题13. 解：∵关于x 的方程（a+c ）x 2-2bx+c-a=0有两个相等的实数根， ∴（-2b ）2-4（a+c ）（c-a ）=0 ∴a 2+b 2=c 2，∴△ABC 是直角三角形，∠C=90°，∴∠A+∠B=90°，∴sinA=cosB ．又∵cosA ，cosB 是二次函数3)]13([)]13([2+-+---=x m x m y 的图象与x 轴的两个交点的横坐标，∴sinA 、cosA 是关于x 的方程 03)]13([)]13([2=+-+---x m x m 的两个根，∴ ⎪⎪⎩⎪⎪⎨⎧+-=+--+=+133sin cos 1313sin cos m A ·A m m A A又∵sin 2A+cos 2A=1， ∴（sinA+cosA ）2-2sinA •cosA=1， ∴（1313+--+m m ）2-2×133+-m =1 解得33+=m经检验，33+=m 是原方程的根.当33+=m 时，原方程变为0332242=++-x )(x ，∴232121==x ,x ∵又△ABC 的外接圆面积为4π，∴外接圆半径R=2， ∴斜边c=2R=4．∴另外两直角边为2，32.14. 解：(1)如图：顶点A 的坐标为（m ，-m 2+4m-8），△AMN 是抛物线的内接正三角形，MN 交对称轴于点B ，tan ∠AMB=tan60°=，则AB=BM=BN ，设BM=BN=a ，则AB=a ， ∴点M 的坐标为（m+a ，a-m 2+4m-8），∵点M 在抛物线上，∴a-m 2+4m-8=（m+a ）2-2m （m+a ）+4m-8，整理得：a 2-a=0得：a= （a=0舍去）所以△AMN 是边长为2的正三角形， S △AMN =×2×3=3，与m 无关；（2）当y=0时，则有x 2-2mx+4m-8=0，解得：，由题意知，(m-2)2+k 为完全平方数，令(m-2)2+4=k 2,则(k+m-2)(k-m+2)=4，又∵m,k 为整数，∴k+m-2，k-m+2的奇偶性相同， ∴⎩⎨⎧=+-=-+2222m k m k 或⎩⎨⎧-=+--=-+2222m k m k ∴⎩⎨⎧==22k m 或⎩⎨⎧-==22k m综上所述，m = 2．∴∠EBD =∠ECB ．∵∠ABI=∠DBI ，∠BIE=∠ECB +∠CBI ，∴∠BIE=∠IBE ． ∴BE=IE ．（2）解：连接QC 、TB ，则∠BCQ+∠CBQ=90°， 又∠BDQ+∠ATD=90°，而∠BCQ=∠BDQ ， ∴∠CBQ=∠ATD=∠ATB ． ∴△ABG ∽△ATB ． ∴AB 2=AG•AT ．∵AI ⊥CE ，∴I 为CE 的中点．∴BE=21EC. 又∵∠OBE =∠ECB ，∠BOE-∠CEB=90°， ∴△O BE ∽△E CB ．∴OE ：OB=BE ：CE=21设⊙A 的半径为R ，由AB 2-OA 2=BO 2，OE=R-3， 得R 2-32=4（R-3）2解得R=5，或R=3（不合题意，舍去）． ∴AT•AG=A B 2=25．(3)证明：作O 1H ⊥MN 于H ，连接O 1N 、PN 、BM ，则MN=2NH ，且∠NO 1H= ∠NPM ，∴sin H NO NHR MN 2NO sin 2211=∠==∠NPM 由直线AB 的解析式：343+=x y ，得OB=OD=4，OM ⊥BD ，∴∠BMO=∠DMO 又∠BMO=∠ABM+∠BAM ，∠DMO=∠MPN+∠PNM ，∠ABM=∠PNM ， ∴∠MPN=∠BAM ，∴17.解：(1)由21212+++-=t tx x y 可得： 对称轴2124122t )t (b ac y ,b x -+=-==-= ∴121==t t(2)如图(1)，∵M （1，2），B （3，0），则直线3+-=x y MB（3）如图（2），由题意得，点A 、B 之间的部分图象的解析式为：)x )(x )(x (y 311321≤≤-+--=，则抛物线向左平移后得到的图象G 的解析式为：)n x n )(n x )(n x (y -≤≤--+++--=311321此时直线平移后的解析式为：n x y ++=64如果平移后直线与平移后的二次函数相切，则方程：)n x )(n x (n x +++--=++132164有两个相等的实数根，即：0913122=--+--n x )n (x 有两个相等的实数根，。

2016年广东省广州市华师附中中考数学一模试卷一、选择题(每小题3分，共30分)1．﹣3的相反数是（）A．3 B．﹣3 C．±3 D．2．下列计算正确的是（）A．2﹣1=﹣2 B．=±3 C．（a4）3=a7 D．﹣（3pq）2=﹣9p2q23．在以下永洁环保、绿色食品、节能、绿色环保四个标志中，是轴对称图形是（）A．B．C．D．4．一组数据3，6，4，5，3，2，则这组数据的中位数和极差是（）A．4.5，2 B．4，6 C．4，4 D．3.5，45．如图所示几何体的俯视图是（）A．B．C．D．6．如图，在▱ABCD中，已知AD=8cm，AB=6cm，DE平分∠ADC交BC边于点E，则BE 等于（）A．cm B．2cm C．3cm D．4cm7．如图，在数轴上所表示的是哪一个不等式的解集（）A．＞﹣1 B．≥﹣3 C．x+1≥﹣1 D．﹣2x＞48．已知一次函数y=kx+b的图象如图，那么正比例函数y=kx和反比例函数y=在同一坐标系中的图象大致是（）A． B． C．D．9．如图，在△ABC中，∠CAB=65°，将△ABC在平面内绕点A旋转到△AB′C′的位置，使CC′∥AB，则旋转角的度数为（）A．35°B．40°C．50°D．65°10．若α、β是方程x2+2x﹣2007=0的两个实数根，则α2+3α+β的值（）A．2007 B．2005 C．﹣2007 D．4010二、填空题(每小题3分，共18分)11．代数式有意义时，x应满足的条件是．12．分解因式：x3﹣xy2=．13．一个不透明的口袋里有4张形状完全相同的卡片，分别写有数字1、2、3、4，口袋外有两张卡片，分别写有数字2、3，现随机从口袋里取出一张卡片，则这张卡片与口袋外的卡片上的数字能构成三角形的概率是．14．如图，在平面直角坐标系中，点O为坐标原点，点P在第一象限，⊙P与x轴交于O，A两点，点A的坐标为（6，0），⊙P的半径为，则点P的坐标为．15．如图，量角器的直径与直角三角板ABC的斜边AB重合，其中量角器0刻度线的端点N与点A重合，射线CP从CA处出发沿顺时针方向以每秒3度的速度旋转，CP与量角器的半圆弧交于点E，第24秒，点E在量角器上对应的读数是度．16．在Rt△ABC中，∠A=90°，有一个锐角为60°，BC=6．若点P在直线AC上（不与点A，C重合），且∠ABP=30°，则CP的长为．三、解答题17．解方程：x2﹣10x+9=0．18．如图，在△ABC中，AD是BC边上的中线，分别过点C、B作射线AD的垂线段，垂足分别为E、F．求证：BF=CE．19．先化简，再求值：÷（﹣），其中a=，b=2．20．为实施“农村留守儿童关爱计划”，某校结全校各班留守儿童的人数情况进行了统计，发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况，并制成如下两幅不完整的统计图：（1）求该校平均每班有多少名留守儿童？并将该条形统计图补充完整；（2）某爱心人士决定从只有2名留守儿童的这些班级中，任选两名进行生活资助，请用列表法或画树状图的方法，求出所选两名留守儿童来自同一个班级的概率．21．两个城镇A、B与两条公路ME，MF位置如图所示，其中ME是东西方向的公路．现电信部门需在C处修建一座信号发射塔，要求发射塔到两个城镇A、B的距离必须相等，到两条公路ME，MF的距离也必须相等，且在∠FME的内部．（1）点C应选在何处？请在图中，用尺规作图找出符合条件的点C．（不写已知、求作、作法，只保留作图痕迹）（2）点C到公路ME的距离为2km，设AB的垂直平分线交ME于点N，点M处测得点C 位于点M的北偏东60°方向，在N处没得点C位于点N的北偏西45°方向，求MN的长（结果保留根号）22．某药品研究所开发一种抗菌新药，经多年动物实验，首次用于临床人体试验，测得成人服药后血液中药物浓度y（微克/毫升）与服药时间x小时之间函数关系如图所示（当4≤x ≤10时，y与x成反比例）．（1）根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式．（2）问血液中药物浓度不低于4微克/毫升的持续时间多少小时？23．如图，AB是⊙O的弦，D为半径OA的中点，过D作CD⊥OA交弦AB于点E，交⊙O于点F，且CE=CB．（1）求证：BC是⊙O的切线；（2）连接AF、BF，求∠ABF的度数；（3）如果CD=15，BE=10，sinA=，求⊙O的半径．24．类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”．（1）概念理解：如图1，在四边形ABCD中，添加一个条件使得四边形ABCD是“等邻边四边形”．请写出你添加的一个条件．（2）问题探究：①小红猜想：对角线互相平分的“等邻边四边形”是菱形，她的猜想正确吗？请说明理由．②如图2，小红画了一个Rt△ABC，其中∠ABC=90°，AB=2，BC=1，并将Rt△ABC沿∠ABC的平分线BB′方向平移得到△A′B′C′，连结AA′，BC′，小红要使平移后的四边形ABC′A′是“等邻边四边形”，应平移多少距离（即线段BB′的长）？（3）拓展应用：如图3，“等邻边四边形”ABCD中，AB=AD，∠BAD+∠BCD=90°，AC，BD为对角线，AC= AB，试探究BC，CD，BD的数量关系．25．在平面直角坐标系中，已知抛物线y=x2+bx+c（b，c为常数）的顶点为P，等腰直角三角形ABC的顶点A的坐标为（0，﹣1），C的坐标为（4，3），直角顶点B在第四象限．（1）如图，若该抛物线过A，B两点，求该抛物线的函数表达式；（2）平移（1）中的抛物线，使顶点P在直线AC上滑动，且与AC交于另一点Q．（i）若点M在直线AC下方，且为平移前（1）中的抛物线上的点，当以M、P、Q三点为顶点的三角形是等腰直角三角形时，求出所有符合条件的点M的坐标；（ii）取BC的中点N，连接NP，BQ．试探究是否存在最大值？若存在，求出该最大值；若不存在，请说明理由．2016年广东省广州市华师附中中考数学一模试卷参考答案与试题解析一、选择题(每小题3分，共30分)1．﹣3的相反数是（）A．3 B．﹣3 C．±3 D．【考点】相反数．【分析】依据相反数的概念求解．相反数的定义：只有符号不同的两个数互为相反数，0的相反数是0．【解答】解：﹣3的相反数就是3．故选A．2．下列计算正确的是（）A．2﹣1=﹣2 B．=±3 C．（a4）3=a7 D．﹣（3pq）2=﹣9p2q2【考点】幂的乘方与积的乘方；算术平方根；负整数指数幂．【分析】分别利用积的乘方运算以及幂的乘方运算法则和算术平方根、负整数指数幂的性质计算得出答案．【解答】解：A、2﹣1=，故此选项错误；B、=3，故此选项错误；C、（a4）3=a12，故此选项错误；D、﹣（3pq）2=﹣9p2q2，正确．故选：D．3．在以下永洁环保、绿色食品、节能、绿色环保四个标志中，是轴对称图形是（）A．B．C．D．【考点】轴对称图形．【分析】据轴对称图形的概念求解．如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴．【解答】解：A、不是轴对称图形，不符合题意；B、是轴对称图形，符合题意；C、不是轴对称图形，不符合题意；D、不是轴对称图形，不符合题意．故选B．4．一组数据3，6，4，5，3，2，则这组数据的中位数和极差是（）A．4.5，2 B．4，6 C．4，4 D．3.5，4【考点】极差；中位数．【分析】根据中位数的定义和求极差的方法分别进行计算即可．【解答】解：把这组数据从小到大排列为：2，3，3，4，5，6，中位数是第3、4个数的平均数，则这组数据的中位数=3.5；极差是：6﹣2=4；故选D．5．如图所示几何体的俯视图是（）A．B．C．D．【考点】简单几何体的三视图．【分析】根据定义，俯视图是从物体上面看所得到的图形，即可得出答案．【解答】解：从上面看可得到三个左右相邻的中间有两个界限的长方形，故选D．6．如图，在▱ABCD中，已知AD=8cm，AB=6cm，DE平分∠ADC交BC边于点E，则BE 等于（）A．cm B．2cm C．3cm D．4cm【考点】平行四边形的性质．【分析】由在▱ABCD中，可得CD=AD=6cm，BC=AD=8cm，又由DE平分∠ADC，易证得△CDE是等腰三角形，即可求得CE的长，继而求得答案．【解答】解：∵四边形ABCD是平行四边形，∴BC=AD=8cm，CD=AB=6cm，AD∥BC，∴∠ADE=∠CED，∵DE平分∠ADC，∴∠ADE=∠CDE，∴∠CDE=∠CED，∴CE=CD=6cm，∴BE=BC﹣CE=2cm．故选B．7．如图，在数轴上所表示的是哪一个不等式的解集（）A．＞﹣1 B．≥﹣3 C．x+1≥﹣1 D．﹣2x＞4【考点】在数轴上表示不等式的解集．【分析】本题先观察数轴表示的不等式的解集，再对选项分别化简，看是否与题意相符．若是，则该选项为正确的答案．【解答】解：依题意得：数轴表示的解集是：x≥﹣2A、解得：x＞﹣2B、解x+3≥﹣6，不等式的解集是x≥﹣9C、解得：x≥﹣2D、解得x＜﹣2故应选C．8．已知一次函数y=kx+b的图象如图，那么正比例函数y=kx和反比例函数y=在同一坐标系中的图象大致是（）A． B． C．D．【考点】反比例函数的图象；一次函数的图象；一次函数图象与系数的关系．【分析】根据一次函数图象可以确定k、b的符号，根据k、b的符号来判定正比例函数y=kx和反比例函数y=图象所在的象限．【解答】解：如图所示，∵一次函数y=kx+b的图象经过第一、三、四象限，∴k＞0，b＜0．∴正比例函数y=kx的图象经过第一、三象限，反比例函数y=的图象经过第二、四象限．综上所述，符合条件的图象是C选项．故选：C．9．如图，在△ABC中，∠CAB=65°，将△ABC在平面内绕点A旋转到△AB′C′的位置，使CC′∥AB，则旋转角的度数为（）A．35°B．40°C．50°D．65°【考点】旋转的性质．【分析】根据两直线平行，内错角相等可得∠ACC′=∠CAB，根据旋转的性质可得AC=AC′，然后利用等腰三角形两底角相等求∠CAC′，再根据∠CAC′、∠BAB′都是旋转角解答．【解答】解：∵CC′∥AB，∴∠ACC′=∠CAB=65°，∵△ABC绕点A旋转得到△AB′C′，∴AC=AC′，∴∠CAC′=180°﹣2∠ACC′=180°﹣2×65°=50°，∴∠CAC′=∠BAB′=50°．故选C．10．若α、β是方程x2+2x﹣2007=0的两个实数根，则α2+3α+β的值（）A．2007 B．2005 C．﹣2007 D．4010【考点】根与系数的关系．【分析】根据方程的解的概念及根与系数的关系得α+β=﹣2、α2+2α=2007，整体代入到α2+3α+β=α2+2α+α+β可得．【解答】解：∵α、β是方程x2+2x﹣2007=0的两个实数根，∴α+β=﹣2，α2+2α﹣2007=0，即α2+2α=2007，则α2+3α+β=α2+2α+α+β=2007﹣2=2005，故选：B．二、填空题(每小题3分，共18分)11．代数式有意义时，x应满足的条件是x＞1．【考点】二次根式有意义的条件．【分析】直接利用二次根式的定义求出x的取值范围．【解答】解：代数式有意义时，x﹣1＞0，解得：x＞1．故答案为：x＞1．12．分解因式：x3﹣xy2=x（x+y）（x﹣y）．【考点】提公因式法与公式法的综合运用．【分析】首先提取公因式x，进而利用平方差公式分解因式得出答案．【解答】解：x3﹣xy2=x（x2﹣y2）=x（x+y）（x﹣y）．故答案为：x（x+y）（x﹣y）．13．一个不透明的口袋里有4张形状完全相同的卡片，分别写有数字1、2、3、4，口袋外有两张卡片，分别写有数字2、3，现随机从口袋里取出一张卡片，则这张卡片与口袋外的卡片上的数字能构成三角形的概率是．【考点】概率公式；三角形三边关系．【分析】由一个不透明的口袋里有4张形状完全相同的卡片，分别写有数字1，2，3，4，可得共有4种等可能的结果，又由这张卡片与口袋外的两张卡片上的数作为三角形三边的长，能构成三角形的有：2，2，3；3，2，3；4，2，3；共3种情况，然后利用概率公式求解即可求得答案．【解答】解：∵一个不透明的口袋里有4张形状完全相同的卡片，分别写有数字1，2，3，4，∴共有4种等可能的结果，∵这张卡片与口袋外的两张卡片上的数作为三角形三边的长，能构成三角形的有：2，2，3；3，2，3；4，2，3；共3种情况，∴能构成三角形的概率是：．故答案为：．14．如图，在平面直角坐标系中，点O为坐标原点，点P在第一象限，⊙P与x轴交于O，A两点，点A的坐标为（6，0），⊙P的半径为，则点P的坐标为（3，2）．【考点】垂径定理；坐标与图形性质；勾股定理．【分析】过点P作PD⊥x轴于点D，连接OP，先由垂径定理求出OD的长，再根据勾股定理求出PD的长，故可得出答案．【解答】解：过点P作PD⊥x轴于点D，连接OP，∵A（6，0），PD⊥OA，∴OD=OA=3，在Rt△OPD中，∵OP=，OD=3，∴PD===2，∴P（3，2）．故答案为：（3，2）．15．如图，量角器的直径与直角三角板ABC的斜边AB重合，其中量角器0刻度线的端点N与点A重合，射线CP从CA处出发沿顺时针方向以每秒3度的速度旋转，CP与量角器的半圆弧交于点E，第24秒，点E在量角器上对应的读数是144度．【考点】圆周角定理．【分析】首先连接OE，由∠ACB=90°，易得点E，A，B，C共圆，然后由圆周角定理，求得点E在量角器上对应的读数．【解答】解：连接OE，∵∠ACB=90°，∴A，B，C在以点O为圆心，AB为直径的圆上，∴点E，A，B，C共圆，∵∠ACE=3×24=72°，∴∠AOE=2∠ACE=144°．∴点E在量角器上对应的读数是：144°．故答案为：144．16．在Rt△ABC中，∠A=90°，有一个锐角为60°，BC=6．若点P在直线AC上（不与点A，C重合），且∠ABP=30°，则CP的长为6或2或4．【考点】解直角三角形．【分析】根据题意画出图形，分4种情况进行讨论，利用直角三角形的性质解答．【解答】解：如图1：当∠C=60°时，∠ABC=30°，与∠ABP=30°矛盾；如图2：当∠C=60°时，∠ABC=30°，∵∠ABP=30°，∴∠CBP=60°，∴△PBC是等边三角形，∴CP=BC=6；如图3：当∠ABC=60°时，∠C=30°，∵∠ABP=30°，∴∠PBC=60°﹣30°=30°，∴PC=PB，∵BC=6，∴AB=3，∴PC=PB===2；如图4：当∠ABC=60°时，∠C=30°，∵∠ABP=30°，∴∠PBC=60°+30°=90°，∴PC=BC÷cos30°=4．故答案为：6或2或4．三、解答题17．解方程：x2﹣10x+9=0．【考点】解一元二次方程-因式分解法．【分析】先分解因式，即可得出两个一元一次方程，求出方程的解即可．【解答】解：x2﹣10x+9=0，（x﹣1）（x﹣9）=0，x﹣1=0，x﹣9=0，x1=1，x2=9．18．如图，在△ABC中，AD是BC边上的中线，分别过点C、B作射线AD的垂线段，垂足分别为E、F．求证：BF=CE．【考点】全等三角形的判定与性质．【分析】求出∠DEC=∠DFB=90°，DB=DC，根据AAS证△BFD≌△CED，根据全等三角形的性质推出即可．【解答】证明：∵CE⊥AF，FB⊥AF，∴∠DEC=∠DFB=90°，又∵AD为BC边上的中线，∴BD=CD，在△BFD和△CED中∴△BFD≌△CED（AAS），∴BF=CE．19．先化简，再求值：÷（﹣），其中a=，b=2．【考点】实数的运算．【分析】先算括号里面的，再算除法，最后把a、b的值代入进行计算即可．【解答】解：原式=÷=•=，当a=，b=2时，原式==．20．为实施“农村留守儿童关爱计划”，某校结全校各班留守儿童的人数情况进行了统计，发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况，并制成如下两幅不完整的统计图：（1）求该校平均每班有多少名留守儿童？并将该条形统计图补充完整；（2）某爱心人士决定从只有2名留守儿童的这些班级中，任选两名进行生活资助，请用列表法或画树状图的方法，求出所选两名留守儿童来自同一个班级的概率．【考点】条形统计图；扇形统计图；列表法与树状图法．【分析】（1）根据留守儿童有6名的班级有4个，占20%，可求得有留守儿童的班级总数，再求得留守儿童是2名的班数；（2）由（1）得只有2名留守儿童的班级有2个，共4名学生．设A1，A2来自一个班，B1，B2来自一个班，列出树状图可得出来自一个班的共有4种情况，则所选两名留守儿童来自同一个班级的概率．【解答】解：（1）该校班级个数为4÷20%=20（个），只有2名留守儿童的班级个数为：20﹣（2+3+4+5+4）=2（个），该校平均每班留守儿童的人数为：=4（名），补图如下：；（2）由（1）得只有2名留守儿童的班级有2个，共4名学生．设A1，A2来自一个班，B1，B2来自一个班，由树状图可知，共有12种可能的情况，并且每种结果出现的可能性相等，其中来自一个班的共有4种情况，则所选两名留守儿童来自同一个班级的概率为：=．21．两个城镇A、B与两条公路ME，MF位置如图所示，其中ME是东西方向的公路．现电信部门需在C处修建一座信号发射塔，要求发射塔到两个城镇A、B的距离必须相等，到两条公路ME，MF的距离也必须相等，且在∠FME的内部．（1）点C应选在何处？请在图中，用尺规作图找出符合条件的点C．（不写已知、求作、作法，只保留作图痕迹）（2）点C到公路ME的距离为2km，设AB的垂直平分线交ME于点N，点M处测得点C 位于点M的北偏东60°方向，在N处没得点C位于点N的北偏西45°方向，求MN的长（结果保留根号）【考点】解直角三角形的应用-方向角问题；线段垂直平分线的性质．【分析】（1）到城镇A、B距离相等的点在线段AB的垂直平分线上，到两条公路距离相等的点在两条公路所夹角的角平分线上，分别作出垂直平分线与角平分线，它们的交点即为所求作的点C；（2）作CD⊥MN于点D．由三角函数得出MD=CD，DN=CD，于是得到结论．【解答】解：（1）如图所示，点C即为所求；（2）作CD⊥MN于点D，由题意得：∠CMN=30°，∠CND=45°，∵在Rt△CMD中，=tan∠CMN，∴MD==2；∵在Rt△CND中，=tan∠CNM，∴ND=CD=2，∵MN=DM+DN=2+2km，22．某药品研究所开发一种抗菌新药，经多年动物实验，首次用于临床人体试验，测得成人服药后血液中药物浓度y（微克/毫升）与服药时间x小时之间函数关系如图所示（当4≤x ≤10时，y与x成反比例）．（1）根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式．（2）问血液中药物浓度不低于4微克/毫升的持续时间多少小时？【考点】反比例函数的应用；一次函数的应用．【分析】（1）分别利用正比例函数以及反比例函数解析式求法得出即可；（2）利用y=4分别得出x的值，进而得出答案．【解答】解：（1）当0≤x≤4时，设直线解析式为：y=kx，将（4，8）代入得：8=4k，解得：k=2，故直线解析式为：y=2x，当4≤x≤10时，设直反比例函数解析式为：y=，将（4，8）代入得：8=，解得：a=32，故反比例函数解析式为：y=；因此血液中药物浓度上升阶段的函数关系式为y=2x（0≤x≤4），下降阶段的函数关系式为y=（4≤x≤10）．（2）当y=4，则4=2x，解得：x=2，当y=4，则4=，解得：x=8，∵8﹣2=6（小时），∴血液中药物浓度不低于4微克/毫升的持续时间6小时．23．如图，AB是⊙O的弦，D为半径OA的中点，过D作CD⊥OA交弦AB于点E，交⊙O于点F，且CE=CB．（1）求证：BC是⊙O的切线；（2）连接AF、BF，求∠ABF的度数；（3）如果CD=15，BE=10，sinA=，求⊙O的半径．【考点】切线的判定；相似三角形的判定与性质．【分析】（1）连接OB，由圆的半径相等和已知条件证明∠OBC=90°，即可证明BC是⊙O 的切线；（2）连接OF，AF，BF，首先证明△OAF是等边三角形，再利用圆周角定理：同弧所对的圆周角是所对圆心角的一半即可求出∠ABF的度数；（3）过点C作CG⊥BE于G，根据等腰三角形的性质得到EG=BE=5，由两角相等的三角形相似，△ADE∽△CGE，利用相似三角形对应角相等得到sin∠ECG=sinA=，在Rt△ECG中，利用勾股定理求出CG的长，根据三角形相似得到比例式，代入数据即可得到结果．【解答】（1）证明：连接OB，∵OB=OA，CE=CB，∴∠A=∠OBA，∠CEB=∠ABC，又∵CD⊥OA，∴∠A+∠AED=∠A+∠CEB=90°，∴∠OBA+∠ABC=90°，∴OB⊥BC，∴BC是⊙O的切线；（2）解：如图1，连接OF，AF，BF，∵DA=DO，CD⊥OA，∴AF=OF，∵OA=OF，∴△OAF是等边三角形，∴∠AOF=60°，∴∠ABF=∠AOF=30°；（3）解：如图2，过点C作CG⊥BE于G，∵CE=CB，∴EG=BE=5，∵∠ADE=∠CGE=90°，∠AED=∠GEC，∴∠GCE=∠A，∴△ADE∽△CGE，∴sin∠ECG=sinA==，即CE=13，在Rt△ECG中，∵CG==12，∵CD=15，CE=13，∴DE=2，∵△ADE∽△CGE，∴=，∴AD=，CG=，∴⊙O的半径OA=2AD=．24．类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”．（1）概念理解：如图1，在四边形ABCD中，添加一个条件使得四边形ABCD是“等邻边四边形”．请写出你添加的一个条件．（2）问题探究：①小红猜想：对角线互相平分的“等邻边四边形”是菱形，她的猜想正确吗？请说明理由．②如图2，小红画了一个Rt△ABC，其中∠ABC=90°，AB=2，BC=1，并将Rt△ABC沿∠ABC的平分线BB′方向平移得到△A′B′C′，连结AA′，BC′，小红要使平移后的四边形ABC′A′是“等邻边四边形”，应平移多少距离（即线段BB′的长）？（3）拓展应用：如图3，“等邻边四边形”ABCD中，AB=AD，∠BAD+∠BCD=90°，AC，BD为对角线，AC= AB，试探究BC，CD，BD的数量关系．【考点】四边形综合题．【分析】（1）由“等邻边四边形”的定义易得出结论；（2）①先利用平行四边形的判定定理得平行四边形，再利用“等邻边四边形”定义得邻边相等，得出结论；②由平移的性质易得BB′=AA′，A′B′∥AB，A′B′=AB=2，B′C′=BC=1，A′C′=AC=，再利用“等邻边四边形”定义分类讨论，由勾股定理得出结论；（3）由旋转的性质可得△ABF≌△ADC，由全等性质得∠ABF=∠ADC，∠BAF=∠DAC，AF=AC，FB=CD，利用相似三角形判定得△ACF∽△ABD，由相似的性质和四边形内角和得∠CBF=90°，利用勾股定理，等量代换得出结论．【解答】解：（1）AB=BC或BC=CD或CD=AD或AD=AB（任写一个即可）；（2）①正确，理由为：∵四边形的对角线互相平分，∴这个四边形是平行四边形，∵四边形是“等邻边四边形”，∴这个四边形有一组邻边相等，∴这个“等邻边四边形”是菱形；②∵∠ABC=90°，AB=2，BC=1，∴AC=，∵将Rt△ABC平移得到△A′B′C′，∴BB′=AA′，A′B′∥AB，A′B′=AB=2，B′C′=BC=1，A′C′=AC=，（I）如图1，当AA′=AB时，BB′=AA′=AB=2；（II）如图2，当AA′=A′C′时，BB′=AA′=A′C′=；（III）当A′C′=BC′=时，如图3，延长C′B′交AB于点D，则C′B′⊥AB，∵BB′平分∠ABC，∴∠ABB′=∠ABC=45°，∴∠BB′D=′∠ABB′=45°∴B′D=B，设B′D=BD=x，则C′D=x+1，BB′=x，∵在Rt△BC′D中，BD2+（C′D）2=（BC′）2∴x2+（x+1）2=（）2，解得：x1=1，x2=﹣2（不合题意，舍去），∴BB′=x=（Ⅳ）当BC′=AB=2时，如图4，与（Ⅲ）方法一同理可得：BD2+（C′D）2=（BC′）2，设B′D=BD=x，则x2+（x+1）2=22，解得：x1=，x2=（不合题意，舍去），∴BB′=x=；（3）BC，CD，BD的数量关系为：BC2+CD2=2BD2，如图5，∵AB=AD，∴将△ADC绕点A旋转到△ABF，连接CF，∴△ABF≌△ADC，∴∠ABF=∠ADC，∠BAF=∠DAC，AF=AC，FB=CD，∴∠BAD=∠CAF，==1，∴△ACF∽△ABD，∴==，∴BD，∵∠BAD+∠ADC+∠BCD+∠ABC=360°，∴∠ABC+∠ADC﹣360°﹣（∠BAD+∠BCD）=360°﹣90°=270°，∴∠ABC+∠ABF=270°，∴∠CBF=90°，∴BC2+FB2=CF2=（BD）2=2BD2，∴BC2+CD2=2BD2．25．在平面直角坐标系中，已知抛物线y=x2+bx+c（b，c为常数）的顶点为P，等腰直角三角形ABC的顶点A的坐标为（0，﹣1），C的坐标为（4，3），直角顶点B在第四象限．（1）如图，若该抛物线过A，B两点，求该抛物线的函数表达式；（2）平移（1）中的抛物线，使顶点P在直线AC上滑动，且与AC交于另一点Q．（i）若点M在直线AC下方，且为平移前（1）中的抛物线上的点，当以M、P、Q三点为顶点的三角形是等腰直角三角形时，求出所有符合条件的点M的坐标；（ii）取BC的中点N，连接NP，BQ．试探究是否存在最大值？若存在，求出该最大值；若不存在，请说明理由．【考点】二次函数综合题．【分析】（1）先求出点B的坐标，然后利用待定系数法求出抛物线的函数表达式；（2）i）首先求出直线AC的解析式和线段PQ的长度，作为后续计算的基础．若△MPQ为等腰直角三角形，则可分为以下两种情况：①当PQ为直角边时：点M到PQ的距离为．此时，将直线AC向右平移4个单位后所得直线（y=x﹣5）与抛物线的交点，即为所求之M点；②当PQ为斜边时：点M到PQ的距离为．此时，将直线AC向右平移2个单位后所得直线（y=x﹣3）与抛物线的交点，即为所求之M点．ii）由（i）可知，PQ=为定值，因此当NP+BQ取最小值时，有最大值．如答图2所示，作点B关于直线AC的对称点B′，由分析可知，当B′、Q、F（AB中点）三点共线时，NP+BQ最小，最小值为线段B′F的长度．【解答】解：（1）∵等腰直角三角形ABC的顶点A的坐标为（0，﹣1），C的坐标为（4，3）∴点B的坐标为（4，﹣1）．∵抛物线过A（0，﹣1），B（4，﹣1）两点，∴，解得：b=2，c=﹣1，∴抛物线的函数表达式为：y=x2+2x﹣1．（2）方法一：i）∵A（0，﹣1），C（4，3），∴直线AC的解析式为：y=x﹣1．设平移前抛物线的顶点为P0，则由（1）可得P0的坐标为（2，1），且P0在直线AC上．∵点P在直线AC上滑动，∴可设P的坐标为（m，m﹣1），则平移后抛物线的函数表达式为：y=（x﹣m）2+m﹣1．解方程组：，解得，∴P（m，m﹣1），Q（m﹣2，m﹣3）．过点P作PE∥x轴，过点Q作QF∥y轴，则PE=m﹣（m﹣2）=2，QF=（m﹣1）﹣（m﹣3）=2．∴PQ==AP0．若以M、P、Q三点为顶点的等腰直角三角形，则可分为以下两种情况：①当PQ为直角边时：点M到PQ的距离为（即为PQ的长）．由A（0，﹣1），B（4，﹣1），P0（2，1）可知，△ABP0为等腰直角三角形，且BP0⊥AC，BP0=．如答图1，过点B作直线l1∥AC，交抛物线y=x2+2x﹣1于点M，则M为符合条件的点．∴可设直线l1的解析式为：y=x+b1，∵B（4，﹣1），∴﹣1=4+b1，解得b1=﹣5，∴直线l1的解析式为：y=x﹣5．解方程组，得：，∴M1（4，﹣1），M2（﹣2，﹣7）．②当PQ为斜边时：MP=MQ=2，可求得点M到PQ的距离为．如答图2，取AB的中点F，则点F的坐标为（2，﹣1）．由A（0，﹣1），F（2，﹣1），P0（2，1）可知：△AFP0为等腰直角三角形，且点F到直线AC的距离为．过点F作直线l2∥AC，交抛物线y=x2+2x﹣1于点M，则M为符合条件的点．∴可设直线l2的解析式为：y=x+b2，∵F（2，﹣1），∴﹣1=2+b2，解得b2=﹣3，∴直线l2的解析式为：y=x﹣3．解方程组，得：，∴M3（1+，﹣2+），M4（1﹣，﹣2﹣）．综上所述，所有符合条件的点M的坐标为：M1（4，﹣1），M2（﹣2，﹣7），M3（1+，﹣2+），M4（1﹣，﹣2﹣）．方法二：∵A（0，1），C（4，3），∴l AC：y=x﹣1，∵抛物线顶点P在直线AC上，设P（t，t﹣1），∴抛物线表达式：，∴l AC与抛物线的交点Q（t﹣2，t﹣3），∵一M、P、Q三点为顶点的三角形是等腰直角三角形，P（t，t﹣1），①当M为直角顶点时，M（t，t﹣3），，∴t=1±，∴M1（1+，﹣2），M2（1﹣，﹣2﹣），②当Q为直角顶点时，点M可视为点P绕点Q顺时针旋转90°而成，将点Q（t﹣2，t﹣3）平移至原点Q′（0，0），则点P平移后P′（2，2），将点P′绕原点顺时针旋转90°，则点M′（2，﹣2），将Q′（0，0）平移至点Q（t﹣2，t﹣3），则点M′平移后即为点M（t，t﹣5），∴，∴t1=4，t2=﹣2，∴M1（4，﹣1），M2（﹣2，﹣7），③当P为直角顶点时，同理可得M1（4，﹣1），M2（﹣2，﹣7），综上所述，所有符合条件的点M的坐标为：M1（4，﹣1），M2（﹣2，﹣7），M3（1+，﹣2+），M4（1﹣，﹣2﹣）．ii）存在最大值．理由如下：由i）知PQ=为定值，则当NP+BQ取最小值时，有最大值．如答图2，取点B关于AC的对称点B′，易得点B′的坐标为（0，3），BQ=B′Q．连接QF，FN，QB′，易得FN∥PQ，且FN=PQ，∴四边形PQFN为平行四边形．∴NP=FQ．∴NP+BQ=FQ+B′Q≥FB′==．∴当B′、Q、F三点共线时，NP+BQ最小，最小值为．∴的最大值为=．2016年8月1日。

华中师大一附中2015—2016学年度上学期高三期中检测数学试题（文科）考试时限：120分钟 卷面满分：150分 命题人：方 钢党宇飞 审题人：帅建成第I 卷（选择题共60分）注意事项：务必将每小题的答案填在答题卡的相应位置.答在试卷上无效.一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的，请将你认为正确的选项代号涂填在选择题的答题卡内. 1、设全集U R =，集合{}2log 2x x A =≤，()(){}310x x x B =-+≥，则()UB A =ð（ ）A ．(],1-∞-B ．(](),10,3-∞-C ．()0,3D ．[)0,32、已知复数12()z ai a R =+∈，i z 212-=，若21z z 为纯虚数，则=||1z( ) A ．2B ．3C ．2D ．53、已知命题:,1lg 2p x R x x ∃∈-<，命题2:,0q x R x ∀∈>，则 ( )A ．命题p q ∨是假命题B ．命题p q ∧是真命题C ．命题()p q ∧⌝是真命题D ．命题()p q ∧⌝是假命题4、已知向量(1,2),(2,1)a x b =-=错误！未找到引用源。

，则“0x >”是“a 与b 错误！未找到引用源。

夹角为锐角”的 ( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件5、在ABC中，已知030,8,A a b ===，则三角形的面积为（ ） A． B ．16 C．或16D．或6、已知2211(2),()()22x p a a q x R a -=+>=∈-，则,p q的大小关系为（ ）A ．p q ≥B ．p q >C ．p q <D ．p q ≤ 7、函数()sin()(0,0,0)f x A x A ωϕωϕπ=+>><<的图象如图所示，为了得到()sin g x A x ω=的图象，可以将()f x 的图象 ( )A ．向右平移12π个单位长度 B ．向右平移6π个单位长度C ．向左平移12π个单位长度 D ．向左平移6π个单位长度8、已知函数223log (2),2(),,2x x f x xx -<⎧⎪=⎨⎪≥⎩则不等式(31)4f x +<的解集为（ ）A ．1{5}3x x -<< B ．5{3}3x x -<< C ．7{5}3x x -<<D ．1{2}3x x <<9、M 是ABC ∆所在平面内一点，33022MB MA MC ++=，D 为AC 中点，则MD BM的值为（ ）A ．13B ．12C ．1D ．210、数列{n a ｝的通项公式为12n n a -=，则使不等式22211252n n a a a ++++<⨯成立的n 的最大值为（ ）A ．2B ．3C ．4D ．511、已知()f x =33x x m -+，在区间[]0,2上任取三个数,,a b c ,均存在以(),(),()f a f b f c 为边长的三 角形，则m 的取值范围是 （ ）A ．8m >B ．6m >C ．4m >D ．2m >12、定义在),1(+∞上的函数)(x f 满足下列两个条件：（1）对任意的),1(+∞∈x 恒有)(2)2(x f x f =成立；（2）当(]2,1∈x 时，x x f -=2)(．记函数=)(x g )1()(--x k x f ，若函数)(x g 恰有两个零点，则实数k 的取值范围是 （ ）A ． ⎪⎭⎫⎢⎣⎡2,34 B ．⎪⎭⎫ ⎝⎛2,34 C ．⎥⎦⎤⎢⎣⎡2,34D ． [)2,1第II 卷(非选择题共90分)二、填空题：本大题共4小题，每小题5分，共20分.把答案填在答题卡内相应题号对应的横线上. 13、已知tan 2α=-，则()2sin cos αα-= ．14、()f x '为定义在R 上的函数()f x而()3f x y '=的图象如图所示， 则()y f x =的单调递增区间是______ ．15、若数列{}n a 满足212332n a a a a n n =++⋅⋅⋅⋅⋅⋅⋅，则数列{}n a 的通项公式为___________. 16、设函数21()ln(1||)1f x x x =+-+，则使得()(21)f x f x >-成立的x 的取值范围为_______.三、解答题：本大题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤.17、(本小题满分10分)已知函数22()sin )2sin cos f x x x x x =-+．（Ⅰ）求()f x 的最小正周期；（Ⅱ）设[,]33x ππ∈-，求()f x 的值域和单调递减区间．18、(本小题满分12分)已知等差数列{a n }的前n 项和为,(1)()n n S S kn n n k R =+-∈，公差d 为2.（Ⅰ）求k 与n a ；（Ⅱ）若数列{}n b 满足112,2(2)na n nb b b n n -=-=⋅≥，求n b .19、(本小题满分12分)在ABC ∆中，角,,A B C 的对边分别为,,a b c ，已知2c =，向量(,3),m c =(cos ,sin )n C B =，且m ∥n ．（Ⅰ）求角C 的大小；（Ⅱ）若sin(),sin 2,sin()A B A B A +-成等差数列，求边a 的大小．20、(本小题满分12分)已知函数x bx ax x f ln )(2-+=，R b a ∈,．（Ⅰ）若0<a 且2=-b a ，试讨论()f x 的单调性；（Ⅱ）若8b =-，总存在10,x e ⎛⎤∈ ⎥⎝⎦使得()0<f x 成立，求实数a 的取值范围．21、(本小题满分12分)已知数列{a }n 的前n 项和为n S ，211,(1),1,2,2n n a S n a n n n ==--=L（Ⅰ）证明：数列1n n S n+⎧⎫⎨⎬⎩⎭是等差数列，并求n S ； （Ⅱ）设323nn S b n n =+，求证：12512n b b b +++<L．22、(本小题满分12分)已知函数()ln f x x a x =+，在1x =处的切线与直线20x y +=垂直，函数()()212g x f x x bx =+-．（Ⅰ）求实数a 的值；（Ⅱ）设1212,()x x x x <是函数()g x 的两个极值点，记12x t x =，若133b ≥， ①求t 的取值范围；②求()()12g x g x -的最小值．华中师大一附中2015—2016学年度上学期高三期中检测数学试题（文科）答案一、选择题 题号 1 2 3 4 5 6 7 8 9 10 11 12答案 C D C B D A B C A C B A二、填空13、95 14、(),3-∞ 15、6,12,2,n n a n n n N n *=⎧⎪=+⎨≥∈⎪⎩ 16、1,13⎛⎫⎪⎝⎭三、解答题 17、（1）()2sin 22sin(2)3f x x x x T ππ=+=+= (5)分（2）∵[,]33x ππ∈-， 233x πππ∴-≤+≤，1)32sin(23≤+≤-∴πx ． )(x f ∴的值域为[2]． (7)分()f x 的递减区间为⎥⎦⎤⎢⎣⎡3,12ππ． …………………………10分18、（1）由题意可得1121a S k ==- ，22141a S S k =-=- (2)分所以 2122a a k -==，即 1k = 故数列{}n a 是首项为1，公差为2的等差数列，即21n a n =- (4)分（2）由题意112,2(2)n a n n b b b n n -=-=⋅≥ 即21112,2(2)n n n b b b n n --=-=⋅≥由累加法可得1122112()()()n n n n n n b b b b b b b b ---≥=-+-+⋅⋅⋅+-+时，1323211222(1)22n n n n --=⨯+⨯+⋅⋅⋅+-⨯+⨯ (6)分 错位相减法2[(31)41]9n n n b -+=…………………………10分 显然1n =，也成立， 故2[(31)41],9n n n b n N *-+=∈ (12)分19、（1）m ∥n ，得sin cos 0c B C -=，由正弦定理可得sin sin cos 0C B B C = (2)分tan C =()0,C π∈3C π=…………………………4分（2）sin(),sin 2,sin()A B A B A +-成等差，所以sin()sin()2sin 2A B B A A ++-= 化简整理得：cos (sin 2sin )0A B A -= (6)分即cos 0A =或sin 2sin B A =得22A b a π==或 (8)分若=22sin c A C a C ππ===，由，则 …………………………10分若222,4b a a b ab a =+-==由得 …………………………12分20、（1）由2b a =-11(1)(21)()222(0)ax x f x ax b ax a x x x x+-'=+-=+--=>………………2分 当112a -<，即2a <-时，()f x 的单调递增区间为11(,)2a -，单调递减区间为11(0,),,2a ⎛⎫-+∞ ⎪⎝⎭………………4分 当112a -=，即2a =-时，()f x 的单调递增区间为(0,)+∞ (5)分当112a->，即20a -<<时，()f x 的单调递增区间为11(,)2a-，单调递减区间为11(0,),,2a ⎛⎫-+∞ ⎪⎝⎭………………6分（2）2()8ln f x ax x x =--由题意总存在10,x e ⎛⎤∈ ⎥⎝⎦，使得()0<f x 成立即存在10,x e ⎛⎤∈ ⎥⎝⎦，使28ln x x a x+< 记28ln ()x xg x x +=，10,x e ⎛⎤∈ ⎥⎝⎦，问题等价于()a g x 小于的最大值。

湖北省华中师范大学第一附属中学中考提前招生提前招生数学模拟试卷一、选择题1．如图所示物态变化过程中，放出热量的是（）A．樟脑丸逐渐变小B．露珠的形成C．正在消融的冰凌D．夏天湿衣服晒干2．如图是一种手摇式手机充电器，只要摇转手柄，就可以给手机充电。

以下四幅图中能反映手摇充电器原理的是（）A．B．C．D．3．小明把上钩后的鱼匀速拉出水面过程中，会感觉鱼逐渐“变重”，关于小明用该鱼竿钓鱼的过程，下列说法正确的是（）A．鱼竿是省力杠杆，鱼受到的浮力逐渐增大B．鱼竿是省力杠杆，细绳上的拉力逐渐减小C．鱼竿是费力杠杆，鱼受到的重力逐渐增大D．鱼竿是费力杠杆，细绳上的拉力逐渐增大4．关于声现象，下列说法中正确的是（）A．“闻其声而知其人”主要是根据声音的响度来判断的B．“上课回答问题要大声”是要求学生回答问题的声音音调要高一些C．用超声波能粉碎人体内的“小石头”，说明超声波能够传递信息D．临街房子的窗户装上双层玻璃，可以在传播过程中减弱噪声5．夏天，从冰箱里取出一瓶矿泉水，一会儿瓶的外壁上出现了许多“小水珠”，下列现象中的物态变化方式与“小水珠”形成原因相同的是（）A．饮料中的冰块变小B．水烧开时，壶嘴出现了“白气”C．晒在太阳下的湿衣服变干D．冬天，树枝上出现了“雾凇”6．如图所示，对下列电磁现象相应的说明正确的是（）A．如图表明通电导线周围有磁场，这个现象是法拉第首先发现的B．如图可以判断电磁铁的左端为N极C．如图是研究电磁感应现象的实验装置，只要导体棒AB运动就一定能产生感应电流D．按如图中的方法把线圈两端导线上的漆刮去，通电后线圈可以持续转动7．如图,手机扫描二维码,相当于绘二码拍了一张照片,手机摄像头相当于凸透镜,影像传感器相当于光屏,下列说法正确的是A．物体上的二维码是光源B．扫码时二维码要位于摄像头二倍焦距以外C．要使屏幕上二维码的像变小,只需将二维码靠近凸透镜D．影像传感器上成的是正立的实像8．如图所示，一个不能打开的盒子外面露出一段细长的导线，在不损坏导线的情况下，用如下一些器材来判断导线中是否有电流，可行的是（）①小磁针②U形磁铁③铁棒、大头针④铁棒、铁块、弹簧测力计A．①②③④B．①②③C．①③④D．①②9．如图甲所示的电路中，电源电压恒定，灯泡L标有“6V 6W”，R0为定值电阻。

2016届湖北武汉华中师大一附等高三上学期第一次联考数学（理）试题及解析一、选择题1．已知集合2{|230}A x x x =--≥，2{|log (1)2}B x x =-<，则()R C A B =（ ）A ．(1,3)B ．(1,3)-C ．(3,5)D ．(1,5)- 【答案】A【解析】试题分析：由已知{|13}A x x x =≤-≥或，{|13}R C A x x =-<<，{|014}{|15}B x x x x =<-<=<<，所以()(|13}R C A B x x =<<，故选A ．【考点】集合的运算．2．命题“若220x y +=，则0x y ==”的否命题为（ ）A ．若220x y +=，则0x ≠且0y ≠ B ．若220x y +=，则0x ≠或0y ≠ C ．若220x y +≠，则0x ≠且0y ≠ D ．若220x y +≠，则0x ≠或0y ≠ 【答案】D【解析】试题分析：命题“若220x y +=，则0x y ==”的否命题是“若220x y +≠，则0x ≠或0y ≠”．故选D ． 【考点】四种命题．3．欧拉公式cos sin ix e x i x =+（i 为虚数单位）是由瑞士著名数学家欧拉发明的，它将指数函数的定义域扩大到复数，建立了三角函数和指数函数的关系，它在复变函数论里占有非常重要的地位，被誉为“数学中的天桥”，根据欧拉公式可知，2i e 表示的复数在复平面中位于（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 【答案】B【解析】试题分析：2cos 2sin 2i e i =+，对应点为(cos 2,sin 2)，由于22ππ<<，因此cos 20,sin 20<>，点(cos 2,sin 2)在第二象限，故选B ． 【考点】复数的几何意义．4．函数222,1,()log (1),1,x x f x x x ⎧-≤=⎨-⎩>则52f f ⎡⎤⎛⎫= ⎪⎢⎥⎝⎭⎣⎦（ ） A ．12-B ．1-C ．5-D ．12【答案】A【解析】试题分析：22553()log (1)log 1222f =-=<，所以23log 225331(())(log )2222222f f f ==-=-=-．故选A ．【考点】分段函数．5．等差数列{}n a 前n 项和为n S ，且20162015120162015S S =+，则数列{}n a 的公差为（ ）A ．1B ．2C ．2015D ．2016 【答案】B 【解析】试题分析：由1(1)2n n n S na d -=+得201620151120152014()()12016201522S S a d a d -=+-+=，所以2d =，故选B ． 【考点】等差数列的前n 项和公式．6．若ln 2a =，125b -=，01sin 4c xdx π=⎰，则,,a b c 的大小关系（ ） A ．a b c << B ．b a c << C ．c b a << D ．b c a << 【答案】D【解析】试题分析：111(cos )(cos cos0)0442c x ππ=-=--=，121552b -==<，121ln 2ln 2a e =>=，所以a c b >>，故选D ． 【考点】比较大小，定积分． 7．已知1sin cos 63παα⎛⎫--= ⎪⎝⎭，则cos 23πα⎛⎫+= ⎪⎝⎭（ ）A ．518 B ．518- C ．79 D ．79- 【答案】C 【解析】试题分析：sin()cos sin cos cos sin cos 666πππααααα--=--1cos sin 22αα=--= 1sin()63πα-+=，1sin()63πα+=-，所以2219cos(2)12sin ()12()3637ππαα+=-+=-⨯-=．故选C ．【考点】两角和与差的正弦（余弦）公式，二倍角公式．【名师点睛】1．当“已知角”有两个时，“所求角”一般表示为两个“已知角”的和或差的形式； 2．当“已知角”有一个时，此时应着眼于“所求角”与“已知角”的和或差的关系，然后应用诱导公式把“所求角”变成“已知角”． 3．常见的配角技巧：22αα=⋅；()()ααββββα=+-=--；1[()()]2ααβαβ=++-，1[()()]2βαβαβ=+--，()424πππαα+=--等等．8．已知某几何体的三视图的侧视图是一个正三角形，如图所示，则该几何体的体积等于（ ）A．．．．【答案】C【解析】试题分析：题设三视图是下图中几何体ABCDEF 的三视图，由三视图中的尺寸，知其体积为11146(43)232V =⨯⨯-⨯⨯⨯⨯=，故选C ． FEDCBA【考点】三视图与几何体的体积． 9．已知函数21()sin ()2f x x ω=-，(0)ω>的周期为π，若将其图象沿x 轴向右平移a 个单位(0)a >，所得图象关于原点对称，则实数a 的最小值为（ ） A ．π B ．34π C ．2π D ．4π 【答案】D【解析】试题分析：22111()sin ()(12sin ())cos 2222f x x x x ωωω=-=--=-，由22T ππω==得1ω=，即()cos 2f x x =-，向右平移a 个单位后得()cos 2()cos(22)g x x a x a =--=--，其图象关于原点对称，即为奇函数，(0)cos(2)cos 20g a a =--=-=，2,2a k k Z ππ=+∈，,24k a k Z ππ=+∈，最小的正数4a π=，故选D ．【考点】函数图象的平移，函数的奇偶性．410．如图所示，在正六边形ABCDEF 中，点P 是CDE ∆内（包括边界）的一个动点，设(,)AP AF AB R λμλμ=+∈，则λμ+的取值范围是（ ）A ．3,42⎡⎤⎢⎥⎣⎦ B ．[]3,4 C ．35,22⎡⎤⎢⎥⎣⎦ D ．3,24⎡⎤⎢⎥⎣⎦【答案】B【解析】试题分析：建立如图所求的直角坐标系，设2AB =，则(0,0)A ，(2,0)B，C，(2,D，(0,E，(F -， 设(,)P x y ，即(,)AP x y =，Ey BA x所以EC的方程为60x +-=，CD的方程为0y +-=，因为P 是CDE ∆内（含边界）的动点，则可行域为600x y y ⎧+-≥≤+-≤，由AP AB AF λμ=+及(2,0)AB =，(AF =-得(,)(2,0)(x y λμ=+-，所以2x y λμ=-⎧⎪⎨=⎪⎩，代入可行域得3122λμμλ+≥⎧⎪≤≤⎨⎪≤⎩，34λμ⇒≤+≤．故选B ．【考点】向量在几何中的应用；平面向量的基本定理及其意义．CF11．若一个四棱锥底面为正方形，顶点在底面的射影为正方形的中心，且该四棱锥的体积为9，当其外接球表面积最小时，它的高为（ ） A ．3 B．．．【答案】A【解析】试题分析：此四棱锥为正四棱锥，设此正四棱锥的底面边长为a ，高为h ，则2193a h =，227a h=，再设其外接球半径为R ，则222())R R h =-+，22212224h a h a R h +==+22724h h =+227444h h h =++94≥=，当且仅当22744h h=，即3h =时，等号成立，此时球面积最小，故选A ．【考点】正四棱锥与外接球．【名师点睛】本题考查多面体及其外接球问题．我们应该掌握一些特殊的多面体与外接球的特征．正四面体外接球的球在其高上，且把高分成3:1两部分，正方体，长方体的对角线就是其外接球的直径，正三棱锥，正四棱锥的外接球的球心在其高上，具体计算可借助相应的直角三角形． 12．关于函数2()ln f x x x=+，下列说法错误的是（ ） A ．2x =是()f x 的极小值点B ．函数()y f x x =-有且只有1个零点C ．存在正实数k ，使得()f x kx >恒成立D ．对任意两个正实数12,x x ，且21x x >，若12()()f x f x =，则124x x +> 【答案】C【解析】试题分析：22212'()x f x x x x-=-+=，'(2)0f =，且当02x <<时，'()0f x <，函数递减，当2x >时，'()0f x >，函数递增，因此2x =是()f x 的极小值点，A 正确；()()g x f x x =-，221'()1g x x x=-+- 2217()24x x -+=-，所以当0x >时，'()0g x <恒成立，即()g x 单调递减，又11()210g e e e =+->，2222()20g e e e=+-<，所以()g x 有零点且只有一个零点，B 正确；设2()2ln ()f x xh x x x x==+，易知当2x >时，222ln 21112()x h x x x x x x x x =+<+<+=，对任意的正实数k ，显然当2x k >时，2k x<，即()f x k x<，()f x kx <，所以()f x kx >不成立，C 错误；作为选择题这时可得结论，选C ，下面对D 研究，因为12()()f x f x =，即121222ln ln x x x x +=+，变形为2122112()ln x x x x x x -=，设21(1)x t t x =>，21x tx =，代入上式解得122(1)ln 2(1)ln t t x tt x t -⎧=⎪⎪⎨-⎪=⎪⎩，所以2121()2(1)ln t g t x x t t-=+=⋅>，由导数的知识可证明()(1)g t t >是增函数，又1lim ()4t g t →=（洛必达法则），所以()4g t >，即124x x +>． 【考点】命题的判断，函数的性质．【名师点睛】本题考查命题的判断，实质上考查函数的性质，一般要对每一个选择支进行判断，所考查的知识点较多，难度较大．A 考查函数的极值，B 考查函数的零点，C 考查不等式恒成立问题，D 考查函数的性质，涉及到转化与化归思想，导数与函数的单调性，甚至还有函数的极限，当然从选择题的角度考虑，D 可以不必证明（因为C 是错误的，只能选C ）． 二、填空题13．已知平面直角坐标系中，(3,4)b =，3a b ⋅=-，则向量a 在向量b 的方向上的投影是 ． 【答案】35-【解析】试题分析：向量a 在向量b 的方向上的投影是2353a b b⋅==-+．【考点】向量的数量积的概念．14．若函数1,02()1,20x x f x x -<≤⎧=⎨--≤≤⎩，[]()(),2,2g x f x ax x =+∈-为偶函数，则实数a = ．【答案】12-【解析】试题分析：由题意(1)1,02()1,20a x x g x ax x +-<≤⎧=⎨--≤≤⎩，则(2)(2)f f -=，即212(1)1a a --=+-，12a =-．【考点】函数的奇偶性．15．设实数x ，y 满足约束条件202x y y x -≥⎧⎪⎨≥-⎪⎩，则2z x y =+的最大值为 ．【答案】10【解析】试题分析：作出题高约束条件表示的可行域，如图ABC ∆内部（含边界），作直线:20l x y+=，把直线l向上平移时2z x y=+在增大，当l过点(4,2)A时，z取得最大值10．【考点】简单的线性规划问题．【名师点睛】求目标函数的最大值或最小值，必须先求出准确的可行域，令目标函数等于0，将其对应的直线平行移动，最先通过或最后通过的顶点便是最优解．具体地就是：（1）线性目标函数z=ax+by与y轴交点为(0,)zb，zz b bb=⨯=⨯（线性目标函数在y 轴上的截距）．故对b的符号一定要注意：当b>0时，当直线过可行域且在y轴上的截距最大时，z值最大，在y轴上的截距最小时，z值最小；当b<0时，当直线过可行域且在y轴上的截距最大时，z值最小，在y轴上的截距最小时，z值最大．（2）如果可行域是一个多边形，那么一般在其顶点处使目标函数取得最大或最小值，最优解一般就是多边形的某个顶点．16．如图所示，已知ABC∆中，90C∠=，6AC=，8BC=，D为边AC上的一点，K为BD上的一点，且ABC KAD AKD∠=∠=∠，则DC=．【答案】73【解析】试题分析：由题意3sin5ABC∠=，4cos5ABC∠=，sin sin()sin2BDC DKA DAK ABC∠=∠+∠=∠34242sin cos25525ABC ABC=∠∠=⨯⨯=，所以7cos25BDC∠=，ABCK24tan 7BDC ∠=，8724tan 37BC CD BDC ===∠． 【考点】解三角形．【名师点睛】本题考查解直角三角形．直角三角形中除勾股定理外，还有三角函数的定义，而涉及到三角函数问题时，它就与三角函数公式（如两角和与差的正（余）弦公式、正切公式，二倍角公式等）建立联系，所以本题还考查了二倍角的正弦公式，同角关系式．本题已知直角ABC ∆中的所有量（三边，三角），要求的线段长可能在直角BDC ∆中，此三角形中已知一直角边，要求另一直角边，要么先求得斜边，要么先求得一锐角，再结合已知条件发现锐角BDC ∠与直角ABC ∆中的角有联系，由此得出解法． 三、解答题17．在等比数列{}n a 中，332a =，392S =． （1）求数列{}n a 的通项公式； （2）设2216log n n b a +=，且{}n b 为递增数列，若11n n n c b b +=⋅，求证：12314n c c c c ++++<． 【答案】（1）32n a =或116()2n n a -=⋅-；（2）见解析． 【解析】试题分析：（1）要分类，按1q =和1q ≠分类求得首项1a ，公比q ；（2）由于{}n b 是递增数列，因此{}n a 不是常数数列，从而116()2n n a -=⋅-，由此得2n b n =，而1111()2(22)41n c n n n n ==-++，即数列{}n c 采用裂项相消法求和．试题解析：（1）1q =时，32n a =； 1q ≠时，116()2n n a -=⋅-（2）由题意知：116()2n n a -=⋅-∴2116()4nn a +=⋅ ∴2n b n = ∴111111()2(2n 2)4(n 1)41n c n n n n ===-⋅+⋅++∴123111(1)414n c c c c n ++++=-<+【考点】等比数列的通项公式，裂项相消法求和．18．如图，ABC ∆中，三个内角B 、A 、C 成等差数列，且10AC =，15BC =．（1）求ABC ∆的面积；（2）已知平面直角坐标系xOy ，点(10,0)D ，若函数()sin()f x M x ωϕ=+(0,0,)2M πωϕ>><的图象经过A 、C 、B 三点，且A 、B为()f x 的图象与x 轴相邻的两个交点，求()f x 的解析式．【答案】（1）252；（2）(x)10sin()153f x ππ∴=+． 【解析】试题分析：（1）已知两边一角，三角形可解，由已知60A =︒，由余弦定理求得边c ，从而有ABC S ∆1sin 2bc A =，当然也可求得高OC ；（2）由（1）求得,A C坐标，(5,0),A C -，要求三角函数式()sin()f x M x ωϕ=+，首先且A 、B 为()f x 的图象与x 轴相邻的两个交点，得周期2[10(5)]30T =--=，于是有215T ππω==，把(5,0)A -代入，再结合2πϕ<可得ϕ=3π，再把点C 坐标代入可得M ． 试题解析：（1）在△ABC 中，60A = 由余弦定理可知：2222cos60a b c bc =+-∴2101250c c --=5c AB ∴==+又∵10cos605AO =⋅=BO ∴=125(522ABCS∴=+⨯=． （2）T=2×（10+5）=30，∴15πω=∵(5)Msin((5))015f π-=⋅-+ϕ= sin()03π∴-+ϕ=，,3k k Z π∴-+ϕ=π∈2πϕ<，3π∴ϕ=。

湖北省华中师范大学第一附属中学中考提前招生提前招生数学模拟试卷一、选择题1．在抗击病毒一线的医护人员为防止患者的传染，必须穿着厚厚的防护服、戴上口罩和眼罩。

眼罩的玻璃片有时会变得模糊不清，是由于医护人员呼出的气体中的水蒸气在眼罩的玻璃片处（）A．遇热熔化形成的B．遇热汽化形成的C．遇冷液化形成的D．遇冷凝华形成的2．在图（a）（b）所示的电路中，电源电压相等且保持不变。

若通过闭合或断开开关S1、S2，使电流表A1与A2示数的比值最小，则（）A．S1、S2均断开B．S1、S2均闭合C．S1闭合，S2断开D．S1断开，S2闭合3．晾晒三条相同的湿毛巾，下列做法最有可能让衣架保持水平的是A．B．C．D．4．如图所示为探究“焦耳定律”的实验装置。

两个透明容器中密封着等量的空气，U型管中液面高度的变化反映密闭空气温度的变化。

将容器中的电阻丝R1、R2串联在电路中，且R1<R2。

下列说法正确的是A．该实验装置用于探究“电压和通电时间一定时，电热与电阻的关系”B．闭合开关后，通过R1的电流大于R2的电流C．闭合开关后，甲管中液面上升比乙慢D．闭合开关后，要使电流增大，应将滑动变阻器滑片P向左移动5．如图所示，炎热的夏季，在无风的环境中，剥开冰棒纸后，可以看到冰棒周围会冒“白气”，下列关于“白气”的说法正确的是（）A．“白气”属于液化现象，要放热B．“白气”属于升华现象，要吸热C．“白气”属于汽化现象，要放热D．“白气”属于凝华现象，要吸热6．有6位同学用一把刻度尺测量同一本《科学》课本的长度，测得数据分别为26.02厘米，26.09厘米、26.10厘米、26.00厘米和26.08厘米、31.38厘米。

下列测量结果最接近真实值的是（）A．26.058厘米B．26.06厘米C．26.95厘米D．无法确定，因为真实值未知7．以下事例与物理知识对应的是（）A．高压锅的原理﹣﹣﹣沸点与气压的关系B．用验钞机检验人民币的真伪﹣﹣﹣利用红外线使荧光物质发光C．吹电风扇感到凉爽﹣﹣﹣风扇转动降低了室温D．运动员打鼓用的力越大，鼓声越高﹣﹣﹣振幅越大，音调越高8．下列说法错误的是A．足球被踢出后仍继续向前运动，是因为它运动时产生惯性B．汽车在转弯时减速，是为了防止惯性带来的危害C．闻到花香说明分子在不停地做无规则运动D．游泳时向后划水，人向前运动，是因为物体间力的作用是相互的9．生活中常常需要估测，下列估测符合实际的是（）A．一个人的正常体温为37.6℃B．一间普通教室的面积约为60m2C．紫外线消毒灯的功率为200W D．新型肺炎冠状病毒的直径约为1mm 10．如图所示，在“探究二力平衡的条件”时，选质量为10g的卡片作为研究对象．在线的两端分别挂上等质量的重物，对卡片施加两个拉力．为探究这两个力满足什么条件才能平衡，则所挂重物质量合适的是A．5gB．10gC．200gD．任意质量均可11．如图所示，防治新冠疫情的医护人员佩戴护目镜一段时间后，护目镜内会出现水雾。

华中师大一附中2016年高中招生考试数学试题考试时间：80分钟 卷面满分：150分说明：所有答案一律书写在答题卡上，写在试卷上作答无效．一、选择题 (本大题共6小题，每小题7分，共42分．在每小题给出的四个选项中，有且只有一项是正确的．)1.已知方程1x ax =+有一个负根，而且没有正根，则a 的取值范围是( ) A ．1a >- B ．1a ≥C ．1a =D ．1a >2.关于x 的方程21212x x ax x x x +-=+-+-的根为负数，则a 的值为( ) A ．3a ≠-B ．3a ≠C ．1a <-且3a ≠-D ．1a >-且3a ≠3.如图，抛物线21(0)y ax bx c a =++≠的顶点为(1,3)A ，且与x 轴有一个交点为(4,0)B ，直线2y mx n =+与抛物线交于A 、B 两点，下列结论： ①20a b +=；②0abc >；③方程23ax bx c ++=有两个相等的实数根； ④抛物线与x 轴的另一个交点坐标是(1,0)-，⑤当14x <<时，有21y y <．其中正确的是( ) A ．①②③B ．①③④C ．①③⑤D ．②④⑤4.已知,αβ是方程2260x ax a -++=的两实数根，那么22(1)(1)αβ+++的最小值为( ) A ．414-B ．2C ．10D ．325.设S ⋅⋅⋅+S 最接近的整数是( ) A ．2015B ．2016C ．2017D ．20186.如图，菱形ABCD 中，60A ∠=︒，6AB =，⊙A 、⊙B 的半径分别为4和2，P 、E 、F 分别是线段CD 、⊙A 和⊙B 上的动点，则PE PF +的最大值是( ) A．12 B．16 C ．18D ．6CBD二、填空题(本大题共6小题，每小题7分，共42分)．7.如图，四边形ABCD 是菱形，E 、F 、G 、H 分别是各边的中点，随机地向菱形ABCD 内掷一粒米，则米粒落在阴影区域内的概率是 . 8.已知222x y z x y z x y z z y x +--+-++==且0xyz ≠，则()()()x y y z z x xyz+++= .9.满足1mx m n +-=的整数对(,)m n 共有 对.10.已知22(1)56p q p p q pq ++=⎧⎨+=⎩，则以p 、q 为实数根的一元二次方程为 . 11.函数3max{4,,}y t t t =-+表示对于给定的t 的值，代数式4t -+、t 、3t的值中最大的数，例如当1t =-时，max{5,1,3}5y =--=，当1t =时，max{3,1,3}3y ==，则当t = 时函数y 的值最小.12.在平面直角坐标系中，同时满足下列两个条件的点的坐标为 . (1)直线23y x =-+通过这样的点；(2)不论m 取何非零实数值，抛物线2(21)3y mx m x m =+--都不通过这样的点. 三、解答题(本大题共4小题，共66分．解答应写出文字说明、证明过程和演算步骤) 13. (本小题满分16分)对于任意实数k ，方程2222(1)2()40k x k a x k k b +-++++=总有一个根是1.(1)求实数a 、b ； (2)求另一个根的范围.14. (本小题满分16分)如图，在平面直角坐标系中，直线y ＝－12x ＋4与x 轴交于A 点，与y 轴交于B 点，以AB 为直径作⊙1O ，过B 作⊙1O 的切线交x 轴于点C . (1)求C 点的坐标；(2)设点D 为BC 延长线上一点，CD BC =，P 为线段BC 上的一个动点(异于B 、C )，过P 点作x 轴的平行线交AB 于M ，交DA 的延长线于N ，试判断PM PN +是否为定值，如果是，求出这个值，若不是，说明理由.15. (本小题满分16分)在四边形ABCD 中，AD ∥BC ，BAC D ∠=∠，点E 在边BC (点C 除外)上运动，点F 在边CD 上运动，且AEF ACD ∠=∠.(1)如图1，若AB kBC =(k 为常数)，则AE 与EF 之间是否存在某种确定的数量关系？若存在，请证明，若不存在，请说明理由； (2)如图2，若5AB AC ==，2425sin BAC ∠=，BAC ∠为锐角，设EF 的长度为m ，当E 、F 点运动时，求m 的变化范围.16. (本小题满分16分)已知抛物线2:24C y x x =-+，其顶点为E ，与y 轴交于点D . (1)直线2:(0)l y kx k =>与抛物线C 交于不同两点P 、Q ，并与直线1:28l y x =-+交于点R ，分别过P 、Q 、R 作x 轴的垂线，其垂足依次为1P 、1Q 、1R ，若11111u OP OQ OR +=，求u 的值； (2)若直线31:83l y x =-+与抛物线C 在第一象限交于点B ，交y 轴于点A ，求ABD DBE∠-∠的值； (3)若13(1,)4F 、(0,8)A ，请在抛物线C 上找一点K ，使得KFA ∆的周长最小，并求出周长的最小值.EDBB华中师大一附中2016年高中招生考试数学试题参考答案及评分标准考试时间：80分钟 卷面满分：150分说明：所有答案一律书写在答题卡上，写在试卷上作答无效．一、选择题(本大题共6小题，每小题7分，共42分．在每小题给出的四个选项中，有且只有一项是正确的．)7．１２8．－1或8(只填对一个只得3分) 9．6 10．x 2－3x ＋2 =0 (填了x 2－2x ＋3 =0给4分)11．212．(－3，9)，(1，1)，(3，－3)[(正确答案个数－错误答案个数)×2。

2016届湖北华中师大一附中高三五月适应性考试数学（文）试题一、选择题1．已知全集{}U=1,234,5，，，集合{}1,2,3A =，集合{}3,4B =，则()U C A B ⋃= A ．{}4 B ．{}2,3,4,5 C ．{}3,4,5 D ．{}2,3,4 【答案】C【解析】试题分析：{}(){}4,5,3,4,5U U C A C A B =∴⋃=,故选C. 【考点】集合的运算.2．计算0107cos 47cos 17cos 47sin +的结果等于A ．12-B ．2C ．2D ．12【答案】D【解析】试题分析：)1747sin()17sin (47cos 17cos 47sin 107cos 47cos 17cos 47sin 0000000000-=-+=+2130sin 0==，故选D. 【考点】诱导公式；两角差的正弦公式． 3．已知复数1023z i i=-+（其中i 是虚数单位），则z =A ．．．．【答案】C【解析】试题分析： 1023233,3z i i i i z i=-=--=-∴==+故选C.【考点】复数的运算．4．已知五个数2,,,,8a m b 构成一个等比数列，则圆锥曲线2212x y m +=的离心率为A ．2 B 2．2【答案】A【解析】试题分析：由题意得28,4ab m m ⨯==∴=±当4-=m 时圆锥曲线表示双曲线，2222,4,6,a b c e ==∴=∴=当4=m 时圆锥曲线表示椭圆， 2224,2,2,2a b c e ==∴=∴=故选A. 【考点】双曲线的简单几何性质．5．若()xxf x e ae -=+为偶函数，则()211e f x e+-<的解集为A ．()2,+∞B ．()0,2C ．(),2-∞D ．()(),02,-∞⋃+∞ 【答案】B【解析】试题分析：()x x f x e ae -=+为偶函数可得1,()x x a f x e e -=∴=+，由xx e e x f --=)('在),0(+∞上为增函数，()2111(1)(1)(1),111,02e f x f x e e f x f x x e-+-<⇒-<+⇒-<∴-<-<∴<<．故选B.【考点】函数的奇偶性；函数的单调性．6．ABC ∆的外接圆圆心为O ，半径为2，OA AB AC ++为零向量，且OA AB =.则CA 在BC 方向上的投影为A ．3-B ．．3 D 【答案】B【解析】试题分析：由题意可得四边形A B O C 为菱形，且边长为2，00120,30A ACB =∴∠=,则CA 在BC 方向上的投影为3)30180cos(00-=-CA ，故选B ．【考点】向量的投影．7．已知函数()()()sin 0,0,62f x x x f f f x ππωωω⎛⎫⎛⎫=>+=⎪ ⎪⎝⎭⎝⎭在区间,62ππ⎛⎫⎪⎝⎭上单调， 则ω=A ．2B ．3C ．1D ．5 【答案】A【解析】试题分析：()sin 2sin()3f x x x x πωωω=+=+，由()0,62f f f x ππ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭在区间,62ππ⎛⎫ ⎪⎝⎭上单调可知函数的对称中心为62(,0),(,0),2sin()0,()233333k k πππππππωωπ+∴∴+=∴+=∈Z ， k 31+-=∴ω，当1=k 时，2=ω，故选A.【考点】三角函数的性质．8．已知某几何体的三视图如图所示，则该几何体的各侧面中，面积最小值为A．2 B．2D ．12【答案】D【解析】试题分析： 由三视图可得几何体的直观图，平面⊥AED 平面BCDE ,四棱锥的高为1，四边形BCDE 为边长为1的正方形，则255121,222121,211121=⨯⨯==⨯⨯===⨯⨯=ACD ABE ABC AED S S S S ,故该几何体的各侧面中，面积最小的为21，故选D. EDCBA【考点】由三视图求面积，体积．【易错点睛】本题主要考查了由三视图求面积，体积．求解有关多面体表面积的问题，关键是找到其特征几何图形，如棱柱中的矩形，棱台中的直角梯形，棱锥中的直角三角形，它们是联系高与斜高、边长等几何元素的桥梁，从而架起侧面积公式中的未知量与条件中已知几何元素的联系．由三视图还原几何体是本题的难点． 9．阅读如图所示的程序框图，则输出结果S 的值为A ．18 B ．12 CD ．116 【答案】D【解析】试题分析：第一次循环：2,9cos==n S π；第二次循环：3,92cos 9cos ==n S ππ；第三次循环：4,3cos 92cos 9cos ==n S πππ；第四次循环：24cos cos cos cos 9939S ππππ=242sin cos cos cos cos199939,5162sin 9n ππππππ===；故选D. 【考点】算法初步；二倍角公式．10．直线y a =分别与曲线2ln ,2y x x y x =-=-交于点P Q 、，则PQ 的最小值为 A ．2 B．1 D【答案】A 【解析】试题分析：设),(),,(21a x Q a x P ,则2ln 2ln 12122121+-=∴-=-x x x x x x ,21PQ x x ∴=- 2111ln 2x x x =--+,令2ln 2+--=x x x y ,则)0()12)(1(121122'>+-=--=--=x x x x x x x x x y ,函数在)1,0(上单调递减,在),0(+∞上单调递增,1=∴x 时,函数的最小值为2，所以A 选项是正确的.【考点】导数与函数的单调性．11．如图，AB 是平面α外固定的斜线段，B 为斜足，若点C 在平面α内运动，且CAB ∠等于直线AB 与平面α所成的角，则动点C 的轨迹为A ．圆B ．椭圆C ．双曲线D ．抛物线 【答案】D 【解析】试题分析：如下图所示，作α⊥AO ,垂足为O ，连结BO ，在α内过O 作BO 的垂线，建立空间直角坐标系，由题意得，设=∴∴==∠=∠AC a B a A y x C a AB CAB ABO ),0,cos ,0(),sin ,0,0(),0,,(,,θθθ()222422222222222222cos sin (,,sin ),(0,cos ,sin ),cos cos sin sin cos sin cos (sin )2sin ,cos cos ay a AC ABx y a AB a AC AB ay aa x y a x a y a a C θθθθθθθθθθθθθθθθ+⋅-=-∴===⇒+=++⇒=+-∴的轨迹是抛物线，故选D.【考点】立体几何中的动态问题．【易错点睛】在立体几何中，某些点、线、面依一定的规则运动，构成各式各样的轨迹，探求空间轨迹与平面轨迹类似，就注意几何条件，善于基本轨迹化，对于较为复杂的轨迹，常常要分段考虑，注意特定情况下的动点的位置，然后对任意情形加以分析判定，也可能化为平面问题，也可利用空间直角坐标系求出轨迹方程，即可知其对应的轨迹类型，对每一道轨迹命题特别注意轨迹的纯粹性与完备性．12．定义在R 上的函数()x f 是减函数，且函数()x f y =的图像关于原点中心对称，若t s 、满足不等式()()2222t t f s s f --≤-，其中s k t ⋅=，则当42<<s 时，k 的取值范围是A ．⎥⎦⎤⎢⎣⎡-1,21 B ．()[)+∞⋃∞-,10, C ．⎥⎦⎤⎝⎛-1,21 D ．(][)+∞⋃∞-,10, 【答案】C【解析】试题分析： 定义在R 上的函数()x f 是减函数,且函数()x f y =的图象关于原点中心对称,故()x f 为奇函数.若t s 、满足不等式()()2222t t f s s f --≤-,其中sk t ⋅=,42<<s .则()()2222f s s f t t -≤-+，2222,2s s t t s t s ∴-≥-+∴-≤≤，--==s t s t k 表示图中四边形ABCD 及其内部区域内的点与原点O 连线的斜率,故当点),(t s 位于线段AD 上时, k 取得最大值为1,当点),(t s 位于点)2,4(-D 时, k 取得最小值为21-.故k 的取值范围为]1,21(-,所以C 选项是正确的．【考点】奇偶性与单调性的综合．【易错点睛】本题综合考查了函数的奇偶性，单调性知识，同时考查由最大值，最小值求取值范围的策略，以及运算能力，属于中档题．另本题还考查了转化与化归思想和数形结合思想．将函数问题转化为简单的线性规划问题是本题的难点，也是关键点，这样方便了不等式的解决．数形结合是解决线性规划问题必要的步骤．二、填空题13．若幂函数()()22233--⋅+-=m m xm m x f 的图像不过原点，则m 的值为 . 【答案】1m =或2=m【解析】试题分析：由幂函数定义可得2331,1,2m m m m -+=∴==． 【考点】幂函数的定义；性质．14．从{}5,4,3,2,1中随机选取一个数为a ，从{}3,2,1中随机选取一个数为b ，则a b >的概率是 .【答案】51 【解析】试题分析：由题意可得如下基本事件：(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),(4,1),(4,2),(4,3),(5,1),(5,2),(5,3)共15个，其中满足a b >的基本事件包括3个，故概率为31155=． 【考点】古典概型． 15．在A B C ∆中，10103cos ,21tan ==B A ，若最长为1，则最短边的长为 . 【答案】55【解析】试题分析：由10103cos ,21tan ==B A得sin sin 2A ABC ===∴=,由最长为1得1=c ，则最短边为,b由正弦定理可得sin sin c b B C =⨯==. 【考点】正弦定理．【易错点睛】解三角形问题的两重性：①作为三角形问题，它必须要用到三角形的内角和定理，正弦、余弦定理及其有关三角形的性质，及时进行边角转化，有利于发现解题的思路；②它毕竟是三角变换，只是角的范围受到了限制，因此常见的三角变换方法和原则都是适用的，注意“三统一”（即“统一角、统一函数、统一结构”）是使问题获得解决的突破口．16．定义在R 上的函数()x f 对任意两个不等的实数21x x 、都()()()()12212211x f x x f x x f x x f x +>+，则称函数()x f 为“Z 函数”，以下函数中为“Z 函数”的序号 为 .⎪⎩⎪⎨⎧<+-≥+=⎩⎨⎧=≠=--=+-=0,0,4)4(0,00,ln )3(cos 2sin 23)2(1)1(222x x x x x x y x x x y x x x y x y【答案】（2）（4）【解析】试题分析：由()()()()12212211x f x x f x x f x x f x +>+得()()0])[(2121>--x f x f x x ，即函数()x f 在R 为增函数，（1）函数在R 上为先增后减，（2） 223)4sin(223sin 2cos 23'-≥++=+-=πx x x y ，函数为增函数，符合题意；（3）函数在R 上先减后增；（4）函数在R 为增函数，符合题意．故本题答案为（2） （4）．【考点】函数的单调性． 【易错点睛】本题主要考查了函数的单调性．判断（或证明）函数单调性的主要方法（1）函数单调性的定义；（2）观察函数的图象；（3）利用函数和、差、积、商和复合函数单调性的判断法则；（4）利用函数的导数等．其中（2）（3）一般用于选择、填空题．对初等函数的单调性的判断要依赖于图象，对于分段函数的单调性的判断一定要注意自变量的取值范围．三、解答题17．设等差数列{}n a 的前n 项和为n S ，143,241165==+S a a ，数列{}n b 的 前n 项和为n T ，满足)(211N n a T n a n ∈-=-．（Ⅰ）求数列{}n a 的通项公式及数列⎭⎬⎫⎩⎨⎧+11n n a a 的前n 项和；（Ⅱ）判断数列{}n b 是否为等比数列？并说明理由. 【答案】（I ）21n a n =+，69nn +；（II ）数列{}n b 不是等比数列【解析】试题分析：（I ）由等差数列的性质可求得511a =，2d =，进而可得{}n a 的通项公式是21n a n =+()n N *∈，利用裂项相消对数列进而求和可得数列⎭⎬⎫⎩⎨⎧+11n n a a 的前n 项和；（II ）由)(211N n a T n a n ∈-=-可得43n n T =+，进而可求当1n =时，17b =；当2n ≥时，1114434n n n n n n b T T ---=-=-=⨯；可验证得该数列不是等比数列． 试题解析：（I ）设数列{}n a 的公差为d ，由11611143,S a ==613a ∴=. 又5624,a a +=解得511a =，2d =， 因此{}n a 的通项公式是21n a n =+()n N *∈， 所以111111()(21)(23)22123n n a a n n n n +==-++++， 从而前n 项的和为1113557(21)(23)n n +++⨯⨯++ 1111111()235572123n n =-+-++-++111()2323n =-+69n n =+.（II ）因为13a =，124n a n -=，43n n T =+.当1n =时，17b =；当2n ≥时，1114434n n n n n n b T T ---=-=-=⨯；所以14n n b b +=（2n ≥．若{}n b 是等比数列，则有214b b =，而127,12b b ==，所以与214b b =矛盾，故数列{}n b 不是等比数列．【考点】等差数列的性质；裂项相消数列求和；等比数列的定义．【易错点睛】本题主要考查了等差数列的性质；裂项相消数列求和；等比数列的定义．用裂项相消法求和应注意的问题：利用裂项相消法求和时，应注意抵消后并不一定只剩下第一项和最后一项，也有可能前面剩两项，后面也剩两项，再就是将通项公式裂项后，有时候需要调整前面的系数，使裂开的两项之差与系数相乘后与原项相等．18．如图，在四棱锥ABCD P -中，底面ABCD 为直角梯形，BC AD //，⊥PD 底面ABCD ，Q BC AD ADC ,2,90==∠ 为AD 的中点，M 为棱PC 的中点.（Ⅰ）证明：//PA 平面BMQ ；（Ⅱ）已知2===AD DC PD ，求点P 到平面BMQ 的距离.【答案】（I ）证明见解析；（Ⅱ）2【解析】试题分析：（I ）连接AC 交BQ 于N ，连接MN ，可知N 为AC 的中点，利用三角形中位线性质可得MN ∥PA ，利用直线与平面平行的判定定理可得//PA 平面BMQ ．（Ⅱ）由（I ）可知，PA ∥平面BMQ ，所以点P 到平面BMQ 的距离等于点A到平面BMQ 的距离，计算得13P BMQ A BMQ M ABQ V V V ---===，BMQ S ∆=P 到平面BMQ的距离32P BMQ BMQV d S -∆==. 试题解析：（I ）证明连接AC 交BQ 于N ，连接MN ，因为090ADC ∠=，Q 为AD 的中点，所以N 为AC 的中点，又M 为PC 的中点，故MN ∥PA ，又MN ⊂平面BMQ ，所以PA ∥平面BMQ .（II ）解由（1）可知，PA ∥平面BMQ ，所以点P 到平面BMQ 的距离等于点A 到平面BMQ 的距离，所以P BMQ A BMQ M ABQ V V V ---==，取CD 的中点K ，连接MK ，所以MK ∥PD ，112MK PD ==. 又PD ⊥底面ABCD ，所以MK ⊥底面ABCD . 又112BC AD ==，2PD DC ==，所以1,2AQ BQ ==，1MQ NQ ==，所以13P BMQ A BMQ M ABQ V V V ---===，BMQ S ∆=则点P 到平面BMQ的距离32P BMQ BMQV d S -∆==. 【考点】直线与平面平行的判定定理；点到平面的距离．19．某校高中三个年级共有学生1800名，各年级男生、女生的人数如下表： 高一年级 高二年级 高三年级 男生 290 b 344女生260c a已知在高中学生中随机抽取一名同学时，抽到高三年级女生的概率为17.0. （Ⅰ）求a 的值；（Ⅱ）现用分层抽样的方法在全校抽取60名学生，则在高二年级应抽取多少名学生？（Ⅲ）已知200,260≥≥c b ，求高二年级男生比女生多的概率. 【答案】（I ）306=a ；（II ）20；（Ⅲ）141100)(=A P 【解析】试题分析：（I ）很容易得306=a ；（II ）由题意可知高一、高二、高三人数，用分层抽样的方法全校抽取60名学生，可知高二年级应抽取20180060060=⨯人；（Ⅲ）写出满足200,260≥≥c b 的所有基本事件的个数，找到c b >的基本事件的个数，即可求得高二年级男生比女生多的概率.试题解析：（I ）根据题意得高三年级女生抽到的概率为1800a ，所以17.01800=a所以30617.01800=⨯=a （人）（II ）由表格知高二年级的总人数为600)306344()290260(1800=+-+-人， 所以高二年级应抽取的人数为20180060060=⨯（人） （III ）设事件A=“高二年级男生比女生多”，求概率)(A P用b 表示高二年级男生的人数，用c 表示高二年级女生的人数，且600=+c b 则满足200,260≥≥c b 的),(c b 配对的情况为)200,400()339,261(),340,260( ，共有141种情况，而事件A 发生的),(c b 配对的情况为)298,302(),299,301(，)200,400(, 共有100种情况，所以高二年级男生比女生多的概率为141100)(=A P 【考点】分层抽样；古典概型．20．已知椭圆)0(1:2222>>=+b a by a x C 的离心率为21，过右焦点F 且垂直于x 轴的直线与椭圆C 相交于N M ,两点，且3=MN .（Ⅰ）求椭圆C 的方程；（Ⅱ）设直线l 经过点F 且斜率为k ，l 与椭圆C 相交于,A B 两点，与以椭圆C 的右顶点E 为圆心的圆相交于,P Q 两点（,,,A P B Q 自下至上排列），O 为坐标原点.95OA OB ⋅=-，且Ap BQ =，求直线l 和圆E 的方程.【答案】（Ⅰ）22143y x +=；（Ⅱ）0y -=与0y +，()223312100x y -+= 【解析】试题分析：（Ⅰ）由椭圆的离心率32,,2222=⋅-==ab b ac a c e ，可求得cb a ,,的值，求得椭圆方程；（Ⅱ）设直线方程及B A ,坐标，将直线方程代入椭圆方程，整理得到关于x 的一元二次方程，根据根与系数的关系求得21x x +及21x x ⋅的值，并求得21y y ⋅，利用向量的坐标表示，整理可求得k 的值，由Ap BQ =可知AB PQ =，分别表示出,AB PQ 将k 代入，可求得圆的半径，即可求得圆的方程和直线的方程．试题解析：（Ⅰ）设(,0)F c ，则由题意得222c a b =-，12c a =，223b a⋅=，解得2,1a b c ==，∴椭圆C 的方程为221y x +=． （Ⅱ）由题意，直线l 的斜率k 存在．设l 的方程为()1y k x =-， 联立椭圆方程得()22223484120k x k x k +-+-=．设()()1122,,,A x y B x y ，则2122834k x x k +=+，212241234k x x k -=+， ∴2122934k y y k=-+．∴21212212534k OA OB x x y y k +⋅=+=-+ ． ∵95OA OB ⋅=- ，∴221259534k k+-=-+，解得23k =．由题意可得，AP BQ =等价于AB PQ =． 设圆E 的半径为r ，∵2122121234k AB x k +=-=+，PQ = 将23k =代入AB PQ =解得2331100r =．故所求直线l 的方程为)1y x =-0y -0y +；圆E 的方程为()223312100x y -+=．【考点】椭圆的简单性质．【易错点睛】本题综合考查了椭圆的标准方程及其简单性质，直线与椭圆相交问题转化为方程联立得到根与系数的关系，向是垂直与数量积的关系等基础知识与基本技能，考查了推理能力和计算能力，属于难题．本题的难点在于利用一元二次方程与根与系数的关系建立等式，求得23k =，利用圆的有关知识可求得半径． 21．设函数()ln ,mf x x m R x=+∈． （Ⅰ）当m e =（e 为自然对数的底数）时，求()f x 的最小值； （Ⅱ）讨论函数()()3xg x f x '=-的零点的个数； （Ⅲ）若对任意()()0,1f b f a b a b a ->><-恒成立，求实数m 的取值范围.【答案】（I ）2；（II ）当32>m 时，函数)(x g 无零点，当32=m 或0≤m 时，函数)(x g 有且仅有一个零点，当320<<m 时，函数)(x g 有两个零点；（III ）⎪⎭⎫⎢⎣⎡+∞,41 【解析】试题分析：（I ）当e m =时，221)(xex x e x x f -=-='，0>x ，由此，利用导数性质能求出)(x f 的极小值；（II ）因为函数),0(313)()(2>--=-'=x xx m x x x f x g 令0)(=x g ，得),0(313>+-=x x x m 令),0(31)(3>+-=x x x x h ),1)(1(1)(2+--=+-='x x x x h 32131)1(=+-=h ，由此利用导数性质能求得函数3)()(xx f x g -'=的零点个数；（III ）当0b a >>时，1)(<'x f 在),0(+∞上恒成立，由此能求出m 的取值范围． 试题解析：（I ）当e m =时，xex x f +=ln )(，易知函数)(x f 的定义域为),0(+∞，所以221)(xex x e x x f -=-='，当),0(e x ∈时，0)(<'x f ，此时)(x f 在),0(e 上是减函数；当),(+∞∈e x 时，0)(>'x f ，此时)(x f 在),(+∞e 上是增函数，所以当e x =时，)(x f 取得极小值2ln )(=+=eee ef （II ）因为函数),0(313)()(2>--=-'=x xx m x x x f x g 令0)(=x g ，得),0(313>+-=x x x m 设),0(31)(3>+-=x x x x h 所以),1)(1(1)(2+--=+-='x x x x h 当)1,0(∈x 时，0)(>'x h ，此时)(x h 在)1,0(上为增函数；当),1(+∞∈x 时，0)(<'x h ，此时)(x h 在),1(+∞上为减函数，所以当1=x 时，)(x h 取极大值32131)1(=+-=h ，令0)(=x h ，即0313=+-x x ，解得0=x 或3=x ，由函数)(x h 的图像知：①当32>m 时，函数m y =和函数)(x h y =无交点； ②当32=m 时，函数m y =和函数)(x h y =有且仅有一个交点；③当320<<m 时，函数m y =和函数)(x h y =有两个交点；④当0≤m 时，函数m y =和函数)(x h y =有且仅有一个交点。