当前位置：文档之家 › 4_4矩阵的秩

4_4矩阵的秩

  • 格式：ppt
  • 大小：934.50 KB
  • 文档页数：47

下载文档原格式

  / 47

合集下载

线性代数：矩阵秩的求法

线性代数：矩阵秩的求法

齐次线性方程组 Ax=0 总是有解的，x=0 就是一个解， 称为零解。 所以我们更关心的是它是否有非零解.
6/44
定理 Ax=0 的解的情况：
1.Ax=0 有非零解 r(A)<n 只有零解 r(A)=n
2.若A是方阵，Ax 0有非零解 A 0 只有零解 A 0
3.Ax 0,若m n,则一定有非零解。 m :方程个数 n :未知量个数
k
2
1 2
0
3 2
1
.
其中k1
,
k
为任意常数。
2
12/44
定理 3 线性方程组 Ax=b 有解 r(A)=r(Ab)
定理 4 设线性方程组 Ax=b 有解。 若A为方阵，
如果 r(A)=n，则它有唯一解; A 0,唯一解
如果
r(A)<n，则它有无穷多解。
A
0，无穷解
13/44
x1 x2 a1
a4
x5 x1 a5
RA RB
5
ai 0
i 1
15/44
5
方程组有解的充要条件是 ai 0.
i 1
x1 x2 a1
由于原方程组等价于方程组
x2 x3
x3 x4
a2 a3
例４
证明方
程组
x2 x3
x3 x4
a2 a3
x4
x5
a4
x5 x1 a5
有解的充要条件
是a1 a2 a3 a4 a5 0.在有解的情况下，
求出它的一切解．
解证 对增广矩阵B进行初等变换， 方程组的增广矩阵为
14/44
1 1 0 0 0 a1
0 1 1 0 0 a2
第十-十一次
4矩阵的秩

4矩阵的秩


(i ) r ( Am×n ) ≤ min{m, n};
显然:r(O)=0;只要 不是零阵 就有 r(A)>0.并且 只要A不是零阵 并且: 显然 只要 不是零阵,就有 并且
(ii ) 若有一个r阶子式不为零，则 r ( A) ≥ r; 若所有的r阶子式全为零，则 r ( A) < r.
r ( A ) = r ( A). 求矩阵A的秩 例:求矩阵 的秩 a11 a12 L a1r L a1n 求矩阵 的秩. a 22 L a 2 r L a 2 n O M L M A= a rr L a rn 0 L L L L 0 M M M M M M 0 L L L L 0 显然 r ( A) = r. ( a 11 a 22 L a rr ≠ 0 ) 利用初等变换可以求矩阵的秩. (iii )
1 4 1 4 1 3 1 3 A → 2 12 − 2 12 → 0 6 − 4 4 r →r3 1 0 − 9 6 − 6 2 − 3 8 2
求矩阵的秩: 例:求矩阵的秩 求矩阵的秩
1 3 1 4 → 0 6 − 4 4 0 0 0 0
T
定理:矩阵经初等变换后其秩不变 矩阵经初等变换后其秩不变. 秩的求法 定理 矩阵经初等变换后其秩不变
秩的求法 定理 矩阵经初等变换后其秩不变. 定理:矩阵经初等变换后其秩不变 矩阵经初等变换后其秩不变
2 2 − 3 8 1. A = 2 12 − 2 12 1 3 1 4
1 2 − 2 3 → 0 −1 1 0 ⇒ t = −3, r ( A) < 3. 0 0 t + 3 0
矩阵的秩
1.k阶子式：在Am×n中任取k行k列，位于这些 行、列相交处的k 个元素，按原次序组成的
4_4矩阵的秩

4_4矩阵的秩


Page 6
例1
1 2 3 求矩阵 A 2 3 5 的秩. 4 7 1
解
1 2 在 A 中， 0. 2 3
又 A的 3 阶子式只有一个 A，且 A 0，
R( A) 2.
Page 7
3 2 2 1 0 3 1 2 5 0 例2 求矩阵 B 的秩. 0 0 0 4 3 0 0 0 0 0
关的列向量， 这说明A的列秩p r; 根据引理，A的极大无关列构成的矩阵一定有
一个非零的p阶子式， p r , 所以p r。 故
类似地，有r rA rAT AT的列秩 A的行秩。
Page 14
结论 若Dr 是矩阵A的一个最高阶非零子式，
则Dr 所在的r列即是列向量组的一个极大无关组， Dr 所在的r 行即是行向量组的一个极大无关组.
奇异矩阵为降秩矩阵.
Page 3
1 1 0 2 例如：矩阵 A 0 0 0 0 a1 (1,1, 3,1), a2
3 1 1 4 的行向量组是 0 5 0 0 (0, 2, -1, 4),
a3 (0, 0, 0, 5), a4 (0, 0, 0, 0) 可以证明 1 , 2 , 3 是A的行向量组的一个极大无关组.
3 2 2 2 1 3 ，求该矩阵的秩． 0 1 5
计算A的3阶子式，
1 3 2 3 2 2 1 2 2 0 , 0 2 1 00 2 3 2 , 1 3 0, 1 3 0, 0 2 0 1 2 0 5 0 1 5 2 1 5
0.
§４.4
矩阵的秩
一、矩阵秩的概念
二、矩阵秩的求法 0011 0010 1010 1101 0001 0100 1011
第四节 矩 阵 的 秩

第四节 矩 阵 的 秩

一个 k 级子式.
例如，在矩阵
1 1 3 1
A


0 0
2 0
1 0
4

5

0
0
0
0

中，选第 1, 3 行和第 3, 4 列，它们交点上的元素
所成的 2就是一个 2 级子式. 又如选第 1, 2, 3 行和第1, 2, 4
列，相应的 3 级子式就是
求向量组的极大线性无关组的方法是：把向量 组中的每一个向量作为矩 阵的一列构成一个矩阵, 然后用矩阵的初等行变换把矩阵化成阶梯形矩阵， 在阶梯形矩阵中，每个阶梯中的第一个非零元所在 的列所对应的向量即为极大线性无关组中的向量.
若要用极大线性无关组来表示其余向量，则需进一 步把阶梯形矩阵化成行最简形，这时，不在极大线 性无关组中的列中的元素即为用极大线性无关组表 示该列所对应的向量的表示系数.


2 3

,
3


3 5

,

4


7
;
1

1


1


4


1

本若请本若请本若请本若请本本若若请请本若节想请单节想本单若节想请单节想本单若节节想想请单单节想内结本单若击内请结节击想内结本单若击内请结节击想内 内结 结本单若击击内请结容束节击想返本容单若束内请返结容束节击想返本容单若束内请返结容 容束 束节击想返返本容单若束已本内请返结回节已击想本本容单若回束已本内请返结回节已击想本本容单若回束已 已本 本内请返结回回节已击想本结本堂容单若回束按内结请返结本堂若节已击想按本结请本 本堂容单若 若回束按内结请 请返结本堂若节已击想按本结 结请本堂 堂容单若回束按按内结请返结堂束节课已击想按本钮容束单回束节课想内结返结钮堂束单节 节课已击想 想按本钮容束单单回束节课想内结返结钮堂束 束单节课 课已击想按本钮钮容束单回束课内,结返结钮堂.已击按本内,!结容束回束课.击内 内,结!返结 结钮堂.已击击按本内,!结容束回束课.击内,,结!返结钮堂..已击按本,!!容束回束课.结!返钮堂容束已按本,返容 容束回束 束课.结!返返钮堂容束已按本,返容束回束课.结!返钮堂已按本,束回课.已本结!钮堂回已 已按本 本,束回回课.已本结!钮堂回已按本,束回课.结!钮堂按,结堂束课.按结 结!钮堂堂按按,结堂束课.按结!钮堂按,束课.!钮束课,钮束束课课.!钮钮束课,钮束课.!钮,.,!.,,!..,!!.,!.!
矩阵的秩求法

矩阵的秩求法

定义2 在 m×n 矩阵 A 中任取 k 行、k 列（k ≤ m , k ≤ n ），位于这些行列交叉处的 k2 个元 素，不改变它们在 A 中所处的位置次序而得到的 k 阶行列式，称为矩阵 A 的 k 阶子式。 m×n 矩阵A 的 k 阶子式共有CmkCnk个。 定义2 设在矩阵A 中有一个不等于0的 r 阶子式 D，且所有 r +1 阶子式（如果有的话）全等于0，那 么 D 称为矩阵A 的最高阶非零子式，数 r 称为矩阵 A 的秩，记作R ( A ) = r 。规定零矩阵的秩等于 0 。
4 3 9 12
1 1 7 8
4 1 11 12
上页 下页
返回
1 0 0 0
6 4 12 16
4 3 9 12
1 1 7 8
4 1 11 12
1 r3 3r2 0 ~ 0 r4 4r2 0
6 4 0 0
4 3 0 0
1 1 4 4
4 1 8 8
上页 下页
返回
1 0 0 0 1 r4 3r3 0 ~ 0 0
6 4 0 0 6 4 0 0
4 3 0 0 4 3 0 0
1 1 4 4 1 1 4 0
2 0 0 1 3 0 3 2 24 0, 4
因此R（B）= 3 。
上页 下页 返回
从本例可知，由矩阵A 的秩的定义求秩，关键在 于找 A 中不等于 0 的子式的最高阶数。 一般当行数与列数都较高时，按定义求秩是很麻 烦的。 对于行阶梯形矩阵，显然它的秩就等于非零行的 行数。 因此自然想到用初等变换把矩阵化为行阶梯形矩 阵，但两个等价的矩阵的秩是否相等呢？
上页 下页 下页 返回 上页
2.6-矩阵的秩

2.6-矩阵的秩

001
1 0 5 1 0 5 1 0 5 1 0 0
E(1, 3(5)) = 0 1 0 , 0 1 0 0 1 0 = 0 1 0 .
00 1 001 00 1 001
第二章 矩阵
§2.6 方阵的逆矩阵
2. 可逆矩阵的分解
***
(1) * * *
** * ***
***
= ***
10 0
010.
000 *** 000 001
第二章 矩阵
2 0 4 1
0 1 3 2 的3阶子式有14个:
4 0 8 2
§2.5矩阵的秩
2 0 4 2 0 1 2 4 1 0 4 1
0 1 3 = 0 1 2 = 0 3 2 = 1 3 2 = 0. 4 0 8 4 0 2 4 8 2 0 8 2
第二章 矩阵
§2.5矩阵的秩
问题: 假若一个56的矩阵中所有3阶子式都等
1 0
0 1
3/2 1
3 1
5/2 1
1 3 2 故A1 = 3/2 3 5/2 .
1 1 1
第二章 矩阵
§2.6 方阵的逆矩阵
三. 用初等变换解矩阵方程
设A可逆, 则A可以经过有限次初等行变换化为 行最简形——单位矩阵E.
下面用初等变换解矩阵方程AX = B. 注意到X = A1B.
(A B) … (E ?)
第二章 矩阵
§2.5 矩阵的秩
定理2. 设A是满秩方阵，则存在初等方阵
P1, P2, , Ps. 使得 Ps Ps1 , P2P1A E
第二章 矩阵
§2.5 矩阵的秩
定理3. mn矩阵A, m阶初等矩阵
P1, P2, …, Ps 及m阶初等矩阵
线性代数 矩阵的秩

线性代数 矩阵的秩


小结. 求m × n 矩阵A 的秩r(A), 可用以下方法: 1. 对于比较简单的矩阵, 直接用秩的定义 直接用秩的定义. .
∼
1 0 0 0
0 1 0 4
0 1 0 −1 0 0 5 0
2. 用有限次初等变换, 用有限次初等变换, 将矩阵A变为它的等价 标准形 , 则 r = r( A ) . O O 3. 用有限次行初等变换, 用有限次行初等变换,将矩阵A变为梯矩阵, 则 r(A)等于该梯矩阵的非零行的行数 等于该梯矩阵的非零行的行数. （方法2 与方法3 相比, 方法3 较为简单.）
例1 求下列矩阵的秩: 求下列矩阵的秩:
(1) A = 2 2
1 1
2 4 8 (2) B = 1 2 1
(3) C = 2
1 2 4 1 4 8 2 3 6 2 0
.
解 (1)因为
1 1 a = 1 ≠ 0 而 det A = 1 1 = 0 A= 11 , 2 2 2 2 故 r ( A) = 1
又B 并无3阶子式, 阶子式,故 r (B) =2.
8 2 2 0
故, 矩阵C 的秩不小于2.
= −3 ≠ 0
另外, 因为矩阵 C 不存在高于3阶的子式, 可知r (C) ≤ 3. 又因矩阵C 的第1, 2行元是对应成比例的, 行元是对应成比例的, 故C 的任一 3阶 子式皆等于零. 子式皆等于零.因此
0 0 1 0
4 3 −3 4
1 0 B= 0 0
0 1 0 0
−1 −1 2 0
0 0 1 0
4 3 −3 4
1 0 (2) 每个台阶只有一行， 每个台阶只有一行，台阶 A = 0 数即是非零行的行数， ，阶梯 数即是非零行的行数 0 线的竖线后面的第一个元素
关于矩阵秩的几个重要不等式

关于矩阵秩的几个重要不等式

第28卷第1期2021年3月辽东学院学报(自然科学版)Journal of Eastern Liaoning University(Natural Science Edition)Vol.28No.1Mar.2021［基础科学与应用】DOI：10.14168/j.issn.1673-4939.2021.01.12关于矩阵秩的几个重要不等式黄述亮①(滁州学院数学与金融学院，安徽滁州239001)摘要：针对学生学习矩阵秩的不等式比较困难的问题，综合运用演绎、分析与综合、化归的数学论证方法对秩的估计、秩的降阶及互素多项式等方面的重要不等式进行研究，并举例说明这些不等式在分块矩阵、线性方程组及判断线面位置关系等问题中的应用，这将有助于学生更好地掌握矩阵的基本理论，提高学生的抽象思维能力和逻辑思维能力。

关键词：矩阵的秩；初等变换；齐次线性方程组中图分类号：0153.3文献标志码：A文章编号：1673-4939(2021)01-0061-05众所周知，在线性代数(或高等代数)课程中最主要的内容就是矩阵及其相关运算。

在学习矩阵的过程中会遇到的一个非常重要的概念——矩阵的秩。

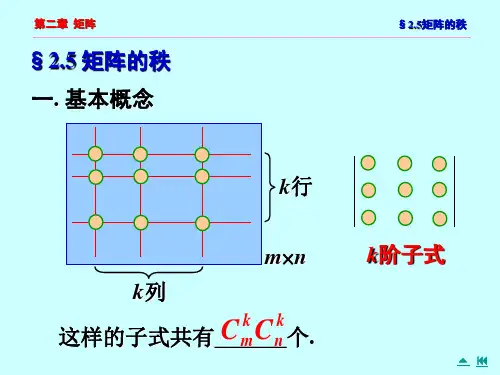
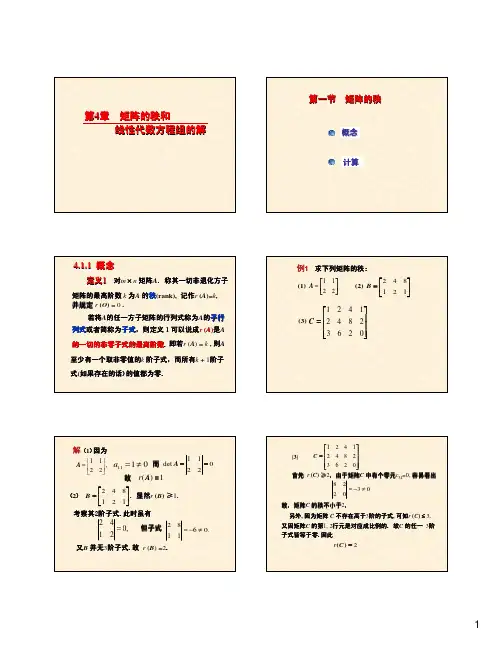
在一般的教科书和文献中，习惯上用数学符号rank(A)来表示一个矩阵的秩，其定义是矩阵A 中的某个非零子式的最高阶数。

考虑到向量组、向量空间等概念，对矩阵分别进行行分块和列分块，且设A=(兔心，…,a”)=(肉,0；,…屈)，则下列几个论断等价：(l)rank(A)=r；(2)rank(兔，他，…，a”)=r；(3)rank(0；,0：,…屈)=r；(4)dim®?如aj,a2,•••,a n|；(5)dimSpan W 嵐,…,0：}=r；(6)矩阵4的阶梯形矩阵中非零行(列)的行(列)数为r o矩阵的秩在很多领域中具有重要的理论意义和实际应用价值，比如在通信复杂性领域中，函数的通信矩阵的秩可以给出计算函数所需的通信量的界限。

此外，利用矩阵的秩可以定义数学中的等价关系，因此一个数域F上的全体"阶矩阵M”(F)可以被划分成n+1个子集(即等价类)的不交并M(F) =U U…U T”,其中7；={A e M”(F)I rank(4) =i}o换言之，矩阵的秩可以实现对全体矩阵的分类，这对进一步研究矩阵有着重要的意义。

第二章 矩阵的运算及与矩阵的秩ppt课件

第二章 矩阵的运算及与矩阵的秩ppt课件


钢笔 100 150
铅笔 300 260
.
§2.1 矩阵的基本运算
每种商品进货单价和销售单价（元）如下表：
圆珠笔 钢笔 铅笔
进货单价 6 9 3
销售单价 8 12 4
.
§2.1 矩阵的基本运算
求每个月的总进货额和总销售额。
金额 月份
总进货额
总销售额
九月 200×6+100×9+300×3 200×8+100×12+300×4
0 0 2 5
0 1 8
0
0 0
A1
A2
0 0 0 3 2 0
A3
0 0 0 0 0 9
.
二、分块矩阵的运算
§2.2 分块矩阵
1．分块矩阵相加、减
设A、B是两个用相同方法分块的同型矩阵
A11
设Amn
A21 M
A12 L A22 L MO
Ap1 Ap2 L
A1q
B11 B12 L
001 a 31 a 32 a 33 a 3 4 a 31 a 32 a 33 a 34
.
§2.1 矩阵的基本运算
1 0 0 0
a11 A(E 2,3)a21
a12 a22
a13 a23
a a1 24 40 0
0 1
1 0
0 0a a1 21 1
a13 a23
a12 a22
a14 a24
P 1 P 2LP sA Q 1 Q 2LQ tB
.
三、矩阵的转置
§2.1 矩阵的基本运算
定义2.3：把m×n矩阵A的行和列依次互换得到的一个 n×m 矩阵，称为A的转置，记作AT或A’.
3-4矩阵的秩

3-4矩阵的秩

向量组 α1 , α 2 ,L , α n 称为矩阵A的列向量组.
α1
α2
αj
αn
高等代数
类似地 , 矩阵A = (a ij )m×n 又有m 个n维行向量
a 11 a 21 M A= a i1 M a m1
a a a
12 22
M
i2
M
a
m2
L 2n M L a in M L a mn L
个线性无关的行向量， 是r个线性无关的行向量， 则该向量组的延伸组 个线性无关的行向量
(a11 , a21 ,L , ar 1 , ar +1,1 ,L , a s1 ),L ,(a1r , a2 r ,L , arr , ar +1,r ,L , a sr )
也线性无关． 于是矩阵A的列秩 也线性无关． 于是矩阵 的列秩 r1 ≥ r ． 同理可证 r1 ≤ r. 所以 r1 = r ．
高等代数
a11 0 A= L 0
a12 ′ a22 L ′ an 2
L L L L
a1n ′ a2 n = a11 L ′ ann
′ a22 L ′ an 2
L L L
′ a2 n L a′ nn
ai 1 ′ 其中 (0, ai′2 ,L , ain ) = α i − α1 , i = 2,L , n a11
a11 x1 + a12 x 2 + L + a1n xn = 0 a21 x1 + a22 x2 + L + a2 n xn = 0 LLLLLLLLLL = 0 a x + a x +L + a x = 0 r2 2 rn n r1 1
3§4 矩阵的秩

3§4 矩阵的秩

上页 下页 返回 结束
从而r(A)=列秩 < n . 若A的第一列的元素有一个不为零，不失一般性， ai1 a 0. 将第一行的( ) 倍加到第i行(2≤i≤n), 则 设 11 a11 从第二行直到第n行的第一个元素 a21 ,, an1全变为零 .
即得
a11 0 | A | 0 a12 a1n a2 n a22 a2 n a22 a11 2 ann an 2 ann an
2
n n个m维列向量
上页 下页 返回 结束
例如 矩阵
1 0 A 0 0
1
1 2 1 4 0 0 5 0 0 0 3
行向量组
1 (1,1,3,1), 2 (0, 2, 1, 4), 3 (0, 0, 0,5), 4 (0, 0, 0, 0).
上页
下页
返回
结束
先证 r r1.
设矩阵A的行向量组为1 , 2 ,, s , 不失一般性，
设1 , 2 ,, r 为它的一个极大线性无关组 . 因为1 , 2 ,, r 是线性无关的，所以方程
x11 x2 2 xr r 0
只有零解， 即
a11 x1 a21 x2 ar1 xr 0, a x a x a x 0, 12 1 22 2 r2 r a1n x1 a2 n x2 arn xr 0
2 ,, r 等价，故方程组（1）与方程组
a11 x1 a12 x2 a1n xn 0, a x a x a x 0, 21 1 22 2 2n n ar1 x1 ar 2 x2 arn xn 0

矩阵的秩4


同解,则对应齐次方程组AX=O的基础解系
(1)不存在
(2)仅含有一个非零向量
(3)含有两个非零向量 (4)含有三个非零向量
4.设向量 1 (1,2,0)T , 2 (1, a 2,3a)T ,
3 (1,b 2, a 2b)T 及 (1,3,3)T ,试讨论当a,b
为何值时,
, , (1) 不能由 1 2 2
2x1 x2 2x3 2x4 3
解
增广矩阵
1 3
2 1
3 5
1 3
1 2
2 1 2 2 3
1 2 3 1 1 1 2 3 1 1 0 5 4 0 1 0 5 4 0 1
0 5 4 0 1 0 0 0 0 2
上计算结果表明，增广矩阵的秩=3，而原方程组系数矩阵 A 的
若 A 经过有限次行的初等变换化为梯形矩阵 B，称 A、B 等价(equivalent)，记为 A~B。 性质：若 A~B，则 B~A；若 A~B，B~C，则 A~C。 定理 若 A~B，则 R(A)=R(B) 证明略。
所以，为求 R(A)，可将 A 先化为梯形矩阵，再计算 R(A)。
3 2 0 5 0
矩阵的秩及其性质
(The rank of matrixs and its properties)
定义 设矩阵Amn ，在其中任取 k 行和 k 列（k m, k n），位
于这些行、列交叉位置元素所构成的 k 级行列式叫做 A 的一个 k 阶子式 (k-order minor determinant)
x21
b11 b21
a11 a21
x12
a12 a22
x22
b12 b22
即B中的向量可以用A中向量表示。

矩阵的秩的求法

矩阵的秩的求法
矩阵秩是用来衡量矩阵行（列）列向量空间的维数，它也是描述矩阵线性变换能力的量，是矩阵分解的重要指标，它的求法有多种，主要有下面几种：
一、基本定义法：
秩（Rank）是一个矩阵中非零的最大线性无关列数，也就是说矩阵有n列向量，如果它们的线性组合能够得到任意的列向量，就称这n列向量线性无关，它们之间构成一种基，n就是该矩阵的秩。

二、行列式法
用行列式法求解矩阵秩，是把矩阵的秩定义为矩阵的行列式值的非零因子的个数，例如矩阵的行列式值是 = 31 + 42 + 53，那么矩阵的秩便是三个非零因子的个数。

三、矩阵初等行变换法
采用该法求解矩阵秩的目的是要把原矩阵变换为一个列向量极
简行阶梯形矩阵，然后该矩阵的秩就等于非零行的数量。

4-4向量组的秩

若记向量组 A : a1 , a2 ,, as ;
B : b1 , b2 ,, bt
若 B能由 A线性表示,即对每个向量 b j ( j 1, 2,, t )
存在数 k1 j , k2 j , ksj ,
使
b j k1 j a1 k2 j a2 ksj as k1 j k 2 j , ( j 1, 2,, t ) a1 , a2 ,, as ) （ k sj
T
关向量组表示.
分析 根据矩阵的初等变换不改变矩阵的秩而且行变 换不改变列向量之间的线性关系,利用初等行变换将 以 a1 , a2 , a3 , a4 , a5为列向量的矩阵化为行阶梯形,然 后在每一个阶梯中选取一个“元素”即构成此向量 组的一个最大无关组,同时求得向量组的秩.当阶梯形 化为 “最简形”时，还可直接得到其余向量用最大 无关组的线性表达式. 解 (1)以 a1 , a2 , a3 , a4 , a5 为列向量作矩阵A ,用初等行 变换将矩阵 A 化为行阶梯形
R( A, b j ) R( A)，
( j 1, 2,, t )
所以b j可由向量组A线性表示，
所以向量组B可由向量组A线性表示.
推论
向量组 A : a1 , a2 ,, am ; B : b1 , b2 ,, bs
等价的充分必要条件是 R( A) R( B) R( A, B) 其中A和 B 是向量组 A和向量组 B 所构成的矩 阵.




二. 向量组的最大无关组
已知向量组 T T T T 1＝ 1，0 ， 2＝ 0，1 , 3＝ 1，1 ， 4＝ 3，-4
1， 2 是线性无关的; 向量组中的任一个向量都可以由 1， 2 线性表示.

3-4矩阵的秩


（若(1)只有零解，则 r n. ）
§3.4 矩阵的秩
4/21
证：设矩阵 A 的行向量组 i (ai 1 , ai 2 ,, ain ), i 1,2,, s
的秩为r，且不妨设 1 , 2 ,, r为其一个极大无关组. 由于向量组1 , 2 ,, s 与向量组 1 , 2 ,, r 等价， 于是方程组(1)与方程组(1')是同解的.
线性相关
a11 a21 行列式 a n1 a11 a21 行列式 a n1
a12 a22 an 2 a12 a22 an 2

a1n a2 n 0. ann a1n a2 n 0. ann
线性无关
§3.4 矩阵的秩
16/21
k 级子式
定义
1 , 2 ,, n 线性相关 R( A) n.
§3.4 矩阵的秩
14/21
推论1
齐次线性方程组
a11 x1 a12 x 2 a1n xn 0 a21 x1 a22 x2 a2 n xn 0 a x a x a x 0 n2 2 nn n n1 1
中一定可以找到 r 个线性无关的向量. 不妨设
(a11 , a21 ,, ar 1 ,),(a12 , a22 ,, ar 2 ),,(a1r , a2 r ,, arr )
a
是r个线性无关的行向量， 则该向量组的延伸组
11
, a21 ,, ar1, ar 1,1,, as1 ,a1r , a2r ,, arr , ar 1,r ,, asr

sn
,
所以A有 r 个行向量线性无关，
a11 a12 a1n A1 a a a rn r1 r 2

线性代数2-4 矩阵的秩


5 2 3 1
A


4
0
1 6
1 2
7

3
取A的第1，2行 和2，4列
2 1 1 7
m n 矩阵 A的 k 阶子式共有 Cmk Cnk 个.
关于矩阵的秩，也可以这样定义：
第二章 矩阵与向量
矩阵A的不为零的子式的最高阶数，叫做矩阵A的秩. 可以证明，该定义与矩阵的秩的定义2.4.2是等价的.
1 0
1 1
0 0
3 1 0 0
2

r1 r2
~
0
1
0
1
2


B
0 0 1 1 0 0 1 1
容易看出，B的列向量1
,

2
,

3
,

间也有
4
线性关系4 1 22 3 .
实际上，如果把以上每作一次初等行变换
所得到的矩阵叫做B的话, B的列向量间同样 存在上述线性关系.
推论 初等行(列)变换不改变矩阵的列(行)秩.
第二章 矩阵与向量
定理2.4.1 初等行(列)变换不改变矩阵的行(列)秩. 定理2.4.2 初等行(列)变换不改变矩阵列(行)
向量间的线性关系. 推论 初等行(列)变换不改变矩阵的列(行)秩. 综上，矩阵的初等变换不改变矩阵的行秩与列秩。
第二章 矩阵与向量
第二章 矩阵与向量
定理2.4.1亦可作为初等变换不改变线性方程组中 独立方程的个数的理论依据
定理2.4.2 初等行(列)变换不改变矩阵列(行) 向量间的线性关系.
1 1 3 0 例32 设矩阵A 0 2 1 5 其列向量
6 0 2 4

第三章 矩阵的秩


Ax = b
b=0,齐次线性方程组 齐次线性方程组 b≠0,非齐次线性方程组 非齐次线性方程组
定理 1 线性方程组 = b有解⇔ r( A) = r( A| b). Ax 证明： 不妨设r(A)=r,利用初等行变换把增广 不妨设r(A)=r,利用初等行变换把增广 r(A)=r 初等行变换 矩阵化为行阶梯形 矩阵化为行阶梯形
推论2 推论2
当
m<n
时，齐次线性方程组
a11 x1 + a12 x2 +⋯+ a1n xn = 0 a21 x1 + a22 x2 +⋯+ a2n xn = 0 ⋯⋯⋯⋯⋯⋯ am1 x1 + am2 x2 +⋯+ amn xn = 0
必有非零解。 必有非零解。
1 A 矩阵， r A中必成立（） 例 已知 为m× n矩阵，且 ( A) = r，则 中必成立（）
丞相买鸡与不定方程 《张丘建算经》是我国南北朝时期写成的一本数 张丘建算经》 学书，距现在有1500多年了，里面共有 个问题， 多年了， 个问题， 学书，距现在有 多年了 里面共有92个问题 其中有一道著名的“百鸡问题” 其中有一道著名的“百鸡问题”： 今有鸡翁一，直钱五；鸡母一，直钱三； 今有鸡翁一，直钱五；鸡母一，直钱三； 鸡雏三，直钱一。凡百钱买鸡百只。 鸡雏三，直钱一。凡百钱买鸡百只。问鸡 母雏各几何？ 翁、母雏各几何？
(4)a = b = 0, r( A) = 0.
(1)a ≠ b且a + (n −1)b ≠ 0, r( A) = n.
对于m个方程 个未知数的线性方程组 对于 个方程n个未知数的线性方程组 个方程 a11 x1 + a12 x2 +⋯+ a1n xn = b1 a21 x1 + a22 x2 +⋯+ a2n xn = b2 ........................................... a x + a x +⋯+ a x = b m n n m m1 1 m2 2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
奇异矩阵为降秩矩阵.
Page 3
1 1 0 2 例如：矩阵 A 0 0 0 0 a1 (1,1, 3,1), a2
3 1 1 4 的行向量组是 0 5 0 0 (0, 2, -1, 4),
a3 (0, 0, 0, 5), a4 (0, 0, 0, 0) 可以证明 1 , 2 , 3 是A的行向量组的一个极大无关组.
只有零解，也就是方程个数s n . 因为任意n 1个n维向量线性相关，故A的行秩t n.
若t n，则A的行向量可由行极大无关组 Ai1 , Ai2 , L , Ait 线性表出，
则A可以通过一系列的初等行变换变化为
Page 11
Ai1 M B ， Ait 0 α 2 L xn αn 0
x1a11 x 2 a12 L xn a1n 0 x1a 21 x 2 a 22 L xn a 2n 0 或 L x1as1 x 2 as2 L xn asn 0
当A 0时，设rA r , A的列秩为p.由于A的秩为r ,
根据定义A中一定有一个非零r阶子式
而 4 为零向量，包含零向量的向量组线性相关，
1 , 2 , 3 , 4 线性相关。 所以向量组 1 , 2 , 3 , 4 的秩为3，
所以矩阵A的行秩为3。 矩阵A的列向量组是
1 1 3 1 0 2 1 4 1 , 2 , 3 , 4 0 0 0 5 0 0 0 0
二、矩阵秩的求法
引理
设矩阵A aij

s n
的列秩等于A的列数n，
则A的行秩、秩都等于n。
证明：对A进行列分块和行分块。
A1 A 2 A α1 ,α 2 , L ,α n ,A , M As
由于A的列秩＝n, A的列向量线性无关，即
则BX 0一定有非零解， 由于AX 0与BX 0是同解方程组， 所以AX 0也有非零解。
这与前面的结论矛盾，所以t n.
Page 12
Ai1 在A中可以找出一个n阶子式 M 0， Ain
而且它为阶数最高的子式，所以A的秩为n。
定理１ 矩阵的行秩、列秩、秩都相等。 证明 如果A＝0，则结论显然成立。
注： m n 矩阵 A 的 k 阶子式共有 C C 个.
k m k n
定义2
设在矩阵A中有一个不等于0的r阶子式D，
且所有r 1阶子式（如果存在的话）全等于0， 那末D称为矩阵A的最高阶非零子式，数r 称为矩 阵A的秩，记作R( A).并规定零矩阵的秩等于零.
Page 2
注： m n 矩阵A的秩R( A)是A中不等于零的子
式的最高阶数.
对于AT， 显然有R( AT ) R( A).
定义3 矩阵的行向量组的秩，称为矩阵的行秩; 矩阵的列向量组的秩，称为矩阵的列秩。
设 n 阶可逆矩阵 A， A 0,
A 的最高阶非零子式为 A , R( A) n, 故A的标准形为单位阵E ,A E .
可逆矩阵的秩等于阶数，故称可逆矩阵 为满秩矩阵.
Page 6
例1
1 2 3 求矩阵 A 2 3 5 的秩. 4 7 1
解
1 2 在 A 中， 0. 2 3
又 A的 3 阶子式只有一个 A，且 A 0，
R( A) 2.
Page 7
3 2 2 1 0 3 1 2 5 0 的秩. 例2 求矩阵 B 0 0 0 4 3 0 0 0 0 0
其非零行有3行， 解 B是一个行阶梯形矩阵，
B 的所有 4 阶子式全为零.
2 1 而0 0 3 0
3 2 0, 4
R( B ) 3.
Page 8
1 7 例３ 求矩阵A 2 6 的秩、行秩与列秩。 3 1 1 7 解：A的二阶子式d 0， 2 6
Page 5
可以验证1 , 2 , 4 线性无关，
7 1 而 3 1 2 0 4 2 2 所以向量组 1 , 2 , 3 , 4 的一个极大无关组是 1 , 2 , 4
所以向量组 1 , 2 , 3 , 4 的秩是3， 所以矩阵A的列秩是3。
A没有三阶子式，故rA 2 ；
1 7 又 0, , 线性无关， 2 6 2 6 添加分量得A的两个列向量线性无关，A的列秩＝２。 1 7
A的1,2行线性无关，三个2维行向量线性相关，
A的行秩 = 2，于是rA A的行秩 A的列秩 2 。 Page 9
§４.4 矩阵的秩
一、矩阵秩的概念
二、矩阵秩的求法 0011 0010 1010 1101 0001 0100 1011
三、矩阵与向量组秩的关系 四、小结
4
1
2
1
一、矩阵秩的概念
定义1 在m n矩阵A中任取k 行k列（k m , k n）,
位于这些行列交叉处的个k 2 元素, 不改变它们在A中 所处的位置次序而得的k阶行列式，称为矩阵A的 k阶子式.
因为，由 k11 k2 2 k3 3 0 即
k1 (1,1,3,1) k2 (0,2, 1,4) k3 (0,0,0,5) ( k1 , k1 2k2 ,3k1 k2 , k1 4k2 5k3 ) (0,0,0,0)
Page 4
可知 k1 k2 k3 0, 即 1 , 2 , 3 线性无关；