DX各种问题解决方法汇总

利用积分解决平面曲线面积问题的方法在数学中，平面曲线的面积问题是一个常见的难题。

然而，通过利用积分这一强大的数学工具，我们能够有效地解决这类问题。

本文将介绍利用积分来求解平面曲线面积的方法，帮助读者理解并掌握相关的数学知识。

一、求解平面曲线与 x 轴之间的面积首先，我们考虑最简单的情况，即求解平面曲线与x 轴之间的面积。

假设给定一条曲线 y = f(x)，我们希望计算曲线与 x 轴之间的面积。

为了实现这一目标，我们可以将该面积划分为无穷多个矩形，然后将这些矩形的面积相加，从而得到整个区域的面积。

具体而言，我们可以选择一个宽度趋近于零的矩形，其宽度为 dx，高度为曲线在该点上的函数值 f(x)。

因此，该矩形的面积可以表示为 dA = f(x)dx。

为了计算整个区域的面积，我们需要对矩形的面积进行积分。

因此，曲线与 x 轴之间的面积可以表示为：A = ∫f(x)dx这里的积分符号∫ 表示对 x 进行积分，A 表示所求得的面积。

二、求解平面曲线与 y 轴之间的面积接下来，我们来思考另一种情况，即求解平面曲线与 y 轴之间的面积。

假设给定一条曲线 x = g(y)，我们的目标是计算曲线与 y 轴之间的面积。

为了实现这一目标，我们可以采用与之前类似的方法。

我们将该面积划分为无穷多个矩形，并对其面积进行积分。

具体而言，在曲线 x =g(y) 上某一点 (g(y), y) 处，我们可以选择一个宽度为 dy、高度为曲线在该点上的函数值 g(y) 的矩形，其面积可以表示为 dA = g(y)dy。

整个区域的面积通过对矩形的面积进行积分得到，因此曲线与 y 轴之间的面积可以表示为：A = ∫g(y)dy这里的积分符号∫ 表示对 y 进行积分，A 表示所求得的面积。

三、求解两条曲线所围成的面积除了求解曲线与坐标轴之间的面积外，我们还可以利用积分来求解两条曲线所围成的面积。

假设给定两条曲线 y = f(x) 和 y = g(x)，我们希望计算这两条曲线所围成的面积。

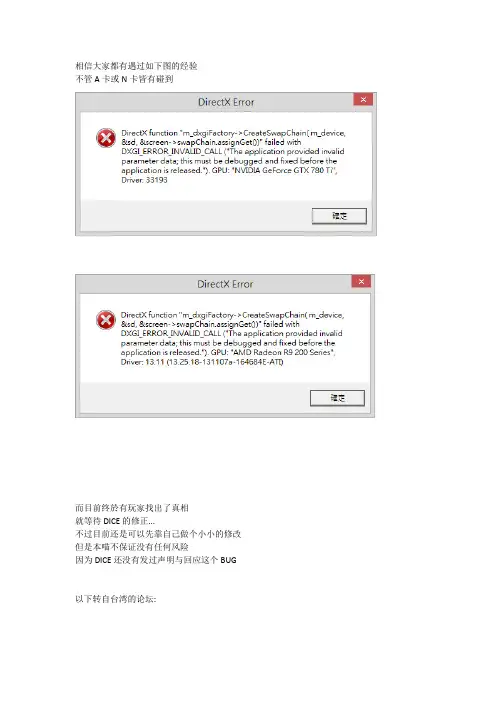
相信大家都有遇过如下图的经验不管A卡或N卡皆有碰到而目前终於有玩家找出了真相就等待DICE的修正...不过目前还是可以先靠自己做个小小的修改但是本喵不保证没有任何风险因为DICE还没有发过声明与回应这个BUG 以下转自台湾的论坛:英文原文(中文翻译在下面):Cause: The character string which displays 'Battlefield 4™' or 'Battlefield 3™' in BF4/BF3 client causes this problem. In other words, the character '™' causes confilcts between the character set in your system locale and those games.Solution: You can solve this problem by replacing the character '™' with the NULL character, which is in the string(s) in BF3.exe, BF4.exe, or BF4_x86.exe. You can use a hex editor to do this.1. By using a hex editor, open BF3.exe, BF4.exe, or BF4_x86.exe and then find the only one string (displayed as bunch of hex values) as below (I take the example of BF4.exe).42 61 74 74 6C 65 66 69 65 6C 64 20 34 99 00 (In BF3.exe, you have to find different strings of '42 61 74 74 6C 65 66 69 65 6C 64 20 33 99 00' at two places. You have to correct all the two strings, if you opened BF3.exe.)'99' -------> means '™'2. Correct '99' to '00' in that string. Then the string will be changed as below.42 61 74 74 6C 65 66 69 65 6C 64 20 34 00 00 (In BF3.exe, the two strings you corrected should be '42 61 74 74 6C 65 66 69 65 6C 64 20 33 00 00'. )3. Save what you opened and enjoy your Battlefield on Windows 8.1.简单翻译:主要原因是当启动程式时，战地风云4传送给Directx的名称是Battlefield 4™，而红字那个很小的TM在中文系统语言不支援，因此才导致出错。

导数隐零点问题处理的8大技巧(附30道经典题目)导数隐零点问题处理的8大技巧如下：1.分类讨论：对于含参数的零点问题，常常需要根据参数的不同取值范围进行分类讨论。

2.构造函数：利用导数研究函数的单调性，进而研究不等式恒成立问题。

3.分离参数：通过分离参数将参数与变量分开，转化为求最值问题。

4.数形结合：利用数形结合思想，将函数图像与x轴的交点问题转化为求函数的最值问题。

5.转化与化归：将复杂问题转化为简单问题，将陌生问题转化为熟悉问题。

6.构造法：通过构造新的函数或方程，将问题转化为已知的问题进行求解。

7.放缩法：通过对不等式进行放缩，将问题转化为易于处理的形式。

8.判别式法：通过引入判别式，将方程问题转化为二次方程的判别式问题。

以下是30道经典题目，以供练习：1.已知函数f(x)=x3−3x2+5，则f(x)的单调递增区间为( )A.(−∞,1)和(2,+∞)B.(−∞,−1)和(1,+∞)C.(−∞,−1)和(2,+∞)D.(−∞,2)和(1,+∞)2.已知函数f(x)=x3−3x2+5，则f(x)在区间[−2,3]上的最大值是____．3.已知函数f(x)=x3+ax2+bx+c在x=1和x=−21时取极值．(1)求a，b的值；(2)求函数极值．4. 已知函数f(x)=x3−3ax2+4，若x∈[0,2]时，f(x)的最大值为417，求实数a的取值范围．5. 已知函数f(x)=ln x−mx+m有唯一的零点，则实数m的取值范围是____．6. 已知函数 f(x) = x^3 - 3ax^2 + 3x + 1，若 x ∈ [0,1] 时，f(x) ≤ f(0) 恒成立，则 m 的取值范围是 _______．7. 已知函数 f(x) = ax^3 + bx^2 - 3x (a、b ∈ Z) 在 x = ±1 和x = ±2 时取极值．(1) 求 f(x) 的解析式；(2) 求 f(x) 的单调区间和极值；8. 已知函数 f(x) = x^3 + ax^2 + bx + c 在 x = ±1 和 x = ±3时取极值．(1) 求 a，b 的值；(2) 求 f(x) 的单调区间和极值．1.已知函数 f(x) = x^3 - 3x^2 + 4 在 [0,3] 上的最大值和最小值分别为 M, N，则 M + N = _______．2.设f(x)=x3−3x2+4，则f(−x)+f(x)的值等于____3.已知函数f(x)=x3−3x2+4，则f(x)在(−3,2)上的最大值是____．4.已知函数f(x)=x3−3x2+4，则f(x)在区间[−1,3]上的最大值是____．5.已知函数f(x)=x3−3ax2+bx+c在x=±1时取极值，且函数y=f(x)图象过原点．(1) 求函数y=f(x)的表达式；(2) 求函数的单调区间和极值；14. 已知函数 f(x) = x^3 - 3ax^2 + bx 在 x = -1 和 x = 3 时取极值．(1) 求 a，b 的值；(2) 求 f(x) 在区间 [-2,4] 上的最大值和最小值．15. 已知函数 f(x) = ax^3 + bx^2 + c 在 x = ±1 和 x = ±2 时取极值．(1) 求 a，b 的值；(2) 若 f(x) 的最大值为 8，求 c 的值．16. 已知函数 f(x) = ax^3 + bx^2 + c 在 x = ±1 和 x = ±√2 时取极值，且 f(-2) = -4．(1) 求 a，b，c 的值；(2) 求 f(x) 在区间 [-3,3] 上的最大值和最小值．17. 已知函数 f(x) = x^3 - 3ax^2 + b (a > 0)，若 f(x) 在区间[-1,0] 上是减函数，则 a 的取值范围是 _______．18. 若关于 x 的方程 x^3 - 3ax + a^3 = 0 有实根，则实数 a 的取值范围是 _______．19. 若关于 x 的方程 x^3 - ax^2 + b = 0 有三个不同的实根，则 a，b 应满足的条件是 _______．20. 若关于 x 的方程 x^3 - ax^2 + b = 0 有三个不同的实根，则 b应满足的条件是 _______．1.函数 f(x) = x^3 - 3x^2 + 4 在区间 [-1,3] 上的最大值和最小值分别为 _______．2.已知函数 f(x) = x^3 - 3x^2 + 4，若实数 x，y 满足 f(x) +3x^2 ≤ f(y) + 3y^2，则 x + y 的取值范围是 _______．3.已知函数 f(x) = x^3 - 3x^2 + 4，若实数 x，y 满足 f(x) ≤f(y) + 3，则 x + y 的取值范围是 _______．4.若关于 x 的方程 x^3 - ax^2 + b = 0 有三个不同的实根，则a，b 应满足的条件是 _______．5.已知函数 f(x) = x^3 - 3ax^2 + b 在 x = -1 和 x = 3 时取极值．(1) 求 a，b 的值；(2) 求 f(x) 在区间 [-3,3] 上的最大值和最小值．26. 若关于 x 的方程 x^3 - ax^2 + b = 0 有三个不同的实根，则 b 应满足的条件是 _______．27. 若关于 x 的方程 x^3 - ax^2 + b = 0 有两个不同的实根，则 a，b 应满足的条件是 _______．28. 若关于 x 的方程 x^3 - ax^2 + b = 0 有两个不同的实根，则 a，b 应满足的条件是 _______．29. 若关于 x 的方程 x^3 - ax^2 + b = 0 有两个相等的实根，则 a，b 应满足的条件是 _______．30. 若关于 x 的方程 x^3 - ax^2 + b = 0 有三个相等的实根，则 a，b 应满足的条件是 _______．。

不定积分题目技巧
不定积分题目技巧主要包括凑微分、利用基本公式、分段函数的不定积分和换元法的技巧等。

1. 凑微分：凑微分是解决不定积分问题的一种常用技巧。

通过观察被积函数的形式，尝试将其变形为微分的形式，从而简化积分过程。

2. 利用基本公式：熟练掌握不定积分的基本公式是解决不定积分问题的关键。

要能够熟练地运用基本公式，包括基本的微分公式、导数公式等。

3. 分段函数的不定积分：对于分段函数的不定积分问题，需要先分析分段函数的特性，再根据函数的特点选择适当的积分方法。

4. 换元法的技巧：换元法也是解决不定积分问题的一种重要技巧。

通过换元，可以将复杂的积分问题转化为简单的积分问题，从而简化计算过程。

掌握这些技巧，对于解决不定积分题目会有很大帮助。

同时，也要多做练习题，不断积累经验，提高自己的解题能力。

应用微积分解决实际问题微积分是数学中的一门重要学科，广泛应用于科学、工程以及经济学等领域。

它能够帮助我们解决各种实际问题，从物理学中的运动分析到经济学中的最优化，都离不开微积分的应用。

本文将探讨一些常见的实际问题，并通过微积分的方法进行解决。

一. 物体的运动分析在物理学中，微积分被用来研究物体的运动。

以一维运动为例，假设一个物体在时间t时刻的位置为x(t)，我们可以通过微积分求解物体的速度和加速度。

1. 速度：速度是物体位置随时间的变化率，即v(t) = dx(t)/dt。

通过微分计算，我们可以求解出速度函数v(t)。

2. 加速度：加速度是速度随时间的变化率，即a(t) = dv(t)/dt。

同样，通过微分计算，我们可以求解出加速度函数a(t)。

通过对速度和加速度的分析，我们可以得到物体运动的各种特性，比如最大速度、最大加速度等。

二. 经济学中的最优化问题微积分在经济学中也扮演着重要的角色。

许多经济现象都可以使用最优化问题来描述，通过微积分的方法，我们可以找到最优解。

1. 利润最大化问题：在市场经济中，一个企业的目标通常是追求利润最大化。

假设一个企业的成本函数为C(x)，收入函数为R(x)，则利润函数为P(x) = R(x) - C(x)。

我们可以通过微积分的方法，找到使利润函数取得最大值的产量水平x*。

2. 消费最优化问题：在经济学中，消费者通常追求利益最大化。

假设一个消费者的效用函数为U(x)，约束条件为消费者的收入不超过一定的限制B。

我们可以通过微积分的方法，找到消费者在给定收入限制下，使效用函数取得最大值的最优消费组合。

三. 物理学中的积分应用在物理学中，微积分的积分部分也有广泛的应用。

1. 曲线长度计算：如果我们需要计算一个曲线的长度，可以通过对曲线方程进行积分来得到结果。

假设曲线方程为y=f(x)，则曲线长度L可以表示为积分形式的定积分：L = ∫[a,b] √(1+(dy/dx)²)dx2. 质量中心计算：质量中心是一个物体在空间中的平衡点，可以通过对物体的质量分布进行积分来求解。

告诉你DirectX修复工具到底能解决什么问题DirectX修复工具从发布至今已经过去整整一年的时间了，通过大家的反馈及交流我发现有一部分人并不清楚DirectX修复工具到底可以解决什么问题。

虽说网上有众多网友的解释，但毕竟不是很全面，都只介绍了某一方面的应用。

因此，在这里，就由作者为大家全面地阐释一下本程序的用途。

本程序可以解决的问题。

No.1 应用程序无法正常启动(0xc000007b)。

请单击“确定”关闭应用程序。

修复时推荐使用版本：增强版解决概率：大于95%（使用V3.0及以上版本）由于本程序主要针对0xc000007b问题设计，因此把这一条放在了第一位。

从目前的反馈情况来看，使用增强版修复该问题时，解决概率可以达到95%以上（仅限使用V3.0及以上版本，使用低版本可能无法达到这个成功概率）。

至于剩下的5%之所以不能解决，是由于有些软件不仅需要DirectX的支持，还需要其他组件的支持，而这些组件异常导致的0xc000007b问题本程序无法解决。

还有很少的一部分人遇到了蓝屏问题，其提示代码为0x0000007b，这种情况通常都是由于硬盘设置造成的，因此本程序也无法解决。

No.2 无法启动此程序，因为计算机中丢失d3dx9_42.dll。

尝试重新安装该程序以解决此问题。

修复时推荐使用版本：增强版解决概率：大于99%这个问题是新系统普遍存在的问题。

不管是正版系统还是盗版系统由于默认都未包含DirectX相关组件，因此在首次运行大型游戏时普遍都会遇到这个问题。

由于造成这个问题的机理简单，解决办法简单，因此针对该问题的解决概率也较高。

除了标题中提到的d3dx9_42.dll文件外，类似的还有以下这些文件。

注意，本程序只能解决在以下列表中包含的文件所遇到的问题：d3dcompiler_33.dll、d3dcompiler_34.dll、d3dcompiler_35.dll、d3dcompiler_36.dll、d3dcompiler_37.dll、d3dcompiler_38.dll、d3dcompiler_39.dll、d3dcompiler_40.dll、d3dcompiler_41.dll、d3dcompiler_42.dll、d3dcompiler_43.dll、d3dcsx_42.dll、d3dcsx_43.dll、d3dx9_24.dll、d3dx9_25.dll、d3dx9_26.dll、d3dx9_27.dll、d3dx9_28.dll、d3dx9_29.dll、d3dx9_30.dll、d3dx9_31.dll、d3dx9_32.dll、d3dx9_33.dll、d3dx9_34.dll、d3dx9_35.dll、d3dx9_36.dll、d3dx9_37.dll、d3dx9_38.dll、d3dx9_39.dll、d3dx9_40.dll、d3dx9_41.dll、d3dx9_42.dll、d3dx9_43.dll、d3dx10.dll、d3dx10_33.dll、d3dx10_34.dll、d3dx10_35.dll、d3dx10_36.dll、d3dx10_37.dll、d3dx10_38.dll、d3dx10_39.dll、d3dx10_40.dll、d3dx10_41.dll、d3dx10_42.dll、d3dx10_43.dll、d3dx11_42.dll、d3dx11_43.dll、X3DAudio1_0.dll、X3DAudio1_1.dll、X3DAudio1_2.dll、X3DAudio1_3.dll、X3DAudio1_4.dll、X3DAudio1_5.dll、X3DAudio1_6.dll、X3DAudio1_7.dll、xactengine2_0.dll、xactengine2_1.dll、xactengine2_2.dll、xactengine2_3.dll、xactengine2_4.dll、xactengine2_5.dll、xactengine2_6.dll、xactengine2_7.dll、xactengine2_8.dll、xactengine2_9.dll、xactengine2_10.dll、xactengine3_0.dll、xactengine3_1.dll、xactengine3_2.dll、xactengine3_3.dll、xactengine3_4.dll、xactengine3_5.dll、xactengine3_6.dll、xactengine3_7.dll、XAPOFX1_0.dll、XAPOFX1_1.dll、XAPOFX1_2.dll、XAPOFX1_3.dll、XAPOFX1_4.dll、XAPOFX1_5.dll、XAudio2_0.dll、XAudio2_1.dll、XAudio2_2.dll、XAudio2_3.dll、XAudio2_4.dll、XAudio2_5.dll、XAudio2_6.dll、XAudio2_7.dll、xinput1_1.dll、xinput1_2.dll、xinput1_3.dll、xinput9_1_0.dll(WindowsXP)、atl100.dll、mfc100.dll、mfc100chs.dll、mfc100cht.dll、mfc100deu.dll、mfc100enu.dll、mfc100esn.dll、mfc100fra.dll、mfc100ita.dll、mfc100jpn.dll、mfc100kor.dll、mfc100rus.dll、mfc100u.dll、mfcm100.dll、mfcm100u.dll、msvcp100.dll、msvcr100.dll、vcomp100.dll、atl110.dll、mfc110.dll、mfc110chs.dll、mfc110cht.dll、mfc110deu.dll、mfc110enu.dll、mfc110esn.dll、mfc110fra.dll、mfc110ita.dll、mfc110jpn.dll、mfc110kor.dll、mfc110rus.dll、mfc110u.dll、mfcm110.dll、mfcm110u.dll、msvcp110.dll、msvcr110.dll、vccorlib110.dll、vcamp110.dll、vcomp110.dll、MSVCRTD.dll、mfc120.dll、mfc120chs.dll、mfc120cht.dll、mfc120deu.dll、mfc120enu.dll、mfc120esn.dll、mfc120fra.dll、mfc120ita.dll、mfc120jpn.dll、mfc120kor.dll、mfc120rus.dll、mfc120u.dll、mfcm120.dll、mfcm120u.dll、msvcp120.dll、msvcr120.dll、vccorlib120.dll、vcamp120.dll、vcomp120.dllNo.3 C:\Windows\system32\d3dx9_42.dll没有被指定在Windows上运行，或者它包含错误。

考研高数必背微分方程初值问题的求解方法微分方程初值问题是高等数学中的重要内容，在考研高数中也是一个必备的知识点。

解决微分方程的初值问题可以帮助我们找到函数的特定解，为后续的计算和分析提供基础。

本文将介绍几种常见的求解微分方程初值问题的方法，帮助考生掌握这一知识点。

方法一：分离变量法分离变量法是求解微分方程中常见的一种方法，适用于一阶常微分方程。

其基本思想是将微分方程中的变量分开后，逐个求解。

下面以一个具体的例子来说明分离变量法的具体步骤。

例题：求解微分方程 dy/dx = x/y, y(0) = 1 的特解。

解答：将变量分离得到 y dy = x dx，然后对方程两边同时积分，得到∫dy/y = ∫xdx。

分别求解这两个积分，得到ln|y| = 1/2*x^2 + C1，再两边取指数得到 |y| = e^(1/2*x^2 + C1)。

利用初值条件 y(0) = 1，得到 C1 = 0，因此特解为 y = e^(1/2*x^2)。

方法二：常系数线性齐次微分方程的求解常系数线性齐次微分方程是一类特殊的微分方程，具有形如dy/dx + Py = 0 的特点。

其中，P表示常系数。

这类微分方程的初值问题可以通过特征方程来求解。

例题：求解微分方程 dy/dx + 2y = 0, y(0) = 1 的特解。

解答：首先根据方程的形式可知，这是一个常系数线性齐次微分方程。

它的特征方程为 r + 2 = 0，解得 r = -2。

由于根为实数且不相等，所以特解可以写为 y = C*e^(-2x)，其中C为待定系数。

利用初值条件y(0) = 1，得到 C = 1，因此特解为 y = e^(-2x)。

方法三：二阶线性非齐次微分方程的求解二阶线性非齐次微分方程是一类常见的微分方程，具有形如d^2y/dx^2 + P(x)dy/dx + Q(x)y = f(x) 的特点。

其中，P(x)、Q(x)和f(x)分别表示一阶导数、常数和非齐次项。

dxdvr行车记录仪说明书篇一：dxdvr行车记录仪说明书本说明书适用于使用Dxdvr行车记录仪的用户。

本说明书将介绍Dxdvr行车记录仪的基本信息,包括安装和使用,以及常见问题和解决方法。

1. 安装安装Dxdvr行车记录仪时,请确保将机器放在稳定、安全的地方。

为了避免机器受损,请确保机器与电源、网络和电视连接正确。

安装完成后,将Dxdvr行车记录仪放置在需要记录的位置,并调整机器角度和高度以确保图像清晰。

2. 使用使用Dxdvr行车记录仪时,请按照机器上的说明操作。

如果不确定如何操作,请查看机器上的手册或联系Dxdvr技术支持。

3. 设置在安装Dxdvr行车记录仪后,可以进入设置菜单进行设置。

在设置菜单中,可以调整图像分辨率、速度、定时器、声音等选项。

还可以更改机器的位置和角度,以获得最佳图像效果。

4. 常见问题在使用Dxdvr行车记录仪时,可能会出现一些问题。

以下是一些常见问题及其解决方法:- 图像模糊:可能是由于图像分辨率或机器角度不正确导致的。

请检查机器设置是否正确,并调整机器角度和高度。

- 视频不连续:可能是由于视频速度不正确或网络连接问题导致的。

请检查网络连接是否正常,并尝试调整视频速度。

- 声音不同步:可能是由于机器设置不正确或网络连接问题导致的。

请检查机器设置是否正确,并尝试调整网络连接。

5. 维护为了维护Dxdvr行车记录仪的性能,请定期清洁机器。

如果机器出现任何问题,请联系Dxdvr技术支持。

篇二：dxdvr行车记录仪说明书本说明书适用于使用Dxdvr行车记录仪的用户。

目录:1. 简介2. 安装与设置3. 拍摄功能4. 存储功能5. 电源与电池6. 操作说明1. 简介Dxdvr行车记录仪是一种专门用于记录行车过程的电子设备,可以实时记录车辆行进过程中的视频和音频信息,并将这些数据存储在SD卡或其他存储设备中。

该设备通常具有多个摄像头,用于捕捉不同的场景,例如前方、侧面和后方。

如何用积分解决面积和体积问题积分方法在解决面积和体积问题中具有重要作用。

积分是一种数学工具，可以帮助我们计算曲线下的面积或者曲线围成的图形的体积。

本文将介绍如何使用积分来解决面积和体积问题。

一、解决面积问题在解决面积问题中，我们经常需要计算曲线与坐标轴围成的曲边梯形、曲边三角形或者曲线与直线围成的图形的面积。

下面将以曲边梯形为例，介绍如何使用积分来计算其面积。

假设曲边梯形的上底为y=f(x)，下底为y=g(x)，宽度为dx。

那么，曲边梯形面积的微小元素可以表示为dA=(f(x)-g(x))dx。

我们可以将整个曲边梯形划分成无穷多个微小元素，然后对这些微小元素进行求和，即可得到曲边梯形的面积。

使用积分符号来表示求和的过程，我们可以得到曲边梯形的面积公式：A = ∫[a,b] (f(x) - g(x)) dx其中，[a,b]表示积分的区间，f(x)和g(x)分别为曲边梯形的上底和下底函数。

通过求解上述积分，可以准确计算出曲边梯形的面积。

同样的方法，我们也可以计算其他类型的面积，例如曲边三角形或者曲线与直线围成的图形，只需要根据具体情况调整积分的上下限和积分函数。

二、解决体积问题在解决体积问题中，积分同样可以帮助我们计算曲线围成的立体图形的体积。

下面将以旋转曲线为例，介绍如何使用积分来计算其围成的旋转体的体积。

假设曲线y=f(x)在区间[a,b]上旋转一周，我们可以得到一个旋转体。

该旋转体的截面是一个圆，其面积可以表示为dA=πy²dx。

我们可以将整个旋转体划分成无穷多个微小元素，然后对这些微小元素进行求和，即可得到旋转体的体积。

使用积分符号来表示求和的过程，我们可以得到旋转体的体积公式：V = ∫[a,b] πf(x)² dx其中，[a,b]表示积分的区间，f(x)为旋转曲线的函数。

通过求解上述积分，可以获得旋转体的准确体积。

除了旋转曲线，我们还可以使用积分来计算其他类型的立体图形的体积，例如通过平移或者放缩变换所得的图形。

某市部分站点PDU建立概率性失败问题反馈【摘要】随着5G网络的快速发展，SA网络商用迫在眉睫，在SA组网结构网络建网初期，经常会遇到很多接入、切换等问题，本次反馈一个PDU建立概率性失败问题。

【关键字】SA网络PDU SESSION ESTABLISHMENT REJECT【业务类别】数据业务1、问题背景按照集团的指标定义方式：空闲态UE对FTP服务器发起PING业务，终端发出第一条RACH preamble至终端发出RRC Connection Reconfiguration Complete的时间差记为接入时延差。

验收标准：对于NR接入时延，当5GC为本省部署时，按照120ms进行验收；当5GC 控制面为大区制非本省部署时，按照280ms进行验收；图1-1：UU口跟踪信令图跟踪信令发现RRC建立时延在700ms左右，无法达标，单验要求在当5GC为本省部署时，按照120ms为达标标准。

2、问题分析图2-1：前台LOG记录图从LOG可以看出，终端收到RRC建立请求后，终端仅3ms后就向基站回复RRC建立消息。

图2-2：UU口信令跟踪截图跟踪信令发现RRC建立时延在700ms左右。

从L3启动RRC_SETUP到L1将消息发送给UE内部会有很多流程要处理，也需要申请一些资源，比较核心资源就是需要申请PDCCH资源(包括PUCCH和PDCCH资源)图2-3：信令流程图图2-4：CELL DT信令跟踪分析图在CELLTD537跟踪中看到大量出现公共信道REG资源调度不出来的情况，因此怀疑是PDCCH资源分配不出来。

分析配置发现该站点开通了PDCC_RATEMATCH功能，且配置的PDCCH资源较少，属于极限峰值配置场景：MOD NRDUCELLPDCCH: NrDuCellId=1, UlMaxCcePct=50, OccupiedRbNum=2;MOD NRDUCELLPDSCH: NrDuCellId=1, RateMatchSwitch=PDCCH_RATEMATCH_SW-1;而且设置的RBNUM是2(单位是12RB)，对应的只有4个CCE资源(上下行各占50%)，下行CCE资源只有2个，当前版本调度需要的CCE的最小单位就是2个，这些CCE资源不足有且只能满足一个用户接入，当已经有一个用户占用了CCE资源就会导致当前用户接入不了，除非等上个用户释放了所占用的下行CCE资源之后，该用户在近点才能重新接入。

DX局点系统频点优先级组漏配导致EPSFB失败
关键字：系统频点优先级组、EPSFB
【问题描述】
DX某局点SA商用网络，收到用户投诉，局部区域5G语音失败，呼入或呼出均有很大概率失败。

11月9日12时，通过重刷开站脚本解决，客户要求具体定位该问题原因。

【问题分析】
处理前，到达用户投诉所在5G基站，现场复现问题，100%复现，当切换至周边其他站点时语音业务恢复正常。

从测试log看，终端发送完invite消息之后，核心网下发503服务不可用导致EPSFB失败，期间基站未下发B1测控。

分析CHR日志，AMF触发了5QI1的建立，基站也回复了拒绝5QI1建立的响应，但是携带原因值是4G频点不支持。

查看话统，11月9日12点修改参数之前从未触发过EPSFB。

查看原配置文件，发现未配置4G频点组，导致基站无法触发EPSFB。

【问题根因】
11月9号12点之前EPSFB失败的主要原因为基站未配置4G频点组GNBFREQPRIORITYGROUP，导致基站无法下发4G B1测量，从而无法触发EPSFB。

12点之后添加完4G频点组GNBFREQPRIORITYGROUP之后，EPSFB正常触发。

【解决方案】
系统频点优先级组GNBFREQPRIORITYGROUP添加完善的4G频点信息。

【优化效果】
系统频点优先级组GNBFREQPRIORITYGROUP添加4G频点后，现场复测EPSFB业务正常。

算式的应用之积分问题解决积分的算式在数学中，积分是解决积分问题的一种重要方法。

它允许我们计算函数曲线下的面积、求解定积分、求解微分方程等多种应用。

本文将探讨一些常见的积分问题，并介绍如何解决这些问题。

一、定积分的计算定积分是积分中最基本的概念之一。

我们可以利用定积分来计算给定区间上函数曲线下的面积。

定积分的计算可以通过求解不定积分来实现。

以求取函数f(x)在区间[a, b]上的定积分为例。

我们可以首先求解f(x)的不定积分F(x)，然后分别计算F(x)在区间[a, b]两个端点的取值F(a)和F(b)，最后计算两者之差F(b) - F(a)即可得到定积分的值。

例如，要计算函数f(x) = x^2在区间[0, 1]上的定积分，我们可以先求解不定积分F(x) = (1/3)x^3，然后计算F(1) - F(0) = 1/3，即可得到定积分的值为1/3。

二、面积计算问题积分还可以用来计算函数曲线下的面积。

对于给定的函数f(x)和区间[a, b]，我们可以利用积分的性质计算函数曲线与x轴之间的面积。

具体做法是首先确定函数f(x)与x轴之间的正部分和负部分，然后计算这两部分的积分值的绝对值之和。

最后，用正部分的积分值减去负部分的积分值，即可得到函数曲线与x轴之间的面积。

举例来说，要计算函数f(x) = x在区间[0, 1]上的面积，我们可以将其分为两部分，一部分是f(x)在区间[0, 1]上的正部分，另一部分是f(x)在区间[0, 1]上的负部分。

根据函数图像可以看出，f(x)在[0, 1]上的正部分面积为1/2，负部分面积为0。

因此，函数f(x)在[0, 1]上的面积为1/2。

三、微分方程的求解积分在解决微分方程问题时也起着重要的作用。

微分方程是描述函数与其导数之间关系的方程。

利用积分可以将微分方程转化为更容易求解的形式，从而找到函数的解析解。

例如，考虑一阶线性非齐次微分方程形式为dy/dx + p(x)y = g(x)，其中p(x)和g(x)是已知函数。

三角函数的微分计算与最值问题解答三角函数是数学中的重要概念，它在解决各种问题中起到了关键作用。

在本文中，我们将探讨三角函数的微分计算以及最值问题的解答，并提供相应的示例和解析。

一、三角函数的微分计算在微积分中，我们经常需要计算三角函数的微分，以便求解相关问题。

下面是常见的三角函数及其微分公式：1. 正弦函数（sin(x)）的微分公式：d/dx[sin(x)] = cos(x)2. 余弦函数（cos(x)）的微分公式：d/dx[cos(x)] = -sin(x)3. 正切函数（tan(x)）的微分公式：d/dx[tan(x)] = sec^2(x)这些微分公式是我们计算三角函数微分的基础，可以根据具体问题进行灵活运用。

二、最值问题的解答在实际问题中，我们经常需要求解三角函数的最值，以确定最优解或者边界条件。

下面是最常见的三角函数最值问题：1. 求解正弦函数的最大值和最小值：对于正弦函数sin(x)，它的最大值为1，最小值为-1。

在定义域内，正弦函数的取值范围位于闭区间[-1, 1]之间。

2. 求解余弦函数的最大值和最小值：对于余弦函数cos(x)，它的最大值为1，最小值为-1。

和正弦函数一样，余弦函数的取值范围也位于闭区间[-1, 1]之间。

3. 求解正切函数的最大值和最小值：对于正切函数tan(x)，它在某些点上没有最大值和最小值。

但是在定义域内，正切函数的取值范围是整个实数集。

以上是最常见的三角函数最值问题，根据具体问题的要求和条件，我们可以运用数学方法求解最优解或边界条件。

三、示例与解析为了更好地理解三角函数的微分计算与最值问题的解答，我们提供以下示例：1. 示例一：求解函数y = sin(x)的导数和最大值解析：根据微分公式，导数d/dx[sin(x)] = cos(x)。

然后，求解导数为0的解，即cos(x) = 0，可知x = π/2。

进一步，代入原函数，可以求得y = sin(π/2) = 1，即函数y = sin(x)的最大值为1。

directx功能不可用DirectX是由微软公司开发的一套多媒体应用程序接口（API），用于在Microsoft Windows操作系统上实现高性能的图形和音频处理。

DirectX功能的不可用可能会导致在Windows平台上无法正常运行基于DirectX的游戏和应用程序。

出现DirectX功能不可用的情况可能有多种原因。

以下是一些常见的问题和解决方法：1. DirectX版本不匹配：某些游戏或应用程序可能需要特定版本的DirectX才能正常运行。

如果您的系统中安装的DirectX版本不兼容，可能会导致功能不可用。

解决方法是升级或重新安装最新版本的DirectX。

2. 显卡驱动过期：显卡驱动程序是用于控制和优化显卡性能的软件。

如果显卡驱动程序过期，可能会导致DirectX功能不可用。

解决方法是从显卡制造商的官方网站上下载并安装最新的显卡驱动程序。

3. 硬件不支持：某些较旧或低端的显卡、声卡或其他硬件设备可能不支持某些DirectX功能。

在购买或升级硬件之前，应该仔细检查硬件的规格和要求，以确保其兼容性。

4. 病毒或恶意软件感染：有时，计算机上的病毒或恶意软件可能会破坏或修改DirectX相关文件，导致功能不可用。

解决方法是使用可靠的杀毒软件进行全面的系统扫描和清理。

5. 计算机配置不足：某些高级的DirectX功能可能需要更强大的计算机配置才能完全支持。

如果您的计算机配置较低，您可能需要升级硬件或调整游戏或应用程序的图形和音频设置。

总之，当出现DirectX功能不可用的问题时，您应该首先检查和更新DirectX版本、显卡驱动程序和系统安全状况。

如果问题仍然存在，您可以考虑升级硬件或调整计算机配置来提高DirectX功能的兼容性和性能。

另外，您还可以与游戏或应用程序的开发者或技术支持团队联系，以获取更专业的帮助和解决方案。

注塑件常见品质问题及原因分析、解决方法一、注塑件常见品质问题塑胶件成型后，与预定的质量标准（检验标准）有一定的差异，而不能满足下工序要求，这就是塑胶件缺陷，即常说的品质问题，要研究这些缺陷产生原因，并将其降至最低程度，总体来说，这些缺陷不外乎是由如下几方面造成：模具、原材料、工艺参数、设备、环境、人员。

现将缺陷问题总结如下：1、色差：注塑件颜色与该单标准色样用肉眼观看有差异，判为色差，在标准的光源下（D65）。

2、填充不足（缺胶）：注塑件不饱满，出现气泡、空隙、缩孔等，与标准样板不符称为缺胶。

3、翘曲变形：塑胶件形状在塑件脱模后或稍后一段时间内产生旋转和扭曲现象，如有直边朝里，或朝外变曲或平坦部分有起伏，如产品脚不平等与原模具设计有差异称为变形，有局部和整体变形之分。

4、熔接痕（纹）：在塑胶件表面的线状痕迹，由塑胶在模具内汇合在一起所形成, 而熔体在其交汇处未完全熔合在一起，彼此不能熔为一体即产生熔接纹，多表现为一直线，由深向浅发展，此现象对外观和力学性能有一定影响。

5、波纹：注塑件表面有螺旋状或云雾状的波形凹凸不平的表征现象，或透明产品的里面有波状纹，称为波纹。

6、溢边（飞边、披锋）：在注塑件四周沿分型线的地方或模具密封面出现薄薄的（飞边）胶料，称为溢边。

7、银丝纹：注塑件表面的很长的、针状银白色如霜一般的细纹，开口方向沿着料流方向，在塑件未完全充满的地方，流体前端较粗糙，称为银丝纹（银纹）。

8、色泽不均（混色）：注塑件表面的色泽不是均一的，有深浅和不同色相，称为混色9、光泽不良（暗色）：注塑件表面为灰暗无光或光泽不均匀称为暗色或光泽不良。

10、脱模不良（脱模变形）：与翘曲变形相似，注塑件成型后不能顺利的从模具中脱出，有变形、拉裂、拉伤等、称为脱模不良。

11、裂纹及破裂：塑胶件表面出现空隙的裂纹和由此形成的破损现象。

12、糊斑（烧焦）：在塑件的表面或内部出现许多暗黑色的条纹或黑点，称为糊斑或烧焦。

dx7导航刷机教程摘要：一、前言二、准备工作1.下载刷机工具2.下载导航数据包三、刷机步骤1.连接设备2.打开刷机工具3.选择刷机模式4.导入导航数据包5.开始刷机6.刷机完成四、常见问题及解决方法五、结语正文：一、前言本文将详细介绍dx7 导航刷机教程，帮助用户轻松完成刷机操作。

在刷机前，请确保设备连接正常，并备份好重要数据。

二、准备工作1.下载刷机工具：首先，请从官方网站或可靠渠道下载dx7 导航刷机工具。

2.下载导航数据包：同样，需要下载适用于dx7 设备的导航数据包，以保证刷机后的导航功能正常使用。

三、刷机步骤1.连接设备：将dx7 导航设备通过USB 数据线连接至电脑。

2.打开刷机工具：双击下载好的刷机工具，启动刷机程序。

3.选择刷机模式：在刷机工具界面中，选择“更新模式”或“恢复模式”，根据个人需求进行选择。

4.导入导航数据包：点击“浏览”按钮，选择下载好的导航数据包，将其导入刷机工具。

5.开始刷机：点击“开始刷机”按钮，刷机程序将自动进行刷机操作。

6.刷机完成：刷机成功后，设备会自动重启。

此时，刷机过程已全部完成。

四、常见问题及解决方法1.刷机过程中出现异常中断：请检查设备连接是否正常，或重新启动刷机工具后再次尝试。

2.刷机后导航功能无法使用：请检查是否正确导入导航数据包，或重新刷机。

3.设备无法开机：请尝试重新连接设备，或联系售后服务。

五、结语通过以上教程，相信你已经掌握了dx7 导航刷机的方法。

在刷机过程中，请务必耐心操作，并注意观察设备反应，避免因操作不当导致设备损坏。

如遇到问题，请及时与售后服务联系。