光在球面上反射和折射

§1.4、光在球面上的反射与折射1.4.1、球面镜成像<1）球面镜的焦距球面镜的反射仍遵从反射定律，法线是球面的半径。

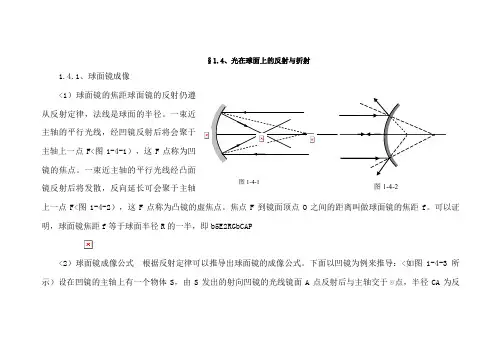
一束近主轴的平行光线，经凹镜反射后将会聚于主轴上一点F<图1-4-1），这F 点称为凹镜的焦点。

一束近主轴的平行光线经凸面镜反射后将发散，反向延长可会聚于主轴上一点F<图1-4-2），这F 点称为凸镜的虚焦点。

焦点F 到镜面顶点O 之间的距离叫做球面镜的焦距f 。

可以证明，球面镜焦距f 等于球面半径R 的一半，即b5E2RGbCAP<2）球面镜成像公式 根据反射定律可以推导出球面镜的成像公式。

下面以凹镜为例来推导：<如图1-4-3所示）设在凹镜的主轴上有一个物体S ，由S 发出的射向凹镜的光线镜面A 点反射后与主轴交于点，半径CA为反图1-4-1图1-4-2射的法线，即S的像。

根据反射定律，，则CA为角A的平分线，根据角平分线的性质有p1EanqFDPw①由为SA为近轴光线，所以，，①式可改写为②②式中OS叫物距u，叫像距v，设凹镜焦距为f，则代入①式化简这个公式同样适用于凸镜。

使用球面镜的成像公式时要注意：凹镜焦距f取正，凸镜焦距f取负；实物u取正，虚物u取负；实像v为正，虚像v为负。

DXDiTa9E3d上式是球面镜成像公式。

它适用于凹面镜成像和凸面镜成像，各量符号遵循“实取正，虚取负”的原则。

凸面镜的焦点是虚的，因此焦距为负值。

在成像中，像长和物长h之比为成像放大率，用m表示，RTCrpUDGiT由成像公式和放大率关系式可以讨论球面镜成像情况，对于凹镜，如表Ⅰ所列；对于凸镜，如表Ⅱ所列。

表Ⅰ 凹镜成像情况～2f表Ⅱ 凸镜成像情况～～2f同侧～<3）球面镜多次成像 球面镜多次成像原则：只要多次运用球面镜成像公式即可，但有时前一个球面镜反射的光线尚未成像便又遇上了后一个球面镜，此时就要引进虚像的概念。

5PCzVD7HxA 如图1-4-4所示，半径为R 的凸镜和凹镜主轴相互重合放置，两镜顶点O1 、 O2 相距2.6R ，现于主轴上距凹镜顶点O1为0.6R 处放一点光源S 。

§3-5 光在球面上的反射和折射单独一个球面不仅是一个简单的光学系统，而且是组成光学仪器的基本元件，研究光经由球面的反射和折射，是一般光学系统成象的基础。

一、符号法则为了研究光线经由球面反射和折射后的光路，必须先说明一些概念以及规定一些适当的符号法则，以便使所得的结果能普遍适用。

(图3－12)图3-12中的AOB 所示球面的一部分，这部分球面的中心点O 称为顶点，球面的球心C 称为曲率中心，球面的半径称为曲率半径，连接顶点的曲率中心的直线CO 称为主轴，通过主轴的平面称为主截面，主轴对于所有的主截面具有对称性，因而我们只须讨论一个主截面内光线的反射。

图3-12表示球面的一个主截面。

在计算任一条光线的线段长度和角度时，我们对符号作如下规定。

（1）光线和主轴交点的位置都从顶点算起，凡在顶点右方者，其间距离的数值为正；凡在顶点左方者，其间距离的数值为负，物点或象点至主轴的距离，在主轴上方为正，在下方为负。

（2）光线方向的倾斜角度都从主轴（或球面法线）算起，并取小于2π的角度，由主轴（或球面法线）转向有关光线时，若沿顺时针方向转，则该角度的数值为正；若沿逆时针方向转动的，则该角度的数值为负（在考虑角度的符号时，不必考虑组成该角度两边的线段的符号）。

（3）在图中出现的长度和角度（几何量）只用正值，例如s 表示的某线段值是负的，则应用()s -来表示该线值的几何长度。

以下讨论的都是假定光线自左向右进行。

二、球面反射对光束单心性的破坏在图3-12中，一个从点光源P 发出的光波从左向右入射到曲率中心为C ，顶点为O ，曲率半径为γ的一个凹球面镜上，光线PA 经球面镜AOB 反射后，在'P 点与主轴相交，令 '',,'',ττ==-=-=AP PA s O P s PO半径AC 与主轴的夹角为ϕ，则光线'PAP 的光程为 (')'P A P n n ττ=+ 在PAC ∆和'ACP ∆中应用余弦定理，并注意c o s c o s ()()()'()(')',P C sr r s C P r s s r ϕπϕ=--=---=-=---=- 从而可得()()()()[]2122cos 2ϕs r r s r r l --+-+-=（3-10）以及()()()()[]2122'cos '2'ϕr s r r s r l ----+-= （3-11）因此，光线'PAP 的光程可写成12221222(')()()2()()cos ()(')2()(')cos PAP n r r s r r s n r s r r s r ϕϕ⎡⎤=-+-+--⎣⎦⎡⎤+-+----⎣⎦（3－12）由于当A 点在镜面上移动时，半径r 是常数，而ϕ才是位置的变量，根据费马原理，物象间的光程应取稳定值，为此，把（3-12）式对ϕ求导，并令其等于零，即()()[]()[]0sin '21sin 21''=-+--=ϕϕϕr s r ln s r r l n d PAP d 由此可得 0''=---l rs l s r 或者⎪⎭⎫⎝⎛+=+l s l s r l l ''111'（3-13） 如果发光点P 至O 点的距离s 为已知，从此式即可算出任一反射线和主轴的交点'P 到 O 点的距离's 的值，显然's 的值将随着所取入射线的倾斜角u ，亦即角ϕ的变化而变化，这就是说，从物点发散的单心光束经球面反射后，将不再保持单心（即使平等光束入射时也不例外），关于这一点可说明如下：PC A 1A 2OP 2P'P 3 (图3－13)图3-13中，相应于1PA 及2PA 两入射光线的反射线分别交主轴于1P 和2P 两点，且相交于'P 点，把该图绕主轴PO 转过一个小角度，使三角形12PA A 展成一单心的空间光束，此时'P 点描出一条很短的弧线，它垂直于图面即反射光束的子午象线，而图面中的12PP 则为弧矢象线。

什么是光的反射和折射光的反射和折射是物理学中的基本概念，涉及到光在不同介质中传播时的现象。

下面将分别对光的反射和折射进行详细的介绍。

一、光的反射光的反射是指光线在传播过程中遇到障碍物被反射出去的现象。

光线传播到两种不同介质的表面上时，会发生反射现象。

例如，光线传播到平面镜、球面镜等光滑的表面上时，会发生反射。

1.反射定律：反射定律是描述光的反射现象的基本规律，包括以下三个方面的内容：（1）入射光线、反射光线和法线在同一平面内；（2）入射光线和反射光线分居在法线的两侧；（3）入射角等于反射角。

2.镜面反射和漫反射：根据反射面的不同，光的反射分为镜面反射和漫反射。

镜面反射是指光线射到光滑表面上的反射，如平面镜、球面镜等。

漫反射是指光线射到粗糙表面上的反射，如光线照到地面上、物体表面等。

二、光的折射光的折射是指光线在传播过程中，从一种介质进入另一种介质时，传播方向发生改变的现象。

光线传播到两种不同介质的界面时，会发生折射。

1.折射定律：折射定律是描述光在介质界面折射现象的基本规律，包括以下三个方面的内容：（1）入射光线、折射光线和法线在同一平面内；（2）入射光线和折射光线分居在法线的两侧；（3）入射角和折射角之间满足正弦定律：n1sin(θ1) = n2sin(θ2)，其中n1和n2分别为入射介质和折射介质的折射率，θ1和θ2分别为入射角和折射角。

2.斯涅尔定律：斯涅尔定律是光的折射现象的另一种表达方式，即入射光线、折射光线和法线三者之间的夹角关系：cos(θ1)/cos(θ2) = n2/n1。

3.正常折射和全反射：当光线从光密介质进入光疏介质时，折射角小于入射角，这种折射现象称为正常折射；当光线从光密介质进入光疏介质时，折射角大于90°，这种现象称为全反射。

通过以上介绍，我们可以了解到光的反射和折射是光在传播过程中遇到不同介质时产生的现象，它们遵循相应的定律和规律。

这些知识点对于中学生来说，是光学学习的基础内容，对于深入理解光的传播和光学设备的工作原理具有重要意义。