土木工程制图第七章截交线与相贯线
- 格式:ppt
- 大小:9.08 MB
- 文档页数:64

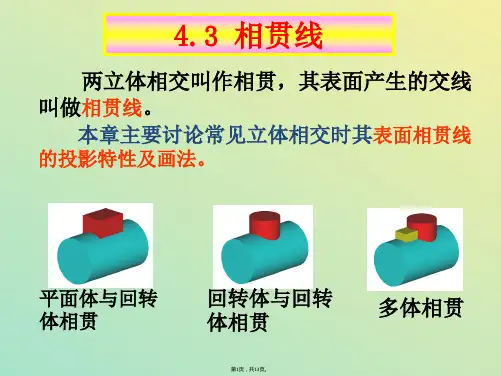
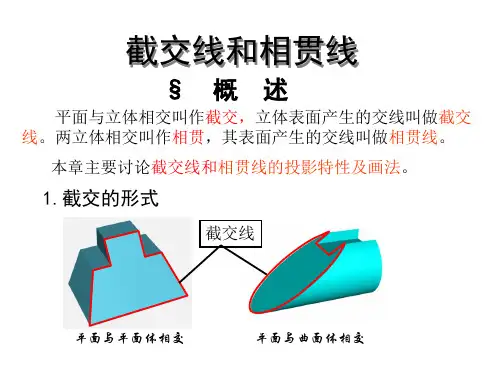






截交线和相贯线第一节基本体表面上交线的投影一、平面与平面立体表面相交:平面与平面立体表面相交,可看成是立体被平面截切,截切立体的平面称为截平面,截平面与立体表面的交线称为截交线。
1、截交线的性质:1)共有性:截交线是截平面和立体表面的共有线,截交线上任何一点都是截平面和立体表面的共有点。
2)封闭性:任何立体都有一定范围,截交线是封闭的平面图形。
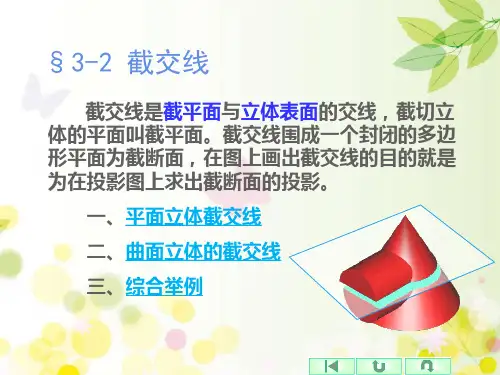
2、截交线的作图方法:平面立体被某一平面所截后其截交线为多边形,该多边形各边交点是截平面与平面立体棱线上的点,该多边形各边是截平面与立体相应棱面的交线。
要想求出平面立体上的截交线,只需求出立体棱线与截平面的交点即可。
然后,依次连接各点。
例,三棱锥被一正垂面所截,求其截交线投影。
步骤如下:1)利用正垂面的积聚性,求棱线与截平面的三个交点的正面投影1、2、3。
2)求得水平投影1、2、3,连接即可。
二、平面与圆柱体表面相交可根据截平面与圆柱体轴线的位置不同,截交线有三种情况:见表4-1分析下列圆柱体切片、开槽的作图方法,及截交线的形状特点。
1、求斜切圆柱体的投影:用一正垂面截切圆柱,截交线为一椭圆,正面投影为一直线,水平投影为一椭圆。
作图步骤:a)求特殊点,即最高点、最低点、最前点、最后点。
b)求一般位置点。
c)依次连接2、圆柱切片的投影:3、圆柱切口的投影4、平面与圆锥体相交:截交线为抛物线截交线为椭圆截交线为双曲线三、平面与圆球相交:例、半圆头螺钉头部的投影作图方法:第二节两回转体表面的相贯线一、基本概念:相贯线:两立体表面相交,产生的交线成为相贯线。
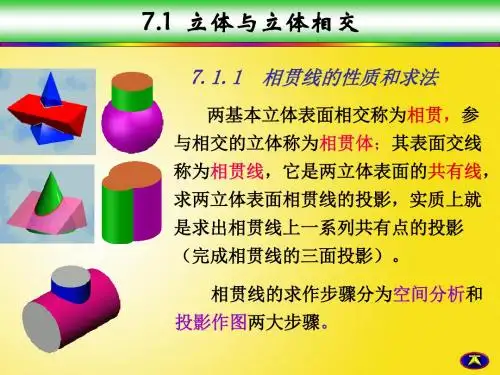
1、相贯线的基本性质:1)共有性:相贯线是立体表面的共有线,也是两立体表面的分界线,相贯线上的点是两立体表面的共有点。
2)封闭性:一般为封闭的空间曲线,少数情况为平面曲线或直线。
2、相贯线的画法:(1)分析首先分析两曲面立体的几何形状、相对大小和相对位置,进一步分析相贯线是空间曲线,还是处于特殊情况(平面曲线或直线)。