201X版中考数学学业水平考试一轮复习 专题 图形的相似强化练习题

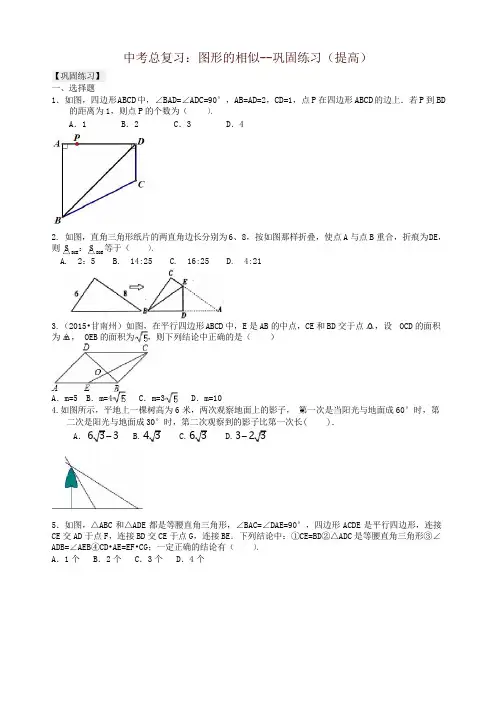
•中考总复习：图形的相似--巩固练习（提高）【巩固练习】一、选择题1．如图，四边形ABCD中，∠BAD=∠ADC=90°，AB=AD=2，CD=1，点P在四边形ABCD的边上．若P到BD 的距离为1，则点P的个数为（）．A．1B．2C．3D．42.如图，直角三角形纸片的两直角边长分别为6、8，按如图那样折叠，使点A与点B重合，折痕为D E，则△SB CE：△SB DE等于（）．A.2：5B.14:25C.16:25D.4:213.（2015•甘南州）如图，在平行四边形ABCD中，E是AB的中点，CE和BD交于点△O，设OCD的面积为△m，OEB的面积为，则下列结论中正确的是（）A．m=5B．m=4C．m=3D．m=104.如图所示，平地上一棵树高为6米，两次观察地面上的影子，第一次是当阳光与地面成60°时，第二次是阳光与地面成30°时，第二次观察到的影子比第一次长()．A．63-3 B.43 C.63 D.3-235．如图，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，四边形ACDE是平行四边形，连接CE交AD于点F，连接BD交CE于点G，连接BE．下列结论中：①CE=BD②△ADC是等腰直角三角形③∠ADB=∠AEB④CD•AE=EF•CG；一定正确的结论有（）．A．1个B．2个C．3个D．4个=，③∠B+∠2=90°④BC∶AC∶AB=3∶4∶5，⑤AC⋅BD=AC⋅C D，②6．如图，△A BC中，CD⊥AB于D，一定能确定△A BC为直角三角形的条件的个数是（）．①∠1=∠A，CD DBAD CDA．1B．2C．3D．4二、填空题7.如图已知△ABC的面积是3的等边三角形，△ABC∽△ADE，AB=2AD，∠BAD=45°，AC与DE相交于点△F，则AEF的面积等于__________（结果保留根号）.第7题第8题8.已知三个边长分别为2、3、5的正三角形从左到右如图排列，则图中阴影部分面积为．9.如图，等边三角形ABC的边长为3，点P为BC边上一点，且BP=1，点D为AC边上一点，若∠APD= 60°，则CD的长为．第9题第10题10．如图，在直角三角形ABC中（∠C=90°），放置边长分别3，4，x的三个正方形，则x的值为．11.如图，边长为6的大正方形中有两个小正方形，若两个小正方形的面积分别为S，S，则S+S的1212值为．3．．．．．．．．．．．．．． ．．12. （2015•湖州）已知正方形 ABC 1D 1 的边长为 1，延长 C 1D 1 到 A 1，以 A 1C 1 为边向右作正方形 A 1C 1C 2D 2，延 长 C 2D 2 到 A 2，以 A 2C 2 为边向右作正方形 A 2C 2C 3D （如图所示），以此类推…．若 A 1C 1=2，且点 A ，D 2，D 3，…，D 10 都在同一直线上，则正方形 A 9C 9C 10D 10 的边长是 ．三、解答题13.（2015•杭州模拟）如图，正方形 ABCD 的边长为 2，点 E ，F 分别是 DC 和 BC 两边上的动点且始终保 持∠EAF=45°，连接 AE 与 AF 交 DB 于点 N ，△M ．下列结论：① △A D M∽ NBA ；②△CEF 的周长始终保持 不变其值是 4；③AE×AM=AF×AN；④DN 2+BM 2=NM 2．其中正确的结论有哪些？14. 如图（△1）， ABC 与△EFD 为等腰直角三角形，AC 与 DE 重合，AB =EF =9，∠BAC ＝∠DEF ＝90°，固 定△ABC ，将△EFD 绕点 A 顺时针旋转，当 DF 边与 AB 边重合时，旋转中止.不考虑旋转开始和结束时重 合的情况，设 DE 、DF （或它们的延长线）分别交 BC （或它的延长线）于 G 、H 点，如图（2）. （△1）问：始终与 AGC 相似的三角形有及；（2）设 CG ＝x ，BH ＝y ，求 y 关于 x 的函数关系式（只要求根据 2 的情况说明理由）； （3）问：当 x 为何值时，△AGH 是等腰三角形？15.已知:直角梯形 OABC 中，BC∥OA，∠AOC=90°，以AB 为直径的圆 M 交 OC 于 D ．E ，连结 AD 、BD 、BE.(1)在不添加其他字母和线的前提下，直接写出图 1 中的两对相似三角形._____________________，______________________；(2)直角梯形OABC中，以O为坐标原点，A在x轴正半轴上建立直角坐标系（如图2），若抛物线y=ax2-2ax-3a(a<0)经过点A．B．D，且B为抛物线的顶点.①写出顶点B的坐标（用a的代数式表示）___________；②求抛物线的解析式；③在x轴下方的抛物线上是否存在这样的点P：过点P做PN⊥x轴于△N，使得PAN与△OAD相似？若存在，求出点P的坐标；若不存在，说明理由.16．（2011上海）在△R t ABC中，∠ACB=90°，BC=30，AB=50．点P是AB边上任意一点，直线PE⊥AB，与边AC或BC相交于E．点M在线段AP上，点N在线段BP上，EM=EN，sin∠EMP=1213．（1）如图1，当点E与点C重合时，求CM的长；（2）如图2，当点E在边AC上时，点E不与点A、C重合，设AP=x，BN=y，求y关于x的函数关系式，并写出函数的定义域；（△3）若AME∽△ENB（△AME的顶点A、M、E分别与△ENB的顶点E、N、B对应），求AP的长．图1图2备用图【答案与解析】一．选择题1．【答案】B．2．【答案】B．3．【答案】B；【解析】∵AB∥CD，∴△OCD∽△OEB，又∵E 是 AB 的中点， ∴2EB=AB=CD，∴=（ ）2，即=（ ）2，解得 m=4 ．故选 B ． 4．【答案】B ． 5．【答案】Ｄ；【解析】①利用 SAS 证明△BAD ≌△CAE ，可得到 CE=BD ，②利用平行四边形的性质可得 AE=CD ，再结合△ADE 是等腰直角三角形可得到△ADC 是等腰直角三角形； ③利用 SAS 证明△BAE ≌△BAD 可得到∠ADB=∠AEB ；④利用已知得出∠GFD=∠AFE ，以及∠GDF+∠GFD=90°，得出∠GCD=∠AEF ，进而得出△CGD ∽△EAF ，得 出比例式． 6．【答案】Ｃ；【解析】①因为∠A+∠2=90°，∠1=∠A ，所以∠1+∠2=90°，即△ABC 为直角三角形，故正确；②根据 CD 2=AD•DB 得到 AD CD =CD DB，再根据∠ADC=∠CDB=90°，则△ACD ∽△CBD ，∴∠1=∠A ，∠2=∠B ，根据三角形内角和定理可得：∠ACB=90°，故正确；③因为∠B+∠2=90°，∠B+∠1=90°，所以推出∠1=∠2，无法得到两角和为 90°，故错误；④设 BC 的长为 3x ，那么 AC 为 4x ，AB 为 5x ，由 9x 2+16x 2=25x 2，符合勾股定理的逆定理，故正确； ⑤由三角形的相似无法推出 AC•BD=AD•CD 成立，所以△ABC 不是直角三角形，故错误． 所以正确的有三个．故选 C ． 二．填空题7．【答案】 3 - 3 4．8．【答案】 3 8．29．【答案】 ；3【解析】∵△ABC 是等边三角形，∴∠B=∠C=60°， ∵∠APB=∠PAC+∠C ，∠PDC=∠PAC+∠APD ，∵∠APD=60°，∴∠APB=∠PAC+60°，∠PDC=∠PAC+60°，∴∠APB=∠PDC ， 又∵∠B=∠C=60°，∴△ABP ∽△PCD ，∴ AB BP 3 1 = ，即 = ，PC CD 2 CD2∴CD= ．310．【答案】７；【解析】根据已知条件可以推出△CEF ∽△OME ∽△PFN 然后把它们的直角边用含 x 的表达式表示出来， 利用对应边的比相等，即可推出 x 的值答题． 11.【答案】17；【解析】如图，设正方形 S 2 的边长为 x ，根据等腰直角三角形的性质知，AC= 2 x ，x= 2 CD ，∴AC=2CD ，CD=2，∴EC 2=22+22，即 EC=2 2 ，∴S 2 的面积为 EC 2=8， ∵S 1 的边长为 3，S 1 的面积为 3×3=9， ∴S 1+S 2=8+9=17．12．【答案】．【解析】延长 D 4A 和 C 1B 交于 O ， ∵AB∥A 2C 1，∴ AOB∽ D △2OC 2，∴ = ，∵AB=BC 1=1，DC 2=C 1C 2=2，∴==∴OC 2=2OB ， ∴OB=BC 2=3， ∴OC 2=6，设正方形 A 2C 2C 3D 3 的边长为 x 1， 同理证得： D △2OC △2∽ D 3OC 3，∴= ，解得，x 1=3，∴正方形 A 2C 2C 3D 3 的边长为 3，设正方形 A 3C 3C 4D 4 的边长为 x 2， 同理证得： D △3OC △3∽ D 4OC 4，∴=，解得 x 2= ，∴正方形 A 3C 3C 4D 4 的边长为 ；设正方形 A 4C 4C 5D 5 的边长为 x 3， 同理证得： D △4OC △4∽ D 5OC 5，∴= ，解得 x= ，∴正方形 A 4C 4C 5D 5 的边长为 以此类推…．；正方形 A n ﹣1C n ﹣1C n D n 的边长为 ； ∴正方形 A 9C 9C 10D 10 的边长为 ．故答案为．三.综合题 13．【解析】解：①∠ANB=∠NDA+∠NAD=45°+∠NAD，∠MAD=∠MAN+∠NAD=45°+∠NAD，∴∠ANB=∠MAD，又∠ADM=∠ABN=45°，∴△ADM∽△NBA，①正确；②如图△1，把ADE顺时针旋转90°得到△ABG，则BG=DE，∠FAG=∠FAB+∠DAE=45°，在△AEF和△AGF中，，∴△AEF≌△AGF，∴DG=EF，∴△CEF的周长=CE+CF+EF=CE+DE+CF+FG=4，②正确；③当MN∥EF时，AE×AM=AF×AN，∵MN与EF的位置关系不确定，∴③错误；④如图△2，把ADN顺时针旋转90°得到△ABH，则BH=DN，∠MAH=∠MAB+∠BAH=∠MAB+∠DAN45°，在△NAM和△HAM中，，∴△AEF≌△AGF，∴MN=MH，又∵∠MBH=∠MBA+∠ABH=90°，∴BH2+BM2=MH2，即DN2+BM2=NM2，④正确．∴正确的结论有：①②④.14．【解析】（△1）HGA及△HAB；（2）由（△1）可知AGC∽△HAB∴CG AC=AB BHx9，即=，9y所以，y=81 x 1（3）当CG＜BC时，∠GAC=∠H＜∠HAC，∴AC＜CH2∵AG＜AC，∴AG＜GH又AH＞AG，AH＞GH此时，△AGH不可能是等腰三角形；当CG=12BC时，G为BC的中点，H与C重合，△AGH是等腰三角形；99此时，GC=2，即x=2221当CG＞BC时，由（△1）可知AGC∽△HGA2所以，若△AGH必是等腰三角形，只可能存在AG=AH 若AG=AH，则AC=CG，此时x=9综上，当x=9或92时，△AGH是等腰三角形．2∴ DC∴1 = ， ∴ a2 = 1 ， ∴CP = = =24．在 Rt△CPM 中，∵sin ∠EMP = ，∴CM = CP = ⨯ 24 =26．，∴PE = x ． 在 Rt△MPE 中，∵sin∠EMP = ，∴ = ．∴EM = PE = ⨯ x = x ．∴PM =PN = ME2 - PE2 = x ⎪ - x ⎪ = x ． ∵AP +PN +NB =50，∴x + x +y =50．∴y = - x + 50 (0<x <32)．15．【解析】（△1）OAD∽△CDB.△ADB∽△ECB；（2）①（1，－4a ）；②∵△OAD ∽△CDBCB=OA OD∵ax 2－2ax －3a=0，可得 A （3，0）又 OC=－4a ，OD=－3a ，CD=－a ，CB=1，-a - 3a 3∵ a < 0 ，∴ a = -1．故抛物线的解析式为： y = - x 2 + 2x + 3 ．③存在，设 P （x ，－x 2+2x+3），∵△PAN 与△OAD 相似，且△OAD 为等腰三角形， ∴PN=AN ．当 x<0（x<－1）时，－x+3=－(－x 2+2x+3)，x 1=－2，x 2=3(舍去)， ∴P （－2，－5），当 x>0（x>3）时，x －3=－(－x 2+2x+3)，x 1=0，x 2=3(都不合题意舍去)， 符合条件的点 P 为（－2，－5）．16.【解析】（1）∵∠ACB =90°，∴AC = AB 2 - BC 2 = 502 - 302 =40．∵S = 1 ⋅ AB ⋅ CP = 21 2⋅ AC ⋅ BC ,AC ⋅ BC 40 ⨯ 30AB 501213CP 12 ∴ = ．CM 1313 1312 12（△2）由 APE ∽△ACB ，得 PE AP =BC AC ，即 PE x 3= 30 40 412 PE 1213 ME 1313 13 3 1312 12 4 16⎛ 13 ⎫2 ⎛ 3 ⎫25 ⎝ 16 ⎭ ⎝ 4 ⎭ 16 51621 16设AP=x，由（2）知EM=x，AM=x-PM=x-x=x，NB=-x+50．∴ x⎪=x⋅(-x+50)∴CE=AC=．设AP=x，易得BE=(50-x)，∴CE=30-(50-x)．（3）①当点E在线段AC上时，△AME∽△ENB，AM ME=EN NB．∵EM=EN，∴EM2=A M⋅NB．135112116161616⎛13⎫21121⎝16⎭1616解得x1=22，x2=0（舍去），即AP=22．②当点E在线段BC上时，根据外角定理，△ACE∽△EPM，∴AC EP12==．CE MP55501235353550∴30-(50-x)=．33解得x=42．即AP=42．∴AP的长为22或42．。

中考数学一轮复习专题突破训练—相似三角形一、单选题1．（2022·北京市第十三中学九年级期中）如图，点D，E分别在△ABC的AB，AC边上，且DE△BC，如果AD：AB＝2：3，那么DE：BC等于（）A．3：2B．2：5C．2：3D．3：5【答案】C【分析】根据相似三角形的判定与性质即可得出结果．【详解】解：△DE∥BC，△△ADE△△ABC，△DE：BC＝AD：AB＝2：3；故选：C．2．（2022·辽宁鞍山市·九年级期末）如图，在平行四边形ABCD中，点E是AB 的中点，CE和BD交于点O，若S△EOB＝1，则四边形AEOD的面积为（）A．4B．5C．6D．7【答案】B根据平行四边形的性质和相似的判定和性质，可以得到△BOC和△COD的面积，从而可以得到△BCD的面积，再根据△ABD和△BCD的面积一样，即可得到四边形AEOD的面积．【详解】解：△在平行四边形ABCD中，点E是AB的中点，△CD△AB，CD=AB=2BE△△DOC△△BOE，△OC CDOE BE=2，△S△EOB=1，△S△BOC=2，S△DOC=4，△S△BCD=6，△S△DAB=6，△四边形AEOD的面积为：S△DAB-S△EOB=6-1=5，故选：B．3．（2022·全国九年级专题练习）如图，已知AB△CD△EF，AD：AF=3：5，BE=12，那么CE的长等于（）A．2B．4C．245D．365【分析】根据平行线分线段成比例得到3125BC =，然后利用比例性质计算出BC ，从而求出CE 即可． 【详解】解：△AB △CD △EF ， △BC AD BE AF =，即3125BC =， △BC =365， △CE =BE -BC =12-365=245， 故选C ．4．（2022·全国九年级专题练习）下列四条线段中，不能成比例的是（ ） A．a ＝2，b ＝4，c ＝3，d ＝6 B ．a ，b c ＝1，d C ．a＝6，b ＝4，c ＝10，d ＝5 D ．a b ＝c d ＝2【答案】C 【分析】根据比例线段的概念，让最小的和最大的相乘，另外两条相乘，看它们的积是否相等即可得出答案． 【详解】解：A 、2×6=3×4，能成比例； B1 C 、4×10≠5×6，不能成比例；D 、523152⨯=⨯，能成比例． 故选：C ．5．（2022·四川省成都市石室联合中学）如图，在ABC 中，点E 和点F 分别在边AB ，AC 上，且//EF BC ，若3AE =，6EB =，9BC =，则EF 的长为（ ）A ．1B ．92C ．12D ．3【答案】D 【分析】证明△AEF △△ABC ，根据相似三角形的性质列出比例式，代入计算得到答案． 【详解】 △//EF BC ， △AEF ABC ∽， △EF AEBCAB， △3AE =，6EB =， 9BC =， △399EF =， △3EF =． 故选D ．6．（2022·全国九年级课时练习）将三角形纸片（ABC ）按如图所示的方式折叠，使点C 落在AB 边上的点D ，折痕为EF ．已知3,4AB AC BC ===，若以点B 、D 、F 为顶点的三角形与ABC 相似，那么CF 的长度是（ ）A ．2B ．127或2 C ．127D ．125或2 【答案】B 【分析】分两种情况：若BFD C ∠=∠或若BFD A ∠=∠，再根据相似三角形的性质解题 【详解】△ABC 沿EF 折叠后点C 和点D 重合， △FD CF =，设CF x =，则,4FD CF x BF x ===-，以点B 、D 、F 为顶点的三角形与ABC 相似，分两种情况： △若BFD C ∠=∠，则BF FDBC AC =，即443x x -=，解得127x =； △若BFD A ∠=∠，则BF FD AB AC =，即433x x -=，解得2x =． 综上，CF 的长为127或2， 故选：B ．7．（2022·全国九年级课时练习）已知线段a 、b 、c 、d 满足ab cd =，把它改写成比例式，错误的是（ ） A ．::a d c b = B ．::a b c d =C ．::d a b c =D ．::a c d b =【答案】B【分析】根据比例的基本性质：外项之积等于内项之积，对选项一一分析，选出正确答案即可．【详解】解：A、a：d＝c：b△ab＝cd，故正确；B、a：b＝c：d△ad＝bc，故错误；C、d：a＝b：c△dc＝ab，故正确；D、a：c＝d：b△ab＝cd，故正确．故选：B．8．（2022·全国九年级课时练习）下列结论不正确的是（）A．所有的矩形都相似B．所有的正三角形都相似C．所有的等腰直角三角形都相似D．所有的正八边形都相似【答案】A【分析】根据相似图形的判定判断即可；【详解】所有的矩形不一定都相似，故A错误，符合题意；因为正三角形的每个角都等于60︒，满足两个角对应相等，所有的正三角形都相似，故B正确；︒︒︒，满足两个角对应相等，因为等腰直角三角形的三个角分别为,45,45,90所有的等腰直角三角形都相似，故C正确；因为正八边形的每个角都相等，每条边都相等，所有的正八边形都相似，故D 正确； 故选A ．9．（2022·全国）如果23a b =，那么2a bb-的结果是（ ） A ．12- B ．43-C ．43D ．12【答案】B 【分析】根据比例的性质即可得到结论． 【详解】 △a b＝23，△可设a ＝2k ，b ＝3k ， △2a bb -＝2k-6k 3k ＝－43． 故选B ．10．（2022·沙坪坝·重庆一中）下列命题正确的是（ ） A ．位似图形一定是相似图形 B ．任意两个菱形一定相似CD ．23、24、25能作为直角三角形的三边长 【答案】A 【分析】根据位似图形，相似图形的定义可判断A 、B ，根据平方根的定义和勾股定理的逆定理，可判断C 、D ． 【详解】解：A. 位似图形一定是相似图形，故原命题正确，符合题意； B. 任意两个菱形不一定相似，故原命题错误，不符合题意；C.±D. 23、24、25不能作为直角三角形的三边长，故原命题错误，不符合题意， 故选A ． 二、填空题11．（2022·山东省青岛第二十六中学九年级期中）如果2x ＝3y ，那么x yy +=___． 【答案】52【分析】直接利用已知得出x =32y ，进而代入得出答案． 【详解】 解：△2x =3y ， △x =32y ，△3522y yx y y y ++==．故答案为：52．12．（2022·全国九年级专题练习）ABC 中，D 、E 分别在AB 、AC 上，DE △BC ，ADE 是ABC 缩小后的图形，若DE 把ABC 的面积分成相等的两部分，则AD ：AB =_____【分析】如图根据BC △DE ，可以得到△ADE △△ABC ，则21=2AED ABC S AD S AB ⎛⎫= ⎪⎝⎭△△ ，由此即可求解． 【详解】 解：△BC △DE ， △△ADE △△ABC ，△DE 把△ABC 的面积分成相等的两部分，△21()2AED ABCS AD SAB ∆∆==， △22AD AB =， 故答案为：22．13．（2022·全国）如图，AC 与BD 相交于点O ，在△AOB 和△DOC 中，已知OA OBOD OC=，又因为________，可证明△AOB △△DOC ．【答案】△AOB＝△DOC【分析】根据相似三角形的判定，两边对应成比例，夹角相等，两三角形相似解答．【详解】解：△OA OBOD OC=，△AOB＝△DOC，△△AOB△△DOC（两边对应成比例，夹角相等，两三角形相似）．故答案为：△AOB＝△DOC．14．（2022·全国九年级专题练习）如图：梯形ADFE相似于梯形EFCB，若AD＝3，BC＝4，则AEBE=__．3【分析】根据相似的性质，列出比例式，根据已知条件即可求得．【详解】因为梯形ADFE相似于梯形EFCB，所以AD EFEF BC=，即EF＝23所以323AE ADBE EF===315．（2022·合肥市第四十五中学九年级）如图，正方形ABCD中，点E是BC的中点，点F是CD上一点，分别以AE、AF为对称轴，折叠△ABE、△ADF，使得AB和AD与AG重合，连接BG交AE于点H，连接CG．（1）HE：AH＝______；（2）S△AFE：S正方形ABCD＝______．【答案】1：4 5：12【分析】（1）根据翻折的性质得到△GHE＝△BHE＝90°，再根据△HEB＝△BEA，从而证明△HEB△△BEA，得出HE BEBE AE=，设正方形边长为2x，则BE＝x，AB＝2x，由勾股定理求出AE，从而求出HE和AH，得出结论；（2）由S△AFE＝12（S正方形ABCD﹣S△FCE），正方形ABCD的边长为2x，FG＝DF＝m，则EF ＝x + m，CF＝2 x﹣m，，由勾股定理求出m即可．【详解】解：（1）△AE为对称轴，△△AEG△△AEB，BG△AE，△△GHE＝△BHE＝90°，又△△HEB＝△BEA，△△HEB△△BEA，△HE BEBE AE=，在正方形ABCD 中，设边长为2x ，△点E 是BC 的中点，则BE ＝x ，AB ＝2x ，△AE=，△HE ＝225BE x AE ==，△AH ＝AE ﹣HE=，△HE ：AH x ＝1：4． 故答案为：1：4；（2）设正方形ABCD 的边长为2x ，则S 正方形ABCD ＝4x 2，△S △AFE ＝12（S 正方形ABCD ﹣S △FCE ），CE ＝BE ＝GE ＝x ，设FG ＝DF ＝m ，则EF ＝x + m ，CF ＝2 x ﹣m ，在△EFC 中，△EF 2＝CE 2+CF 2，△（m +x ）2＝（2 x ﹣m ）2+ x 2，解得：m ＝23x ，△CE ＝2 x ﹣m ＝43x ，△S △CFE ＝12×CE ×CF ＝12×24233x x x ⨯=， △S △AFE ＝12×（4 x 2﹣223x ）＝253x ， △S △AFE ：S 正方形ABCD ＝225:43x x ＝5：12．故答案为：5：12．三、解答题16．（2022·辽宁鞍山市·九年级期末）如图，将△ABC绕点A旋转得到△ADE，连接BD，CE．求证：△ADB△△AEC．【答案】见解析．【分析】由题知，将△ABC绕点A旋转得到△ADE，可得到AC＝AE，AB＝AD，△CAE＝△BAD，即可证明．【详解】△将△ABC绕点A旋转得到△ADE，△AC＝AE，AB＝AD，△CAE＝△BAD，△AE AC，AD AB△△ADB△△AEC．17．（2022·广西贺州市·九年级期中）如图，已知在△ABC中，DE△BC，EF△AB，AE＝2CE，AB＝6，BC＝9．求：（1）求BD的长度；（2）求DE的长度．【答案】（1）2；（2）6【分析】（1）由平行线分线段成比例得出比例式，即可得出结果；（2）由平行线分线段成比例得出比例式，即可得出结果．【详解】解：（1）△AE =2CE ， △12CE AE =， △DE △BC ， △13BD CE AB AC ==， △AB =6，△BD =2；（2）△EF △AB ， △23AE BF AC BC ==， △BC =9，△BF =6，又△DE △BC ，△四边形BDEF 是平行四边形，△DE =BF =6．18．（2022·全国九年级专题练习）已知：如图，△ABC ＝△CDB ＝90°，AC ＝a ，BC ＝b ，当BD 与a 、b 之间满足怎样的关系时，这两个三角形相似？【答案】2b BD a =或22b a b BD -=【分析】由AB △BC ，BD △CD 得到△ABC =△BDC =90°，再利用勾股定理计算出22AB a b -根据直角三角形相似的判定方法，当AB BD AC BC =，Rt △ABC △Rt △BDC ；当=BC AC BD BC时然后分别利用比例性质可表示出BD 与a 和b 的关系． 【详解】解：△AC ＝a ，BC ＝b ，△ABC ＝△CDB ＝90°，△AB 22a b -△当BD BC AB AC=时， 即22b a b BD -=Rt △ABC △Rt △BDC ； △当BD BC CB AC=时， 即2b BD a=时，Rt △ABC △Rt △CDB ，． 19．（2020·北京市第六十六中学九年级期中）如图，在Rt△ABC 中，△C ＝90°，D 是AB 上一点，E 是BC 上一点，AC ＝6，BC ＝8，BD ＝4，BE ＝5．求证：DE △AB ．【答案】见解析【分析】利用勾股定理可求得AB ＝10，则有12BE AB =，12BD BC =，结合△B ＝△B ，可证得△BDE △△BCA ，从而有△BDE ＝△C ＝90°，即可得证．【详解】证明：△△C ＝90°，AC ＝6，BC ＝8，△AB 2210AC BC +=，△BD ＝4，BE ＝5， △12BE AB =，12BD BC =， △△B ＝△B ，△△BDE △△BCA ，△△BDE ＝△C ＝90°，即DE △AB ．20．（2022·全国九年级专题练习）如图：小明欲测量一座古塔的高度，他站在该塔的影子上前后移动，直到他本身影子的顶端正好与塔的影子的顶端重叠，此时他距离该塔18 m ，已知小明的身高是1.6 m ，他的影长是2 m ．（1）图中△ABC 与△ADE 是否相似？为什么？（2）求古塔的高度．【答案】（1）相似，见解析；（2）16m【分析】（1）根据在同一时刻物高和影长成正比，即在同一时刻的两个物体，影子，经过物体顶部的太阳光线三者构成的两个直角三角形相似；（2）利用相似三角形的性质求得相应线段的长即可．【详解】解：（1）△ABC△△ADE．△BC△AE，DE△AE，△△ACB=△AED=90°.△△A=△A，△△ABC△△ADE；（2）由(1)得△ABC△△ADE,△AC BC=AE DE△AC=2m，AE=2+18=20m，BC=1.6m，△2 1.6=，20DE△DE=16m，即古塔的高度为16m．21．（2022·全国九年级专题练习）在锐角△ABC中，AD，CE分别为BC，AB边上的高，△ABC 和△BDE 的面积分别等于18和2，DE ＝2，求AC 边上的高．【答案】6【分析】由已知条件得到△CEB ＝△ADB ＝90°，推出△ADB △△CEB ，根据相似三角形的性质得到BD ：AB ＝BE ：BC ，证得△BDE △△BAC ，得到S △BDE ：S △ABC ＝（DE ：AC ）2，于是求得AC ＝6，然后根据三角形的面积公式即可得到结果．【详解】过点B 做BF △AC ,垂足为点F ，△AD ,CE 分别为BC ,AB 边上的高，△△ADB =△CEB =90°，又△△B =△B ，△Rt △ADB △Rt △CEB , △BD AB BE CB =，即BD BE AB CB=， 且△B =△B ，△△EBD △△CBA , △221189BED BCA S DE S AC ⎛⎫=== ⎪⎝⎭, △13DE AC =, 又△DE =2，△AC =6，△1182ABCS AC BF =⋅=， 6BF ∴=．22．（2022·湖南师大附中博才实验中学）如图，在正方形ABCD 中，点G 是对角线上一点，CG 的延长线交AB 于点E ，交DA 的延长线于点F ，连接AG ．（1）求证：AG CG =；（2）若9GE GF ⋅=，求CG 的长．【答案】（1）见解析；（2）CG =3【分析】（1）根据正方形的性质得到△ADB =△CDB =45°，AD =CD ，从而利用全等三角形的判定定理推出△ADG △△CDG （SAS ），进而利用全等三角形的性质进行证明即可；（2）根据正方形的性质得到AD △CB ，推出△FCB =△F ，由（1）可知△ADG △△CDG ，利用全等三角形的性质得到△DAG =△DCG ，结合图形根据角之间的和差关系△DAB -△DAG =△DCB -△DCG ，推出△BCF =△BAG ，从而结合图形可利用相似三角形的判定定理得到△AEG △△F AG ，进而根据相似三角形的性质进行求解即可．【详解】解：（1）证明：△BD 是正方形ABCD 的对角线，△△ADB =△CDB =45°，又AD =CD ，在△ADG 和△CDG 中，AD CD ADG CDG DG DG =⎧⎪∠=∠⎨⎪=⎩， △△ADG △△CDG （SAS ），△AG =CG ；（2）解：△四边形ABCD 是正方形，△AD △CB ，△△FCB =△F ，由（1）可知△ADG △△CDG ，△△DAG =△DCG ，△△DAB -△DAG =△DCB -△DCG ，即△BCF =△BAG ，△△EAG =△F ，又△EGA =△AGF ，△△AEG △△F AG ，△GE GA GA GF =，即GA 2=GE •GF ，△GA =3或GA =-3（舍去），根据（1）中的结论AG =CG ，△CG =3．23．（2022·浙江杭州·翠苑中学九年级）如图，在矩形ABCD 中，E 是CD 上一点，AE AB =，作BF AE ⊥．（1）求证：ADE BFA ≅△△；（2）连结BE ，若BCE 与ADE 相似，求AD AB ． 【答案】（1）见解析；（23【分析】（1）根据矩形的性质得出90D DAB ∠=∠=︒，求出90DAE FAB ∠+∠=︒，90FBA FAB ∠+∠=︒，求出D AFB ∠=∠，DAE FBA ∠=∠，再根据全等三角形的判定推出即可；（2）根据矩形的性质得出90C D ∠=∠=︒，//DC AB ，根据平行线的性质得出CEB ABE ∠=∠，设CEB ABE x ∠=∠=︒，根据等腰三角形的性质求出AEB EBA x ∠=∠=︒，根据相似三角形的性质得出两种情况：△DEA CEB x ∠=∠=︒，根据180DEA AEB CEB ∠+∠+∠=︒得出180x x x ++=，求出x ，再解直角三角形求出AE 和AD ，再求出答案即可；△DEA EBC ∠=∠，设DEA EBC y ∠=∠=︒，求出(2)180DEA AEB CEB y x ∠+∠+∠=+︒=︒，()90EBC CEB y x ∠+∠=+︒=︒，求出x ，再得出答案即可．【详解】解：（1）证明：四边形ABCD 是矩形，90D DAB ∴∠=∠=︒，90DAE FAB ∴∠+∠=︒，BF AE ⊥，90AFB ∴∠=︒，D AFB ∴∠=∠，90FBA FAB ∠+∠=︒，DAE FBA ∴∠=∠，在ADE ∆和BFA ∆中DAE FBA D AFB AE AB ∠=∠⎧⎪∠=∠⎨⎪=⎩， ()ADE BFA AAS ∴∆≅∆；（2）四边形ABCD 是矩形，90C D ∴∠=∠=︒，//DC AB ，CEB ABE ∴∠=∠，设CEB ABE x ∠=∠=︒，AE AB =，AEB EBA x ∴∠=∠=︒，当BCE ∆与ADE ∆相似时，有两种情况：△DEA CEB x ∠=∠=︒，180DEA AEB CEB ∠+∠+∠=︒，180x x x ∴++=，解得：60x =，即60DEA ∠=︒，906030DAE ∴∠=︒-︒=︒，2AE DE ∴=，由勾股定理得：AD ， AE AB =，∴AD AD AB AE = △DEA EBC ∠=∠，设DEA EBC y ∠=∠=︒，CEB EBA AEB x ∠=∠=∠=︒，则(2)180DEA AEB CEB y x x y x ∠+∠+∠=︒+︒+︒=+︒=︒， 在Rt BCE ∆中，()90EBC CEB y x y x ∠+∠=︒+︒=+︒=︒， 即218090y x y x +=⎧⎨+=⎩， 解得：90x =︒，即90CEB ∠=︒，此时点E 和点C 重合，BEC ∆不存在，舍去；△AD AB =。

2019-2020九年级数学一轮复习图形的相似中考真题当堂反馈考点过关训练作业练习含答案解析一．选择题（共4小题）1．如图，在▱ABCD中，点E在对角线BD上，EM∥AD，交AB于点M，EN∥AB，交AD 于点N，则下列式子一定正确的是（）A．＝B．＝C．＝D．＝2．如图，平行于BC的直线DE把△ABC分成面积相等的两部分，则的值为（）A．1B．C．1D．3．学校门口的栏杆如图所示，栏杆从水平位置BD绕O点旋转到AC位置，已知AB⊥BD，CD⊥BD，垂足分别为B，D，AO＝4m，AB＝1.6m，CO＝1m，则栏杆C端应下降的垂直距离CD为（）A．0.2m B．0.3m C．0.4m D．0.5m4．如图，在△ABC中，AC＝2，BC＝4，D为BC边上的一点，且∠CAD＝∠B．若△ADC 的面积为a，则△ABD的面积为（）A．2a B．a C．3a D．a二．填空题（共2小题）5．如图，在Rt△ABC中，∠ACB＝90°，AB＝10，BC＝6，CD∥AB，∠ABC的平分线BD 交AC于点E，DE＝．6．如图，在平面直角坐标系中，正方形OABC和正方形ADEF的边OA、AD分别在x轴上，OA＝2，AD＝3，则正方形OABC和正方形ADEF位似中心的坐标是．三．解答题（共3小题）7．在如图所示的平面直角坐标系中，已知点A（﹣3，﹣3），点B（﹣1，﹣3），点C（﹣1，﹣1）．（1）画出△ABC；（2）画出△ABC关于x轴对称的△A1B1C1，并写出A1点的坐标：；（3）以O为位似中心，在第一象限内把△ABC扩大到原来的两倍，得到△A2B2C2，并写出A2点的坐标：．8．如图，在正方形ABCD中，E为边AD的中点，点F在边CD上，且∠BEF＝90°，延长EF交BC的延长线于点G．（1）求证：△ABE∽△EGB；（2）若AB＝4，求CG的长．9．如图，⊙O的半径为5，△ABC是⊙O的内接三角形，AB＝8．AD和过点B的切线互相垂直，垂足为D．（1）求证：∠BAD+∠C＝90°；（2）求线段AD的长．图形的相似参考答案与试题解析一．选择题（共4小题）1．如图，在▱ABCD中，点E在对角线BD上，EM∥AD，交AB于点M，EN∥AB，交AD 于点N，则下列式子一定正确的是（）A．＝B．＝C．＝D．＝【解答】解：∵在▱ABCD中，EM∥AD∴易证四边形AMEN为平行四边形∴易证△BEM∽△BAD∽△END∴＝＝，A项错误＝，B项错误＝＝，C项错误＝＝，D项正确故选：D．2．如图，平行于BC的直线DE把△ABC分成面积相等的两部分，则的值为（）A．1B．C．1D．【解答】解：∵DE∥BC，∴∠ADE＝∠B，∠AED＝∠C，∴△ADE∽△ABC，∴（）2＝．∵S△ADE＝S四边形BCED，∴＝，∴＝＝＝﹣1．故选：C．3．学校门口的栏杆如图所示，栏杆从水平位置BD绕O点旋转到AC位置，已知AB⊥BD，CD⊥BD，垂足分别为B，D，AO＝4m，AB＝1.6m，CO＝1m，则栏杆C端应下降的垂直距离CD为（）A．0.2m B．0.3m C．0.4m D．0.5m【解答】解：∵AB⊥BD，CD⊥BD，∴∠ABO＝∠CDO＝90°，又∵∠AOB＝∠COD，∴△ABO∽△CDO，则＝，∵AO＝4m，AB＝1.6m，CO＝1m，∴＝，解得：CD＝0.4，故选：C．4．如图，在△ABC中，AC＝2，BC＝4，D为BC边上的一点，且∠CAD＝∠B．若△ADC 的面积为a，则△ABD的面积为（）A．2a B．a C．3a D．a【解答】解：∵∠CAD＝∠B，∠ACD＝∠BCA，∴△ACD∽△BCA，∴＝（）2，即＝，解得，△BCA的面积为4a，∴△ABD的面积为：4a﹣a＝3a，故选：C．二．填空题（共2小题）5．如图，在Rt△ABC中，∠ACB＝90°，AB＝10，BC＝6，CD∥AB，∠ABC的平分线BD 交AC于点E，DE＝．【解答】解：∵∠ACB＝90°，AB＝10，BC＝6，∴AC＝8，∵BD平分∠ABC，∴∠ABE＝∠CDE，∵CD∥AB，∴∠D＝∠ABE，∴∠D＝∠CBE，∴CD＝BC＝6，∴△AEB∽△CED，∴，∴CE＝AC＝×8＝3，BE＝，DE＝BE＝×＝，故答案为．6．如图，在平面直角坐标系中，正方形OABC和正方形ADEF的边OA、AD分别在x轴上，OA＝2，AD＝3，则正方形OABC和正方形ADEF位似中心的坐标是（﹣4，0）或（2，）．【解答】解：连接FC并延长交x轴于点M，由题意可得：△MOC∽△MAF，则＝＝，∴＝，解得：MO＝4，故M点的坐标为：（﹣4，0）．连接DC，OE，交点为N，可得△CNO∽△END，则＝＝，解得：AN＝，故N点坐标为：（2，），综上所述：正方形OABC和正方形ADEF位似中心的坐标是（﹣4，0）或（2，）．故答案为：（﹣4，0）或（2，）．三．解答题（共3小题）7．在如图所示的平面直角坐标系中，已知点A（﹣3，﹣3），点B（﹣1，﹣3），点C（﹣1，﹣1）．（1）画出△ABC；（2）画出△ABC关于x轴对称的△A1B1C1，并写出A1点的坐标：（﹣3，3）；（3）以O为位似中心，在第一象限内把△ABC扩大到原来的两倍，得到△A2B2C2，并写出A2点的坐标：（6，6）．【解答】解：（1）△ABC如图所示；（2）△A1B1C1如图所示；A1（﹣3，3），（3）△A2B2C2如图所示；A2（6，6）．故答案为（﹣3，3），（6，6）．8．如图，在正方形ABCD中，E为边AD的中点，点F在边CD上，且∠BEF＝90°，延长EF交BC的延长线于点G．（1）求证：△ABE∽△EGB；（2）若AB＝4，求CG的长．【解答】（1）证明：∵四边形ABCD为正方形，且∠BEG＝90°，∴∠A＝∠BEG，∵∠ABE+∠EBG＝90°，∠G+∠EBG＝90°，∴∠ABE＝∠G，∴△ABE∽△EGB；（2）∵AB＝AD＝4，E为AD的中点，∴AE＝DE＝2，在Rt△ABE中，BE＝＝＝2，由（1）知，△ABE∽△EGB，∴＝，即：＝，∴BG＝10，∴CG＝BG﹣BC＝10﹣4＝6．9．如图，⊙O的半径为5，△ABC是⊙O的内接三角形，AB＝8．AD和过点B的切线互相垂直，垂足为D．（1）求证：∠BAD+∠C＝90°；（2）求线段AD的长．【解答】解：（1）连接BO延长交⊙O于E，连接AE．∵DB为⊙O的切线，∴EB⊥BD．∵AD⊥BD，∴AD∥BE，∴∠BAD＝∠EBA．∵BE为直径，∴∠EBA+∠E＝90°，由圆周角定理得，∠E＝∠C．∴∠BAD+∠C＝90°；（2）∵⊙O的半径为5，∴BE＝10．∵∠BAD＝∠EBA，∠D＝∠BAE，∴△ABE∽△DAB，∴，∵AB＝8，BE＝10，∴AD＝6.4．∴线段AD的长度为6.4．。

中考数学复习专题综合过关检测—图形的相似与位似（含解析）（考试时间：90分钟，试卷满分：100分）一、选择题（本题共10小题，每小题3分，共30分）。

1．若，则等于（）A．B．C．D．【答案】C【解答】解：∵，∴设x＝10k，y＝7k，∴＝＝＝，故选：C．2．如图所示，在△ABC中，DE∥BC，若AD＝2，AB＝6，则＝（）A．B．C．D．【答案】C【解答】解：∵DE∥BC，∴＝，∵AD＝2，AB＝6，∴DB＝AB﹣AD＝4，∴＝＝，故选：C．3．如图，DF∥AC，DE∥BC，下列各式中正确的是（）A．＝B．＝C．＝D．＝【答案】D【解答】解：∵DF∥AC，∴＝，所以A选项错误；∵DE∥BC，∴＝，所以C选项错误；而＝，∴＝，∵DE∥CF，DF∥CE，∴四边形DECF为平行四边形，∴CF＝DE，∴＝，即＝，所以B选项错误；∵DE∥BC，∴＝，即＝，所以D选项正确．故选：D．4．如图，△ABC与△DEF位似，点O为位似中心．已知OA：OD＝1：3，则△ABC与△DEF的面积比为（）A．1：3B．2：3C．4：5D．1：9【答案】D【解答】解：∵△ABC与△DEF位似，∴△ABC∽△DEF，AB∥DE，∴△OAB∽△ODE，∴AB：DE＝OA：OD＝1：3，∴△ABC与△DEF的面积比为1：9，故选：D．5．如图，△ABC中，∠B＝60°，AB＝6，BC＝8．将△ABC沿图中的DE剪开．剪下的阴影三角形与原三角形不相似的是（）A．B．C．D．【答案】D【解答】解：A、∵∠C＝∠C，∠DEC＝∠B＝60°，∴△DEC∽△ABC，故A不符合题意；B、∵∠C＝∠C，∠CDE＝∠B，∴△CDE∽△CBA，故B不符合题意；C、由图形可知，BE＝AB﹣AE＝6﹣2＝4，BD＝BC﹣CD＝8﹣5＝3，∵，，∴，又∵∠B＝∠B，∴△BDE∽△BAC，故C不符合题意；D、由已知条件无法证明△ADE与△ABC相似，故D符合题意，故选：D．6．如图，数学活动课上，为了测量学校旗杆的高度，小明同学在脚下水平放置一平面镜，然后向后退（保持脚、镜和旗杆底端在同一直线上），直到他刚好在镜子中看到旗杆的顶端．已知小明的眼睛离地面高度为1.6m，同时量得小明与镜子的水平距离为2m，镜子与旗杆的水平距离为12m，则旗杆高度为（）A．6.4m B．8m C．9.6m D．12.5m【答案】C【解答】解：如图，由题意得，AB＝1.6m，BC＝2m，CD＝12m，根据镜面反射可知：∠ACB＝∠ECD，∵AB⊥BD，DE⊥BD，∴∠ABC＝∠EDC＝90°，∴△ACB∽△ECD，∴，即，∴ED＝9.6（m），故选：C．7．在三角形ABO中，已知点A（﹣6，3），B（﹣6，﹣4），以原点O为位似中心，相似比为，把△ABO 缩小，则点A的对称点A′的坐标是（）A．（﹣2，1）B．（﹣8，4）C．（﹣8，4）或（8，﹣4）D．（﹣2，1）或（2，﹣1）【答案】D【解答】解：∵以原点O为位似中心，相似比为，把△ABO缩小，点A的坐标为（﹣6，3），∴点A的对称点A′的坐标为（﹣6×，3×）或（6×，﹣3×），即（﹣2，1）或（2，﹣1），故选：D．8．如图，在等边三角形ABC中，BC＝6，点D是边AB上一点，且BD＝2，点P是边BC上一动点（D、P 两点均不与端点重合），作∠DPE＝60°，PE交边AC于点E．若CE＝a，当满足条件的点P有且只有一个时，则a的值为（）A．4B．C．D．5【答案】C【解答】解：∵△ABC是等边三角形，∴∠B＝∠C＝60°，∴∠BDP+∠BPD＝180°﹣∠B＝120°，∵∠DPE＝60°，∴∠BPD+∠CPE＝120°，∴∠BDP＝∠CPE，∵∠B＝∠C＝60°，∴△BDP∽△CPE；∴，∴，∴BP2﹣6BP+2a＝0，∵满足条件的点P有且只有一个，∴方程BP2﹣6BP+2a＝0有两个相等的实数根，∴△＝62﹣4×2a＝0，∴a＝．故选：C．9．如图，四边形ABCD是一张矩形纸片．将其按如图所示的方式折叠：使DA边落在DC边上，点A落在点H处，折痕为DE；使CB边落在CD边上，点B落在点G处，折痕为CF．若矩形HEFG与原矩形A BCD相似，AD＝1，则CD的长为（）A．﹣1B．﹣1C．+1D．+1【答案】C【解答】解：设HG＝x，∵四边形ABCD是矩形，∴∠A＝∠ADH＝90°，AD＝BC＝1，由折叠得：∠A＝∠AHE＝90°，AD＝DH＝1，BC＝CG＝1，∴四边形ADHE是矩形，∵AD＝DH，∴四边形ADHE是正方形，∴AD＝HE＝1，∵矩形HEFG与原矩形ABCD相似，∴＝，∴＝，解得：x＝﹣1或x＝﹣﹣1，经检验：x＝﹣1或x＝﹣﹣1都是原方程的根，∵GH＞0，∴GH＝﹣1，∴DC＝2+x＝+1，故选：C．10．如图，正方形ABCD的边长为4，点E，F分别在边DC，BC上，且BF＝CE，AE平分∠CAD，连接D F，分别交AE，AC于点G，M．P是线段AG上的一个动点，过点P作PN⊥AC，垂足为N，连接PM．有下列四个结论：①AE垂直平分DM；②PM+PN的最小值为3；③CF2＝GE•AE；④S△ADM＝6．其中正确的是（）A．①②B．②③④C．①③④D．①③【答案】D【解答】解：①∵四边形ABCD是正方形，∴AD＝DC＝BC，∠ADC＝∠DCB＝90°，∵BF＝CE，∴BC﹣BF＝DC﹣CE，即CF＝DE，在△ADE和△DCF中，，∴△ADE≌△DCF（SAS），∴∠DAE＝∠CDF，∵∠CDF+∠ADG＝90°，∴∠DAE+∠ADG＝90°，∴∠AGD＝90°，∴∠AGM＝90°，∴∠AGM＝∠AGD，∵AE平分∠CAD，∴∠MAG＝∠DAG，又AG为公共边，∴△AGM≌△AGD（ASA），∴GM＝GD，又∵∠AGM＝∠AGD＝90°，∴AE垂直平分DM，故①正确；②如图，连接BD与AC交于点O，交AG于点H，连接HM，∵四边形ABCD是正方形，∴AC⊥BD，即DO⊥AM，∵AE垂直平分DM，∴HM＝HD，当点P与点H重合时，PM+PN的值最小，此时PM+PN＝HM+HO＝HD+HO＝DO，即PM+PN的最小值是DO的长，∵正方形ABCD的边长为4，∴AC＝BD＝，∴，即PM+PN的最小值为，故②错误；③∵AE垂直平分DM，∴∠DGE＝90°，∵∠ADC＝90°，∴∠DGE＝∠ADE，又∵∠DEG＝∠AED，∴△DGE∽△ADE，∴，即DE2＝GE•AE，由①知CF＝DE，∴CF2＝GE•AE，故③正确；④∵AE垂直平分DM，∴AM＝AD＝4，又，∴，故④错误；综上，正确的是：①③，故选：D．二、填空题(本题共6题，每小题2分，共12分）。

《图形相似》提升训练.一．选择题（共14小题）1．如图，将矩形ABCD沿AE折叠，点D的对应点落在BC上点F处，过点F作FG∥CD，连接EF，DG，下列结论中正确的有（）①∠ADG=∠AFG；②四边形DEFG是菱形；③DG2=AE•EG；④若AB=4，AD=5，则CE=1．A．①②③④B．①②③C．①③④D．①②2．如图，在△ABC中，D为AB边上一点，E为CD中点，AC=，∠ABC=30°，∠A=∠BED=45°，则BD的长为（）A．B． +1﹣C．﹣D．﹣13．如图，在Rt△ABC中，∠ABC=90°，AB=6，AC=10，∠BAC和∠ACB的平分线相交于点E，过点E作EF∥BC交AC于点F，那么EF的长为（）A．B．C．D．4．（易错题）已知：如图，∠ADE=∠ACD=∠ABC，图中相似三角形共有（）A．1对 B．2对 C．3对 D．4对5．如图，平面直角坐标系中O是原点，平行四边形ABCO的顶点A、C的坐标分别（8，0）、（3，4），点D，E把线段OB三等分，延长CD、CE分别交OA、AB 于点F，G，连接FG．则下列结论：①F是OA的中点；②△OFD与△BEG相似；③四边形DEGF的面积是；④OD=．正确的个数是（）A．4个 B．3个 C．2个 D．1个6．如图，点P是边长为的正方形ABCD的对角线BD上的动点，过点P分别作PE⊥BC于点E，PF⊥DC于点F，连接AP并延长，交射线BC于点H，交射线DC于点M，连接EF交AH于点G，当点P在BD上运动时（不包括B、D两点），以下结论中：①MF=MC；②AH⊥EF；③AP2=PM•PH；④EF的最小值是．其中正确结论是（）A．①③B．②③C．②③④D．②④7．如图，在正方形ABCD中，O是对角线AC与BD的交点，M是BC边上的动点（点M不与B，C重合），CN⊥DM，CN与AB交于点N，连接OM，ON，MN．下列五个结论：①△CNB≌△DMC；②△CON≌△DOM；③△OMN∽△OAD；④AN2+CM2=MN2；⑤若AB=2，则S△OMN的最小值是，其中正确结论的个数是（）A．2 B．3 C．4 D．58．如图，△ABC中，D、E是BC边上的点，BD：DE：EC=3：2：1，M在AC边上，CM：MA=1：2，BM交AD，AE于H，G，则BH：HG：GM等于（）A．3：2：1 B．5：3：1 C．25：12：5 D．51：24：109．如图，矩形纸片ABCD中，G、F分别为AD、BC的中点，将纸片折叠，使D 点落在GF上，得到△HAE，再过H点折叠纸片，使B点落在直线AB上，折痕为PQ．连接AF、EF，已知HE=HF，下列结论：①△MEH为等边三角形；②AE⊥EF；③△PHE∽△HAE；④=，其中正确的结论是（）A．①②③B．①②④C．①③④D．①②③④10．如图，在Rt△ABC中，∠C=90°，P是BC边上不同于B，C的一动点，过点P 作PQ⊥AB，垂足为Q，连接AP．若AC=3，BC=4，则△AQP的面积的最大值是（）A．B．C．D．11．如图，在梯形ABCD中，AD∥BC，对角线AC与BD相交于点O，如果S△ACD：S△ABC=1：2，那么S△AOD：S△BOC是（）A．1：3 B．1：4 C．1：5 D．1：612．在△ABC与△A′B′C′中，有下列条件：（1），（2）；（3）∠A=∠A′；（4）∠C=∠C′，如果从中任取两个条件组成一组，那么能判断△ABC∽△A′B′C′的共有（）A．1组 B．2组 C．3组 D．4组13．如图，在正方形ABCD中，AC为对角线，E为AB上一点，过点E作EF∥AD，与AC、DC分别交于点G，F，H为CG的中点，连接DE，EH，DH，FH．下列结论中结论正确的有（）①EG=DF；②∠AEH+∠ADH=180°；③△EHF≌△DHC；④若=，则S△EDH =13S△CFH．A．1个 B．2个 C．3个 D．4个14．如图，在正方形ABCD中，AC为对角线，E为AB上一点，过点E作EF∥AD，与AC、DC 分别交于点G，F，H为CG的中点，连结DE、EH、DH、FH．下列结论：①EG=DF；②△EHF≌△DHC；③∠AEH+∠ADH=180°；④若=，则=．其中结论正确的有（）A．1个 B．2个 C．3个 D．4个二．填空题（共5小题）15．大自然是美的设计师，即使是一片小小的树叶，也蕴含着“黄金分割”，如图，P为AB的黄金分割点（AP＞PB），如果AB的长度为10cm，那么PB的长度为cm．16．如图，在正方形ABCD中，△BPC是等边三角形，BP、CP的延长线分别交AD于点E、F，连结BD、DP，BD与CF相交于点H，给出下列结论：①△DFP～△BPH；②==；③PD2=PH•CD；④=，其中正确的是（写出所有正确结论的序号）．17．如图，在△ABC中，点D、E分别是边AB、AC的中点，DF过EC的中点G并与BC的延长线交于点F，BE与DF交于点O．若△ADE的面积为4，则四边形BOGC的面积=．18．如图，在菱形ABCD中，∠B=60°，BC=6，E为BC中点，F是AB上一点，G 为AD上一点，且BF=2，∠FEG=60°，EG交AC于点H，下列结论正确的是．（填序号即可）①△BEF∽△CHE②AG=1③EH==3S△AGH④S△BEF19．已知菱形A1B1C1D1的边长为2，∠A1B1C1=60°，对角线A1C1、B1D1相交于点O，以点O为坐标原点，分别以OB1，OA1所在直线为x轴、y轴建立如图所示的直角坐标系，以B1D1为对角线作菱形B1C2D1A2∽菱形A1B1C1D1，再以A2C2为对角线作菱形A2B2C2D2∽菱形B1C2D1A2，再以B2D2为对角线作菱形B2C3D2A3∽菱形A2B2C2D2，…，按此规律继续作下去，在y轴的正半轴上得到点A1，A2，A3，…，A n，则点A2022的坐标为三．解答题（共7小题）20．如图，在△ABC中，点D在边BC上，联结AD，∠ADB=∠CDE，DE交边AC 于点E，DE交BA延长线于点F，且AD2=DE•DF．（1）求证：△BFD∽△CAD；（2）求证：BF•DE=AB•AD．21．已知四边形ABCD中，AB=AD，对角线AC平分∠DAB，过点C作CE⊥AB于点E，点F为AB上一点，且EF=EB，连结DF．（1）求证：CD=CF；（2）连结DF，交AC于点G，求证：△DGC∽△ADC；（3）若点H为线段DG上一点，连结AH，若∠ADC=2∠HAG，AD=3，DC=2，求的值．22．如图①，OP为一墙面，它与地面OQ垂直，有一根木棒AB如图放置，点C是它的中点，现在将木棒的A点在OP上由A点向下滑动，点B由O点向OQ方向滑动，直到AB横放在地面为止．（1）在AB滑动过程中，点C经过的路径可以用下列哪个图象来描述（）（2）若木棒长度为2m，如图②射线OM与地面夹角∠MOQ=60°，当AB滑动过程中，与OM并于点D，分别求出当AD=、AD=1、AD=时，OD的值．（3）如图③，是一个城市下水道，下水道入口宽40cm，下水道水平段高度为40cm，现在要想把整根木棒AB通入下水道水平段进行工作，那么这根木棒最长可以是（cm）（直接写出结果，结果四舍五入取整数）．23．如图，△ABC和△BEC均为等腰直角三角形，且∠ACB=∠BEC=90°，点P为线段BE延长线上一点，连接CP，以CP为直角边向下作等腰直角△CPD，线段BE与CD相交于点F．（1）求证：=；（2）连接BD，请你判断AC与BD有什么位置关系？并说明理由．24．如图（1），P为△ABC所在平面上一点，且∠APB=∠BPC=∠CPA=120°，则点P叫做△ABC的费马点．（1）如果点P为锐角△ABC的费马点，且∠ABC=60°．①求证：△ABP∽△BCP；②若PA=3，PC=4，则PB=．（2）已知锐角△ABC，分别以AB、AC为边向外作正△ABE和正△ACD，CE和BD 相交于P点．如图（2）①求∠CPD的度数；②求证：P点为△ABC的费马点．25．如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别为A（﹣1，2），B（﹣3，4），C（﹣2，6）．（1）画出△ABC绕点A顺时针旋转90°后得到的△A1B1C1；（2）以原点O为位似中心，在图中画出将△A1B1C1三条边放大为原来的2倍后的△A2B2C2，并写出A2、B2、C2的坐标．26．在四边形ABCD中，点E为AB边上的一点，点F为对角线BD上的一点，且EF⊥AB．（1）若四边形ABCD为正方形．①如图1，请直接写出AE与DF的数量关系；②将△EBF绕点B逆时针旋转到图2所示的位置，连接AE，DF，猜想AE与DF 的数量关系并说明理由．（2）若四边形ABCD为矩形，BC=mAB，其他条件都不变．①如图3，猜想AE与DF的数量关系并说明理由；②将△EBF绕点B顺时针旋转α（0°＜α＜90°）得到△E′BF′，连接AE′，DF′，请在图4中画出草图，并直接写出AE′和DF′的数量关系．参考答案与试题解析一．选择题（共14小题）1．如图，将矩形ABCD沿AE折叠，点D的对应点落在BC上点F处，过点F作FG∥CD，连接EF，DG，下列结论中正确的有（）①∠ADG=∠AFG；②四边形DEFG是菱形；③DG2=AE•EG；④若AB=4，AD=5，则CE=1．A．①②③④B．①②③C．①③④D．①②【解答】解：①由折叠可得，AD=AF，DG=FG，在△ADG和△AFG中，，∴△ADG≌△AFG（SSS），∴∠ADG=∠AFG，故①正确；②∵GF∥DC，∴∠EGF=∠DEG，由翻折的性质可知：GD=GF，DE=EF，∠DGE=∠EGF，∴∠DGE=∠DEG，∴GD=DE，∴DG=GF=DE=EF，∴四边形DEFG为菱形，故②正确；③如图所示，连接DF交AE于O，∵四边形DEFG为菱形，∴GE⊥DF，OG=OE=GE，∵∠DOE=∠ADE=90°，∠OED=∠DEA，∴△DOE∽△ADE，∴=，即DE2=EO•AE，∵EO=GE，DE=DG，∴DG2=AE•EG，故③正确；④由折叠可得，AF=AD=5，∴Rt△ABF中，BF==3，∴CF=5﹣3=2，设CE=x，则DE=EF=4﹣x，∵Rt△CEF中，CE2+CF2=EF2，∴x2+22=（4﹣x）2，解得x=，∴CE=，故④错误；故选：B．2．如图，在△ABC中，D为AB边上一点，E为CD中点，AC=，∠ABC=30°，∠A=∠BED=45°，则BD的长为（）A．B． +1﹣C．﹣D．﹣1【解答】解：如图，过C作CF⊥AB于F，过点B作BG⊥CD于G，在Rt△BEG 中，∠BED=45°，则GE=GB．在Rt△AFC中，∠A=45°，AC=，则AF=CF==1，在Rt△BFC中，∠ABC=30°，CF=1，则BC=2CF=2，BF=CF=，设DF=x，CE=DE=y，则BD=﹣x，∴△CDF∽△BDG，∴==，∴==，∴DG=，BG=，∵GE=GB，∴y+=，∴2y2+x（﹣x）=﹣x，在Rt△CDF中，∵CF2+DF2=CD2，∴1+x2=4y2，∴+x（﹣x）=﹣x，整理得：x2﹣（2+2）x+2﹣1=0，解得x=1+﹣或1+﹣（舍弃），∴BD=﹣x=﹣1．故选：D．3．如图，在Rt△ABC中，∠ABC=90°，AB=6，AC=10，∠BAC和∠ACB的平分线相交于点E，过点E作EF∥BC交AC于点F，那么EF的长为（）A．B．C．D．【解答】解：如图，延长FE交AB于点D，作EG⊥BC于点G，作EH⊥AC于点H，∵EF∥BC、∠ABC=90°，∴FD⊥AB，∵EG⊥BC，∴四边形BDEG是矩形，∵AE平分∠BAC、CE平分∠ACB，∴ED=EH=EG，∠DAE=∠HAE，∴四边形BDEG是正方形，在△DAE和△HAE中，，∴△DAE≌△HAE（SAS），∴AD=AH，同理△CGE≌△CHE，∴CG=CH，∵BC===8，设BD=BG=x，则AD=AH=6﹣x、CG=CH=8﹣x，∴6﹣x+8﹣x=10，解得：x=2，∴BD=DE=2，AD=4，∵DF∥BC，∴△ADF∽△ABC，∴=，即=，解得：DF=，则EF=DF﹣DE=﹣2=．故选：C．4．（易错题）已知：如图，∠ADE=∠ACD=∠ABC，图中相似三角形共有（）A．1对 B．2对 C．3对 D．4对【解答】解：∵∠ADE=∠ACD=∠ABC∴DE∥BC∴△ADE∽△ABC，∵DE∥BC∴∠EDC=∠DCB，∵∠ACD=∠ABC，∴△EDC∽△DCB，同理：∠ACD=∠ABC，∠A=∠A，∴△ABC∽△ACD，∵△ADE∽△ABC，△ABC∽△ACD，∴△ADE∽△ACD∴共4对故选：D．5．如图，平面直角坐标系中O是原点，平行四边形ABCO的顶点A、C的坐标分别（8，0）、（3，4），点D，E把线段OB三等分，延长CD、CE分别交OA、AB 于点F，G，连接FG．则下列结论：①F是OA的中点；②△OFD与△BEG相似；③四边形DEGF的面积是；④OD=．正确的个数是（）A．4个 B．3个 C．2个 D．1个【解答】解：①∵四边形OABC是平行四边形，∴BC∥OA，BC=OA，∴△CDB∽△FDO，∴=，∵D、E为OB的三等分点，∴==2，∴=2，∴BC=2OF，∴OA=2OF，∴F是OA的中点；所以①结论正确；②如图2，延长BC交y轴于H，由C（3，4）知：OH=4，CH=3，∴OC=5，∴AB=OC=5，∵A（8，0），∴OA=8，∴OA≠AB，∴∠AOB≠∠EBG，∴△OFD∽△BEG不成立，所以②结论不正确；③由①知：F为OA的中点，同理得；G是AB的中点，∴FG是△OAB的中位线，∴FG=OB，FG∥OB，∵OB=3DE，∴FG=DE，∴=，过C作CQ⊥AB于Q，如图3．S▱OABC=OA•OH=AB•CQ，∴4×8=5CQ，∴CQ=，S△OCF=OF•OH=×4×4=8，S△CGB=BG•CQ=××=8，S△AFG=×4×2=4，∴S△CFG=S▱OABC﹣S△OFC﹣S△CBG﹣S△AFG=8×4﹣8﹣8﹣4=12，∵DE∥FG，∴△CDE∽△CFG，∴=（）2=，∴=，∴S四边形DEGF =S△CFG=；所以③结论正确；④在Rt△OHB中，由勾股定理得：OB2=BH2+OH2，∴OB==，∴OD=，所以④结论不正确；本题结论正确的有：①③．故选：C．6．如图，点P是边长为的正方形ABCD的对角线BD上的动点，过点P分别作PE⊥BC于点E，PF⊥DC于点F，连接AP并延长，交射线BC于点H，交射线DC于点M，连接EF交AH于点G，当点P在BD上运动时（不包括B、D两点），以下结论中：①MF=MC；②AH⊥EF；③AP2=PM•PH；④EF的最小值是．其中正确结论是（）A．①③B．②③C．②③④D．②④【解答】解：①错误．因为当点P与BD中点重合时，CM=0，显然FM≠CM；②正确．连接PC交EF于O．根据对称性可知∠DAP=∠DCP，∵四边形PECF是矩形，∴OF=OC，∴∠OCF=∠OFC，∴∠OFC=∠DAP，∵∠DAP+∠AMD=90°，∴∠GFM+∠AMD=90°，∴∠FGM=90°，∴AH⊥EF．③正确．∵AD∥BH，∴∠DAP=∠H，∵∠DAP=∠PCM，∴∠PCM=∠H，∵∠CPM=∠HPC，∴△CPM∽△HPC，∴=，∴PC2=PM•PH，根据对称性可知：PA=PC，∴PA2=PM•PH．④正错误．∵四边形PECF是矩形，∴EF=PC，∴当CP⊥BD时，PC的值最小，此时A、P、C共线，∵AC=2，∴PC的最小值为1，∴EF的最小值为1；故选：B．7．如图，在正方形ABCD中，O是对角线AC与BD的交点，M是BC边上的动点（点M不与B，C重合），CN⊥DM，CN与AB交于点N，连接OM，ON，MN．下列五个结论：①△CNB≌△DMC；②△CON≌△DOM；③△OMN∽△OAD；④AN2+CM2=MN2；⑤若AB=2，则S△OMN的最小值是，其中正确结论的个数是（）A．2 B．3 C．4 D．5【解答】解：∵正方形ABCD中，CD=BC，∠BCD=90°，∴∠BCN+∠DCN=90°，又∵CN⊥DM，∴∠CDM+∠DCN=90°，∴∠BCN=∠CDM，又∵∠CBN=∠DCM=90°，∴△CNB≌△DMC（ASA），故①正确；根据△CNB≌△DMC，可得CM=BN，又∵∠OC M=∠OBN=45°，OC=OB，∴△OCM≌△OBN（SAS），∴OM=ON，∠COM=∠BON，∴∠DOC+∠COM=∠COB+∠BPN，即∠DOM=∠CON，又∵DO=CO，∴△CON≌△DOM（SAS），故②正确；∵∠BON+∠BOM=∠COM+∠BOM=90°，∴∠MON=90°，即△MON是等腰直角三角形，又∵△AOD是等腰直角三角形，∴△OMN∽△OAD，故③正确；∵AB=BC，CM=BN，∴BM=AN，又∵Rt△BMN中，BM2+BN2=MN2，∴AN2+CM2=MN2，故④正确；∵△OCM≌△OBN，∴四边形BMON的面积=△BOC的面积=1，即四边形BMON的面积是定值1，∴当△MNB的面积最大时，△MNO的面积最小，设BN=x=CM，则BM=2﹣x，∴△MNB的面积=x（2﹣x）=﹣x2+x，∴当x=1时，△MNB的面积有最大值，的最小值是1﹣=，故⑤正确；此时S△OMN综上所述，正确结论的个数是5个，故选：D．8．如图，△ABC中，D、E是BC边上的点，BD：DE：EC=3：2：1，M在AC边上，CM：MA=1：2，BM交AD，AE于H，G，则BH：HG：GM等于（）A．3：2：1 B．5：3：1 C．25：12：5 D．51：24：10【解答】解：连接EM，CE：CD=CM：CA=1：3∴EM平行于AD∴△BHD∽△BME，△CEM∽△CDA∴HD：ME=BD：BE=3：5，ME：AD=CM：AC=1：3∴AH=（3﹣）ME，∴AH：ME=12：5∴HG：GM=AH：EM=12：5设GM=5k，GH=12k，∵BH：HM=3：2=BH：17k∴BH=K，∴BH：HG：GM=k：12k：5k=51：24：10故选：D．9．如图，矩形纸片ABCD中，G、F分别为AD、BC的中点，将纸片折叠，使D 点落在GF上，得到△HAE，再过H点折叠纸片，使B点落在直线AB上，折痕为PQ．连接AF、EF，已知HE=HF，下列结论：①△MEH为等边三角形；②AE⊥EF；③△PHE∽△HAE；④=，其中正确的结论是（）A．①②③B．①②④C．①③④D．①②③④【解答】解：∵矩形纸片ABCD中，G、F分别为AD、BC的中点，∴GF⊥AD，由折叠可得，AH=AD=2AG，∠AHE=∠D=90°，∴∠AHG=30°，∠EHM=90°﹣30°=60°，∴∠HAG=60°=∠AED=∠MEH，∴△EHM中，∠EMH=60°=∠EHM=∠MEH，∴△MEH为等边三角形，故①正确；∵∠EHM=60°，HE=HF，∴∠HEF=30°，∴∠FEM=60°+30°=90°，即AE⊥EF，故②正确；∵∠PEH=∠MHE=60°=∠HEA，∠EPH=∠EHA=90°，∴△PHE∽△HAE，故③正确；设AD=2=AH，则AG=1，∴Rt△AGH中，GH=AG=，Rt△AEH中，EH===HF，∴GF==AB，∴==，故④正确，综上所述，正确的结论是①②③④，故选：D．10．如图，在Rt△ABC中，∠C=90°，P是BC边上不同于B，C的一动点，过点P 作PQ⊥AB，垂足为Q，连接AP．若AC=3，BC=4，则△AQP的面积的最大值是（）A．B．C．D．【解答】解：设BP=x（0＜x＜4），由勾股定理得AB=5，∵∠PQB=∠C=90°，∠B=∠B，∴△PBQ∽△ABC，∴==，即==∴PQ=x，QB=xS △APQ =PQ ×AQ=+x= ∴当x=时，△APQ 的面积最大，最大值是．故选：C ．11．如图，在梯形ABCD 中，AD ∥BC ，对角线AC 与BD 相交于点O ，如果S △ACD ：S △ABC =1：2，那么S △AOD ：S △BOC 是（ ）A ．1：3B ．1：4C ．1：5D ．1：6【解答】解：∵在梯形ABCD 中，AD ∥BC ，而且S △ACD ：S △ABC =1：2，∴AD ：BC=1：2；∵AD ∥BC ，∴△AOD ～△BOC ，∵AD ：BC=1：2，∴S △AOD ：S △BOC =1：4．故选：B ．12．在△ABC 与△A′B′C′中，有下列条件：（1），（2）；（3）∠A=∠A′；（4）∠C=∠C′，如果从中任取两个条件组成一组，那么能判断△ABC ∽△A′B′C′的共有（ ）A ．1组B ．2组C ．3组D ．4组【解答】解：共有3组，其组合分别是（1）和（2）三边对应成比例的两个三角形相似；（2）和（4）两边对应成比例且夹角相等的两个三角形相似；（3）和（4）两角对应相等的两个三角形相似．故选：C．13．如图，在正方形ABCD中，AC为对角线，E为AB上一点，过点E作EF∥AD，与AC、DC分别交于点G，F，H为CG的中点，连接DE，EH，DH，FH．下列结论中结论正确的有（）①EG=DF；②∠AEH+∠ADH=180°；③△EHF≌△DHC；=13S△CFH．④若=，则S△EDHA．1个 B．2个 C．3个 D．4个【解答】解：①∵四边形ABCD为正方形，EF∥AD，∴EF=AD=CD，∠ACD=45°，∠GFC=90°，∴△CFG为等腰直角三角形，∴GF=FC，∵EG=EF﹣GF，DF=CD﹣FC，∴EG=DF，故①正确；②∵△CFG为等腰直角三角形，H为CG的中点，∴FH=CH，∠GFH=∠GFC=45°=∠HCD，在△EHF和△DHC中，，∴△EHF ≌△DHC （SAS ），∴∠HEF=∠HDC ，∴∠AEH +∠ADH=∠AEF +∠HEF +∠ADF ﹣∠HDC=∠AEF +∠ADF=180°，故②正确；③由②知：△EHF ≌△DHC ，故③正确； ④∵=，∴AE=2BE ，∵△CFG 为等腰直角三角形，H 为CG 的中点，∴FH=GH ，∠FHG=90°，∵∠EGH=∠FHG +∠HFG=90°+∠HFG=∠HFD ，在△EGH 和△DFH 中，，∴△EGH ≌△DFH （SAS ），∴∠EHG=∠DHF ，EH=DH ，∠DHE=∠EHG +∠DHG=∠DHF +∠DHG=∠FHG=90°， ∴△EHD 为等腰直角三角形，过H 点作HM 垂直于CD 于M 点，如图所示：设HM=x ，则CF=2x ，∴DF=2FC=4x ，∴DM=5x ，DH=x ，CD=6x ，则S △CFH =×HM ×CF=•x•2x=x 2，S △EDH =×DH 2=×=13x 2， ∴则S △EDH =13S △CFH ，故④正确；其中结论正确的有：①②③④，4个；故选：D ．14．如图，在正方形ABCD中，AC为对角线，E为AB上一点，过点E作EF∥AD，与AC、DC 分别交于点G，F，H为CG的中点，连结DE、EH、DH、FH．下列结论：①EG=DF；②△EHF≌△DHC；③∠AEH+∠ADH=180°；④若=，则=．其中结论正确的有（）A．1个 B．2个 C．3个 D．4个【解答】解：①∵四边形ABCD为正方形，EF∥AD，∴EF=AD=CD，∠ACD=45°，∠GFC=90°，∴△CFG为等腰直角三角形，∴GF=FC，∵EG=EF﹣GF，DF=CD﹣FC，∴EG=DF，故①正确；②∵△CFG为等腰直角三角形，H为CG的中点，∴FH=CH，∠GFH=∠GFC=45°=∠HCD，在△EHF和△DHC中，，∴△EHF≌△DHC（SAS），故②正确；③∵△EHF≌△DHC（已证），∴∠HEF=∠HDC，∴∠AEH+∠ADH=∠AEF+∠HEF+∠ADF﹣∠HDC=∠AEF+∠ADF=180°，故③正确；④∵=，∴AE=2BE，∵△CFG为等腰直角三角形，H为CG的中点，∴FH=GH，∠FHG=90°，∵∠EGH=∠FHG+∠HFG=90°+∠HFG=∠HFD，在△EGH和△DFH中，，∴△EGH≌△DFH（SAS），∴∠EHG=∠DHF，EH=DH，∠DHE=∠EHG+∠DHG=∠DHF+∠DHG=∠FHG=90°，∴△EHD为等腰直角三角形，如图，过H点作HM⊥CD于M，设HM=x，则DM=5x，DH=x，CD=6x，则S△DHC =×HM×CD=3x2，S△EDH=×DH2=13x2，∴3S△EDH =13S△DHC，故④正确；故选：D．二．填空题（共5小题）15．大自然是美的设计师，即使是一片小小的树叶，也蕴含着“黄金分割”，如图，P为AB的黄金分割点（AP＞PB），如果AB的长度为10cm，那么PB的长度为（15﹣5）cm．【解答】解：∵P为AB的黄金分割点（AP＞PB），∴AP=AB=×10=5﹣5，∴PB=AB﹣PA=10﹣（5﹣5）=（15﹣5）cm．故答案为（15﹣5）．16．如图，在正方形ABCD中，△BPC是等边三角形，BP、CP的延长线分别交AD于点E、F，连结BD、DP，BD与CF相交于点H，给出下列结论：①△DFP～△BPH；②==；③PD2=PH•CD；④=，其中正确的是①②③（写出所有正确结论的序号）．【解答】解：∵PC=CD，∠PCD=30°，∴∠PDC=75°，∴∠FDP=15°，∵∠DBA=45°，∴∠PBD=15°，∴∠FDP=∠PBD，∵∠DFP=∠BPC=60°，∴△DFP∽△BPH，故①正确；∵∠DCF=90°﹣60°=30°，∴tan∠DCF==，∵△DFP∽△BPH，∴==，∵BP=CP=CD，∴==，故②正确；∵PC=DC，∠DCP=30°，∴∠CDP=75°，又∵∠DHP=∠DCH+∠CDH=75°，∴∠DHP=∠CDP，而∠DPH=∠CPD，∴△DPH∽△CPD，∴，即PD2=PH•CP，又∵CP=CD，∴PD2=PH•CD，故③正确；如图，过P作PM⊥CD，PN⊥BC，设正方形ABCD的边长是4，△BPC为正三角形，则正方形ABCD的面积为16，∴∠PBC=∠PCB=60°，PB=PC=BC=CD=4，∴∠PCD=30°∴PN=PB•sin60°=4×=2，PM=PC•sin30°=2，=S四边形PBCD﹣S△BCD=S△PBC+S△PDC﹣S△BCD∵S△BPD=×4×2+×2×4﹣×4×4=4+4﹣8=4﹣4，∴=，故④错误；故答案为：①②③．17．如图，在△ABC中，点D、E分别是边AB、AC的中点，DF过EC的中点G 并与BC的延长线交于点F，BE与DF交于点O．若△ADE的面积为4，则四边形BOGC的面积=7．【解答】解：∵点D、E分别是边AB、AC的中点，∴DE∥BC，DE=BC，∴△ADE∽△ABC，∴==，∵△ADE的面积为4，=16，∴S△ABC∵DE∥BC，∴△ODE∽△OFB，∠EDG=∠F，∠DEG=∠GCF，∴=，又EG=CG，∴△DEG≌△FCG（AAS），∴DE=CF，∴BF=3DE，∵DE∥BC，∴△ODE∽△OFB，∴==，∵AD=BD，=S△ADE=4，∴S△BDE∵AE=CE=2EG，∴S △DEG =S △ADE =×4=2， ∵=，∴S △ODE =S △BDE =×4=1，∴S △OEG =S △DEG ﹣S △ODE =×4=1，∵S 四边形DBCE =S △ABC ﹣S △ADE =3×4=12，∴S 四边形OBCG =S 四边形DBCE ﹣S △BDE ﹣S △OEG =7．故答案为：7．18．如图，在菱形ABCD 中，∠B=60°，BC=6，E 为BC 中点，F 是AB 上一点，G 为AD 上一点，且BF=2，∠FEG=60°，EG 交AC 于点H ，下列结论正确的是①②③．（填序号即可）①△BEF ∽△CHE②AG=1③EH=④S △BEF =3S △AGH【解答】解：∵菱形ABCD 中，∠B=60°，∠FEG=60°，∴∠B=∠ECH=60°，∠BEF=CHE=120°﹣∠CEH ，∴△BEF ∽△CHE ，故①正确；∴=，又∵BC=6，E为BC中点，BF=2，∴，即CH=4.5，又∵AC=BC=6，∴AH=1.5，∵AG∥CE，∴△AGH∽△CEH，∴，∴AG=CE=1，故②正确；如图，过F作FP⊥BC于P，则∠BFP=30°∴BP=BF=1，PE=3﹣1=2，PF=，∴Rt△EFP中，EF==，又∵，∴EH=EF=，故③正确；∵AG=CE，BF=CE，△△BEF∽△CHE，△AGH∽△CEH，∴S△CEH=9S△AGH，S△CEH=S△BEF，∴9S△AGH =S△BEF，∴S△BEF =4S△AGH，故④错误；故答案为：①②③．19．已知菱形A1B1C1D1的边长为2，∠A1B1C1=60°，对角线A1C1、B1D1相交于点O，以点O为坐标原点，分别以OB1，OA1所在直线为x轴、y轴建立如图所示的直角坐标系，以B1D1为对角线作菱形B1C2D1A2∽菱形A1B1C1D1，再以A2C2为对角线作菱形A2B2C2D2∽菱形B1C2D1A2，再以B2D2为对角线作菱形B2C3D2A3∽菱形A2B2C2D2，…，按此规律继续作下去，在y轴的正半轴上得到点A1，A2，A3，…，A n，则点A2022的坐标为（0，32021）【解答】解：∵菱形A1B1C1D1的边长为2，∠A1B1C1=60°，∴OA1=A1B1•sin30°=2×=1，OB1=A1B1•cos30°=2×=，∴A1（0，1）．∵1C2D1A2∽菱形A1B1C1D1，∴OA2===3，∴A2（0，3）．同理可得A3（0，9）…∴A2022（0，32021）．故答案为：（0，32021）．三．解答题（共7小题）20．如图，在△ABC中，点D在边BC上，联结AD，∠ADB=∠CDE，DE交边AC 于点E，DE交BA延长线于点F，且AD2=DE•DF．（1）求证：△BFD∽△CAD；（2）求证：BF•DE=AB•AD．【解答】证明：（1）∵AD2=DE•DF，∴，∵∠ADF=∠EDA，∴△ADF∽△EDA，∴∠F=∠DAE，又∵∠ADB=∠CDE，∴∠ADB+∠ADF=∠CDE+∠ADF，即∠BDF=∠CDA，∴△BFD∽△CAD；（2）∵△BFD∽△CAD，∴，∵，∴，∵△BFD∽△CAD，∴∠B=∠C，∴AB=AC，∴，∴BF•DE=AB•AD．21．已知四边形ABCD中，AB=AD，对角线AC平分∠DAB，过点C作CE⊥AB于点E，点F为AB上一点，且EF=EB，连结DF．（1）求证：CD=CF；（2）连结DF，交AC于点G，求证：△DGC∽△ADC；（3）若点H为线段DG上一点，连结AH，若∠ADC=2∠HAG，AD=3，DC=2，求的值．【解答】（1）证明：∵AC平分∠DAB，∴∠DAC=∠BAC，在△ADC和△ABC中∴△ADC≌△ABC，∴CD=CB，∵CE⊥AB，EF=EB，∴CF=CB，∴CD=CF；（2）解：∵△ADC≌△ABC，∴∠ADC=∠B，∵CF=CB，∴∠CFB=∠B，∴∠ADC=∠CFB，∴∠ADC+∠AFC=180°，∵四边形AFCD的内角和等于360°，∴∠DCF+∠DAF=180°，∵CD=CF，∴∠CDG=∠CFD，∵∠DCF+∠CDF+∠CFD=180°，∴∠DAF=∠CDF+∠CFD=2∠CDG，∵∠DAB=2∠DAC，∴∠CDG=∠DAC，∵∠DCG=∠ACD，∴△DGC∽△ADC；（3）解：∵△DGC∽△ADC，∴∠DGC=∠ADC，=，∵∠ADC=2∠HAG，AD=3，DC=2，∴∠HAG=∠DGC，=，∴∠HAG=∠AHG，=，∴HG=AG，∵∠GDC=∠DAC=∠FAG，∠DGC=∠AGF，∴△DGC∞△AGF，∴==，∴=．22．如图①，OP为一墙面，它与地面OQ垂直，有一根木棒AB如图放置，点C 是它的中点，现在将木棒的A点在OP上由A点向下滑动，点B由O点向OQ方向滑动，直到AB横放在地面为止．（1）在AB滑动过程中，点C经过的路径可以用下列哪个图象来描述（）（2）若木棒长度为2m，如图②射线OM与地面夹角∠MOQ=60°，当AB滑动过程中，与OM并于点D，分别求出当AD=、AD=1、AD=时，OD的值．（3）如图③，是一个城市下水道，下水道入口宽40cm，下水道水平段高度为40cm，现在要想把整根木棒AB通入下水道水平段进行工作，那么这根木棒最长可以是113（cm）（直接写出结果，结果四舍五入取整数）．【解答】解：（1）∵点C是AB的中点，∴OC=AB，∴点C的运动轨迹是以O为圆心，AB长为半径的圆弧，经过的路程的圆周．故选甲．（2）过D作DH⊥OP于H，设DH=a，在Rt△OHD中，∵∠AOD=90°﹣600=300，∴OD=2a，OH=a，∵DH⊥OA，OQ⊥OA，∴DH∥QO，∴=，当AD=时，BD=，∴=，∴AH=a，在Rt△AHD中，∵AH2+DH2=AD2，∴a2+a2=，解得a=，OD=，当AD=1时，BD=1，∴=，∴AH=a，在Rt△AHD中，∵AH2+DH2=AD2，∴3a2+a2=1，解得a=，OD=1，当AD=时，BD=，∴=，∴AH=2a，在Rt△AHD中，∵AH2+DH2=AD2，∴12a2+a2=，解得a=，OD=．（3）由题意当等腰直角三角形的直角边为80cm时，斜边为≈113cm，所以这根木棒最长可以是113cm．故答案为113cm．23．如图，△ABC和△BEC均为等腰直角三角形，且∠ACB=∠BEC=90°，点P为线段BE延长线上一点，连接CP，以CP为直角边向下作等腰直角△CPD，线段BE与CD相交于点F．（1）求证：=；（2）连接BD，请你判断AC与BD有什么位置关系？并说明理由．【解答】（1）证明：∵，△ABC和△BEC均为等腰直角三角形，且∠ACB=∠BEC=90°，∴∠ECB=∠PCD=45°，∠CEB=∠CPD=90°，∴△BCE∽△DCP，∴=；（2）AC∥BD，理由：∵∠PCE+∠ECD=∠BCD+∠ECD=45°，∴∠PCE=∠BCD，∵=，∴△PCE∽△DCB，∴∠CBD=∠CEP=90°，∵∠ACB=90°，∴∠ACB=∠CBD，∴AC∥BD．24．如图（1），P为△ABC所在平面上一点，且∠APB=∠BPC=∠CPA=120°，则点P叫做△ABC的费马点．（1）如果点P为锐角△ABC的费马点，且∠ABC=60°．①求证：△ABP∽△BCP；②若PA=3，PC=4，则PB=2．（2）已知锐角△ABC，分别以AB、AC为边向外作正△ABE和正△ACD，CE和BD 相交于P点．如图（2）①求∠CPD的度数；②求证：P点为△ABC的费马点．【解答】（1）证明：①∵∠PAB+∠PBA=180°﹣∠APB=60°，∠PBC+∠PBA=∠ABC=60°，∴∠PAB=∠PBC，又∵∠APB=∠BPC=120°，∴△ABP∽△BCP，②解：∵△ABP∽△BCP，∴=，∴PB2=PA•PC=12，∴PB=2；故答案为：2；（2）解：①∵△ABE与△ACD都为等边三角形，∴∠BAE=∠CAD=60°，AE=AB，AC=AD，∴∠BAE+∠BAC=∠CAD+∠BAC，即∠EAC=∠BAD，在△ACE和△ABD中，，∴△ACE≌△ABD（SAS），∴∠1=∠2，∵∠3=∠4，∴∠CPD=∠6=∠5=60°；②证明：∵△ADF∽△CFP，∴AF•PF=DF•CF，∵∠AFP=∠CFD，∴△AFP∽△CDF．∴∠APF=∠ACD=60°，∴∠APC=∠CPD+∠APF=120°，∴∠BPC=120°，∴∠APB=360°﹣∠BPC﹣∠APC=120°，∴P点为△ABC的费马点．25．如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别为A（﹣1，2），B（﹣3，4），C（﹣2，6）．（1）画出△ABC绕点A顺时针旋转90°后得到的△A1B1C1；（2）以原点O为位似中心，在图中画出将△A1B1C1三条边放大为原来的2倍后的△A2B2C2，并写出A2、B2、C2的坐标．【解答】解：（1）如图，△A1B1C1为所求；（2）如图，△A2B2C2为所作，点A2、B2、C2的坐标分别为（﹣2，4），B（2，8），C（6，6）．26．在四边形ABCD中，点E为AB边上的一点，点F为对角线BD上的一点，且EF⊥AB．（1）若四边形ABCD为正方形．①如图1，请直接写出AE与DF的数量关系DF=AE；②将△EBF绕点B逆时针旋转到图2所示的位置，连接AE，DF，猜想AE与DF 的数量关系并说明理由．（2）若四边形ABCD为矩形，BC=mAB，其他条件都不变．①如图3，猜想AE与DF的数量关系并说明理由；②将△EBF绕点B顺时针旋转α（0°＜α＜90°）得到△E′BF′，连接AE′，DF′，请在图4中画出草图，并直接写出AE′和DF′的数量关系．【解答】解：（1）①∵四边形ABCD为正方形，∴△ABD为等腰直角三角形，∴BD=AB，∵EF⊥AB，∴△BEF为等腰直角三角形，BF=BE，∴BD﹣BF=AB﹣BE，即DF=AE，故答案为：DF=AE；②DF=AE．理由如下：∵△EBF绕点B逆时针旋转到图2所示的位置，∴∠ABE=∠DBF，∵=，=，∴=，∴△ABE∽△DBF，∴==，即AE与DF的数量关系是：DF=AE；（2）①AE与DF的数量关系是：DF=AE；理由：在图3中，作FM⊥AD，垂足为M．∵∠A=∠AEF=∠AMF=90°，∴四边形AEFM是矩形，∴FM=AE，∵AD=BC=mAB，∴Rt△ABD中，BD==AB，∵MF∥AB，∴△DMF∽△ABD，∴==，∴DF=MF=AE；②AE′和DF′的数量关系：DF'=AE'．如图3，∵四边形ABCD为矩形，∴AD=BC=mAB，∴B D==AB，∵EF⊥AB，∴EF∥AD，∴△BEF∽△BAD，∴=，∴==，如图4，∵△EBF绕点B顺时针旋转α（0°＜α＜90°）得到△E'BF'，∴∠ABE′=∠DBF′，BE′=BE，BF′=BF，∴==，∴△ABE′∽△DBF′，∴==，即DF′=AE′．。

2019年中考数学一轮复习相似三角形一、选择题1.下列叙述正确的是（）A．任意两个正方形一定是相似的B．任意两个矩形一定是相似的C．任意两个菱形一定是相似的D．任意两个等腰梯形一定是相似的2.Rt△ABC的两条直角边分别为3cm、4cm,与它相似的Rt△A/B/C/的斜边为20cm,那么Rt△A/B/C/的周长为（）A．48cm B．28cm C．12cm D．10cm3.如图,已知在△ABC中，点D、E、F分别是边AB、AC、BC上的点,DE∥BC，EF∥AB,且AD：DB=3：5，那么CF：CB等于（）A．5：8 B．3：8 C．3：5 D．2：54.如图,已知直线a∥b∥c,直线m,n与a,b,c分别交于点A,C,E,B,D,F,若AC=4,CE=6,BD=3,则DF的值是（）A．4 B．4.5 C．5 D．5.55.下列说法中正确的是（）①在两个边数相同的多边形中，如果对应边成比例，那么这两个多边形相似；②如果两个矩形有一组邻边对应成比例，那么这两个矩形相似；③有一个角对应相等的平行四边形都相似；④有一个角对应相等的菱形都相似.A．①②B．②③C．③④D．②④6.如图，在△ABC中，∠A=78°，AB=4，AC=6，将△ABC沿图示中的虚线剪开，剪下的阴影三角形与原三角形不相．．似．的是 ( )7.如图，在▱ABCD中，F是AD延长线上一点，连接BF交DC于点E，则图中相似三角形共有（）对.A．2对B．3对C．4对D．5对8.如图，在△ABC中，D、E分别为AB、AC边上的点，DE∥BC，BE与CD相交于点F，则下列结论一定正确的是（）A． =B．C．D．9.下列关于位似图形的表述：①相似图形一定是位似图形，位似图形一定是相似图形；②位似图形一定有位似中心；③如果两个图形是相似图形，且每组对应点的连线所在的直线都经过同一个点，那么，这两个图形是位似图形；④位似图形上任意两点与位似中心的距离之比等于位似比．其中正确命题的序号是（）A．②B．①②C．③④D．②③④10.如图，在长为8cm、宽为4cm的矩形中，截去一个矩形，使得留下的矩形（图中阴影部分）与原矩形相似，则留下矩形的面积是（）A．2cm2B．4cm2C．8cm2D．16cm211.如图，数学兴趣小组的小颖想测量教学楼前的一棵树的树高，下午课外活动时她测得一根长为1m的竹竿的影长是0.8m，但当她马上测量树高时，发现树的影子不全落在地面上，有一部分影子落在教学楼的墙壁上(如图)，她先测得留在墙壁上的影高为1.2m，又测得地面的影长为2.6m，请你帮她算一下树高是( )A．3.25m B．4.25m C．4.45m D．4.75m12.将一副三角尺（在Rt△ABC中,∠ACB=90°,∠B=60°,在Rt△EDF中，∠EDF=90°,∠E=45°)如图摆放，点D 为AB的中点，DE交AC于点P，DF经过点C，将△EDF绕点D顺时针方向旋转α（0°<α<60°），DE′交AC于点M，DF′交BC于点N，则PM：CN的值为（）A．B．C．D．13.在一张比例尺为1：50000的地图上，如果一块多边形地的面积是100cm2，那么这块地的实际面积是________m2（用科学记数法表示）．14.如图，AB∥CD∥EF，如果AC=2，AE=5.5，DF=3，那么BD= .15.如图278，正方形OABC与正方形ODEF是位似图形，O为位似中心，相似比为1：，则这两个四边形每组对应顶点到位似中心的距离之比是__________．16.如图，在菱形ABCD中，点M，N在AC上，ME⊥AD，NF⊥AB，若NF=NM=2，ME=3，则AN的长度为 .17.如图，在Rt△ABC中，∠ABC=90°，AB=3，BC=4.Rt△MPN中，∠MPN=90°，点P在AC上，PM交AB于点E，PN交BC于点F，当PE=2PF时，AP=________.18.如图，点A1、A2、A3、…，点B1、B2、B3、…，分别在射线OM、ON上，A1B1∥A2B2∥A3B3∥A4B4∥…．如果A1B1=2，A1A2=2OA1，A2A3=3OA1， A3A4=4OA1，…．那么A2B2=________，A n B n=________．（n为正整数）三、解答题19.如图，已知在△ABC中，∠ACB的平分线CD交AB于D，过B作BE∥CD交AC的延长线于点E．(1)求证：BC=CE；(2)求证：AD:BD=AC:BC;20.如图，点C、D在线段AB上，△PCD是等边三角形，若∠APB=120°.求证：△ACP∽△PDB．21.如图，在△ABC中，点D在BC边上，∠DAC=∠B.点E在AD边上，CD=CE.（1）求证：△ABD∽△CAE；（2）若AB=6，AC=4.5，BD=2，求AE的长.22.如图，在正方形ABCD中，点M是边BC上的一点（不与B、C重合），点N在CD边的延长线上，且满足∠MAN=90°，联结MN、AC，N与边AD交于点E．（1）求证；AM=AN；（2）如果∠CAD=2∠NAD，求证：AM2=AC•AE．23.如图，△ABC中，∠ACB=90°，D为AB上一点，以CD为直径的⊙O交BC于点E，连接AE交CD于点P，交⊙O于点F，连接DF，∠CAE=∠ADF.(1)判断AB与⊙O的位置关系，并说明理由；(2)若PF:PC=1:2，AF=5，求CP的长.24.如图，矩形OABC的顶点A．C分别在x轴和y轴上，点B的坐标为(2，3)，双曲线y=错误！未找到引用源。

中考数学一轮复习《相似》专项练习-带含参考答案学校:___________班级：___________姓名：___________考号：___________一、单选题1．下列四组图形中，不是相似图形的是（）A．B．C．D．2．如图，已知，那么添加下列一个条件后，仍无法判定的是（）A．B．C．D．3．小刚身高1.7m，测得他站立在阳光下的影子长为0.85m，紧接着他把手臂竖直举起，测得影子长为1.1m，那么小刚举起的手臂超出头顶（）A．0.5m B．0.55m C．0.6m D．2.2m4．如图所示，四边形中，AD//BC，∠B=90°，AB=7，AD=3，BC=4，若与相似，则符合条件的点个数是（）A．0 B．1 C．2 D．35．如图，在平面直角坐标系中，已知点，以原点为位似中心，相似比为，把缩小，则点的对应点的坐标是（）A．或B．C． D．或6．如图，四边形是平行四边形，点E在边上，连接交于点F，则（）A．2：1 B．2：3 C．2：5 D．1：37．如图，点为的重心连结CG并延长交AB于点，作于点，过点作交AC于点，则的值为（）A．1 B．C．D．8．如图，是等腰直角三角形，点O是的中点，点D是延长线上的一点，以为斜边向左侧作等腰，与交于点F，连接，平分．下列结论不成立的是（）A．B．C．D．二、填空题9．如果，那么的值为．10．如图，与交于点，若，则．11．如图，平行四边形中，E为延长线上的一点，且，交于点F.若，则的长为.12．如图，将正方形ABCD的边AB，BC绕着点A逆时针旋转一定角度，得到线段，连接交CD于点E，连接，若，则.13．如图，在中，∠C=60°，D为线段的中点，点E，F分别在，上，且，沿将折叠得到，若，则的长是．三、解答题14．如图，为了测量山坡的护坡石坝高，把一根长为的竹竿斜靠在石坝旁，量出竿上长为时，它离地面的高度为，则坝高为多少．15．已知a，b，c是的三边长，且．（1）求的值；（2）若的周长为81，求三边a，b，c的长．16．如图，在中，BC=20，BA=10，点是边上的一点，且，联结，过点作，交的延长线于点．（1）求证：；（2）如果，求的面积．17．如图，在中，点、分别在边，上，线段分别交线段，于点，G，且．（1）求证：；（2）若，求的值．18．如图，在锐角中，过点A作于点D，过点B作于点E，与相交于点H，连接.的平分线交于点F，连接交于点G. （1）求证：（2）试探究线段，BE，DE之间的数量关系；（3）若，求的长.参考答案：1．D2．C3．A4．C5．D6．C7．B8．C9．510．11．2.512．75°13．14．解：如图，过作于，则∴，即解得答：坝高为．15．（1）解：因为设，则（2）解：令，得所以，和．16．（1）证明：∵∴∵∴∴在与中∴∴∵∴∴．（2）解：∵∴设∵在中，由勾股定理得∴．∴∵∴△CAD∽△CEB ．∴∵∴．∴∴．17．（1）证明：．又；（2）解：．18．（1）证明：∵∴∴∴；（2）解：过点作，交于点则：∵∴，AD=BD ∴又∵∴∴∴是等腰直角三角形∴∴（3）解：由（2）知：∵∴∴∵的平分线交于点F∴∴∵∴∴∴∵∴∵∴∴∴过点作，垂足为则：∴∵∴∴∴∴，即：∴∴∴∵∴∴∴作，交于点则：∴，即：∴∴∵∴∴，即：∴。

第3课时 图形的相似1．已知5x ＝6y (y ≠0)，那么下列比例式中正确的是( B ) A ．x 5＝y6B ．x 6＝y5C ．x y ＝56D ．x 5＝6y2．(改编题)如图，△ABC ∽△ADE ，且∠ADE ＝∠B ，则下列比例式正确的是( D )A ．AE BE ＝AD DCB ．AE AB ＝ADACC ．AD AC ＝DE BCD ．AE AC ＝DEBC3．(2018·临沂)如图，利用标杆BE 测量建筑物的高度．已知标杆BE 高1.2 m ，测得AB ＝1.6 m ，BC ＝12.4 m ．则建筑物CD 的高是( B )A ．9.3 mB ．10.5 mC ．12.4 mD ．14 m4．(2018·梧州)如图，AG ∶GD ＝4∶1，BD ∶DC ＝2∶3，则AE ∶EC 的值是( D )A ．3∶2B ．4∶3C ．6∶5D ．8∶55．(2018·泸州)如图所示，正方形ABCD 中，E ，F 分别在边AD ，CD 上，AF ，BE 相交于点G ，若AE ＝3ED ，DF ＝CF ，则AGGF的值是( C )A ．43B ．54C ．65D ．766．(原创题)△ABC 中，AB ＝10 cm ，BC ＝20 cm ，点P 从点A 开始沿AB 边向B 点以2 cm/s 的速度移动，点Q 从点B 开始沿BC 边向点C 以4 cm/s 的速度移动，如果P ，Q 分别从A ，B 同时出发，经过多少秒钟△PBQ 与△ABC 相似( C )A ．2.5 sB ．3.5 sC ．1 s 和2.5 sD ．1 s 和3.5 s7．(改编题)在比例尺1∶6 000 000的地图上，量得南京到北京的距离是15 cm ，这两地的实际距离是__900 km __.8．(原创题)如图，∠1＝∠B ，AD ＝5 cm ，AB ＝10 cm ，则AC ＝__52 cm __.9．经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形，如果其中一个是等腰三角形，另外一个三角形和原三角形相似，那么把这条线段定义为原三角形的“和谐分割线”．如图，线段CD 是△ABC 的“和谐分割线”，△ACD 为等腰三角形，△CBD 和△ABC 相似，∠A ＝46°，则∠ACB 的度数为__113°或92°__.10．(2018·宜宾)如图，在矩形ABCD 中，AB ＝3，CB ＝2，点E 为线段AB 上的动点，将△CBE 沿CE 折叠，使点B 落在矩形内点F 处，下列结论正确的是__①②③__(写出所有正确结论的序号)．①当E 为线段AB 中点时，AF ∥CE ；②当E 为线段AB 中点时，AF ＝95；③当A ，F ，C 三点共线时，AE ＝13－2133；④当A ，F ，C 三点共线时，△CEF ≌△AEF .11．(2018·福建)求证：相似三角形对应边上的中线之比等于相似比．要求：①根据给出的△ABC 及线段A ′B ′，∠A ′(∠A ′＝∠A )，以线段A ′B ′为一边，在给出的图形上用尺规作出△A ′B ′C ′，使得△A ′B ′C ′∽△ABC ，不写作法，保留作图痕迹；②在已有的图形上画出一组对应中线，并据此写出已知、求证和证明过程． (1)如图(1)，△A′B′C′就是所求作的三角形．(2)已知：如图(2)，△A′B′C′∽△ABC ，A′B′AB ＝B′C′BC ＝A′C′AC＝k ，AD ＝DB ，A′D′＝D′B′.求证：C′D′CD＝k.证明：∵AD ＝DB ，A′D′＝D′B′，∴AD ＝12AB ，A′D′＝12A′B′，∴A′D′AD ＝12A′B′12AB ＝A′B′AB .∵△A′B′C′∽△ABC ，A′B′AB ＝A′C′AC ＝k ，∴A′D′AD ＝A′C′AC ＝k.在△C′A′D′和△CAD 中，A′D′AD ＝A′C′AC ，且∠A′＝∠A ，∴△C′A′D′∽△CAD ，∴C′D′CD ＝A′C′AC＝k. 12．(2018·合肥一模)已知四边形ABCD 中，AB ＝AD ，对角线AC 平分∠DAB ，过点C 作CE ⊥AB 于点E ，点F 为AB 上一点，且EF ＝EB ，连接DF .(1)求证：CD ＝CF ；(2)连接DF ，交AC 于点G ，求证：△DGC ∽△ADC ；(3)若点H 为线段DG 上一点，连接AH ，若∠ADC ＝2∠HAG ，AD ＝3，DC ＝2，求FGGH的值．(1)证明：∵AC 平分∠DAB ，∴∠DAC ＝∠BAC ，在△ADC 和△ABC 中，⎩⎪⎨⎪⎧AC ＝AC ，∠DAC ＝∠BAC ，AD ＝AB ，∴△ADC≌△ABC ，∴CD ＝CB ，∵CE ⊥AB ，EF ＝EB ，∴CF ＝CB ，∴CD ＝CF ；(2)解：∵△ADC≌△ABC ，∴∠ADC ＝∠B ，∵CF ＝CB ，∴∠CFB ＝∠B ，∴∠ADC ＝∠CFB ，∴∠ADC ＋∠AFC ＝180°，∵四边形AFCD 的内角和等于360°，∴∠DCF ＋∠DAF ＝180°，∵CD ＝CF ，∴∠CDG ＝∠CFD ，∵∠DCF ＋∠CDF ＋∠CFD ＝180°，∴∠DAF ＝∠CDF ＋∠CFD ＝2∠CDG ，∵∠DAB ＝2∠DAC ，∴∠CDG ＝∠DAC ，∵∠DCG ＝∠ACD ，∴△DGC ∽△ADC ；(3)解：∵△DGC ∽△ADC ，∴∠DGC ＝∠ADC ，CG CD ＝DG AD ，∵∠ADC ＝2∠HAG ，AD ＝3，DC ＝2，∴∠HAG ＝12∠DGC ，CG 2＝DG3，∴∠HAG ＝∠AHG ，CG DG ＝23，∴HG ＝AG ，∵∠GDC ＝∠DAC ＝∠FAG ，∠DGC ＝∠AGF ，∴△DGC ∽△AGF ，∴GF AG ＝CG DG ＝23，∴FG GH ＝23。

2019中考数学一轮系列复习图形的相似提升训练A （含答案）1．如图，下列条件中不能判定△ACD ∽△ABC 的是（ ）A ．AB AC BC CDB ．∠ADC ＝∠ACB C ．∠ACD ＝∠B D ．AC 2=AD ·AB 2．△ABC 与△DEF 满足下列条件，其中能使△ABC ∽△DEF 的是( )A ．AB ＝1，BC ＝1.5，AC ＝2，DE ＝8，EF ＝12，DF ＝16B ．AB ＝，BC ＝，AC ＝，DE ＝，EF ＝3，DF ＝3C ．AB ＝3，BC ＝4，AC ＝6，DE ＝6，EF ＝8，DF ＝16D ．AB ＝3，BC ＝4，AC ＝5，DE ＝，EF ＝2，DF ＝ 3．如图，已知是坐标原点，与是以点为位似中心的位似图形，且与的相似比为，如果内部一点的坐标为，则在中的对应点的坐标为（ ） A ．(-x, -y) B ．(-2x, -2y) C ．(-2x, 2y) D ．(2x, -2y)4．如图， CD 、BE 分别为ABC 的两条中线， CD 、BE 相交于点O ，连接DE ，若ABC 的面积为12，则ODE 的面积为（ ）．A ．2B ．56 C ．23 D ．15．如图，在中，，，已知，则的长是A ．B ．3C ．D ．46．如图，是以点O 为位似中心经过位似变换得到的，若的面积与的面积比是4：9，则：OB 为A ．2：3B ．3：2C ．4：5D ．4：97．如图，为了估计荆河的宽度，在荆河的对岸选定一个目标点，在近岸取点和，使点、、在一条直线上，且直线与河垂直，在过点且与垂直的直线上选择适当，则荆河的宽度为（）A．B．C．D．8．已知：如图，在▱ABCD中，E、F分别是边AD、BC的中点，AC分别交BE、DF于C、H．请判断下列结论：（1）BE=DF；（2）AG=GH=HC；（3）EG=BG；（4）S△ABE=3S△AGE．其中正确的结论有（）A．1个B．2个C．3个D．4个9．如图，在中，，于点．，，则A．B．C．D．10．下列各组图形中，不是位似图形的是A．B．C．D．11．4与9的比例中项是_____．12．如图，锐角三角形的边，上的高分别为和，和相交于点，图中相似三角形有________对．13．如图，E是▱ABCD的边AD上一点，AE=ED，CE与BD相交于点F，BD=10，那么DF=__．14．放映电影时，屏幕上的图象和胶片上对应的图形之间的关系：________．15．如图，在△ABC中，点D，E，F分别在边AB，AC，BC上，四边形DEFB是菱形，AB＝6，BC＝4，那么AD＝__________．16．如图，矩形中，，、分别是、的中点，，若矩形与矩形相似，则的长为________．17．如图，以点O为位似中心，将△ABC缩小后得到△A′B′C′，已知OB=3OB′，若△ABC的面积为9，则△A′B′C′的面积为_____；18．如图，在△ABC 中，∠C=90°，AB 的垂直平分线分别交AB、AC 于点D、E，AE=5，AD=4，线段CE 的长为________.19．如图，DE是△ABC的中位线，F是DE的中点，CF的延长线交AB于G，AB=6，则AG=_____．20．如图，将边长为4的正方形ABCD折叠，使点D落在AB边的中点E处，折痕为FH，点C落在Q处，EQ与BC交于点G，则△EBG的周长是______．21．（1）如图1，已知正方形ABCD，E是AD上一点，F是BC上一点，G是AB上一点，H是CD上一点，线段EF、GH交于点O，∠EOH=∠C，求证：EF=GH；（2）如图2，若将“正方形ABCD”改为“菱形ABCD”，其他条件不变，探索线段EF与线段GH的关系并加以证明；（3）如图3，若将“正方形ABCD”改为“矩形ABCD”，且AD=mAB，其他条件不变，探索线段EF与线段GH的关系并加以证明；附加题：根据前面的探究，你能否将本题推广到一般的平行四边形情况？若能，写出推广命题，画出图形，并证明，若不能，说明理由．22．某学习小组的学生在学习中遇到了下面的问题：如图1，在△ABC和△ADE中，∠ACB=∠AED=90°，∠CAB=∠EAD=60°，点E，A，C在同一条直线上，连接BD，点F是BD的中点，连接EF，CF，试判断△CEF的形状并说明理由．问题探究：（1）小婷同学提出解题思路：先探究△CEF的两条边是否相等，如EF=CF，以下是她的证明过程CF=EF=EG请根据以上证明过程，解答下列两个问题：①在图1中作出证明中所描述的辅助线；②在证明的括号中填写理由（请在SAS，ASA，AAS，SSS中选择）．（2）在（1）探究结论的基础上，请你帮助小婷求出∠CEF的度数，并判断△CEF的形状．问题拓展：（3）如图2，当△ADE绕点A逆时针旋转某个角度时，连接CE，延长DE交BC的延长线于点P，其他条件不变，求的值．23．如图，已知CD为Rt△ABC斜边上的中线，过点D作AC的平行线，过点C作CD 的垂线，两线相交于点E．求证：△ABC∽△DEC.24．（10分）如图，在正方形网格中，四边形TABC 的顶点坐标分别为()()()()1,1,2,3,3,3,4,2T A B C .（1）以点()1,1T 为位似中心，在位似中心的同侧将四边形TABC 放大为原来的2倍，放大后点A ， B ， C 的对应点分别为'A ， 'B ， 'C 画出四边形'''TA B C ；（2）写出点'A ， 'B ， 'C 的坐标：'A （ ），'B （ ），'C （ ）；（3）在（1）中，若(),D a b 为线段AC 上任一点，则变化后点D 的对应点'D 的坐标为（ ）.25．如图，在一块三角形区域ABC 中，∠C=90°，边AC=8m ，BC=6m ，现要在△ABC 内建造一个矩形水池DEFG ，如图的设计方案是使DE 在AB 上．（1）求△ABC 中AB 边上的高h ；（2）设DG=x ，当x 取何值时，水池DEFG 的面积（S ）最大？26．如图，、为山两侧的两个村庄，为了两村交通方便，根据国家的惠民政策，政府决定打一直线涵洞．工程人员为了计算工程量，必须计算、两点之间的直线距离，选择测量点、、，点、分别在、上，现测得千米、千米，米、米、米，求、两点之间的直线距离．27．如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别是A（2，2），B（4，0），C（4，﹣4）．（1）请在图中，画出△ABC向左平移6个单位长度后得到的△A1B1C1；（2）以点O为位似中心，将△ABC缩小为原来的，得到△A2B2C2，请在图中y轴右侧，画出△A2B2C2，并求出∠A2C2B2的正弦值．28．如图，为了估算河的宽度，我们可以在河对岸选定一个目标点P，在近岸取点Q和S，使点P、Q、S共线且直线PS与河垂直，接着再过点S且与PS垂直的直线a上选择适当的点T，确定PT与过点Q且垂直PS的直线b的交点R．如果测得QS=45m，ST=90m，QR=60m，求河的宽度PQ．参考答案1．A解析：根据两边对应成比例且夹角相等，可由AB BCBC CD=，∠B=∠B，可得△ACD∽△ABC，故A不能判定两三角形相似；根据两角对应相等的两三角形相似，可知B、C均可以判定两三角形相似；根据两边对应成比例且夹角相等，可由AC2=AD·AB，∠A为公共角，可判定两三角形相似.故选：A.2．A解：若使△ABC∽△DEF,则三边应满足,A选项中,,,所以,所以△ABC∽△DEF,符合题意,故选A.3．B解：∵△OBC与△ODE是以0点为位似中心的位似图形，即关于原点对称，且其位似比为1：2，M的坐标为（x，y），∴M在△ODE中的对应点M′的坐标为（-2x，-2y）．故选B．4．D解析：因为CD, BE分别为ABC的两条中线,所以可得: DE ODBC OC==12,因为ABC的面积为12,且BE是中线,所以ACD的面积是6,在ACD中,DE是中线,所以CDE的面积是3,又因为ODOC=12,所以ODE的面积为113CDES=,故选D.5．B解：∵AD=DE=EF=FB，AG=GH=HI=IC，∴DG∥EH∥FI；∴，即DG=BC；同理可得：EH=BC，FI=BC；∴DG+EH+FI=BC+BC+BC=BC=3；故选B．6．A分析：先求出位似比，根据位似比等于相似比，再由相似三角形的面积比等于相似比的平方即可．解：由位似变换的性质可知，A′B′∥AB，A′C′∥AC，∴△A′B′C′∽△ABC．∵△A'B'C'与△ABC的面积的比4：9，∴△A'B'C'与△ABC的相似比为2：3，∴OB'：OB=2：3.故选：A．7．B解：由题意可知：QR∥ST，∴△PQR∽△PST，∴设PQ=x，∴解得：x=120故PQ=120m故选B．8．D解：（1）∵▱ABCD，∴AD=BC，AD∥BC．E、F分别是边AD、BC的中点，∴BF∥DE，BF=DE．∴BEDF为平行四边形，BE=DF．故正确；（2）根据平行线等分线段定理可得AG=GH=HC．故正确；（3）∵AD∥BC，AE=AD=BC，∴△AGE∽△CGB，AE：BC=EG：BG=1：2，∴EG=BG．故正确．（4）∵BG=2EG，∴△ABG的面积=△AGE面积×2，∴S△ABE=3S△AGE．故正确．故选：D．9．A解：∵Rt△ABC中,，CD⊥AB于点D，∴△ACD∽△ABC，∴AC:AB=AD:AC,即∵AC=3，AB=6，∴AD=.故选:A.10．B解：根据位似图形的定义，可得A，C，D是位似图形，A与C的位似中心是交点，D的为中心是圆心；B不是位似图形．故选B．11．±6解：设它们的比例中项是x，则x2=4×9，x=±6．故答案为:±6．12．解：∵边，上的高分别为和，∴∠BED=∠CEA=∠CFD=∠BF A=90°,∴图中有△ABF∽△ACE，△BDE∽△CDF，△CDF∽△ACE，△CDF∽△ABF，△BDE∽△BF A，△BDE∽△CAE，6对三角形相似．故答案为6．13．4解：∵AE=ED，AE+ED=AD，∴ED=AD，∵四边形ABCD是平行四边形，∴AD=BC，AD//BC，∴△DEF∽△BCF，∴DF：BF=DE：BC=2：3，∵DF+BF=BD=10，∴DF=4，故答案为：4.14．位似解：放映电影时，屏幕上的图象和胶片上对应的图形是位似图形，因为图形形状相同，对应边平行，因此屏幕上的图象和胶片上对应的图形之间的关系：位似．15．解析：设菱形的边长为x，∵DE∥BC∴，即，同理：，即，由于∴解得：x=2.4，即BD=2.4∴AD=AB-BD=6-2.4=3.6.16．解：矩形与矩形相似所以DM:AB=MN:BC即DM:4=4:2DM解得DM=2，所以的长为.17．1分析：由题意可得△A′B′C′∽△ABC，，从而可得S△A′B′C′：S△ABC=1：9结合S△ABC=9即可求得S△A′B′C′的值.解：∵OB=3OB′，∴，∵以点O为位似中心，将△ABC缩小后得到△A′B′C′，∴△A′B′C′∽△ABC，∴．∴S△A′B′C′：S△ABC=1：9，∵△ABC的面积为9，∴△A′B′C′的面积为：1．故答案为：1．18．1.4解：∵DE 是AB 的垂直平分线，∴AB=2AD=8，∠ADE=∠C=90°，∵∠A=∠A，∴△ADE∽△ACB，∴，即，∴AC=6.4，∴CE=1.4，故答案为：1.4．19．2解：过E作EM∥AB与GC交于点M，如图所示：∴△EMF≌△DGF，∴EM=GD，∵DE是中位线，∴CE=12 AC，又∵EM∥AG，∴△CME∽△CGA，∴EM：AG=CE：AC=1：2，又∵EM=GD，∴AG：GD=2：1．∵AB=6，∴AD=3，∴AG=232 21⨯= +.故答案为：2.20．8分析：首先根据勾股定理求出EF的长度；然后证明，列出关于的三边长的比例式，求出三边的长度即可解决问题．解：由题意得：EF=DF(设为x)，则AF=4−x；而AE=2，由勾股定理得：解得：由题意得：∴∠AEF+∠AFE=∠AEF+∠BEG，∴∠AFE=∠BEG；∴△AEF∽△BGE，∴∴∴△EBG的周长故答案为：8.21．（1）证明见解析；（2）EF=GH；证明见解析；（3）；证明见解析；附加题：能；证明见解析；分析：（1）过点F作FM⊥AD于M，过点G作GN⊥CD于N，易证△GNH≌△FME，根据全等三角形的性质即可证得结论；（2）EF=GH，过点F作FM⊥AD于M，过点G作GN⊥CD于N，设EF、GN交于R、GN、MF交于Q，证明△GNH≌△FME，，根据全等三角形的性质即可证得结论；（3）过点F作FM⊥AD于M，过点G作GN⊥CD于N，设EF、GN交于R、GN、MF交于Q，证明△GNH∽△FME，根据相似三角形的性质即可证得结论；附加题：如图，过点F作FM⊥AD于M，过点G作GN⊥CD于N，设EF、GN交于R、GN、MF交于Q，证明△GNH∽△FME，根据相似三角形的性质及（3）的结论即可求解.解：（1）如图1，过点F作FM⊥AD于M，过点G作GN⊥CD于N，则FM=GN=AD=BC，且GN⊥FM，设它们的垂足为Q，设EF、GN交于R∵∠GOF=∠A=90°，∴∠OGR=90°﹣∠GRO=90°﹣∠QRF=∠OFM．∵∠GNH=∠FME=90°，FM=GN，∴△GNH≌△FME．∴EF=GH．（2）如图2，过点F作FM⊥AD于M，过点G作GN⊥CD于N，设EF、GN交于R、GN、MF 交于Q，在四边形MQND中，∠QMD=∠QND=90°∴∠ADC+∠MQN=180°．∴∠MQN=∠A=∠GOF．∵∠ORG=∠QRF，∴∠HGN=∠EFM．∵∠A=∠C，AB=BC，∴FM=AB•sinA=BC•sinC=GN．∵∠FEM=∠GNH=90°，∴△GNH≌△FME．∴EF=GH．（3）如图3，过点F作FM⊥AD于M，过点G作GN⊥CD于N，设EF、GN交于R、GN、MF 交于Q，∵∠GOF=∠A=90°，∴∠OGR=90°﹣∠GRO=90°﹣∠QRF=∠OFM．∵∠GNH=∠FME=90°，∴△GNH∽△FME．∴．∵GN=AD，FM=AB,AD=mAB，∴.附加题：已知平行四边形ABCD，E是AD上一点，F是BC上一点，G是AB上一点，H是CD上一点，线段EF、GH交于点O，∠EOH=∠C，AD=mAB，则GH=mEF．证明：如图，过点F作FM⊥AD于M，过点G作GN⊥CD于N，设EF、GN交于R、GN、MF交于Q，在四边形MQND中，∠QMD=∠QND=90°，∴∠MDN+∠MQN=180°．∴∠MQN=∠A=∠GOF．∵∠ORG=∠QRF，∴∠HGN=∠EFM．∵∠FME=∠GNH=90°，∴△GNH∽△FME．∴=m．即GH=mEF．22．（1）①图形见解析，②证明见解析，ASA；（2）证明见解析（3）1分析：（1）①按要求画出辅助线即可；②由小婷的解题过程可知，括号里的推理依据是“ASA”；（2）在（1）中图的基础上，延长BA，DE相交于点H（图3），先证EH=DE，再证四边形BGEH是平行四边形，得出∠DEF=∠H=30°，即可求出∠CEF=∠AED-∠DEF=60°，即可得出结论；（3）延长EF至G，使FG=EF，连接BG，CG（图4），由题意可证△DEF≌△BGF，得出∠CAE=∠CBG，再利用60°角的正切函数证，进而可证得△BCG∽△ACE，可得∠BCG=∠ACE，就可证得∠ECG=90°，即可得到CF=EF=EG，再由tan∠GEC=，可得∠GEC=60°，就可得出结论来了.解析：（1）①由题意作图如图1所示：②延长线段EF交CB的延长线于点G．∵F是BD的中点，∴BF=DF．∵∠ACB=∠AED=90°，∴ED∥CG．∴∠BGF=∠DEF．又∵∠BFG=∠DFE，∴△BGF≌△DEF（ ASA）．∴EF=FG，∴CF=EF=EG．故括号中的依据为ASA；（2）如图3，延长BA，DE相交于点H，∵∠BAC=60°，∴∠EAH=60°=∠EAD，∵∠AED=90°，∴∠H=30°，EH=DE，由（1）②知，△BGF≌△DEF，∴DE=BG，∴EH=BG，∵DE∥BG，∴四边形BGEH是平行四边形，∠DEF=∠H=30°，∴∠CEF=∠AED﹣∠DEF=60°，∵CF=EF，∴△CEF是等边三角形；（3）如图4，延长EF至G使FG=EF，连接CG，∵点F是BD的中点，∴DF=BF，∵∠DFE=∠BFG，∴△DEF≌△BGF（SAS），∴∠DEF=∠BGF，DE=BG，∴BG∥DP，∴∠P+∠CBG=180°，∵在四边形ACPE中，∠AEP=∠ACP=90°，∴∠CAE+∠P=180°，∴∠CAE=∠CBG，∵在Rt△ADE中，∠DAE=60°，∴tan∠DAE=，∴，同理：，∴，又∵∠CBG=∠CAE，∴△BCG∽△ACE，∴∠BCG=∠ACE，∴∠ECG=∠ACE+∠ACG=∠BCG+∠ACG=90°，∵在Rt △CEG 中，tan ∠CEG=，∴∠CEG=60°.∵在Rt △CEG 中，∠ECG=90°，EF=FG ，∴CF=EG=EF ，∴△CEF 是等边三角形，∴CE=CF ， ∴.23．解：∵CD 为Rt △ABC 斜边上的中线， ∴. ∴.∵DE ∥AC . ∴. ∴. ∵，CE ⊥CD ，∴ .∴△ABC ∽△DEC.24．（1）见解析;(2) ()'3,5A ， ()'5,5B ， ()'7,3C ；(3) ()21,21a b --分析：（1）利用位似图形的性质得出变化后图形即可；（2）利用已知图形得出对应点坐标；（3）利用各点变化规律，进而得出答案．解析：（1）如图所示：四边形'''TA B C 即为所求；（2）()'3,5A ， ()'5,5B ， ()'7,3C ；（3）'D 的坐标为()21,21a b --.25．（1）h=4.8；（2）当x 取2.4m 时，水池DEFG 的面积（S ）最大，且S=12m 2． 解：（1）如图，作于点H ，交FG 于点K ． 由，易得．，．（2）如图，设，，，由此可得．，当时，S有最大值12．答：当x取2.4m时，水池DEFG的面积（S）最大，且S=12m2．26．、两点之间的直线距离是米；解：连接MN，如图所示：∵,，∴,∵∠BAC=∠NAM，，∴△ABC∽△ANM，∴，∵BC=45米，AC=30米，AM=1千米=1000米，∴，∴MN=1500．故M、N之间的直线距离是米．27．（1）见解析（2）分析：（1）直接利用平移的性质得出对应点位置进而得出答案；（2）利用位似图形的性质得出对应点位置，再利用锐角三角三角函数关系得出答案．解析：（1）如图所示：△A1B1C1，即为所求；（2）如图所示：△A2B2C2，即为所求，由图形可知，∠A2C2B2=∠ACB，过点A作AD⊥BC交BC的延长线于点D，由A（2，2），C（4，﹣4），B（4，0），易得D（4，2），故AD=2，CD=6，AC==，∴sin∠ACB===，即sin∠A2C2B2=．28．90米解：根据题意得出：QR∥ST ，则△PQR∽△PST ，故，∵QS=45m，ST=90m，QR=60m，∴，解得：PQ=90（m），∴河的宽度为90米．。

2023年九年级数学中考一轮复习《图形的位似》专题提升训练一．选择题1．如图，线段AB两个端点的坐标分别为A（2，2）、B（2.5，0.8），以原点O为位似中心，在第一象限内将线段AB扩大为原来的2倍后得到线段CD，则端点C的坐标为（ ）A．（3，1.6）B．（4，3.2）C．（4，4）D．（6，1.6）2．如图，四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形，若OA：OA′＝：，则四边形ABCD与四边形A′B′C′D′的面积比为（ ）A．：B．2：3C．2：5D．4：93．如图，两个三角形是位似图形，它们的位似中心是（ ）A．点N B．点O C．点M D．点P4．如图，△ABC与△DEF位似，点O为位似中心，△ABC与△DEF的面积之比为1：4，若OB＝2，则OE的长为（ ）A．1B．2C．4D．85．如图，在平面直角坐标系xOy中有两点A（﹣2，0）和B（﹣2，﹣1），以原点O为位似中心作△COD，△COD与△AOB的相似比为2，其中点C与点A对应，点D与点B 对应，且CD在y轴左侧，则点D的坐标为（ ）A．（4，2）B．（﹣4，﹣2）C．（1，）D．（﹣1，﹣）6．如图，直角坐标系中，△OAB顶点为O（0，0），A（4，3），B（3，0）．以点O为位似中心，在第三象限内作与△OAB的位似比为的位似图形△OCD，则点C坐标（ ）A．（﹣1，﹣1）B．（﹣1，﹣）C．（﹣，﹣1）D．（﹣2，﹣1）7．在如图所示的网格中，四边形ABCD的位似图形是四边形NPMQ，位似中心是点O，则四边形ABCD与四边形NPMQ的位似比是（ ）A．1：2B．2：1C．1：D．：18．如图，以点O为位似中心，把△ABC中放大到原来的2倍得到△A'B'C'．以下说法中错误的是（ ）A．△ABC∽△A'B'C'B．点C，O，C'三点在同一条直线上C．AO：AA'＝1：2D．AB∥A'B'二．填空题9．如图，在平面直角坐标系中，矩形OABC的顶点坐标分别是O（0，0），C（6，0），B（6，4），A（0，4），已知矩形OA'B'C'与矩形OABC位似，位似中心是原点O，且矩形OA′B'C'的面积等于矩形OABC面积的，则点B'的坐标是 ．10．如图，正方形OABC与正方形ODEF是位似图形，点O为位似中心，位似比为2：3，点A的坐标为（0，2），则点E的坐标是 ．11．在平面直角坐标系中，△ABC和△A1B1C1的相似比等于，并且是关于原点O的位似图形，若点A的坐标为（2，4），则其对应点A1的坐标是 ．12．如图，△ABC∽△DEF，则△ABC与△DEF是以 为位似中心的位似图形，若＝，则△DEF与△ABC的位似比是 ．三．解答题13．如图所示，在矩形ABCD中，对角线AC，BD相交于点O．过点O作OE⊥BC于点E，连接DE交OC于点F，过点F作FG⊥BC于点G，则△ABC与△FGC是位似图形吗？若是，请说出位似中心，并求出相似比；若不是，请说明理由．14．如图，点A，D在∠XOY的边OX上，点B，E在OY边上，射线OZ在∠XOY内，且点C，F在OZ上，AC∥DF，BC∥EF．＝．（1）试说明△ABC与△DEF是位似图形；（2）求△ABC与△DEF的位似比．15．如图，在6×6的正方形方格中，每个小正方形的边长都为1，顶点都在网格线交点处的三角形叫做格点三角形，如图①中，△ABC是一个格点三角形．（1）在图①中，请判断△ABC与△DEF是否相似，并说明理由；（2）在图②中，以O为位似中心，画一个格点三角形△A1B1C1，使它与△ABC的位似比为2：1．16．在平面直角坐标系中，△ABC的顶点坐标分别为A（0，2）、B（1，3）、C（2，1）．（1）在坐标系中原点O的异侧，画出以O为位似中心的位似图形△A'B'C，使得△A'B'C与△ABC的位似比为2，则点C′的坐标为： ．（2）△A'B'C的面积为： ．（3）在x轴上找一点P，使得△PAC的周长最小，则点P的坐标是： ．17．如图，在正方形网格中，△OBC的顶点分别为O（0，0），B（3，﹣1）、C（2，1）．（1）以点O（0，0）为位似中心，按比例尺2：1在位似中心的异侧将△OBC放大为△OB'C'，放大后点B、C两点的对应点分别为B'、C'，画出△OB'C'，并写出点B'、C'的坐标；（2）在（1）中，若点M（x，y）为线段BC上任一点，写出变化后点M的对应点M'的坐标．18．小明同学在研究如何在△ABC内做一个面积最大的正方形时，想到了可以利用位似知识解决这个问题，他的做法是：（如图1）先在△ABC内作一个小正方形DEFG，使得顶点D落在边AB上，顶点E、F落在边BC上，然后连接BG并延长交AC边于点H，作HK⊥BC，HI∥BC，再作IJ⊥BC于J，则正方形HIJK就是所作的面积最大的正方形．（1）若△ABC中，AB＝4，∠ABC＝60°，∠ACB＝45°，请求出小明所作的面积最大的正方形的边长．（2）拓展运用：如图2，已知∠BAC P，请画一个⊙M，使得⊙M经过点P，且与AB、AC都相切．（注：并简要说明画法）19．如图，正三角形ABC的边长为3+．（1）如图①，正方形EFPN的顶点E、F在边AB上，顶点N在边AC上，在正三角形ABC及其内部，以点A为位似中心，作正方形EFPN的位似正方形E′F′P′N′，且使正方形E′F′P′N′的面积最大（不要求写作法）；（2）求（1）中作出的正方形E′F′P′N′的边长；（3）如图②，在正三角形ABC中放入正方形DEMN和正方形EFPH，使得DE、EF 在边AB上，点P、N分别在边CB、CA上，求这两个正方形面积和的最大值和最小值，并说明理由．20．我们知道：如果两个三角形不仅是相似三角形，而且每对对应点所在的直线都经过同一个点，那么这两个三角形叫做位似三角形，它们的相似比又称为位似比，这个点叫做位似中心．利用三角形的位似可以将一个三角形缩小或放大．（1）选择：如图1，点O是等边三角形PQR的中心，P′、Q′、R′分别是OP、OQ、OR的中点，则△P′Q′R′与△PQR是位似三角形．此时，△P′Q′R′与△PQR的位似比、位似中心分别为 ；（A）2、点P，（B）、点P，（C）2、点O，（D）、点O；（2）如图2，用下面的方法可以画△AOB的内接等边三角形．阅读后证明相应问题．画法：①在△AOB内画等边三角形CDE，使点C在OA上，点D在OB上；②连接OE并延长，交AB于点E′，过点E′作E′C′∥EC，交OA于点C′，作E′D′∥ED，交OB于点D′；③连接C′D′，则△C′D′E′是△AOB的内接三角形．求证：△C′D′E′是等边三角形．参考答案一．选择题1．解：∵以原点O为位似中心，在第一象限内将线段AB扩大为原来的2倍后得到线段CD，∴A点与C点是对应点，∵C点的对应点A的坐标为（2，2），位似比为1：2，∴点C的坐标为：（4，4）故选：C．2．解：∵四边形ABCD和A'B'C'D'是以点O为位似中心的位似图形，OA：OA'＝：，∴四边形ABCD与四边形A'B'C'D'的面积比：（）2：（）2＝2：3，故选：B．3．解：如图，因为位似图形的位似中心位于对应点连线所在的直线上，点M、N为对应点，所以位似中心在M、N所在的直线上．因为点P在直线MN上，所以点P为位似中心．故选：D．4．解：∵＝（）2＝，∴＝＝，∴＝，∴EO＝4，故选：C．5．解：∵点A（﹣2，0）和B（﹣2，﹣1），以原点O为位似中心作△COD，△COD与△AOB的相似比为2，点C与点A对应，点D与点B对应，且CD在y轴左侧，∴点D的坐标为（﹣4，﹣2）．故选：B．6．解：∵以点O为位似中心，在第三象限内作与△OAB的位似比为的位似图形△OCD，∴点C坐标为（﹣×4，﹣×3），即（﹣1，﹣）．故选：B．7．解：如图，连接OD，OQ，∵四边形ABCD的位似图形是四边形NPMQ，位似中心是点O，∴四边形ABCD与四边形NPMQ的位似比＝OD：OQ＝：2＝1：2．故选：A．8．解：∵点O为位似中心，把△ABC中放大到原来的2倍得到△A'B'C'，∴△ABC∽△A'B'C'，OA：OA′＝1：2，AB∥A′B′，CC′经过点O．故选：C．二．填空题9．解：∵矩形OA′B'C'的面积等于矩形OABC面积的，∴矩形OA'B'C'与矩形OABC位似比为1：2，∵B（6，4），∴B′点的坐标为（3，2）或（﹣3，﹣2）．故答案为（3，2）或（﹣3，﹣2）．10．解：∵四边形ABCO为正方形，而A（0，2），∴B（2，2），∵正方形OABC与正方形ODEF是位似图，点O为位似中心，位似比为2：3，∴E点坐标为（2×，2×），即E（3，3）．故答案为（3，3）．11．解：∵△ABC和△A1B1C1的相似比等于，并且是关于原点O的位似图形，而点A的坐标为（2，4），∴点A对应点A1的坐标为（2×2，2×4）或（﹣2×2，﹣2×4），即（4，8）或（﹣4，﹣8）．故答案为（4，8）或（﹣4，﹣8）．12．解：如图所示：△ABC∽△DEF，则△ABC与△DEF是以O为位似中心的位似图形，若＝，则△DEF与△ABC的位似比是：．故答案为：O，．三．解答题13．解：△ABC与△FGC∵OE⊥BC，FG⊥BC，∴OE∥FG，又OF、EG的连线相交于点C，∴△ABC与△FGC是位似图形，位似中心是点C，∵四边形ABCD是矩形，∴∠BCD＝90°，OB＝OD，又OE⊥BC，∴OE∥CD，∴OE是△BCD的中位线，∴OE＝CD，∵OE∥CD，∴＝＝，则＝，∴△ABC与△FGC的相似比是3．14．解：（1）∵AC∥DF，BC∥EF，∴∠DFO＝∠ACO，∠OFE＝∠OCB，＝＝，＝，∴∠DFE＝∠ACB，＝，∴△ACB∽△DFE，∴△ABC与△DEF是位似图形；（2）∵△ABC与△DEF是位似图形，＝，∴△ABC与△DEF的位似比为：．15．解：（1）相似．理由如下：∵AB＝1，BC＝＝，AC＝＝2，DE＝＝，EF＝＝，DF＝4，∴＝，＝＝，＝＝，∴＝＝，∴△ABC∽△DEF；（2）如图②，△A1B1C1为所作．16．解：（1）如图，△A'B'C即为所求，点C′的坐标为（﹣4，﹣2）．故答案为：（﹣4，﹣2）；（2）S△A′B′C′＝4×4﹣×2×4﹣×2×2﹣×2×4＝6，故答案为：6；（3）如图，点P即为所求，P（，0），故答案为：（，0）．17．解：（1）如图，△OB′C′即为所求．B′（﹣6，2），C′（﹣4，﹣2）．（2）M′（﹣2x，﹣2y）．18．解：（1）如图1中，作AM⊥BC于M，交IH于N，设正方形边长为x．在RT△ABM中，∵∠AMB＝90°，∠B＝60°，AB＝4，∴BM＝2，AM＝2，∵∠C＝∠MAC＝45°，∴AM＝MC＝2，∴BC＝2+2∵IH∥BC，∴＝，∴＝，∴x＝∴小明所作的面积最大的正方形的边长为．（2）如图2中，①作∠BAC的平分线AQ，②在AQ上取一点O，作⊙O和AB、AC相切，③连接AP交⊙O于E、F．④作PM1∥OE交AQ于M1，⑤以M1为圆心PM1为半径作⊙M1，⊙M1即为所求．同法，作PM2∥OF，交AQ于M2，以M2为圆心PM2为半径作⊙M2，⊙M2即为所求．19．解：（1）如图①，正方形E′F′P′N′即为所求．（2）设正方形E′F′P′N′的边长为x，∵△ABC为正三角形，∴AE′＝BF′＝x．∵E′F′+AE′+BF′＝AB，∴x+x+x＝3+，∴x＝，即x＝3﹣3，（x≈2.20也正确）（3）如图②，连接NE、EP、PN，则∠NEP＝90°．设正方形DEMN、正方形EFPH的边长分别为m、n（m≥n），它们的面积和为S，则NE＝，PE＝n．∴PN2＝NE2+PE2＝2m2+2n2＝2（m2+n2）．∴S＝m2+n2＝PN2，延长PH交ND于点G，则PG⊥ND．在Rt△PGN中，PN2＝PG2+GN2＝（m+n）2+（m﹣n）2．∵AD+DE+EF+BF＝AB，即m+m+n+n＝+3，化简得m+n＝3．∴S＝[32+（m﹣n）2]＝+（m﹣n）2①当（m﹣n）2＝0时，即m＝n时，S最小．∴S最小＝；②当（m﹣n）2最大时，S最大．即当m最大且n最小时，S最大．∵m+n＝3，由（2）知，m最大＝3﹣3．∴S最大＝[9+（m最大﹣n最小）2]＝[9+（3﹣3﹣6+3）2]＝99﹣54…．（S最大≈5.47也正确）综上所述，S最大＝99﹣54，S最小＝．20．（1）解：选择D．∵△P′Q′R′∽△PQR，且相似比是1：2，∴位似比是1：2，位似中心为点O．故选D；（2）证明：∵E′C′∥EC，E′D′∥ED，∴△OCE∽△OC′E′，△ODE∽△OD′E′∴CE：C′E′＝OE：OE′，DE：D′E′＝OE：OE′，∠CEO＝∠C′E′O，∠DE O＝∠D′E′O∴CE：C′E′＝DE：D′E′，∠CED＝∠C′E′D′∴△CDE∽△C′D′E′∵△CDE是等边三角形，∴△C′D′E′是等边三角形．。

米． 33 7
则
x y y
_2_7_:7________．
整理课件
2.过矩形ABCD的顶点A作对角线AC的垂线 分别与CB,CD的延长线交于E,F.则图中与
△ABC相似的三角C形（ ）。
A.4个
C
B. 5个
D
C. 6个
B
D. 7个E
A
F
整理课件
• 3．如果在△ABC中，点D、 E、F分别为BC、AC、AB的 中 点 ， AB ＝ 5 ， BC ＝ 12 ， AC＝13，那么△DEF的周长 ＝ _______1_5__ ， 面 积 ＝ ______7_._5__．
整理课件
相似三角形的性质：
1.对应角相等，对应边成比例.
2.相似三角形对应高的比，对应 中线的比，对应角平分线的比， 周长的比都等于相似比. 3.相似三角形面积的比等于相似 比的平方.
整理课件
1． 地图上两地间的距离（图上距离）
为 3 厘 米 ， 比 例 尺 是 1∶1000000 ， 那
么两地间的实际距离是____________
6.如图4—8—5，△ABC是一块锐角三角形余 料，其中BC=12 cm，高AD=8 cm，现在要
把它裁剪成一个正方形材料备用，使正方形的
一边在BC上，其余两个顶点分别在AB、AC
上，问这个正方形材料的边长是多少？
图4—8—5
整理课件
解：设这个正方形材料的边长 为x cm
则△PAN的边PN上的高为（8 －x） cm
∵由已知得：△APN∽△ABC ∴=，即=解得：x=4.8
答：这个正方形材料的边长为 4.8 cm.
整理课件
7.如图，梯形ABCD中AB∥CD, AB=a, BD=b, CD=c,若∠DBC=∠A,则a,b,c使方程

《图形的相似》全章复习与巩固--巩固练习（基础）【巩固练习】一、选择题1．如图，已知，那么下列结论正确的是( ).A．B． C．D．2. 在和中，，如果的周长是16，面积是12，那么的周长、面积依次为( ).A．8，3 B．8，6 C．4，3 D．4，63．如图，小正方形的边长均为1，则下列图中的三角形(阴影部分)与相似的是( ).4.如图，△ABC中，A，B两个顶点在x轴的上方，点C的坐标是(-1，0)．以点C为位似中心，在x轴的下方作△ABC的位似图形△A′B′C，并把△ABC的边长放大到原来的2倍．设点B的对应点B′的横坐标是，则点B的横坐标是（）.A．B． C．D．5.如图，以点O为位似中心，将△ABC放大得到△DEF．若AD=OA，则△ABC与△DEF的面积之比为（）A．1：2 B．1：4 C．1：5 D．1：66. 如图，在正方形ABCD中，E是CD的中点，P是BC边上的点，下列条件中不能推出△ABP与以点E、C、P为顶点的三角形相似的是( ).A．∠APB=∠EPC B．∠APE=90° C．P是BC的中点D．BP：BC=2：3 7. （2016•盐城）如图，点F在平行四边形ABCD的边AB上，射线CF交DA的延长线于点E，在不添加辅助线的情况下，与△AEF相似的三角形有（）A．0个B．1个C．2个D．3个8.如图，六边形ABCDEF∽六边形GHIJKL，相似比为2：1，则下列结论正确的是（）.A．∠E=2∠K B．BC=2HIC．六边形ABCDEF的周长=六边形GHIJKL的周长D．S六边形ABCDEF=2S六边形GHIJKL二、填空题9. 在□ABCD中，在上，若，则___________.10. 如图，在△ABC中，D、E分别是AB和AC中点，F是BC延长线上一点，DF平分CE于点G，CF=1，则BC=_______，△ADE•与△ABC•的面积之比为_______，•△CFG与△BFD的面积之比为________.11. （2016•衡阳）若△ABC与△DEF相似且面积之比为25：16，则△ABC与△DEF的周长之比为．12. 在相同时刻的物高与影长成比例.小明的身高为1.5米，在地面上的影长为2米，同时一古塔在面上的影长为40米，则古塔高为________.13.如图，直线l1、l2、…l6是一组等距的平行线，过直线l1上的点A作两条射线，分别与直线l3、l6相交于点B、E、C、F．若BC=2，则EF的长是．14．如图，在△ABC中，MN∥BC，若∠C=68°，AM：MB＝1：2，则∠MNA=_______度，AN：NC＝_____________.15.如图，点D,E分别在AB、AC上，且∠ABC=∠AED。

中考数学一轮复习《图形的相似》练习题（含答案）(建议答题时间：40分钟)1. (2017兰州)已知2x＝3y(y≠0)，则下列结论成立的是()A. xy＝32 B.x3＝2y C.xy＝23 D.x2＝y32. (2017连云港)如图，已知△ABC∽△DEF，AB∶DE＝1∶2，则下列等式一定成立的是()A. BCDF＝12B.∠A的度数∠D的度数＝12C. ABCDEFSS＝12D. ABCDEFCC＝12第2题图3. (2017重庆西大附中三模)已知△ABC∽△DEF，△ABC与△DEF的面积之比为4∶25，若BC＝8，则EF的长度为()A. 50B. 20C. 10D. 404. (2017重庆南岸区模拟)两个相似三角形的最短边分别是5 cm和3 cm，它们的周长之差为12 cm，那么小三角形的周长为()A. 14cmB. 16cmC. 18cmD. 30cm5. (北师九上84页第1题改编)如图，已知直线a∥b∥c，直线m交直线a，b，c于点A，B，C，直线n交直线a，b，c于点D，E，F，若ABBC＝12，则DEEF＝()A. 13 B.12 C.23 D. 1第5题图第6题图6. (2017杭州)如图，在△ABC中，点D、E分别在边AB、AC上，DE∥BC，若BD＝2AD，则()A. ADAB＝12 B.AEEC＝12 C.ADEC＝12 D.DEBC＝127. (2017哈尔滨)如图，在△ABC中，D、E分别是边AB、AC边上的点，DE∥BC，点F为BC边上一点，连接AF交DE于点G.则下列结论中一定正确的是()A. ADAB＝AEEC B.AGGF＝AEBD C.BDAD＝CEAE D.AGAF＝ACEC 第7题图第8题图8. (2017青海)如图，在平行四边形ABCD中，点E在边DC上，DE∶EC＝3∶1，连接AE交BD于点F，则△DEF的面积与△BAF的面积之比为()A. 1∶3B. 3∶4C. 1∶9 D．9∶169. (2017恩施州)如图，在△ABC中，DE∥BC，∠ADE＝∠EFC，AD∶BD＝5∶3，CF＝6，则DE的长为()A. 6B. 8C. 10D. 12第9题图第10题图10. (2017枣庄)如图，在△ABC中，∠A＝78°，AB＝4，AC＝6.将△ABC沿图示中的虚线剪开，剪下的阴影三角形与原三角形不相似．．．的是()11. (2017绵阳)为测量操场上旗杆的高度，小丽同学想到了物理学中平面镜成像的原理．她拿出随身携带的镜子和卷尺，先将镜子放在脚下的地面上，然后后退，直到她站直身子刚好能从镜子里看到旗杆的顶端E，标记好脚掌中心位置为B. 测得脚掌中心位置B到镜面中心C的距离是50 cm，镜面中心C距旗杆底部D 的距离为4 m，如图所示，已知小丽同学的身高是1.54 m，眼睛位置A距离小丽头顶的距离是4 cm，则旗杆DE的高度等于()A. 10 mB. 12 mC. 12.4 mD. 12.32 m第11题图第13题图12. (2018原创)如果两个相似三角形的面积比是9∶25，其中小三角形一边上的中线长是12 cm，那么大三角形对应边上的中线长是________cm.13. (2017临沂)已知AB∥CD，AD与BC相交于点O.若BOOC＝23，AD＝10，则AO＝________.14. (2017北京)如图，在△ABC中，M、N分别为AC，BC的中点．若S△CMN＝1，则S四边形ABNM＝________．第14题图第16题图15. (2017随州)在△ABC中，AB＝6，AC＝5，点D在边AB上，且AD＝2，点E 在边AC上，当AE＝________时，以A、D、E为顶点的三角形与△ABC相似．16. (2017齐齐哈尔)经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形，如果其中一个是等腰三角形，另外一个三角形和原三角形相似，那么把这条线段定义为原三角形的“和谐分割线”．如图，线段CD是△ABC的“和谐分割线”，△ACD为等腰三角形，△CBD和△ABC相似，∠A＝46°，则∠ACB的度数为________．17. (2017杭州)如图，在锐角三角形ABC中，点D，E分别在边AC，AB上，AG ⊥BC于点G，AF⊥DE于点F，∠EAF＝∠GAC.(1)求证：△ADE∽△ABC；(2)若AD＝3，AB＝5，求AFAG的值．第17题图18. (2017泰安)如图，四边形ABCD中，AB＝AC＝AD，AC平分∠BAD，点P是AC延长线上一点，且PD⊥AD.(1)证明：∠BDC＝∠PDC；(2)若AC与BD相交于点E，AB＝1，CE∶CP＝2∶3，求AE的长．第18题图答案1. A2. D3. B4. C 【解析】根据题意得两三角形的周长的比为5∶3，设两三角形的周长分别为5x cm ，3x cm ，则5x －3x ＝12，解得x ＝6，所以3x ＝18，即小三角形的周长为18 cm .5. B 【解析】∵a ∥b ∥c ，∴DE EF ＝AB BC ＝12.6. B 【解析】∵DE ∥BC ，∴△ADE ∽△ABC ，∵BD ＝2AD ，∴AD AB ＝AE AC ＝DE BC ＝13，∴AE EC ＝12，故选B .7. C 【解析】A 、∵DE ∥BC ，∴△ADE ∽△ABC ，∴AD AB ＝AE AC ，故A 错误；B 、∵DE ∥BC ，∴AG GF ＝AE EC ，故B 错误；C 、∵DE ∥BC ，BD AD ＝CE AE ，故C 正确；D 、∵DE ∥BC ，∴△AGE ∽△AFC ，∴AG AF ＝AE AC ，故D 错误；故选C .8. D 【解析】∵四边形ABCD 是平行四边形，∴DC ∥AB ，∴△DFE ∽△BF A ，又∵DE ∶EC ＝3∶1，∴DE ∶AB ＝3∶4，∴△DEF 的面积与△BAF 的面积之比为9∶16.9. C 【解析】∵DE ∥BC ，∴∠ADE ＝∠B ，∵∠ADE ＝∠EFC ，∴∠B ＝∠EFC ，∴EF ∥AB ，∴四边形DEFB 为平行四边形，∴DB ＝EF ，DE ＝BF ，又∵AD DB ＝53，∴EF AB ＝38，又∵EF ∥AB ，∴CF BC ＝EF AB 即66＋BF＝38，∴BF ＝10，∴DE ＝BF ＝10. 10. C 【解析】根据相似三角形的判定定理对各选项进行逐一判定即可．A . 阴影部分的三角形与原三角形有两个角相等，故两三角形相似，故本选项不符合题意；B . 阴影部分的三角形与原三角形有两个角相等，故两三角形相似，故本选项不符合题意；C . 两三角形的对应边不成比例，故两三角形不相似，故本选项符合题意；D . 两三角形对应边成比例且夹角相等，故两三角形相似，故本选项不符合题意．故选C .11. B 【解析】由平面镜成像原理得∠ACB ＝∠ECD ，又∵∠ABC ＝∠EDC ＝90°，∴△ABC ∽△EDC ，∴AB DE ＝BC CD ，即1.54－0.04DE＝0.54，解得DE ＝12 m . 12. 20 【解析】∵两个相似三角形的面积比是9∶25，∴大三角形的中线长∶小三角形的对应中线长是5∶3，∵小三角形一边上的中线长是12 cm ，∴12÷35＝20 cm ，∴大三角形对应边上的中线长是20 cm . 13. 4 【解析】由AB ∥CD 可得OA OD ＝OB OC ＝23，所以OA ＝25AD ，又由AD ＝10，可得OA ＝25×10＝4.14. 3 【解析】∵点M ，N 分别为AC ，BC 的中点，∴MN 为△ABC 的中位线，∴△ABC ∽△MNC 且AC ＝2AM ，又∵S △CMN ＝1，∴S △ABC ＝4S △CMN ＝4，∴S 四边形ABNM ＝S △ABC －S △CMN ＝ 4－1＝3.15. 53或125 【解析】先根据题意画出图形，然后分为△ADE ∽△ABC 和△ADE ∽△ACB 两种情况：如解图①所示：∵∠A ＝∠A ，∴当AD AB ＝AE AC 时，△ADE ∽△ABC ，∴26＝AE 5，解得AE ＝53；如解图②所示：∵∠A ＝∠A ，∴当AD AC ＝AE AB 时，△ADE ∽△ACB ，∴25＝AE 6，解得AE ＝125.第15题解图16 . 113°或92° 【解析】∵△BCD ∽△BAC ，∴∠BCD ＝∠A ＝46°，∵△ACD 是等腰三角形，∠ADC ＞∠BCD ，∴∠ADC ＞∠A ，即AC ≠CD ，①当AC ＝AD时，∠ACD ＝∠ADC ＝12(180°－46°)＝67°，∴∠ACB ＝67°＋46°＝113°，②当DA＝DC 时，∠ACD ＝∠A ＝46°，∴∠ACB ＝46°＋46°＝92°.17. (1)证明：∵AF ⊥DE ，AG ⊥BC ，∴∠AFE ＝90°，∠AGC ＝90°，∴∠AEF ＝90°－∠EAF ，∠C ＝90°－∠GAC ，又∵∠EAF ＝∠GAC ，∴∠AEF ＝∠C ，又∵∠DAE ＝∠BAC ，∴△ADE ∽△ABC ；(2)解：∵△ADE ∽△ABC ，∴∠ADE ＝∠B ，又∵∠AFD ＝∠AGB ＝90°，∴△AFD ∽△AGB ，∴AF AG ＝AD AB ，∵AD ＝3，AB ＝5，∴AF AG ＝35.18. (1)证明：∵AB ＝AD ，AC 平分∠BAD ，∴AC ⊥BD ，∴∠ACD ＋∠BDC ＝90°，∵AC ＝AD ，∴∠ACD ＝∠ADC ，∴∠ADC ＋∠BDC ＝90°，∵PD ⊥AD ，∴∠PDC ＋∠ADC ＝90°，∴∠BDC ＝∠PDC ；(2)解：如解图，过点C 作CM ⊥PD 于点M ， ∵∠BDC ＝∠PDC ，∠CED ＝∠CMD ＝90°， ∴CE ＝CM .∵∠CMP ＝∠ADP ＝90°，∠P ＝∠P ， ∴△CPM ∽△APD ；∴CM AD ＝PC PA. 设CM ＝CE ＝x ，∵CE ∶PC ＝2∶3，∴PC ＝32x ，∵AB ＝AD ＝AC ＝1，∴x 1＝32x32x ＋1， 解得x ＝13， ∴AE ＝1－13＝23.第18题解图。

xx学校xx学年xx学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx 题总分得分一、xx题评卷人得分（每空xx 分，共xx分）试题1:在比例尺1：10000的地图上，相距2cm的两地的实际距离是（）。

A．200cm B．200dm C．200m D．200km试题2:已知线段a=10，线段b是线段a上黄金分割的较长部分，则线段b的长是（）。

A．B．C．D．试题3:若则下列各式中不正确的是（）。

A．B．C．D．试题4:下列图形一定相似的是（）。

A．所有的直角三角形B．所有的等腰三角形C．所有的矩形 D．所有的正方形试题5:三角形三边之比3：5：7，与它相似的三角形最长边是21cm，另两边之和是（）。

A．15cm B．18cm C．21cm D．24cm试题6:△ABC∽△A1B1C1，相似比为2：3，△A1B1C1∽△A2B2C2，相似比为5：4，则△ABC与△A2B2C2的相似比为（）。

A．B．C． D．试题7:如图，P是Rt△ABC的斜边BC上异于B，C的一点，过P点作直线截△ABC，使截得的三角形与△ABC相似，满足这样条件的直线共有（）。

A．1条 B．2条 C．3条 D．4条试题8:如图，电灯P在横杆AB的正上方，AB在灯光下的影子为CD，AB∥CD，AB=2m，CD=5m，点P到CD的距离是3m，则P到AB的距离是（）。

A. B. C. D.试题9:若，则=_________。

试题10:已知，则=_________。

试题11:若且，则∶=_________。

试题12:2和8的比例中项是_________；线段2与8的比例中项为_________。

试题13:如果两个相似三角形的面积比为3∶4，则它们的周长比为_________。

试题14:若，且∠A＝45°，∠B＝30°，则∠C′＝_________。

2021中考数学一轮知识点系统复习之图形的相似优生提升测试题（附答案详解）1．已知△ABC的三边长分别为a，b，c，且(a－c)∶(a＋b)∶(c－b)＝－2∶7∶1，则△ABC 是( )A．等腰三角形B．等边三角形C．直角三角形D．等腰直角三角形2．如图，AB、CD分别垂直于直线BC，AC和BD相交于E，过点E作EF⊥BC于F，若AB=80，CD=20，那么EF等于（）A．40B．25C．20D．163．如图，在△ABC中，点D、E分别在边BA、CA的延长线上，ABAD=2，那么下列条件中能判断DE∥BC的是（）A．12AEEC=B．2ECAC=C．12DEBC=D．2ACAE=4．下列阴影三角形分别在小正方形组成的网格中，则与图中的三角形相似的是（）．A．B．C．D．5．四边形ABCD相似四边形A'B'C'D'，且AB:A'B'=1:2,已知BC=8，则B'C'的长是( ) A．4 B．16 C．24 D．646．在一张比例尺为1:1000的地图上，21cm的面积表示的实际面积是（）A．1000 cm2B．100m2C．10m2D．100000cm27．如图，在边长为1的正方形ABCD中，动点F，E分别以相同的速度从D，C两点同时出发向C和B运动（任何一个点到达即停止），过点P作PM∥CD交BC于M点，PN∥BC交CD于N点，连接MN，在运动过程中，则下列结论：①△ABE≌△BCF；②AE=BF；③AE⊥BF；④CF2=PE•BF；⑤线段MN的最小值为51-．其中正确的结论有（）A．2个B．3个C．4个D ．5个8．如图，在△ABC 中，∠AED=∠B ，DE=6，AB=10，AE=8，则BC 的长度为( )A ．152B ．154C ．3D ．839．如图，在ABC 中，//DE BC ，分别交AB ，AC 于点D ，E ．若1AD =，2DB =，则ADE 的面积与ABC 的面积的比等于（ ）A ．12B ．14C ．18 D ．1910．如图，三角形ABC 中，D 、E 、F 分别是AB ，AC ，BC 上的点，且DE ∥BC ，EF ∥AB ，AD ：DB=1：2，BC=30cm ，则FC 的长为（ ）A ．10cmB ．20cmC ．5cmD ．6cm11．如图，要使ADB ABC ∽，还需添加的条件________．12．如图，在□ABCD 中，F 是AD 延长线上一点，连接BF 交DC 于点E ，在不添加辅助线的情况下，请写出图中一对相似三角形：__________________.13．矩形纸片ABCD ，AB=9，BC=6，在矩形边上有一点P ，且DP=3．将矩形纸片折叠，使点B 与点P 重合，折痕所在直线交矩形两边于点E ，F ，则EF 长为________． 14．如图，在△ABC 中，D 、F 在BC 上，且BD=DF=FC ，连接AD 、AF ，E 、G 分别在AF 、AC 上，且ED ∥AB ，GF ∥AB ，则ED GF 的值为____． 15．如图，直线AB 与坐标轴交于()1,0A 、()0,2B 两点，过A ，B 两点的抛物线与x 轴的另一交点为()3,0，P 为抛物线上的一动点，当45PBA ∠=时，P 点的坐标为________．16．在ABC 中，D 为AB 上一点，F 为AC 上一点，CD 与BF 交于点E ，32AD DB =，3CA CF =，则BE BF=________．17．已知：AD ∥BE ∥FC,AB=2，BC=3，DE=4，则DF=_____.18．如图，梯形ABCD 中，//AD BC ，且AD ：1BC =：3，对角线AC ，BD 交于点O ，那么AOD S ：BOC S ：AOB S =______．19．如图1，西沙河属马刨泉河支流，发源于房山区城关街道迎风坡村，流域面积11平方公里，为估算西沙河某段的宽度，如图2，在河岸边选定一个目标点A ，在对岸取点B,C,D ．使得AB ⊥BC,CD ⊥BC,点E 在BC 上，并且点A,E,D 在同一条直线上，若测得BE=2m,EC=1m,CD=3m,则河的宽度AB 等于_____m.20．如果，那么=_____21．如图，已知△ABC 是面积为3的等边三角形，△ABC ∽△ADE ，AB=2AD ，∠BAD=45°，AC 与DE 相交于点F ，则点D 到线段AB 的距离等于（结果保留根号）_____．22．如图1所示，已知抛物线245y x x =-++的顶点为D ，与x 轴交于A 、B 两点，与y 轴交于C 点，E 为对称轴上的一点，连接CE ，将线段CE 绕点E 按逆时针方向旋转90°后，点C 的对应点C′恰好落在y 轴上．（1）直接写出D 点和E 点的坐标；（2）点F 为直线C′E 与已知抛物线的一个交点，点H 是抛物线上C 与F 之间的一个动点，若过点H 作直线HG 与y 轴平行，且与直线C′E 交于点G ，设点H 的横坐标为m （0＜m ＜4），那么当m 为何值时，ΔHGF ΔBGF :S S =5：6；（3）图2所示的抛物线是由245y x x =-++向右平移1个单位后得到的，点T （5，y ）在抛物线上，点P 是抛物线上O 与T 之间的任意一点，在线段OT 上是否存在一点Q ，使△PQT 是等腰直角三角形？若存在，求出点Q 的坐标；若不存在，请说明理由． 23．如图，在矩形ABCD 中，6AB =，8BC =，沿直线MN 对折，使A 、C 重合，直线MN 交AC 于O ．(1)求证：COM CBA ∽； (2)求线段MN 的长度．24．如图已知OB 是半径，弦EF 垂直OB 于H ，点A 是HF 上的一点，BA 和O 相交于另一点C ，过点C 的切线和EF 的延长线交于点D ，（1）求证：DA DC =；（2）当:1:8DF EF =，2DF =时，求AB AC ⋅的值．25．如图1，D 是ABC 的BC 边上的中点，过点D 的一条直线交AC 于F ，交BA 的延长线于E ，//AG BC 交EF 于G ，我们可以证明EG DC ED AG ⋅=⋅成立（不要求考生证明）．()1如图2，若将图1中的过点D 的一条直线交AC 于F ，改为交CA 的延长线于F ，交BA 的延长线于E ，改为交BA 于E ，其它条件不变，则EG DC ED AG ⋅=⋅还成立吗？如果成立，请给出证明；如果不成立，请说出理由；()2根据图2，请你找出EG 、FD 、ED 、FG 四条线段之间的关系，并给出证明； ()3如图3，若将图1中的过点D 的一条直线交AC 于F ，改为交CA 的反向延长线于F ，交BA 的延长线于E ，改为交BA 于E ，其它条件不变，则()2得到的结论是否成立？26．如图，抛物线212y ax ax b =-+经过()1,0A -，30,2C ⎛⎫ ⎪⎝⎭两点，与x 轴交于另一点B ．()1求此抛物线的解析式；()2若抛物线的顶点为M ，点P 为线段OB 上一动点(不与点B 重合)，点Q 在线段MB 上移动，且45MPQ ∠=，设线段OP x =，22MQ y =，求2y 与x 的函数关系式，并直接写出自变量x 的取值范围； ()3在同一平面直角坐标系中，两条直线x m =，x n =分别与抛物线交于点E 、G ，与()2中的函数图象交于点F 、.H 问四边形EFHG 能否成为平行四边形？若能，求m 、n 之间的数量关系；若不能，请说明理由．27．已知：如图，△ADE ∽△ABC ，AB=10cm ，AD=6cm ，BC=12cm ，∠A=56°，∠ADE=40°．求： （1）∠ACB 的度数；（2）DE 的长．28．如图，△ABC 内接于⊙O，且AB ＝AC ．延长BC 到点D ，使CD ＝CA ，连接AD 交⊙O 于点E.（1）求证：△ABE ≌△CDE ；（2）填空：①当∠ABC 的度数为 时，四边形AOCE 是菱形；②若AE ＝6，BE=8，则EF 的长为 .29．如图，有三条线段AB 、BD 、DC ，AB 6=，BD 8=，DC 2=，且AB//DC ．点E 和点F 分别为BD 上的两个动点，且DF 1BE 3=．()1求证：ABE CDF ∽；()2当EF 2=时，求BE 的长度；()3在以上2个问题的解题过程中，概括（或者描述）你所用到数学基本知识（定义、定理等）或者是利用的数学思想方法．（共写出2点即可）30．已知△ABC 中，D 为AB 边上任意一点，DF ∥AC 交BC 于F ，AE ∥BC ，∠CDE=∠ABC ＝∠ACB ＝α，(1)如图1所示，当α=60°时，求证：△DCE 是等边三角形；(2)如图2所示，当α=45°时，求证：CD DE=2； (3)如图3所示，当α为任意锐角时，请直接写出线段CE 与DE 的数量关系：CE DE＝_____.参考答案1．C【解析】【分析】根据题目给出的条件推出三角形三边的比，再确定三角形的形状．【详解】∵（a-c）：（a+b）=-2：7，∴9a+2b-7c=0 ①，∵（a-c）：（c-b）=-2：1，∴a-2b+c=0 ②，∵（a+b）：（c-b）=7：1，∴a+8b-7c=0 ③，∵①+②得a：c=3：5，①-③得a：b=3：4，∴a：b：c=3：4：5，∴△ABC是直角三角形，故选C.【点睛】本题考查了比例的基本性质以及勾股定理的逆定理，根据比例的基本性质进行变形找出三角形三边的比是解题的关键.2．D【解析】【分析】由AB⊥BC，CD⊥BC，EF⊥BC，即可得AB∥EF∥CD，然后根据平行线分线段成比例定理，即可求得AB AECD CE=与CE EFAC AB=，又由AB=80，CD=20，即可求得CEAC的值，即可求得答案．【详解】∵AB⊥BC，CD⊥BC，EF⊥BC，∴AB∥EF∥CD，∴AB AE CD CE=，∵AB=80，CD=20， ∴80420AE CE ==， ∴15CE AC =， ∵CE EF AC AB=， ∴1805EF =， ∴EF=16．故选D ．【点睛】考查了平行线分线段成比例定理．此题难度不大，解题的关键是注意数形结合思想的应用与比例变形．3．D【解析】【分析】 只要证明AC AB AE AD=，即可解决问题． 【详解】解:A.12AE EC = ，可得AE ：AC=1：1，与已知2AB AD =不成比例，故不能判定 B. 2EC AC =，可得AC ：AE=1：1，与已知2AB AD=不成比例，故不能判定； C 选项与已知的2AB AD=，可得两组边对应成比例，但夹角不知是否相等，因此不一定能判定； 12DE BC = D. 2AC AB AE AD==，可得DE//BC ， 故选D.【点睛】本题考查平行线的判定，解题的关键是灵活运用所学知识解决问题，属于中考常考题型． 4．D【解析】设小正方形的边长为1，则图中的三角形是一个直角三角形，A选项，由图可知这是一个钝角三角形，所以不能选A；B选项，由图可知这是一个锐角三角形，所以不能选B；C选项，由图可知这是一个直角三角形，两直角边分别为2、3，和原直角三角形两直角边对应不成比例，所以不能选C；D选项，由图可知这是一个直角三角形，两直角边分别为2、4，和原直角三角形两直角边对应成比例，所以可以选D；故选D.5．B【解析】【分析】根据相似三角形对应边长比等于相似比即可解答.【详解】已知四边形ABCD相似四边形A'B'C'D'，且AB:A'B'=1:2,已知BC=8，则B'C'的长=16.即答案选B.【点睛】熟悉掌握相似三角形对应边长比等于相似比这一性质是解答本题的关键.6．D【解析】【分析】根据面积比是比例尺的平方比，列比例式求得该地方的实际面积即可．【详解】设该地方的实际面积为xcm2，则1：x=（1：1000）2，解得x=1000000．故1cm2的面积表示的实际面积是100000cm2．故选D．【点睛】本题考查了比例尺的定义，关键是熟悉面积比是比例尺的平方比的知识点．7．D【解析】试题分析：如图，∵动点F ，E 的速度相同，∴DF ＝CE ，又∵CD ＝BC ，∴CF ＝BE ，在△ABE 和△BCF 中，190AB BC ABE BCF BE CF ==⎧⎪∠=∠=⎨⎪=⎩，∴△ABE ≌△BCF （SAS ），故①正确；∴∠BAE ＝∠CBF ，AE ＝BF ，故②正确；∵∠BAE ＋∠BEA ＝90°， ∴∠CBF ＋∠BEA ＝90°， ∴∠APB ＝90°，故③正确；在△BPE 和△BCF 中，∵∠BPE ＝∠BCF ，∠PBE ＝∠CBF ，∴△BPE ∽△BCF ， ∴PE BE CF BF=， ∴CF •BE ＝PE •BF ，∵CF ＝BE ，∴CF 2＝PE •BF ，故④正确；∵点P 在运动中保持∠APB ＝90°， ∴点P 的路径是一段以AB 为直径的弧，设AB 的中点为G ，连接CG 交弧于点P ，此时CP 的长度最小，在Rt △BCG 中，CG， ∵PG ＝12AB ＝12，∴CP＝CG﹣PG＝5﹣12＝51-，即线段CP的最小值为512-，故⑤正确；综上可知正确的有5个，故选D．点睛：本题为四边形的综合应用，涉及全等三角形、相似三角形的判定和性质、勾股定理、正方形的性质等知识点．在判定三角形全等时，关键是选择恰当的判定条件，证明△ABE≌△BCF是解题的关键．本题考查知识点较多，综合性较强，难度较大．8．A【解析】∵∠AED=∠B，∠A=∠A∴△ADE∽△ACB∴AE DE AB BC=，∵DE=6，AB=10，AE=8，∴8610BC=，解得BC＝15 2.故选A.9．D【解析】【分析】根据DE∥BC，即可证得△ADE∽△ABC，然后根据相似三角形的面积的比等于相似比的平方，即可求解．【详解】∵AD=1，DB=2，∴AB=AD+DB=3，∵DE ∥BC ，∴△ADE ∽△ABC ， ∴221193ADE ABC S AD S AB ===（）（）： ． 故选D ．【点睛】本题考查了相似三角形的判定和性质：相似三角形的面积比是相似比的平方．10．B【解析】∵DE ∥BC ，EF ∥AB ，∴四边形BDEF 是平行四边形，∴BF=DE ．∵AD ：DB=1：2，∴AD ：AB=1：3．∵DE ∥BC ，∴DE ：BC=AD ：AB=1：3，即DE ：30=1：3，∴DE=10，∴BF=10．故FC 的长为20cm ．故选B.【点睛】运用了平行线分线段成比例定理，平行四边形的判定与性质，比例的性质，难度不大，得出BF=DE ，从而利用转化思想是解题的关键．11．ADB ABC ∠=∠或ABD ACB ∠=∠或AB AD AC AB= 【解析】【分析】根据相似三角形的判定定理（1）两角对应相等两三角形相似，（2）两边对应成比例且夹角相等两三角形相似，（3）三边对应成比例两三角形相似．此题有个公共角∠A ，所以应该应用（1），（2）两个判定方法，可补充如∠ADB=∠ABC 或∠ABD=∠ACB 或AB AD AC AB=． 【详解】解：此题答案不唯一，∵∠A=∠A ， ∴可以添加：如∠ADB=∠ABC 或∠ABD=∠ACB 或AB AD AC AB=． 故答案为：ADB ABC ∠=∠或ABD ACB ∠=∠或AB AD AC AB = 12．答案不唯一，如△DFE ∽△CBE【解析】【分析】根据平行四边形的性质可得AB//CD ，BC//AD ，再根据平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似即可得.【详解】∵四边形ABCD 是平行四边形，∴BC//AD ，即BC//DF ，∴△DEF ∽△CEB ，故答案为：△DEF ∽△CEB （答案不唯一）.【点睛】本题考查了平行四边形的性质、相似三角形的判定，熟练掌握“平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似”是解本题的关键.13．62或210．【解析】试题分析：根据P 点的不同位置，此题分两种情况计算：①点P 在CD 上；②点P 在AD 上．①点P 在CD 上时,如图：∵PD=3，CD=AB=9，∴CP=6，∵EF 垂直平分PB ，∴四边形PFBE 是邻边相等的矩形即正方形，EF 过点C ，∵BF=BC=6，∴由勾股定理求得EF=62②点P 在AD 上时，如图：先建立相似三角形，过E 作EQ ⊥AB 于Q ，∵PD=3，AD=6，∴AP=3，AB=9，由勾股定理求得2239+10，∵EF 垂直平分PB ，∴∠1=∠2（同角的余角相等），又∵∠A=∠EQF=90°，∴△ABP ∽△EFQ （两角对应相等，两三角形相似），∴对应线段成比例：EF EQ PB AB=,代入相应数值：69310=，∴10．综上所述：EF 长为2或10． 考点：翻折变换（折叠问题）． 14．32【解析】【分析】由BD=DF=FC 知DF BF =12、CF BC =13，证△ABF ∽△EDF 得DE=12AB ，证△ABC ∽△GFC 得GF=13AB ，从而得出答案． 【详解】解：∵BD=DF=FC ，∴DF BF =12、CF BC =13， ∵ED ∥AB ，∴△ABF ∽△EDF ，则AB DE =BF DF=2， ∴DE=12AB ， ∵GF ∥AB ，∴△ABC ∽△GFC ，∴ABGF=BCFC=3，∴GF=13 AB，则EDGF=1213ABAB=32，故答案为32．【点睛】本题主要考查相似三角形的判定与性质，寻找相似三角形的一般方法是通过作平行线构造相似三角形；或依据基本图形对图形进行分解、组合；或作辅助线构造相似三角形，判定三角形相似的方法有时可单独使用，有时需要综合运用，无论是单独使用还是综合运用，都要具备应有的条件方可．15．75, 26⎛⎫ ⎪⎝⎭【解析】【分析】先求出二次函数的解析式，然后过点B作BC⊥BP，交x轴于点C，延长BP交x轴于点D，可得∠CBA=45°，设点C坐标为（a，0），利用面积公式求出a值，然后得出点C坐标，根据BC⊥BD，BO⊥CD，可得△BCO∽DCB，进而得出BC CDCO BC=，求出点D的坐标，然后求出直线BD的解析式，与二次函数解析式联立求出点P的坐标．【详解】设二次函数的解析式为y=ax2+bx+c，则{2930 a b cca b c++++＝＝＝，解得：238 {32abc-＝＝＝，二次函数的解析式为：y=23x2-83x+2，过点B作BC⊥BP，交x轴于点C，延长BP交x轴于点D，则有∠CBA=45°，设点C坐标为（a，0）（a＜0），∵S△ABC=12BC•ABsin∠ABC=12AC•BO，21214?5?(1)?2222a a+=-，整理得：3a2-16a-12=0，解得：a=-23或a=6（不合题意，舍去），∴点C（-23，0），∵BC⊥BD，BO⊥CD，∴△BCO∽DCB，则有BC CDCO BC=，即BC2=CO•CD，∴4022933OD=+（），解得：OD=6，即点D（6，0），∵B（0，2），∴设直线BD的解析式为y=kx+m，代入得：2{60mk m+＝＝，解得：1{32km-＝＝，∴直线BD 的解析式为y=-13x+2， 与二次函数的解析式联立得： 2123{28233y x y x x -+-+＝＝， 解得：110{2x y ＝＝，2272{56x y ＝＝， 即点P 的坐标为（72，56）． 故答案为（72，56）． 【点睛】本题考查了二次函数的综合知识，涉及到待定系数法求一次函数和二次函数的解析式、三角形的面积公式、相似三角形的判定和性质等知识点，涉及考点众多，综合性较强，计算量大，有一定的难度．16．23【解析】【分析】先过点F 作FG ∥CD ，交AB 与点G ，得出AG AF DG CF =，BE BD BF BG=，再根据CA=3CF ，求出DG=12AG ，设DG=x ，则AG=2x ，再根据32AD DB =，得出BG=3x ，从而求出BD BG 即可． 【详解】过点F 作FG ∥CD ，交AB 与点G ，则AG AF DG CF =，BE BD BF BG=，∵CA=3CF，∴AG AFDG CF==2，∴DG=12 AG，∴设DG=x，则AG=2x，∵32 ADDB=，∴BD=2x，∴BG=3x，∴2233 BE BD xBF BG x===．故答案为：23．【点睛】此题主要考查了平行线分线段成比例定理，关键是作出平行线，得到成比例的线段，注意要把比例线段对应起来．17．10【解析】【分析】先根据平行线分线段成比例定理求出EF的长，进而可求出DF的长.【详解】∵AD∥BE∥FC，∴.∵AB=2，BC=3，DE=4，∴,∴EF=6,∴DF=DE+EF=4+6=10.故答案为：10.【点睛】本题考查了平行线分线段成比例定理，平行线分线段成比例定理指的是两条直线被一组平行线所截，截得的对应线段的长度成比例.推论：平行于三角形一边，并且和其他两边相交的直线，所截得的三角形的三边与原三角形的三边对应成比例.18．1：9：3【解析】【分析】先根据AD∥BC,可判定△AOD∽△COB,由于AD：BC=1：3,可得OD：OB=AD：BC=1：3,根据等高的两个三角形,两个三角形的面积比等于对应的底边之比,可得S△AOD：S△AOB=1：3,再根据相似三角形的面积比等于相似比的平方倍可得S△AOD：S△BOC=1：9.【详解】∵梯形ABCD中,AD∥BC,∴△AOD∽△COB,∵AD：BC=1：3,∴OD：OB=AD：BC=1：3,∴S△AOD：S△AOB=1：3,∴S△AOD：S△BOC=1：9,∴S△AOD：S△BOC：S△AOB=1：9：3,故答案为:1:9:3.【点睛】本题主要考查三角形的面积比,解决本题的关键是要掌握相似三角形的面积比等于相似比的平方倍,非相似三角形,在等高的情况下,两三角形的面积比等于对应的底边之比.19．6【解析】如图2，∵AB⊥BC，CD⊥BC，∴∠ABE=∠DCE=90°，又∵∠AEB=∠DEC，∴△ABE∽△DCE，∴AB BECD EC=，即：231AB=，解得：AB=6（m）.故答案为6. 20．【解析】【分析】直接用同一未知数表示出x，y的值，进而得出答案．【详解】解：∵，∴设x=4a，则y=3a ，那么故答案为：．【点睛】此题主要考查了比例式的性质，正确用同一未知数表示各数是解题关键．21．2【解析】【分析】先根据相似三角形面积比等于相似比的平方求得三角形ADE的面积，再根据等边三角形的面积公式求出其边长，进而求出点D到线段AB的距离．【详解】解：∵△ABC∽△ADE，AB=2AD，∴2ABCADES ABS AD⎛⎫= ⎪⎝⎭=4，∵S△ABC=3，∴S△ADE=3∵△ABC是等边三角形，△ABC∽△ADE，∴△ADE是等边三角形，2 ∴AD=1．如图，过点D 作DH ⊥AB 于H ．在△ADH 中，∵∠HAD=45°，∴DH=AD•sin ∠HAD=1×2=2．故答案为2． 【点睛】 此题考查了相似三角形的性质，等边三角形的性质，锐角三角函数，解此题的关键是根据相似三角形面积比等于相似比的平方求得三角形ADE 的面积，求出边长AD ．22．（1）D （2，9），E （2，3）；（2）1m =，232m =；（3）存在，（1，1）或（3，3）或（2，2）．【解析】【分析】（1）把抛物线配方，即可得到顶点为D 的坐标，然后设点E 的坐标是（2，m ），点C′的坐标是（0，n ），根据△CEC′是等腰直角三角形，求出E 点的坐标；（2）令抛物线的y=0，可求得A 、B 的坐标，然后再根据ΔHGF ΔBGF :S S =5：6，得到：56HM BN =，然后再证明△HGM ∽△ABN ，HG HM AB BN =，从而可证得56HG AB =，所以HG=5，设点H （m ，﹣m 2+4m+5），G （m ，m+1），最后根据HG=5，列出关于m 的方程求解即可；（3）分别根据∠P 、∠Q 、∠T 为直角画出图形，然后利用等腰直角三角形的性质和一次函数的图象的性质求得点Q 的坐标即可．【详解】解：（1）∵抛物线245y x x =-++=2(2)9x --+，∴D 点的坐标是（2，9），∵E 为对称轴上的一点，∴点E 的横坐标是2，设点E的坐标是（2，m），点C′的坐标是（0，n），∵将线段CE绕点E按逆时针方向旋转90°后，点C的对应点C′恰好落在y轴上，∴△CEC′是等腰直角三角形，∴2222222(5)2(5)(20)(5)2()2n mm m n⎧⎡⎤-=-+-⎪⎣⎦⎨-+=-+⎪⎩解得：31mn⎧⎨⎩==或79mn⎧⎨⎩==（舍去），∴点E的坐标是（2，3），点C′的坐标是（0，1）．综上，可得D点的坐标是（2，9），点E的坐标是（2，3）．（2）如图1所示：令抛物线245y x x=-++的y=0得：2450x x-++=，解得：11x=-，25x=，所以点A（﹣1，0），B（5，0）．设直线C′E的解析式是y kx b=+，将E（2，3），C′（0，1），代入得123bk b=+=⎧⎨⎩，解得：11kb=⎧⎨=⎩，∴直线C′E的解析式为1y x=+，联立得：2145y xy x x⎧⎨⎩=+=-++，解得：45xy⎧⎨⎩==，或1xy⎧⎨⎩=-=，∴点F得坐标为（4，5），点A（﹣1，0）在直线C′E上．∵直线C′E 的解析式为1y x =+，∴∠FAB=45°．过点B 、H 分别作BN ⊥AF 、HM ⊥AF ，垂足分别为N 、M ．∴∠HMN=90°，∠ADN=90°，又∵∠NAD=∠HNM=45°，∴△HGM ∽△ABN ， ∴HG HM AB BN=， ∵ΔHGF ΔBGF :S S =5：6， ∴56HM BN =． ∴56HG AB =，即566HG =， ∴HG=5．设点H 的横坐标为m ，则点H 的纵坐标为245m m -++，则点G 的坐标为（m ，m+1）， ∴245(1)5m m m -++-+=．解得：132m +=，232m =； （3）由平移的规律可知：平移后抛物线的解析式为2(1)4(1)5y x x =--+-+=26x x -+．将x=5代入26y x x =-+得：y=5，∴点T 的坐标为（5，5）．设直线OT 的解析式为y kx =，将x=5，y=5代入得；k=1，∴直线OT 的解析式为y x =，①如图2所示：当PT ∥x 轴时，△PTQ 为等腰直角三角形，将y=5代入抛物线26y x x =-+得：265x x -+，解得：11x =，25x =．∴点P 的坐标为（1，5）．将x=1代入y x =得：y=1，∴点Q 的坐标为（1，1）；②如图3所示：由①可知：点P 的坐标为（1，5）．∵△PTQ 为等腰直角三角形，∴点Q 的横坐标为3，将x=3代入y x =得；y=3，∴点Q 得坐标为（3，3）；③如图4所示：设直线PT 解析式为y kx b =+，∵直线PT ⊥QT ，∴k=﹣1，将k=﹣1，x=5，y=5代入y kx b =+得：b=10，∴直线PT 的解析式为10y x =-+．联立得：2106y x y x x ⎧⎨⎩=-+=-+， 解得：28x y ==⎧⎨⎩，55x y =⎧⎨=⎩， ∴点P 的横坐标为2，将x=2代入y x =得，y=2，∴点Q 的坐标为（2，2）．综上所述：点Q 的坐标为（1，1）或（3，3）或（2，2）．【点睛】本题主要考查的是二次函数的综合应用，明确△HGF 和△BGF 的面积比等于HG 和AB 的边长比是解题的关键，同时解答本题主要应用了分类讨论的思想需要同学们分别根据∠P 、∠Q 、∠T 为直角进行分类计算．23．(1)证明见解析；(2)152MN =． 【解析】【分析】(1) 由折叠判断垂直, 进而判断两直角相等, 又有一公共角, 可以判断△COM ∽△CBA(AA);(2) 利用 (1) 的结论, 得到线段成比例OC OM BC AB=, AB 、BC 已知, 由勾股定理求出AC 的值, 根据矩形的性质, 可得到OC 的值,进而求解.【详解】(1)∵沿直线MN 对折，使A 、C 重合．∴A 与C 关于直线MN 对称，∴AC MN ⊥，∴90COM ∠=．在矩形ABCD 中，90B ∠=，∴COM B ∠=∠，又∵ACB ACB ∠=∠，∴COM CBA ∽；(2)∵在Rt CBA 中，6AB =，8BC =，∴10AC =，∴5OC =，∵COM CBA ∽，∴OC OM BC BA=， ∴154OM =， ∴1522MN OM ==． 【点睛】本题主要考查相似三角形的应用、勾股定理的应用以及矩形的性质.24．（1）见解析；（2）24.【解析】【分析】（1）作出辅助线，利用等角的余角相等即可解题，（2）利用相似比，找到比例中项即可解题.【详解】（1）连接OC ，则有12∠=∠，又CD 是切线，∴OC CD ⊥，而4∠与1∠互余，3∠与2∠互余，∴34∠=∠，∴DA DC =（2）∵2DF =∴EF =又∵218CD DF DE =⋅==，∴CD AD ==∴AF AE ===∴24AB AC AE AF ⋅=⋅=．【点睛】本题考查了相似三角形的性质，作出辅助线是解题关键.25．(1)成立,证明见解析;(2)见解析;()3成立.【解析】【分析】（1）由于BD CD =，，那么本题要证得实际是EAG EBD ∽，因为//AG BC 由此可得证．（2）本题要根据两组相似三角形来求解，根据//AG BC ，得出FGA FDC ∽．可得出::FG FD AG DC =．根据EAG EBD ∽．可得出::EG ED AG BD =．由于BD CD =，将相等值进行替换即可得出FG FD EG ED ，，，的比例关系．（3）成立，和（2）的证法完全一样．【详解】解：()1成立．证明：∵//AG BC ，∴EAG EBD ∽．∴::EG ED AG BD =．即EG BD ED AG ⋅=⋅．∵BD CD =，∴EG CD ED AG ⋅=⋅．()2FG ED FD EG ⋅=⋅．证明：∵//AG BC ，∴FGA FDC ∽．∴::FG FD AG DC =．∵BD DC =，∴::FG FD AG BD =．由()1，得::EG ED AG BD =．∴::FG FD EG ED =，即FG ED FD EG ⋅=⋅．()3成立，证明过程同()2．【点睛】考查相似三角形的判定与性质，相似三角形的对应边的比相等是解题的关键.26．（1）211322y x x =-++；（2）2215(03)22y x x x =-+≤<；（3）m 、n 之间的数量关系是2(02m n m +=≤≤且1)m ≠．【解析】【分析】()1将A 、C 的坐标代入抛物线的解析式中，即可求出1y 的函数解析式；()2过M 作MN x ⊥轴于N ，根据抛物线1y 的函数解析式，即可得到M 点的坐标，可分别在Rt MPN 和Rt MBN 中，用勾股定理表示出MN 的长，由此可得到关于PM 、x 的函数关系式；由于45MPQ MBP ∠=∠=，易证得MPQ ∽MBP ，根据相似三角形得到的比例线段即可得到关于PM 、2y 的关系式，联立两式即可求出2y 、x 的函数关系式； ()3根据两根抛物线的解析式和两条直线的解析式，可求出E 、F 、G 、H 四点的坐标，即可得到EF 、GH 的长，由于//EF GH ，若四边形EFHG 是平行四边形，那么必有EF GH =，可据此求出m 、n 的数量关系．【详解】解：()1抛物线212y ax ax b =-+经过()1,0A -，30,2C ⎛⎫ ⎪⎝⎭两点； 2032a a b b ++=⎧⎪∴⎨=⎪⎩，解得1232ab⎧=-⎪⎪⎨⎪=⎪⎩．∴抛物线的解析式为211322y x x=-++；()2作MN AB⊥，垂足为N．由211322y x x=-++，易得()1,2M，()1,0N，()1,0A-，()3,0B；4AB∴=，2MN BN==，22MB=45MBN∠=；根据勾股定理有：2222BM BN PM PN-=-，2222(22)2(1)PM x∴-=--⋯①；又45MPQ MBP∠==∠，(PMQ BMP∠=∠公共角)，MPQ∴∽MBP，22222222PM MQ MB y y∴=⋅=⋅=⋯②；由①②得：221522y x x=-+；03x≤<，2y∴与x的函数关系式为2215(03)22y x x x=-+≤<；()3四边形EFHG可以为平行四边形，m、n之间的数量关系是：2(02m n m+=≤<且1)m≠；点E、G是抛物线211322y x x=-++分别与直线x m=，x n=的交点，∴点E 、G 坐标为213,22E m m m ⎛⎫-++ ⎪⎝⎭，213,22G n n n ⎛⎫-++ ⎪⎝⎭； 同理，点F 、H 坐标为215,22F m m m ⎛⎫-+ ⎪⎝⎭，215,.22H n n n ⎛⎫-+ ⎪⎝⎭ 2221513212222EF m m m m m m ⎛⎫∴=-+--++=-+ ⎪⎝⎭，2221513212222GH n n n n n n ⎛⎫=-+--++=-+ ⎪⎝⎭； 四边形EFHG 是平行四边形，EF GH =，222121m m n n ∴-+=-+，()()20m n m n ∴+--=；由题意知m n ≠，()21m n m ∴+=≠；因此四边形EFHG 可以为平行四边形，m 、n 之间的数量关系是2(02m n m +=≤≤且1)m ≠．【点睛】此题考查了二次函数解析式的确定、勾股定理、相似三角形的判定和性质、平行四边形的判定等知识，综合性强，难度较大．27．（1）84°；（2）7.2.【解析】【分析】（1）（2）根据三角形相似，对应角相等，对应边的比相等，可以把本题转化为求∠AED的问题，再根据对应边的比相等，就可以求出DE的长．【详解】（1）△AED中已知，∵∠A=56°，∠ADE=40°，∴∠AED=84°．∵△ADE∽△ABC，∴∠ACB=∠AED=84°．（2）∵△ADE∽△ABC，∴DE AD BC AB=∴6 1210 DE=．∴DE=7.2（cm）．【点睛】本题主要考查了相似三角形的性质，对应角相等，对应边的比相等．28．（1）证明见解析（2）①60②9 2【解析】分析：（1）根据AAS证明两三角形全等；（2）①先证明∠AOC=∠AEC=120°，∠OAE=∠OCE=60°，可得▱AOCE，由OA=OC可得结论；②根据（1）中的全等得：BE=DE=8，AE=CE=6，证明△ECD∽△CFB，列式可得：EC CFED BC==68，证明△AEF∽△BCF，则可得EF的长．详解：（1）证明：∵AB=AC，CD=CA，∴∠ABC=∠ACB，AB=CD．∵四边形ABCE是圆内接四边形，∴∠ECD=∠BAE，∠CED=∠ABC．∵∠ABC=∠ACB=∠AEB，∴∠CED=∠AEB，∴△ABE≌△CDE（AAS）；（2）①当∠ABC的度数为60°时，四边形AOCE是菱形；理由是：连接AO、OC．∵四边形ABCE是圆内接四边形，∴∠ABC+∠AEC=180°．∵∠ABC=60，∴∠AEC=120°=∠AOC．∵OA=OC，∴∠OAC=∠OCA=30°．∵AB=AC，∴△ABC是等边三角形，∴∠ACB=60°．∵∠ACB=∠CAD+∠D．∵AC=CD，∴∠CAD=∠D=30°，∴∠ACE=180°﹣120°﹣30°=30°，∴∠OAE=∠OC E=60°，∴四边形AOCE是平行四边形．∵OA=OC，∴▱AOCE是菱形；②由（1）得：△ABE≌△CDE，∴BE=DE=8，AE=CE=6，∴∠D=∠EBC．∵∠CED=∠ABC=∠ACB，∴△ECD∽△CFB，∴EC CFED BC==68．∵∠AFE=∠BFC，∠AEB=∠FCB，∴△AEF∽△BCF，∴6AE BCEF CF EF=∴，=86，∴EF=368=92．故答案为①60°；②92．点睛：本题是圆的综合题，考查了等腰三角形的性质、等边三角形的性质和判定、三角形相似和全等的性质和判定、四点共圆的性质、菱形的判定等知识，难度适中，正确判断圆中角的关系是关键．29．（1）证明见解析；（2）BE的长度为92；（3）见解析.【解析】【分析】（1）由“SAS”可以判定,∴△ABE∽△CDF．（2）设BE=x，则1DF x3=，又∵BD=8，∴1x x823+=-，解方程即可得到答案．（3）本题用到的数学基本知识较多，如：①两直线平行，内错角相等；②相似三角形对应边成比例；③两边对应成比例，且夹角相等的两个三角形相似；④分类讨论思想；⑤数形结合思想…．【详解】()1证明：∵AB//CD∴B D∠∠=，又∵CD1AB3=，DE1BE3=，∴ABE CDF∽．()2解：设BE x=，则1DF x3=，又∵BD8=，∴1x x823+=-，解得：9x2 =，∴BE的长度为：92．()3解：①两直线平行，内错角相等,②相似三角形对应边成比例③两边对应成比例，且夹角相等的两个三角形相似④分类讨论思想,⑤数形结合思想,⑥方程思想（列方程解决实际问题）．【点睛】考查相似三角形的判定与性质，掌握相似三角形的判定方法是解题的关键. 30．1【解析】试题分析：（1）证明△CFD≌△DAE即可解决问题．（2）如图2中，作FG⊥AC于G．只要证明△CFD∽△DAE，推出DCDE=CFAD，再证明CF即可．（3）证明EC=ED即可解决问题．试题解析：（1）证明：如图1中，∵∠ABC=∠ACB=60°，∴△ABC是等边三角形，∴BC=BA．∵DF∥AC，∴∠BFD=∠BCA=60°，∠BDF=∠BAC=60°，∴△BDF是等边三角形，∴BF=BD，∴CF=AD，∠CFD=120°．∵AE∥BC，∴∠B+∠DAE=180°，∴∠DAE=∠CFD=120°．∵∠CDA=∠B+∠BCD=∠CDE+∠ADE．∵∠CDE=∠B=60°，∴∠FCD=∠AD E，∴△CFD≌△DAE，∴DC=DE．∵∠CDE=60°，∴△CDE是等边三角形．（2）证明：如图2中，作FG⊥AC于G．∵∠B=∠ACB=45°，∴∠BAC=90°，∴△ABC是等腰直角三角形．∵DF∥AC，∴∠BDF=∠BAC=90°，∴∠BFD=45°，∠DFC=135°．∵AE∥BC，∴∠B AE+∠B=180°，∴∠DFC=∠DAE=135°．∵∠CDA=∠B+∠BCD=∠CDE+∠ADE．∵∠CDE=∠B=45°，∴∠FCD=∠ADE，∴△CFD∽△DAE，∴DCDE=CFAD．∵四边形ADFG是矩形，FC=2FG，∴FG=AD，CF=2AD，∴CDDE=2．（3）解：如图3中，设AC与DE交于点O．∵AE∥BC，∴∠EAO=∠ACB．∵∠CDE=∠ACB，∴∠CDO=∠OAE．∵∠COD=∠EOA，∴△COD∽△EOA，∴COEO=ODOA，∴COOD=EOOA．∵∠COE=∠DOA，∴△COE∽△DOA，∴∠CEO=∠DAO．∵∠CED+∠CDE+∠DCE=180°，∠BAC+∠B+∠ACB=180°．∵∠CDE=∠B=∠ACB，∴∠EDC=∠ECD，∴EC=ED，∴CEDE=1．点睛：本题考查了相似三角形综合题、全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，灵活运用所学知识解决问题，属于中考压轴题．。

乏公仓州月氏勿市运河学校2021届鲍沟学业水平考试数学一轮复习专题：图形的相似强化练习题一、单项选择题1．如图，在△ABC中，∠AED=∠B，DE=6，AB=10，AE=8，那么BC的长度为〔〕A．B．C．3 D．2．如图，物理课上张明做小孔成像实验，蜡烛与成像板之间的距离BB'为36cm，要使烛焰的像A′B′是烛焰AB的2倍，那么蜡烛与成像板之间的小孔纸板应放在离蜡烛〔〕cm的地方．A．12 B．24 C．18 D．93．如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，把△ABC绕AB边上的点D顺时针旋转90°得到△A′B′C′，A′C′交AB于点E，假设AD=BE，那么△A′DE的面积是〔〕A．3 B．5 C．11 D．64．如图,在菱形ABCB中,点E在AD边上,EF∥CD,交对角线BD于点F,那么以下结论中错误的选项是( )A．B．C．D．5．如图，矩形的顶点分别落在轴、轴，那么点的坐标是〔〕A．B．C．D．6．如图，线段AB两个端点的坐标分别为A〔6,6〕，B〔8,2〕，以原点O为位似中心，在第一象限内将线段AB缩小为原来的后得到线段CD，那么端点C的坐标为〔〕A．〔3,3〕B．〔4,3〕C．3,1〕D．〔4,1〕7．点C在线段AB上，且点C是线段AB的黄金分割点〔AC＞BC〕，那么以下结论正确的选项是〔〕A. AB2=AC•BC B. BC2=AC•BC C. AC=BC D. BC=AB8．如图，在平行四边形ABCD中，AB=10，AD=6，E是AD的中点，在AB上取一点F，使△CBF∽△CDE，那么BF的长是〔〕A．5 B．C．D．9．如图，梯形ABCD中，AD∥BC，AB=DC，∠DBC=45°，点E在BC上，点F在AB上，将梯形ABCD沿直线EF翻折，使得点B与点D重合．如果，那么的值是〔〕A．B．C．D．10．如图，△，△，△，△是4个全等的等腰三角形，底边，，，在同一条直线上，且，．连接，交于点，那么〔〕A．1 B．C．D．11．如图，在平行四边形ABCD中，点E是AB的中点，BD与CE相交于点F，那么△BEF与△DCF的面积比为〔〕A．1：2 B．2：1 C．4：1 D．1：412．如图，正方形OEFG和正方形ABCD是位似图形，且点F与点C是一对对应点，点F的坐标是〔1，1〕，点C的坐标是〔4，2〕；那么它们的位似中心的坐标是〔〕A．〔0，0〕B．〔﹣1，0〕C．〔﹣2，0〕D．〔﹣3，0〕二、填空题13．如图，矩形ABCD的边AB上有一点P，且AD=，BP=，以点P为直角顶点的直角三角形两条直角边分别交线段DC，线段BC于点E，F，连接EF，那么tan∠PEF= _______．14．如图，在△ABC中，DE垂直平分BC，垂足为点D，交AB于点E，且AD=AC，EC交AD于点F，以下说法：①△ABC∽△FDC；②点F是线段AD的中点；③S△AEF：S△AFC=1：4；④假设CE平分∠ACD，那么∠B=30°，其中正确的结论有_____〔填写所有正确结论的序号〕．15．如图在正方形ABCD中，点M为BC边上一点，BM＝4MC，以M为直角顶点作等腰直角三角形MEF，点E 在对角线BD上，点F在正方形外EF交BC于点N，连CF，假设BE＝2，S△CMF＝3，那么MN＝_____.16．如图,第一象限内的点在反比例函数的图象上,第四象限内的点在反比例函数图象上,且度,那么值为______17．如图，DE是△ABC的中位线，F是DE的中点，CF的延长线交AB于G，AB=6，那么AG=_____．18．在Rt△内有边长分别为2，，3的三个正方形如图摆放，那么中间的正方形的边长的值为________．三、解答题19．如图，边长为2的正方形ABCD中，P是对角线AC上的一个动点〔点P与A、C不重合〕，连接BP，将BP绕点B顺时针旋转90°到BQ；连接PQ，PQ与BC交于点E，QP延长线与AD〔或AD延长线〕交于点F，连接CQ．求证：〔1〕CQ=AP；〔2〕△APB∽△CEP．20．如图，点E是正方形ABCD的边BC延长线上一点，联结DE，过顶点B作BF⊥DE，垂足为F，BF交边DC于点G．〔1〕求证：GD•AB=DF•BG；〔2〕联结CF，求证：∠CFB=45°．21．如图，在△ABC中，∠C=90°，点O在AC上，以OA为半径的⊙O交AB于点D，BD的垂直平分线交BC 于点E，交BD于点F，连接DE．〔1〕求证：直线DE是⊙O的切线；〔2〕假设AC=6，BC=8，OA=2，求线段AD和DE的长．22．如图，在平行四边形ABCD中，过B作BE⊥CD，垂足为点E，连接AE，F为AE上一点，且∠BFE=∠C．〔1〕求证：△ABF∽△EAD；〔2〕假设AB=4，∠BAE=30°，求AE的长．23．如图，在△ABC中，点D，E分别在边AB，AC上，且BE平分∠ABC，∠ABE=∠ACD，BE，CD交于点F．〔1〕求证：；〔2〕请探究线段DE，CE的数量关系，并说明理由；〔3〕假设CD⊥AB，AD=2，BD=3，求线段EF的长．24．如图1 ，一次函数(k,b为常数，k≠0)的图象与反比例函数〔m为常数，m≠0〕的图象相交于点M(1，4)和点N〔4，n〕．(1)填空：①反比例函数的解析式是；②根据图象写出时自变量x的取值范围是；(2) 假设将直线MN向下平移a(a>0)个单位长度后与反比例函数的图象有且只有一个公共点，求a的值；(3) 如图2，函数的图象〔x＞0〕上有一个动点C，假设先将直线MN平移使它过点C，再绕点C 旋转得到直线PQ，PQ交轴于点A，交轴点B，假设BC=2CA，求OA·OB的值.。

考点强化练25 图形的相似基础达标一、选择题1.如图,在△ABC中,点D,E分别是AB,AC的中点,则下列结论不正确的是()A.BC=2DEB.△ADE∽△ABCC.AAAA =AAAAD.S△ABC=3S△ADE2.若△ABC与△DEF的相似比为1∶4,则△ABC与△DEF的周长比为()A.1∶2B.1∶3C.1∶4D.1∶16△ABC与△DEF的相似比为1∶4,∴△ABC与△DEF的周长比为1∶4.故选C.3.为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据:①BC,∠ACB;②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根据所测数据,求出A,B间距离的有()A.1组B.2组C.3组D.4组因为知道∠ACB和BC的长,所以可利用∠ACB的正切来求AB的长;②可利用∠ACB和∠ADB的正切求出AB;③因为△ABD∽△FED,可利用AAAA =AAAA,求出AB;④无法求出A,B间距离.故共有3组可以求出A,B间距离.4.下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是()5.如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA'B'C'与矩形OABC关于点O位似,且矩形OA'B'C'的面积等于矩形OABC面积的14,那么点B'的坐标是()A.(-2,3)B.(2,-3)C.(3,-2)或(-2,3)D.(-2,3)或(2,-3)6.如图是跷跷板示意图,横板AB绕中点O上下转动,立柱OC与地面垂直,设B点的最大高度为h1.若将横板AB换成横板A'B',且A'B'=2AB,O仍为A'B'的中点,设B'点的最大高度为h2,则下列结论正确的是()A.h2=2h1B.h2=1.5h1C.h2=h1D.h2=12h1B作BD⊥AC于D,∵O为AB的中点,OC⊥AD,BD⊥AD,∴OC∥BD,∴OC是△ABD的中位线,∴h1=2OC,同理,当将横板AB换成横板A'B',且A'B'=2AB,O仍为A'B'的中点,设B'点的最大高度为h2,则h2=2OC,∴h1=h2.7.(2018重庆)要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5 cm,6 cm和9 cm,另一个三角形的最短边长为2.5 cm,则它的最长边为()A.3 cmB.4 cmC.4.5 cmD.5 cmx cm,根据题意,得52.5=9A,解得x=4.5,即另一个三角形的最长边长为4.5cm,故选C.8.(2018浙江杭州)如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是(),∠ACB=180°-45°=135°,A,C,D图形中的钝角都不等于135°,由勾股定理得,BC=√2,AC=2,对应的图形B中的边长分别为1和√2,∵√2=√22,∴图B中的三角形(阴影部分)与△ABC相似,故选B.二、填空题9.如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,则AAAA的值等于.10.如图,已知∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是.(只需写一个条件,不添加辅助线和字母)∥DE(答案不唯一)11.如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,若S△DEC=3,则S△BCF=.三、解答题12.(2018湖南张家界)如图,点P 是☉O 的直径AB 延长线上一点,且AB=4,点M 为AA ⏜上一个动点(不与A ,B 重合),射线PM 与☉O 交于点N (不与M 重合). (1)当M 在什么位置时,△MAB 的面积最大,并求岀这个最大值; (2)求证:△PAN ∽△PMB.M 在AA ⏜的中点处时,△MAB 面积最大,此时OM ⊥AB ,∵OM=12AB=12×4=2,∴S △ABM =12AB ·OM=12×4×2=4.∠PMB=∠PAN ,∠P=∠P ,∴△PAN ∽△PMB.能力提升一、选择题 1.如图,D ,E 分别是△ABC 的边AB ,BC 上的点,且DE ∥AC ,AE ,CD 相交于点O ,若S △DOE ∶S △COA =1∶25,则S △BDE 与S △CDE 的比是( )A.1∶3B.1∶4C.1∶5D.1∶25DE ∥AC ,∴△DOE ∽△COA.又S △DOE ∶S △COA =1∶25,∴AA AA =15.∵DE ∥AC ,∴AAAA =AAAA =15.∴AA AA =14. ∴S △BDE 与S △CDE 的比是1∶4.2.(2018贵州遵义)如图,四边形ABCD 中,AD ∥BC ,∠ABC=90°,AB=5,BC=10,连接AC ,BD ,以BD 为直径的圆交AC 于点E.若DE=3,则AD 的长为( ) A.5 B.4C.3√5D.2√5,在Rt △ABC 中,AB=5,BC=10,∴AC=5√5.过点D 作DF ⊥AC 于点F ,∴∠AFD=∠CBA ,∵AD ∥BC ,∴∠DAF=∠ACB , ∴△ADF ∽△CAB ,∴AA AA =AAAA , ∴AA 5=,设DF=x ,则AD=√5x ,在Rt △ABD 中,BD=√AA 2+AA 2=√5A 2+25,∵∠DEF=∠DBA ,∠DFE=∠DAB=90°, ∴△DEF ∽△DBA ,∴AA AA =AAAA , ∴√=√5A, ∴x=2,∴AD=√5x=2√5,故选D .二、填空题3.(2018北京)如图,在矩形ABCD 中,E 是边AB 的中点,连接DE 交对角线AC 于点F ,若AB=4,AD=3,则CF 的长为 .四边形ABCD 为矩形,∴AB=CD ,AD=BC ,AB ∥CD ,∴∠FAE=∠FCD ,又∵∠AFE=∠CFD ,∴△AFE ∽△CFD ,∴AA AA =AAAA =2. ∵AC=√AA 2+AA 2=5, ∴CF=AAAA +AA ·AC=22+1×5=103.三、解答题4.(2018湖南株洲)如图,在Rt △ABM 和Rt △ADN 的斜边分别为正方形的边AB 和AD ,其中AM=AN. (1)求证:Rt △ABM ≌Rt △ADN ;(2)线段MN 与线段AD 相交于T ,若AT=14AD ,求tan ∠ABM 的值.AD=AB ,AM=AN ,∠AMB=∠AND=90°,∴Rt △ABM ≌Rt △ADN (HL).Rt △ABM ≌Rt △ADN 易得∠DAN=∠BAM ,DN=BM.∵∠BAM+∠DAM=90°,∠DAN+∠ADN=90°, ∴∠DAM=∠AND ,∴ND ∥AM , ∴△DNT ∽△AMT. ∴AA AA =AAAA . ∵AT=14AD ,∴AA AA =13. ∴tan ∠ABM=AAAA =AAAA =13。