材料力学 杆件的变形计算

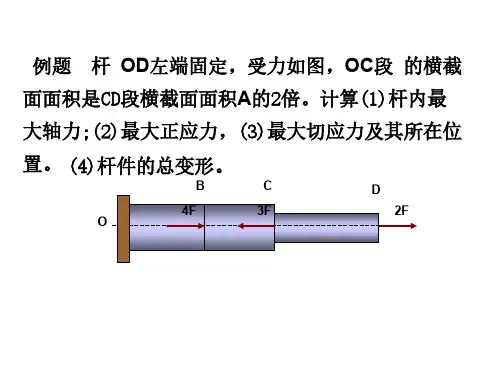
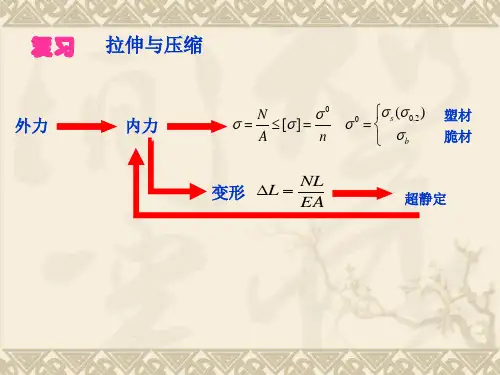
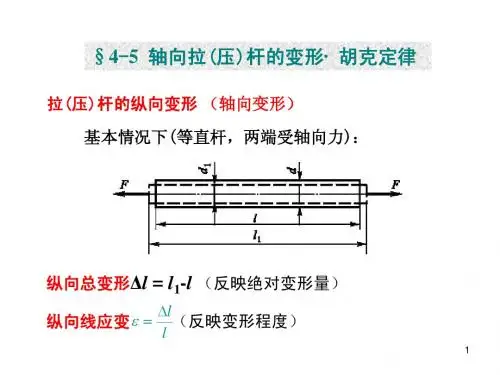
面积A，拉应力为正）d，拉伸后试样直径 d1）纵向线应变和横向线应变外力偶P 功率， n 转速）弯矩、剪力和荷载集度之间的关系式轴向拉压杆横截面上正应力的计算公式杆件横截面轴力F N，横截面1.2.3.4.5.6.7.8.9.10.11.12.泊松比胡克定律受多个力作用的杆件纵向变形计算公式轴向拉压杆斜截面上的正应力与切应力计算公式夹角a 从x 轴正方向逆时针转至外法线的方位角为正）纵向变形和横向变形（拉伸前试样标距l ，拉伸后试样标距 l1 ；拉伸前试样直径承受轴向分布力或变截面的杆件，纵向变形计算公式轴向拉压杆的强度计算公式许用应力，脆性材料延伸率截面收缩率剪切胡克定律拉压弹性模量，塑性材料切变模量G，切应变gE、泊松比和切变模量圆截面对圆心的极惯性矩（ a）实心圆b）空心圆）G之间关系式圆轴扭转时横截面上任一点切应力计算公式圆截面周边各点处最大切应力计算公式扭转截面系数，（ a）实心圆扭矩T，所求点到圆心距离r ）13.14.15.16.17.18.19.20.21.22.23.24.薄壁圆管（壁厚 δ≤ R 0 /10 ，R 0 为圆管的平均半径）扭转切应力计算公式圆轴扭转角 与扭矩 T 、杆长 l 、 扭转刚度 GH p 的关系式 同一材料制成的圆轴各段内的扭矩不同或各段的直径不同（如阶梯轴）时等直圆轴强度条件受内压圆筒形薄壁容器横截面和纵截面上的应力计算公式平面应力状态下斜截面应力的一般公式b ）空心圆25.26. 27. 28. 29. 30.31.32.33.或 塑性材料或 扭转圆轴的刚度条件 ? ；脆性材料平面应力状态的三个主应力 主平面方位的计算公式 ，面内最大切应力 三向应力状态最大切应力 广义胡克定律 四种强度理论的相当应力34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44.任意截面图形对一点的极惯性矩与以该点为原点的任意两正交坐标轴的惯性矩之 和的关系式平行移轴公式（形心轴 z c 与平行轴 z 1的距离为 a ，图形面积为 A ）纯弯曲梁的正应力计算公式45. 46.47.48.49. 50.51.52.53.54.， 组合图形的形心坐标计算公式 截面图形对轴 z 和轴y 的惯性半径 ?矩形、圆形、空心圆形的弯曲截面系数几种常见截面的最大弯曲切应力计算公式（ 轴 z 的静矩， b 为横截面在中性轴处的宽度）为中性轴一侧的横截面对中性横力弯曲最大正应力计算公式工字形截面梁腹板上的弯曲切应力近似公式轧制工字钢梁最大弯曲切应力计算公式 圆形截面梁最大弯曲切应力发生在中性轴处弯曲正应力强度条件弯曲梁危险点上既有正应力 σ 又有切应力 τ 作用时的强度条件 或，梁的挠曲线近似微分方程 轴向荷载与横向均布荷载联合作用时杆件截面底部边缘和顶部边缘处的正应力计弯扭组合变形时圆截面杆按第三和第四强度理论建立的强度条件表达式55.56.57.58.59. 60.61.62.63.64.65. 66.算公式偏心拉伸（压缩） 圆环形薄壁截面梁最大弯曲切应力发生在中性轴处 几种常见截面梁的弯曲切应力强度条件梁的转角方程梁的挠曲线方程圆截面杆横截面上有两个弯矩 和 同时作用时，合成弯矩为圆截面杆横截面上有两个弯矩和同时作用时强度计算公式弯拉扭或弯压扭组合作用时强度计算公式剪切实用计算的强度条件挤压实用计算的强度条件 等截面细长压杆在四种杆端约束情况下的临界力计算公式 压杆的约束条件：（ a ）两端铰支 μ =l（ b ）一端固定、一端自由 μ =2（ c ）一端固定、一端铰支d ）两端固定 μ =0.567.68.69.70.71.72.73. 74. 75. 76. 77.μ=0.778.压杆的长细比或柔度计算公式79.细长压杆临界应力的欧拉公式80.欧拉公式的适用范围81.压杆稳定性计算的安全系数法82.压杆稳定性计算的折减系数法83. 关系需查表求得3截面的几何参数4应力和应变5应力状态分析6内力和内力图7强度计算刚度校核9 压杆稳定性校核10 动荷载11 能量法和简单超静定问题材料力学公式汇总、应力与强度条件1、拉压maxmax2、剪切max3、4、挤压挤压圆轴扭转P挤压A挤压TWtmax平面弯曲①maxM maxy t maxI z*③ Q max S z max②t max5、斜弯曲max M z M yW z W yW z maxtmaxt maxmax注意：“5”与“ 6”两式仅供参考 ②第四强度理论r4w 2 3 n 2M w 20.75M n 2r4 w 3 n WWz二、变形及刚度条件１拉压LNLNLN i L iN ( x) dxEA EA LEA２扭转TLT i L i T x dx T 180 0（ /GI pGI pGI pL GI p３弯曲(1) 积分法 : EIy ''( x) M(x) E Iy '(x) EI (x) M(x)dx CEIy ( x) [ M (x)dx]dx Cx D(2)叠加法 : f P 1,P 2 ⋯= f P 1 f P 2 +⋯， P 1, P 2 = P 1 P 2 ⋯M 2L =M i 2L i =M 2xdx2EI 2EI i 2EI（5）卡氏第二定理 （ 注：只给出线性弹性弯曲梁的公式 ） 三、应力状态与强度理论 １、 二向应力状态斜截面应力２、 二向应力状态极值正应力及所在截面方位角 ３、 二向应力状态的极值剪应力注：极值正应力所在截面与极值剪应力所在截面夹角为 450４、 三向应力状态的主应力： 1 2 36、拉（压）弯组合 maxNM7、圆轴弯扭组合：①第三强度理论M w 2 M n2Wz（3）基本变形表 （ 注意：以下各公式均指绝对值，使用时要根据具体情 况赋予正负号 ）ML3EI, A MLA6EIBA PL 216EI qL3 24EI （4）弹性变形能 （ 注：以下只给出弯曲构件的变形能 响, 其他变形与此相似 ,不予写出 ） 并忽略剪力影 B最大剪应力 ： max1 325、二向应力状态的广义胡克定律（1）、表达形式之一（用应力表示应变） （2）、表达形式之二（用应变表示应力） 6、三向应力状态的广义胡克定律 强度理论 1) r1 1 1 bnb2)r 3 1 3五、动载荷（只给出冲击问题的有关公式）能量方程TVU7、 sn s8、平面应力状态下的应变分析sin 2x y x y1)2 2xys i n222tg2 0 xyxy四、压杆稳定1、临界压力与临界应力公式（若把直杆分为三类） ① 细长受压杆 p ② 中长受压杆 p ③ 短粗受压杆s2EI minPcr 2PcrL2cr a b“ cr ”2Ecr22、关于柔度的几个公式 或 b2Epasb3、惯性半径公式 i I Az短边长度 ））圆截面 i d4，矩形截面 i min b12（b 为2cos 2xyc o 2s2冲击系数 K d 1 1 2hst （自由落体冲击）K dgv0st（水平冲击）六、截面几何性质1、 惯性矩（以下只给出公式，不注明截面的形状） 442 d D 4 d132 DI P 2dA =2、惯性矩平移轴公式32。

《材料力学》课程中杆件内力与变形计算的Matlab实现李春锋;蒲兴龙;于彬;杨旭辉;王丽【摘要】杆件的内力与变形计算是材料力学课程教学的主要任务之一，其确定往往涉及较大的计算量，学生在学习中易形成重计算而轻力学原理与力学思想的学习观念。

将Matlab科学计算软件引入材料力学课程，将杆件内力与变形中比较繁杂的数学运算由计算机完成，一方面能使学生将大量时间用于掌握力学原理和力学思想，提高教学质量和教学效果，另一方面对培养学生用计算机解决问题与创新能力的提高有着积极的推动作用，为相关力学类课程的教学与学习提供一些参考。

%Internal forces and deformation calculation of the prismatic bar is one of the main tasks of mechanics of materials,and its calculation often takes much time. Hence, many students spend much time learning the calculation but neglect the learning of the mechanical calculation principle and mechanics. However, there’re solutions of putting the Matlab scientific computing software into the material mechanics course and making more complex mathematical operations done by the computer on internal forces and deformation calculation, which enable students to focus on the principles of mechanics and mechanical thinking,which also improve teaching quality and teaching effectiveness. In addition, students are promoted to use computers actively to solve problems and to improve their innovation capability. And the solutions also provide some reference for the teaching and learning of other mechanics courses.【期刊名称】《河西学院学报》【年(卷),期】2015(000)002【总页数】12页(P55-65,9)【关键词】材料力学;内力;变形;Matlab;计算【作者】李春锋;蒲兴龙;于彬;杨旭辉;王丽【作者单位】河西学院土木工程学院，甘肃张掖734000;河西学院土木工程学院，甘肃张掖 734000;河西学院土木工程学院，甘肃张掖 734000;河西学院土木工程学院，甘肃张掖 734000;河西学院土木工程学院，甘肃张掖 734000【正文语种】中文【中图分类】O3材料力学课程是土木、机械等专业的核心基础课程，传统力学类课程教学及学习过程中经常要面对大量而繁杂的数学计算，使得教学、学习过程中容易产生重计算而轻视或忽略力学模型的建立及力学原理的学习，其已经暴露出许多不尽如人意的方面，国内很多理工科院校在材料力学课程的教学中进行了较多的探讨与研究.将计算机技术与现代数值计算方法引入材料力学课程的教学，给力学类课程的教学提供了新的教学视野，对提高教学质量，加强学生力学建模与力学原理思想及培养学生创新思维提供了积极的因素.Matlab软件以其强大的计算与图形仿真能力正逐渐成为理工科大学本科生、硕士生、博士生必需掌握的基本技能之一，国内很多学者已将其引入到力学类课程教学中并取得了丰富的成果.罗义银、邓旭辉等［1-4］通过运用Matlab来分析运动学、动力学问题来讲述Matlab在理论力学教学中的运用，李银山［5-6］将 Maple软件作为学习理论力学、材料力学的工具，并将之编写为教材，王玉山等［7］介绍了Matlab在材料力学超静定问题求解及梁变形可视化中的应用，张宁等［8］利用Simmechanics对曲柄连杆机构进行了运动学和动力学仿真，敖文刚［9］利用Matlab设计了虚拟实验可视化用户界面，可将分析结果以曲线动画和表格表达出来.内力与变形计算是《材料力学》课程教学的重要内容，采用Matlab软件进行较为系统的构件、简单结构内力与变形计算的研究还不是很多，较系统的对材料力学课程中的拉压、扭转、弯曲及梁的剪力与弯矩问题进行计算机分析仿真，并利用Matlab自身强大的数据图形处理能力对分析结果以图形输出，使学生能在课堂上直观了解工程实际问题的处理过程，既可提高学生的学习兴趣，又可增强学生对工程实际的感性认识和解决工程问题的能力，对《材料力学》课程的教学方法改革将有着重要的补充意义.1.1 静定问题1.1.1 拉（压）杆件计算的Matlab仿真（1）计算方法拉压杆的内力与应力计算是《材料力学》课程四种基本计算内容之一.对于常见的杆系结构，其求解往往涉及线性方程组的求解，耗时耗力.运用Matlab软件只需针对所建立力学模型列出方程（组），运用Matlab软件下的solve命令即可得到结果.其计算的基本思路可概括如下：①确定荷载；②画受力分析图；③静力平衡方程，求解.（2）举例与Matlab仿真计算例题1：如图1所示，实心圆钢杆AB和AC在点A铰接连接，在A点作用有铅垂向下的力F= 35KN.已知杆AB和AC的直径分别为d1=12mm和d2=15mm，钢的弹性模量E=210Gpa.试求各杆轴力及A点的铅垂位移.Matlab程序：%考虑节点位移问题；以水平向右为X正方向1.1.2 等直圆杆的扭转计算与Matlab仿真（1）计算方法等直圆杆扭转时的应力计算，需要先从变形几何方面和物理方面两方面确定切应力在横截面上的分布规律，然后再考虑静力平衡进行求解.几何方面通过一点处切应变随该点在横截面上的位置变化而变化的规律，通过下面公式计算.在物理方面，由剪切胡克定律可知，在线弹性范围内，切应力与切应变成正比计算，即在静力学方面，由合力矩原理可得扭矩T.结合三方面便可算出等直圆杆在扭转时的切应力.其计算的基本思路可概括为：①确定作用在圆杆上的外力偶；②列静力平衡方程；③求解并画扭矩图.（2）举例与Matlab仿真计算例题2：一传动轴如图2所示，其转速n=300r/min，主动轮输入的功率P1=500kW.若不计轴承摩擦所耗的功率，三个从动轮输出的功率分别为P2=150kW，P3=150kW及P4=200kW，试做轴的扭矩图.运行结果：如图2所示.1.1.3 静定梁的计算与仿真（1）计算方法梁截面内力求解的基本方法是截面法，工程常根据梁截面内力图以确定梁构件的配筋计算图，依据所绘制梁的内力图，一方面可直观地确定出梁的“危险点”、“危险截面”.另一方面是完成梁的截面尺寸设计和强度、刚度校核的关键环节.其计算的基本思路可概括如下：①计算支座约束力；②建立剪力函数（剪力的单位kN）；③建立弯矩函数（弯矩的单位kN·m）；④绘制剪力图；⑤绘制弯矩图；（2）举例与Matlab仿真计算例题3：已知简支梁上均布荷载与力偶共同作用时，Me=4KN.m，q=0.2KN/m，l=10m，b=2m，绘制其剪力及弯矩图，计算简图如图3所示.运行结果：如图3所示.1.2 超静定问题1.2.1 拉（压）杆件超静定问题计算与Matlab仿真（1）计算方法实际工程中，大多数杆件结构为超静定结构，其特点是未知力的数目多于独立静力平衡方程的数目，在计算时首先要确定体系的超静定次数，根据变形协调条件，得出补充方程，再依据平衡条件求出未知力，最后得到结构体系的内力图，计算思路简单，但计算量非常之大.其常用基本计算思路可概括如下：①确定荷载；②画受力分析图，确定超静定次数并列静力平衡方程；③建立杆件的变形方程（几何关系）；④建立物理方程（力与变形之间的关系）；⑤求解.（2）举例与Matlab仿真计算例题4：如图4所示，支架承受荷载F=10KN，1、2、3各干由同一材料制成，其横截面积分别为A1=100mm2，A2=150mm2和A3=200mm2.试求各杆轴力.1.2.2 扭转超静定计算与Matlab仿真（1）计算方法扭转变形是结构体系中杆件的基本变形之一，工程中的大部分构件在正常工作阶段需考虑其扭转效应，扭转超静定问题比简单的扭转问题更为复杂，需要考虑杆件在扭转时的几何条件、物理条件，然后联合求解.其计算的基本思路可概括如下：①确定荷载；②画受力分析图，确定超静定次数并列静力平衡方程；③建立杆件的变形方程（几何关系）；④建立物理方程（力与变形之间的关系）；⑤联合求解.（2）举例与Matlab仿真计算例题5：如图5所示，圆截面杆AC的直径d1=100mm，A端固定，在截面B承受外力偶矩Me= 7kN.m，截面C的上、下两点处的直径均为d2=20mm的圆杆EF、GH铰接.已知各杆件材料相同，弹性常数间的关系为G=0.4E.试求杆AC的最大切应力.Matlab程序：%考虑杆件的扭转问题1.2.3 简单超静定梁的计算与Matlab仿真（1）计算方法在超静定梁的计算中，需要运用变形计算法来对其求解，确定超静定次数是解决此问题的首要条件，超静定次数决定了补充方程的个数，将梁所受的约束去掉加为未知力，根据叠加原理求解此问题.其解决思路可概括如下：①确定超静定次数；②确定静定基（去约束，加未知力）；③建立补充方程（变形条件）；④联合静力方程求解；⑤绘制内力图.（2）举例与Matlab仿真计算例题6：如图6所示，矩形梁AB受到均布荷载q=5kN/m的作用，其梁的截面尺寸为b=250mm，h=500mm，梁的跨度为l=6m，弹性模量E=210Gpa.绘制梁的内力图.2.1 拉（压）杆件的变形计算与Matlab仿真（1）计算方法拉压杆件的变形计算主要以轴向变形与横向变形为主，其主要计算思路可概括如下：①确定荷载，用截面法确定杆件的轴力.②由于材料力学范围内主要讨论线弹性范围内变形，故广义胡克定律成立，可用下述公式来计算出轴线方向的变形.③由所求的轴向变形根据泊松比即可计算出杆件在拉压时的横向变形.（2）举例与Matlab仿真计算例题7：图7所示结构中AB为水平放置的刚性杆，杆1、2、3材料相同，其弹性模量为E= 210Gpa，已知l=1m，A1=A2=A3=100mm2，F=20kN.求C点的水平位移与铅垂位移.解题思路：设图示中各杆件受拉为正，C点因各杆变形而引起X方向位移，Y方向位移.①由胡克定律，得杆件变形表达式为：②节点的变形几何关系为：式中，ls表示水平位移，lv表示竖直位移，由于3杆为刚性杆，故不发生形变.③由于以上计算均为线性方程，可利用Matlab矩阵左除命令求解.2.2 等直圆杆的扭转变形计算与Matlab仿真（1）计算方法等直圆杆扭转时的变形为一端固定不动，另一端相对固定端扭转角来表现.主要计算思路如下：①确定扭矩，运用截面法通过已知的外力偶确定杆件内部的扭矩.②根据已知杆件尺寸确定杆件极惯性矩IP.③圆轴扭转的变形（扭转角）可根据下列公式确定.对于扭转问题来说，通常极惯性矩的计算是在扭转变形计算中是非常繁琐且耗费大量时间，而在Matlab中只需根据不同类型的杆件来选择相应的计算方法，之后便是矩阵形式的线性方程组的运用，大大的简化了复杂的计算过程.（2）举例与Matlab仿真计算例题8：已知Ma=5.4kN.m，Mb=1.8kN.m，Mc=3.6kN.m，G=80×103pa，D=125mm，d=100mm，计算扭转角Φ.解题思路：首先，通过外力偶计算杆件扭矩T.其次，由于是空心圆杆，故采用下列公式来计算其极惯性矩.最后，将求得的极惯性矩以及扭矩代入扭矩下述公式，即可计算出杆件的转角. 2.3 静定梁的变形计算与Matlab仿真（1）计算方法静定梁变形的主要指标是：挠度和转角.其主要的计算思路如下：①确定荷载，确定杆件上作用的剪力及弯矩.②写出杆件的弯矩方程.③对弯矩方程一次积分得到转角方程且含有未知常数C，再次积分得到杆件的挠度方程且含有未知常数C和D.④利用杆件特殊位置的挠度与转角的边界条件，求出未知数C，D.⑤将所求位置点代入挠度转角方程，即可得到所求的挠度与转角方程.在静定梁的变形计算中最为繁琐之处在于采用积分方法确定挠度与转角的方程，积分会耗费大量的时间且容易出错，运用Matlab强大的计算能力，可以用计算机来计算积分，从而得到变形方程，节省大量时间.（2）举例与Matlab仿真计算例题9：如图8所示，一悬臂梁在端部受集中力F=10kN作用，其梁的截面尺寸为b=250mm，h= 500mm，梁的跨度为l=3m，弹性模量E=210Gpa.求梁的转角和挠度并绘制变形曲线.通过上面分析可以看出，《材料力学》课程中引入Matlab编程功能，进行杆件或杆系结构内力与变形计算将对课程的教学与学生学习、创新能力的培养有着积极的作用，具体为：（1）使学生从力学类课程繁杂的数学手算中解脱出来，将课程学习的主要精力集中到力学建模与力学分析思路的养成上，把繁杂的计算任务交给计算机去完成. （2）通过Matlab科学计算平台，引导学生建立数值求解的思想和方法，提高学生的工程素养与工程意识.（3）Matlab软件在课程教学中的引进，有利于提高教学效率，加强学生对基本概念和原理的理解，为学生创新思维的发挥拓展了广阔的空间，给学生自主学习和研究性学习提供了一个良好的平台，为相关力学类课程教学与学习提供一些参考.【相关文献】［1］罗义银.机械类专业理论力学教学改革的发展与思考［J］.力学与实践，2000，22（3）：56-57.［2］邓旭辉，张平，肖攀.Matlab在理论力学教学中应用［J］.力学与践，2006，28（5）：82-83.［3］胡超，程建钢.《理论力学》多媒体仿真教学实验［J］.力学与实践，2003，25（1）：67-70.［4］李校兵，扬芳，王军.Matlab在理论力学教学中的应用［C］.2009力学课程报告论坛论文集，2009：63-65.［5］李银山.Maplel理论力学［M］.北京：机械工业出版社，2006.［6］李银山.Maplel材料力学［M］.北京：机械工业出版社，2009.［7］王玉山，王锐.Matlab在材料力学超静定问题求解及梁变形可视化中的应用［J］.石河子大学学报，2007，25（1）：109-111.［8］张宁，田杰，陈奇.基于simmechanics的曲柄压力机机构仿真分析［J］.宜春学院学报，2013，35（3）：35-36.［9］敖文刚.基于Matlab的可视化理论力学虚拟实验［J］.重庆工商大学学报：自然科学版，2012，29（9）：101-105.［10］孙训方，方孝淑，关来泰.材料力学（Ⅰ）［M］.北京：高等教育出版社，2013.。

材料力学常用公式MJgi = 9 549 TJ1. 外力偶矩计算公式（P功率，n转速）2. 弯矩、剪力和荷载集度之间的关系式『Mg —叭㈤dx2既飢3. 轴向拉压杆横截面上正应力的计算公式（杆件横截面轴力FN,横截面面积A,拉应力为正）4. 轴向拉压杆斜截面上的正应力与切应力计算公式（夹角a从x轴正方向逆时针转至外法线的方位角为正）b.=辛軒casa= CTcna^ <f = —（1 + c口當2®5. 纵向变形和横向变形（拉伸前试样标距I，拉伸后试样标距I1 ;拉伸前试样直径d，拉伸后试样直径di）6. 纵向线应变和横向线应变r = sincr= crcDs<rsina =7.泊松比2328. 胡克定律9. 受多个力作用的杆件纵向变形计算公式S - =1 xLOO%13.延伸率 1A -爭-1xlQO%14. 截面收缩率A15. 剪切胡克定律 （切变模量 G 切应变g ）匸” 16.拉压弹性模量E 、泊松比'和切变模量G 之间关系式E2(1+ v)（b ）空心圆10.承受轴向分布力或变截面的杆件，纵向变形计算公11.轴向拉压杆的强度计算公式12. . 许用应力 性材料％ =込脆性材料17.圆截面对圆心的极惯性矩（a ）实心圆18.圆轴扭转时横截面上任一点切应力计算公式(扭矩19.圆截面周边各点处最大切应力计算公式(b )空心圆21.薄壁圆管(壁厚 8< R/10 , Ro 为圆管的平均半_ T 径)扭转切应力计算公式'注耳22.圆轴扭转角二与扭矩T 、杆长I 、扭转刚度GH 的关系式23.同一材料制成的圆轴各段内的扭矩不同或各段的直径不同(如阶梯轴)时或卩24.等直圆轴强度条件25. 塑性材料"1 = (D •界 阿［叫脆性材料[r] = (0T 8-L0)[cr] 26.扭转圆轴的刚度条件? s 侥L<1^1或T ,所求点到圆心距离 r )20.扭转截面系数(a )实心圆 1“TL27.受内压圆筒形薄壁容器横截面和纵截面上的应力计算公式，28.平面应力状态下斜截面应力的一般公式G.十6 CT — (Tcr = --------------- - 十 -------------- cns2ar — sinlcr■>|H]fl再29.平面应力状态的三个主应力叼二吉巧一叭円+°i )l叼=云|“ —叭巧十込)]0*=030.主平面方位的计算公式沁吗“玉-碍一円31. 宀土兰三面内最大切应力232.受扭圆轴表面某点的三个主应力33. 三向应力状态最大与最小正应力 °maji 二 °1qirin 二 °3534. 三向应力状态最大切应力 t,H'35. 广义胡克定律36. 四种强度理论的相当应力=°i弔二巧一叭还+巧）殆=硏—円|%二普[何-阿f晋何-碍F十何一巧）'】37. 一种常见的应力状态的强度条件込3 = J/ +4F < 0] 込厶二Jc/ 十痒< [tr]_刀毘38. 组合图形的形心坐标计算公式39. 任意截面图形对一点的极惯性矩与以该点为原点的任意两正交坐标轴的惯性矩之和的关系式41. 平行移轴公式（形心轴z c与平行轴z1的距离为a，图形面积为A）' □+宀cr 二42. 纯弯曲梁的正应力计算公式43. 横力弯曲最大正应力计算公式40. 截面图形对轴z和轴y的惯性半径」MA44. 矩形、圆形、空心圆形的弯曲截面系数3245. 几种常见截面的最大弯曲切应力计算公式（;—为中性轴一侧的横截面对中性轴z的静矩，b为横截面在46. 矩形截面梁最大弯曲切应力发生在中性轴处弘= lbh = l~^47. 工字形截面梁腹板上的弯曲切应力近似公式48. 轧制工字钢梁最大弯曲切应力计算公式49. 圆形截面梁最大弯曲切应力发生在中性轴处50. 圆环形薄壁截面梁最大弯曲切应力发生在中性轴52. 几种常见截面梁的弯曲切应力强度条件处51. 弯曲正应力强度条件260.圆截面杆横截面上有两个弯矩和同时作用时，合成弯矩为61.圆截面杆横截面上有两个弯矩 5和-同时作用时62. 占皿W 誌阿乔而訥53.弯曲梁危险点上既有正应力a 又有切应力T 作用时的强度条件 爼 」”14工、1叫 或 込丄 b 鳥L 兰[E54. 55. 梁的挠曲线近似微分方程 梁的转角方程56. 梁的挠曲线方程？57.轴向荷载与横向均布荷载联合作用时杆件截面底部边缘和顶部边缘处的正应力计算公式> = £li_ 58. 59.偏心拉伸（压缩）弯扭组合变形时圆截面杆按第三和第四强度理论建立的强度条件表达式5 -亠 ‘ | 厂 T°l强度计算公式占血+尸二占祠+可+严如d 2w_ A/U ）计=—[f “djcdx 4-C.JC + /J 】63. 弯拉扭或弯压扭组合作用时强度计算公式 % =十记=J (氐+乐尸+4说＜[cr\ c^4 = 2十卅=加M +丐尸+玩＜ [E64. 剪切实用计算的强度条件65. 挤压实用计算的强度条件66.等截面细长压杆在四种杆端约束情况下的临界力F =輕计算公式，(阳 67. (b )一端固定、一端自由 1 =2 (c ) 一端固定、 一端铰支 1 =0.7(d )两端固定(1 =0.5\L压杆的长细比或柔度计算公式I*1• >7?遲 细长压杆临界应力的欧拉公式%丑只工召=药匡压杆的约束条件：(68. 69. 欧拉公式的适用范围a )两端铰支卩=1F 站 cr^A n = ------ = -------- >70. 71. 压杆稳定性计算的安全系数法 72.压杆稳定性计算的折减系数法 73.「卩关系需查表求得。