当前位置：文档之家 › 梁的正应力

梁的正应力

  • 格式：ppt
  • 大小：1000.00 KB
  • 文档页数：23

下载文档原格式

  / 23

合集下载

6第六章-梁的应力详解精选全文完整版

6第六章-梁的应力详解精选全文完整版
等直梁横截面上的最大正应力发生在最大弯矩所在横 截面上距中性轴最远的边缘处，而且在这些边缘处，即使 是横力弯曲情况，由剪力引起的切应力也等于零或其值很 小(详见下节)，至于由横向力引起的挤压应力可以忽略不 计。因此可以认为梁的危险截面上最大正应力所在各点处 于单向应力状态。于是可按单向应力状态下的强度条件形 式来建立梁的正应力强度条件：
需要注意的是，型钢规格表中所示的x轴是我们所标示 的z轴。
Ⅱ. 纯弯曲理论的推广
工程中实际的梁大多发生横力弯曲，此时梁的横截面
由于切应力的存在而发生翘曲。此外，横向力还使各纵向
线之间发生挤压。因此，对于梁在纯弯曲时所作的平面假
设和纵向线之间无挤压的假设实际上都不再成立。但弹性
力学的分析结果表明，受分布荷载的矩形截面简支梁，当
A
将
E
y
r
代入上述三个静力学条件，有
FN
dA E
A
r
y d A ESz
A
r
0
(a)
M y
z d A E
A
r
yz d A EIyz
A
r
0
(b)
M z
y d A E
A
r
y2 d A EIz
A
r
M
(c)
以上三式中的Sz，Iyz，Iz都是只与截面的形状和尺寸相 关的几何量，统称为截面的几何性质，而
图b所示的简支梁。钢的许用弯曲正应力[]=152 MPa 。试
选择工字钢的号码。
(a)
(b)
解：在不计梁的自重的情况下，弯矩图如图所示 Mmax 375kN m
强度条件 Mmax 要求：
Wz
Wz
M max

梁的正应力

梁的正应力

点的正应力；
1m
2m
1
（2）此截面上的最大正应力； （3）全梁的最大正应力；
12 z
120 y
180 30
（4）已知 E = 200 GPa，
求1—1截面的曲率半径。
1 q=60kN/m
A
1m
2m
1
+
M
qL2
8 M1 Mmax
180 30
12 z
120 y
解：1 画 M 图求有关弯矩
B
M1
( qLx 2
( A) max (a) max (b) max (c)； (B) max (a) max (b) max (c)； (C) max (a) max (b) max (c)； (D) max (a) max (b) max (c)。
[σ] ＝160MPa ，试计算：1.F加在辅助梁的什么位置，才能保证两台吊 车都不超载？2.辅助梁应该选择多大型号的工字钢？
200kN吊车
150kN吊车
2 x 2.667
2.确定工字钢型号
A
C 辅助梁
B Mmax A 200l 2.667 266.6kNm
FA
F
x
FB Mmax B 150 2 300kNm
A
0
M y
zdA
A

E

A
zydA
0
M z
ydA
A
E

A
y 2 dA

EIZ

1 MZ
EIZ
Mzy
Iz
M
M
中性轴

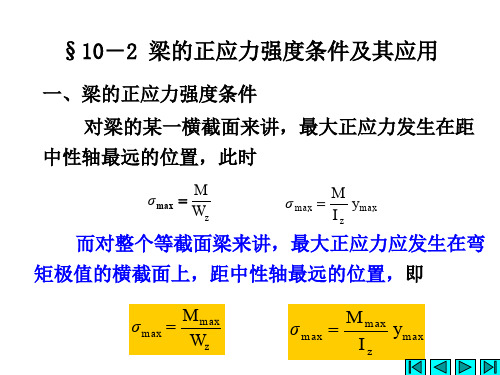
工程力学梁的正应力强度条件及其应用1

工程力学梁的正应力强度条件及其应用1

ymax
对矩形截面
Wz

bh3 12 h2

bh2 6
Wz

bh2 6
对圆形截面
Wz

d 4
d
64 2

d 3
32
Wz

d 3
32
各种型钢的截面惯性矩Iz和弯曲截面系数Wz的 数值，可以在型钢表中查得。
为了保证梁能安全的工作，必须使梁横截面上的
最大正应力不超过材料的许用应力，所以梁的正应力
强度条件为
σmax
M max Wz

σ
二、三种强度问题的计算
σmax
M max Wz

σ
（1）强度校核 （2）选择截面 （3）确定许用荷载
σmax

M max Wz

σ
Wz

M max σ
M max Wz σ
例题10-2 一矩形截面简支木梁如图所示，已知l=4m， b=140mm，h=210mm，q=2kN/m，弯曲时木材的许 用正应力[σ]=10MPa，校核该梁的强度。
σc,max

MC Iz
y1

2.7 103 0.072 0.573105
33.9 106 Pa
33.9MPa [σc]
由以上分析知该梁满足强度要求。
例题10−4 如图所示的简支梁由工字钢制成，钢的 许用应力[σ ]=150MPa，试选择工字钢的型号。
解：先画出弯矩图如图b所示。 梁的最大弯矩值为
y1

1.8103 0.072 0.573105

22.5106 Pa

22.5MPa

梁正应力

梁正应力

8 hb2
12MPa
6
例题3：图示T形截面简支梁在中点承受集中力F＝32kN，梁的长度L＝
2m。T形截面的形心坐标yc＝96.4mm，横截面对于z轴的惯性矩Iz＝
1.02×108mm4。求弯矩最大截面上的最大拉应力和y最大压应力。
F
150
A
B
L
L
2
2
M max
FL 4
16kNm
y max
200
例题1:长为L的矩形截面悬臂梁，在自由端作用一集中力F， 已知b＝120mm，h＝180mm、L＝2m，F＝1.6kN，试
求B截面上a、b、c各点的正应力。
A L2
F
h6
B
C
L2
h2
()
1 FL h
FL
a
M B ya IZ
2 bh3
3
1.65MPa
b 0
c
M B yc IZ
12
1 FL h
2 bh3
2
2.47MPa （-）
12
a
bh
c b
1 M B 2 FL
IZ
bh3 12
例题2：试计算图示简支矩形截面木梁平放与竖放时的 最大正应力，并加以比较。
q 2 kN m
200
100
4m qL2
200 100
8
竖放
qL2
max
M max WZ
8 bh2
6MPa
横放
6
qL2
max
M max WZ
一 基本概念与假设
1 纯弯曲与横力弯曲 纯纯弯弯曲曲：: 横截面上弯矩为常量，而切力为零。
A
横横力力弯弯曲曲：: 横截面上既有弯矩，又有切力。

梁的应力计算

梁的应力计算

Mmax WZ
§6-2 梁的正应力强度条件及其应用
q=2kN/m
A
xm
FAY
C
l = 4m
例题6-2
140
[σ]=10MPa，试校核该梁
B
的强度。
x
210
FBY
解：1. 求支反力 FAy 4kN FBy 4kN
M
ql2 / 8 4kN m
2. 求最大弯矩
Mmax
ql2 8
4kN m
物理关系 E E y
静力学关系
1 M
EI
Z
1
为曲率半径， 为梁弯曲变形后的曲
正应力公式 My (6-6)
率
IZ
§6-1 （纯弯曲）梁的正应力
正应力分布
My
IZ M • 正应力大小与其到
中性轴距离成正比；
• 与中性轴距离相等 的点， 正应力相等；
• 中性轴上,正应力等于零
M
max
bh3 12
Wz
bh2 6
Wz
D3
32
(1 4 )
Wz
( b0 h03 12
bh3 12
) /(h0
/
2)
§6-1 （纯弯曲）梁的正应力
横力弯曲
弹性力学精确分析表明， 当跨度 l 与横截面高度 h 之 比 l / h > 5 （细长梁）时， 纯弯曲正应力公式对于横力 弯曲近似成立。
§6-1 梁的正应力
2.离中性轴最远处
3.变截面梁要综合考虑 M 与 Iz
4.脆性材料抗拉和抗压性能不同，两方面都要考虑
t,max t
c,max c
§6-2 梁的正应力强度条件及其应用
根据弯曲正应力强度条件

梁应力强度计算

梁应力强度计算
纵向对称面仍为平面在同一截面上变形公式共同作用横截面翘曲纵向截面间有挤压
第五章 平面弯曲梁的强度
内容： 梁的应力、强度计算
τ→FS
z
dA
FS y
σ→M
M
z
dA
dA
y
M =∫yσσd
A
§5.1 梁的正应力
一、纯弯曲梁横截面上的正应力
F
F
a
l
a
FS F
M
x
F Fa
x
FS M
纯弯曲梁
Me
l
x
Me
450×0.03 2×45×10－9
=150
MPa
（－）
习题5-13 当20号槽钢受纯弯曲变形时，测出A、B两点间长度
Δl=27×10－3mm，材料的E=200GPa。试求梁截面上的弯矩M。
解：
50
5
M
AB
M
●
●
ε=
Δl l
=
27×10－3 50
=5.4×10－4
σ=Eε=200×109×5.4×10－4=108MPa
BC段： d2 ≥ 3
32×455×103 π140×106
= 321 mm
取: d1=250mm d2=322mm
例11. 已知：[σ]=160MPa，[τ]=100MPa，
试选工字钢梁的型号。
解： Fsmax=6kN
1.σ计算：
σmax =
M max Wz
≤ [σ]
M max = 8 kN • m
=
1 2
qab+
1 8
qb2
=
0.02375q
N
•
m

梁的正应力强度计算.

§7-2 梁的正应力强度计算一、最大正应力在强度计算时，必须算出梁的最大正应力。

产生最大正应力的截面，称为危险截面。

对于等直梁，弯矩最大的截面就是危险截面。

危险截面上的最大应力处称为危险点，它发生在距中性轴最远的上、下边缘处。

对于中性轴是截面对称轴的梁，最大正应力的值为：maxmax max zM y I σ=令zz maxI W y =，则 maxmax zM W σ=式中z W 称为抗弯截面系数，是一个与截面形状和尺寸有关的几何量。

常用单位是m 3或mm 3。

z W 值越大，max σ就越小，它也反映了截面形状及尺寸对梁的强度的影响。

对高为h 、宽为b 的矩形截面，其抗弯截面系数为：32z z max /12/26I bh bh W y h ===对直径为d 的圆形截面，其抗弯截面系数为：43z z max /64/232I d d W y d ππ===对于中性轴不是截面对称轴的梁，例如图7-9所示的T 形截面梁，在正弯矩M 作用下梁下边缘处产生最大拉应力，上边缘处产生最大压应力，其值分别为：+1max z My I σ=2maxzMy I σ-=令z 11I W y =、z 22IW y =，则有： +max 1M W σ=max2M W σ-=maxσ-图7-9二、正应力强度条件为了保证梁能安全地工作，必须使梁截面上的最大正应力max σ不超过材料的许用应力，这就是梁的正应力强度条件。

现分两种情况表达如下：1、材料的抗拉和抗压能力相同，其正应力强度条件为：maxmax z[]M W σσ=≤ 2、材料的抗拉和抗压能力不同，应分别对拉应力和压应力建立强度条件：+maxmax 1[]M W σσ+=≤ max max2[]MW σσ--=≤ 根据强度条件可解决有关强度方面的三类问题：1）强度校核：在已知梁的材料和横截面的形状、尺寸（即已知[]σ、z W ）以及所受荷载（即已知max M ）的情况下，可以检查梁是否满足正应力强度条件。

纯弯曲梁的正应力实验报告

姓名：班级：学号：实验报告纯弯曲梁的正应力实验一、实验目的：1.测定梁在纯弯曲时横截面上正应力大小和分布规律2.验证纯弯曲梁的正应力公式二、实验设备及工具：1.材料力学多功能试验台中的纯弯曲梁实验装置2.数字测力仪、电阻应变仪三、实验原理及方法：在纯弯曲条件下，根据平面假设和纵向纤维间无挤压的假设，可得到梁横截面上任意一点的正应力，计算公式：σ=My/I z为测量梁横截面上的正应力分布规律，在梁的弯曲段沿梁侧面不同高度，平行于轴线贴有应变片。

贴法：中性层一片，中性层上下1/4梁高处各一片，梁上下两侧各一片，共计五片。

采用增量法加载，每增加等量荷载△P（500N）测出各点的应变增量△ε，求的各点应变增量的平均值△ε实i，从而求出应力增量：σ实i=E△ε实i将实验应力值与理论应力值进行比较，已验证弯曲正应力公式。

四、原始数据：五、实验步骤：1.打开应变仪、测力仪电源开关2.连接应变仪上电桥的连线，确定第一测点到第五测点在电桥通道上的序号。

3. 检查测力仪，选择力值加载单位N或kg，按动按键直至显示N上的红灯亮起。

按清零键，使测力计显示零。

4.应变仪调零。

按下“自动平衡”键，使应变仪显示为零。

5.转动手轮，按铭牌指示加载，加力的学生要缓慢匀速加载，到测力计上显示500N，读数的学生读下5个测点的应变值，（注意记录下正、负号）。

用应变仪右下角的通道切换键来显示第5测点的读数。

以后，加力每次500N，到3000N 为止。

6.读完3000N应变读数后，卸下载荷，关闭电源。

六、实验结果及处理：1.各点实验应力值计算根据上表数据求得应变增量平均值△εPi，带入胡克定律计算各点实验值：σ实i=E△εPi×10-62.各点理论应力值计算载荷增量△P=500N弯矩增量△M=△P/2×a应力理论值计算σ理i=∆M∙YiI z（验证的就是它）3.绘出实验应力值和理论应力值的分布图以横坐标表示各测点的应力σ实和σ理，以纵坐标表示各测点距梁中性层的位置。

材料力学04梁截面正应力

E E
y
M

这表明，直梁的横截面上的 正应力沿垂直于中性轴的方向按 直线规律变化(如图)。 11
三、静力学方面
横截面上的应力合成内力，则
FN d A
A
(d)
M y z d A
A
M z y d A
A
12
EI yz E M y z d A yz d A 0 A A
所以梁的强度由最大拉应力控制:
33
C截面：
F 3 2 m 13410 m M C 134103 m 4 t,max 30106 Pa Iz Iz




F 24.6kN
B截面：
F 3 2 m 8610 m M B 86103 m 2 t,max 30106 Pa Iz Iz




F 19.2kN
所以，该梁的许可荷载为[F]=19.2 kN。
34
§4-5 梁横截面上的切应力· 梁的切 应力强度条件
Ⅰ. 梁横截面上的切应力
• • • • 矩形截面梁 工字形截面梁 薄壁圆环形截面梁 圆截面梁
研究表明：截面上各点的切应力不相等
求解的理论根据：切应力互等定理
35
一、矩形截面梁
29
根据强度条件要求：
Wz M max

375 kN m 2460106 m3 152106 Pa
由型钢规格表查得56b号工字钢的Wz为
Wz 2447cm3 2447106 m3
此值虽略小于要求的Wz但相差不到1%，故 可以选用56b工字钢。
工程实践中，如果最大工作应力超过许用应力 不到5%，则通常还是允许的。

建筑力学第12章梁的应力

n
b1b2 yd bb2 dx
d 1 dx
m
o1 b m1
o2
y dx

y
b2
b1 n1

——纯弯曲时应变分布规律

y

z M
Hooke定律： E
E E
y
dA

——纯弯曲时应力分布规律
沿梁高线性分布，中性轴上为零，外边缘上最大
E 中性轴必然通过截面的形心
强度条件： 1－ 2＋ 3
适用于脆性材料
最大剪应力理论（第三强度理论） 破坏条件： max 达到危险值
max 1 3
2
强度条件： 1 3
适用于塑性材料
形状改变比能理论（第四强度理论）
引起单元体形状改变的能量超过危险值 破坏条件：
强度条件： ＋ － 1 3
2 1 2 3
适用于塑性材料
l
+
100kN 100kN 2m 2m 2m
-
q
* z *
*
I z：横截面对中性轴的惯性矩
b：横截面的宽度
QS Izb
b h2 2 * * * Sz A y y 2 4 h 1 h b y 2 2 2 1 3 I z bh 12
* z
* z
y
m2
3.6 kN
m
3.6 kN
m
max
5m
M max Wz
M max
1 2 1 ql 3.6 25 11.25 kN m 8 8
W z 2 39.7 103 79.4 106 m 3
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
31.9
查表
N0 12.6工字钢
15 3.75
WZ=77.5cm3
kN
28.1
kNm
13.16
例题 4.25
铸铁制作的悬臂梁，尺寸及受力如图示，图中F＝20kN。梁 的截面为T字形，形心坐标yc=96.4mm。已知材料的拉伸许用应 力和压缩许用应力分别为[σ]+＝40MPa， [σ]－＝100MPa。试 校核梁的强度是否安全。 y
o

IZ:截面对中性轴的惯性矩

z
m
dx
n
y

Mzy Iz
max
Mz Wz
M
M
max
M x Wz
中性轴
正应力计算公式适用范围

M Iz
y
横力弯曲时，截面上有切应力，平面假设不严格成立 但当梁跨度 l 与高度 h 之比大于5（即为细长梁）时 弹性力学指出：上述公式近似成立 截面惯性积 Iyz = 0 推导时用到郑玄-胡克定律，但可用于已屈服的梁截面
WZ
M max B
1.875 1.86 1.875

1.875 10 cm
3
3
100
％
0.8％
例题 4.27
图示结构承受均布载荷，AC为10号工字钢梁，B处用直 径d=20mm的钢杆BD悬吊，梁和杆的许用应力[σ] ＝ 160MPa 。不考虑切应力，试计算结构的许可载荷[q]。
FL
h
IZ
bh
3
12
2 3 3 bh 12
1.65MPa
1
b 0
c
M B yc IZ
FL
h
2 3 2 bh 12
2.47MPa
（压）
例题 4.21
试计算图示简支矩形截面木梁平放与竖放时的最大 正应力，并加以比较。
q 2 kN m
200
100
200
4m
100
竖放
max
F
150
A
B
50
96 . 4
l 2
l 2
200
C
z
M max

FL 4
50
16kNm
ymax 200 50 96.4 153.6mm ymax 96.4mm

max

My max IZ My max IZ


24.09MPa
max

15.12MPa
qL 8
2
qL
2
M max WZ
8 6MPa 2 bh 6
横放
qL
2
max
M max WZ

8 12MPa 2 hb 6
例题 4.22
图示T形截面简支梁在中点承受集中力F＝32kN，梁的长度L＝2m。T形 截面的形心坐标yc＝96.4mm，横截面对于z轴的惯性矩Iz＝1.02×108mm4。求 弯矩最大截面上的最大拉应力和最大压应力。 y
150 kN 吊车
200 kN 吊车
1.确定F加在辅助梁的位置
A
B
C
F
l
辅助梁
x
M
A
0
FP l x FB l F l x 0 FB l
FA
FB
MB 0
F Fx FAx FAl 0 l
令: FA
Fx l
200kN
FB
F l x l
1 2

M1 y Iz 10 61.7 MPa
5
120 y
60 60 5.832
1max
max
M1 Wz

60 6.48
10 92.6MPa
4
M max Wz

67.5 6.48
10 104.2MPa
4
3 求曲率半径
1
EI z M1
A
(-) B
D
(+) 10kN*m
y2
C
拉应力
a
e
压应力
y1
压应力 B截面
b
d
拉应力 D截面
危险点：
a, b, d
（3）计算危险点应力 拉应力
a
e
压应力
校核强度
a
M B y2 Iz
M B y1 Iz

30 MPa （拉）
压应力 B截面
b
d
拉应力
D截面
b
最大压应力：
70 MPa （压）
3
B
M By y IZ
12 10 250 96.4 18.07MPa 1.02
3
例题 4.26
为了起吊重量为F＝300kN的大型设备，采用一台150kN和一台 200kN的吊车，以及一根工字形轧制型钢作为辅助梁，组成临时的 附加悬挂系统，如图示。如果已知辅助梁的长度l=4m，型钢材料的 许用应力[σ] ＝160MPa ，试计算：1.F加在辅助梁的什么位置，才 能保证两台吊车都不超载？2.辅助梁应该选择多大型号的工字钢？
c max b 70 MPa [ c ]
最大拉应力：
d
M d y1 Iz
t max d 35 MPa [ t ]
梁的强度符合要求
35 MPa （拉）
150kN
2 x 2.667
x 2.667m
x 2m
为了起吊重量为F＝300kN的大型设备，采用一台150kN和一台 200kN的吊车，以及一根工字形轧制型钢作为辅助梁，组成临时的附加 悬挂系统，如图示。如果已知辅助梁的长度l=4m，型钢材料的许用应力 [σ] ＝160MPa ，试计算：1.F加在辅助梁的什么位置，才能保证两台吊 车都不超载？2.辅助梁应该选择多大型号的工字钢？
F
B
C
A
B
A
50
150
2F
1400 600
96 . 4
z
200
12kNm
50
A
16kNm

M Ayl IZ

16 10 250 96.4 24.09MPa 8 1.02 10
3
A

M Ay y IZ
16 10 96.4 15.12MPa 8 1.02 10
FN dA
A
m
n o
dA
z
y
E E

ydA
A
0

o
z
M y zdA
A A

E
zydA 0 y dA
2
A
m
dx
n
d
y

M z ydA
1 MZ EI Z

EI Z
A

dx
y



Mzy Iz
M
M
中性轴
MZ:横截面上的弯矩
m
n o
dA
z
y
y:到中性轴的距离

200 5.832 60
10 194.4m
例2
外伸梁
P＝20kN q=10kN/m y2
A
B
2m 2m
D
2m
E
C
y1
T形梁截面，用铸铁制成，
I z 4.0 10 mm , y1 140mm,
7 4
y2 60mm
[ t ] 35 MPa, [ c ] 100 MPa
m
n
线,变形后仍为直线，且仍与弯曲 了的纵向线正交，但两条横向线 间相对转动了一个角度。
平面假设：
变形前杆件的横截面变形后仍 为平面。
中性层
中性轴：
m
n
中性层与横截面的交线称 为中性轴。
o1 o2
m
中性轴
n
F
F
m
n

y d d
d

y

m
n
M
M
中性轴
E y E
B M ( qLx qx ) 1 2 2 2m + M
qL 8
2
2
x 1
60kNm
M max qL / 8 67.5kNm
2
x
2 求应力
Iz
bh
3
5.832 10 m
5
4
12
4
M1 Mmax 180 30
Wz I z / ymax 6.48 10
m
3
1
2 z
梁横截面上的正应力.梁的正应力条件
纯弯曲时梁横截面上的正应力
a
A
C
F
F
a
D B
F
F
纯弯曲：梁 受力弯曲后，如 其横截面上只有 弯矩而无剪力， 这种弯曲称为纯 弯曲。
Fa
实验现象：
F F
1、变形前互相平行的纵向直线、
m
n
变形后变成弧线，且凹边纤维缩 短、凸边纤维伸长。
2、变形前垂直于纵向线的横向
D
d
FA
3q 4
kN
FB
9q 4
kN
q
A B
FB
C
梁的强度

M max WZ 0.5q WZ
FA
2m
1m
1 2
q
q
WZ 0.5
15.68kN / m
9q 4 1 4