数学方法论丛书
- 格式:docx
- 大小:14.08 KB
- 文档页数:1

数学基础知识丛书
1. 《数学分析基础》(A Course in Mathematical Analysis)- 弗尔多(Walter Rudin)著
这本书是分析学领域的经典教材,适合学习数学分析的初学者。
2. 《高等代数(下卷)》(Abstract Algebra)- 迈克尔·阿廷(Michael Artin)著
这本书介绍了抽象代数的基本概念和技术,对于学习抽象代数非常有帮助。
3. 《概率论与数理统计基础》(Introduction to Probability Theory and Mathematical Statistics)- 禹志豪、李汐著
这本书从数理统计和概率论的基本概念出发,介绍了一些基本的数学统计理论和方法。
4. 《微分几何与外微分》(Differential Geometry and Exterior Calculus)- Andrew Pressley著
这本书介绍了微分几何和外微分的基本概念和技术,对于对几何形式的数学建模非常有帮助。
5. 《数论导引》(An Introduction to the Theory of Numbers)- Ivan Niven, Herbert S. Zuckerman, Hugh L. Montgomery著
这本书是一本介绍数论基础知识的经典教材,非常适合想要深入了解数论的读者。
这些书籍都是基础的数学知识丛书,适合有一定数学基础的读者使用。

方法论的书籍推荐方法论是研究探索问题解决方法和规律的学科,它具有广泛的应用领域,对个人发展、团队合作、组织管理等方面都有着重要的指导意义。
下面我将为您推荐几本关于方法论的书籍,这些书籍涵盖了不同领域的方法论思考和方法实践,希望能够帮助您更好地理解和运用方法论。
1.《方法论》- 钱穆这本书是中国著名历史学家、哲学家钱穆的经典之作,探讨了方法的历史沿革和发展,对于方法论的基本概念、原则和分类进行了系统的阐释。
该书注重方法论在不同领域的应用,包括科学、人文、艺术等,并提出了方法论的价值与局限。
对于初学者来说,这本书可以作为入门读物,了解方法论的基本概念和理论框架。
2.《写作的艺术》- 罗伯特·麦基这本书是好莱坞编剧导师罗伯特·麦基的传世之作,虽然它的主题是写作,但其中运用了很多方法论的思想和技巧。
麦基通过剖析经典电影的情节和结构,总结出了许多创作原则和技巧,对于任何一个需要进行创作的领域来说都具有启发意义。
他通过角色、冲突、转折等要素,系统讲解了如何构建一个精彩的故事,并阐述了许多方法论的思考和实践。
3.《奇特的一生》- 哈罗德·阿布拉哈姆斯这是一本关于系统思维和创造力的经典之作,作者通过对伟大科学家、艺术家和发明家的研究,总结出了他们的共同特点和成功之道。
他认为这些成功的人都具备系统思维的能力,能够从整体的角度看待问题,并运用方法论的思维方式解决问题。
这本书不仅对方法论的思维方式进行了深入探讨,还给出了许多实用的例子和练习,帮助读者培养系统思维和创造力。
4.《黑天鹅效应》- 尼古拉斯·塔勒布尼古拉斯·塔勒布是一位知名的风险分析师和思想家,他通过对历史和实证研究的探索,提出了黑天鹅效应的理论。
该书强调了我们对事件的预测和解释常常是不准确的,因为我们通常只看到发生的事情,而忽视了潜在的不确定性因素。
对于方法论的研究来说,这本书提醒我们要认识到方法的局限性和不确定性,从而提醒我们在应用方法论时要保持谨慎和灵活性。

学习数学的方法和技巧的书
以下是一些关于学习数学方法和技巧的书籍:
1.《数学思维导图》- Tony Buzan
这本书介绍了利用思维导图来提高数学学习和解题能力的方法。
思维导图是一种图形化的思考方式,可以帮助学生组织和理清数学概念和思考过程。
2.《数学自学法》- George Pólya
这本书总结了数学思维和解题的一般方法和策略。
它介绍了如何构建数学问题的解决方案,如何提出假设和证明,以及如何培养探索和创新的数学思维。
3.《数学之美》- 吴军
这本书通过一系列有趣的数学问题和案例,展示了数学在现实生活中的应用和美妙之处。
它不仅帮助读者更好地理解数学的概念和原理,同时也培养了数学思维和解题的能力。
4.《数学的启示》- 賀韻堂、郭小衛
这本书通过一系列的趣味数学问题,揭示了数学思维和解题的一些技巧和方法。
它通过生动的例子和解析,帮助学习者更好地理解和应用数学知识。
5.《数学创造性思维的培养》- George Pólya
这本书着重讲解了如何培养数学创造性思维,通过发散性思维来解决数学问题。
它探讨了如何通过提出问题、试探性猜测和积极探索来培养学生的创新能力。
这些书籍提供了各种不同的方法和技巧,旨在帮助读者更好地学习数学和解决数学问题。
每个人的学习风格和需求不同,可以根据个人的兴趣和目标选择适合自己的一本或几本书来阅读和学习。

高中数学解题基本方法书籍在高中学习阶段,数学是一门非常重要的科目,需要掌握一定的解题基本方法。
为了帮助广大高中生更好地掌握数学解题技巧,我推荐以下几本经典的高中数学解题基本方法书籍。
一、《高中数学解题秘籍》《高中数学解题秘籍》是一本经典的数学解题指南,详细介绍了高中数学中常见的各类题型以及解题技巧。
该书以通俗易懂的语言,结合大量例题和实例,系统地介绍了数学解题的基本方法。
不仅涵盖了代数、几何、概率等各个方面的知识,还提供了大量实用的解题技巧和思维导图,帮助读者迅速掌握解题的要领。
二、《高中数学全解与定理导读》《高中数学全解与定理导读》是一本全面介绍高中数学基本解题方法和定理的参考书。
该书以解题为主线,详细解析了高中数学中的典型题型,并提供了详细的解题步骤和思路。
同时,该书还对高中数学中的重要定理进行了概述和导读,帮助读者理解定理的来龙去脉,掌握定理的应用技巧。
三、《高中数学解题思路与方法》《高中数学解题思路与方法》是一本针对高中生的解题指南。
该书注重培养学生的思维能力和解题思路,通过举一反三的方法,帮助读者理解题目的本质,抓住解题的关键。
同时,该书还介绍了一些高效的解题技巧和方法,如逆向思维、巧妙运用代数变换等,帮助读者提高解题的效率。
四、《高中数学解题技巧与方法大全》《高中数学解题技巧与方法大全》是一本全面介绍高中数学解题技巧和方法的参考书。
该书从问题分析到解题方法的选择,再到解题过程的详细展示,全面系统地介绍了高中数学中各类题型的解题技巧和方法。
此外,该书还提供了大量习题和试题,读者可以进行针对性的练习,提高解题能力。
五、《高中数学解题实战指南》《高中数学解题实战指南》是一本注重实际应用的解题指南。
该书通过实战演练的方式,结合实际问题,帮助读者理解数学知识的应用场景,掌握解决实际问题的方法。
同时,该书还提供了大量实战题目和解题思路,可以让读者在实践中不断提高解题的能力。
总结:以上是我为大家推荐的几本高中数学解题基本方法书籍。

中学数学方法丛书是一系列针对中学数学学习方法的书籍。
这些书籍通常涵盖了数学的不同领域,包括代数、几何、概率统计等,并提供了一系列实用的解题方法和技巧。
这些方法丛书通常包括以下内容:
1. 代数方法:代数是中学数学的重要部分,包括方程、不等式、函数等。
这些方法丛书通常会介绍一些代数的基本概念和解题方法,如因式分解、化简、解方程等。
2. 几何方法:几何是中学数学的另一个重要部分,包括平面几何和立体几何。
这些方法丛书通常会介绍一些几何的基本概念和解题方法,如勾股定理、相似三角形、圆的性质等。
3. 概率统计方法:概率统计是中学数学的一个新领域,包括概率、统计等。
这些方法丛书通常会介绍一些概率统计的基本概念和解题方法,如概率计算、统计图表、回归分析等。
此外,还有一些专门针对某个领域的数学方法丛书,如代数解题方法、几何解题方法等。
这些书籍通常更加详细地介绍该领域的解题方法和技巧,帮助读者更好地理解和掌握该领域的知识。
总之,中学数学方法丛书是一系列非常有用的书籍,可以帮助读者更好地理解和掌握中学数学的知识和方法。


绪论数学思想方法的对象和意义第一节中学数学思想方法的研究对象第二节学习中学数学思想方法的意义第三节中学数学思想方法的学习方法第一章数学的起源与发展第一节数学发展各个时期简析第二节中国数学的起源与发展第三节数学发展的动力第二章数学概观第一节数学的对象和特征第二节数学的地位第三节辩证唯物主义数学观第四节数学基础论及其简要评介第三章数学研究的一般方法第一节观察与实验第二节划分与比较第三节分析与综合第四节抽象与概括‘第五节特殊与一般第四章数学的逻辑方法第一节逻辑思维的基本形式第二节形式逻辑方法与辩证逻辑方法第三节逻辑推理规则第四节常用逻辑推理方法第五节数学证明与逻辑推理错误剖析第五章几种重要的数学方法第一节模型方法第二节化归方法第三节公理化方法第六章数学思维方法第一节思维及数学思维第二节数学逻辑思维方法第三节数学形象思维方法第四节创造性思维及其培养第七章数学思想方法的教学第一节数学思想方法教学的原理第二节符号化意识的培养第三节化归意识的培养第四节整体化意识的培养第五节帮助学生形成正确的数学观1、方法:就是人们处理某种事物的策略、思路、途径和步骤,解决不同学科的不同问题,需要用不同的方法。
2、方法论:研究各种方法共同规律和原则的学问3、数学方法论:狭义:解决数学问题的方法和手段,包括:数学概念的定义方法、数学的推理和证明方法、数学的计算和解决问题的思想方法等。
广义:还应包括对数学概念、数学理论的概念、数学理论的概念认识,包括对各种数学方法进行分类、整理和总结,从中寻找某些共同的规律,从而使我们能更好地学习数学和运用数学。
更广义:研究数学的发展规律,数学的思想、方法、原则,数学的发现、发明和创新的学科。
4、正确的数学观应该包含如下成分:数学的整体观;数学的价值观;数学的问题观;数学的审美观;数学教学和数学学习观。
第一章数学的起源与发展一、数学发展史1、数学萌芽时期(公元前600年以前)(1)数学的对象:社会生活的农业生产上的实际计算和测量的问题。

这20本经典数学著作,值得对数学有兴趣的人一睹为快1. 莫里斯·克莱因:《古今数学思想》全书共三册,是数学史的经典名著。
著作洋洋百万余言,阐述了从古代直到20世纪头几十年中的数学创造和发展,特别着重于主流数学的工作。
大量第一手资料的旁征博引,非常全面地提及各个历史时期的数学家特别是著名数学家的贡献,是全书的一大特色。
中国科学院院士李大潜这样评价:“本书通过对漫长而丰富多彩的数学历史的介绍,突出了古今数学思想及其发展脉络,抓住了核心和灵魂,对推动和吸引读者走近数学、品味数学、理解数学和热爱数学必将大有助益。
”2. 波利亚:《怎样解题:数学思维的新方法》这是国际著名数学家波利亚论述中学数学教学法的普及名著,对数学教育产生了深刻的影响。
波利亚认为中学数学教育的根本宗旨是教会年轻人思考,他把“解题“作为培养学生数学才能和教会他们思考的一种手段和途径。
全书的核心是在分解解题思维过程中得到的一张“怎样解题”表。
作者在书中引导学生按照“表”中的问题和建议思考问题,探索解题途径,进而逐步掌握解题过程的一般规律。
书中还有一部“探索法小词典”,对解题过程中典型有用的智力活动做进一步解释。
3. 艾格纳(MartinAigner) & 齐格勒:《数学天书中的证明》书中介绍了40个著名数学问题的极富创造性和独具匠心的证明。
其中有些证明不仅想法奇特、构思精巧,作为一个整体更是天衣无缝。
难怪,西方有些虔诚的数学家将这类杰作比喻为上帝的创造。
这不是一本教科书,也不是一本专著,而是一本开阔数学视野和提高数学修养的著作。
4. 西蒙·辛格:《费马大定理:一个困惑了世间智者358年的谜》生动的故事和流畅的语言使《费马大定理:一个困惑了世间智者358年的谜》形神兼备。
全书分两条主线,一条是历代数学家征服费马大定理的努力,另一条是费马大定理证明者怀尔斯的成长之路。
其间穿插各位数学家的轶事,精彩纷呈。
5. 高斯:《算术探索》《算术研究》是被誉为“数学王子”的德国大数学家高斯的第一部杰作,该书写于1797年,1801年正式出版,这是一部用拉丁文写成的巨著,是数论的最经典及最具权威性的著作。

《数学方法论简明教程》是2006年南京大学出版社出版的图书。
《数学方法论简明教程》共10章,在介绍数学方法论的学科性质、研究对象、发展简史、研究意义的基础上,结合实际介绍化归法、类比与归纳、联想与直觉、抽象方法、论证方法、模型方法、试验方法、美学方法等最重要最基本的数学思想方法及其数学语言的运用等,既包括数学中的逻辑方法。
当前,人类社会正由工业时代向信息时代转变,世界性的新技术革命正在到来,在现代科学技术的飞速发展中,方法论正在迅速崛起,成为一门引人注目的新兴学科。
数学方法论是方法论学科中一门独立的学科,它在数学研究和教学中的地位与作用日益受到人们的普遍重视,本章首先对什么是数学方法论,数学方法论的学科性质、研究对象、发展简史和研究意义进行介绍。

《数学方法论》教学大纲数学方法论是关于数学研究的基本方法,是数学研究的基本策略。
数学思想方法是数学教育的重要依据。
通过中学数学思想方法概论的学习,让学生理解观察、实验、类比、归纳、联想、分析、综合、抽象、概括等基本的研究方法,把握数学的逻辑方法、思维方法、模型方法等。
通过这些内容的学习无疑有益于学生数学教育素养的提高。
一、课时总数: 108学时,其中自学52学时,面授56学时。
二、课程内容:第一章数学的起源与发展第一节数学发展各个时期简析第二节中国数学的起源与发展第三节数学发展的动力本章内容要求学生了解数学史的分期,初步掌握数学发展的规律,把握中国数学发展的线索,通过了解九章算术认识中国数学的历史,正确认识数学与世界的关系,正确认识数学。
把握数学发展的动力。
P.60练习题1—15第二章数学概观第一节数学的对象和特征第二节数学的地位第三节辩证唯物主义数学观第四节数学基础论及其简要评价通过本章学习,要求学生了解关于数学的特征的主要观点,把握数学的三大特征,认识数学在科学、自然科学、人类文化中的地位和作用。
形成辩证唯物主义的数学观,能运用辩证唯物观去把握数学、理解数学,了解数学悖论形成的原因,了解逻辑主义、直觉主义、形成主义等数学三大学派的主要观点,并能指出其不足。
P.108 练习题1~11,13,14,15,17第三章数学研究的一般方法第一节观察与实验第二节划分与比较第三节分析与综合第四节抽象与概括第五节特殊与一般通过本章学习,认识观察与实验、划分与比较、分析与综合、抽象与概括、特殊与一般在数学研究中的重要作用,要求学生掌握观察与实验的一般规律,了解概念划分的原则,理解划分的标准,掌握划分的方法;能灵活运用分析与综合方法去解决各种问题,理解抽象与概括的涵义,学会抽象与概括数学概念、原理等;掌握特殊化与一般化解决问题的策略。
P.144 练习题 3~5,6~8, 9,10第四章数学中的逻辑方法第一节逻辑思维的基本形式第二节形式逻辑方法与辩证逻辑方法第三节逻辑推理规则第四节常用的逻辑推理方法第五节数学证明与逻辑推理错误剖析通过本章学习,让学生理解概念、判断和推理是逻辑思维的基本形式,理解概念的内涵与外延的涵义以及概念间的各种关系;认识判断与推理的各种形式,了解形式逻辑与辩证逻辑的关系;掌握命题基本形式以及逻辑等价的涵义,灵活运用逻辑推理规则,掌握正确的逻辑推理方法,理解数学证明的意义,避免逻辑推理中的错误。
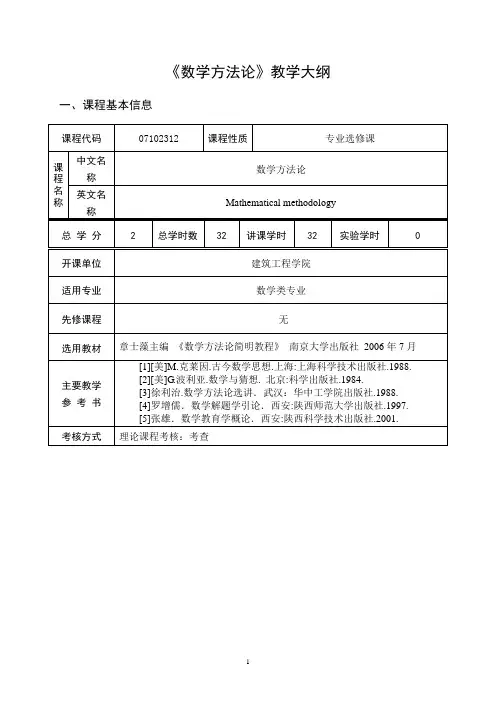
《数学方法论》教学大纲一、课程基本信息二、课程性质和任务课程的性质:是数学与应用数学专业的专业选修课,在第7学期开设。
课程的任务:本课程是四年年制师范类院校数学专业选修课程。
是数学科学与思维科学的一门交叉学科,是一门对数学方法进行概括、抽象、综合化和系统化,使数学方法不断地得到丰富和发展的学科。
它与数学、哲学、思维科学、心理学、教育学、人才学、数学史等学科有着密切的关系。
通过本课程的学习,培养学生运用辩证唯物主义的观点看待数学科学及数学教育,使学生全面掌握数学方法的本质与发展规律,引导和启发学生的思维和创新精神。
三、学时分配表四、教学内容及基本要求知识目标:掌握与数学教育相关的数学思想方法,培养学生的数学素养和能力,认识数学及其教育的本质。
技能目标:培养学生运用所学知识分析问题和解决问题的能力以及较强的自主学习能力,逐步培养学生的创新能力。
素质目标:培养学生严谨的学习态度、良好的学习习惯、一定的数学修养。
学会运用辩证唯物主义的观点看待数学科学及数学教育。
第一章绪论(2学时)教学内容:数学方法论;数学方法论的性质与对象;数学方法论的产生与发展;研究数学方法论的意义。
教学目的:掌握数学方法论的概念;掌握数学方法论的性质与对象;掌握数学方法论的产生与发展;了解研究数学方法论的意义。
教学重点与难点重点:数学方法论难点:数学方法论的概念、意义主要教学内容1.1 数学方法论1.2 数学方法论的性质与对象1.3 数学方法论的产生与发展1.4 研究数学方法论的意义思考题第二章化归(4学时)教学内容:化归方法概述;化归的方向;化归的策略;化归的方法;辩证地认识化归。
教学目的:掌握化归方法的基本方法(化归的方向、化归的策略和化归的方法)。
教学重点与难点:重点:化归难点:化归方法的基本方法主要教学内容2.1 化归方法概述2.2 化归的方向2.3 化归的策略2.4 化归的方法2.5 辩证地认识化归思考题与练习题第三章类比与归纳(4学时)教学内容:类比法;常见的几种类比;归纳法;数学归纳法;类比与归纳的再认识。
数学与应用数学专业必读书目1.《怎样解题》波利亚著,科学出版社1982年版2.《数学与猜想》波利亚著,科学出版社1984年版3.《数学与似真推理》波利亚著,福建人民出版社1985年版4.《数学的发现》波利亚著,科学出版社1982年版5.《古今数学思想》(1—4卷)克莱茵著,上海科技出版社1979—1981年版6.《数学的精神、思想与方法》朱芷国著,四川教育出版社1986年版7.《高观点下的初等数学》 F.克莱茵著,湖北教育出版社1986年版8.《数学手稿》马克思著,人民出版社1976年版9.《数学领域中的发明心理学》江苏教育出版社1989年版10.《人人关心数学教育的未来》世界图书出版社1993年版11.《美国数学的现在和未来》复旦大学出版社1986年版12.《从惊讶到思考—数学悖论》科学技术文献出版社1984年版13.《数学加德纳》戴维·A.克拉纳著,上海教育出版社1987年版14.《从混沌到有序》伊·普里戈金等著,上海译文出版社1986年自版15.《猜想与反驳》波普尔著,上海译文出版社1986年版16.《数学—它的内容、方法与意义》(1—3卷)亚历山大著,科学出版社2001年版17.《数学史上的里程碑》伊夫斯著,北京科学技术出版社1993年版18.《数论妙趣》阿尔伯特著,上海教育出版社1998年版19.《大众数学》(上下册)范格本著,科学普及出版社1992年版20.《数学确定性的丧失》M.克莱茵著,湖南科技出版社1997年版21.《数学:新的黄金时代》德夫林著,上海教育出版社1998年版22.《自然哲学之数学原理宇宙体系》牛顿著,武汉大学出版社1977年版23.《数学方法论先讲》徐利治著,华中工学院出版社1983年版24.《数学与文化》邓东皋等著,北京大学出版社1990年版25.《数学与教育》丁石孙等著,湖南教育出版社1991年版26.《数学与社会》胡作玄著,湖南教育出版社1991年版27.《数学与经济》史济怀著,湖南教育出版社1990年版28.《数学与语言》冯志伟著,湖南教育出版社1991年版29.《数学分析的方法及例题选讲》徐利治等著,高等教育出版社1982年版30.《数学思想发展简史》袁小明等著,高等教育出版社1992年版31.《从数学教育到教育数学》井中等著,四川教育出版社1989年版32.《几何中机器证明的基本定律》吴文俊著,科学出版社1984年版33.《21世纪数学展望》江苏教育出版社1992年版34.《中国数学通史》李迪著,辽宁教育出版社1997年版35.《世界数学通史》梁宗巨著,辽宁教育出版社1995年版36.《九章算术》辽宁教育出版社2000年版37.《华罗庚》王元著,开明出版社1994年版38.《数:上帝的宠物》谈祥柏著,上海教育出版社1998年版39.《科学发现纵横谈》王梓坤著,湖南教育出版社1979年版40.《科学发现纵横新编》王梓坤著,北京师范大学出版社1992年版41.《中国数学史》钱金琛著,科学出版社1992年版42.《现代数学设计论》盛群力等编,浙江教育出版社1998年版43.《混沌控制》胡岗著,上海科技出版社2000年版44.《Mathcad7.0实用教程》思索著,人民邮电出版社1998年版45.《Matlab应用程序接口用户指南》刘志俭著,科学出版社2000年版46.《数学奇妙》西奥妮.帕帕著,上海科技出版社1999年版47.《数学的源与流》张顺燕著,高等教育出版社2000年版48.《世界著名数学家评传》袁小明著,江苏教育出版社1990年版。
数学书刊书名大全
1. 《数学简史》
2. 《数学之美》
3. 《数学基础教程》
4. 《线性代数与几何初步》
5. 《数学分析教程》
6. 《离散数学导论》
7. 《概率论与数理统计》
8. 《实变函数与泛函分析》
9. 《复变函数引论》
10. 《微分几何初步》
11. 《组合数学》
12. 《图论及其应用》
13. 《拓扑学基础》
14. 《数学建模入门教程》
15. 《微积分学教程》
16. 《数理逻辑基础教程》
17. 《代数学教程》
18. 《解析几何学教程》
19. 《数学物理方程教程》
20. 《数学实验教程》
21. 《应用数学导论》
22. 《运筹学导论》
23. 《数学软件教程》
24. 《数值计算方法教程》
25. 《离散概率论教程》
26. 《随机过程教程》
27. 《无穷级数与积分学教程》
28. 《常微分方程教程》
29. 《偏微分方程教程》
30. 《实分析与复分析教程》。
数学书籍的推荐列表本文旨在推荐一些数学书籍,供读者研究和提高数学知识之用。
以下是一些优秀的数学书籍,涵盖了不同层次和领域的内容。
1. 初级数学书籍- 《数学分析引论》:作者:哈代。
这本书对数学分析的基本概念和方法进行了清晰而深入的介绍,适合初学者入门。
- 《高等代数导论》:作者:阿廷,作者:麦克拉肯。
这是一本深入浅出的高等代数入门书籍,适合有一定数学基础的读者。
- 《几何学教程》:作者:哈特。
该书介绍了基本的几何学概念和定理,对几何学的理解有很大帮助。
2. 中级数学书籍- 《实变函数与泛函分析导引》:作者:柯面。
该书对实变函数和泛函分析的基本理论进行了系统的阐述,适合具有一定数学基础的读者。
- 《微分几何与拓扑学导论》:作者:李文泰。
该书介绍了微分几何和拓扑学的基本概念和方法,适合对几何学和拓扑学感兴趣的读者。
- 《概率论导论》:作者:邹民。
该书介绍了概率论的基本概念和理论,适合对概率论感兴趣的读者。
3. 高级数学书籍- 《函数解析导论》:作者:郑民定。
该书对函数分析的基本理论和方法进行了全面而深入的介绍,适合高级数学研究者。
- 《代数拓扑导论》:作者:罗伯特。
该书介绍了代数拓扑学的基本内容和研究方法,适合对代数拓扑学感兴趣的读者。
- 《微分方程与动力系统导论》:作者:霍普芙。
该书介绍了微分方程和动力系统的基本理论和研究进展,适合对微分方程和动力系统感兴趣的读者。
以上是一些值得推荐的数学书籍,希望能对读者学习和提高数学知识有所帮助。
读者可以根据自己的数学水平和兴趣选择合适的书籍进行学习。
与数学文化素养提高相关好书推荐[1][美]M.克莱因古今数学思想(1-4)上海科技出版社 2003[2][美]M.克莱因现代世界中的数学上海科技出版社 2004[3][美]M.克莱因西方文化中的数学复旦大学出版社 2004[4][美]M.克莱因数学与知识的探求复旦大学出版社 2005[5][美]M.克莱因数学:确定性能丧失湖南科学技术出版社 2000[6][美]R.柯朗什么是数学复旦大学出版社 2005[7][美]G.波利亚数学与猜想九章出版社 2000[8][美]G.波利亚数学发现九章出版社 2000[9][美]G.波利亚怎样解题九章出版社 2000[10][美]J.戴维斯数学经验江苏教育出版社 1991[11][美]J.katz 数学史通论高等教育出版社 2004[12][英]D.韦尔斯数学与联想上海教育出版社 1999[13][英]G.德夫林数学新的黄金时代上海教育出版社 1999[14][法]L.迪厄多内当代数学为了人类心智的荣耀上海教育出版社 1999[15][美]L.A.斯蒂恩站在巨人的肩膀上上海教育出版社 1999[16][美]J.L.卡斯蒂 20世纪数学的五大指导理论上海教育出版社 1999[17][美]J.S.玛达其数学娱乐问题上海教育出版社 1999[18][美]K.A.约翰逊近代欧氏几何学上海教育出版社 1999[19][德]M.艾根游戏——自然规律支配偶然性上海教育出版社 2005[20][日]平山谛东西数学物语上海教育出版社 2005[21][德]A.恩格尔解决问题的策略上海教育出版社 2005[22][美]C.R.劳统计与真理科学出版社 2004[23][美]J.A.保罗士数盲上海教育出版社 2006[24][美]K.C.柯尔数学与头脑相遇的地方长春出版社 2004[25][日]小室直树给讨厌数学的人哈尔滨出版社 2003[26][波]H.施旦豪斯数学万花镜湖南教育出版社 2000[27][美]西蒙辛格费马大定理上海译文出版社 2005[28][美]卡尔克劳森数学魔法湖南科学技术出版社 2005[29][韩]李光延有趣的数学(1,2)北京理工大学出版社 2003[30][美]李学数数学和数学家的故事(1-4)新华出版社 1999[31][美]K.瑞德希尔伯特——数学世界的亚历山大上海科技出版社 2001[32][美]约瑟夫.马祖尔雨林中的欧几里德重庆出版社 2006[33][美]G.伽莫夫从一到无穷大科学出版社 2007[34][美]爱德华.伯格等数学爵士乐湖南科学技术出版社 2007[35][美]H.W.伊夫斯数学圈(1,2,3)湖南科学技术出版社 2007[36][美]马里奥.利维奥ϕ的故事长春出版社,2003[37][美]C.A.匹克奥弗果戈尔博士数学奇遇记上海科技出版社 2006[38][美]X.帕帕斯数学的奇妙上海科技出版社 1999[39][美]X.帕帕斯数学走遍天涯上海教育出版社 2006[40][美]大卫.布拉特纳神奇的π汕头大学出版社 2003[41]张景中主编好玩的数学(注:共10本)科学出版社[42]张景中主编院士数学讲座专辑(注:共7本)[43]韩雪涛数学悖论与三次数学危机长沙,湖南教育出版社 2006[44]韩雪涛从惊呀到思考长沙,湖南教育出版社 2007[45]周述岐数学思想和数学哲学北京,中国人民大学出版社 1993[46]梁宗巨世界数学史(上)沈阳,辽宁教育出版社 2001[47]杜瑞芝数学史辞典济南,山东教育出版社 1990[48]王恩大,郭维亮主编数学教育辞典济南,山东教育出版社 1990[49]郝宁湘数学历史文化成都,四川教育出版社 2002[50]徐品方,张红数学符号史北京,科学出版社 2006[51]沈康身数学的魅力(1-4)上海新书出版社 2006[52]刘培杰数学智力趣题哈尔滨工业大学出版社 2006[53]刘培杰数学奥林匹克与数学文化哈尔滨工业大学出版社 2006[54]欧阳维城寓言与数学湖南教育出版社 2001[55]欧阳维城数学、科学与人文的共同基因湖南教育出版社 2000[56]郑毓信数学文化四川教育出版社 2000[57]郑毓信数学教育哲学四川教育出版社 2000[58]郑毓信数学思维与数学方法论四川教育出版社 2000[59]张顺燕数学的源与流高等教育出版社 2000[60]张顺燕数学的美与理北京大学出版社 2004[61]张顺燕数学的思想和方法应用北京大学出版社1997[62]史树中诺贝尔奖经济学奖与数学清华大学出版社 2002[63]史树中数学与金融上海教育出版社 2006[64]淡祥柏数学与文史上海教育出版社 2006[65]李心灿当代数学大师北京航天大学出版社 2005[66]李心灿数坛英豪科学出版社 1989[67]张楚廷数学文化高等教育出版社 2000[68]张楚廷数学方法论湖南科学技术出版社 1989[69]王庚数学文化与数学教育科学出版社 2004[70]傅海伦传统文化与数学机械化科学出版社 2005[71]张维忠文化传统与数学教育现代化北京大学出版社 2006[72]丁石孙数学与教育湖南教育出版社 1998[73]李浙生数学科学与辩证法首都师范大学出版社 1995[74]高隆昌数学及其认识高等教育出版社 2004[75]吴振奎数学的创造上海教育出版社 2003[76]盛立人社会科学中的数学科学出版社 2006[77]徐炎章,王剑峰敲开数学之门北京,中国青年出版社 2003[78]邹瑾,杨国安开心数学哈尔滨,哈尔滨工业大学出版社 2003[79]李蕊科学门——数学号中国少年儿童出版社 2002[80]陈敏寻找身边的科学——数学篇新疆人民出版社 2002[81]王志雄数学美食城民主与建设出版社 2000[82]吴鹤龄娱乐数学经典名题科学出版社 2003[83]郭凯声等数学迷宫科学技术文献出版社 2005[84]葛帆数学的故事哈尔滨出版社 2007[85] 邱庆剑财富数学机械工业出版社 2004[86] 王之明数学是什么东南大学出版社 2003。
讲解数值方法的书籍
以下是一些关于数值方法的书籍:
1.《数值方法与计算实验》(邓俊辉著)- 本书是数值计算的经典教材,介绍了数值计算的基本概念和常见方法,包括插值、数值积分、解非线性方程、数值微分和数值解微分方程等内容。
2.《数值分析》(Richard L. Burden和J. Douglas Faires著)- 这本书是一本广泛使用的数值分析教材,详细介绍了数值计算中的各种算法和技术,包括线性方程组、矩阵特征值、插值和逼近、数值积分、常微分方程的数值方法等内容。
3.《数值计算方法》(李乃成著)- 本书系统地介绍了数值计算的基本原理和方法,包括求根、线性方程组、插值、数值微积分、常微分方程数值解、数值积分和数值求解偏微分方程等内容。
4.《数值计算方法(第3版)》(陈尚平著)- 这本书详细介绍了数值计算的应用和算法实现,包括数值代数方程的求解、插值和多项式逼近、数值积分、常微分方程的数值解法、偏微分方程的差分法等内容。
5.《科学计算中的数值方法》(William H. Press等著)- 这本书是一本经典的科学计算教材,涵盖了数值方法的基本原理和实现方法,包括线性代数、插值和逼近、数值积分、常微分方程的数值解法、偏微分方程的有限差分法等内容。
这些书籍涵盖了数值方法中的基本概念、常用算法和实际应用,适合需要学习和应用数值计算方法的学生和专业人员阅读。
根据自身的需求和数学背景,选择适合自己的书籍进行学习和探索。
数学方法论丛书
《数学证明》萧文强著
《关系映射反演方法》徐利治郑毓信著
《化归与归纳·类比·联想》史久一朱梧槚著
《康托的无穷的数学和哲学》[美]周·道本著郑毓信刘晓力译《数学中的美学方法》徐本顺殷启正著
《数学家言行录》莫里兹编著朱剑英编译
《数学抽象方法与抽象度分析法》徐利治郑毓信著
《数学方法溯源》欧阳绛著
《数学的思维方式》席振伟著
《数学直觉与发现》刘云章马复
《数学领域中的发明心理学》[法]雅克·阿达玛著
《智力游戏中的数学方法》倪进朱明书著
《泛系理论与数学方法》吴学谋著
《数学中的特殊化与一般化》阴东升卞瑞玲徐本顺著
《中国古代数学思想方法》王鸿钧孙宏安著。