博弈论第四章
- 格式:doc
- 大小:338.00 KB
- 文档页数:33


第四章动态不完全信息博弈第一节. 序贯均衡的内涵一.问题的提出1.序贯理性2.一致信念二.序贯均衡的内涵1.例子2.定义a.行为战略b.序贯理性c.一致信念3.存在性三.序贯均衡的计算1.例子:一般计算2.例子:分析应用第二节. 序贯均衡的应用一.教育和信号传递1.假设2.分析二.垄断限价模型1.假设2.分析三.声誉模型1.假设2.分析四.序贯均衡之再精炼1.剔除劣弱战略2.直观标准3.垄断限价模型第四章不完全信息动态博弈第一节.序贯均衡的内涵一.问题的提出1.序贯理性——参与人在所有情况决策都是理性的,即在给定信念的条件下,以及其他参与人的选择条件下,自身选择是最优的例1:子博弈最优——纳什均衡(,)L l是否合理?——如果参与人2有机会选择,肯定选r而不是l;——(,)L l不是子博弈精炼纳什均衡。
例2:单点信息集最优——纳什均衡(,,)D a l是子博弈纳什均衡;——但如果参与人2有机会选择,但肯定选择d;——(,,)D a l不满足单点信息集理性。
例3:多点信息集最优——纳什均衡(,)A r是子博弈精炼纳什均衡;——(,)A r不满足多点信息集理性。
2.一致信念例1:与客观事实一致u=是否合理?——参与人2的信念2/3——2/3u=是不合理的,因为任何到达参与人2信息集都不可能产生此后验概率;——后验信念必须与先念信念保持一致。
例2:前后信念一致——参与人2的第2个信息集上的信念,是否合理?——不合理,给定参与人战略和第1个信息集的信念,利用贝叶斯法则计算信念与此不一致;——参与人前后信念保持一致。
例3:独立偏离——参与人3的信念0.9u =是否合理?——参与人1和参与人3的偏离是独立的,所以参与人3的合理信念为0.1u =;——不同参与人之间的偏离是独立的总结,一致信念要求:参与人偏离最小化,,参与人之间偏离是独立的;二.序贯均衡的定义1.例子——定义参与人1在信息集1.1和1.3以及参与人2在2.2上的序贯理性;——定义信息集1.3和2.2的信念?2.定义a.行为战略:参与人在某个信息集到行动集映射,——如果某个状态真正发生,参与人如何决策;——序贯理性是否满足?b.序贯理性:在任何信息集上,参与人在给定信念和所有后续行为战略,选择自身行为战略最大化预期效用。






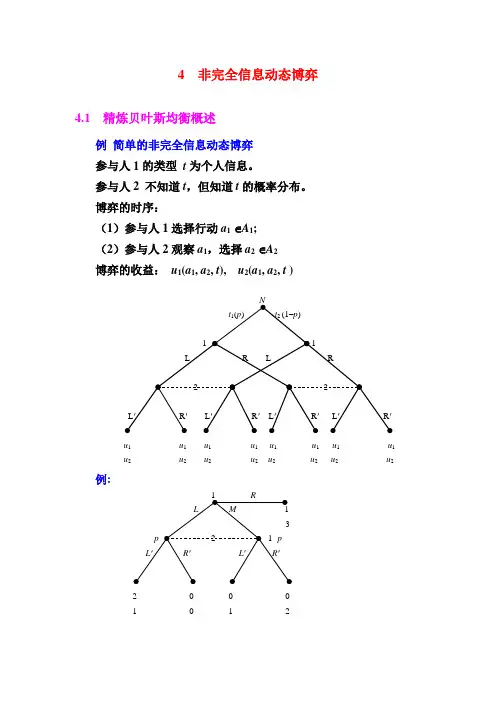
4 非完全信息动态博弈4.1 精炼贝叶斯均衡概述例简单的非完全信息动态博弈参与人1的类型t为个人信息。
参与人2 不知道t,但知道t的概率分布。
博弈的时序:(1)参与人1选择行动a1∈A1;(2)参与人2观察a1,选择a2∈A2博弈的收益:u1(a1, a2, t), u2(a1, a2, t )u1u1u1u1 u1u1u1u1u2u2u2u2 u2u2u2u2例:1 RL M 13p 2 1- pL'R'L'R'2 0 0 01 0 1 2标准式表示参与人 2L'R'L2,10,0参与人 1 M0, 20,1R1, 31, 3纯战略纳什均衡: (L,L'), (R,R')均为子博弈精炼纳什均衡(无子博弈)。
但是(R, R')不可信。
排除不可信的纳什均衡:要求1 参与人必须有一个推断(belief).要求2 参与者的战略必须满足序贯理性(sequentially rational).定义: 处于均衡路径上(on the equilibrium path)的信息集: 在均衡战略下,博弈以正的概率到达该集.要求3 在处于均衡路径上的信息集上, 推断由贝叶斯法则和参与人的均衡战略决定。
例要求3的说明参与人1的类型空间:{ t1,t2,t3,t4 }行动空间:A= { L,R}推断p i: 观察到L后,参与人1的类型是t i的概率。
推断q i: 观察到R后,参与人1的类型是t i的概率。
p1 + p2 + p3 + p4 = 1q1 + q2 + q3 + q4= 1N如果参与人1的战略: t 1选 L ,t 2选 L , t 3选R ,t 4 选R 。
参与人2对p i 与 q i 的推断:p 1 = 3.02.02.0+= 0.4, p 2 = 3.02.03.0+= 0.6, p 3 = 0, p 4 =0; q 1 = 0, q 2= 0, q 3 =3.02.02.0+= 0.4, q 4= 3.02.03.0+= 0.6,例 3个参与人的博弈。


第四章完全信息动态博弈更为现实的考虑是将静态博弈动态化,动态化后,纳什均衡这一概念是否仍然有效呢?答案是部分有效的。
如果不存在动态不一致,那么纳什均衡在完全信息动态博弈中仍不失为一个有用的均衡概念,但纳什均衡概念本身并不能保证不出现动态不一致,为了克服这一点在纳什均衡的基础上生产了所谓子博弈完美均衡。
而这一章,我们将围绕这子博弈完美均衡来展开。
第一节完美信息与完全但不完美信息完全信息动态博弈可以分为两类,即完美信息与完全但不完美信息。
所谓的完美信息博弈,是指博弈中的后行动者始终能够观察到前行动者的行动,因而动态博弈中不存在参与者同时行动这样的情况。
而完全但不完美信息博弈,则指动态博弈中,至少存在两个参与者同时行动的情况,因而“后行动者”无法观察到“前行动者”的行动。
我们不妨用两个例子来加以说明。
例4.1 动态囚徒困境囚徒1图4-1 动态囚徒困境例4.2 取消管制政府图4-2 取消管制与图4-2完全等价的表示方法见图4-3。
政府图4-3 取消管制定义4.1完美信息动态博弈就是不存在同时行动的完全信息动态博弈。
显然,运用策略式来描述动态博弈会非常不便,特别是当信息不完全时更是如此,为了更简便地描述动态博弈,我们将引入一种新的博弈表达式——扩展式。
第二节动态博弈的扩展式我们把博弈中所有从开始到结束的行动序列称为全历史(Terminal history),而用参与者函数来表示在每一个全历史上,在博弈进行到某个阶段时谁来行动。
因而要完整地描述一个动态博弈,必须具备四个要素:(1)参与者集合;(2)全历史集合;(3)参与者函数;(4)偏好。
如果我们把全历史表示成一个行动序列(a1, a2,…, a K)(K为自然数,当K→∞时,就表示无穷动态博弈),那么(a1, a2, …, a m),其中m K≤,就称为全历史(a1, a2, …, a K)的子历史(Subhistory)。
当m < K时,(a1,a2, …, a m)就是全历史(a1, a2, …, a K)的真子历史(Proper subhistory)。
R R M 4.1.a 标准式1↖2 L ’ R ’4,1 0,0 3,0 0,1 2,2 2,2纯战略纳什均衡:( L, L ’ ) ( R, R ’ )子博弈精炼纳什均衡:( L, L ’ ) ( R, R ’ )精炼贝叶斯纳什均衡:( L, L ’ )4.1.b 标准式1↖2 L ’ M ’ R ’1, 3 1, 2 4, 0 4, 0 0, 2 3, 3 2, 4 2, 4 2, 4纯战略纳什均衡:( R, M ’ )子博弈精炼纳什均衡:( R, M ’ )精炼贝叶斯均衡: 没有4.2标准式1↖2 L ’ R ’2,2 2,2 3,0 0,1 0,1 3,0六种纯战略组合,每种组合中都至少有一方存在偏离的动机,因此不存在纯战略纳什均衡,因此也就不存在纯战略精炼贝叶斯均衡。
求混合战略精炼贝叶斯均衡:设参与者1选择L 、M 、R 的概率分别为1,2,12(1)p p p p −−参与者2选择L ’和R ’的概率分别为,(1)q q −在给定参与者1的战略下,参与者2选择L ’和R ’的收益无差异,则: 1212120*1*1*0*p p p p p p +=+⇒=给定参与者2的战略,参与者1选择L 、M 、R 的收益无差异,则:12121212[3*0*(1)][0*3*(1)]2*(1)41:**,*112p q q p q q p p p p p p q +−=+−=−−====又 联立得 所以 L LML LM L RL4.3答案(见4.5)4.4表示方法第一个括号,逗号左边为type 1发送者信号,逗号右边为type 1发送者信号;第二个括号,逗号左边为接收到L 信号的反应,逗号右边为接收到R 信号的反应; P 为信号接收者对type 1发送L 的推断,q 为信号接收者对type 1发送R 的推断 (a )[(,),(,),1/2][(,),(,),1/2][(,),((1),),1/2][(,),(,),1,0]R R u u p R R d u p R R d u u p L R u d p q αα><+−===(b )[(,),(,),1/2,2/3][(,),(,),1,0][(,),(,),0,1]L L u u p q L R d u p q R L u d p q =<====中文版习题4.5答案(a )[(,),(,),1/3,1/2]R R u d p q >=(b )12121212[(,,),(,),1/3,1/2][(,,),(,),1/2,0]L L L u u p p q q L L R u d p p q q ==+<==+=。
第四章习题一、如果T次重复齐威王田忌赛马,双方在该重复博弈中的策略是什么?博弈结果如何?答:因为这是零和博弈,结论比较具体。
重复Nash 均衡,均以1/6的概率选择各个策略,期望收益分别为1和-1。
因为这是竞争性的零和博弈,无论是有限次重复博弈还是无限次的重复博弈,均不能达成合作的条件。
二、举出现实生活中的一个重复博弈与一次性博弈效率不同的例子。
答:火车站和机场餐饮业的服务的顾客往往是一次性的,回头客和常客也比较少,价格高,质量差,一次性博弈。
效率也比较低。
商业区和居民区的餐饮业和商业服务业,回头客和常客比较多,比较注重信誉,质优、价廉,重复博弈。
效率也比较高。
三、有限次重复博弈和无限次重复博弈有什么区别?这些区别对我们有什么启发?答:动态博弈的逆向归纳法可以用于有限次重复博弈,但不能用于无限次重复博弈,主要用逆向归纳法。
无限次重复博弈的效率往往高于有限次重复博弈。
当重复次数较少不一定考虑贴现问题,但无限次重复博弈必须考虑贴现问题。
启发:重视有限次与无限次的区别,区分和研究这两类博弈,在实践方面重要启发是促进和保持经济的长期稳定和可持续发展,提高社会经济效率是非常有意义的。
四、判断下列表述是否正确,并作简单讨论:(1)有限次重复博弈的子博弈完美纳什均衡每次重复采用的都是原博弈的纳什均衡。
答:不一定。
对于有两个以上纯策略纳什均衡的条件下就不一定。
如“触发策略”就不是。
(2)有限次重复博弈的子博弈完美纳什均衡的最后一次重复必定是原博弈的一个纳什均衡。
答:是,根据子博弈完美纳什均衡的要求,最后一次必须是原博弈的一个纳什均衡。
(3)无限次重复博弈均衡解的得益一定优于原博弈均衡解的得益。
答:错。
如严格竞争的零和博弈就不优于。
(4)无限次重复古诺产量博弈不一定会出现合谋生产垄断产量的现象。
答:正确。
合谋生产垄断产量是有条件的,由贴现率来反映,当不满足条件时,就不能构成激励。
(5)如果博弈重复无限次或者每次结束的概率足够小,而得益的时间贴现率 充分接近1,那么任何个体理性的可实现得益都可以作为子博弈完美纳什均衡的结果出现。
4 非完全信息动态博弈4.1 精炼贝叶斯均衡概述例简单的非完全信息动态博弈参与人1的类型t为个人信息。
参与人2 不知道t,但知道t的概率分布。
博弈的时序:(1)参与人1选择行动a1∈A1;(2)参与人2观察a1,选择a2∈A2博弈的收益:u1 (a1, a2, t ), u2 (a1, a2, t )u1u1u1u1 u1u1u1u1u2u2u2u2 u2u2u2u2例:1 RL M 13p 2 1- pL'R'L'R'2 0 0 01 0 1 2标准式表示参与人2L'R'L2,10,0参与人1 M0, 20, 1R1, 31, 3纯战略纳什均衡: (L,L'), (R,R')均为子博弈精炼纳什均衡(无子博弈)。
但是(R, R')不可信。
排除不可信的纳什均衡:要求1 参与人必须有一个推断(belief).要求2 参与者的战略必须满足序贯理性(sequentially rational).定义处于均衡路径上(on the equilibrium path)的信息集: 在均衡战略下,博弈以正的概率到达该集.处于均衡路径之外(off the equilibrium path)的信息集: 在均衡战略下,博弈不会到达此集.要求 3 在处于均衡路径上的信息集上, 推断由贝叶斯法则和参与人的均衡战略决定。
例要求3的说明参与人1的类型空间:{ t1,t2,t3,t4 }行动空间:A= { L,R}推断p i : 观察到L 后,参与人1的类型是t i 的概率。
推断q i : 观察到R 后,参与人1的类型是t i 的概率。
p 1 + p 2 + p 3 + p 4 = 1q 1 + q 2 + q 3 + q 4= 1如果参与人1的战略: t 1选 L ,t 2选 L , t 3选R ,t 4 选R 。
参与人2对p i 与 q i 的推断:p 1 = 3.02.02.0+= 0.4, p 2 = 3.02.03.0+= 0.6, p 3 = 0, p 4 =0; q 1 = 0, q 2= 0, q 3 =3.02.02.0+= 0.4, q 4= 3.02.03.0+= 0.6,要求 4 在处于均衡路径之外的信息集上, 可能情况下,推断由贝叶斯法则和参与人的均衡战略决定。
原文:At information sets off the equilibrium path, beliefs are determined by Bayes ’ rule and the players ’ equilibrium strategies where possible.精炼贝叶斯均衡(perfect Bayesian equilibrium):在一个非完全信息的动态博弈中,满足要求1 – 4 的战略与推断构成的均衡。
例不满足要求4的情形。
3个参与人的博弈。
1 A 2D 02L R[p] [1 –p]3L'R'L'R'1 3 0 02 3 1 11 32 1子博弈精炼纳什均衡: (D, L, R')另有战略(A, L, L')和推断p = 0:----纳什均衡----满足要求1-3.----不是精炼贝叶斯均衡: 不满足要求4: p= 0 与2的战略不相容.例要求4中“不可能”的情形。
1 AD2 A'L R1-q1-q2[q1] [q2]3L'R'L'R'如果(A, A', L') 是均衡,则参与人3的战略要针对参与人2的L 或R。
参与人3的推断必须是p = q1/(q1 + q2)但是参与人2选A',q1 + q2 =0, 因此无法计算p。
4.2 信号博弈4.2.A 信号博弈中的精炼贝叶斯均衡信号博弈的参与人:信号发送者S,接收者R。
信号博弈的时间顺序自然按照概率分布为S产生一个t i∈TS观察t,并选择m j∈MR观察m并选择a k∈A收益U S(t i,m j,a k)和U R(t i,m j,a k)信号博弈的例T = {t1, t2}, M = {m1, m2}, A = {a1, a2},Pr{t 1} = p , Pr{t 2} = 1 - p 。
发送者战略: 在类型为t 1时发出的信号与t 2时发出的信号:{m 1, m 1}, {m 1, m 2}, {m 2, m 1}, {m 2, m 2}混同(pooling)战略: 所有的类型发出相同的信号:{m 1, m 1}, {m 2, m 2}分离(separating)战略:不同的类型发出不同的信号:{m 1, m 2}, {m 2, m 1}接收者战略: 在收到信号m 1时与信号m 2时选择的行动: { a 1, a 1}, {a 1, a 2}, {a 2, a 1}, {a 2, a 2}1,3,12,2,03,1,01,2,2信号要求 1: 接收者在观察信号m j 后,必须对发送m j 的类型有一个推断∑∈T t i μ( t i ∣m j ) = 1信号要求 2R : 对每一 m j , 接收者的行动 a *(m j ) 必须在给定推断 μ( t i | m j ) 后,最大化他的期望效用,A a k ∈max ∑∈T t i μ( t i | m j ) U R (t i , m j , a k )信号要求 2S : 对每一t i , 在给定a *(m j ) 后,发送者的信号 m *(t i )必须最大化他的效用Mm j ∈max U S (t i , m j , a *(m j )) 信号要求 3: 对每一 m j , 如果存在 t i 使得 m *(t i ) = m j , 则接收者的推断:μ( t i | m j ) =∑)()(i i t p t p 精炼贝叶斯均衡: 战略 (m *(t i ), a *(m j ))和推断 μ(t i | m j ) 满足信号要求 (1), (2R), (2S),和 (3)。
为什么没有要求4?例 T = {t 1, t 2, t 3, t 4}, M = {m 1, m 2, m 3}如果在均衡中,发送者的战略:m *(t 1) = m 1,m *(t 2) = m 1,m *(t 3) = m 2,m *(t 4) = m 2则m 3处于均衡路径以外,若用贝叶斯公式,分母为0。
例 (Figure 4.2.2)1, 2,14, 0,02, 1,00, 1,2求精炼贝叶斯均衡:对4种情况逐一分析。
1. 混同于L ?发送者: (L, L).如果为均衡,p = 0.5接收者收益分别为: 3.5(u),或0.5(d)。
将选择u。
发送者收益分别为:1 (t1),2 (t2)如果发送者发送R, 当q + (1 –q)×0 ≤q×0 + (1 –q)×2q≤ 2/3接收者将选择d. 发送者收益为0(t1),和1(t2), 小于发送L时分别所得。
均衡: { (L, L), (u, d), p = 0.5, q≤ 2/3}2. 混同于R?发送者: (R, R)如果是均衡,q = 0.5.接收者的收益: 0.5 (u), 1 (d)。
他选择d发送者的收益分别为: 0 (t1), 1 (t2)如果发送者在t1时发送L, 收益至少为1。
不是均衡。
3. 分离(L, R)?发送者: (L, R).接收者推断:p = 1 , q = 0接收者战略: (u, d)。
发送者的收益分别为:1 (t1), 1 (t2)但是对t2, 如果发送者发送L, 接收者选择u, 发送者的收益将为2。
发送者在t2时,将发送L。
不是均衡。
4. 分离(R, L)?发送者: (R, L)。
接收者推断:p = 0, q = 1,战略:(u, u)发送者的收益分别为:2(t1), 2 (t2)如果发送者不这样, 收益将为1(t1发送L),和1(t2发送R)。
分离精炼贝叶斯均衡:[(R, L), (u, u), p = 0, q = 1]4.2.B就业市场的信号博弈。
1.自然决定工人的能力η,以概率q为高H,以概率1 –q为低L。
2.工人了解自己的能力,选择一个教育水平e≥ 0,教育的成本为c(H,e)或c( L,e)。
假设对于获得相同的教育,低能力工人的边际成本要高于高能力的工人的,即c e(L, e ) > c e ( H, e)c e c e(L, e )c e ( H, e)e3.企业观察e,决定工人的工资w。
工人的收益w–c( η,e)工人的无差异曲线I(e, w) = w–c( η,e)斜率 k = -//dI de dI dw= c e w I LI He企业的收益 y ( η,e ) – w假设企业是完全竞争的,即w = y ( η,e )wy (H , e )w H *y (L , e )w L *e L * e s e H *具有能力η 的工人选择教育水平e 使得emax w – c (η, e ) s . t . y (η, e ) = w最优解表示为e *(η),对应的工资w *(η) = y [η, e *(η)]低能力工人不冒充高能力工人的情形,即w *(L ) – c [L , e *(L )] > w *(H ) – c [L , e *(H )]ww H*w L*e L* e s e H*在有冒充的情形,即w*(H) –c[L, e*(H)] > w*(L) –c[L, e*(L)]wy(H, e s )w H*w L*e L* e H* e s e' e1.混同均衡只有存在冒充时,才可能有混同均衡。
两种工人选择同一种教育水平e p,公司观察到e p后的判断为p(H|e p) = q支付的工资为w p = qy (H, e p) + (1 –q) y(L, e p) (4.2.2)对于不在均衡路径上的判断,可以是p(H|e) = 0 e≠e p工资支付为w(e) = y(L,e) e≠e pwy(H, e s )w L*e L* e p e'e''e s e其他的混同均衡:e0: e p < e0 < e',类似给出公司的判断及工资的支付,也构成完备贝叶斯均衡。
另一种混同均衡:e p,但公司对不在均衡路径上的判断不同。
0 e≤e"e≠e pμ(H| e) = q e = e pq e > e"公司的工资支付为y(L, e) e≤e"e≠e pw(e) = w(e p ) e = e pw(e) e > e"2.分离均衡(1)不存在冒充的时候e(L) = e L*,e(H) = e H*,公司的判断:p(H| e) = 0,e < e H*p(H| e) = 1,e≥e H*公司支付工资w (e) = y(L,e H*),e < e H*w (e) = y(H,e L*),e≥e H*这是完备贝叶斯均衡。