A4长方体和正方体填空小提纲

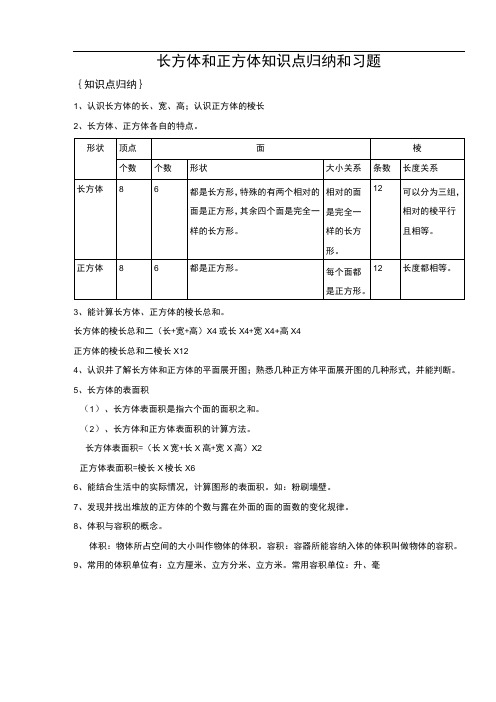
长方体和正方体知识点归纳和习题｛知识点归纳｝1、认识长方体的长、宽、高；认识正方体的棱长2、长方体、正方体各自的特点。

3、能计算长方体、正方体的棱长总和。

长方体的棱长总和二（长+宽+高）X4或长X4+宽X4+高X4正方体的棱长总和二棱长X124、认识并了解长方体和正方体的平面展开图；熟悉几种正方体平面展开图的几种形式，并能判断。

5、长方体的表面积（1）、长方体表面积是指六个面的面积之和。

（2）、长方体和正方体表面积的计算方法。

长方体表面积=（长X宽+长X高+宽X高）X2正方体表面积=棱长X棱长X66、能结合生活中的实际情况，计算图形的表面积。

如：粉刷墙壁。

7、发现并找出堆放的正方体的个数与露在外面的面的面数的变化规律。

8、体积与容积的概念。

体积：物体所占空间的大小叫作物体的体积。

容积：容器所能容纳入体的体积叫做物体的容积。

9、常用的体积单位有：立方厘米、立方分米、立方米。

常用容积单位：升、毫如：冰箱的容积用“升”作单位；我们饮用的自来水用“立方米”作单位。

10、长方体的体积二长X宽X高正方体的体积二棱长X棱长X棱长长方体（正方体）的体积二底面积X高11、能利用长方体（正方体）的体积及其他两个条件求出问题。

如：长方体的高二体积三（长X宽）12、相邻两个体积单位、容积单位之间的进率是1000。

如：1dm3=1000cm31L=1000mL1m3=1000dm3高级单位化低级单位乘进率，低级单位化高级单位除以进率。

13、不规则物体体积测量方法：将物体体积转化成可测量的水的体积。

如：容器中上升水的体积=不规则物体体积专题练习一、填空：1、长方体和正方体都有（）个面，（）条棱，（）个顶点。

2、长方体的长是8厘米，宽是6厘米，高是5厘米，它的棱长和是（）厘米；六个面中最大的一个面积是（）平方厘米，表面积是（）平方厘米。

3、2850平方厘米二（）平方分米（）平方厘米12.8米二（）分米二（）厘米4、一个棱长是1分米的正方体，锯成2个小长方体，其中一个长方体的表面积是（）平方分米。

长方体与正方体复习提纲一、知识再现二、综合练习基础知识填空1、长方体的12条棱按长度可以分成（ ）组，每组有（ ）条。

2、当长方体的四个面相同时，另两个相对的面一定是（ ）形；当长方体的六个面都相同时，它就是（ ）体，又叫做（ ）体。

3、一个长方体的所有棱长总和是36厘米，从一个顶点引出的三条棱的长度和是（ ）分米。

4、用橡皮泥小球和小棒插一个长8厘米，宽5厘米，高3厘米的长方体，一共需要（ ）个橡皮泥小球，小棒（ ）根，这些小棒的长度之和是（ ）厘米5、右图是一个长方体纸盒的表面展开图（单位：分米）这个纸盒的最大的一个面的面积是（ ）平方分米，最小的一个面的面积是（ ）平方分米，它的表面积（ ）平方分米。

6、把一个棱长6cm 的正方体切成棱长2cm 的小正方体，能得到（ ）个小正方体。

7、把一个长5厘米，宽3厘米，高2厘米的长方体，切割成一个最大的正方体，长方体：基本要素： 1、顶点：（ ）个 2、棱：（ ）条 特征（ ） 3、面：（ ）个 特征（ ） 表面积： 1、定义： 2、公式： 体积： 1、定义： 2、公式： 正方体：基本要素： 1、顶点：（ ）个 3、面：（ ）个 特征（ ）表面积： 体 积： 棱长和=（ ） 2、棱：（ ）条 特征（ ） 棱长和=（ ）这个正方体的体积是（）立方厘米。

8、一块长2米，横截面是边长1分米的正方形方木，它的表面积是（）平方分米，体积是（）立方分米。

9、把一个长16厘米，宽和高都是8厘米的长方体分割成两个大小相等的正方体，表面积比原来增加（）平方厘米。

10、用棱长2厘米的两个正方体木块拼成长方体，长方体的表面积是（）平方厘米。

11、把3个完全一样的正方体拼成一个长方体后，表面积减少了16平方厘米，原来每个正方体的表面积是（）平方厘米。

12、用4块棱长为5厘米的正方体拼成一个长方体，这个长方体的表面积最小是（）平方厘米，最大是（）平方厘米。

13、棱长1米的正方体可以分成（）个体积是1立方厘米的小正方体，若将这些小正方体排成一个长方体，长方体的长是（）米，体积是（）立方米。

长方体与正方体练习一一、填空1.长方体或者正方体（）叫做它的表面积。

2.一个正方体的棱长是10厘米，它的表面积是（）平方厘米。

3.一个长方体长4分米，宽3分米，高2分米，它的表面积是（）平方分米。

4.正方体的棱长之和是60分米，它的表面积是（）平方分米。

5.用两个长6厘米，宽3厘米，高1厘米的长方体拼成一个表面积尽可能小的正方体，这个拼成的长方体的表面积是（）平方厘米。

二、选择题。

1.用两个棱长是1分米的正方体小木块拼成一个长方体，拼成的长方体的表面积是（）。

A.增加了B.减少了C.没有变2.如果把一个棱长是10厘米的正方体切成两个完全相同的长方体，这两个长方体的表面积之和比原来的正方体表面积（）。

A.增加了B.减少了C.没有变化3.正方体的棱长扩大2倍，它的表面积就（）。

A.扩大2倍B.扩大4倍C.扩大6倍4.大正方体的表面积是小正方体的4倍，那么大正方体的棱长之和是小正方体的（）A.2倍B.4倍C.6倍D.8倍5.把一个正方体切成大小相等的8个小正方体，8个小正方体的表面积之和（）。

A.等于大正方体的表面积B.等于大正方体表面积的2倍C.等于大正方体表面积的3倍三、一个房间长5米，宽3米，高2.8米，现需油漆四壁和天花板，扣除门窗的面积4.5平方米，求油漆的总面积有多大？四、要做一种管口周长40厘米的通气管子10根，管子长2米，至少需要铁皮多少平方米？五、一个正方体的表面积是54平方分米，这个正方体所有棱长之和是多少？六、有一个长方体木箱，长0.7米，宽0.5米，高0.3米。

怎样放，这个木箱占地面积最小？最小是多少平方米？长方体与正方体练习二1．填空（l）长方体或正方体（）个面的总面积，叫做它们的表面积。

（2）计算正方体的表面积可以用（）×（）×（）的方法计算。

这是因为正方体有（）个面，每个面都是（）形，而且（）都相等。

（3）一个正方体的表面积是36平方厘米，把它放在桌子上占的面积是（）平方厘米。

长方体正方体的认识预习提纲1、读一读朗读教材85-86页的内容。

完成自主学习。

2、观察信息窗1的图片，思考这些物体可以分为几类？想一想从哪几个方面研究长方体？从哪几个方面研究正方体？3、（1）找一个长方体，结合自己手中的长方体实物，数一数，摸一摸，长方体有（）个面，分别是（）面、（）面、（）面、（）面、（）面、（）面，相对的面（），从一个方向观察长方体最多可以看到（）个面。

思考：长方体的六个面可能是什么形状？举例说明生活中哪些物体的形状是长方体？（2）观察手中的长方体，想一想，长方体的棱在哪？怎样数棱才能做到不重复？长方体共有（）条棱，按照棱的长度可以分为（）组，每组有（）条棱，相对的四条棱（）。

（3）观察手中的长方体，思考;长方体的顶点在哪？怎样数顶点才能做到不重复？长方体共有（）个顶点。

（4）叫做长方体的长、宽、高。

长方体有条长，条宽，条高。

（5）、怎样计算长方体的棱长总和？4、（1）找一个正方体，结合自己手中的正方体实物，数一数，摸一摸，正方体有（）个面，每个面是（）形状，6个面大小（）；正方体有（）条棱，12条棱长度（）；正方体有（）定点。

（2）举例说明生活中哪些物体的形状是正方体？（3）怎样计算正方体的棱长总和？5、记一记，试着记一记课本86页中的概念和结论。

6、说一说，将预习获得的知识说给家长听一听，征求家长的意见。

7、画一画，试着画一个长方体直观图。

8、做一做课本第87页1、2、4题。

做在练习本上。

长方体正方体的表面积预习提纲认真阅读课本p33－35页，完成自主学习。

1、观察操作，理解意义。

（1））拿一个长方体和正方体的盒子，沿着棱剪开，并在图中，分别用“上”、“下”、“前”、“后”、“左”“右”标明6个面。

长方体哪些面的面积相等？正方体哪些面的面积相等？（2）每个面的长和宽与长方体的长、宽、高有什么关系？（）面与（）面的长和宽就是长方体的长和高；面与面的长和宽就是长方体的和；面与面的长和宽就是长方体的和；（3）通过阅读课本与观察操作，你知道长方体和正方体表面积的含义吗？2、完成课本91页自主练习第2题（列算式解答）3、写出长方体的表面积计算公式。

长方体和正方体复习提纲知识要点1、基本概念1）长方体和正方体都是立体图形；都有6个面，12条棱，8个顶点。

2）从一个顶点引出的3条棱的长度就是长方体的长、宽、高。

3）长方体的6个面都是长方形，特殊的情况有两个相对的面是正方形，相对的面完全相同；相对的棱长度相等（有4条长、4条宽、4条高）。

4）当长方体有两个相对的面是正方形时，其他的4个面是相等的长方形。

（在长方体中最多可以有4个相同的面）5）正方体的6个面都是相等的正方形，12条棱的长度都相等。

6）正方体是特殊的长方体。

7）长方体和正方体最多可以看到3个面。

8）长方体和正方体的表面积是指6个面的总面积；体积是指所占空间的大小；容积是指所容纳物体的体积（比如说，一个洗发液的瓶子里面所能装下的洗发液的体积就是它的容积）；一个物体的容积一般都比它的体积小。

9）常用的体积单位有立方厘米、立方分米、立方米；容积单位一般都用体积单位，但计量液体的体积时用升和毫升。

10）1立方分米=1升；1立方厘米=1毫升。

11）熟悉立方厘米、立方分米、立方米的多少和升和毫升的多少，能填写生活中常用的物体的面积、体积和容积。

12）当计算长方体的表面积时，有时候需要计算的不需要是6个面，因此需要仔细理解题意，求出需要的面的面积和。

求5个面的面积是：无盖的盒子、箱子等；游泳池的四壁和底面、一个抽屉、一个火柴盒的内盒、一本影集的封套；求4个面的面积是：一根方柱的涂漆表面、一个盒子四周的商标纸、一个烟囱或通风管或排水管、一个火柴盒的外盒；2、基本计算公式长方体的棱长总和=（长+宽+高）×4正方体的棱长总和=棱长×12；正方体的棱长总和÷12=棱长长方体的表面积=（长×宽+长×高+宽×高）×2正方体的表面积=棱长×棱长×6长方体的体积=长×宽×高正方体的体积=棱长×棱长×棱长长方体和正方体的体积=底面积×高如果长方体有2个面是正方形时，这个长方体的表面积=正方形的面积×2+长方形的面积×4如果将一个长方体展开，那么长方体的表面积=长×宽×2+×（长+宽）×2×高（底面周长=（长+宽）×2）3、补充的知识点1）如果将长方体沿平行一个面的方向切下去，那么得到的2个长方体的表面积的和比原来一个大长方体的表面积多了，多出了切口的2个面，而且分3种情况：一种是多了2个上面或下面；一种是多了2个左面或右面；一种是多了2个前面或后面。

第二单元 长方体和正方体总结一、 长方体和正方体的特征： 形体 相同点 不同点关系 面 棱 顶点 面的形状 面的大小棱长 长方体 6 12 8 一般六个面都是长方形〔也有两个相对的面是正方形〕。

相对的面面积相等平行的四条棱长度 相等 正方体是特殊的长方体 正方体 6 12 8 六个面都是正方形 六个面的面积相等 十二条棱长都相等长方体：①有6个面，相对的面完全相同；长方体放桌面上，最多只能看到3个面。

②有12条棱，相对的棱长长度相等，而且相对的棱互相平行；12条棱可以分为3组〔分别为长、宽、高〕，每组的4条棱一样长；长方体的棱长总和=长×4+宽×4+高×4=〔长+宽+高〕×4③有8个顶点，每个顶点上的三条棱分别称为长方体的长、宽、高。

正方体：①有6个完全相同的面；正方体放桌面上，最多只能看到3个面。

②有12条长度相等的棱，每条棱的长度称为正方体的棱长； 正方体的总棱长=棱长×12。

上下左后右前③有8个顶点。

练一练：1.一个长方体长、宽、高分别是10cm、7 cm、4 cm ，这个长方体的棱长和是多少厘米？〔提示：根据长方体的总棱长公式计算〕2.一个长方体的棱长和是160dm，其中，长是20dm，宽是8dm，它的高是多少？从一个顶点引出的三条棱的长度总和是多少？3.将一根铁丝长720厘米做成正方体，则正方体的棱长是多少厘米？二、长方体和正方体的外表积定义：长方体或正方体6个面的总面积，叫做它的外表积。

1.法一：(1)长方体的外表积〔有六个面〕=长×宽×2+长×高×2+宽×高×2=〔长×宽+长×高+宽×高〕×2〔因为长方体相对的面完全相同〕法二：前、后面：长×高×2=X左、右面：长×高×2=Y上、下面：长×宽×2=Z则长方体的外表积〔有六个面〕= X + Y + Z2.正方体的外表积〔有六个面〕=棱长×棱长×6〔因为正方体的六个面完全相同〕在解决一些问题时，要充分考虑实际情况，想清楚要算几个面。

13/14苏教版六年级上册数学期末复习二（内容：长方体和正方体）班级姓名座号成绩一、填空（共29分）（第1、2题各4分，第10题3分，其余每题2分）1、 3.02立方米=（）立方分米 90020立方厘米=（）升9.08立方分米=( )升( )毫升 4.07升=( )立方厘米2、在括号里填上适当的单位名称旗杆高15（）教室面积80（）油箱容积16（）一瓶墨水60（）3、一个长方体的体积是72立方厘米，长6厘米，宽5厘米，高( )厘米。

4、用一根12分米长的铁丝围成一个最大的正方体形状的框架，这个正方体的表面积是（）平方分米，体积是( )立方分米。

5、一个长方体的长、宽、高分别是7cm,6cm和5cm，它的棱长之和是（）厘米。

做这样一个无盖的长方体盒子，需要（）平方厘米材料。

6、一个长方体的横截面是边长为3厘米的正方形，它的长是5厘米，这个长方体的表面积是( )平方厘米，体积是( )立方厘米。

7、一个棱长是5分米的正方体水池，蓄水的水面低于池口2分米，水的容量是( )升。

8、一个容量是15升的药桶，装满了止咳药水，把这些药水分别装在100毫升的小瓶里，可以装（）瓶。

9、3个棱长都是8厘米的正方体，拼成一个长方体，表面积（）。

10、一个正方体和一个长方体的底面积都是4平方分米，这个正方体的表面积是（）平方分米，体积是（）立方分米。

长方体的体积是20立方分米，高是（）分米。

11、一个长12厘米，宽4厘米，高5厘米的长方体纸盒，最多能容纳（）个棱长2厘米的小立方体。

12、一个长方体可以切成两个正方体，每个正方体是原长方体体积的( )，两个正方体的表面积是原长方体的（）倍。

( )二、将正确答案的序号填入（）内。

（10分）1、用一根52厘米长的铅丝，正好可以焊成长6厘米，宽4厘米，高（）厘米的长方体教具。

A、2B、3C、4D、52、如果把长方体的长、宽、高都扩大3倍，那么它的体积扩大（）倍。

A、3B、9C、27D、543、食堂的长方体烟囱是用铁皮制成的，求用了多少铁皮，就是求( )。

长方形和正方形单元知识整理长方形和正方形单元知识整理（长），短边的长叫作（宽）；正方形每条边的长叫作（边4、用一张长10厘米，宽6厘米的长方形纸 对边相等）一一四个角（都折直一个最大的正方形，这个正方形的正方形一一四条边（都相等）四个角（都是直角）3、物体某个面一周边线的长就是它的周长。

边长是多少厘米？ 多边形各边的长度之和就是它的周长。

4、 长方形周长计算：1、长+宽+长+宽。

2、先算出2条长、2条宽各是多少，再把结果相加。

3先算长+宽的和，再用和X2o 5、从一张长7厘米，宽5厘米的长方形纸5、 正方形周长计算：边长X 4=正方形的周长片中，剪去一个尽可能大的正方形，剩 6、 正方形边长二周长十4长方形的长二周长十2—宽 长方形的宽二周长十2 —长下部分是一个长（）厘米，宽（）厘1、一个长方形，宽是6厘米，长是宽的3米的长方形，剩下部分的周长是多少？倍，这个长方形的长是（）厘米，周 长是多少厘米?2、一块长方形菜地的宽是15米，长是宽的3倍。

要在这块菜地周围围上篱笆，篱笆长多少 米？【单元知识梳理】 1、 长方形长边的长叫作 长）。

2、 长方形一一四条边（个正方形的周长是多少厘米？剩下部分米？的周长是多少厘米?3、一块长方形菜地，长24米，宽比长少8米，如果沿这块菜地跑5圈，跑了多少 &明明从一张长20厘米，宽12厘米的长方形纸上，剪下一个最大的正方形，这个长方形，拼成长方形的长是（）厘8 —个长方形操场，长55米，宽35米小华沿操场跑了一圈，跑了多少米？9、一个长方形操场，长150米，宽50米，围着这个操场跑3圈，一共跑了多少米？10.用4个边长1厘米的小正方形拼成一个大正方形，拼成大正方形的边长是多少厘米？周长呢？11x用5个边长1厘米的小正方形拼成一个长方形，拼成长方形的周长是多少厘是多少？13、用两个长4厘米、宽2厘米的长方形拼成正方段或长方形，拼成的正方形或长方形的14、用两个长都是6厘米、宽都是3厘米的长方形拼成长方形或正方形，拼成的图形的周长各是多少？15、用四个长都是8厘米、宽都是3厘米的长方形分别拼成下面这样不同白- 艇？这两个大长方形的周长分别是多少7、一个正方形池塘，边长是60米，它的四周有一条小路，这条小路的全长大约是多少米? 12、用3个边长5厘米的正方形纸片拼成一米，宽是（）厘米，周长是多少厘米？米？16、把一张边长20厘米的正方形纸片剪成17、 把边长16厘米的正方形硬纸板剪成4个同样大的小正方形，每个小正方 的周长是多少厘米？18、 把一张边长8厘米的正方形纸对折成两个长 方形再剪开，每个长方形的周长是多少厘 米？19、张大妈打算用篱笆围出一块长方形菜地，这块菜地一面靠墙，长12米，宽7米，篱笆可能长多少？20、小亮家利用一面院墙，用篱笆围成一个 长方形的养鸡场，养鸡场长M 米，宽8米，篱笆21、用一根20厘米的铁丝围成一个正方形，正方形的边长是多少厘米？22、用一根铁丝围成一个长10厘米，宽8 厘米的长方形，如果改围一个正方形， 正方形的边长是多少？23、 一根铁丝正好可以围成一个长5分米，宽3分米的长方形，如果改围成一个正方形，那么这个正方形的边长是多少？24、 一个正方形和一个长方形的周长相等，已知长方形的长是24厘米，宽是16厘米，正方 形的边长是多少分米？25、 用1根1米长的绳子，围成一个边长18厘米的正方形，正方形的周长是多少厘 米？围成 正方形后，这根绳子还剩多少厘米？至少长多少米?26、小英拍了一张照片，要给照片做一个木质相框。

长方体和正方体A卷一、我来填一填。

（每小题2分，共20分。

）1、相交于一个顶点的（）条棱，分别叫做长方体的（）、（）、（）。

因为正方体是长、宽、高都（）的长方体，所以正方体是（）的长方体。

2、一个正方体的棱长为A，棱长之和是（），当A=6厘米时，这个正方体的棱长总和是（）厘米。

3、一个长方体的棱长总和是80厘米，长10厘米，宽是7厘米。

高是（）厘米。

4、一个长方体的长是15厘米，宽是12厘米，高是8厘米，它的上面的面积是（）平方厘米；前面的面积是（）平方厘米；右面的面积是（）平方厘米。

这个长方体的表面积是（）平方厘米。

体积是（）立方厘米。

5、给下面的各题填上适当的单位名称。

一块橡皮的体积约是8（）；一台洗衣机的体积约是300（）一节集装箱所占空间约是60（）；汽车的油箱大约能盛汽油50（）6、在括号里填上适当的数。

7.９立方分米＝（）升 8600平方厘米＝（）平方分米980立方分米＝（）立方米 9.4立方米＝（）立方分米25立方分米50立方厘米＝（）立方分米＝（）立方厘米3.26立方米＝（）立方米（）立方分米7、一个长方体，长4米，宽3米，高2米，它的占地面积最大是（）平方米，最小是（）平方米。

8、一个正方体的表面积是24平方分米，把它分成两个完全相同的长方体，每个长方体的表面积是（）。

9、有一种无盖的玻璃鱼缸，长20厘米，宽15厘米，高10厘米，做这样一对鱼缸需要（）平方厘米的玻璃，能装水（）升。

10、一个长方体，如果高减少3厘米，就成为一个正方体。

这时表面积比原来减少了96平方厘米。

原来长方体的体积是（）立方厘米。

二、我来选一选。

（每小题2分，共10分。

）11、棱长是1米的正方体和棱长是10分米的正方体的体积（）。

A一样大 B棱长是1米的正方体大 C棱长是10分米的正方体大12、正方体的棱长扩大到原来的3倍，它的表面积扩大到原来的（）。

A、3倍B、6倍C、9倍D、27倍13、一本书的封面的周长大约是89（）体积大约是210（）。

《长方体和正方体》知识点归纳知识点一、长方体的特征1、长方体由（）个面围成，相对的面互相（）且形状大小（）。

通常这些面的形状都是（），特殊情况下可有（）个相对的面是正方形。

2、长方体有（）个顶点。

3、长方体两个面相交的边叫做这个长方体的棱，共有（）条棱，且每条棱长都（）。

相邻的三条棱互相（）。

相对的两条棱互相（）。

4、相交于一个顶点的三条棱分别叫做这个长方体的长、宽、高。

底面中较长的一条棱是（），较短的一条棱是（），垂直于底面的棱是（）。

长方体有（）条长、（）条宽、（）条高。

知识点二、正方体的特征1、正方体由（）个面围成，每个面的形状大小都（），且形状都是（），其中相对的两个面互相（）。

2、正方体有（）个顶点。

3、正方体两个面相交的边叫做这个正方体的棱，共（）条棱，且每条棱长都（）。

相邻的三条棱互相（）。

相对的两条棱互相（）。

4、正方体可以视为长、宽、高都相等的（）。

因此正方体是特殊的（）。

5、从某一点观察，能够呈现几何体整体形状的绘图叫做（），其中看见不见的边要用（）表示。

这里长方体和正方体的图都是直观图。

知识点三、长方体和正方体的相关计算1、物体外部各个面的面积之和叫做物体的（）。

2、物体所占空间的大小叫做物体的（）。

3、表面积和面积的单位是一样的，常用的有：（）、（）、（），分别写作（）、（）、（）。

4、常用体积单位有：（）、（）、（），分别可以写作（）、（）、（）。

5、单位换算：①1m=（）dm，1dm=（）cm 。

（进率是____）②1m2=（）dm2 ，1dm2=（）cm2。

（进率是____）③1m3=（）dm3，1dm3=（）cm3。

（进率是____）6、大单位转化为小单位，要（）进率。

小单位转化为大单位，要（）进率。

7、长方体和正方体的表面积公式：温馨提示：计算表面积的时候，要注意物体是否有6个面。

例如游泳池、鱼缸等物体并不是完整长方体，它们只有（）个面，我们算出长方体的表面积后，还要减去那1个缺少的面。