乘公交迎奥运,数学建模

2007B题：乘公交，看奥运（数据有变化）我国人民翘首企盼的第29届奥运会明年8月将在北京举行，届时有大量观众到现场观看奥运比赛，其中大部分人将会乘坐公共交通工具（简称公交，包括公汽、地铁等）出行。

这些年来，城市的公交系统有了很大发展，北京市的公交线路已达800条以上，使得公众的出行更加通畅、便利，但同时也面临多条线路的选择问题。

针对市场需求，某公司准备研制开发一个解决公交线路选择问题的自主查询计算机系统。

为了设计这样一个系统，其核心是线路选择的模型与算法，应该从实际情况出发考虑，满足查询者的各种不同需求。

请你们解决如下问题：1、仅考虑公汽线路，给出任意两公汽站点之间线路选择问题的一般数学模型与算法。

并根据附录数据，利用你们的模型与算法，求出以下6对起始站→终到站之间的最佳路线（要有清晰的评价说明）。

(1)、S3769→S2857 (2)、S1557→S0481 (3)、S1879→S2322(4)、S0008→S0073 (5)、S0148→S0485 (6)、S0087→S36762、同时考虑公汽与地铁线路，解决以上问题。

3、假设又知道所有站点之间的步行时间，请你给出任意两站点之间线路选择问题的数学模型。

【附录1】基本参数设定相邻公汽站平均行驶时间(包括停站时间)：3分钟相邻地铁站平均行驶时间(包括停站时间)： 2.5分钟公汽换乘公汽平均耗时：6分钟(其中步行时间2分钟)地铁换乘地铁平均耗时：5分钟(其中步行时间2分钟)地铁换乘公汽平均耗时：8分钟(其中步行时间4分钟)公汽换乘地铁平均耗时：6分钟(其中步行时间4分钟)公汽票价：分为单一票价与分段计价两种，标记于线路后；其中分段计价的票价为：0～20站：1元；21～40站：2元；40站以上：3元地铁票价：3元（无论地铁线路间是否换乘）注：以上参数均为简化问题而作的假设，未必与实际数据完全吻合。

【附录2】公交线路及相关信息（见公汽线路信息，对原数据文件B2007data.rar 有少量更改）城市公交线路选择优化模型摘要本文针对城市公交线路选择问题建立了两个模型，一个是基于集合寻线算法模型，另一个是图论模型。

07年全国数学建模竞赛试题解答(由于懒得将图片依次贴出，需要者可以下载相关附件)乘公交看奥运相关文件下载点击此处摘要本设计要解决的是合理给出两站点间的最佳路线选择问题，即给出一条经济且省时的路线。

在处理此问题之前，我们根据调查和分析，对影响线路选择的因素进行筛选，最终确定了以下三个影响较大的因素：第一是换乘次数；第二是乘车时间；第三是乘车费用。

依据各因素对路线选择的影响程度,我们按不同的权重对它们进行考虑。

从实际情况分析，人们通常宁愿多乘坐几站地也不愿换车，所以我们赋予换乘次数较大的权重。

为了解决换乘次数最少，乘车时间相对较短、乘车费用相对较少的问题，经过尝试与探索，我们采用了现代分析的方法，对起始站和终点站有无相交站点进行分类讨论，归纳出直达，换乘一次，换乘两次的情况（三次以上的情形可以类推），并通过Matlab编制程序，给出了任意两站点间的最佳乘车路线以及换车的地点，最后还提出了进一步的意见和建议。

关键词：最佳路线换乘次数乘车时间乘车费用一、问题的重述第29届奥运会明年8月将在北京举行，作为城市枢纽的公共交通承担着非常重的运输任务。

近年来，北京市的公交系统有很大的发展，公交线路的条数和公交车数量在迅速增多，给人民生活带来便利的同时，也面临多条线路得选择问题，有时出行往往还需要转乘多辆公交车才能到达目的地。

如何在短时间、换乘次数最少、成本最低的情况到达目的地，是人们所关注的问题。

因此，我们通过建立线路选择的模型与算法，设计一套自主查询计算机系统，查询到出行时所需的最佳公交路线及换乘方法，给人们出行节约更多的时间和金钱。

要求：1、仅考虑公汽线路，建立任意两公汽站点之间线路选择问题的数学模型与算法。

并求出以下6对起始站→终到站之间的最佳路线。

（1）S3359→S1828 （2）S1557→S0481 （3）S0971→S0485（4）S0008→S0073 （5）S0148→S0485 （6）S0087→S36762、同时考虑公汽与地铁线路，解决1中问题。

数学建模全国⼀等奖论⽂系列（27）乘公交，看奥运摘要由于可供选择的车次很多，各种车辆的换乘⽅式也很多，为了避免上下⾏站点不⼀样的车次等对路线产⽣的影响，我们以由易到难的思路来完成模型。

⾸先分析⼀辆车可以直接到达的情况，在这其中⼜考虑到环线的特殊性对其单独进⾏判断讨论；由于⼀辆车可使乘客到达⽬的地的可能性太⼩，我们接下来讨论要进⾏⼀次换乘的情况，在这⾥巧妙地利⽤矩阵来判断两辆车是否含有共同站这个思想，避免了⾄少两重循环，使运算速度⼤⼤提⾼；虽然这样就已经能够解决不少的问题，但并不完全，因此我们继续计算换乘两次的乘车路线，经过⼤量的运算，我们发现基本所有的站点间都可以通过换乘两次到达，⾄此对公交线路的讨论基本完成。

对加⼊地铁的讨论与只有公交车时类似，从最简单的两辆地铁换乘的情况开始考虑，由浅⼊深。

论⽂中并没有运⽤⼤量的符号，⽽是⽤⽂字来说明程序的主要步骤，这样可以让不了解程序的读者也清楚地知道模型的思路，⽽且，只要知道起始与终点，利⽤程序就可以计算所有可能路线，并可以在结果中为读者提供路线的相关信息，⽐如路费及所需时间，以供选择。

对于最优的解释，我们除了以时间最少、车费最省为原则，还对时间与车费进⾏了加权平均，⽽权数便是乘客对时间与⾦钱的偏好程度，当输⼊⾃⼰愿⽤1元钱去换多少分钟乘车时间时，程序会根据个⼈的不同喜好，来选择出适合每个⼈的最优路线。

这样将程序⼈性化，可以更符合实际中⼈们的需要。

关键词：公交线路选择最优化矩阵加权平均数组分类讨论⾃主查询问题重述北京是中国的⾸都，是政治、⽂化中⼼，同时也是国际交往的中⼼。

在成功取得2008年第29届夏季奥运会的举办权后，北京市城市建设的步伐将进⼀步加快。

众所周知，可靠的交通保障是成功举办奥运会的关键之⼀，公共客运交通服务系统尤为重要。

在保持公车票价⼀直相对较低的情况下，北京市⼜已经实⾏机动车单双号出⾏，⽬的就是为了⿎励⼈们乘公共汽车出⾏，缓解交通阻塞状况。

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人（包括指导教师）研究、讨论与赛题有关的问题。

我们知道，抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。

我们郑重承诺，严格遵守竞赛规则，以保证竞赛的公正、公平性。

如有违反竞赛规则的行为，我们将受到严肃处理。

我们参赛选择的题号是（从A/B/C/D中选择一项填写）： B我们的参赛报名号为（如果赛区设置报名号的话）：所属学校（请填写完整的全名）：参赛队员(打印并签名) ：1.2.3.指导教师或指导教师组负责人(打印并签名)：日期：年月日赛区评阅编号（由赛区组委会评阅前进行编号）：编号专用页赛区评阅编号（由赛区组委会评阅前进行编号）：全国评阅编号（由全国组委会评阅前进行编号）：乘公交，看奥运摘要本文要解决的问题是以即将举行的08年北京奥运会为背景而提出的。

人们为了能现场观看奥运会，必然会面对出行方式与路线选择的问题。

因此如何快速、高效地从众多可行路线中选出最优路线成为了解决此问题的关键。

鉴于公交系统网络的复杂性，我们没有采用常规的Dijkstra算法，而采用了高效的广度优先算法。

其基本思想是从经过起（始）点的路线出发，搜寻出转乘次数不超过两次的可行路线，然后对可行解进行进一步处理。

为满足不同查询者要求，我们对三个问题都分别建立了以时间、转乘次数、费用最小为目标的优化模型。

针对问题一（只考虑公汽系统），我们建立了模型一并通过VC++编程得到了任意两个站点间的多种最优路线，并得出所求站点间最优路线的最优值，如下程得到所求站点间的最优路线，如下表所示：进里又建立了图论模型。

本文的主要特点在于，所用算法的效率十分显著。

在对原始数据仅做简单预处理的条件下，搜索任意站点间的最优路线所需的平均时间不超过0.5秒。

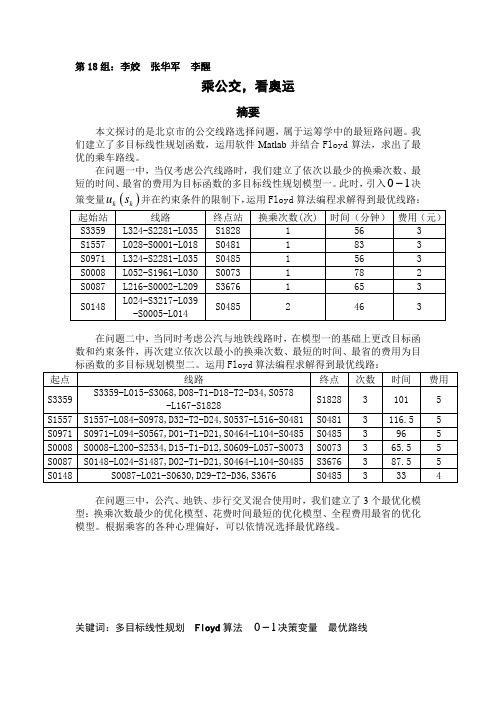
第18组：李姣 张华军 李醒乘公交，看奥运摘要本文探讨的是北京市的公交线路选择问题，属于运筹学中的最短路问题。

我们建立了多目标线性规划函数，运用软件Matlab 并结合Floyd 算法，求出了最优的乘车路线。

在问题一中，当仅考虑公汽线路时，我们建立了依次以最少的换乘次数、最短的时间、最省的费用为目标函数的多目标线性规划模型一。

此时，引入01-决策变量()u s 并在约束条件的限制下，运用Floyd 算法编程求解得到最优线路：在问题二中，当同时考虑公汽与地铁线路时，在模型一的基础上更改目标函数和约束条件，再次建立依次以最小的换乘次数、最短的时间、最省的费用为目在问题三中，公汽、地铁、步行交叉混合使用时，我们建立了3个最优化模型：换乘次数最少的优化模型、花费时间最短的优化模型、全程费用最省的优化模型。

根据乘客的各种心理偏好，可以依情况选择最优路线。

关键词：多目标线性规划 Floyd 算法 01-决策变量 最优路线1、问题重述1.1问题背景2004年在雅典奥运会上使用的info2004信息服务系统，为奥运期间来访的各国运动员、旅游观光者以及本国居民提供了便利，同时也将“数字奥运”、“科技奥运”、“人文奥运”融为一体，向世界宣告了信息化的广泛普及以及科技竞争的日益加剧。

“数字奥运”作为奥运会的亮点，旨在建设各种与奥运相关的信息与基础通信设施和系统，营造良好的信息化环境，提供优质的信息服务，是“科技奥运”的时代特征，是“人文奥运”的弘扬手段，我国人民翘首企盼的第29届奥运会明年8月将在北京举行，届时有大量观众到现场观看奥运比赛，其中大部分人将会乘坐公共交通工具（简称公交，包括公汽、地铁等）出行。

这些年来，城市的公交系统有了很大发展，北京市的公交线路已达800条以上，使得公众的出行更加通畅、便利，但同时也面临多条线路的选择问题。

如何通过高科技信息手段，建立一个公交查询服务系统，充分体现“以人为本”和“科技奥运”的理念，同时，进一步推动首都信息化的长期发展，实现“数字奥运”和北京生活的信息化的双重目标，提高我国的国际竞争力和影响力，便是值得我们深思的问题。

数学建模乘公交-看奥运（含代码)————————————————————————————————作者: ————————————————————————————————日期:乘公交看奥运摘要本设计要解决的是合理给出两站点间的最佳路线选择问题，即给出一条经济且省时的路线。

在处理此问题之前,我们根据调查和分析，对影响线路选择的因素进行筛选,最终确定了以下三个影响较大的因素：第一是换乘次数;第二是乘车时间;第三是乘车费用。

依据各因素对路线选择的影响程度,我们按不同的权重对它们进行考虑。

从实际情况分析,人们通常宁愿多乘坐几站地也不愿换车，所以我们赋予换乘次数较大的权重。

为了解决换乘次数最少,乘车时间相对较短、乘车费用相对较少的问题,经过尝试与探索，我们采用了现代分析的方法,对起始站和终点站有无相交站点进行分类讨论,归纳出直达，换乘一次,换乘两次的情况（三次以上的情形可以类推)，并通过Matlab编制程序，给出了任意两站点间的最佳乘车路线以及换车的地点，最后还提出了进一步的意见和建议。

关键词：最佳路线换乘次数乘车时间乘车费用一、问题的重述第29届奥运会明年8月将在北京举行，作为城市枢纽的公共交通承担着非常重的运输任务。

近年来，北京市的公交系统有很大的发展,公交线路的条数和公交车数量在迅速增多，给人民生活带来便利的同时，也面临多条线路得选择问题,有时出行往往还需要转乘多辆公交车才能到达目的地。

如何在短时间、换乘次数最少、成本最低的情况到达目的地,是人们所关注的问题。

因此，我们通过建立线路选择的模型与算法,设计一套自主查询计算机系统，查询到出行时所需的最佳公交路线及换乘方法，给人们出行节约更多的时间和金钱。

要求:1、仅考虑公汽线路，建立任意两公汽站点之间线路选择问题的数学模型与算法。

并求出以下６对起始站→终到站之间的最佳路线。

(1）S3359→S1828(2）Ｓ1557→S0４81 (3)Ｓ0９71→S0485(4)S０008→Ｓ０07３(5）Ｓ0１４8→S0４8５(6）S0087→S36７62、同时考虑公汽与地铁线路，解决１中问题。

乘公交,看亚运摘要本文解决的是最佳乘车路线问题, 分析乘车路线选择的主要影响因素建立了相应的求解模型,确定不同情况下的最佳乘车路线.并分析各线路的交通情况,给出了缓解交通困难的方案.对于问题一: 根据题目所给出的公交线路信息数据,利用逐步搜索法求出任意两公汽站点间的直达线路,在最少换乘次数的基础上以时间为主要目标并考虑乘车费用建立多目标优化模型.通过编程找出三对站点的最佳方案,均需要换乘1次,总花费均为3元,详细结果见下表:华穗路→交通大厦越秀桥→山村江南大道北→策边村换乘方案由408路转到1047路由184路转到893路由235路转到192路换乘站点江南大道口芳村隧道口动物园花费时间116分钟38分钟140分钟对于问题二: 以分别到达所有亚运场馆的总换乘次数最多和所需时间最长为困难地区的评判标准,建立新的多目标优化模型,利用MATLAB软件编程求解得到结果.对于问题三: 在模型二的基础上,建立以总时间最少作为目标的单目标模型.将专线的路线设置分为两种处理办法: 一,对可在公交或地铁线路中得到路线的四条线路用模型三求解;二,对不可在公交或地铁线路中得到路线的直接搜索相关资料得到两站的最短路程再换算成时间.最后统一给定根据行驶时间的收费标准得到专线具体设置情况.对于问题四:以过站点的线路最少为交通困难目标建立相应的整数规划模型,并用MATLAB软件求解得到交通困难区,在增加公交、地铁或专线时重点考虑求得的交通困难区.本文分析考虑不同问题的需求建立了四个相应的模型,但由于时间原因,部分模型没有求得结果.关键词: 逐步搜索法多目标规划整数规划1. 问题重述1.1问题背景:2010年11月12日第16届亚运会在广州举行,为了让全体市民更好观看亚运会,广州市政府决定在亚运期间放假3天、以及全体市民可在亚运及亚残运会期间免费坐公交、地铁30个工作日等惠民政策,这一政策的施行在很大程度上加剧了广州市交通出行的困难.为了方便游客看亚运会,请你用数学建模的方法,为广州市设计一个公交线路查询系统,满足查询者的各种不同需求.1.2题目所给信息交通困难以某条线路上的最困难作为指标;基本参数设定见附录一;公交线路及相关信息见附录二.1.3本文需解决的问题有:问题一: 在亚运会开幕前,仅考虑公汽线路,给出任意两公汽站点之间线路选择问题的一般数学模型与算法.并根据附录数据,利用你们的模型与算法,求出以下3对起始站→终到站之间的最佳路线（要有清晰的评价说明）.(1)、华穗路→交通大厦(2)、越秀桥→山村(3)、江南大道北→策边村问题二: 在亚运会期间考虑公交和地铁的情况下,哪些地区的交通困难,并说明原因.问题三: 在亚运会开幕前现拟建专线,请合理设置专线的路线,运行时间,以及收费标准.问题四: 如何增加公交,地铁或者专线,缓解交通困难.2. 模型的假设与符号说明2.1模型的假设假设1: 各路径上的公交车发车平度相同;假设2: 相邻站点的平均行驶时间一定;假设3: 不出现交通阻塞,公交运行顺畅;假设4: 不出现车辆故障及交通事故;假设5: 公交准点到达,不考虑红绿灯等待时间;假设6: 除环形线路外其他线路均是单向行驶.2.2符号说明符号符号说明(),,G V E W公汽网的有向赋权图,i j站点号 A 直达线路数矩阵 B 引入的中间矩阵 C最少换乘数矩阵ij a 第i 个站点到第j 个站点的直达线路数 ij c第i 个站点到第j 个站点的最少换乘次数ij x ,ij y弧(),i j 是否在该路径上N 总站点数 n两站点的直达线路数 ij t ,'ij t 站点i j →的最短乘车时间 ij P站点i j →的总乘车费用 ij s表示站点i j →的过站数c人为设定参数,乘客可接受的最多换乘次数()'''',,G V E W公汽地铁网的有向赋权图 Q亚运六个主场馆的站点集合{}1057,385,927,1282,2998,874Q ∈ij Z i j →始发的等待时间0T总的乘车时间 1T 总的等待时间 2T总的步行时间ik Yi k →换乘时步行的时间站点i在线路j上ij3. 问题分析为了设计一个公交线路查询系统去满足查询者的各种需求,我们分析题目要求,先对题目给出的公交线路各站点名按一定的顺序进行标号,以便后面的求解叙述.再分析主要的影响因素——换乘次数、行驶时间、乘车费用等,建立相应的求解模型,确定不同情况的最佳乘车路线.并分析各线路的交通情况,给出缓解交通困难的方案.对问题的具体分析如下.针对问题一: 只考虑公交车线路的情况下,要给出任意两公汽站点之间线路选择.首先,我们根据题目所给出的公交线路信息,利用逐步搜索法求出任意两公汽站点间的直达线路,并用矩阵表示出直达线路的条数,这是为后面的目标及约束的考虑做准备.再考虑换乘次数,在最少换乘次数的基础上先后考虑行驶时间及乘车费用,并以它们建立相应的目标函数.通过编程找出供选的多种参考方案.并以时间为主要目标建立任意两站点的行驶时间最短的最优化模型.针对问题二: 在亚运会期间,考虑公交和地铁的情况下,将地铁站点与其对应的公交站点视为一个站点处理.另外,由于亚运期间乘公交地铁免费,故此问少了问题一中的最少乘车费用的目标.但由于要考察地区的交通困难情况,所以在问题一的基础上要增加新的目标函数.交通困难是以某条线路上的最困难作为指标,通过查询我们知道广州亚运的主场馆在六个站点（奥林匹克体育中心、体育中心、大学城体育中心、广州体育馆、黄埔体育馆、增城体育馆）附近,所以我们定义站点的交通困难为分别到达所有亚运场馆的总换乘次数最多和所需时间最长.而增加了地铁后,换乘的情况也相应变化,特别是换乘时间,这对总时间和换乘次数的目标函数都有影响,约束条件基本不变,这样建立新的优化模型,再用matlab编程求解.针对问题三: 要设置合理的专线线路,我们在问题二的基础上,考虑专线设置的总路程最短即耗时最少作为线路设置指标,可直接将问题二的模型改成总时间最少的单目标,并对相应约束条件进行调整得到优化模型三.但考虑到有四条拟建专线的站点不能在公交或地铁线路中得到路线,所以我们将专线的路线设置分为两种处理办法: 对可在公交或地铁线路中得到路线的四条线路用模型三求解;对不可在公交或地铁线路中得到路线的直接搜索相关资料得到两站的最短路程再换算成时间.最后统一给定根据行驶时间的收费标准.针对问题四: 要增加公交、地铁或者专线,缓解交通困难,我们以过站点的线路最少的作为交通困难区,建立相应的整数规划模型,并用MATLAB软件求解得到交通困难区,在增加公交、地铁或专线时重点考虑求得的交通困难区,这样可缓解交通压力.4. 数据分析把题目所给数据信息分类整理:整理一: 将题目所给附录二中的同条线路上的两个相同站点名改后一个为“站名+2”,如第五条线路的“江夏（安华灯饰城）”就在此条线路中出现了两次,我们将第二次出现的改名为“江夏（安华灯饰城）2”.整理二: 根据题目的站点数归类原则,将题中附录二中的线路按: 0—2拟建专线;3—47公交线;47—55地铁线进行归类.最后得到: 公交线路1052条,其中环线39条;地铁线路9条;拟建专线8条.将上述结果制成下图,即:3910529820040060080010001200环线非环线地铁拟建专线图4-1: 附录一的线路分类结果从图中可以看出: 广州市以公交线路为主,其中包括部分+环线公交,地铁和专线数都很少,这主要与城市的交通及需要有关.整理三: 将题中附录二的线路按附录一中的票价标准进行票价分类,即: 站点数小于6的线路为2.5元票价;站点数小于10的线路为2.0元票价;站点数大于等于10的线路为1.5元票价;地铁票价为3元.统计结果见下表（源程序参见附录三）:表4-1: 票价统计结果表票价（元） 3.0 2.5 2.0 1.5 线路数（条）920261044从上表我们看出: 大部分线路的票价为1.5元.接着,我们将每条线路的站点数目进行统计划分得到下面的站点数分布图,即:1020304050102030405060线路站点数目线路条数图4-2: 线路的站点数分布图从上图我们可以看出: 大部分线路的站点数在15—30之间,站点数大于30的线路数比站点数小于15的线路数多.可见,广州市的站点线路设置还是比较合理的,基本符合线路覆盖面广和地铁数量合理的原则.5．问题一的解答针对问题一,我们建立了以时间为主要目标的任意两站点的行驶时间最短的最优化模型一. 5.1模型的准备准备一: 引用图论相关知识,将题目所提供的公汽网络抽象成一个有向赋权图(),,G V E W = ,G中每个顶点代表不同的站点,如果i v 到j v 有直达路线,那么这两点之间就用有向边相连,记做(),i j E ∈,相应用(),i j w v v 表示该有向边的权,这样公汽网络就抽象为了一个有向赋权图.准备二: 问题分析中我们提出为了方便乘客乘车,考虑到换乘既存在时间消耗又有增加乘车费用,所以我们在最少换乘次数的基础上考虑公众对其他因素的需求.所以,我们首先确定最少换乘次数.第一步,构造直达线路数矩阵:通过求得任意两点的直达线路并构造两两间直达路线数目的直达路线数矩阵()ij N NA a ⨯=.其矩阵元素ij a 表示第i 个站点到第j 个站点的直达线路数n ,其中,当i j =时,0ij a =,即:ij n i j a i j≠⎧=⎨=⎩以所有公汽所经过的站点总数为N ,则直达线路数矩阵可表示为:111212122212N N N NijN N N Na a a a a a A a a a a ⨯⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭第二步,建立换乘线路数矩阵:根据矩阵运算法则,2A 的元素212a 可表示为:21211121222133212N N a a a a a a a a a =++++假设上式中等号右边仅13321,1a a ==,其余为0,说明仅第一个站点可直达到第三个站点,第三个站点可直达到第二个站点,那么2121a =,即第一个站点可通过一次换乘到达第二个站点,换乘站点为3.通过上面的例子我们发现,可以用2ij A 表示第i 个站点到第j 个站点通过1次换乘的路线数.依次类推,用nij A 表示方阵的n 次幂,kj A 为站点k j →的直达路线数,则:11Nn n ijik kj k A A A -==∑其中,元素nij A 为通过()1n -次换乘从站点i j →的线路数.如: 34,31A =表示从站点4到站点3有1条两次换乘路线,其换乘站点可通过运算参数记录得到. 第三步,建立最少换乘次数矩阵:先引入矩阵()ij B b =,其矩阵元素ij b 为使得0nij A ≠的n 的最小值,[)1,n ∈∞,即:[){}m in |0,1,0nijij n An i j b i j⎧≠∈∞≠⎪=⎨=⎪⎩则1ij b -表示从站点i j →必要的最少换乘次数,以矩阵()ij C c =表示最少换乘次数矩阵,元素ij c 表示从站点i j →必要的最少换乘次数,则:10B i j C i j -≠⎧=⎨=⎩5.2模型一的建立5.2.1确定目标函数在问题分析中我们已经提出,要满足乘客的不同需求,主要分三个因素考虑: 换乘次数、行驶时间、乘车费用.并且,我们在最少换乘次数的基础上考虑公众对其他因素的需求.这样目标函数就有三个,即:一，换乘次数最少在模型准备中我们建立了公汽网的有向赋权图,在此,我们引入0-1决策变量ij x 表 示弧(),i j 是否在起点与终点的路上,即:()()1,0,i j ij i j i j v v x i j v v ⎧⎪=⎨⎪⎩弧位于顶点至顶点的路上弧不在顶点至顶点的路上若i v 与j v 之间无直接相连的弧,但可以通过中间节点跳转,表明站点i 与j 之间不 可直达,但可通过转乘到达,则两点的转乘次数为经过的总弧数减一,即:(),m in1ij i j Ex ∈-∑二，行驶时间最短以第i 个站点到第j 个站点的时间为元素建立时间权值矩阵:()tij N NW t ⨯=则乘车总时间就为:(),ij ij i j Et x ∈∑由公汽换公汽的时间固定为5分钟,则换乘时间为:(),51ij i j E x ∈⎛⎫- ⎪ ⎪⎝⎭∑ 包含起始站等待时间3分钟的行驶总时间最短为:()(),,m in513ij ij ij i j E i j E t x x ∈∈⎛⎫+-+ ⎪ ⎪⎝⎭∑∑ 三，所需花费最少依题意,i j →的直达费用ij P 满足:[][][)2.51,52.06,91.510,47ij ij ij ij s P s s ⎧∈⎪⎪=∈⎨⎪∈⎪⎩得到行程费用最少为:().minij ij i j EP x ∈∑5.2.2确定约束条件 约束一,换乘次数的约束之前的分析中已经提到,应尽量减少换乘次数,但不同的乘客可能承受的换乘次数不同,所以我们用c （[)0,c ∈∞且为整数）表示乘客所能接受的最大换乘次数,得到换乘次数的约束为:(),1ij i j Ex c ∈-≤∑参数c 为人为设定值,分以下三种情况: 一，当0c =时,严格约束不能换乘;二，当c =∞时,无换乘次数约束,可无限换乘;三，当c 为不为0的常数q 时,约束换乘次数在q 次以内的情况.若单从模型的通用性考虑,c 可取到正无穷;若从实际情况出发,查询系统中c 应由查询者自行设定,当最小换乘次数小于ij b 时输出无解.约束二,最短路始末点的约束因为有向图G中,顶点分为了: 起点、中间点、终点,对于起点只有出的边而无入的边,对于中间点既有入的也有出的边,对于终点只有入的没有出的边.那么,用进入第j 个顶点的边ij x 和出第j 个顶点的边ji x 表示两顶点的最短路径中三类点的约束为:()()11,,110NNij jij j i j Ei j Ei x x i i ==∈∈⎧⎪-=-⎨⎪⎩∑∑为起点为终点为中间点综上所述,得到问题一的最优化模型:(),m in1ij i j Ex ∈-∑()(),,m in513ij ij ij i j E i j E t x x ∈∈⎛⎫+-+ ⎪ ⎪⎝⎭∑∑ ().minij ij i j EP x ∈∑()()()[][][)[){}(),11,,11102.51,5. 2.06,91.510,470,0,1,ij i j E N Nij ji j j i j E i j E ij ij ij ij ijx ci x x i i s s t P s s c x i j E ∈==∈∈⎧-≤⎪⎪⎧⎪⎪⎪-=-⎨⎪⎪⎪⎩⎪⎧∈⎪⎨⎪⎪⎪=∈⎨⎪⎪∈⎪⎪⎩⎪∈∞⎪⎪∈⎪⎪∈⎩∑∑∑为起点为终点为中间点,且为整数 5.3模型一的求解按照以上模型,利用以换乘次数最少为基本目标的逐步搜寻法,把问题一中的三对起始站→终到站输入算法程序（参见附录四）中,即得到基于最少换乘次数c 的选择方式的乘车路线.由于可行方案较多,为了得到最优可行方案,根据以下原则进行筛选:原则一,乘车费用和乘车耗时都大的先剔除; 原则二,三个目标都相同的方案任选其一,其他剔除. 按上诉原则进行筛选后,给出最佳选择方案如下:表5-2: 模型一的求解结果华穗路→交通大厦越秀桥→山村江南大道北→策边村换乘次数 111换乘方案 由408路转到1047路由184路转到893路由235路转到192路换乘站点 江南大道口 芳村隧道口 动物园 花费时间 116分钟 38分钟 140分钟 乘车费用3元3元3元5.4结果分析:通过上面的结果我们看出,题目所求的三对站点都无法直接到达,需要至少换乘一次才能到达,但考虑到多数人可能不会接受多次换乘,故在此以换乘次数最少为第一目标,得到三对站点的一次换乘结果.此结果中的一次换乘方案中华穗路→交通大厦需要的总时间为116分钟,江南大道北→策边村需要的总时间为140分钟,这两个时间都很长,所以在乘客希望更省时间的情况下,考虑两次的换乘可能更符合乘客要求.另外,在乘车费用的角度来讲,一次换乘是既可到达目的地又最省钱的,都只需3元.6．问题二的解答针对问题二我们在问题一模型的基础上建立了新的多目标优化模型,即模型二. 6.1模型的准备用模型一准备中相同的方法将公汽、地铁混合网络抽象成一个有向赋权图()'''',,G V E W = ,图中的含义同模型一.再用模型一准备中相同的方法确定最少换乘次数,得到含义与模型一相同的表达式,即:''1'1Nnn ij ikkj k A AA -==∑[){}''m in |0,1,0nij ijn A n i j b i j⎧≠∈∞≠⎪=⎨=⎪⎩''10B i j C i j ⎧-≠=⎨=⎩6.2模型二的建立6.2.1确定目标函数问题二是在亚运期间考虑地铁的情况下求交通困难的地区,考虑到亚运期间乘车免费,所以去掉费用的目标,以总的行驶时间最长和分别到达所有亚运场馆的总换乘次数最多为目标函数,即:一，分别到达所有亚运场馆的总换乘次数最多在此模型的准备中我们同样建立了公汽网的有向赋权图()'''',,G V E W = ,在此,我们同样引入0-1决策变量ij y 表示弧(),i j 是否在起点与终点的路上,即:()()1,0,i j ij i j i j v v y i j v v ⎧⎪=⎨⎪⎩弧位于顶点至顶点的路上弧不在顶点至顶点的路上同样得到两站点的最少换乘次数:()',m in1ij i j E y ∈-∑不同的是,我们需要给定六个亚运场馆（奥林匹克体育中心、体育中心、大学城体育中心、广州体育馆、黄埔体育馆、增城体育馆）作为终点站,以分别到达所有亚运场馆的总换乘次数最多为目标函数,即:()',m ax m in 1ik k Qi k E y ∈∈⎛⎫- ⎪ ⎪⎝⎭∑∑二，总的行驶时间最长先求到达每个亚运场管的最短时间.在问题一的目标二基础上,由于增加了地铁, 所以,换乘的时间上就有所改变,且给定了终点站k Q ∈.首先,在考虑地铁后,第i 个站点到第k 个站点的时间为元素建立时间权值矩阵:()''tik N NWt ⨯=得到总的乘车时间为:()'',0ik ik i k E T t y ∈=∑i k →始发的等待时间ik Z 满足:23ikZ ⎧=⎨⎩始发坐地铁的等待时间始发坐公汽的等待时间得到总的等待时间为:()',1ik ik i k E T Z y ∈=∑根据题目所给的两两间的换乘所步行的时间ik Y 知道,步行时间与换乘的交通工具是否相同有关,即:24ik Y ⎧=⎨⎩交通工具相同的换乘步行时间交通工具不同的换乘步行时间从上面知道,基础步行时间为2分钟,再加上不同交通工具间换乘多步行的2分钟.得到总的步行时间为:()()''2,,2212ik ik ik Z i k E i k E T y y =∈∈⎛⎫=-+⎪ ⎪⎝⎭∑∑综上所述,得到总的乘车时间最长的目标函数为:()maxmin 012k QT T T ∈++∑5.2.2确定约束条件问题分析中已经知道,本问的约束条件基本不变,即:()',1ik i k E y c ∈-≤∑()()11,,110N Nik kik k i k E i k Ei y y i i ==∈∈⎧⎪-=-⎨⎪⎩∑∑为起点为终点为中间点综上所述,得到问题二的最优化模型:()',m ax m in 1ik k Q i k E y ∈∈⎛⎫- ⎪ ⎪⎝⎭∑∑()maxmin 012k QT T T ∈++∑()()()[][][)()()()(){}{}''''',11,,',,2,,11102.51,52.06,91.510,470.122122,32,4ik ik i k E NNik ki k k i k E i k Eik ik ik ik ik iki k E ik ik i k E ik ikZ i k E i k E ik ik y ci y y i i s P s s T t y s t T Z yT y y Z Y k Q c ∈==∈∈∈∈=∈∈-≤⎧⎪-=-⎨⎪⎩⎧∈⎪=∈⎨⎪∈⎩==⎛⎫=-+ ⎪ ⎪⎝⎭∈∈∈∑∑∑∑∑∑∑为起点为终点为中间点[){}()0,0,1,ik y i k E⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪∈∞⎪∈⎪⎪∈⎩,且为整数6.3模型二的求解 6.4结果分析:7．问题三的解答针对问题三我们建立了新的收益最大的规划模型,即模型三.7.1模型三的建立 7.1.1确定目标函数在问题二的基础上,考虑专线设置的总路程最短即耗时最少作为线路设置指标,可直接将问题二的模型改成总时间最少的单目标,即:()min 012T T T ++7.1.2确定约束条件因为限定了四条可求的拟建专线,则它们的起点站终点站都以确定,它们的编号分别为117,2142,2498,2919,则:{},117,2142,2498,2919i j ∈7.1.3综上所述,得到问题三的单目标优化模型:()min 012T T T ++()()()[][][)()()()(){}{}''''',11,,',,2,,11102.51,52.06,91.510,470.122122,32,4,ij ij i j E NNij jij j i j E i j Eij ij ij ij ij ij i j E ij iji j E ij ij Z i j E i j E ij ij y c i y y i i s P s s T t y s t T Z y T y y Z Y i ∈==∈∈∈∈=∈∈-≤⎧⎪-=-⎨⎪⎩⎧∈⎪⎪=∈⎨⎪∈⎪⎩==⎛⎫=-+ ⎪ ⎪⎝⎭∈∈∑∑∑∑∑∑∑为起点为终点为中间点{}[){}()117,2142,2498,29190,0,1,ij j c y i j E⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪∈⎪⎪∈∞⎪⎪∈⎪∈⎪⎩,且为整数7.2模型三的求解 7.3结果分析:8．问题四的解答针对问题四我们建立了一个经过此站点的线路数最少的整数规划模型,即模型四. 8.1模型四的建立引进0-1变量ij μ,且'i V ∈10ij i j i j μ⎧⎨⎩站点在线路上站点不在线路上以经过站点的线路数最少为目标函数,即:11001m inijj μ=∑综上所述,得到问题四的模型:11001m inijj μ=∑{}'0,1.ij s t i Vμ⎧∈⎪⎨∈⎪⎩ 8.2模型四的求解根据建立的整数规划模型,编写相应的MATLAB 程序（源程序参见附录五）,求得交通困难的站点（具体结果见附录五）.8.3结果分析:9. 模型的评价9.1模型优点:优点一: 问题一中我们综合考虑了转车次数、乘车费用、乘车时间建立了多目标的快速公交模型,能提供多种可行方案同时给出推荐比较好的乘车方案,可以更好满足人们乘车需要.优点二: 在问题一的基础上将地铁线路加入到乘车网络当中在模型一的情况下很容易就能查找相关乘车方案,再去讨论后面的问题,模型简单且容易求解.优点三: 在对题目复杂数据的处理方面,我们先将个站点进行编号,同时巧妙处理环路和非环路的两种情况,有利于模型的建立和求解.优点四: 在考虑亚运会开幕前和亚运会期间的问题时以亚运场馆为基准点向周围搜索,方向比较明确,使模型更为简单.9.2模型缺点缺点一: 建立的模型在综合考虑各方面的因素时,查询算法不够高高效,程序运行时间比较长.缺点二: 在考虑交通困难等方面的问题时,没有结合各站点人流量等实际情况综合各方面因素考虑交通的困难程度.10. 模型的改进及推广10.1模型改进改进一: 定义新的直达矩阵,建立一种基于矩阵运算的高效公交查询算法.改进二: 交通困难并不仅仅是有些地区线路上无法到达目的地还应包括部分地区经过的车次比较多造成交通比较拥挤的情况,我们应该建立综合考虑二者的数学模型.改进三: 通过实地调研广州市各站点人流量的情况,对模型进行改进.10.2模型推广本文所建立的公交查询模型能很快的查得广州市各地区的乘车方案,能很好的满足广大广州市民的生活需求,同时建立了评判交通困难的模型,以及给出了减小交通困难的具体解决办法.这也可以应用于其它城市公交线路的查询和公交线路的优化以及对城市的交通作出合理的指导.参考文献[1] 宋来忠,王志明,《数学建模与实验》,北京:科学出版社,2005.[2] 运筹学教材编写组编,《运筹学(3版)》,北京:清华大学出版社,2005.6[3] 张志涌,杨祖缨,《matlab教程R2011a》,北京:航空航天大学出版社,2011.7附录附录一: 题目所给附录一说明（略）附录二: 题目所给附录二线路（略）附录三: 数据分析整理三的MATLAB源程序clcclearload path[a,data]=xlsread('data.xls');b=path;station=unique(data);station(1)=[];[n1,n2]=size(b);C=zeros(1108,1);for i=1:1108C(i)= sum((b(i,:)~=0)) ;enddisp('票价2.5')ind=find(C<6&C>2)C(ind)n1=length(ind)disp('票价2.0')ind1=find(C<10&C>=6)C(ind1)n2=length(ind1)disp('票价1.5')ind2=find(C<48&C>=10)C(ind2)n3=length(ind2)disp('票价3')ind3=find(C>=48)C(ind3)n4=length(ind3)n=max(C);D=zeros(n-1,1);for i=2:nD(i-1,1)=length(find(C==i));endx=[2:n];plot(x,D','-*b')grid on,axis equalaxis([2,55,0,61])xlabel('线路站点数目'),ylabel('线路条数') 运行结果:'上下九步行街''东乡村口''东环路(东怡新村)''东风中学''东风小学''中医院东''中医院东门''中央酒店''乐捷图广场''五''仁济西路''傍东村''傍江东坊''光属纤维厂''勒竹新村''勒竹村''北斗星''北村路''区星海青少年宫(城北公园)总站''华南工商学院''华工大牌坊''南华东路''南华广场新世纪东''南浦中路''南浦大桥北''南浦大桥南''名雅公司''塘埗西''多宝路(市二医院)''大学城中部枢纽（共54站）''大新路''大石桥底''大龙桥''天成路''姬棠商业街''富华市场〔下行〕''小北花圈仓边路''岐东酒家''市桥镇政府''市第二少年宫' '新桥车站''旧机场北门''星海青少年宫(城北公园)总站' '春晖园''朱村一条街''杨巷''松岗政府''林乐路''林乐路站''横枝岗路北''水荫二横路口''汉基工业区''沙头市场''沙涌亭''沙湾文化中心''沙溪(丽江明珠歌剧院)''洛城中学''洲装饰材料城''海珠保华广场''海珠南路''清湖路口''湖天货运''潭村''环窖旧桥头''珀丽酒店大酒店''珠光路''瑞丽花园''白云货运站''白蟮塘''白鳝塘''省妇幼站''石基村总站''石基牌坊''石牌西''祈福新村路口''窖心工业区''窖心村口''笔岗村委''红场路口''花园酒店④''广东大厦''广东工大北门''广东药学院从化分院''广园客运''广州大厦''广州大道南''广州奥林匹克花园(洛溪新城)' '广源购物中心''广花三站''应元路口''康泰园''惠福西路''成人教育出版社''执信南路''文化公园北门''文昌南路(南方名酒中心)''新华收费站''新厅街''新桥东坊' '萝岗路口''西环路''诗书路''轻工中专''金沙洲大道西''金湾生活区''铸管场''长沙路口''陵园西路''集贤北''集贤庄''青新港码头''面粉厂''骏丰鞋厂''骏景花园(骏景花园门口旁候车亭)' '骏逸苑''黄埔双岗''龙洞林场''龙湖鱼村''。

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人（包括指导教师）研究、讨论与赛题有关的问题。

我们知道，抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。

我们郑重承诺，严格遵守竞赛规则，以保证竞赛的公正、公平性。

如有违反竞赛规则的行为，我们将受到严肃处理。

我们参赛选择的题号是（从A/B/C/D中选择一项填写）： B我们的参赛报名号为（如果赛区设置报名号的话）：所属学校（请填写完整的全名）：重庆大学参赛队员(打印并签名) ：1. 熊国刚2. 王杰3. 黎明指导教师或指导教师组负责人(打印并签名)：龚劬日期： 2007年 9 月 21 日赛区评阅编号（由赛区组委会评阅前进行编号）：编号专用页赛区评阅编号（由赛区组委会评阅前进行编号）：全国统一编号（由赛区组委会送交全国前编号）：全国评阅编号（由全国组委会评阅前进行编号）：乘公交，看奥运【摘要】本文要解决的问题是以即将举行的08年北京奥运会为背景而提出的。

人们为了能现场观看奥运会，必然会面对出行方式与路线选择的问题。

因此如何快速、高效地从众多可行路线中选出最优路线成为了解决此问题的关键。

鉴于公交系统网络的复杂性，我们没有采用常规的Dijkstra算法，而采用了高效的广度优先算法。

其基本思想是从经过起（始）点的路线出发，搜寻出转乘次数不超过两次的可行路线，然后对可行解进行进一步处理。

为满足不同查询者要求，我们对三个问题都分别建立了以时间、转乘次数、费用最小为目标的优化模型。

针对问题一（只考虑公汽系统），我们建立了模型一并通过VC++编程得到了任意两个站点间的多种最优路线，并得出所求站点间最优路线的最优值，如下进里又建立了图论模型。

本文的主要特点在于，所用算法的效率十分显著。

乘公交，看奥运刘其峰，罗礼全，颜焱指导教师： 朱伟摘要：这是一个最优路径选择问题。

在路径选择上我们采用遍历法，找出可能的从路径源到目的地的路径，并根据用户的实际需求（时间最短，费用最少，最方便）作为约束条件进行优化选择，最终得到符合每个客户需求的路径选择方案。

在问题一中只有汽车这种工具可供选择。

问题二在问题一的基础上加入地铁系统，地铁系统和公交系统的信息存在差异性，找出两个系统相关信息的共同点并把这两个系统相关信息整合到一起是求解的关键。

问题三是一个开放性的问题，约束条件少，灵活程度大，我们以现实生活中的实际情况为根据，在建模过程中我们定义了代价P 。

根据P 的定义式计算出从起点到终点全部乘车和步行1站，步行2站……步行全程的所有代价，P 值最小的方案就是最终结果。

关键词：最少换乘；最少时间；最少花费；公交网络；出行路径选择模型；代价1 符号说明i T ：乘汽车、地铁、走路和交通工具转换所花费的时间 (1,2,3,4)i =；i C ：乘汽车和地铁所花的费用(1,2)i =；G ：北京市公共汽车交通图；V ：图G 的所有站点集合；E ：图G 的所有公汽线路集合；P ：代价；L ：公交线路信息矩阵。

2 模型假设1.任意的相邻站点之间的行车时间和步行时间是相同的为一定值2．任意一条公交线路的运力都是足够的，不会出现没有座位的情况3.票价一定，不会变更4.同一地铁站对应的任意两个公共汽车站之间可通过地铁站换乘（无需支付地铁费）5.任意两个站点之间都可以通过有限次的车辆换乘达到对方6.地铁换乘地铁无需支付费用7.地铁1T 为往返线路3 模型的建立通过南京、苏州、广州等城市对居民的公交出行心理问询调查，公交乘客选择出行路径的决策过程主要受到3个因素的作用：换乘次数、所花费用和出行耗时。

本文根据这三个因素，确定查询者的不同需求有三种：第一种情况是最普遍的一种情况，那就是尽量出行方便，少换车；第二种是所花的费用最少；最后一种是所花费的时间最短（路程最短）。