高中数学苏教版必修一函数的表示方法(一)

江苏省泰兴中学高一数学教学案(15)必修1_02 函数 函数的表示方法（1）班级 姓名目标要求1． 了解函数的三种表示法，以及三种表示法的内在联系；2． 根据具体问题的特点，选用恰当的方法表示函数关系．重点难点重点：函数的表示法；难点：解析法与图象法的联系与转化．课前预习1、回顾初中学过的函数及其表示方法2、函数表示方法列表法：用 来表示两个变量之间函数关系的方法。

解析法：用 来表示两个变量之间函数关系的方法。

图像法：用 来表示两个变量之间函数关系的方法。

3、分段函数在定义域内不同部分上，有不同的 ，像这样的函数通常叫做分段函数。

课堂互动例1 购买某种饮料x 听，所需钱数为y 元，若每听2元，试分别用解析法、列表法、图象法将y 表示成x ({1,2,3,4})x 的函数，并指出该函数的值域．例2 某市出租汽车收费标准如下：在km 3以内（含km 3）路程按起步价7元收费，超过km 3以外的路程按2.4元km /收费，试写出收费额关于路程的函数的解析式．回顾小结：分段函数（1） 概念：（2） 理解：例3 （1）已知⎩⎨⎧<-≥=-=)0.(1)0.()(,12)(2x x x x g x x f ，求[][])(,)(x f g x g f ．例4 如图AOB ∆是边长为2的正三角形，这个三角形在直线t x =左侧部分的面积为y,求函数)(t f y =的解析式，并画出)(t f y =的图象.例5 作出函数)1(|2|-+=x x y 的图象，并求函数的定义域与值域．课堂练习１、下列各个图形中，表示函数关系()y f x =的图象的有（１）（２） （３）（４）2、设(),f x π=则2()f x =____________3、1 n mile （海里） 约合1852m ，根据这一关系，写出米数y 关于海里数x 的函数解析式．4、用长为30 cm 的铁丝围成矩形，试将矩形面积Ｓ（cm 2）表示成矩形一边长x （cm ）的函数，并画出函数的图象．5、在学校的洗衣店中，每洗一次衣服（4.5千克以内）需要付费4元，如果在这家洗衣店洗衣10次，则其后可以免费洗一次(1)根据题意填写下表：(2)问：＂费用c是次数n的函数＂还是＂次数n是费用c的函数＂？(3)写出当n 15时函数的解析式．学习反思1、函数关系的表示方法主要有．2、函数的解析式从＂数＂的层面表示了函数关系；而函数的图象从＂形＂的层面表示了函数关系，它们各有特点，要善于＂取长补短＂；3、分段函数在不同的定义域内各有不同的对应关系，因而分段函数的处理常需要分类讨论，再整合出相应的结论．江苏省泰兴中学高一数学作业(15)班级 姓名 得分1、函数()y f x =的图象与直线()x a a R =∈的交点个数是 （ ）A ．至少一个B ．至多一个C ．有且仅有一个D ．一个或两个以上2、物体从静止开始下落，下落的距离与下落时间的平方成正比。

2.1.2 函数的表示方法（1）教学目标：1．进一步理解函数的概念，了解函数表示的多样性，能熟练掌握函数的三种不同的表示方法；2．在理解掌握函数的三种表示方法基础上，了解函数不同表示法的优缺点，针对具体问题能合理地选择表示方法；3．通过教学，培养学生重要的数学思想方法——分类思想方法．教学重点：函数的表示． 教学难点：针对具体问题合理选择表示方法．教学过程：一、问题情境 1． 情境．下表的对应关系能否表示一个函数：2．问题．如何表示一个函数呢？ 二、学生活动1．阅读课本掌握函数的三种常用表示方法； 2．比较三种表示法之间的优缺点． 3．完成练习 三、数学建构 1．函数的表示方法： 2．三种不同方法的优缺点： 列表法—用列表来表示两个变量之间函数关系的方法 解析法—用等式来表示两个变量之间函数关系的方法 图象法—用图象来表示两个变量之间函数关系的方法3．三种不同方法的相互转化：能用解析式表示的，一般都能列出符合条件的表、画出符合条件的图，反之亦然；列表法也能通过图形来表示．四、数学运用（一）例题例1 购买某种饮料x听，所需钱数为y元．若每听2元，试分别用解析法、列表法、图象法将y表示成x(x∈{1，2，3，4})的函数，并指出该函数的值域．跟踪练习：某公司将进货单价为8元一个的商品按10元一个销售，每天可卖出100个，若这种商品的销售价每个上涨1元，则销售量就减少10个．（1）列表：（2）图象：（3）解析式：将条件变换成：“某公司将进货单价为8元一个的商品按10元一个销售，每天可卖出110个”例2 如图，是一个二次函数的图象的一部分，试根据图象中的有关数据，求出函数f(x)的解析式及其定义域．（二）练习：1．1 nmile(海里)约为1854m，根据这一关系，写出米数y关于海里数x的函数解析式．2．用长为30cm的铁丝围成矩形，试将矩形的面积S(cm2)表示为矩形一边长x(cm)的函数，并画出函数的图象．3．已知f(x)是一次函数，且图象经过(1，0)和(－2，3)两点，求f(x)的解析式．4．已知f(x)是一次函数，且f(f(x))＝9x－4，求f(x)的解析式．五、回顾小结1．函数表示的多样性；2．函数不同表示方法之间的联系性；3．待定系数法求函数的解析式．六、作业课堂作业：课本35页习题1，4，5．。

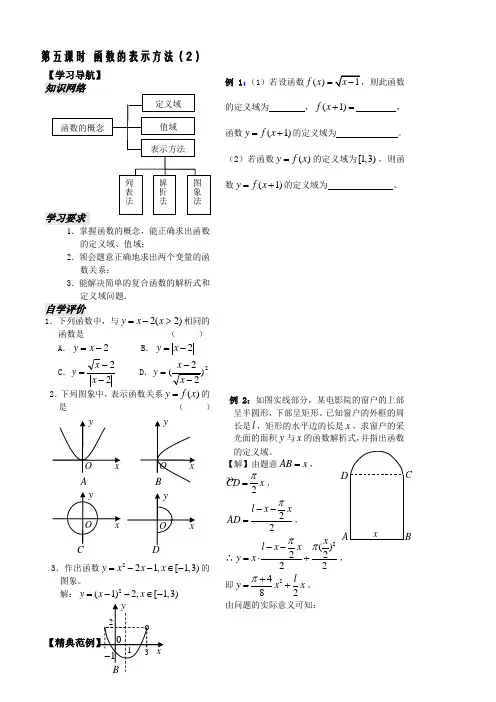
第五课时 函数的表示方法（2）1．掌握函数的概念，能正确求出函数的定义域、值域；2．领会题意正确地求出两个变量的函数关系；3．能解决简单的复合函数的解析式和定义域问题．自学评价1．下列函数中，与2(2)y x x =->相同的函数是 （ ） A ．2-=x y B ．2-=x y C ．22--=x x y D ．2)22(--=x x y 2．下列图象中，表示函数关系()y f x =的是 （ ）3．作出函数221,[1,3)y x x x =--∈-的图象。

解：2(1)2,[1,3)y x x =--∈-例1：（1）若设函数()f x =的定义域为 ，(1)f x += ，函数(1)y f x =+的定义域为 。

（2）若函数()y f x =的定义域为[1,3)，则函数(1)y f x =+的定义域为 。

例2：如图实线部分，某电影院的窗户的上部呈半圆形，下部呈矩形。

已知窗户的外框的周长是l ，矩形的水平边的长是x ，求窗户的采光面的面积y 与x 的函数解析式，并指出函数的定义域。

【解】由题意AB x =，»2CDx π=， 22l x xAD π--=，∴2()2222x l x x y x ππ--=⋅+， 即2482ly x x π+=+。

由问题的实际意义可知：AABCD x0202x l x xπ>⎧⎪⎪⎨--⎪>⎪⎩，解得202l x π<<+。

所以，y 与x 的函数解析式是2482ly x x π+=+，函数的定义域是2(0,)2l π+。

例3．若函数27()43kx f x kx kx +=++的定义域为R ，求实数k 的取值范围．追踪训练一1．函数()f x =的定义域为 （ ） ()A [1,1]- ()B (,1][1,)-∞-+∞U ()C [0,1] ()D {1,1}- 2．动点P 从边长为1的正方形ABCD 的顶点A 出发，顺次经过B 、C 、D 再回到A ，设x 表示点P 的行程，y 表示线段PA 的长，求y 关于x 的函数解析式。

一、复习引入1、复习函数的有关概念及性质2、函数的三种表示方法 （1）列表法（2）解析法（3）图象法（4）三种表示方法各自特点3、分段函数二、例题分析例1、设购买某种饮料x 听，所需钱数为y 元。

若每听2元，试分别用解析法、列表法、图象法将y 表示成x })4,3,2,1{(∈x 的函数，并指出该函数的值域。

例2、设)(x f 是定义在R 上的函数，且1)32(2-+=-x x x f 。

求)(x f 的解析式。

例3、已知)(x f 是一次函数，且[]14)(-=x x f f ，求)(x f 的解析式。

例4、定义在闭区间[]2,1-上的函数)(x f 的图象如图所示，求此函数的解析式、定义域、值域及1()4f ，1()8f -，))41((f f三、随堂练习1、画出函数3)(+=x x f 的图象。

2、用长cm 30为的铁丝围成矩形，试将矩形面积)(2cm S 表示为矩形一边长)(cm x 的函数，并画出函数的图象。

3、某人去公园玩，先步行、后骑自行车，如果S 表示该人离公园的距离，t 表示出发后的时间，则下列图象中符合此人走法的是 。

（1） （2） （3） （4） 4、设函数x x f 31)(-=，它的值域为{}4,3,1,1,2--，求此函数的定义域。

5、已知一次函数)(x f 满足34))((+=x x f f ，求)(x f 。

四、回顾小结1、重点掌握函数的解析方法；2、会用待定系数法、换元法等求函数的解析式；3、分段函数及其简单应用。

课后作业班级：高一（ ）班 姓名__________一、基础题1、若函数52)(+=x x f ，则)(2x f = 。

2、已知1)(2+=x x f ，则=+)1(x f ，=))((x f f 。

3、若函数⎩⎨⎧-+=xx y 212 )0()0(>≤x x 则)3(-f 的值为 。

4、若函数212x y x ⎧+=⎨⎩)0()0(>≤x x 则使函数值为10的x 的集合为 。