下载文档原格式
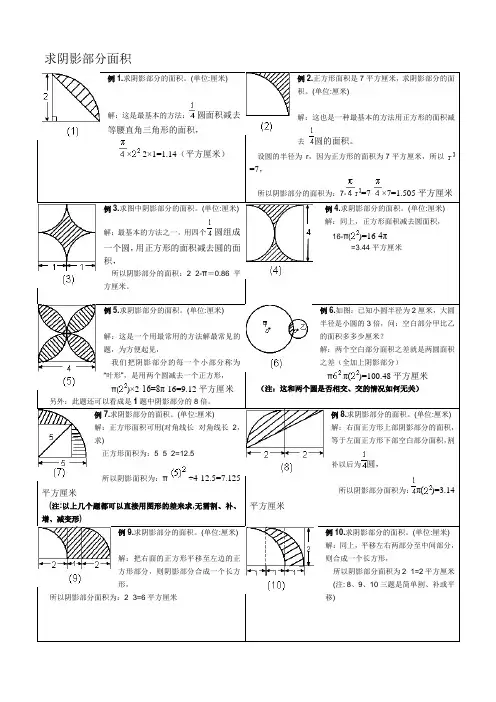
求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解：这是最基本的方法：圆面积减去等腰直角三角形的面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。
(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解：最基本的方法之一。
用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例 5.求阴影部分的面积。
(单位:厘米)解：这是一个用最常用的方法解最常见的题，为方便起见，我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形，π()×2-16=8π-16=9.12平方厘米另外：此题还可以看成是1题中阴影部分的8倍。
例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π()=100.48平方厘米（注：这和两个圆是否相交、交的情况如何无关）例7. 求阴影部分的面积。
(单位:厘米)解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5所以阴影面积为：π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
(单位:厘米)解：右面正方形上部阴影部分的面积，等于左面正方形下部空白部分面积，割补以后为圆，所以阴影部分面积为：π()=3.14平方厘米例9.求阴影部分的面积。
求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解：这是最基本的方法：圆面积减去等腰直角三角形的面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。
(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解：最基本的方法之一。
用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解：这是一个用最常用的方法解最常见的题，为方便起见，我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形，π()×2-16=8π-16=9.12平方厘米另外：此题还可以看成是1题中阴影部分的8倍。
例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π()=100.48平方厘米（注：这和两个圆是否相交、交的情况如何无关）例7.求阴影部分的面积。
(单位:厘米)解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5所以阴影面积为：π÷4-12.5=7.125平方厘米例8.求阴影部分的面积。
(单位:厘米) 解：右面正方形上部阴影部分的面积，等于左面正方形下部空白部分面积，割补以后为圆，(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形) 所以阴影部分面积为：π()=3.14平方厘米例9.求阴影部分的面积。
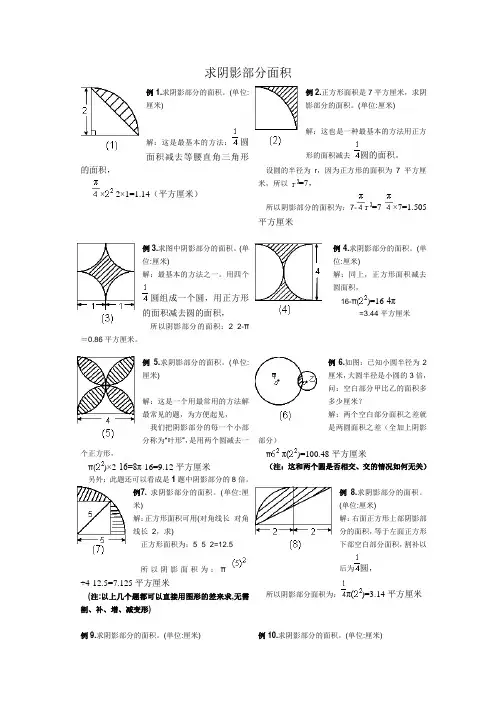
例1.求阴影部分的面积。
(单位:厘米)解：这是最基本的方法：圆面积减去等腰直角三角形的面积，×-2×1=（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。
(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解：最基本的方法之一。
用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=平方厘米例5.求阴影部分的面积。
(单位:厘米)解：这是一个用最常用的方法解最常见的题，为方便起见，我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形，π()×2-16=8π-16=平方厘米另外：此题还可以看成是1题中阴影部分的8倍。
例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π()=平方厘米（注：这和两个圆是否相交、交的情况如何无关）例7.求阴影部分的面积。
(单位:厘米)解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=所以阴影面积为：π÷=平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
(单位:厘米)解：右面正方形上部阴影部分的面积，等于左面正方形下部空白部分面积，割补以后为圆，所以阴影部分面积为：π()=平方厘米例9.求阴影部分的面积。
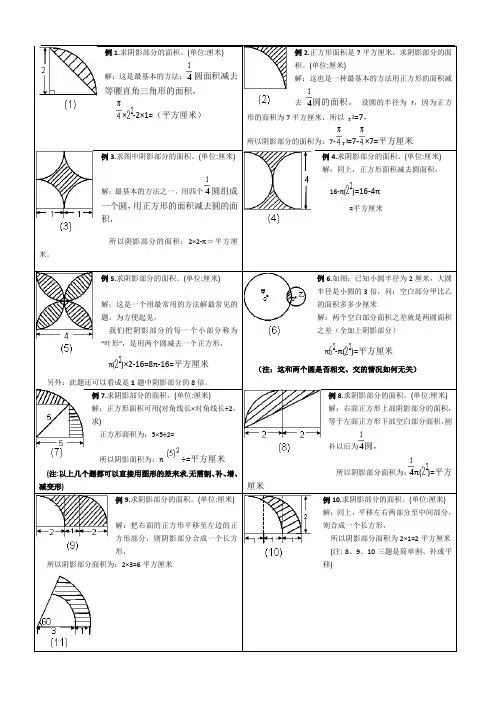
(单位:厘米)解：把右面的正方形平移至左边的正方形部分，则阴影部分合成一个长方形，所以阴影部分面积为：2×3=6平方厘米例10.求阴影部分的面积。
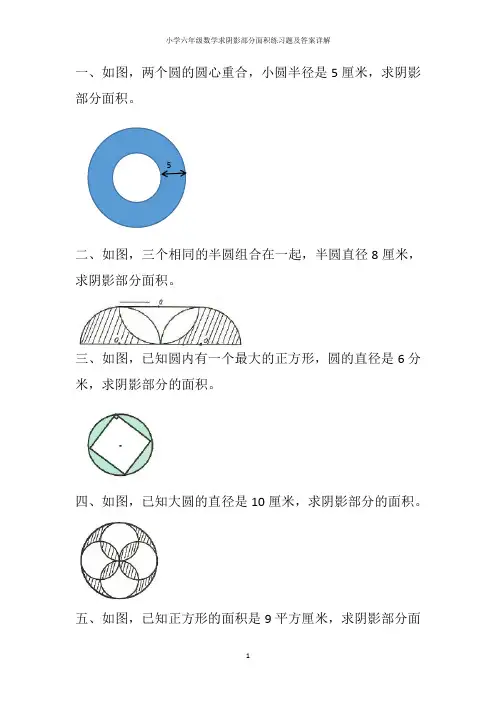
一、如图，两个圆的圆心重合，小圆半径是5厘米，求阴影部分面积。
5二、如图，三个相同的半圆组合在一起，半圆直径8厘米，求阴影部分面积。
三、如图，已知圆内有一个最大的正方形，圆的直径是6分米，求阴影部分的面积。
四、如图，已知大圆的直径是10厘米，求阴影部分的面积。
五、如图，已知正方形的面积是9平方厘米，求阴影部分面六、如图，已知正方形的边长是8厘米，正方形内有四个相同的半圆相交于正方形中心，求阴影部分面积。
七、如图，两个直径为10厘米的半圆，求阴影部分面积。
八、如图，半圆直径是8厘米，求阴影部分面积。
九、如图，已知正方形的边长为6分米，AB长10分米，求阴影部分的面积。
十、如图，两个完全一样的梯形重叠放置，求阴影部分的面十一、如图，在梯形内有四个以梯形顶点为圆心3厘米为半径的扇形，求阴影部分的面积。
十二、如图，求阴影部分的面积。
十三、如图，由三个相同的圆组成的图形，圆的半径是2厘米，求阴影部分的面积。
参考答案一、πr2是圆的面积公式，图中阴影部分是圆环，所以不能直接用公式计算。
图中阴影部分面积等于大圆的面积减去小圆的面积，3.14×（5+5）2－3.14×52=235.5（平方厘米）。
二、画辅助线，如图，用割补法将2区域补到1位置，则右边半圆内的阴影面积就变成了一个三角形的面积；左边同理。
所以，阴影面积相当于两个三角形的面积，即：8×（8÷2）÷2×2=32（平方厘米）。
三、阴影面积等于圆的面积减去正方形的面积，正方形面积公式是边长乘边长，而这个正方形的边长未知；正方形的面积还可以用对角线的乘积除以2，所以，阴影部分的面积是：3.14×（6÷2）2－6×6÷2=10.26（平方分米）。
四、画辅助线，如图，用割补法，将阴影1补到空白3位置，将阴影2补到空白4位置，其它三个小正方形也如此割补，所以，阴影的面积等于大圆的面积减去大正方形的面积（对角线乘积除以2），即3.14×（10÷2）2－10×10÷2=28.5（平方厘米）。
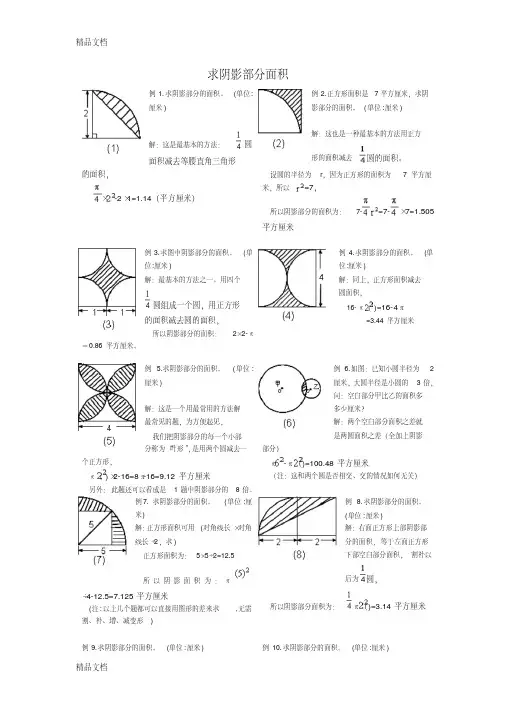
求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解：这是最基本的方法：圆面积减去等腰直角三角形的面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。
(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解：最基本的方法之一。
用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解：同上，正方形面积减去圆面积，16-π（)=16-4π=3.44平方厘米例 5.求阴影部分的面积。
(单位:厘米)解：这是一个用最常用的方法解最常见的题，为方便起见，我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形，π（)×2-16=8π-16=9.12平方厘米另外：此题还可以看成是1题中阴影部分的8倍。
例 6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π（)=100.48平方厘米（注：这和两个圆是否相交、交的情况如何无关）例7.求阴影部分的面积。
(单位:厘米)解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5所以阴影面积为：π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
(单位:厘米)解：右面正方形上部阴影部分的面积，等于左面正方形下部空白部分面积，割补以后为圆，所以阴影部分面积为：π（)=3.14平方厘米例9.求阴影部分的面积。
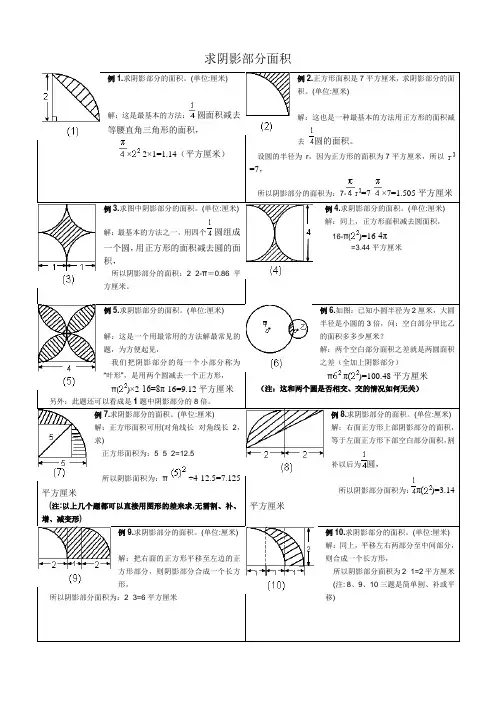
求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解：这是最基本的方法：?圆面积减去等腰直角三角形的面积，?×例2.正方形面积是7平方厘米，求阴影部分的面积。
(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：例3.求图中阴影部分的面积。
(单位:厘米)解：最基本的方法之一。
用四个?圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解：这是一个用最常用的方法解最常见的题，为方便起见，我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形，π()×2-16=8π-16=9.12平方厘米另外：此题还可以看成是1题中阴影部分的8倍。
例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π()=100. 48平方厘米?（注：这和两个圆是否相交、交的情况如何无关）例7.求阴影部分的面积。
(单位:厘米)解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5所以阴影面积为：π÷4-1 2.5=7.125平方厘米?(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
(单位:厘米)解：右面正方形上部阴影部分的面积，等于左面正方形下部空白部分面积，割补以后为圆，所以阴影部分面积为：π()=3.14平方厘米例9.求阴影部分的面积。
(单位:厘米)解：把右面的正方形平移至左边的正方形部分，则阴影部分合成一个长方形，所以阴影部分面积为：2×3=6平方厘米例10.求阴影部分的面积。
求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解：这是最基本的方法：圆面积减去等腰直角三角形的面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。
(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解：最基本的方法之一。
用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解：同上，正方形面积减去圆面积，16-π（)=16-4π=3.44平方厘米例 5.求阴影部分的面积。
(单位:厘米)解：这是一个用最常用的方法解最常见的题，为方便起见，我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形，π（)×2-16=8π-16=9.12平方厘米另外：此题还可以看成是1题中阴影部分的8倍。
例 6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π（)=100.48平方厘米（注：这和两个圆是否相交、交的情况如何无关）例7.求阴影部分的面积。
(单位:厘米)解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5所以阴影面积为：π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
(单位:厘米)解：右面正方形上部阴影部分的面积，等于左面正方形下部空白部分面积，割补以后为圆，所以阴影部分面积为：π（)=3.14平方厘米例9.求阴影部分的面积。
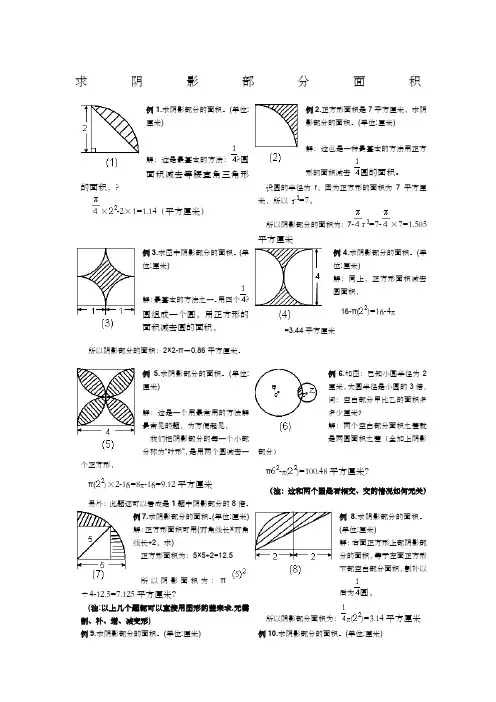
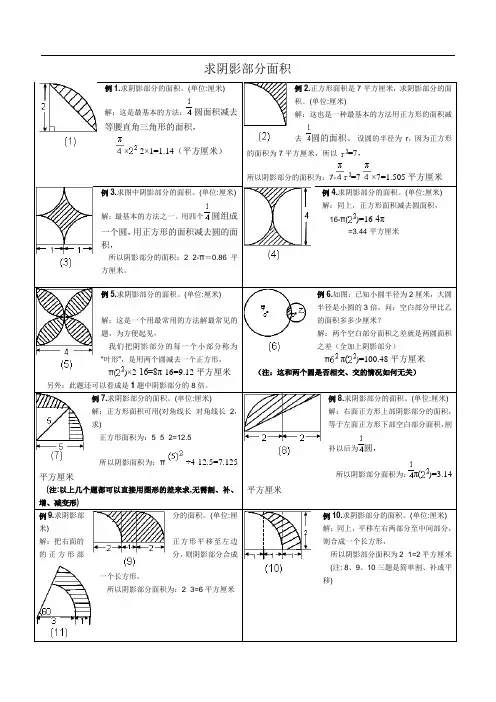
求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解：这是最基本的方法：?圆面积减去等腰直角三角形的面积，?×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。
(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为 r ，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解：最基本的方法之一。
用四个?圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解：同上，正方形面积减去圆面积， 16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解：这是一个用最常用的方法解最常见的题，为方便起见， 我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形， π()×2-16=8π-16=9.12平方厘米另外：此题还可以看成是1题中阴影部分的8倍。
例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分） π-π()=100.48平方厘米?（注：这和两个圆是否相交、交的情况如何无关）例7.求阴影部分的面积。
(单位:厘米) 解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5 所以阴影面积为：π÷4-12.5=7.125平方厘米?(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
(单位:厘米)解：右面正方形上部阴影部分的面积，等于左面正方形下部空白部分面积，割补以后为圆，所以阴影部分面积为：π()=3.14平方厘米例9.求阴影部分的面积。
百度文库
10、已知四边形是一个正方形，空白三角形的面积是56平方厘米，ED长是7厘米，求阴影部分面积。
11、右图中大平行四边形的面积是48平方厘米，A、B是上下两边的中点，你能求出图中小平行四边形（阴影部分）的面积吗？
A
B
12、右图，D、E分别是BC 、AD的中点，如果△ABC的面积为1平方分米，则
△AEC的面积是多少平方分米？（请简要写出理由）
13、求阴影部分的面积。
（单位：米）
14、如图，已知四边形ABCD是正方形，边长为5厘米，三角形ECF的面积比三角形ADF的面积大5平方厘米，求线段CE的
长。
15
152个圆形的瓶盖，材料的利用率是多少？
8厘
米
16、如图，已知小正方形的面积是16平方厘米，求圆的面积是多少？。
