连续分布的电荷元电场强度的计算

电场强度的几种求法一．公式法1．qF E =是电场强度的定义式：适用于任何电场，电场中某点的场强是确定值，其大小和方向与试探电荷无关，试探电荷q 充当“测量工具”的作用。

2．2r k Q E =是真空中点电荷电场强度的决定式，E 由场源电荷Q 和某点到场源电荷的距离r 决定。

3．dU E =是场强与电势差的关系式，只适用于匀强电场，注意式中的d 为两点间的距离在场强方向的投影。

二．对称叠加法当空间的电场由几个点电荷共同激发的时候，空间某点的电场强度等于每个点电荷单独存在时所激发的电场在该点的场强的矢量和，其合成遵守矢量合成的平行四边形定则。

例：如图，带电量为+q 的点电荷与均匀带电。

例：如图，带电量为+q 的点电荷与均匀带电薄板相距为2d ，点电荷到带电薄板的垂线通过板的几何中心，如图中a 点处的场强为零，求图中b 点处的场强多大例：一均匀带负电的半球壳，球心为O 点，AB 为其对称轴，平面L 垂直AB 把半球壳一分为二，L 与AB 相交于M 点，对称轴AB 上的N 点和M 点关于O 点对称。

已知一均匀带电球壳内部任一点的电场强度为零，点电荷q 在距离其为r 处的电势为r qk =ϕ。

假设左侧部分在M 点的电场强度为E 1，电势为1ϕ；右侧部分在M 点的电场强度为E 2，电势为2ϕ；整个半球壳在M 点的电场强度为E 3，在N 点的电场强度为E 4，下列说法中正确的是（ ）A ．若左右两部分的表面积相等，有E 1＞E 2，1ϕ＞2ϕB ．若左右两部分的表面积相等，有E 1＜E 2，1ϕ＜2ϕC ．只有左右两部分的表面积相等，才有E 1＞E 2，E 3=E 4D ．不论左右两部分的表面积是否相等，总有E 1＞E 2，E 3=E 4答案：D例：ab 是长为L 的均匀带电细杆，P1、P2是位于ab 所在直线上的两点，位置如图所示．ab 上电荷产生的静电场在P1处的场强大小为E 1，在P2处的场强大小为E2。

电场强度的几种求法一． 公式法1．qFE =是电场强度的定义式：适用于任何电场，电场中某点的场强是确定值，其大小和方向与试探电荷无关，试探电荷q 充当“测量工具”的作用 2．2rk QE =是真空中点电荷电场强度的决定式，E 由场源电荷Q 和某点到场源电荷的距离r 决定。

3．dUE =是场强与电势差的关系式，只适用于匀强电场，注意式中的d 为两点间的距离在场强方向的投影。

二．对称叠加法当空间的电场由几个点电荷共同激发的时候，空间某点的电场强度等于每个点电荷单独存在时所激发的电场在该点的场强的矢量和，其合成遵守矢量合成的平行四边形定则。

例：如图，带电量为+q 的点电荷与均匀带电。

例：如图，带电量为+q 的点电荷与均匀带电薄板相距为2d ，点电荷到带电薄板的垂线通过板的几何中心，如图中a 点处的场强为零，求图中b 点处的场强多大？例：一均匀带负电的半球壳，球心为O 点，AB 为其对称轴，平面L 垂直AB 把半球壳一分为二，L 与AB 相交于M 点，对称轴AB 上的N 点和M 点关于O 点对称。

已知一均匀带电球壳内部任一点的电场强度为零，点电荷q 在距离其为r 处的电势为rqk=ϕ。

假设左侧部分在M 点的电场强度为E 1，电势为1ϕ；右侧部分在M 点的电场强度为E 2，电势为2ϕ；整个半球壳在M 点的电场强度为E 3，在N 点的电场强度为E 4，下列说法中正确的是（ ） A ．若左右两部分的表面积相等，有E 1＞E 2，1ϕ＞2ϕ B ．若左右两部分的表面积相等，有E 1＜E 2，1ϕ＜2ϕC ．只有左右两部分的表面积相等，才有E 1＞E 2，E 3=E 4D ．不论左右两部分的表面积是否相等，总有E 1＞E 2，E 3=E 4 答案：D例：ab 是长为L 的均匀带电细杆，P1、P2是位于ab 所在直线上的两点，位置如图所示．ab 上电荷产生的静电场在P1处的场强大小为E 1，在P2处的场强大小为E2。

电场与电势的电场强度计算电场强度是描述电场强弱的物理量，是电力学的基本概念之一。

在电场中，带电粒子会受到电场力的作用，而电场强度则是描述这种力的大小和方向。

电场强度的计算涉及到库仑定律、电势、电场线等基本概念和公式。

本文将介绍如何计算电场强度，并给出一些相关的例题。

一、库仑定律库仑定律是描述点电荷之间相互作用的基本规律，它表明电场强度与距离的平方成反比。

库仑定律的数学表达式为：\[F = \frac{{k \cdot q_1 \cdot q_2}}{{r^2}}\]其中，F是电场力的大小，k是一个常数，q1和q2分别是两个电荷的大小，r是两个电荷之间的距离。

根据库仑定律，我们可以通过已知电场力的大小和两个电荷的大小来计算电场强度。

假设已知两个点电荷分别为q1和q2，它们之间的距离为r，且受到的电场力的大小为F。

那么我们可以得到以下关系：\[E = \frac{F}{q_0}\]其中，E是电场强度，q0是测试电荷的大小。

根据库仑定律的公式，我们可以将F代入上式中，得到电场强度的计算公式：\[E = \frac{{k \cdot q_1 \cdot q_2}}{{r^2 \cdot q_0}}\]这个公式描述了点电荷之间的电场强度。

二、电势和电场强度的关系电势是描述电场中某一点的势能大小的物理量，是电场力做功的势能单位。

电势的计算公式为：\[V = \frac{{k \cdot q}}{{r}}\]其中，V是电势，k是常数，q是电荷大小，r是与电荷产生电场力的地点之间的距离。

电场强度与电势之间有一定的关系。

根据电场力和势能之间的关系，我们可以得到以下公式：\[E = \dfrac{-dV}{dr}\]根据这个公式，我们可以通过求解电势函数的导数来计算给定位置处的电场强度。

这个方法在计算连续分布的电荷的电场强度时尤为有用。

三、电场强度的计算实例例1：求解均匀带电长直线的电场强度假设有一根长度为L、线密度为λ的均匀带电长直线。

学习电场中电势与电场强度的计算电场是物理学中的一个重要概念，它描述了电荷受到的力和电势的分布情况。

在学习电场的过程中，我们需要掌握电势和电场强度的计算方法。

一、电势的计算电势是描述电荷周围电场状态的物理量，它是用来衡量电荷所具有的能量。

在电场中，电势的计算可以通过以下公式进行：V = k * Q / r其中，V表示电势，k表示库仑常数，Q表示电荷大小，r表示距离。

通过这个公式，我们可以计算出电荷点周围的电势大小。

需要注意的是，电势是一个标量量，它没有方向性。

因此，我们可以简单地将电势看作是一个点的属性，而不需要考虑具体的方向。

二、电场强度的计算电场强度是描述电荷周围电场状态的物理量，它是用来衡量电荷对其他电荷施加的力的大小。

在电场中，电场强度的计算可以通过以下公式进行：E = k * Q / r^2其中，E表示电场强度，k表示库仑常数，Q表示电荷大小，r表示距离。

通过这个公式，我们可以计算出电荷点周围的电场强度大小。

需要注意的是，电场强度是一个矢量量，它具有方向性。

因此，在计算电场强度时，我们需要考虑具体的方向。

三、电势与电场强度的关系电势和电场强度之间存在着一定的关系。

根据电场的定义，电场强度是电势在空间上的梯度。

也就是说，电场强度的方向是电势下降最快的方向。

具体来说，电场强度的方向是从高电势指向低电势的。

这是因为电势表示了单位正电荷在电场中所具有的能量，而电场强度表示了单位正电荷所受到的力。

因此，电势越高，电场强度越大。

在计算电场强度时，我们可以利用电势的概念。

根据电场强度的定义，我们可以将电场强度表示为电势的负梯度。

也就是说，电场强度的大小可以通过电势的变化率来计算。

四、电势与电场强度的应用电势和电场强度的计算方法在物理学中有着广泛的应用。

它们可以用来描述电荷之间的相互作用，解释电场中的运动规律，以及计算电场中的能量分布等。

例如，在电场中，电荷受到的力可以通过电场强度进行计算。

根据库仑定律，电荷之间的力与电场强度成正比。

电场强度的计算描述电场的物理量——电场强度AFqq F E=++++++q 0BF A B电场中某点的电场强度等于单位正电荷在该点所受的电场力。

电场强度的计算（1）点电荷的电场（3）连续分布电荷的电场（2）场强叠加原理和点电荷系的电场场点源点（1)点电荷的电场qr30e r r r r q q F==,041πε=E 0q F rr q 3041πε=FE+E rErrq i q 0q 对的作用q iq 2qq 1（2)电场强度叠加原理和点电荷系的场强n F F F F +++=21iF0q F E =021q F F F n +++=nE E E+++=21∑=iE E 1F 2F iF ∑==n i iF 1电场强度叠加原理场点点电荷系的电场q 1+q 2-ii i i r q r E3041πε=∑=iE E 2r 2E E 1E 1r电荷面分密度电荷体密度电荷线分布密度d Sd Vld (3) 连续带电体的电场：体分布、面分布、线分布V ΔΔ=→Δq lim0τρlq lim 0l ΔΔ=→ΔηSq lim 0S ΔΔ=→Δσ电荷面分布电荷体分布电荷线分布d Sd Vd qP.l q d d η=所以, 电荷元：q d S q d d σ=dVd ρ=q rE30d 41d r q πε=计算时将上式在坐标系中进行分解，再对坐标分量积分。

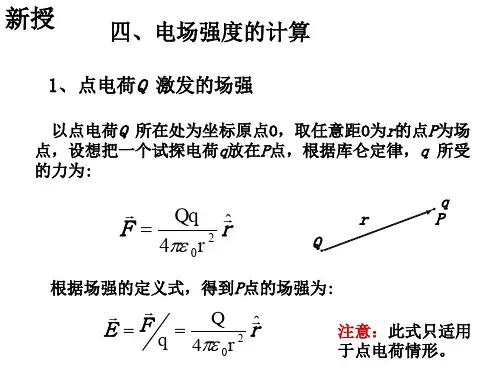
rEd ld •体电荷分布的带电体的电场r r dV E V∫∫∫=304περ•面电荷分布的带电体的电场rr dS E S∫∫=304πεσ•线电荷分布的带电体的电场rr dlE l∫=304πεη计算时将上式在坐标系中进行分解，再对坐标分量积分，即先分后和：,∫=x x dE E ,∫=y y dE E ∫=ZZ dE E 解题思路及步骤：1、根据题意建立坐标系;2、确定电荷密度:4、根据库仑定律确定电荷元的电场强度dE ：6、积分求场强分量：3、求电荷元电量dq;7、求总场的大小和方向222Zy x E E E E ++=xy x i dE E i i ,,,==∫关键是得到电荷元的微分形式，即dqr E30d 41d r q πε=5、确定dE 在坐标系中分量形式：xy x i ,,,=i dE 注意使用对称性解：例1. 求电偶极子中垂面上的电场。

电场强度的几种求法．公式法1．E F q是电场强度的定义式：适用于任何电场，电场中某点的场强是确定值，其大小和方向与试探电荷无关，试探电荷q 充当“测量工具”的作用。

2． E k r Q2 是真空中点电荷电场强度的决定r式，E 由场源电荷Q 和某点到场源电荷的距离r 决定。

3．E U d是场强与电势差的关系式，只适用于匀强电场，注意式中的d 为两点间的距离在场强方向的投影。

二．对称叠加法当空间的电场由几个点电荷共同激发的时候，空间某点的电场强度等于每个点电荷单独存在时所激发的电场在该点的场强的矢量和，其合成遵守矢量合成的平行四边形定则。

例：如图，带电量为+q 的点电荷与均匀带电。

例：如图，带电量为+q 的点电荷与均匀带电薄板相距为2d，点电荷到带电薄板的垂线通过板的几何中心，如图中a 点处的场强为零，求图中b 点处的场强多大b a + ddd 例：一均匀带负电的半球壳，球心为O 点，AB 为其对称轴，平面L垂直AB 把半球壳一分为二，L与AB 相交于M 点，对称轴AB上的N 点和M 点关于O点对称。

已知一均匀带电球壳内部任一点的电场强度为零，点电荷q 在距离其为r 处的电势为k q r。

假设左侧部分在M 点的电场强度为E1，电势为 1 ；右侧部分在M 点的电场强度为E2，电势为 2 ；整个半球壳在M 点的电场强度为E3，在N 点的电场强度为E4，下列说法中正确的是（）A．若左右两部分的表面积相等，有E1> E2，1 > 2B．若左右两部分的表面积相等，有E1<E2， 1 < 2C．只有左右两部分的表面积相等，才有E1>E2，E3=E4D．不论左右两部分的表面积是否相等，总有E1> E2，E3=E4答案：D例：ab 是长为L 的均匀带电细杆，P1、P2 是位于ab 所在直线上的两点，位置如图所示．ab 上电荷产生的静电场在P1 处的场强大小为E1，在P2 处的场强大小为E2。

电场计算技巧电场计算是物理学中非常重要的一部分，它用于研究电荷间相互作用产生的力和能量变化。

在实际应用中，电场计算可以帮助我们确定电场的强度、方向和能量分布，从而更好地理解和解释电荷在电场中的行为。

本文将介绍电场计算的基本原理和一些常用的计算技巧。

首先，我们需要了解什么是电场。

电场是由电荷而产生的物理现象，在空间中形成一种场的分布。

根据库仑定律，电荷之间的相互作用力与它们的电荷量成正比，与它们之间的距离平方成反比。

因此，电荷越大、距离越远，它们之间的相互作用力就越强。

电场的强度描述了电场中某一点所受到的电荷力的大小，通常用N/C（牛顿/库仑）来表示。

计算电场强度的方法有多种，其中一种常用的方法是使用电场线。

电场线是沿着电场方向绘制的虚拟曲线，它给出了该点电场强度的方向和大小。

在计算电场强度时，可以通过电场线的密度来判断电场的强弱。

电场线越密集，表示电场的强度越大；电场线越稀疏，表示电场的强度越小。

因此，通过观察电场线的分布情况，我们可以初步估算电场的强度。

除了电场线法，电场的强度也可以通过电场公式进行计算。

对于一个均匀电场中的点电荷，可以利用库仑定律和电场公式E=kQ/r^2来计算电场强度。

其中，E表示电场强度，k是库仑常数（相当于比例系数），Q是电荷量，r是距离。

通过将这些数值代入电场公式，我们可以快速计算得到电场强度。

在实际应用中，我们通常需要计算不止一个点电荷的电场强度。

这时，我们可以将所有点电荷的电场强度向量按照矢量加法的方式进行叠加。

即将所有点电荷的电场强度向量的x分量相加，y分量相加，z分量相加，从而得到最终的电场强度向量。

这种方法称为“叠加原理”，它是计算多电荷电场的一种常用技巧。

另外，当电场不均匀或存在连续分布的电荷时，我们可以使用积分来计算电场强度。

对于连续分布电荷的情况，可以将其划分为许多微小的电荷元，并将它们的电场强度进行积分求和。

通过对整个分布电荷求和，我们可以得到一个完整的电场强度。

电场强度的四种求法电场类别所用公式任何电场真空中点电荷电场匀强电场多个电场E=E1+E2+E3(矢量叠加）电场强度除通过以上方法求解外，还可以采用镜像法、等效替代法、补偿法等方法求解，用这些独特的方法求解，有时能起到事半功倍的效果。

一、镜像法镜像法是根据某些物理现象、物理规律、物理过程或几何图形的对称性进行解题的一种方法，利用此法分析解决问题可以避免复杂的数学演算和过程推导采用本法解题的关键是根据题设给定情景，发现其对称性，找到事物之间的联系，恰当地建立物理模型【例证1】如图所示，带电量为+q的点电荷与均匀带电薄板相距为2d，点电荷到带电薄板的垂线通过板的几何中心。

若图中a点处的电场强度为零，根据对称性，带电薄板在图中b 点处产生的电场强度大小和方向如何？（静电力常量为k）二、等效替代法等效替代法是指在效果相同的前提下，从A事实出发，用另外的B事实来代替，必要时再由B而C……直至实现所给问题的条件，从而建立与之相对应的联系采用本法解题的关键是找出与研究对象相近的模型或等效的物理参数。

原则是用较简单的因素代替较复杂的因素，常见的有：（1）以合力替代数个分力;（2）以合运动替代数个分运动;（3）电阻的等效替代;（4）电源的等效替代【例证2】如图所示，一带电量为正Q的点电荷A，与一块接地的长金属板MN组成一系统，点电荷A与板MN间的垂直距离为d，试求A与板MN的连线中点C处的电场强度。

三、补偿法求解物理问题，要根据问题给出的条件建立起物理模型，但有时由题给条件建立的模型不是一个完整的模型，这时需要给原来的问题补充一些条件，组成一个完整的新模型，此法即为补偿法采用本法解题的关键有二：（1）找出可以替代的物理模型;（2）将原问题转化为求新模型与补充条件的差值问题例3如图所示，用长为L的金属丝弯成半径为r的圆弧，但在A、B之间留有宽度为d的间隙，且d远远小于r，将电量为Q的正电荷均匀分布于金属丝上，求圆心处的电场强度。

点电荷周围的电场强度公式
点电荷周围的电场强度公式是物理学中一个重要的概念，它可以用来描述电荷在空间中的分布情况。

点电荷周围的电场强度公式可以用来计算电荷在空间中的电场强度，从而更好地理解电荷的作用。

点电荷周围的电场强度公式是由英国物理学家爱因斯坦提出的，它表明，电荷在空间中的电场强度与其距离的倒数成正比。

具体来说，电荷在空间中的电场强度可以用以下公式来表示：
E=KQ/r^2
其中，E表示电场强度，K表示常数，Q表示电荷的大小，r表示电荷与观察点之间的距离。

点电荷周围的电场强度公式可以用来计算电荷在空间中的电场强度，从而更好地理解电荷的作用。

例如，当电荷的大小和距离都是固定的时候，电场强度也是固定的，这就是点电荷周围的电场强度公式的本质。

此外，点电荷周围的电场强度公式还可以用来计算电荷在空间中的电场分布情况。

例如，当电荷的大小和距离都是固定的时候，电场强度会随着距离的增加而减小，这就是点电荷周围的电场强度公式的另一个重要特性。

综上所述，点电荷周围的电场强度公式是物理学中一个重要的概念，它可以用来计算电荷在空间中的电场强度，从而更好地理解电荷的作用。

它的本质是，当电荷的大小和距离都是固定的时候，电场强度也是固定的，而且电场强度会随着距离的增加而减小。

因此，点电荷周围的电场强度公式对于理解电荷的作用具有重要的意义。

电场强度计算的六种方法方法1利用合成法求电场强度空间中的电场通常会是多个场源产生的电场的叠加，电场强度可以应用平行四边形定则进行矢量计算，这是高考常考的考点。

虽然电场强度的定义式为E＝Fq，但公式E＝kQr2反映了某点场强与场源电荷的特性及该点到场源电荷的距离的关系，体现了电场的来源与本质，高考常围绕此公式出题。

【典例1】如图所示，M、N为真空中两根完全相同的均匀带正电绝缘棒，所带电荷量相同，且平行正对放置，两棒中点分别为O1、O2，a、b、c、d、e为O1O2连线上的六等分点，a点处有一带正电的固定点电荷．已知c处和d处的场强大小均为E0，方向相反，则b处的场强大小为()A. E0B.C.D.【跟踪短训】1．如图在半径为R的圆周上均匀分布着六个不同的点电荷，则圆心O处的场强大小和方向为A. ；由O指向FB. ；由O指向FC. ；由O指向CD. ；由O指向C2.在真空中有两个点电荷Q1＝＋3.0×10－8 C和Q2＝－3.0×10－8 C，它们相距0.1 m，A点与两个点电荷的距离均为0.1 m。

试求A点的场强。

方法2利用补偿法求电场强度【典例1】均匀带电的球壳在球外空间产生的电场等效于电荷集中于球心处产生的电场。

如图所示，在半球面AB上均匀分布正电荷，总电荷量为q，球面半径为R，CD为通过半球顶点与球心O的轴线，在轴线上有M、N两点，OM＝ON＝2R。

已知M点的场强大小为E，则N点的场强大小为()A.kq2R2－E B.kq4R2C.kq4R2－E D.kq4R2＋E【跟踪短训】1．均匀带电的球体在球外空间产生的电场等效于电荷集中于球心处产生的电场。

如图所示，在半球体上均匀分布正电荷，总电荷量为q，球半径为R，MN为通过半球顶点与球心O的轴线，在轴线上有A、B 两点，A、B关于O点对称，AB=4R。

已知A点的场强大小为E，则B点的场强大小为A. B.C. D.2．已知均匀带电圆盘在圆外平面内产生的电场与一个位于圆心的、等电量的同种点电荷产生的电场相同。