-互感电路的计算及变压器

互感电路的计算范文互感电路是由两个或多个线圈组成的电路。

每个线圈都有一定的感应电动势，同时也会相互影响。

对于互感电路的计算，一般需要考虑以下几个方面：互感电路的等效电路模型、互感系数、互感电路的电流和电压关系、磁场能量的传递和损耗等。

一、互感电路的等效电路模型互感电路的等效电路模型是两个或多个线圈之间通过互感系数相互连接而成的。

互感电路可以通过理想变压器模型来进行等效。

理想变压器模型假设变压器没有损耗，可以表示为一个多绕组的互感电路。

在等效电路模型中，可以用理想变压器的等效电路来代替实际的互感电路。

二、互感系数互感系数表示了线圈之间的相互影响程度。

一般用k表示，其取值范围在0到1之间。

当k接近于1时，表示线圈之间的相互影响较大；当k接近于0时，表示线圈之间的相互影响较小。

互感系数可以通过几何方法和电磁方法来计算。

三、互感电路的电流和电压关系互感电路中，线圈的电流和电压之间存在相位差。

对于理想变压器模型，可以通过等效电路来计算电流和电压之间的相关关系。

在互感电路中，线圈的电流和电压之间满足相位差为90度的关系。

相位差的方向取决于线圈的极性。

四、磁场能量的传递和损耗互感电路中，线圈之间的磁场能量会相互传递。

当电流在其中一个线圈中产生磁场时，这个磁场会穿透其他线圈，从而诱发出电动势。

这个电动势会导致其他线圈中产生电流。

同时，在互感电路中，存在损耗，主要是由于线圈的电阻引起的。

通过计算这些损耗，可以评估互感电路的性能。

在进行互感电路的计算时，一般可以采用下面的步骤：1.确定互感电路的等效电路模型，即选择合适的理想变压器等效电路模型。

2.计算互感系数，可以通过几何方法或电磁方法来计算。

3.根据互感系数和等效电路模型，建立互感电路的等效电路图。

4.根据等效电路图，进行电流和电压之间的计算，包括计算互感电路中的电流和电压相位差。

5.根据互感电路的等效电路模型和磁场能量的传递关系，计算磁场能量的传递和损耗。

6.进行互感电路的分析和设计，包括选择合适的元器件和参数，优化互感电路的性能。

自感和互感的计算公式
电路中的电感元件可以分为两种，一种是自感，另一种是互感。

自感是指电流在电感元件内部产生的磁场，而互感是指电流在两个电感元件之间产生的磁场。

在电路中，自感和互感都是非常重要的参数，它们的计算公式如下：
自感的计算公式：
L = Φ / I
其中，L表示电感的大小，Φ表示电流在电感元件内部产生的磁通量，I表示电流的大小。

互感的计算公式：
M = k * sqrt(L1 * L2)
其中，M表示两个电感元件之间的互感大小，k表示两个电感元件之间的耦合系数，L1和L2分别表示两个电感元件的自感大小。

在实际的电路设计中，自感和互感的计算是非常重要的。

例如，在变压器的设计中，需要计算变压器的互感大小，以确定变压器的输出电压和输入电压之间的关系。

在电感元件的选择和设计中，也需要计算电感的大小，以满足电路的要求。

自感和互感是电路中非常重要的参数，它们的计算公式可以帮助我们更好地设计和选择电感元件，以满足电路的要求。

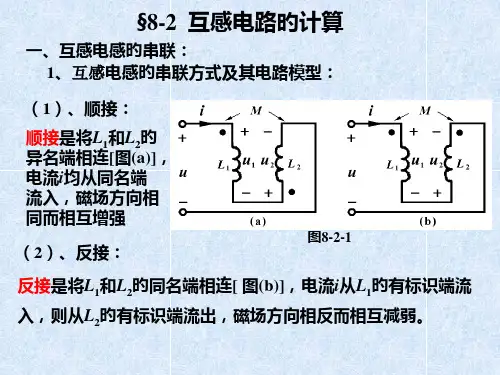
互感的原理与计算方法简介
无论在何处，只要存在两个电流回路，就会有互感。

一个回路的电流产生一个磁场，而该磁场会影响第二个回路。

两个回路相互作用，其相互作用的系数随距离的增加快速地减小。

两个回路之间相互作用的系数称为它们的互感，单位是亨利（H），或伏-秒/安培。

两个电路之间的互感耦合相当于一个连接在
电路A 和电路B 之间的微小变压器，如图1.18 所示。

无论何处，对于两个相邻电流回路的相互作用，可以看成是一个变压器的初级和次级，从面得到互感。

互感LM 将一个噪声电压Y 注入到电路B，按照下列规则，噪声电压Y 与电路A 中的电流变化速率成正比：Y=LM DIA/DT
回路A 中电流的快速变化导致回路B 上产生一个相当大的电压，高速设计中互感耦合的重要性由此面来。

对于实际的耦合噪声电压，式（Y=LM DIA/DT）只是一个简单的近似公式。

完整的公式应该采用初级和次级电路之间的电流差，以及初级和次级线圈对电路的负载效应。

关于式（Y=LM DIA/DT）的前提假设，与式的情况类似，即：
1、LM 上的感应电压远远小于原有信号的电压。

由此附加的LM 不增加电路
A 的负载。

在数字产品中，由感耦合产生的噪声电压总是比源信号小。

2、电路B 中的耦合信号电流小于电路A 中的电流。

可以忽略电路B 中小的耦合电流，并假设耦合变压器的初级和次级的电流差正好等于IA。

3、假设与电路B 的接地阻抗相比，次级的阻抗很小，只在电路B 的电压上加上耦合噪声电压，这个过程忽略了互感和次级电路之间的相互作用。

与互容类似，数字电路中的互感，通常导致电路之间不必要的串扰。

互感系数公式范文互感系数（Mutual Inductance）是电磁学中的一个重要概念，它描述了电路中两个独立线圈之间的电磁耦合。

互感系数可以用于计算变压器的耦合系数、彼此之间的能量传递等。

互感系数可以通过以下公式计算：M = (N1 * Φ2) / (I2 * dt) = (N2 * Φ1) / (I1 * dt)其中，M表示互感系数，N1和N2表示两个线圈的匝数，Φ1和Φ2表示通过线圈1和线圈2的磁通量，I1和I2表示通过线圈1和线圈2的电流，dt表示两个线圈中磁通量变化的时间差。

这个公式可以进一步简化为：M=k*√(L1*L2)其中，k表示耦合系数，L1和L2分别是线圈1和线圈2的自感系数。

这个公式表明互感系数与线圈的自感系数及耦合系数有关。

在实际应用中，我们可以利用互感系数计算两个线圈之间的互感。

例如，当一个线圈上的电流变化时，会在另一个线圈上感应出电动势。

利用互感系数可以计算出在另一个线圈上感应出的电动势大小。

这种现象在变压器中得到了广泛应用，其中一侧的线圈产生的交流电流会诱导另一侧的线圈产生电流。

互感系数还可以用来计算线圈储能和能量传递。

当一个线圈的电流变化时，互感系数表示在另一个线圈上感应出的储能大小。

这个储能可以通过线圈之间的能量传递进行转化。

互感系数的大小范围通常在0到1之间。

当互感系数等于0时，表示两个线圈之间没有耦合，即线圈之间没有能量传递。

当互感系数等于1时，表示线圈之间完全耦合，即线圈之间的能量传递完全。

在设计电路和变压器时，互感系数的选择非常重要。

合适的互感系数可以实现高效的能量传递和电路性能。

同时，互感系数的选择还会影响到系统的稳定性和抗干扰能力。

除了上述互感系数的计算公式，还有其他方法可以计算互感系数，如使用多径时频域反演算法（MPTF）。

利用这种方法，可以更准确地计算互感系数，并研究不同频率和幅度下的线圈之间的耦合。

总而言之，互感系数是描述电路中两个线圈之间电磁耦合效应的一个重要参数。

电路互感的概念和计算公式一、电路互感的概念。

电路互感是指两个电感器件之间由于磁场的相互作用而产生的电压。

在电磁学中，电感是指电流变化时所产生的电动势。

当一个电流通过一个线圈时，会产生一个磁场，而这个磁场又会影响到另一个线圈中的电流，从而产生电动势。

这种现象就是电路互感。

电路互感是一种重要的电磁现象，它在电路中起着至关重要的作用。

在许多电子设备中，都会用到电感器件，而电路互感则是影响电感器件性能的重要因素之一。

了解电路互感的概念和计算公式，有助于我们更好地理解电路中的电磁现象，从而更好地设计和应用电子设备。

二、电路互感的计算公式。

电路互感的计算公式可以通过法拉第定律和楞次定律来推导得到。

根据法拉第定律，电路中的电动势等于电感的变化率乘以电流的变化率。

而根据楞次定律，电路中的电动势等于电感的变化率乘以磁通量的变化率。

结合这两个定律，可以得到电路互感的计算公式：M = k sqrt(L1 L2)。

其中，M表示电路互感，k表示比例系数，L1和L2分别表示两个线圈的电感。

从这个公式可以看出，电路互感与两个线圈的电感和它们之间的相对位置有关。

当两个线圈的电感增大或它们之间的距离减小时，电路互感也会增大。

而当两个线圈之间的磁场耦合程度增强时，电路互感也会增大。

因此，通过调节线圈的电感和它们之间的相对位置，可以改变电路互感的大小，从而实现对电路性能的调控。

三、电路互感的应用。

电路互感在电子设备中有着广泛的应用。

在变压器中，电路互感可以实现电压的变换。

当一个线圈中的电流发生变化时，会产生磁场，从而感应出另一个线圈中的电动势，从而实现电压的变换。

这种原理被广泛应用于变压器中，用于实现电压的升降。

此外，电路互感还可以用于电路的隔离和耦合。

在一些需要隔离的电路中，可以通过增加电路互感来实现线圈之间的电气隔离。

而在一些需要耦合的电路中，可以通过减小电路互感来实现线圈之间的电气耦合。

因此，电路互感在电子设备中有着广泛的应用。

互感电感的计算公式在电路中，互感电感是指两个线圈之间由于磁场的相互作用而产生的电感。

互感电感在电路设计和分析中起着重要的作用，因此了解互感电感的计算公式是很有必要的。

本文将介绍互感电感的计算公式及其应用。

互感电感的计算公式可以通过以下公式来表示：M = k sqrt(L1 L2)。

其中，M表示互感电感，k表示互感系数，L1和L2分别表示两个线圈的自感电感。

互感系数k是一个无量纲的常数，它取决于两个线圈之间的几何形状和相对位置。

一般情况下，k的取值范围在0到1之间。

当两个线圈之间几乎没有磁场相互作用时，k的取值接近于0；而当两个线圈之间的磁场相互作用非常强时，k的取值接近于1。

通过上述公式，我们可以看出互感电感是与两个线圈的自感电感及其相互作用相关的。

当两个线圈的自感电感越大，它们之间的互感电感也会越大；而当它们之间的相互作用越强时，互感电感也会越大。

互感电感的计算公式在电路设计和分析中有着广泛的应用。

首先，它可以帮助我们计算出两个线圈之间的互感电感，从而进一步分析电路的性能和特性。

其次，它可以帮助我们设计出符合要求的互感电感，以满足特定的电路需求。

最后，它还可以帮助我们优化电路结构，以提高电路的效率和性能。

除了上述的计算公式外，我们还可以通过一些实际的例子来进一步理解互感电感的计算。

例如，当我们设计一个变压器时，我们需要计算出其一次线圈和二次线圈之间的互感电感，以确定变压器的性能和特性。

又如，当我们设计一个共振电路时，我们需要计算出其电感元件之间的互感电感，以确定共振电路的频率和带宽。

总之，互感电感的计算公式是电路设计和分析中的重要工具。

通过了解互感电感的计算公式及其应用，我们可以更好地理解电路中的互感电感现象，从而更好地设计和分析电路。

希望本文对读者能有所帮助，谢谢！。

第六章互感电路第一节互感及互感电压学习目标1 ．了解电磁场的基本知识和电感的概念2 ．理解自感和互感现象重点互感对电流的阻碍作用难点自感和互感电动势的判断一、互感图 6-11. 互感现象 :如图6-1所示表示两个有磁耦合的线圈(简称耦合电感)，电流i 1在线圈1和2中产生的磁通分别为Φ11和Φ21，则Φ21≤Φ11。

称为互感现象。

电流i 1 称为施感电流。

Φ11 称为线圈 1 的自感磁通，Φ21 称为耦合磁通或互感磁通。

如果线圈2的匝数为N 2，并假设互感磁通Φ21与线圈2的每一匝都交链，则互感磁链为Ψ21＝N 2Φ21。

图 6-2同理，如图 6-2 所示，电流i 2在线圈2和l中产生的磁通分别为Φ22和Φ12，且Φ12 ≤Φ22。

Φ22称为线圈2的自感磁通，Φ12称为耦合磁通或互感磁通。

如果线圈1的匝数为N 1，并假设互感磁通Φ12与线圈1的每一匝都交链，则互感磁链为Ψ12＝N 1Φ122.互感线圈：上述线圈称为互感线圈。

3.互感系数:上述系数和称互感系数。

对线性电感和相等，记为。

4 ．自感系数：对于线性非时变电感元件，当电流的参考方向与磁通的参考方向符合右螺旋定则时，磁链Ψ电流i成正比，即Ψ＝Li ，式中L为与时间无关的正实常数,即为自感系数。

根据电磁感应定律和线圈的绕向，如果电压的参考正极性指向参考负极性的方向与产生它的磁通的参考方向符合右螺旋定则时，也就是在电压和电流关联参考方向下，则在此电感元件中，磁链Ψ和感应电压u 均由流经本电感元件的电流所产生，此磁链感应电压分别称为自感磁链和自感电压，如图6-3。

图6-3自感磁链 : , 为自感系数 .5 ．耦合系数:上述一个线圈的磁通交链于另一线圈的现象，称为磁耦合，用耦合系数 K 来反应其耦合程度。

，则（“ + ”号表示互感的增强作用；“—”表示互感的削弱作用）第二节互感线圈的同名端学习目标：掌握同名端的几种判断方法。

重点：同名端的判断一．同名端：图6-4如图 6-4 所示，一对互感线圈中，一个线圈的电流发生变化时，在本线圈中产生的自感电压与在相邻线圈中所产生的互感电压极性相同的端点称为同名端，以“ * ” , “ · ” , “ Δ”等符号表示。