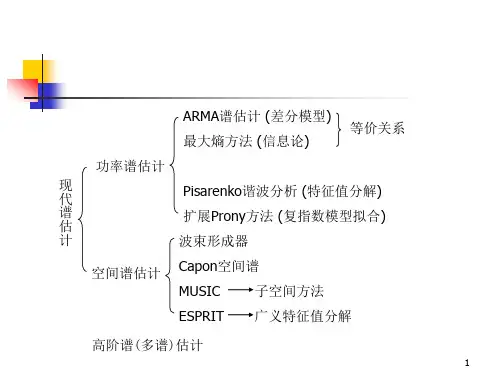
现代谱估计 原理与应用((美)凯 依(Kay, S.M.)著;黄建国等译)思维导图

现代谱估计计算机仿真实验报告胡敏在许多工程应用中，利用观测到的一组样本数据估计并分析一个平稳随机信号的功率谱密度是十分重要的。

例如，在雷达信号处理中，由回波信号的功率谱密度、谱峰的宽度、高度和位置，可以确定目标的位距离和运动速度；在阵列信号处理中，空间功率谱描述了信号功率随空间角度的分布情况。

在许多信号处理应用中，谐波过程经常会遇到，它对应的功率谱为线谱，谐波过程的功率谱估计就是要确定谐波的个数，频率和功率（合称谐波恢复）。

为了更好的学习现代信号处理中该部分的内容，我们做了相应的计算机仿真实验。

1 实验目的1、深入理解现代谱估计和谐波恢复的基本理论，包括ARMA 模型，ARMA 谱估计，ARMA 模型识别，Pisarenko 谐波分解，信号子空间和噪声子空间，旋转不变技术(ESPRIT)；2、熟悉与上述谱估计和谐波恢复理论相关的数学方法以及各自的特点，包括最小二乘估计（LS ），奇异值分解（SVD ），总体最小二乘估计（TLS ），特征值分解和广义特征值分解；3、体会ARMA 功率谱估计中的Cadzow 谱估计子和Kaveh 谱估计子，ARMA 模型的识别方法，Pisarenko 谐波恢复方法，ARMA 建模谐波恢复方法，MUSIC 方法进行谐波恢复，两种ESPRIT 方法（LS-ESPRIT 和TLS-ESPRIT 进行谐波恢复；2 实验原理2.1 ARMA 谱估计相当多的平稳随机过程都可以通过用白噪声激励线性时不变系统来产生，而线性系统又可以用线性差分方程进行描述，这种差分模型就是自回归—滑动平均（ARMA ）模型。

而且，任何一个有理式的功率谱密度都可以用一个ARMA 随机过程的功率谱密度精确逼近。

ARMA 随机过程定义为服足下列线性差分方程的离散随机过程{})(n x ：∑∑==-+=-+qj jpi ij n e bn e i n x an x 11)()()()( （1）式中)(n e 是一离散白噪声；式（1）所示的差分方程称为ARMA 模型，系统p a a ,1和q b b ,,1 分别称为自回归（AR ）参数和滑动平均（MA ）参数，而p 和q 分别叫做AR 阶数和MA 阶数。

现代谱估计实验报告1 实验目的功率谱估计在实际工程中有重要应用价值。

如在语音信号识别、雷达杂波分析、波达方向估计、地震勘探信号处理、水声信号处理、系统辨识中非线性系统识别、物理光学中透镜干涉、流体力学的内波分析、太阳黑子活动周期研究等许多领域发挥了重要作用。

本次实验的目的主要是深入理解现代谱估计的基本理论，包括ARMA 模型、ARMA 谱估计。

掌握现代谱估计的基本方法，包括SVD-TLS 算法等。

利用ARMA 功率谱估计中Cadzow 谱估计子和Kaveh 谱估计子来进行谱估计。

2 实验原理2.1 背景若离散随机过程{x(n)}服从线性差分方程)()()()(11j n e n e i n x n x q j j p i i b a -+=-+∑∑==（1）式中e （n ）是一离散白噪声，则称{x(n)}为ARMA 过程，而式（1）所示的差分方程称为ARMA 模型。

系数a 1,a 2……a p ,和b 1,b 2……b q ,分别称为自回归参数和滑动平均参数，而p 和q 分别叫做AR 阶数和MA 阶数。

式（1）所示的ARMA 过程，其功率谱密度为)()()()()(22e e P jw jw z x B B e z A z B w jw δδ=== （2）ARMA 谱估计的目的是使用N 个已知的观测数据x(0)，x(1)…..x(N-1)计算出ARMA 过程{x(n)}的功率谱密度估计。

在实际中，可以运用cadzow 谱估计子和kaveh 谱估计子来估计，cadzow 谱估计子秩序确定AR 阶数p 和估计AR 参数，而kaveh 谱估计子也只需要确定AR 阶数p 和估计AR 参数以及MA 阶数。

2.2 相关算法AR阶数p的确定用奇异值分解（SVD）,AR参数的估计用总体最小二乘法(TLS),即应用（SVD—TLS）算法来完成ARMA谱估计。

SVD—TLS算法：步骤1 计算增广矩阵B的SVD，并储存奇异值和矩阵V;步骤2 确定增广矩阵B的有效秩p；步骤3 计算矩阵S;步骤4 求S的逆矩阵S--,并计算出未知参数的总体最小二乘估计。